核电厂发生严重事故后,大量的放射性裂变产物以气溶胶的形式释放在安全壳内,并可能通过安全壳缝隙泄漏、 安全壳隔离失效等方式释放到大气中污染环境[1-2]。核电厂放射性气溶胶的迁移特性与热力学现象成为近年来的研究热点,王辉等[3]研究了毛细通道内气溶胶的沉积与滞留现象,结果表明毛细通道有利于阻碍气溶胶泄漏。陈君岩等[4]探究了亚微米级气溶胶聚并对重力沉降行为的影响,聚并后的大颗粒有更快的重力沉降速率。 Han等[5]研究了微米级颗粒的热泳沉积效应, 不同的温度梯度场对热泳沉积速率的影响显著。王竞弘等[6]、 Li等[7]阐释了高温高湿环境下气溶胶的吸湿增长行为。田林涛[8]研究了安全壳源项气溶胶的喷淋去除特性,相比自然沉积,喷淋是一种十分有效的气溶胶去除手段。然而,在涉及核事故放射性气溶胶的传输模型中,荷电现象经常被忽略,颗粒带电的重要性尚未达成共识[9-11]。本研究中开发了一个适用于核电厂严重事故下安全壳内放射性气溶胶荷电-凝并的数值计算模型,以研究颗粒荷电和凝并行为之间的相互影响。
大量研究表明, 放射性气溶胶可以自发地积累电荷, 并且表现出与非放射性气溶胶明显不同的行为[12-16]。 放射性气溶胶首先通过发射α、 β射线在自身留存一定数量的正电荷, 每次β衰变使颗粒带1个正电荷, 每次α衰变带1～20个正电荷, 这一过程称为自荷电。 这些高能射线在空气中沉积能量从而电离出空气离子, 正、 负离子在扩散作用下附着到颗粒表面。 通常情况下, 负离子表现出比正离子更强的流动性, 不对称的流动性使颗粒电荷进一步发生改变, 这一过程称为扩散荷电。 现有研究表明, 颗粒表面积累的电荷量主要受颗粒的放射性活度、 衰变留存电荷数、 颗粒尺寸、 离子电离率和离子流动性差异等的影响。
考虑到静电相互作用改变了微小颗粒间的作用力,电荷会显著影响颗粒的凝并行为[17-19]。气溶胶的放射性可以提高或降低凝并率,这取决于颗粒尺寸和电荷的分布形式。现有的理论和实验大多关注气溶胶带电后的凝并演化,认为气溶胶荷电和凝并先后发生,假设荷电时尺寸分布恒定,并在凝并时不考虑荷电。在真实的事故条件下,放射性是持续的,气溶胶的荷电和凝并行为同时发生并互相影响,特别是当颗粒荷电时间尺度与凝并的时间尺度相当甚至更长时,忽略同时效应会增加预测结果的不确定性[20]。
目前同时考虑荷电-凝并效应的尝试包括:Alonso等[21-22]开发了解析和数值方法来估计单电荷和中性颗粒尺寸随时间的变化,并进行了相关实验。Oron等[23]开发了分区方法来预测同时荷电-凝并行为,没有考虑放射性自荷电,且公式形式过于复杂,不适合数值计算。Kim等[20]使用的分区方法更加简洁,但考虑的机制并不完整。Sharma等[24]使用对数正态矩方法对高温纳米颗粒的同时荷电-凝并进行了计算,计算效率高,但在精度和放射性气溶胶适用性方面有局限。
结合已有的研究成果和实际计算需求,本文中基于分区法开发并验证了适用于放射性多分散气溶胶同时荷电-凝并计算的程序。工程意义在于为评估荷电对放射性气溶胶的凝并迁移特性的影响和在工程计算中忽略放射性荷电这一假设的准确性提供参考,此外也为放射性气溶胶的去除机制(如静电除尘)提供了新的思路。
1 模型开发
1.1 荷电-凝并方程
颗粒体积v和带电量q是描述放射性气溶胶的2个关键参数。放射性气溶胶演化研究的关键在于准确预测颗粒的尺寸和电荷分布随时间的变化。在求解颗粒演化方程的过程中,v的连续分布使数值求解困难,本文中采用的分区法的思想就是将v和q进行二维分区处理。图1所示为尺寸-电荷二维分区及单元平均方法示意图,将v和q划分在具有代表性的分区节点上,基于此将连续方程离散。
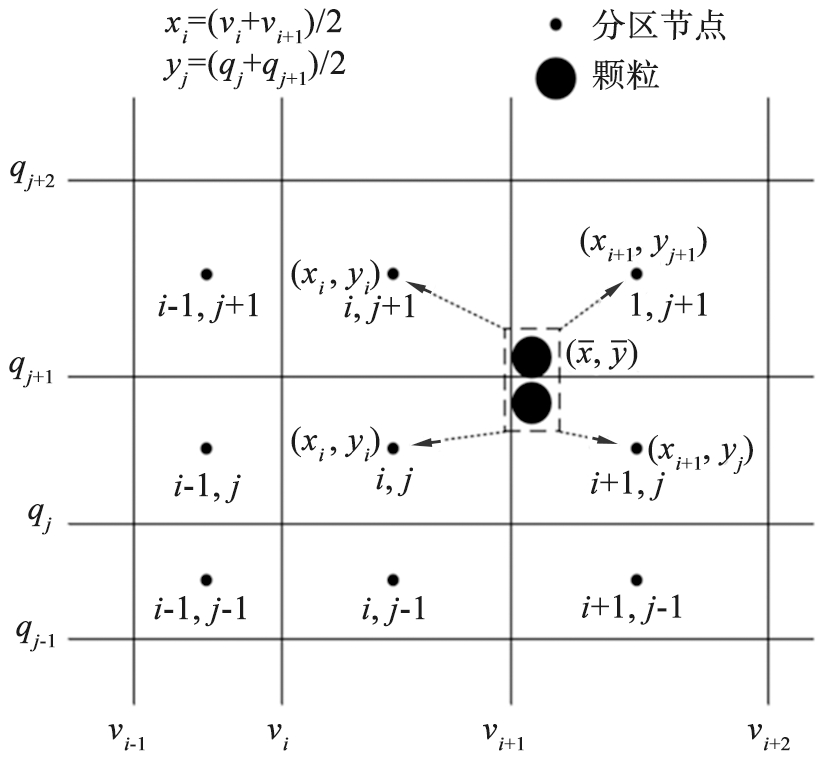
图1 尺寸-电荷二维分区及单元平均方法示意图
Fig.1 Two-dimensional discretization of size-charge and CAT method
基于Clement等[14]所述的放射性气溶胶荷电过程,可以通过以下方程描述荷电引起的离子和颗粒数量浓度的演化:
(1)
(2)
(3)
式中: n+、 n-分别为正、 负离子数量浓度; N为粒子数密度; 
分别为正、 负离子与颗粒的附着系数; αrc为离子间再结合系数; η为颗粒放射性活度; I为电离率系数; qb为背景电离率; 
为平均留存电荷数。
凝并引起的颗粒浓度演化通过双变量群平衡方程(bivariate population balance equations, BVPBE)给出[23]:
(4)
采用分区法离散方程,如公式(4),将Kumar等[25]提出的单元平均技术(cell average technology, CAT)扩展到二维双变量情形,利用到BVPBE的离散上。该技术的特点是同时保留了颗粒的数量和质量特征,比以往的分区方法具有更高的精度。
如图1所示,在单元(xi≤x≤xi+1, yi≤y≤yi+1)中,首先计算该单元内颗粒总数量生成率Bi, j和总体积生成率Vi, j计算公式为
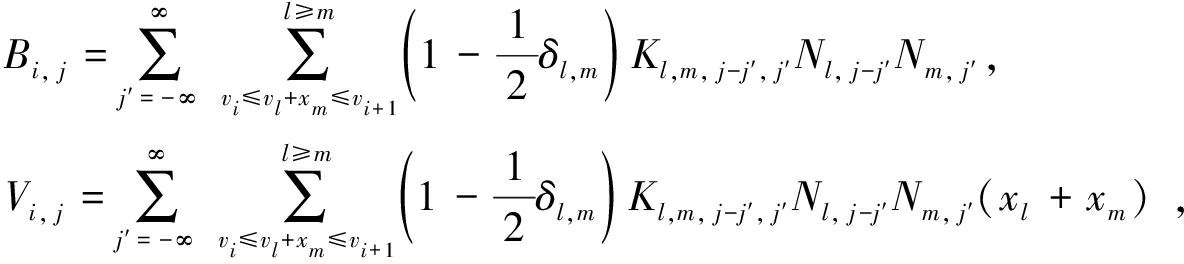
(5)
式中: δ为狄拉克函数; K为凝并核函数。
定义单元内生成颗粒的平均体积计算公式为
(6)
根据生成颗粒的数量和平均质量,保证守恒的前提下将数量和质量分配到邻近的4个节点上,BVPBE被离散公式为
(7)
式中:
为分配系数; H为辅助函数; Di, j为单元内颗粒的消失率。
(8)
由同种电荷相互排斥引起的静电分散作用也在本研究的考虑范围内:
(9)
式中M为颗粒的机械迁移率[17]。
综合考虑以上效应,得到同时荷电和凝并方程如下:
(10)
给定初始离子浓度以及初始颗粒尺寸-电荷分布,联立求解方程(1)、 (2)、 (10)就可以得到各自随时间的演化。
根据模型的涵盖范围,本模型适用于放射性气溶胶的荷电、 凝并2种机制,以及空间均匀分布气溶胶随时间的演化计算。
1.2 数值求解程序
编写Python程序计算模型中各个系数,输入初始条件后使用变系数常微分方程(VODE)求解器向后差分(BDF)方法隐式求解微分方程组(1)、 (2)、 (10) 。设定电荷网格为线性网格,体积网格任意,计算时间和步长可变。
2 模型验证和结果分析
采用放射性颗粒电荷测量和放射性电荷中和器获得的测量结果来验证模型的准确性。
2.1 放射性荷电模拟
Yeh等[12]对β放射性198Au气溶胶进行了荷电实验,测量了粒径为0.53 μm的3种放射性活度下的初始单分散气溶胶的平均电荷。图2所示为198Au气溶胶平均电荷和电荷分布。由图可知,平均电荷随时间迅速增长,达到峰值后缓慢下降至稳定,理论计算值与实验值一致性大。气溶胶从最初带中性电荷到整体带正电,同时电荷分布逐渐展平,在图中显示为分布曲线向右下方移动,最终的稳态电荷与高斯分布很近似。
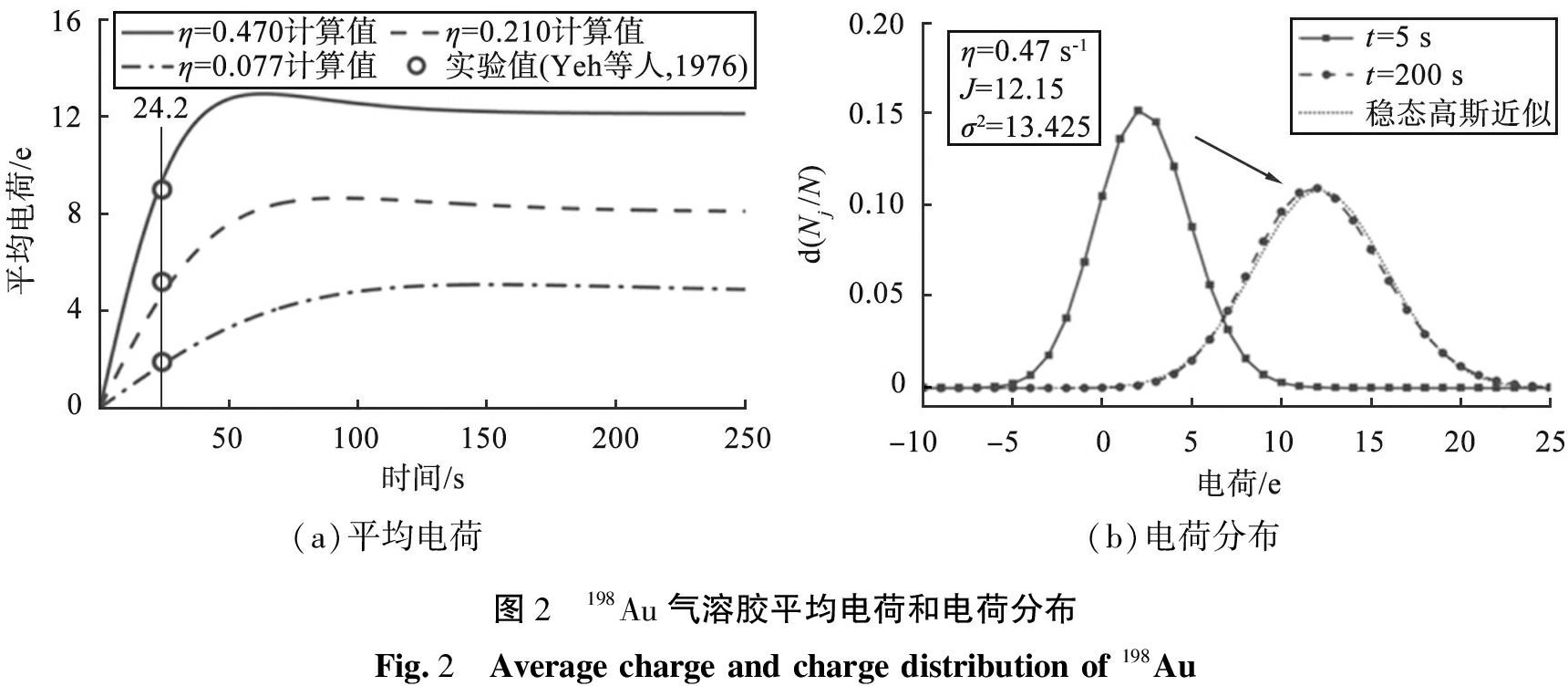
(a)平均电荷(b)电荷分布图2 198Au气溶胶平均电荷和电荷分布Fig.2 Average charge and charge distribution of 198Au
Yeh等[13]对α放射性238PuO2气溶胶进行了荷电实验,测量了粒径为0.96 μm的初始单分散气溶胶的电荷。假设每次衰变平均留存电荷
气溶胶初始不带电,图3所示为238PuO2气溶胶电荷分布。由图可知,在极短的时间内,电荷分布会出现双峰甚至多峰,这是由较大的留存的电荷数引起的。随后,大约2.5 s内电荷分布达到了稳态,相比于上述198Au气溶胶的荷电情况,稳态电荷分布的不对称性更加显著,小于平均电荷的粒子数相对较多,会出现少数带大量正电荷的粒子。此时的高斯分布无法很好地描述实际电荷分布。
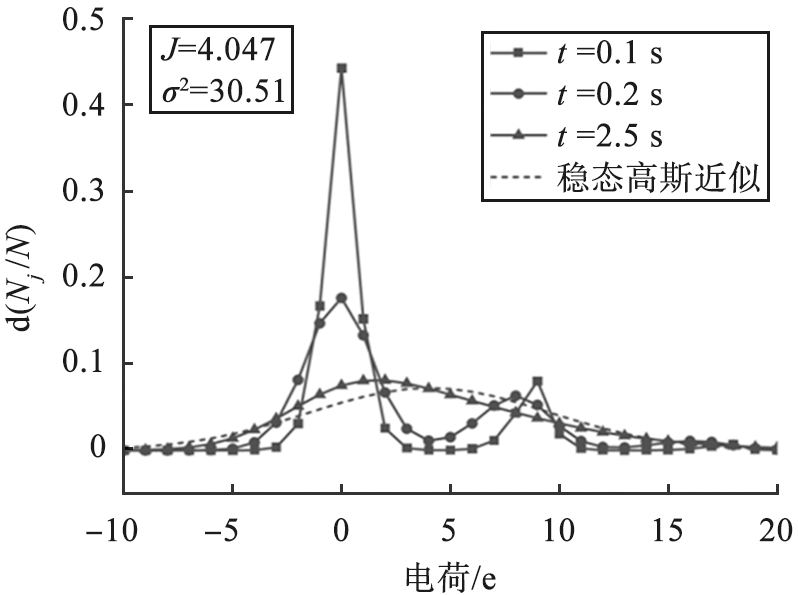
图3 238PuO2气溶胶电荷分布
Fig.3 Charge distribution of 238PuO2
Gensdarmes等[15]对β放射性137Cs气溶胶进行了荷电实验。图4所示为137Cs气溶胶平均电荷和电荷分布。高离子电离率(Exp1)和低离子电离率(Exp2)环境下测量时间分别为第2 500 s和第1 060 s。在Exp1环境下放射性颗粒电荷迅速累积达到稳态,并且与初始电荷近似,此时扩散荷电占主导。Exp2环境下颗粒电荷累积时间更长,稳态电荷向正电荷方向偏移量更大,此时扩散荷电相比于自荷电的主导优势减弱。
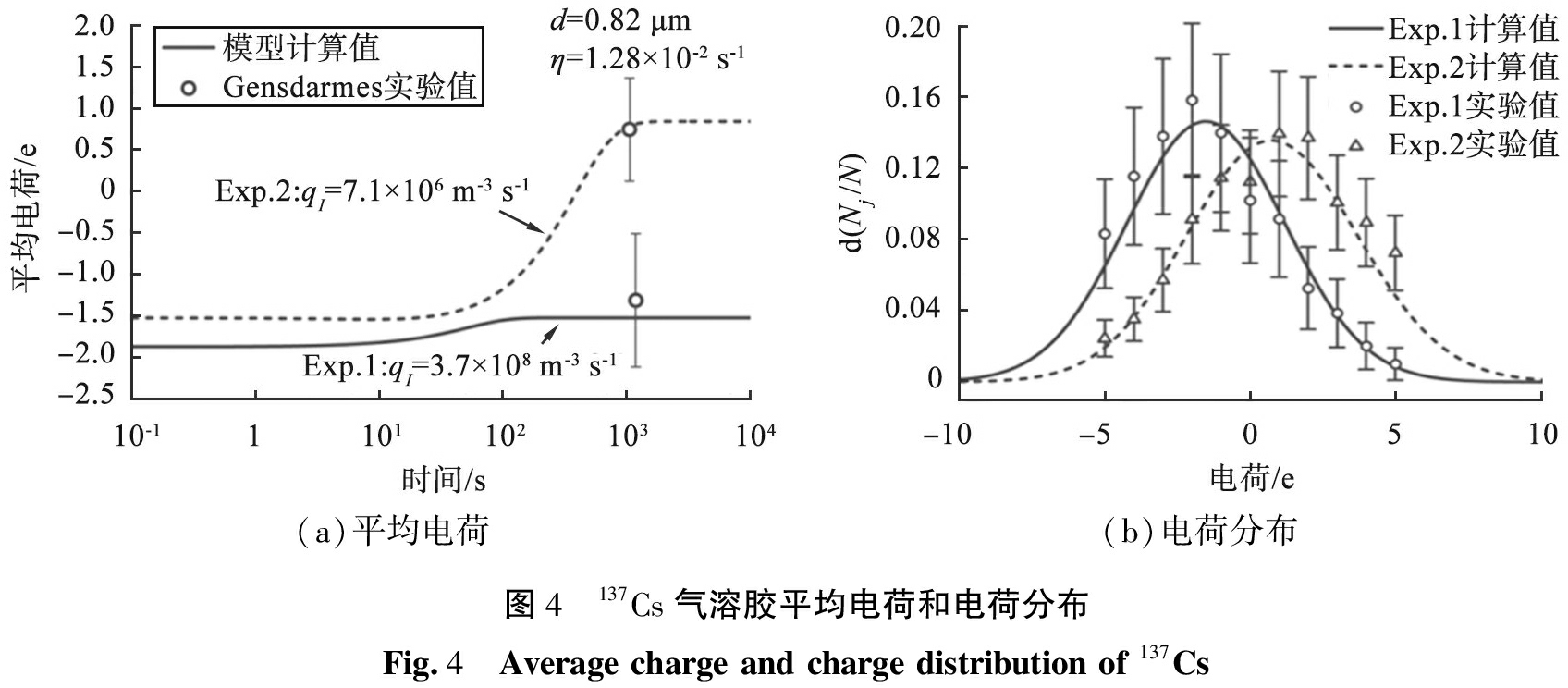
(a)平均电荷(b)电荷分布图4 137Cs气溶胶平均电荷和电荷分布Fig.4 Average charge and charge distribution of 137Cs
计算值和实验值的一致性表明,计算模型能够准确描述扩散荷电和自荷电之间的竞争,并精准地预测了放射性颗粒的电荷分布。
2.2 荷电-凝并模拟
采用Alonso等[21-22]针对纳米级非放射性颗粒的荷电-凝并动力学开展的数值计算和实验进行模型验证。
2.2.1 近似解析方法验证
为了得到近似的解析模型,做出以下假设: 1)纳米颗粒的荷电概率很低,大部分颗粒是电中性的; 2)纳米颗粒最多带1个电荷,且带正、 负电颗粒浓度相当; 3)颗粒间凝并核函数为常数; 4)荷电是对称的,也就是正、 负离子具有相同的迁移特性; 5)正、 负离子浓度在整个过程中保持不变;6)忽略带电颗粒在壁面上的损失。
对于初始单分散气溶胶的凝并过程,不带电颗粒浓度的演化规律公式为
(11)
带电颗粒浓度演化近似解公式为
(12)
(13)
式中: t为时间。
数值计算过程中,设定体积网格为线性Vi=iVp(Vp是初始单个颗粒体积),颗粒初始单分散且不带电(dp=2 nm,N(0)=1015 m-3, n±(0)=2×1013 m-3)。图5所示为不带电和带电颗粒浓度随时间的变化。由图可知,不带电的初始颗粒在凝并和扩散荷电的作用下不断减少;而较大的不带电颗粒随时间不断增多,并且颗粒体积越大,出现的时间越晚,在第3 s时尚未出现大颗粒多于小颗粒的情况。带电的初始颗粒在很短的时间内在荷电作用下迅速增多,随后在凝并作用下缓慢减少,说明相比于纳米颗粒的凝并过程,荷电过程的时间尺度更小,但没有小到可以忽略,也就说明考虑荷电和凝并的同时效应是有必要的。数值模型和解析解具有很好的一致性,能够可靠地预测颗粒的电荷和尺寸演化。
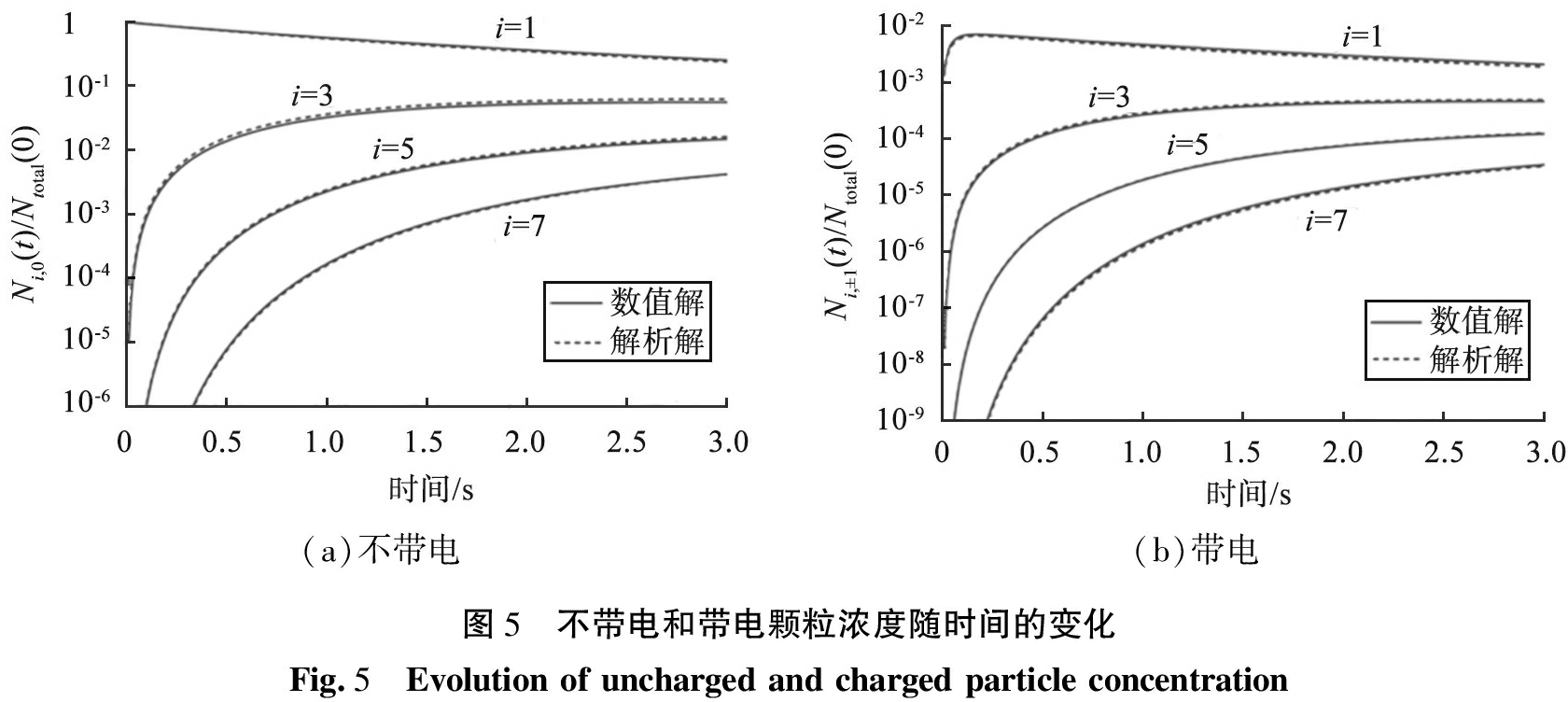
(a)不带电(b)带电图5 不带电和带电颗粒浓度随时间的变化Fig.5 Evolution of uncharged and charged particle concentration
2.2.2 放射性中和器实验验证
Alonso等[21]测量了在不同停留时间时通过241Am放射性中和器的纳米颗粒的尺寸分布,实验结果被用于验证数值模型。
实验中初始颗粒被认为是不带电的,尺寸分布被假定为对数正态分布
(14)
式中: d为粒径; dg为数量中值粒径; σg为几何标准偏差,根据测量结果拟合得到。
实验中通过改变通过中和器的气溶胶载气流速来改变颗粒的停留时间,从而改变出口处的粒径分布和荷电水平。数值计算过程中,设定对于粒径范围2～20 μm,等距划分为81个粒径网格。
图6所示为2种不同初始分布下颗粒尺寸分布的演化。由图可知,在2种条件下,颗粒尺寸分布均随着时间呈右移、展平的趋势,显示了明显的凝并现象。此外,可以看到实验分布比理论分布窄,特别是在停留时间较长时。Alonso等[21]认为可能造成这一现象的原因是理论计算中忽略了颗粒因静电分散或沉积效应而在壁面上的损失,较小的颗粒实际上比大颗粒的损失率更高,所以导致理论过度预测了小颗粒的浓度。
2.2.3 假设条件验证
在对Alonso等实验结果进行理论计算时,保留了解析模型第1)、 2)、 5)、 6)条假设,下面对以上假设的合理性进行验证。
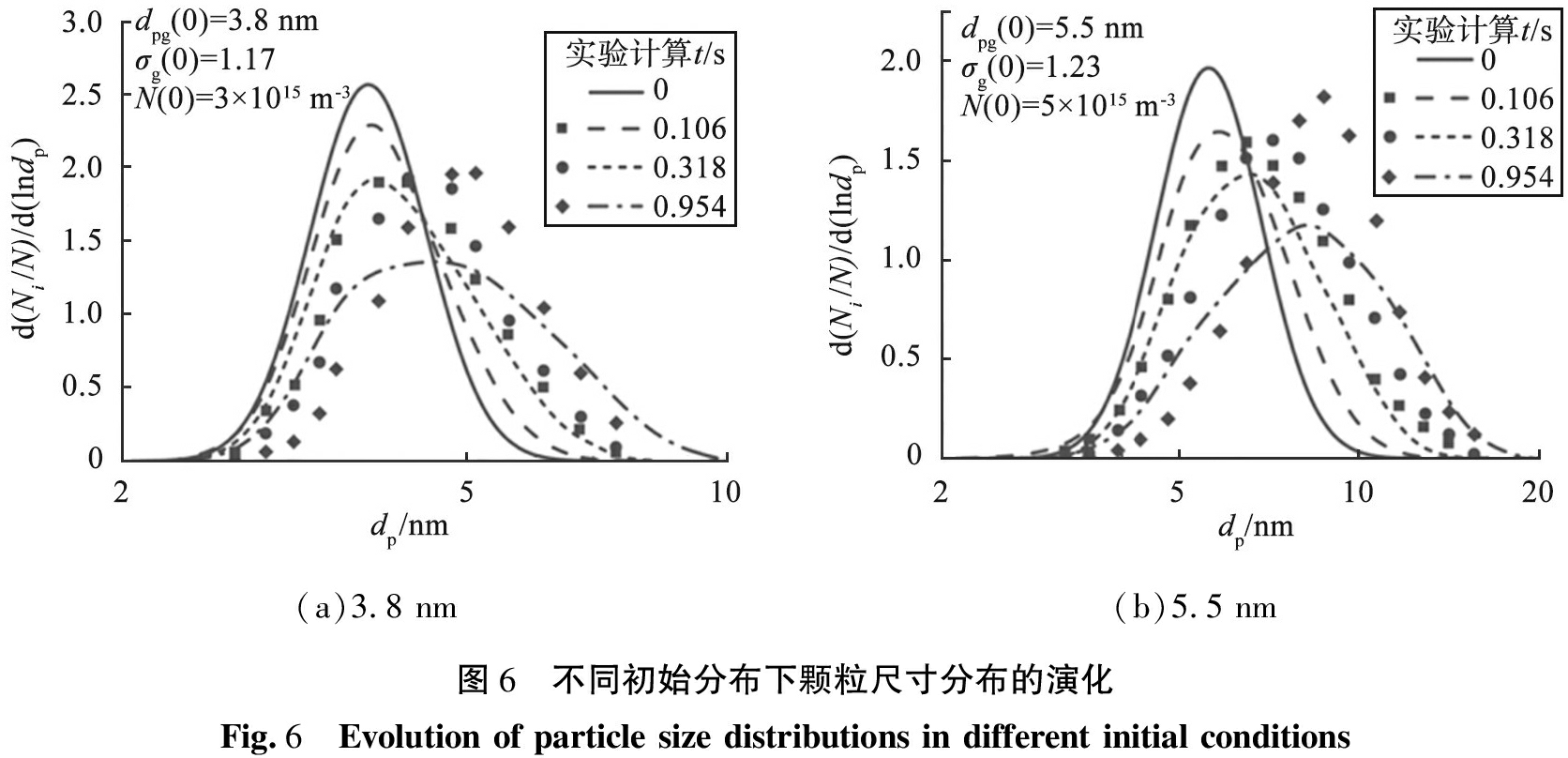
(a)3.8 nm(b)5.5 nm图6 不同初始分布下颗粒尺寸分布的演化Fig.6 Evolution of particle size distributions in different initial conditions
图7所示为不同颗粒浓度、电荷随时间的变化。由图可知,颗粒的荷电概率很低,约有质量分数为3%的颗粒经过中和器后会带电荷,由于扩散附着到颗粒表面的离子数几乎可以忽略,因此假设1)和5)被满足。由于负离子具有较高的流动性,因此带负电的颗粒比带正电的多。此外,将颗粒最大电荷数设置为3,计算得到颗粒电荷分布随时间的变化。由于纳米颗粒与离子的多次碰撞概率更小,因此带大电荷的颗粒数较少,且大多数颗粒不带电。正离子更低的流动性导致带电量大于1的正电颗粒远小于负电颗粒。因此,假设2)中认为颗粒最多带1个电荷基本满足,且带正电颗粒数小于带负电颗粒数。
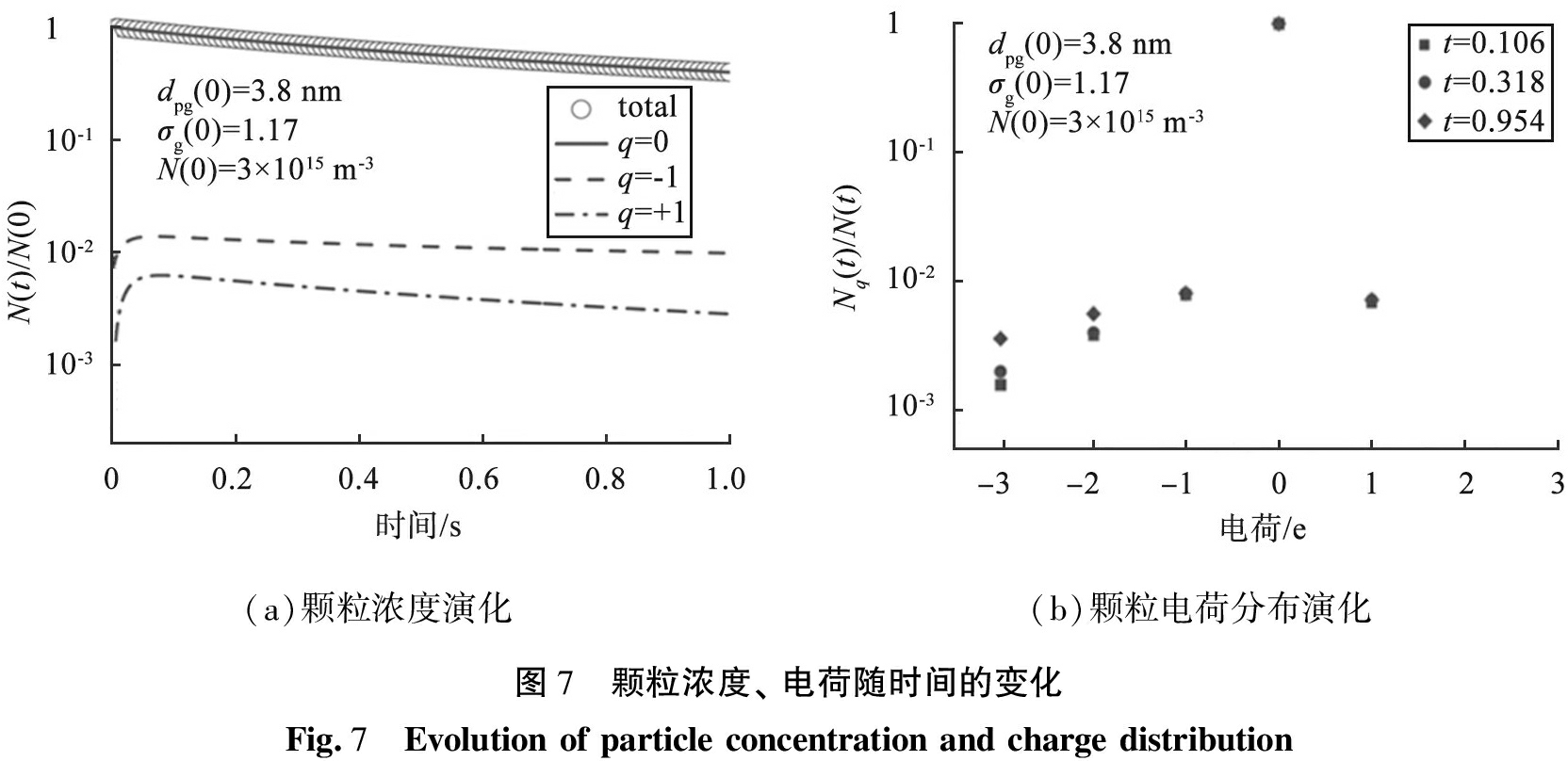
(a)颗粒浓度演化(b)颗粒电荷分布演化图7 颗粒浓度、 电荷随时间的变化Fig.7 Evolution of particle concentration and charge distribution
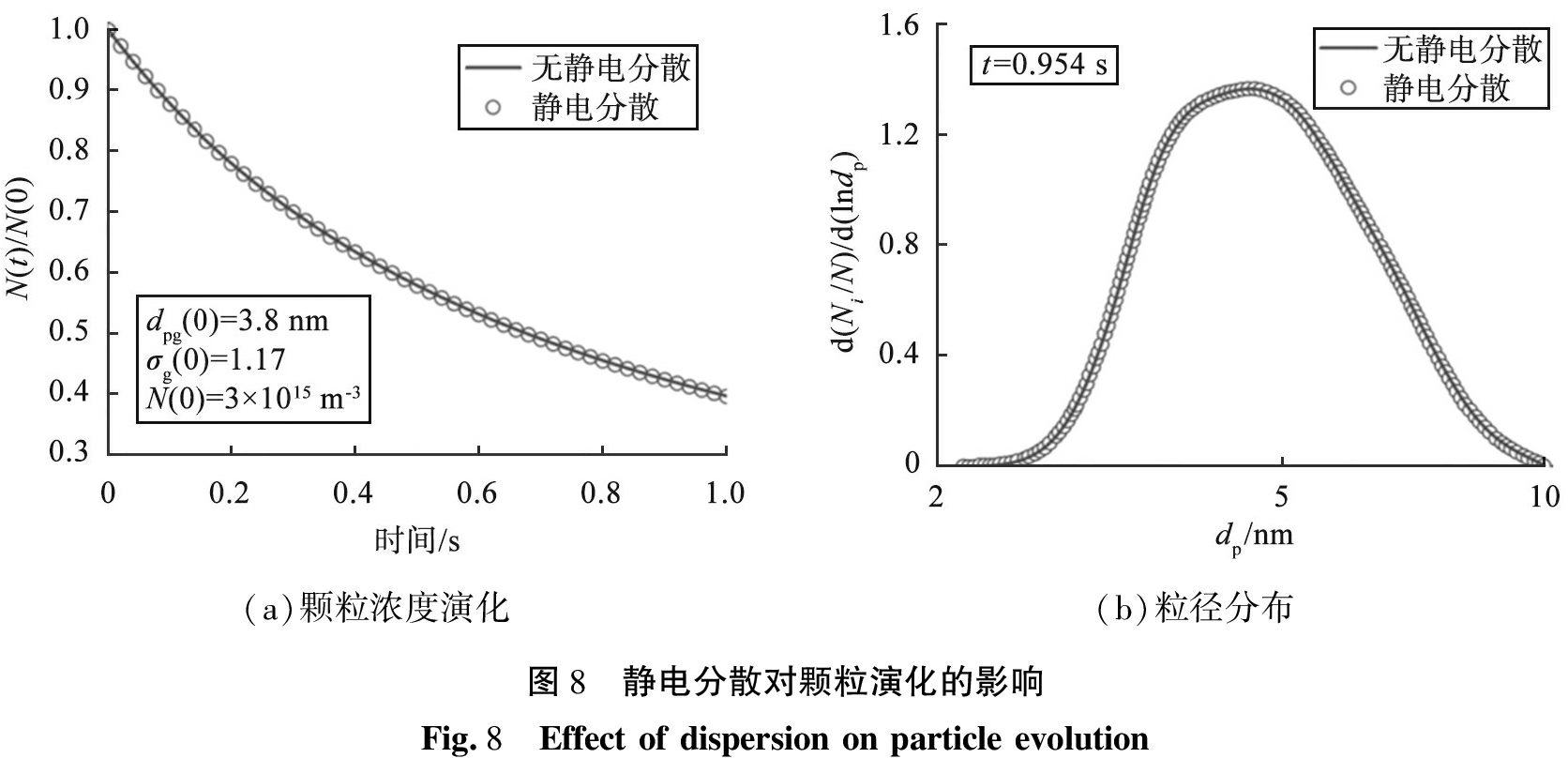
在模型中加入静电分散作用项来评估静电分散对颗粒演化的影响,图8所示为静电分散对颗粒演化的影响。由图可知,静电分散在本实验计算中几乎没有影响,这是因为本实验中颗粒的荷电比例太小,由同种电荷间库伦斥力导致的颗粒损失可以忽略,因此假设6)中由静电分散造成的壁面损失可以忽略。
在计算中发现,改变模型参数(如增大离子附着系数、 增加初始颗粒数、 增加初始离子浓度、 增大正负离子流动性差异等)能显著提高颗粒的荷电水平,此时由静电分散造成的颗粒损失更加显著。
图9所示为不同参数对荷电水平的影响。 由图可知, Gunn[26]推荐的离子附着系数更大, 颗粒荷电比例更高; 图9(b)、 (c)说明在一定范围内增大初始颗粒数、 初始离子浓度能增大颗粒和离子的碰撞概率, 从而增加荷电比例; 图9(d)在固定μ+的前提下增大μ-和μ+的比例实际上是增大了离子的附着系数, 导致荷电比例增加。 此外, 增大正、 负粒子流动性的差异会导致带正、 负电荷的颗粒数差异增大。
(a)颗粒浓度演化(b)粒径分布图8 静电分散对颗粒演化的影响Fig.8 Effect of dispersion on particle evolution
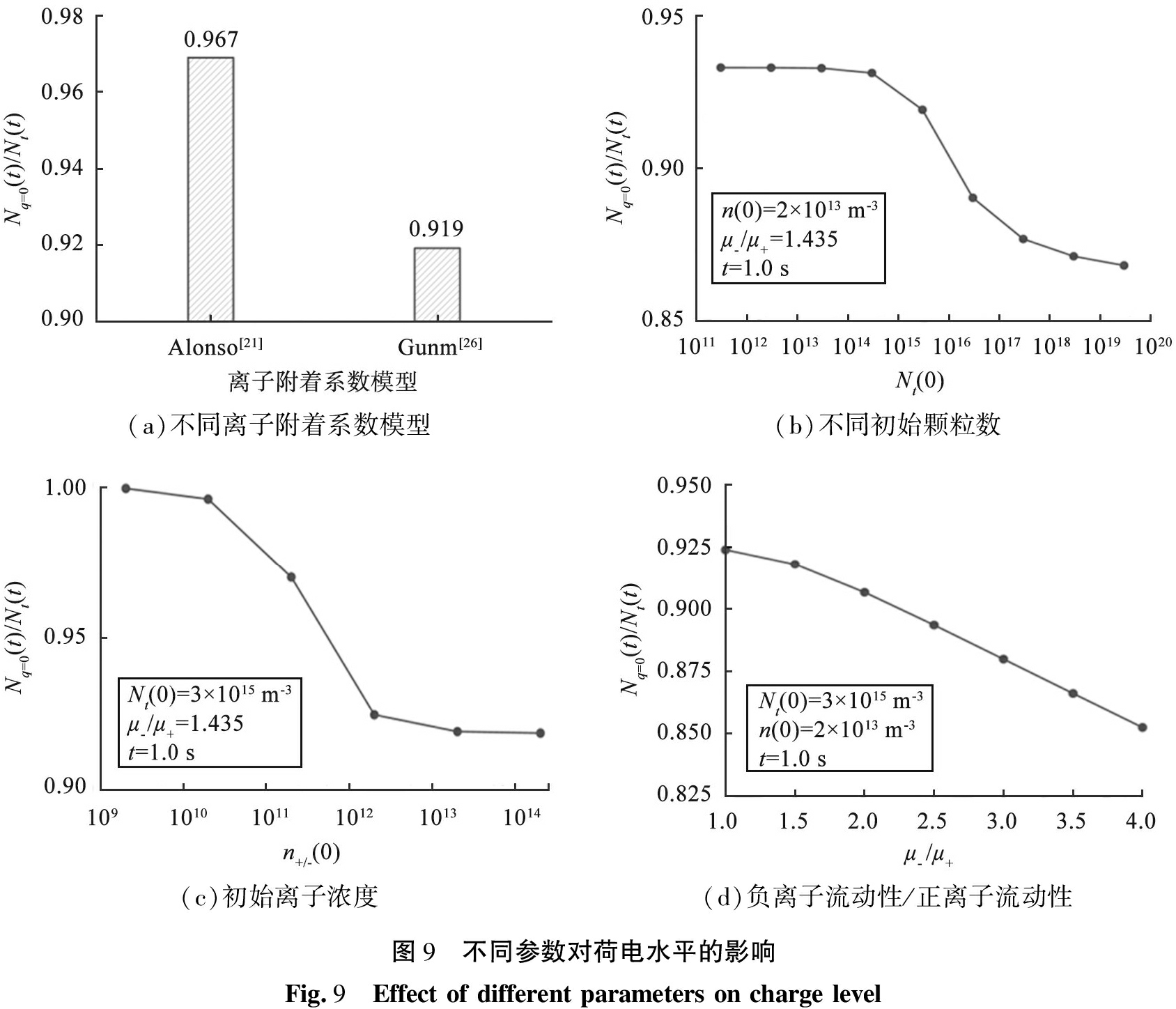
(a)不同离子附着系数模型(b)不同初始颗粒数(c)初始离子浓度(d)负离子流动性/正离子流动性图9 不同参数对荷电水平的影响Fig.9 Effect of different parameters on charge level
图10所示为不同离子附着系数对颗粒演化的影响。由图可知,Gunn模型系数更大,扩散荷电增强的同时,由静电分散导致的颗粒损失显著增加。从粒径分布曲线可以看到,Gunn模型得到的粒径分布更窄,小颗粒由于更大的迁移率更快地损失。在时间为0.954 s内,粒径为4～5 nm的颗粒质量分数增大,更加符合图6(a)中所示的实验数据。
通过与Alonso等开展的数值模拟和实验进行对比验证, 表明本研究中提出的数值模型可以作为模拟带电气溶胶的同时荷电-凝并行为的合理选择。 事实上, 该模型可以适用于更广的范围, 如适用于颗粒的任何粒径分布、 任何颗粒及电荷量范围、 任何活度的放射性气溶胶、 任何荷电及凝并时间尺度等等。
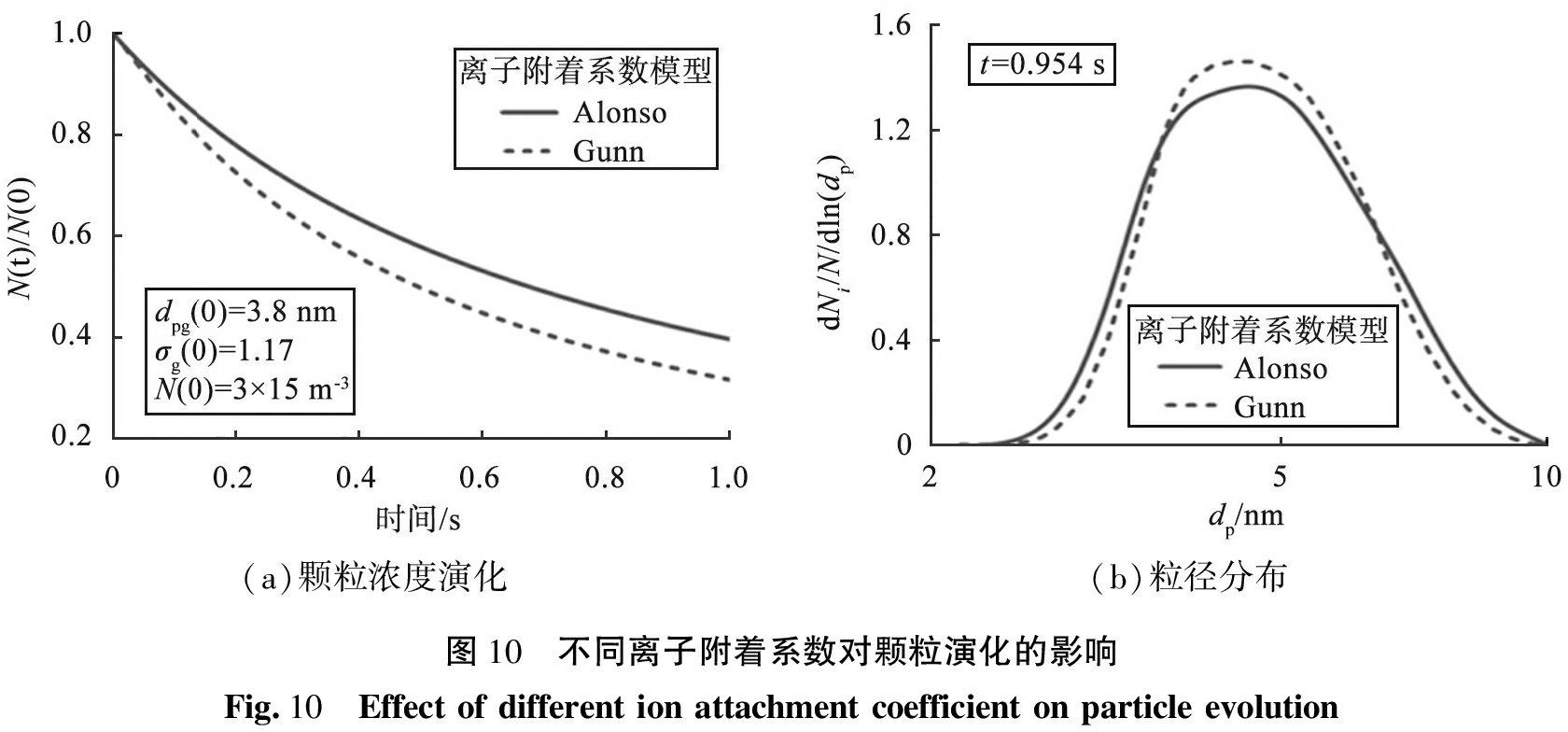
(a)颗粒浓度演化(b)粒径分布图10 不同离子附着系数对颗粒演化的影响Fig.10 Effect of different ion attachment coefficient on particle evolution
3 结论
本文中基于所建立的同时荷电-凝并理论以及分区法和单元平均技术数值求解了放射性气溶胶的同时荷电-凝并问题。模型准确性经过了分析解和经典实验验证, 适用于核电厂严重事故下安全壳内放射性气溶胶的荷电-凝并动力学研究。此外,由于放射性物质的管制以及气溶胶测量技术上的困难,目前国内外还没有可供参考的放射性气溶胶同时荷电-凝并的测量实验,因此本研究为填补这一方面的空白提供了参考和依据。
本模型目前只涵盖颗粒荷电-凝并机制的作用过程,未来将继续探究颗粒荷电和成核、 生长、 沉积、 去除等机制的相互作用。此外,分区法在求解群平衡方程时面临着计算成本较高的问题,未来将探究更加高效且保留良好精度的计算方法。
[1]朱继洲. 核反应堆安全分析[M]. 西安: 西安交通大学出版社, 2004.
ZHU J Z. Nuclear reactor safety analysis[M]. Xi’an: Xi’an Jiaotong University Press, 2004.
[2]颜翠平, 陈海焱, 林龙沅, 等. 放射性气溶胶净化的研究进展[J]. 中国粉体技术, 2008, 14(4): 47-50.
YAN C P, CHEN H Y, LIN L Y, et al. Progression for scavenging radioactive aerosol[J]. China Powder Science and Technology, 2008, 14(4): 47-50.
[3]王辉, 孙晓晖, 邢继, 等. 基于滑移通量模型的毛细管内气溶胶输运与滞留数值研究[J]. 原子能科学技术, 2022, 56(增1): 50-57.
WANG H, SUN X H, XING J, et al. Numerical research on aerosol transport and retention in capillary tubes based on drift-flux model[J]. Atomic Energy Science and Technology, 2022, 56(S1): 50-57.
[4]陈君岩, 高璞珍, 谷海峰, 等. 事故后聚并对亚微米气溶胶重力沉降的影响[J]. 哈尔滨工程大学学报, 2022, 43(12): 1719-1727.
CHEN J Y, GAO P Z, GU H F, et al. Effects of coagulation on the gravity deposition of submicron aerosols under severe accident conditions[J]. Journal of Harbin Engineering University, 2022, 43(12): 1719-1727.
[5]HAN S, LI Y, WEN G, et al. Study on thermophoretic deposition of micron-sized aerosol particles by direct numerical simulation and experiments[J]. Ecotoxicology and environmental safety, 2022, 233: 113316.
[6]王竞弘, 彭威, 于溯源. 核反应堆严重事故中气溶胶的吸湿增长研究进展[J]. 核动力工程, 2022, 43(2): 138-151.
WANG J H, PENG W, YU S Y. A review of research on aerosol hygroscopic growth in severe nuclear reactor accidents[J]. Nuclear Power Engineering, 2022, 43(2): 138-151.
[7]LI Y, ZHOU Y, SUN Z, et al. Analysis of hygroscopic growth properties of soluble aerosol under severe nuclear accidents conditions[J]. Progress in Nuclear Energy, 2020, 127: 103464.
[8]田林涛. 安全壳内源项气溶胶去除特性实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2020.
TIAN L T. Experimental study on aerosol removal characteristics of source term in containment[D]. Harbin: Harbin Engineering University, 2022.
[9]万永鑫. 安全壳内气体与气溶胶输运模型开发与分析[J]. 科学技术创新, 2022(14): 169-172.
WAN Y X. Development and analysis of gas and aerosol transport models in containment[J]. Scientific and Technological Innovation, 2022(14): 169-172.
[10]MA Z, MA T, WANG B, et al. Meso-scale numerical analysis for transport and deposition behaviors of radioactive aerosols under severe nuclear accident[J]. Progress in Nuclear Energy, 2022, 150: 104314.
[11]YUAN X, WEI J, ZHANG B, et al. Development and application of an aerosol model under a severe nuclear accident[J]. Frontiers in Energy Research, 2022, 10: 200.
[12]YEH H, NEWTON G, RAABE O, et al. Self-charging of 198 Au-labeled monodisperse gold aerosols studied with a miniature electrical mobility spectrometer[J]. Journal of Aerosol Science, 1976, 7(3): 245-253.
[13]YEH H, NEWTON G, TEAGUE S. Charge distribution on plutonium-containing aerosols produced in mixed-oxide reactor fuel fabrication and the laboratory[J]. Health physics, 1978, 35(3): 500-503.
[14]CLEMENT C, HARRISON R. The charging of radioactive aerosols[J]. Journal of Aerosol Science, 1992, 23(5): 481-504.
[15]GENSDARMES F, BOULAUD D, RENOUX A. Electrical charging of radioactive aerosols-comparison of the Clement-Harrison models with new experiments[J]. Journal of aerosol science, 2001, 32(12): 1437-1458.
[16]孙晓晖, 孙婧, 王辉, 等. 事故工况下核电厂安全壳内放射性气溶胶电荷分布研究[J]. 原子能科学技术, 2022, 56(增1): 67-73.
SUN X H, SUN J, WANG H, et al. Study on radioactive aerosol charge distribution in containment of nuclear power plant during severe accident[J]. Atomic Energy Science and Technology, 2022, 56(S1): 67-73.
[17]PALSMEIER J F, LOYALKA S K. Evolution of charged aerosols: role of charge on coagulation[J]. Nuclear Technology, 2013, 184(1): 78-95.
[18]DE LA TORRE AGUILAR F, LOYALKA S K. Simulation of multiple-component charged aerosol evolution[J]. Nuclear Science and Engineering, 2020, 194(5): 373-404.
[19]潘陈烨. 荷电颗粒在声场中的凝并特性研究[D]. 常州: 常州大学, 2022.
PAN C Y. Study on condensation characteristics of charged particles in sound field[D]. Changzhou: Changzhou University, 2022.
[20]KIM Y H, YIACOUMI S, NENES A, et al. Charging and coagulation of radioactive and nonradioactive particles in the atmosphere[J]. Atmospheric Chemistry and Physics, 2016, 16(5): 3449-3462.
[21]ALONSO M, HASHIMOTO T, KOUSAKA Y, et al. Transient bipolar charging of a coagulating nanometer aerosol[J]. Journal of Aerosol Science, 1998, 29(3): 263-270.
[22]ALONSO M. Simultaneous charging and Brownian coagulation of nanometre aerosol particles[J]. Journal of Physics A: Mathematical and General, 1999, 32(8): 1313-1327.
[23]ORON A, SEINFELD J H. The dynamic behavior of charged aerosols: III. Simultaneous charging and coagulation[J]. Journal of Colloid and Interface Science, 1989, 133(1): 80-90.
[24]SHARMA G, WANG Y, CHAKRABARTY R, et al. Modeling simultaneous coagulation and charging of nanoparticles at high temperatures using the method of moments[J]. Journal of Aerosol Science, 2019, 132(1): 70-82.
[25]KUMAR J, PEGLOW M, WARNECKE G, et al. The cell average technique for solving multi-dimensional aggregation population balance equations[J]. Computers &Chemical Engineering, 2008, 32(8): 1810-1830.
[26]GUNN R. Diffusion charging of atmospheric droplets by ions and the resulting combination coefficients[J]. Journal of Atmospheric Sciences, 1954, 11(5): 339-347.