世界卫生组织指出, 全球每年约700万人因大气污染过早死亡, 工业活动是引起大气污染的主要成因[1]。 在我国, 工业领域排放的二氧化硫(SO2)、 氮化物(NOx)和颗粒物分别占排放总量的76.3%、 37.3%、 60.5%[2]。“十一五”规划中首次将减少SO2总量作为约束性指标;“十二五”规划中将NOx减排列入约束性指标;“十三五”规划中提出,环境管理策略从总量控制单一目标向环境质量改善和污染物总量控制双目标的转变。在上述政策措施的加持下,我国工业大气污染治理水平显著提升,但目前大气污染呈现跨区域、 复合型特征,经济增长与污染物排放尚未脱钩[3]。由于建厂初期选择污染物治理工艺时忽略了运营成本、 污染物产量、 环境政策等因素间的动态关系,污染物超标和工艺治理设备闲置等现象导致经济发展与环境污染间的冲突加剧,因此,需要借助系统分析法来支持区域工业大气污染的控制管理。
针对区域工业大气污染的控制与管理,Zhu等[4-5]运用了一系列优化方法,如区间数学规划、 随机数学规划、 模糊数学规划等。区间两阶段随机规划 (interval two-stage stochastic programming,ITSP) 方法能够表征数据获取不够精确的区间不确定性,以追索权思想反映随机性事件发生后采取纠正措施的能力[6]。Huang等[7]首次提出两步交互法处理ITSP中区间、概率的不确定性。Chen等[8]将ITSP模型用于碳交易市场进行温室气体排放管理。Guo等[9]利用ITSP模型实现资源短缺的惩罚量化。Jin等[10]基于ITSP与双极交互算法采用空气质量指数评价多种污染物的综合空气质量。Khosrojerdi等[11]将ITSP与模糊数结合,用于处理水资源最优分配过程中的不确定性问题。
尽管ITSP能较好地处理数据不精确与随机事件带来的不确定性,但不能揭示参数及其交互作用对系统输出的影响,因此将析因分析(factorial analysis, FA)方法引入系统分析解决上述问题。Wang等[12]提出基于析因分析的多区域投入产出模型,模拟二氧化碳(CO2)减排路径,揭示多因素、 多部门、 多城市对城市群的个体和交互效应。Wang等[13]将析因分析法与区间线性规划法进行耦合,用于空气质量管理。Liu等[14]提出基于析因分析的模糊机会约束方法,研究城市群中不确定性因子对生态环境的影响。Zhang等[15]将析因分析集合到非确定性优化与混合层次因子分析的耦合模型中,支持发电扩能规划,帮助决策者在不确定性条件下做出最优决策。
在污染物去除效率、 经济数据、 环境政策、 污染物排放速率等不确定性因素中,几个参数的变化可能会导致系统响应发生显著差异,而其他一些参数可能根本不产生影响[16],然而已有研究缺乏针对地区-行业-设备-复合型污染物的协同治理的多目标优化研究。
陕西省安康市是我国“南水北调”工程的水源地城市,2020年环境空气质量优良天数达到346 d,进入国家达标城市行列。尽管安康市空气质量环境整体向优,但受限于“两山夹一川”的盆地因素、静风频率较高且湿度持续较大的气候条件,不利于污染物的扩散和消减。部分水泥企业排放的工业大气中含有烟气污染物,虽然安康市出台一系列环保政策整改“散乱污”企业,但这些企业对地区国民生产总值(GDP)与就业均起着重要的支撑作用,不适合盲目关闭或淘汰,只能通过高效污染物治理工艺等手段实现企业良性发展。通过系统分析优选不同行业污染物治理工艺,研究影响污染物处理成本的深层次原因,实现工业区经济发展和环境保护的双赢局面。
本文中采用基于析因分析法的区间两阶段随机规划法(factorial analysis-interval two-stage stochastic programming,FA-ITSP),研究安康市区域环境中的工业大气的污染控制和管理。以工业大气质量和处理成本为优化目标,以去除水泥厂排放的主要污染物SO2、 NOx和颗粒物为例,在双碱法、 石灰石-石膏法、 选择性催化还原法、 选择性非催化还原法、 袋式除尘法和电除尘法中优选污染物治理工艺组合,分析不确定性因素的主效应及交互效应对处理成本的影响,为制定区域环境工业大气污染管理策略提供技术支持。
1 分析与计算方法
1.1 区间两阶段随机规划法
ITSP是一种具有2层递阶结构的规划模型,适用于包含区间、随机参数且需要进行政策情景分析的问题。随机事件发生前做出第1阶段决定,将最优决策传递,待随机事件发生之后,做出第2阶段决策,用追索权思想纠正由不确定性造成的损失,使全局效益最优。ITSP基本形式的描述见文献[17]。区间参数可计算出区间形式的结果,结果具有上界和下界,上界是由区间数的上限计算所得结果,下界是由区间数的下限计算所得结果。
1.2 析因分析法
析因分析法是一种多元推理方法,可以揭示各参数的主效应与交互关系,并量化参数水平变化对系统性能的影响。当模型中包含k(k=1,2,…,n)个因子,每个因子包含高、 低2个水平时,引入2k次析因分析,系统中包含k个主效应和![]() 个两因子交互效应,其他的交互效应依次类推。k个因子的效应对照展开式参见文献[18],效应与效应的平方和计算公式参见文献[19]。
个两因子交互效应,其他的交互效应依次类推。k个因子的效应对照展开式参见文献[18],效应与效应的平方和计算公式参见文献[19]。
2 案例与建模
2.1 基础数据和行业排放标准以及环境空气质量标准
选择安康市某工业区水泥厂为研究对象,排放的SO2、 NOx、 颗粒物为该区域环境中工业大气的主要污染物。以2021年为基准年,以5 a为1个规划期L, L=1、 2、 3时,分别代表第1、 2、 3个5年规划期,即2021—2025、 2026—2030、 2031—2035年。
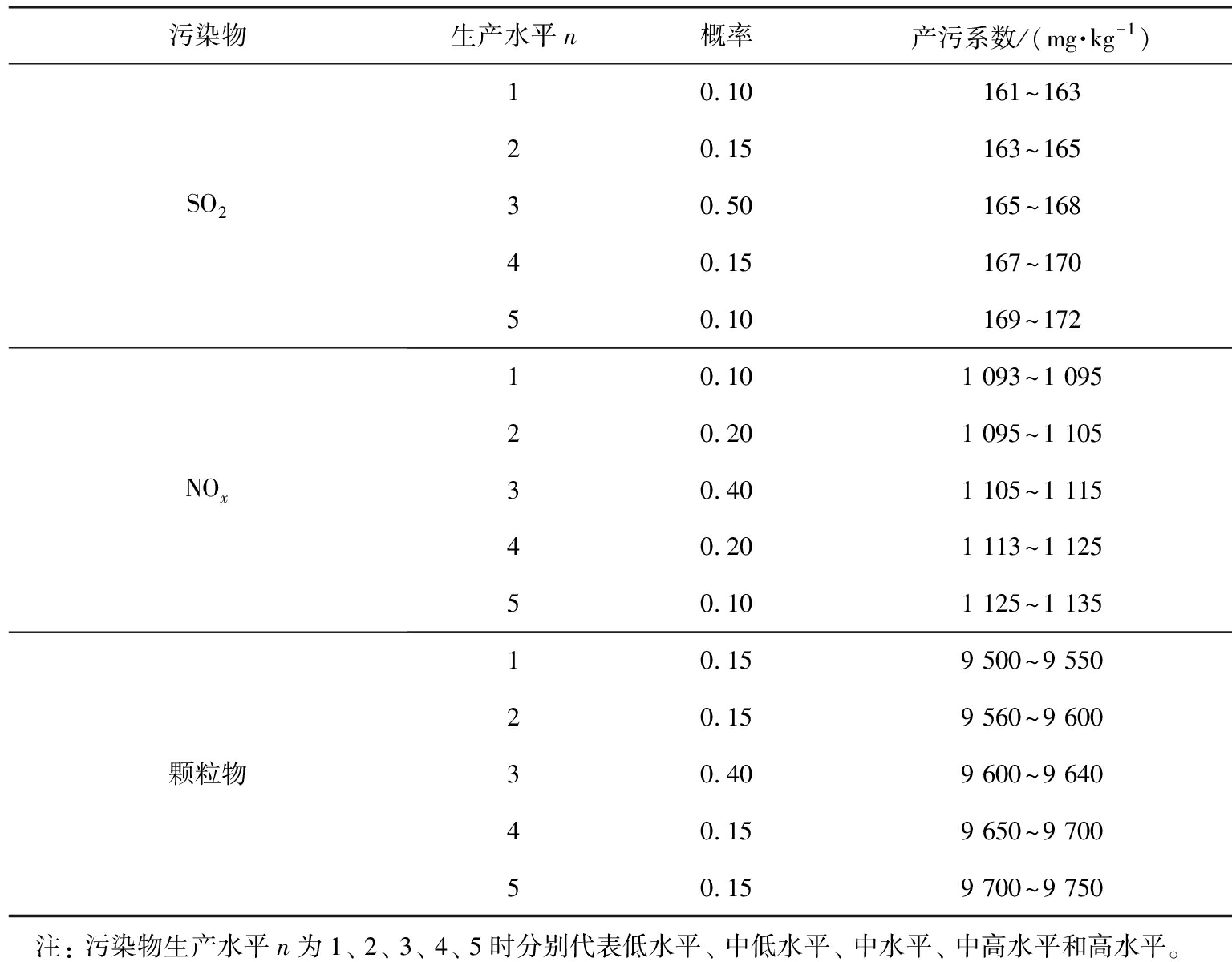
假定每年生产时间为3 600 h,当L=1、 2、 3时,水泥厂产能分别为26 400、 31 500、 36 600 kg/h。 SO2、 NOx、 颗粒物的生产水平n分别取值为1、 2、 3、 4、 5时,各自代表低水平、 中低水平、 中水平、 中高水平和高水平。水泥厂的3种污染物在不同生产水平时的概率和产污系数如表1所示。由表1可知,对于水泥厂的3种污染物,颗粒物的产污系数最大,NOx的产污系数较小,SO2的产污系数极小。
表1 3种污染物在不同生产水平时的概率和产污系数
Tab.1 Probability and pollution coefficient of 3 pollutants at different production levels
污染物生产水平n概率产污系数/(mg·kg-1)SO210.10161~16320.15163~16530.50165~16840.15167~17050.10169~172NOx10.101 093~1 09520.201 095~1 10530.401 105~1 11540.201 113~1 12550.101 125~1 135颗粒物10.159 500~9 55020.159 560~9 60030.409 600~9 64040.159 650~9 70050.159 700~9 750 注: 污染物生产水平n为1、 2、 3、 4、 5时分别代表低水平、 中低水平、 中水平、 中高水平和高水平。
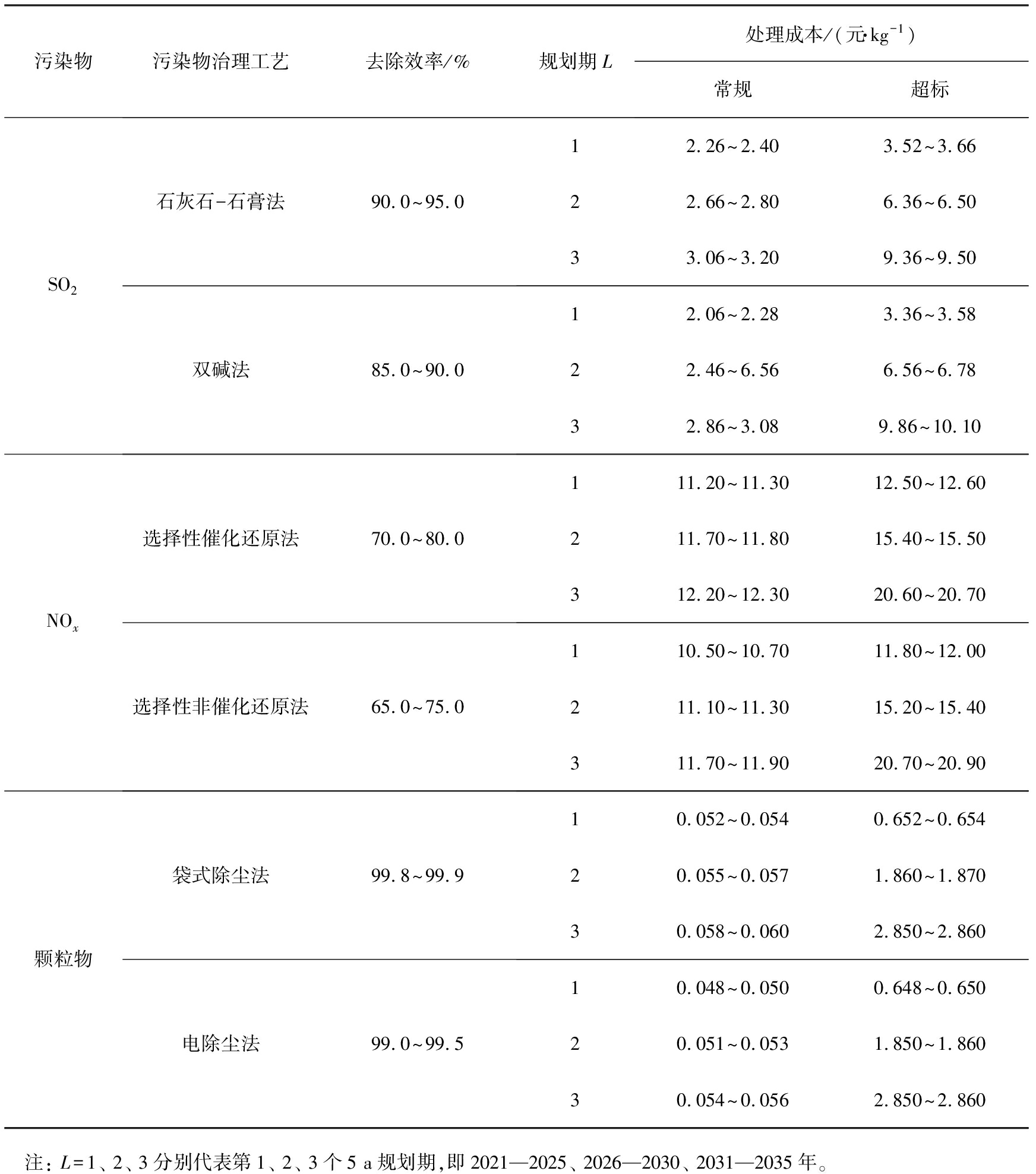
污染物处理成本包括运营成本、 投资成本、 闲置成本、 折旧成本等费用, 模型采用生命周期法的计算值作为污染物处理成本[20]。 3种污染物不同治理工艺的效率及在不同规划期的处理成本表2所示。 由表2可以看出, 对于3种污染物, 常规处理成本在每个规划期都小于超标处理成本,且处理成本随着规划期的增大而增大; 超标污染物处理成本随规划期增大的程度要大于常规污染物处理成本。
表2 3种污染物不同治理工艺的去除效率及在不同规划期的处理成本
Tab.2 Removal efficiency of different treatment technologies and their processing costs of 3 pollutants in different planning periods
污染物污染物治理工艺去除效率/%规划期L处理成本/(元·kg-1)常规超标SO2石灰石-石膏法90.0~95.012.26~2.403.52~3.6622.66~2.806.36~6.5033.06~3.209.36~9.50双碱法85.0~90.012.06~2.283.36~3.5822.46~6.566.56~6.7832.86~3.089.86~10.10NOx选择性催化还原法70.0~80.0111.20~11.3012.50~12.60211.70~11.8015.40~15.50312.20~12.3020.60~20.70选择性非催化还原法65.0~75.0110.50~10.7011.80~12.00211.10~11.3015.20~15.40311.70~11.9020.70~20.90颗粒物袋式除尘法99.8~99.910.052~0.0540.652~0.65420.055~0.0571.860~1.87030.058~0.0602.850~2.860电除尘法99.0~99.510.048~0.0500.648~0.65020.051~0.0531.850~1.86030.054~0.0562.850~2.860 注: L=1、 2、 3分别代表第1、 2、 3个5 a规划期,即2021—2025、 2026—2030、 2031—2035年。
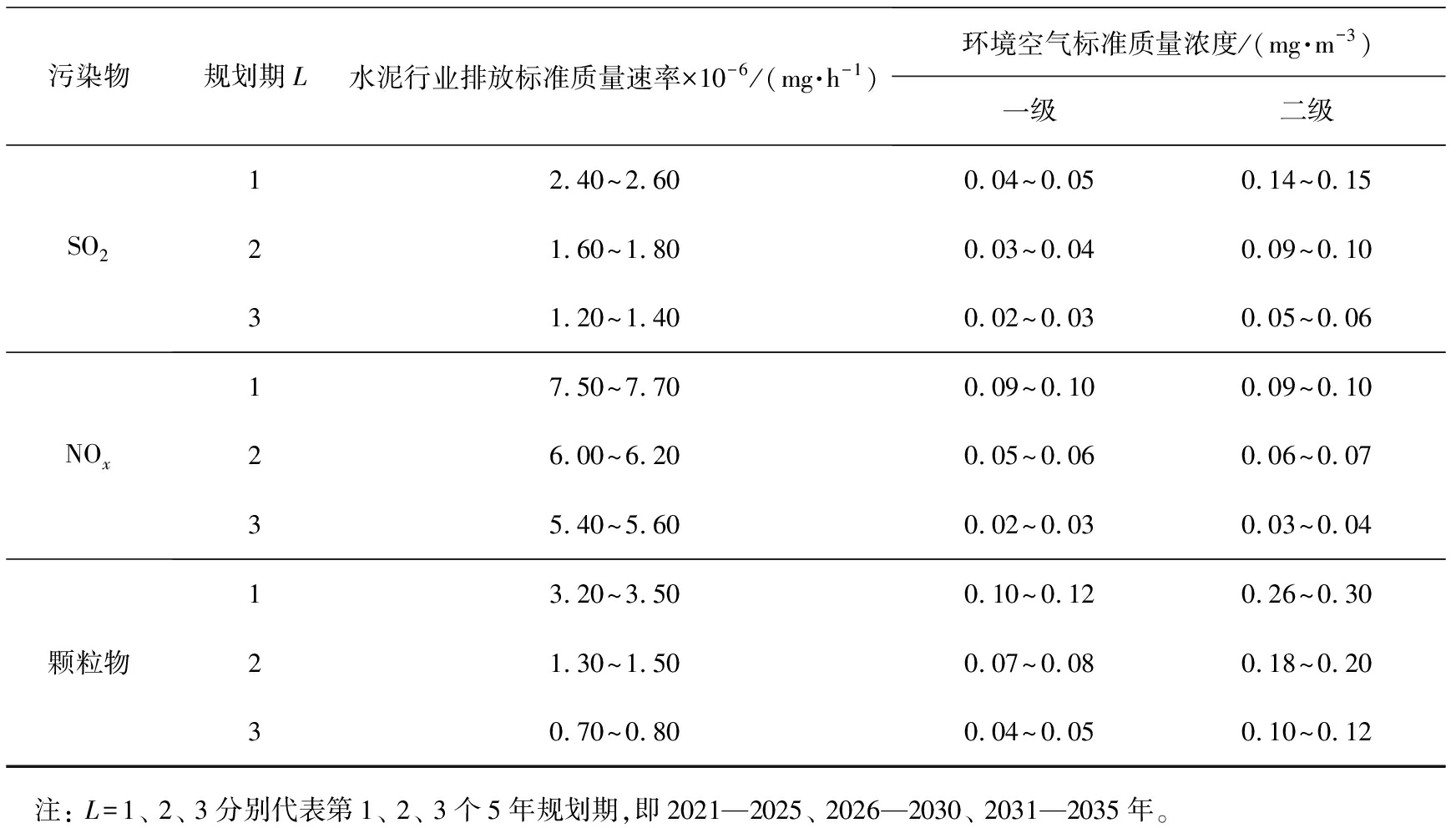
3种污染物不同规划期的行业排放标准质量速率与环境空气标准质量浓度如表3所示。由表3可知,排放标准质量速率均随着规划期的增大而减小;在相同的规划期时,质量速率从大到小依次为NOx、 颗粒物、 SO2;环境空气质量浓度标准中,一级标准要严于二级标准[21-22]。
表3 不同规划期3种污染物的行业排放标准质量速率与环境空气标准质量浓度
Tab.3 Mass rates of industry emission standard and mass concentration of ambient air standards for 3 pollutants during different planning periods
污染物规划期L水泥行业排放标准质量速率×10-6/(mg·h-1)环境空气标准质量浓度/(mg·m-3)一级二级SO212.40~2.600.04~0.050.14~0.1521.60~1.800.03~0.040.09~0.1031.20~1.400.02~0.030.05~0.06NOx17.50~7.700.09~0.100.09~0.1026.00~6.200.05~0.060.06~0.0735.40~5.600.02~0.030.03~0.04颗粒物13.20~3.500.10~0.120.26~0.3021.30~1.500.07~0.080.18~0.2030.70~0.800.04~0.050.10~0.12 注: L=1、 2、 3分别代表第1、 2、 3个5年规划期,即2021—2025、 2026—2030、 2031—2035年。
对于高架点源的工业大气污染物排放扩散,选择高斯扩散模型估算下风向不同位置处的污染物浓度。在估算颗粒物扩散时,应当考虑颗粒物重力沉降、干沉降、湿沉降的过程[23-24]。
2.2 基于环境空气质量达标和处理成本最小化为目标的数学模型
区域环境工业大气污染控制通过安装末端治理措施脱除污染物,同时还要考虑行业排放特征与污染排放空间差异[17]。由于实现污染物近零排放在经济与技术上均不易达成,因此转而追求环境空气质量标准达标、处理成本最小化的方案[18]。基于环境空气质量达标和处理成本最小化方案的数学模型中,主要包括污染物生产和处理成本的目标函数、质量平衡约束条件、排放行业标准质量去除速率的约束条件、环境空气标准质量浓度的约束条件。
污染物生产和处理成本的目标函数为
(1)
式中: f±为污染物治理总成本,上角标“±”表示该物理量的值具有上下限(后续所有物理量符号的上角标同理); Ll为规划期长度,l=1,2,3分别代表3个规划期; j=1,2,3,分别代3种污染物SO2、 NOx、 颗粒物; s=1,2,分别代表脱硫工艺的石灰石-石膏法和双碱法; r=1,2,分别代表脱硝工艺的选择性催化还原法、 选择性非催化还原法; g=1,2,分别代表除尘工艺的袋式除尘法、 电除尘法; ![]() 分别为未超标时规划期l内采用脱硫工艺s治理SO2、 采用脱硝工艺r治理NOx、 采用除尘工艺g治理颗粒物的单位成本;
分别为未超标时规划期l内采用脱硫工艺s治理SO2、 采用脱硝工艺r治理NOx、 采用除尘工艺g治理颗粒物的单位成本; ![]() 分别为规划期l内采用s、 r、 g治理第1个阶段未超标时SO2、 NOx、 颗粒物的质量,非负; Pjn分别为污染物j的污染物概率水平为n的概率[25];
分别为规划期l内采用s、 r、 g治理第1个阶段未超标时SO2、 NOx、 颗粒物的质量,非负; Pjn分别为污染物j的污染物概率水平为n的概率[25]; ![]() 分别为污染物超标排放后,超标部分在规划期l内采用j治理SO2、 采用r治理NOx、 采用g治理颗粒物的单位成本;
分别为污染物超标排放后,超标部分在规划期l内采用j治理SO2、 采用r治理NOx、 采用g治理颗粒物的单位成本; ![]() 分别为规划期l内采用s、 r、 g治理第2阶段超标时SO2、 NOx、 颗粒物的质量,非负。
分别为规划期l内采用s、 r、 g治理第2阶段超标时SO2、 NOx、 颗粒物的质量,非负。
污染物生产和治理的质量平衡约束条件为
(2)
(3)
(4)
式中:![]() 为水泥厂的污染物j在概率水平n下的产污系数; Tl为水泥厂在规划期l内的产能。
为水泥厂的污染物j在概率水平n下的产污系数; Tl为水泥厂在规划期l内的产能。
污染物排放行业标准质量去除速率的约束条件为
(5)
(6)
(7)
式中:![]() 分别代表s、 r、 g的去除效率;
分别代表s、 r、 g的去除效率;![]() 代表水泥厂在规划期l内污染物j的行业排放标准质量去除速率。
代表水泥厂在规划期l内污染物j的行业排放标准质量去除速率。
环境空气标准质量浓度的约束条件为
(8)
(9)
(10)
式中:![]() 代表污染物j的标准质量浓度贡献的转移因子[25];d=1,2,代表环境空气质量功能区(一类区、 二类区),环境空气质量标准(GB 3095—2012)中一类区指自然保护区、 风景名胜区和其他需要特殊保护的地区;二类区指城镇规划中确定的居住区、 商业交通居民混合区、 文化区、 一般工业区和农村地区,以及一、 三类区不包括的地区,三类区指特定工业区;
代表污染物j的标准质量浓度贡献的转移因子[25];d=1,2,代表环境空气质量功能区(一类区、 二类区),环境空气质量标准(GB 3095—2012)中一类区指自然保护区、 风景名胜区和其他需要特殊保护的地区;二类区指城镇规划中确定的居住区、 商业交通居民混合区、 文化区、 一般工业区和农村地区,以及一、 三类区不包括的地区,三类区指特定工业区;![]() 代表d功能区在规划期l内污染物j的标准质量浓度。
代表d功能区在规划期l内污染物j的标准质量浓度。
3 结果与分析
3.1 污染物治理工艺的优选组合
工业大气中水泥厂排放的主要污染物为SO2、 NOx和颗粒物。 去除SO2采用双碱法和石灰石-石膏法; 去除NOx采用选择性催化还原法和选择性非催化还原法; 去除颗粒物采用袋式除尘法和电除尘法。
在基于环境空气质量达标和处理成本最小化方案的数学模型中,以3种污染物处理成本之和为目标函数,所使用的约束包括质量平衡、 行业标准和环境空气质量标准,求解得到的决策变量是各治理工艺所处理的污染物量。根据求得的与治理工艺对应的决策变量,进而得到水泥厂在不同时期的治理工艺,因此,工艺的选择是根据排放标准和成本确定的。根据模型计算出的结果,把每个时期治理污染物所用到的工艺相结合为方案,即最低成本条件下不同时期和污染物的治理工艺组合。水泥厂不同规划期的治理的常规污染物的边界质量与成本如图1所示。由图1可知,在第1个规划期(L=1)处理下界时,电除尘法需要去除6 629.04 t 颗粒物,选择性非催化还原法需要去除698.54 t的NOx,双碱法需要去除106.92 t的SO2,第1个规划期的污染物处理成本为7.83×106元;其他情景可依次类推。
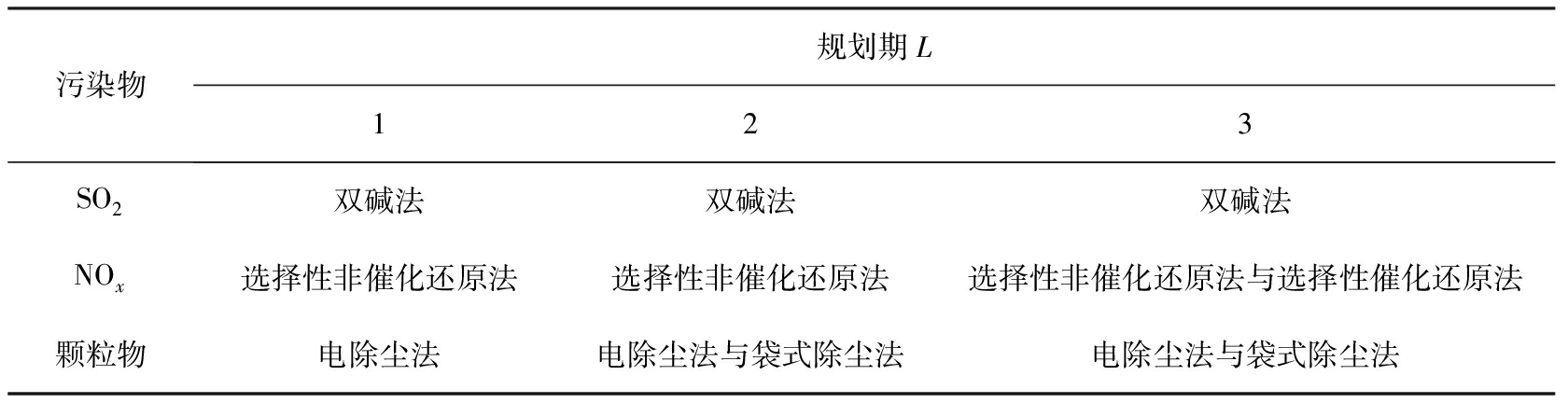
浓度未超标时3种污染物在不同规划期的治理工艺见表4。由表4可知,当污染物排放浓度未超标时,烟气中污染物排量的从大到小依次为颗粒物、 NOx、 SO2。第1个规划期烟气颗粒物治理选择电除尘法;第2、 3个规划期内颗粒物治理工艺组合为电除尘法与袋式除尘法。第1、 2个规划期脱硝工艺为选择性非催化还原法;随着水泥需求量和产量逐年增长,烟气脱硝设备面临着日益加重的污染物治理压力,在第3个规划期时2种工艺协同治理;烟气中的SO2主要来自于有机硫和黄铁矿硫,水泥原料在高温条件下会分解生成氧化钙、 氧化镁,它们能吸收大部分的SO2,反应生成稳定性强的硫酸钙、 硫酸镁等固定在水泥熟料中。常见脱硫工艺均可实现水泥烟气脱硫,因此,水泥厂可以选择处理成本低的烟气脱硫技术双碱法。
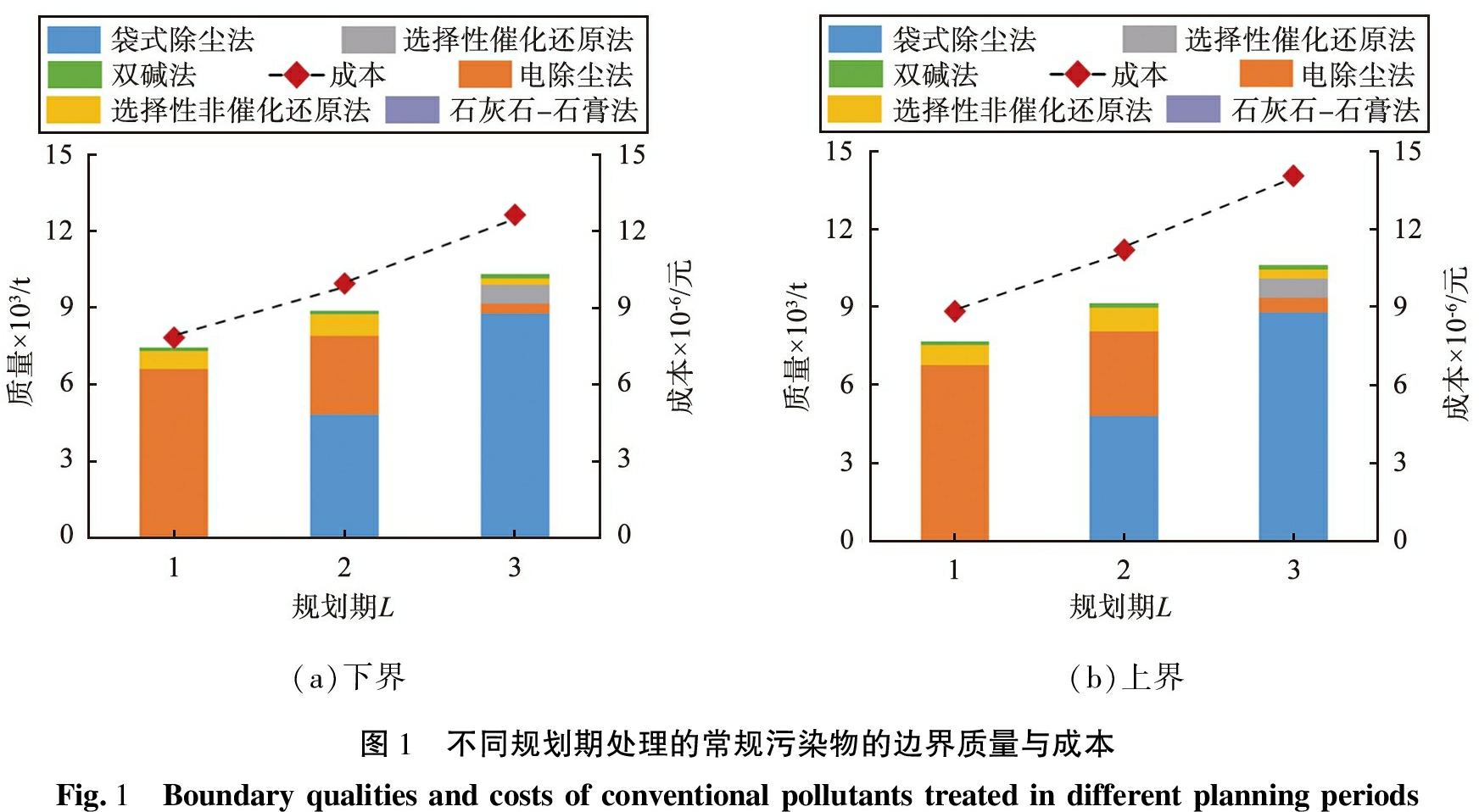
(a)下界(b)上界图1 不同规划期处理的常规污染物的边界质量与成本Fig.1 Boundary qualities and costs of conventional pollutants treated in different planning periods
表4 浓度未超标时3种污染物在不同规划期的治理工艺
Tab.4 Treatment technologies of 3 kinds of pollutants during different planning periods when pollutant concentration is not exceeded
污染物规划期L123SO2双碱法双碱法双碱法NOx选择性非催化还原法选择性非催化还原法选择性非催化还原法与选择性催化还原法颗粒物电除尘法电除尘法与袋式除尘法电除尘法与袋式除尘法
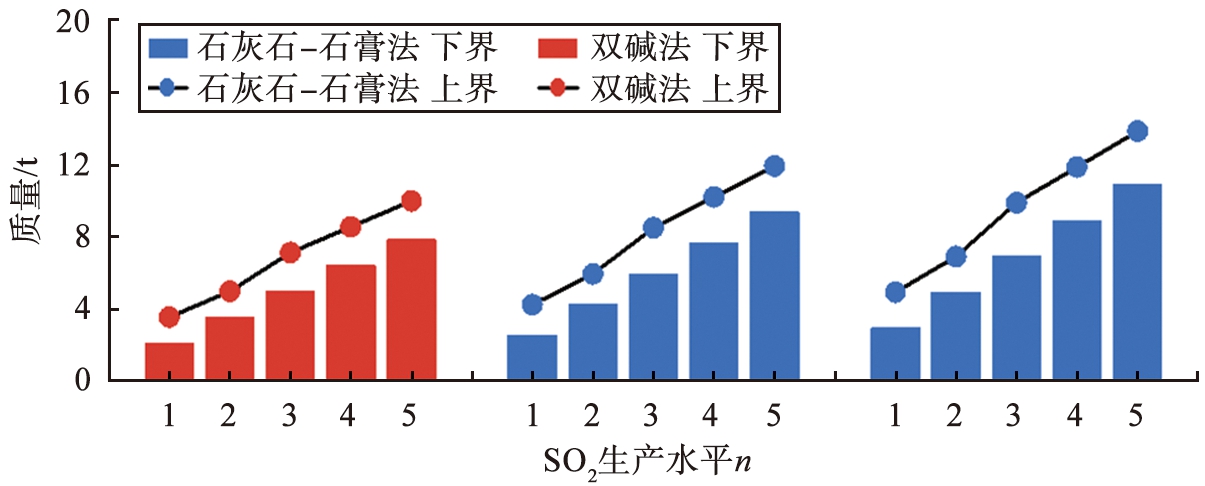
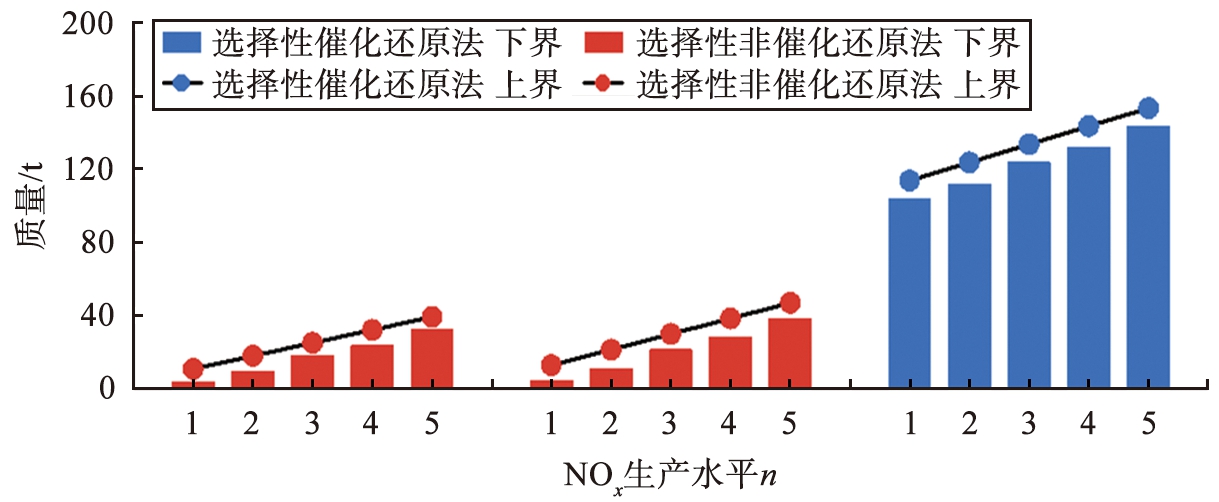
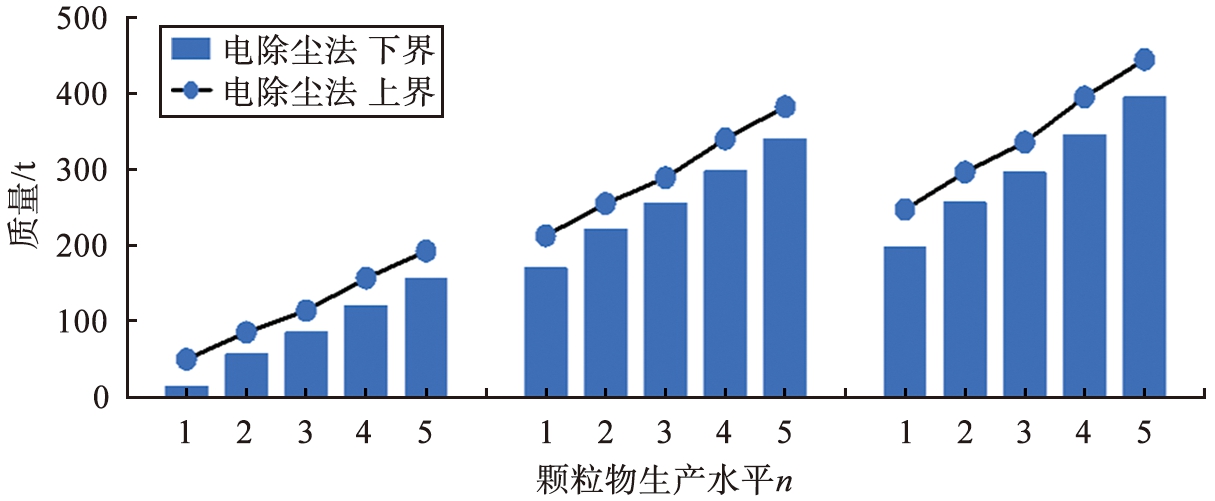
当污染物超标时,不同规划期时超标污染物质量随污染物生产水平的变化如图2—4所示。由图2可见,第1个规划期时,超标SO2全部使用双碱法进行治理,第2、 3个规划期的超标SO2全部使用石灰石-石膏法治理;处理的SO2的质量的上界和下界均随着SO2生产水平的增大而增大。图3、 4同理,不同规划期时超标NOx和颗粒物质量随污染物生产水平的增大而增大。
(a)L=1 (b)L=2 (c)L=3
图2 不同规划期时处理的SO2质量随SO2生产水平的变化
Fig.2 Variation of SO2 mass treated with SO2 production level in different planning periods
(a)L=1 (b)L=2 (c)L=3
图3 不同规划期时处理的NOx质量随NOx生产水平的变化
Fig.3 Variation of NOx mass treated with NOx production level in different planning periods
(a)L=1 (b)L=2 (c)L=3
图4 不同规划期时处理的颗粒物质量随颗粒物生产水平的变化
Fig.4 Variation of mass of particles treated with production level of particles in different planning periods
由于超标排放物较少,而且超标惩罚金额远高于工艺处理成本,因此当污染物超标时,水泥厂选择的治理策略如下:SO2治理策略为第1个规划期选用双碱法,第2、 3个规划期选用石灰石-石膏法应对严格的环境标准与高额的环保处罚。NOx治理策略为第1、 2个规划期使用选择性非催化还原法,第3个规划期使用选择性催化还原法。颗粒物治理策略为规划期内选择电除尘法作为唯一的超标颗粒物治理技术。
3.2 处理成本分析
污染物超标排放的处理成本包括超出行业标准部分的环保处罚和设备治理超标部分产生的成本。 一般来说, 高效率的治理工艺可能会造成效能过剩导致成本升高, 但可以满足逐渐严格的环保要求。 相反, 效率较低的治理措施尽管以较低的成本满足当下环保要求; 但在后期可能会因违反环保要求而面临环保处罚, 不能一味降低运营成本, 因此, 需要探究处理成本、 治理工艺与环保标准之间存在的交互关系。
安康市区域环境工业大气污染物控制管理系统总成本为(30.48~37.16)×106元。若污染物排放量不超过行业允许的排放标准,需支付常规运行成本,即FA-ITSP的第1个阶段成本,约(30.42~34.05)×106元;超标排放时将承担环保处罚造成高额经济损失,即第2个阶段成本。
3种超标污染物在不同规划期和污染物生产水平时的下界处理成本如图5所示。由图5可知,去除SO2,规划期为1时采用双碱法,规划期为2、3时采用石灰石法;去除NOx时,规划期为1、 2时采用选择性非催化还原法;去除颗粒物时,3个规划期全部采用电除尘法;3种超标污染物的下界处理成本随着生产水平和规划期的增大而增大;生产水平为5、 规划期为3时,去除SO2、 颗粒物、 NOx的下界处理成本分别为101.75×103、 112.89×104、 2.95×106元,在3种污染物中去除SO2的下界处理成本最低,去除NOx的下界处理成本最高。
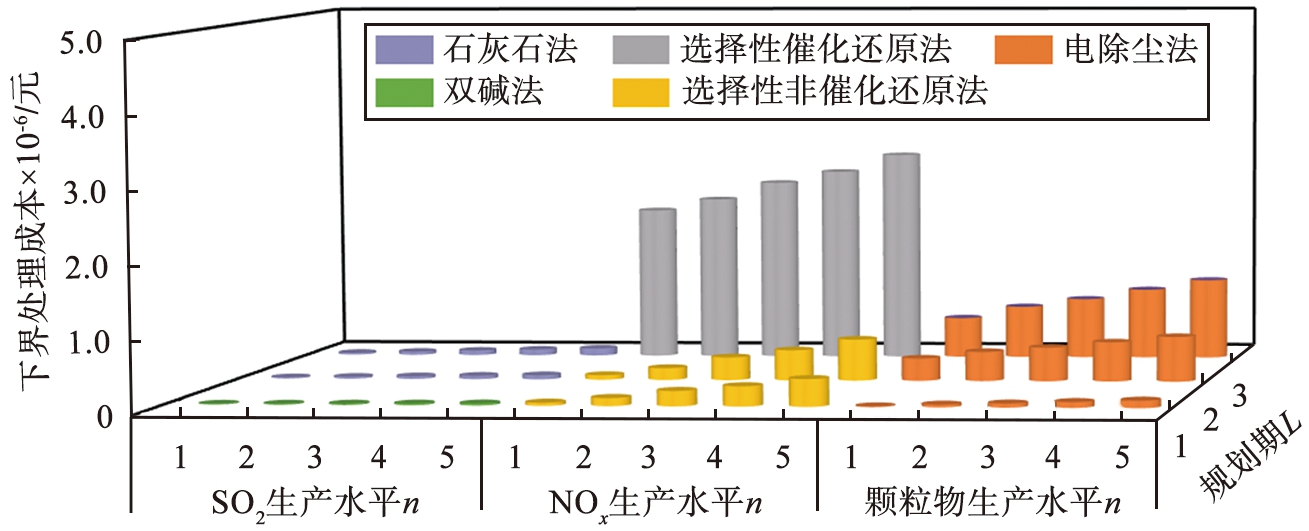
图5 3种超标污染物在不同规划期和污染物生产水平时的下界处理成本
Fig.5 Lower boundary processing cost of three kinds of excessive pollutants in different planning periods and pollutant production levels
3种超标污染物在不同规划期和污染物生产水平时的上界处理成本如图6所示。 由图6可以看出, 上界处理成本的变化趋势与下界的类似, 去除SO2的成本仍为同时期同生产水平成本最低, 最高为131.43×103元;去除NOx的成本仍为同时期同生产水平成本最高,最高为3.17×106元;去除颗粒物的成本位于其后,最高为1.27×106元。
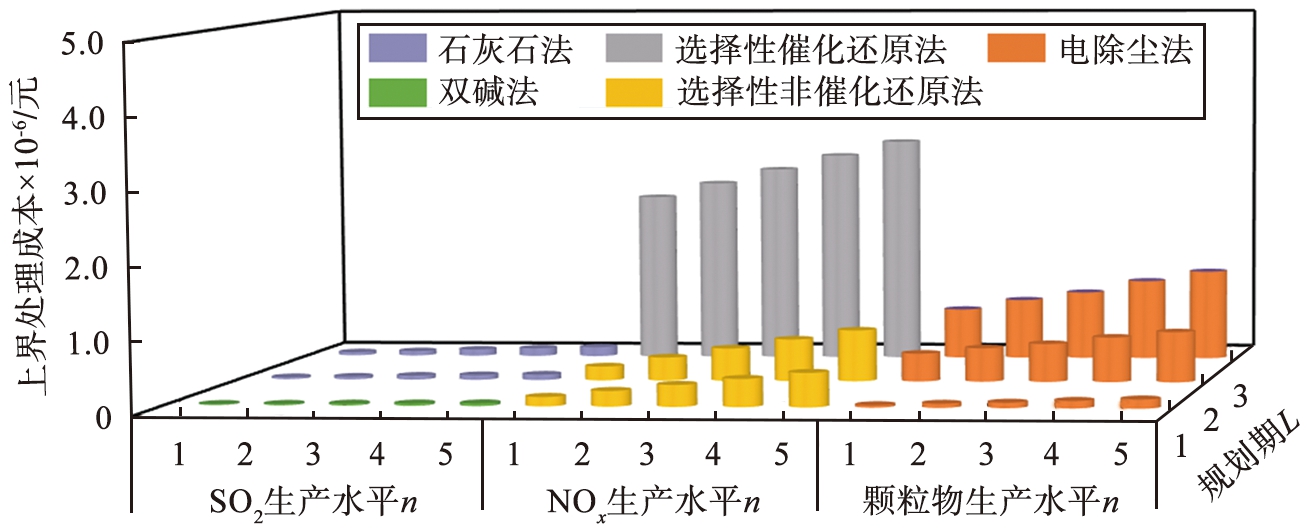
图6 3种超标污染物在不同规划期和污染物生产水平时的处理成本上界
Fig.6 Upper boundary processing cost of three kinds of excessive pollutants in different planning periods and pollutant production levels
由图5、 6可知,在3种污染物超标排放的情况下,污染物生产水平越高,处理成本越大,即区间两阶段随机规划计算出来的第2个阶段的成本越高。
3.3 析因分析
析因分析法可以揭示各参数的主效应与交互关系,并量化参数水平变化对系统性能的影响。本文中,系统包含7个主效应和8个两因子交互效应。经过FA-ITSP模型计算,在析因试验中,仅有水泥厂脱硝、除尘系统中存在明显主效应与交互效应。工艺效率、 行业标准、 环境标准是可能影响到模型输出的不确定性因素。水泥烟气中大部分SO2转化成硫酸盐被固定在水泥熟料中。经过脱硫治理后排放的SO2小于水泥行业排放标准,因此不确定性因素主要干扰着水泥厂烟气的脱硝、 除尘治理。
为了使不同因子的数据能够进行比较,需要将它们的效应进行标准化,成为标准化效应。标准化效应是统计量的一种,是将原始效应大小除以相应的标准差得到的结果,其大小能够度量因子的影响,效应越大则因子的影响越大。
3种污染物治理过程中因子的标准化效应和贡献率如表5所示。由表5可知,在水泥厂烟气脱硝过程中,标准化效应的绝对值和贡献率从高到低的因子依次为D、 C和CD、 F和DF、 CF,因此优先选用选择性非催化还原法;在烟气除尘过程中,标准化效应的绝对值和贡献率从高到低的因子依次为H、 G、 J、 HJ、 I、 GI、 GJ、 GH、 HI,因此优先选用电除尘法。
表5 脱硝及除尘治理过程中因子的标准化效应和贡献率
Tab.5 Standardization effects and contribution rates of factors in process of denitration and dust removal
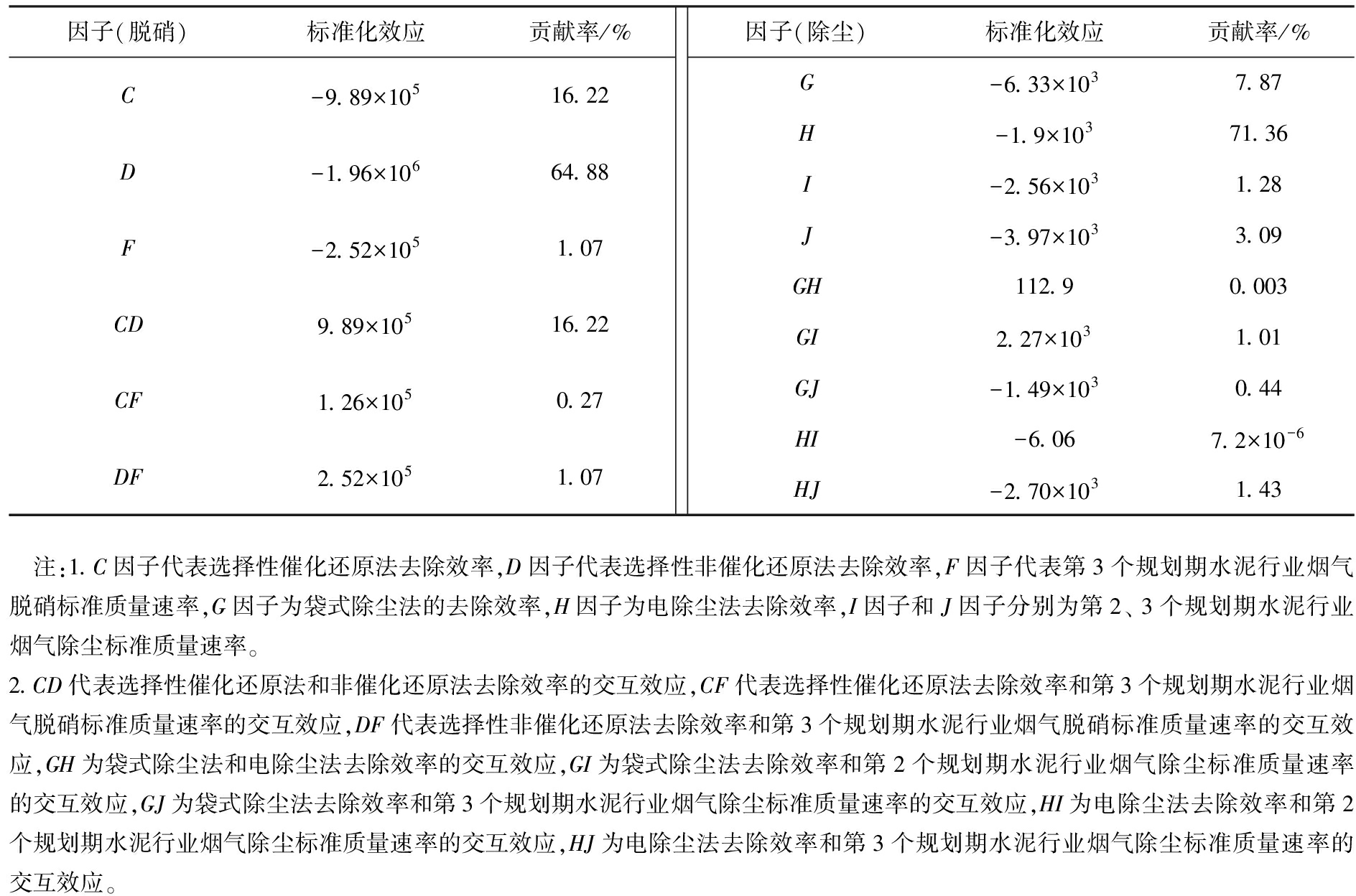
因子(脱硝)标准化效应贡献率/%C-9.89×10516.22D-1.96×10664.88F-2.52×1051.07CD9.89×10516.22CF1.26×1050.27DF2.52×1051.07因子(除尘)标准化效应贡献率/%G-6.33×1037.87H-1.9×10371.36I-2.56×1031.28J-3.97×1033.09GH112.90.003GI2.27×1031.01GJ-1.49×1030.44HI-6.067.2×10-6HJ-2.70×1031.43 注:1.C因子代表选择性催化还原法去除效率,D因子代表选择性非催化还原法去除效率,F因子代表第3个规划期水泥行业烟气脱硝标准质量速率,G因子为袋式除尘法的去除效率,H因子为电除尘法去除效率,I因子和J因子分别为第2、 3个规划期水泥行业烟气除尘标准质量速率。2.CD代表选择性催化还原法和非催化还原法去除效率的交互效应,CF代表选择性催化还原法去除效率和第3个规划期水泥行业烟气脱硝标准质量速率的交互效应,DF代表选择性非催化还原法去除效率和第3个规划期水泥行业烟气脱硝标准质量速率的交互效应,GH为袋式除尘法和电除尘法去除效率的交互效应,GI为袋式除尘法去除效率和第2个规划期水泥行业烟气除尘标准质量速率的交互效应,GJ为袋式除尘法去除效率和第3个规划期水泥行业烟气除尘标准质量速率的交互效应,HI为电除尘法去除效率和第2个规划期水泥行业烟气除尘标准质量速率的交互效应,HJ为电除尘法去除效率和第3个规划期水泥行业烟气除尘标准质量速率的交互效应。
在烟气脱硝系统中,治理工艺的效率对工艺的贡献率占比高达97.32%,因此改良工艺使其在满足脱硝标准的情况下尽可能降低成本是实现成本最优化的重要途径。此外,不同规划区不同功能区的环境空气质量也存在着一定的贡献率,因此除了除尘工艺与行业标准,还不应该忽视环境空气质量标准中关于颗粒物的限制。
烟气脱硝的不确定性因子的半正态效应与标准化效应的关系如图7所示。由图7可见,随着标准化效应的增大,半正态效应也逐渐增大;半正态效应从大到小的因子依次为D、 CD、 C、 DF、 F,因子D(选择性非催化还原法)的效应最显著,这是因为选择性非催化还原法成本较低,在第1、 2个规划期内水泥厂选择其作为烟气脱硝的唯一工艺;因子CD(选择性催化还原法和选择性非催化还原法去除效率的交互效应)与C(选择性催化还原法去除效率)对系统的影响也比较明显;由于第3个规划期的环境要求提高,需要加大污染治理力度以满足环保需求,因此选用选择性催化还原法和选择性非催化还原法协同治理;因子C不仅对模型输出有影响,还参与了CD交互作用;综上,在脱硝工艺中,第1、 2个规划期选用选择性非催化还原法,第3个规划期选用选择性非催化还原法和选择性催化还原法。
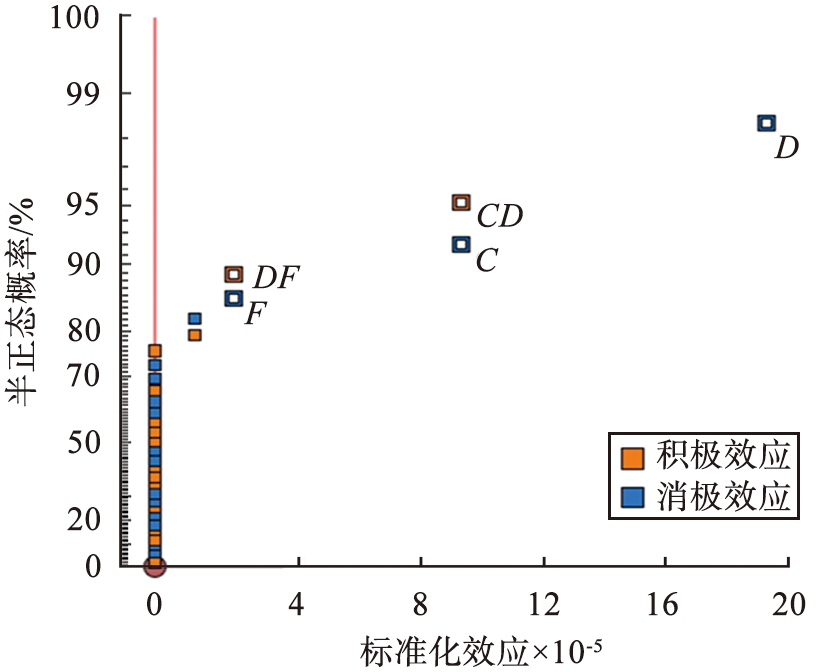
C—选择性催化还原法去除效率; D—选择性非催化还原法去除效率; F—第3个规划期水泥行业烟气脱硝标准质量速率;CD—选择性催化还原法和非催化还原法去除效率的交互效应; DF—选择性非催化还原法去除效率和第3个规划期水泥行业烟气脱硝标准质量速率的交互效应。
图7 烟气脱硝因子的半正态概率与标准化效应的关系
Fig.7 Relationship between semi-normal probability and standardization effects of flue gas denitrification factors
烟气除尘的不确定性因子的半正态效应与标准化效应的关系如图8所示。 由图8可见, 随着标准化效应的增大, 半正态效应也逐渐增大; 半正态效应从大到小的因子依次为H、 G、 J、 HJ、 I、 GI、 GH, 因子H(电除尘法去除效率)的效应最显著, 这是因为在污染物未超标时, 第1、 2、 3个规划时使用了电除尘法; 电除尘法的使用时间最长, 处理量最大, 因此因子H的效应最显著; 因子G(袋式除尘法去除效率)与J(第3个规划期水泥厂行业烟气除尘标准质量速率)对系统的影响也比较明显; 由于后期的环境要求提高, 需要加大污染治理力度以满足环保需求, 因此水泥厂在第2、 3个规划期引入了袋式除尘法与电除尘法共同应对更多的颗粒物和更加严格的环境质量标准; 因子H不仅对模型输出有影响, 还参与了HJ交互作用; 综上, 在除尘工艺中, 第1个规划期选用电除尘法,第2、 3个规划期选用电除尘法和袋式除尘法。
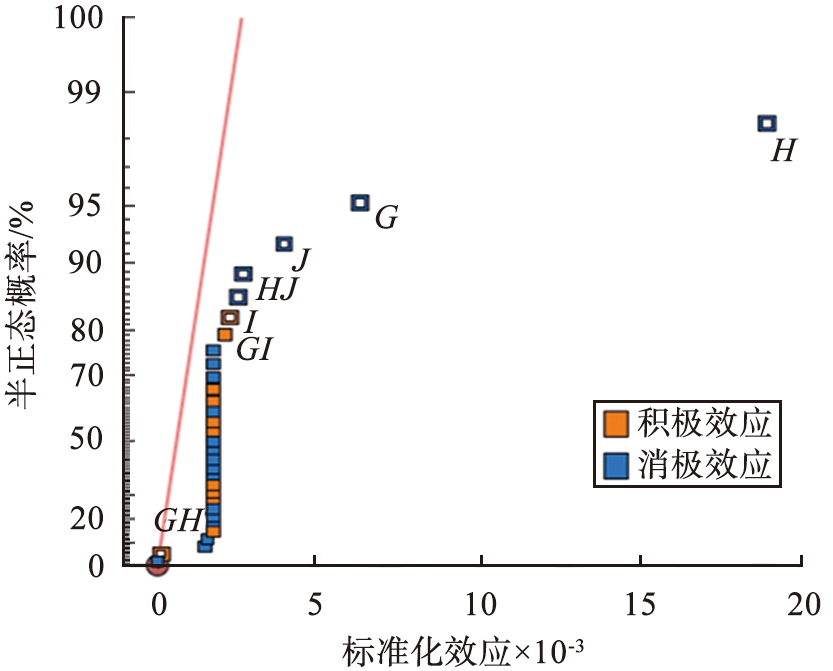
G—袋式除尘法的去除效率; H—电除尘法去除效率; I、 J—第2、 3个规划期水泥行业烟气除尘标准质量速率;GH—袋式除尘法和电除尘法去除效率的交互效应; GI—袋式除尘法去除效率和第2个规划期水泥行业烟气除尘标准质量速率的交互效应; HJ—电除尘法去除效率和第3个规划期水泥行业烟气除尘标准质量速率的交互效应。
图8 烟气除尘因子的半正态概率与标准化效应的关系
Fig.8 Relationship between semi-normal probability and standardization effects of flue gas dust removal factors
由图7、 8可知,低效率、 低成本类工艺依旧对模型输出影响最大,均为负效应,即去除效率越高,污染物处理成本越低;其他对系统影响较大的因子主要为行业排放标准、 治理工艺与行业标准的交互效应。在FA-ITSP模型中,前期环境约束宽松时,低效率类烟气治理工艺能满足排放要求,低成本的优势被放大,这些工艺成为首选工艺;到规划末期,增加的生产压力和严格的环境要求迫使工业区安装更高效率的工艺;工艺组合交互效应也对模型有着不小的贡献率,因此第2、 3个规划期会出现2种工艺协同治理,共同实现区域环境工业大气污染控制管理成本最小化。
水泥厂烟气脱硝包括选择性非催化还原法分别与选择性催化还原法、 水泥行业脱硝标准的交互效应, 表6为水泥厂脱硝系统不确定性因子的交互效应。 由表6可知, 选择性催化还原法去除效率80%和选择性非催化还原法去除效率75%时处理成本为25.97×106元; 选择性非催化还原法去除效率0.75、 第3个规划期水泥行业烟气脱硝标准质量速率5.6×106 mg/h时有利于实现处理成本最低, 因此选择性催化还原法效率应为80%, 选择性非催化还原法效率应为75%。
表6 水泥厂不同脱硝因子效应交互的成本
Tab.6 Interaction costs of different denitration factor effects in cement plant
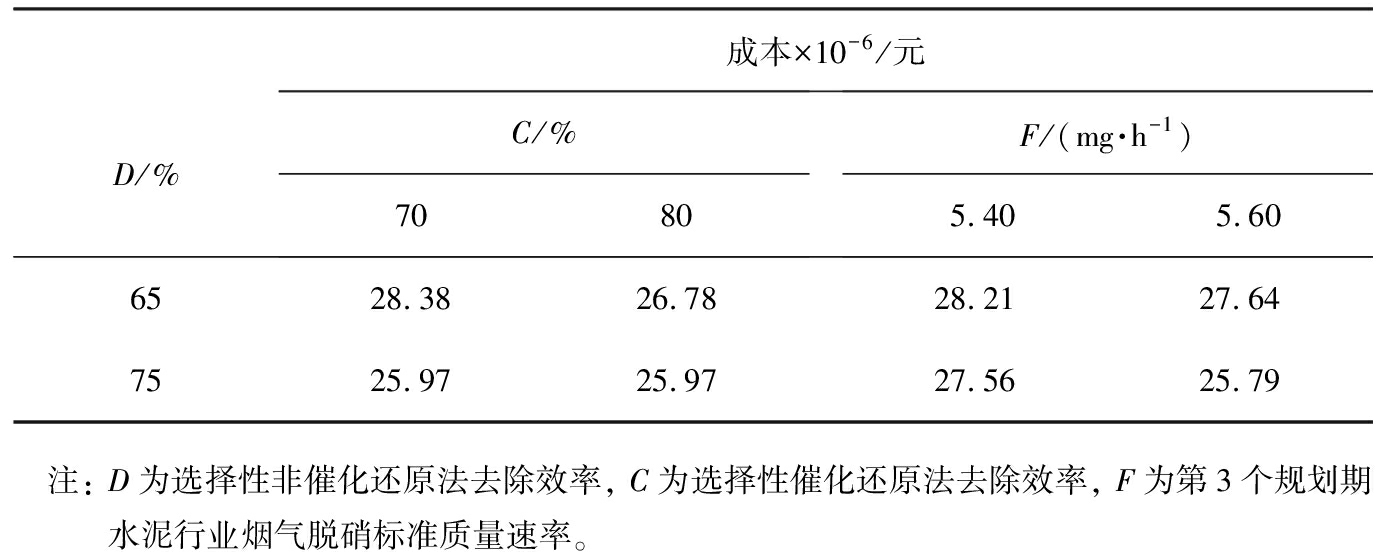
D/%成本×10-6/元C/%7080F/(mg·h-1)5.405.606528.3826.7828.2127.647525.9725.9727.5625.79 注: D为选择性非催化还原法去除效率, C为选择性催化还原法去除效率, F为第3个规划期水泥行业烟气脱硝标准质量速率。
水泥厂烟气除尘系统不确定性因子的交互效应如表7所示。水泥厂烟气除尘过程包括袋式除尘法、电除尘法分别与水泥行业除尘标准限制的交互效应。由表7可知,第2个规划期水泥行业颗粒物排放标准在袋式除尘法去除效率99.9%高水平下影响不大,但在袋式除尘法去除效率99.8%水平下存在较大负影响;第3个规划期水泥行业颗粒物排放标准在电除尘法去除效率99%低水平下对成本影响不大,但在电除尘法去除效率99.5%水平下存在较大负影响。因此,袋式除尘法效率应为99.9%,电除尘法效率应为99.5%。治理工艺与行业排放标准达到高水平时,有利于整个系统的成本最小化。
表7 水泥厂在不同除尘因子效应交互下的成本
Tab.7 Costs of cement plant under interaction of different dust removal factors
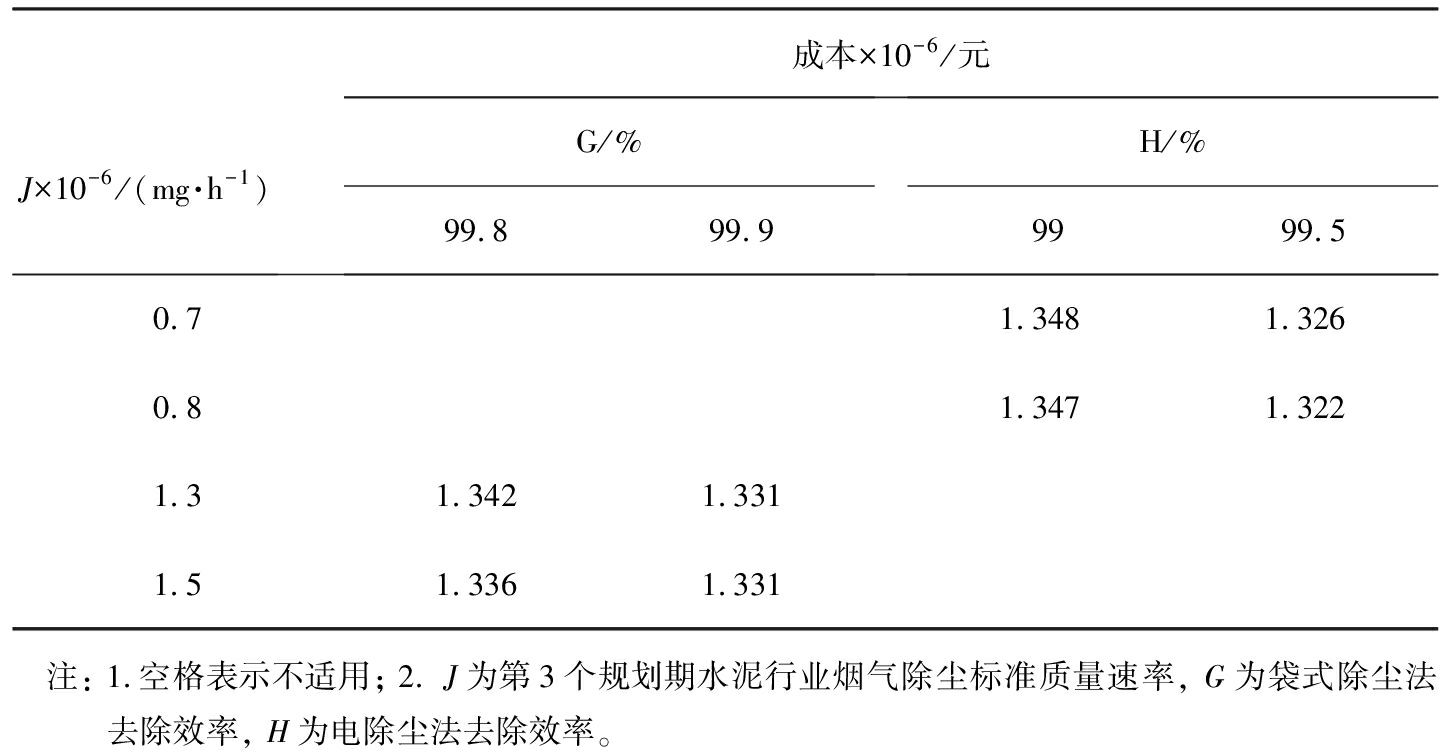
J×10-6/(mg·h-1)成本×10-6/元G/%99.899.9H/%9999.50.71.3481.3260.81.3471.3221.31.3421.3311.51.3361.331 注: 1.空格表示不适用; 2. J为第3个规划期水泥行业烟气除尘标准质量速率, G为袋式除尘法去除效率, H为电除尘法去除效率。
4 结论
本文中基于FA-ITSP研究安康市区域环境中的工业大气的污染控制和管理,建立以工业大气环境质量达标和处理成本最小化为目标的数学模型,依据水泥厂的环境治理数据、 行业排放标准以及环境空气质量标准,针对去除工业大气中的主要污染物SO2、 NOx和颗粒物的烟气治理过程,进行治理工艺组合优选、 处理成本分析和数学模型析因分析。主要结论如下:
1)去除SO2时,在3个规划期内都采用双碱法;去除NOx时,在第1、 2个规划期采用选择性非催化还原法,在第3个规划期采用选择性非催化还原法和选择性催化还原法;去除颗粒物时,在第1个规划期采用电除尘法,在第2、 3个规划期采用电除尘法和袋式除尘法;
2)数学模型最优决策条件下区域环境工业大气污染物管理处理成本为(30.42~34.05)×106元, 成本下限对应的污染物产量较低, 但存在更高的越界风险, 成本上限会产生较高处理成本, 但降低了越界风险, 提高了系统的可靠性。
3)由析因分析法可知,应该重点关注水泥厂脱硝和除尘系统,控制好这2类系统中的不确定性是实现处理成本最优的有效途径。不确定性参数对系统输出的影响从高到低依次是低效率类治理工艺(贡献率为64.88%~71.36%),高效率类治理工艺(贡献率为7.87%~16.22%),高、 低效率治理工艺组合的交互效应(贡献率为0.003%~16.22%)、 行业排放标准(贡献率为1.07%~3.09%)、 治理工艺与行业排放标准的交互效应(贡献率为7.2×10-6%~1.43%)。
针对区域环境工业大气污染控制管理建立的FA-ITSP方法不仅表征了区间、随机的不确定性,还揭示了不确定性参数对系统输出的贡献率和交互效应,后续研究有必要引入模糊不确定性,进一步提升数学模型的鲁棒性。
[1]XU W, SUN J, LIU Y, et al. Spatiotemporal variation and socioeconomic drivers of air pollution in China during 2005-2016[J]. Journal of Environmental Management, 2019, 245: 66-75.
[2]中华人民共和国生态环境部. 2021年中国生态环境统计年报[EB/OL]. (2023-01-18)[2023-08-25]. https://www.mee.gov.cn/hjzl/sthjzk/sthjtjnb/202301/W020230118392178258531.pdf.
Ministry of Ecology and Environment, People’s Republic of China. Annual report of China ecological and environmental statistics 2021[EB/OL]. (2023-01-18) [2023-08-25]. https://www.mee.gov.cn/hjzl/sthjzk/sthjtjnb/202301/W020230118392178258531.pdf.
[3]唐湘博, 陈晓红. 我国区域空气质量精准管理最优决策方法研究[J]. 系统工程理论与实践, 2021, 41(12): 3199-3211.
TAND X B, CHEN X H. Research on the optimal decision method for precise management of regional air quality in China[J]. Systems Engineering: Theory and Practice, 2021, 41(12): 3199-3211.
[4]ZHU Y, YAN X X, CHEN C, et al. Analysis of industry-air quality control in ecologically fragile coal-dependent cities by an uncertain Gaussian diffusion-Hurwicz criterion model[J]. Energy Policy, 2019, 132: 1191-1205.
[5]ZHU Y, WEI Z, LI Y X, et al. Energy and atmosphere system planning of coal-dependent cities based on an interval minimax-regret coupled joint-probabilistic cost-benefit approach[J]. Energy, 2021, 239: 122154.
[6]LI Y P, HUANG G H, VEAWAB A, et al. Two-stage fuzzy-stochastic robust programming: a hybrid model for regional air quality management[J]. Journal of the Air and Waste Management Association, 2006, 56(8): 1070-1082.
[7]HUANG G H, LOUCKS D P. An inexact two-stage stochastic programming model for water resources management under uncertainty[J]. Civil Engineering and Environmental Systems, 2000, 17(2): 95-118.
[8]CHEN W T, LI Y P, HUANG G H, et al. A two-stage inexact-stochastic programming model for planning carbon dioxide emission trading under uncertainty[J]. Applied Energy, 2010, 87(3): 1033-1047.
[9]GUO S S, ZHANG F, ZHANG C L, et al. An improved intuitionistic fuzzy interval two-stage stochastic programming for resources planning management integrating recourse penalty from resources scarcity and surplus[J]. Journal of Cleaner Production, 2019, 234: 185-199.
[10]JIN S W, LI Y P, NIE S. An integrated bi-level optimization model for air quality management of Beijing’s energy system under uncertainty[J]. Journal of Hazardous Materials, 2018, 350: 27-37.
[11]KHOSROJERDI T, MOOSAVIRAD S H, ARIAFAR S, et al. Optimal allocation of water resources using a two-stage stochastic programming method with interval and fuzzy parameters[J]. Natural Resources Research, 2019, 28: 1107-1124.
[12]WANG P P, LI Y P, HUANG G H, et al. A multi-scenario factorial analysis and multi-regional input-output model for analyzing CO2 emission reduction path in Jing-Jin-Ji Region[J]. Journal of Cleaner Production, 2021, 2: 126782.
[13]WANG S, HUANG G H, VEAWAB A. A sequential factorial analysis approach to characterize the effects of uncertainties for supporting air quality management[J]. Atmospheric Environment, 2013, 67: 304-312.
[14]LIU H X, LI Y P, YU L. Urban Agglomeration (Guangzhou-Foshan-Zhaoqing) ecosystem management under uncertainty: a factorial fuzzy chance-constrained programming method[J]. Environmental Research, 2019, 173: 97-111.
[15]ZHANG X Y ,HUANG G H, XIE Y L, et al. A coupled non-deterministic optimization and mixed-level factorial analysis model for power generation expansion planning: a case study of Jing-Jin-Ji Metropolitan Region, China[J]. Applied Energy, 2022, 311: 118621.
[16]JAMES E, JUAN S M, JORGE E P, et al. Air quality modeling to inform pollution mitigation strategies in a Latin American Megacity[J]. Science of the Total Environment, 2021, 776: 145894.
[17]LV Y, HUANG G H , LI Y P, et al. A two-stage inexact joint-probabilistic programming method for air quality management under uncertainty[J]. Journal of Environmental Management, 2011, 92(3): 813-826.
[18]WANG S, HUANG G H. A coupled factorial-analysis-based interval programming approach and its application to air quality management[J]. Journal of the Air and Waste Management Association, 2013, 63(2): 179-189.
[19]WANG S, HUANG G H, ZHOU Y. A fractional-factorial probabilistic-possibilistic optimization framework for planning water resources management systems with multi-level parametric interactions[J]. Journal of Environmental Management, 2016 ,172: 97-106.
[20]洪巧巧. 燃煤电厂烟气脱硫脱硝除尘技术生命周期评价[D]. 杭州: 浙江大学, 2015: 71-76.
HONG Q Q. Life cycle evaluation of flue gas desulfurization, denitrification and dust removal technology in coal-fired power plants[D]. Hangzhou: Zhejiang University, 2015: 71-76.
[21]中国环境科学研究院, 合肥水泥研究设计院. 水泥工业大气污染物排放标准: GB 4915—2013[S]. 北京: 中国环境科学出版社, 2014.
Chinese Academy of Environmental Sciences,Hefei Cement Research and Design Institute. Emission standard of air pollutants for cement industry: GB 4915—2013[S].Beijing: China Environmental Science Press, 2014.
[22]中国环境科学研究院, 中国环境监测总站. 环境空气质量标准: GB 3095—2012[S].中国环境科学出版社, 2019.
Chinese Academy of Environmental Sciences, China Environmental Monitoring Station. Ambient air quality standards: GB 3095—2012[S]. Beijing: China Environmental Science Press,2019.
[23]LU H W, HUANG G H, LIU L, et al. An interval-parameter fuzzy-stochastic programming approach for air quality management under uncertainty[J]. Environmental Engineering Science, 2008, 25(6): 895-910.
[24]LV Y, HUANG G H, LI Y P, et al. Interval-based air quality index optimization model for regional environmental management under uncertainty[J]. Environmental Engineering Science, 2009, 26(11): 1585-1597.
[25]LI, Y P, HUANG, G H. An inexact two-stage mixed integer linear programming method for solid waste management in the city of Regina[J]. Journal of Environmental Management, 2005, 81(3): 188-209.