海泡石是一种含水硅酸镁非金属矿物,具有典型的纤维状和层链状结构[1]。工业上经过破碎后的海泡石矿粉的粒径范围通常为1~110 μm。颗粒分级是粉体制备过程中的重要工艺过程。海泡石矿粉产品的粒度分布决定着颗粒的应用价值和产品的性能,且不同粒径范围的颗粒具有不同的使用价值,所以要对破碎后的海泡石颗粒进行分级[2]。
颗粒分级主要分为离心式分级和重力式分级2种方式。为了提高分级器的性能,国内外学者对这2种分级器进行了广泛研究。在颗粒离心式分级方面, 国内外学者主要在离心式分级器的结构创新和参数优化等方面进行了相关研究。例如,使用方形分级器[3],调整进料或进风口位置[4-5],改变分级器入口数量[6], 优化圆柱与锥体的高度比[7], 优化入口形状、 布置方式和入口角度[8]等, 但当前研究中大部分离心式分级器只能获得2种粒径范围的颗粒,即细颗粒和粗颗粒,而工业上对颗粒要求为具有良好单分散性和不同的平均粒径[9],因此,能够获得多种粒径范围的颗粒分级器更加符合当前工业发展需求。
重力式分级器具有能够实现颗粒多粒径分级的研究潜力,近年来受到了更多的研究关注。当前研究中,国内外学者主要通过构建不同流场和改变分级器的结构等方法对重力式分级器展开研究。Wang等[10]和Lai等[11]通过构建横流流场,实现了细颗粒的分离;但由于颗粒收集装置位于分级器底部,因此横流流场速度不能过大,产量较低,且需要较大的分离空间。Banjac等[12]研究了颗粒在一种重力逆流式分级器流场中的受力对分级效率的影响。研究表明,流体曳力对较细颗粒的分级有较大影响,但是这类分级器横向尺寸小,通常难以获得多种颗粒产品。周友行等[13]基于射流效应和康达效应研制了一种射流分级装置。分析了在射流分级过程中,海泡石颗粒的粒径越小,附壁效应作用越明显,该分级装置可以筛选出细粉产品。Johansson等[14]研制了一种可获得多种粒径范围颗粒的重力逆流式耦合分级器,但该分级器结构复杂,实际操作难度较大,实用性不强。重力式分级器虽然适合解决多粒径分级问题;但当前的重力式分级器难以兼顾分级效果和结构复杂程度等方面的问题,因此,一种结构简单的重力式多粒径颗粒分级器具有一定的应用价值。
本文中通过构建重力横流域和顺流域相叠加的分级流场,在分级器的2侧设置多个出口,不同粒径颗粒随气流从不同出口流出,有效地实现细颗粒与粗颗粒的分离,从而获得多种粒径分布的海泡石颗粒产品,并分析各出口处的颗粒粒径分布来判断分级效果。重力分级方法可为重力式分级器的设计提供借鉴。
1 计算模型和分级原理
1.1 湍流模型
空气被假设为连续且不可压缩湍流,使用欧拉方法描述流体相。湍流模型选用雷诺应力模型(Reynolds stress model,RSM),该模型考虑了湍流的各向异性,相比标准k-ε模型,计算结果更加精确、 可靠。流体区域计算基于质量和动量守恒方程,流体控制方程表达式如下:
(1)
(2)
式中:![]() 为流体速度;
为流体速度;![]() 为流体压力; ρ为流体密度; μ为流体动力黏度;
为流体压力; ρ为流体密度; μ为流体动力黏度;![]() 为雷诺应力张量; t为时间; xj为空间坐标。
为雷诺应力张量; t为时间; xj为空间坐标。
RSM模型雷诺应力输运方程如下:
(3)
式中: Dij为湍流扩散项; Pij为剪应力产生相; Πij为压力应变相; εij黏性耗散项。
1.2 离散相模型
本研究中所使用离散相体积分数远小于10%,故采用离散相模型(discrete phase model,DPM)模型追踪颗粒轨迹,欧拉-拉格朗日方法用来描述流体与颗粒运动。不考虑颗粒运动对流体产生的影响,将颗粒形状视为球形并忽略颗粒间碰撞,得到颗粒的动力学平衡方程如下:
(4)
式中: vf、 vp分别为流体和颗粒的速度; FD(vf-vp)为流场作用在单位质量颗粒上的曳力; g为重力加速度; ρp、 ρ分别为颗粒和流体的密度; Fx为其他力,其他力Fx包括浮力、 压力梯度力、 附加质量力、 萨夫曼升力、 热泳力等[15]。
海泡石颗粒的分级主要是依靠不同粒径颗粒产生不同运动轨迹实现, 属于物理过程, 不涉及温度变化和其他化学反应, 故忽略热泳力。 在气体流场中,浮力和萨夫曼升力会对亚微米级颗粒产生影响, 而其他力对海泡石颗粒运动的影响可以忽略不计, 因此, 本研究中仅考虑重力、 曳力、 浮力和萨夫曼升力。
1.3 重力分级装置与原理
重力分级装置结构示意图如图1所示。 重力分级装置主要由进料装置、 重力分级室和粉体颗粒收集装置等结构部件构成。 加速气流、 分级气流由高压鼓风机产生, 高压鼓风机与分级器通过转换接口连接, 再通过变频器控制高压鼓风机来调节管内流量至设定值, 以保证分级气流均匀稳定。 球阀用于调节流量, 气体流量传感器用于显示管内流量以控制管内气流平均速度, 保证颗粒入口处的速度是均一的。
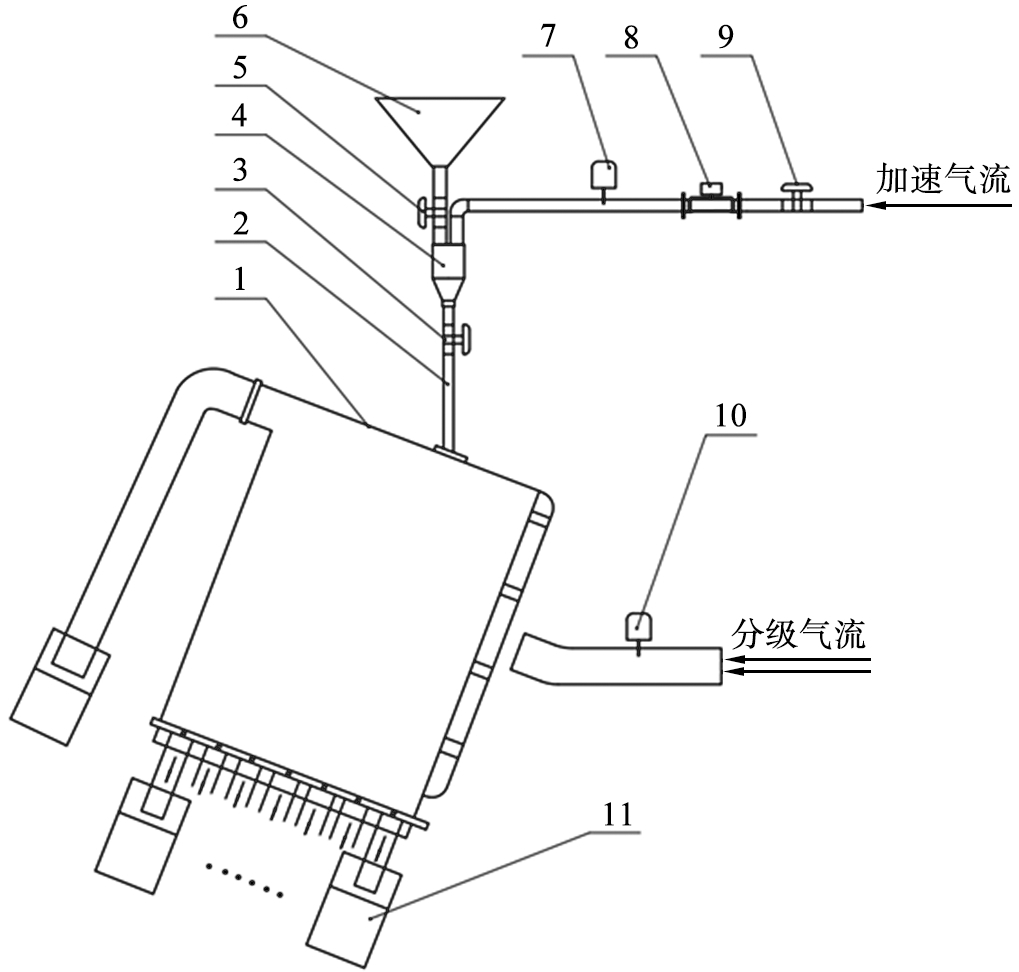
1—重力分级室; 2—直圆管; 3—球阀Ⅰ; 4—气固混合器; 5—球阀Ⅱ; 6—颗粒进料斗; 7—气体流量传感器; 8—压力调节阀; 9—球阀Ⅲ; 10—气体流量传感器; 11—粉体收集袋。
图1 重力分级装置结构示意图
Fig.1 Schematic diagram of structure of gravity classification device
多级粉体重力分级器的分级原理如图2所示。颗粒在加速气流的作用下以气-固两相流形式从直圆管中射入分级器分级流场中,分级流场与水平成一定夹角向上布置,形成了顺流域与横流域相叠加的分级流场,不同粒径颗粒在曳力、 重力和浮力的作用下,产生不同的运动轨迹,随气流进入不同的出口,从而获得不同粒径分布的颗粒产品。
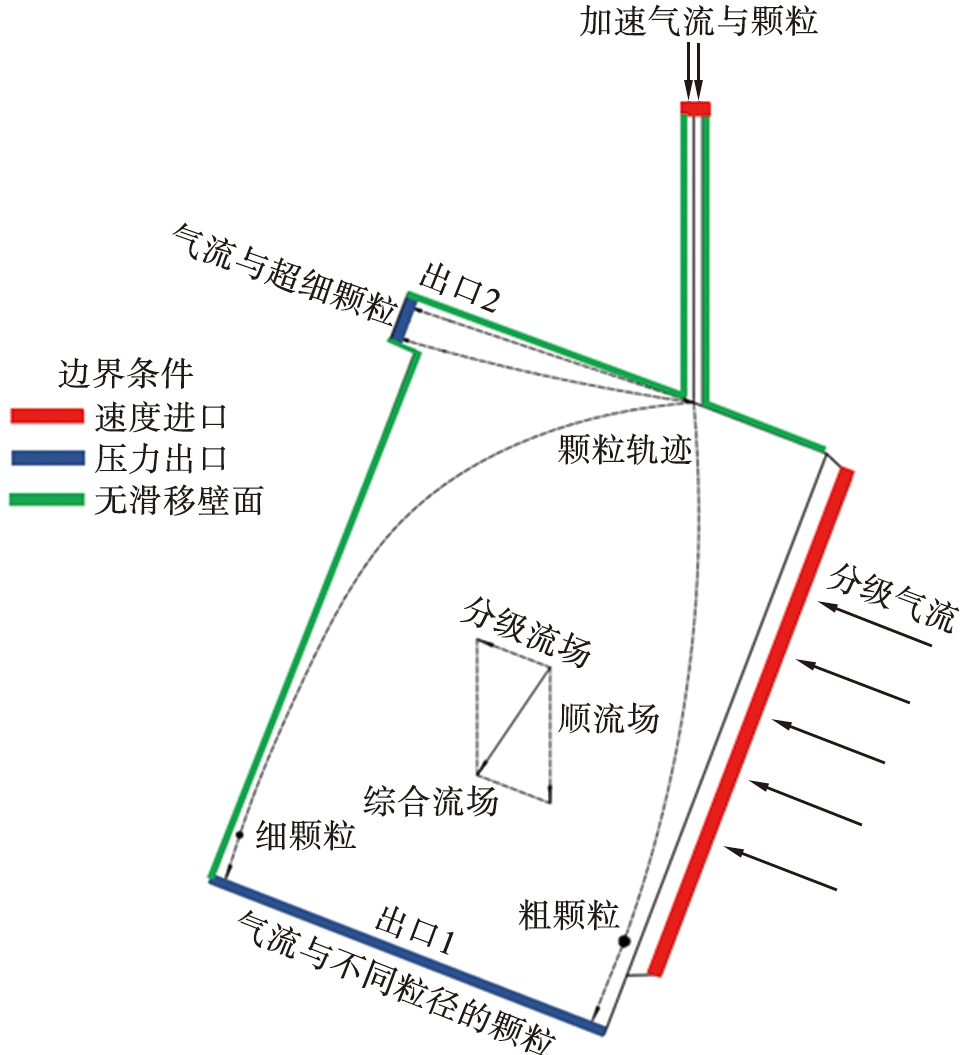
图2 分级原理与分级参数
Fig.2 Geometric model of bend
分级流场由分级流域和顺流域叠加构成,使得不同粒径颗粒附有不同动能,形成不同运动轨迹,实现颗粒分级。超细颗粒主要受分级流场的作用,在气流曳力的主导下随气流从分级器左上侧出口2流出,其余颗粒受综合流场作用由小到大、 从左到右在分级器下侧出口1流出。
2 数值模拟条件
2.1 几何结构
本次数值模拟主要是计算分析分级器内部的流场分布,计算流体力学(computational fluid dynamics,CFD)模拟所涉及的几何结构如图3所示。分级器的具体结构参数见表1。
表1 重力分级器的结构参数
Tab.1 Structural parameters of gravity classifier
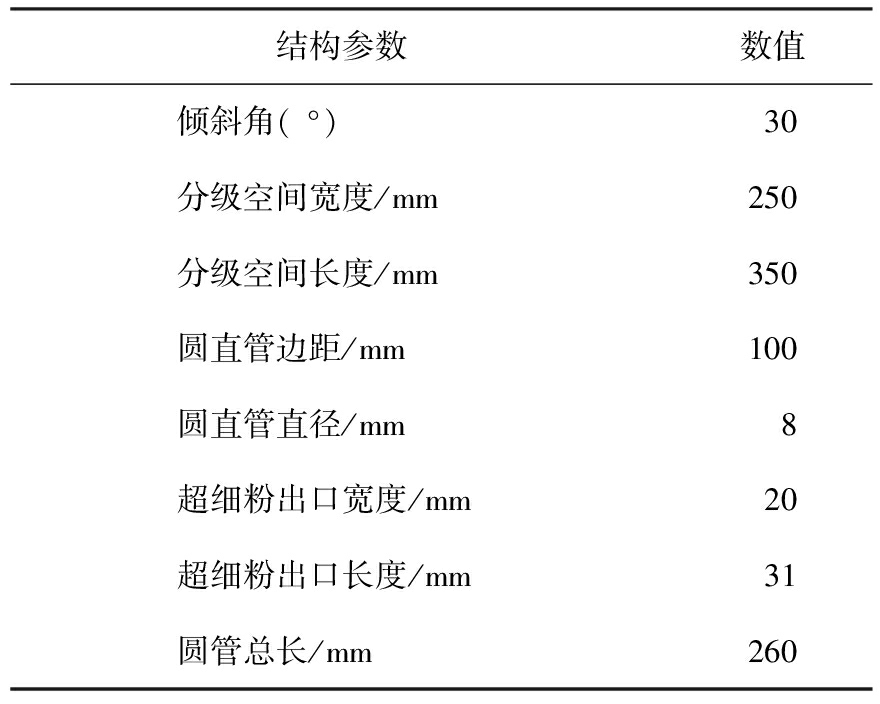
结构参数数值倾斜角( °)30分级空间宽度/mm250分级空间长度/mm350圆直管边距/mm100圆直管直径/mm8超细粉出口宽度/mm20超细粉出口长度/mm31圆管总长/mm260
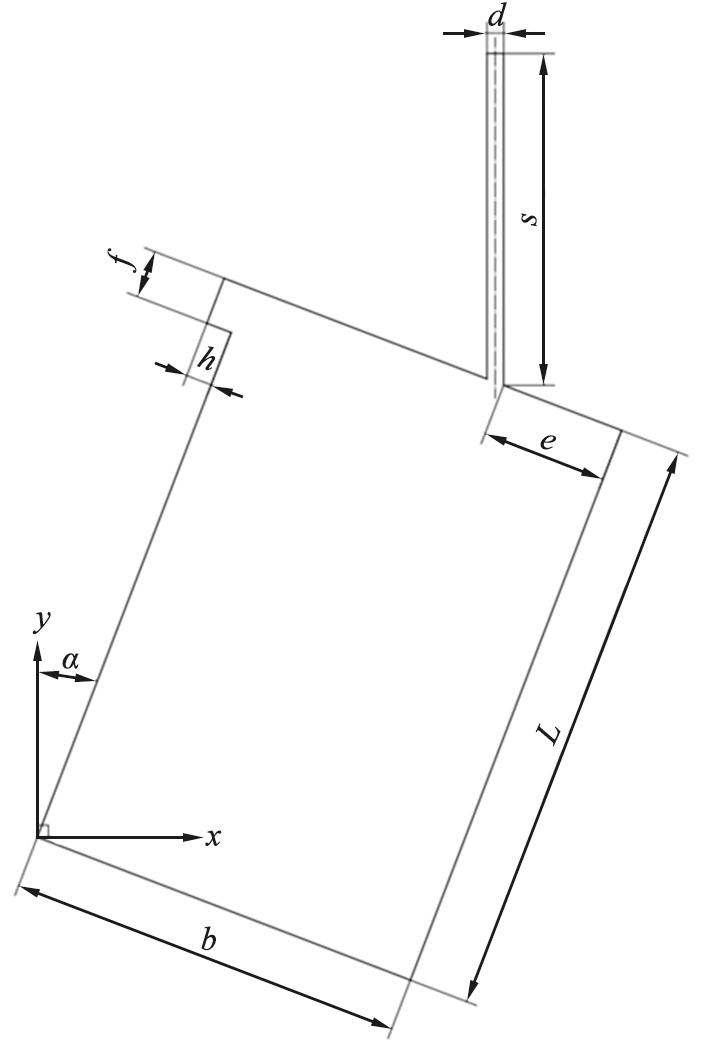
α—倾斜角; b—分级空间宽度; L—分级空间长度; e—圆直管边距; d—圆直管直径;h—超细粉出口宽度; f—超细粉出口长度; s—圆管总长。
图3 分级器几何结构
Fig.3 Geometric structure

图4 网格划分
Fig.4 Mesh division
2.2 网格划分与无关性验证
本文中开展的是三维仿真,使用前处理软件Workbench Meshing对分级流域采用四面体结构化网格进行离散化。为了在尽量少的网格下准确地计算出分级器的分级流场,在分级流域出口1和出口2设置检测点,采集2个出口处的平均速度和气体流量值,进行网格无关性验证。采用5种网格方案(A—E)进行检验,网格方案的网格数量分别为10万、 15万、 23万、 35万和50万。网格无关性检验数据如表2和表3所示。
表2 网格无关性检验(出口1)
Tab.2 Mesh independence test(outlet 1)
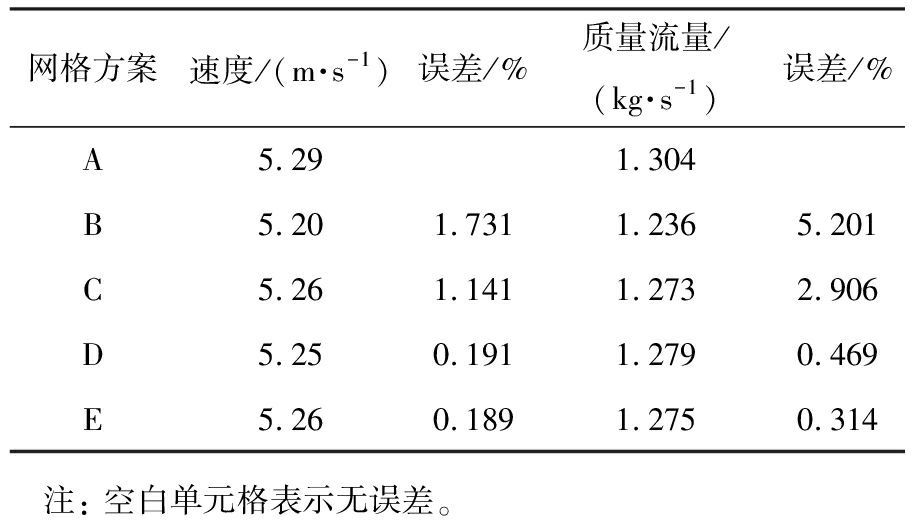
网格方案速度/(m·s-1)误差/%质量流量/(kg·s-1)误差/%A5.291.304B5.201.7311.2365.201C5.261.1411.2732.906D5.250.1911.2790.469E5.260.1891.2750.314 注: 空白单元格表示无误差。
表3 网格无关性检验(出口2)
Tab.3 Mesh independence test(outlet 2)
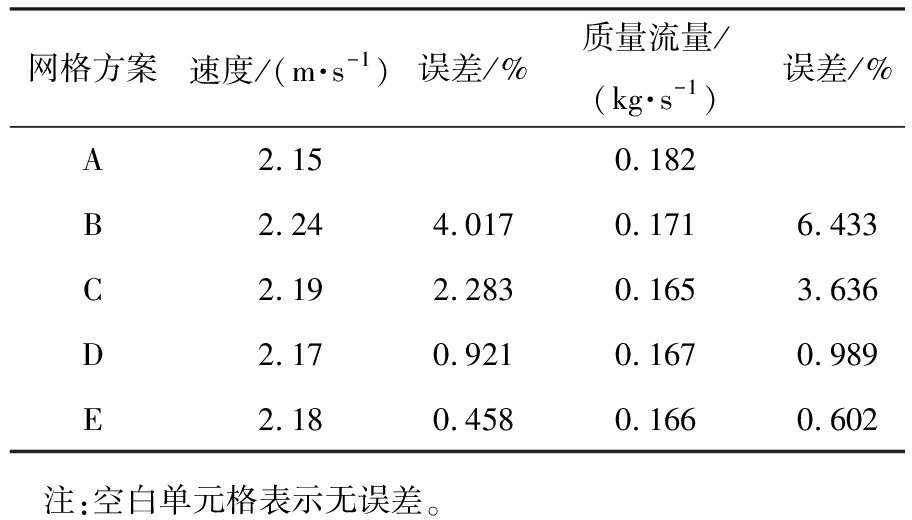
网格方案速度/(m·s-1)误差/%质量流量/(kg·s-1)误差/%A2.150.182B2.244.0170.1716.433C2.192.2830.1653.636D2.170.9210.1670.989E2.180.4580.1660.602 注:空白单元格表示无误差。
由表2、 3的数据可知,当网格数量大于35万时,网格方案D和网格方案E的模型模拟结果的计算偏差小于1%,网格数量对出口平均速度和流量的影响可以忽略不计,故最终采用方案D的网格划分模型进行数值模拟。
2.3 模拟材料参数
为模拟真实状态下不同粒径的颗粒分级状况,模拟中所使用的离散相材料为海泡石颗粒,流体为空气。海泡石矿粉样品(湖南源远海泡石有限公司);KW-510型激光粒度仪(厦门科王电子有限公司)。实验测得粉体材料真实密度为2 481 kg/m3。海泡石矿粉的物理参数如表4所示。粒度分析结果如图5所示。
表4 材料属性
Tab.4 Material properties

物理参数数值流体密度/(kg·m-3)1.225流体动力黏度/ [kg·(m·s)-1]1.789物理参数数值流体运动黏度/(Pa·s)0.759颗粒密度/(kg·m-3)2 481
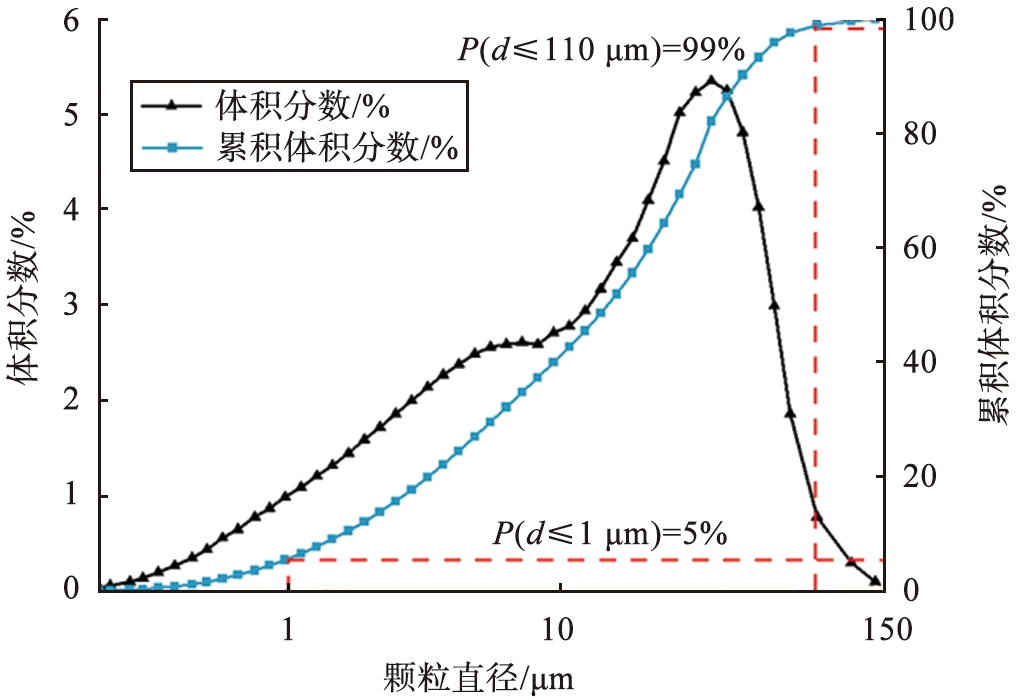
图5 颗粒粒径分布
Fig.5 Particle size distribution of sepiolite powder
本次模拟中共选用8组单分散颗粒,用于研究不同粒径颗粒的运动特性。模拟所用颗粒由多种单一尺寸的颗粒组成,颗粒的粒径取值计算方法[16]如下:
(5)
式中: δmin为颗粒最小粒径; δmax为颗粒最大粒径; n为颗粒种数; i为颗粒序号; N*为非负整数集。
由图5可知,累积体积分数为5%以下对应的粒径小于1 μm,颗粒粒径110 μm以上的含量极少。本文中研究微米级的颗粒分级,粒径为1 μm以下的颗粒不在研究范围,即最小粒径和最大粒径分别取累积体积分数为5%和累积体积分数为99%所对应的海泡石颗粒粒径。
本研究中,取δmin=1 μm, δmax=110 μm, n=8,在该条件下,计算出的颗粒直径如表5所示。参考表5数据,模拟所取海泡石颗粒的粒径分别为1、 15、 30、 50、 65、 80、 95、 110 μm。
表5 颗粒直径
Tab.5 Particle diameter

序号12345678粒径/μm1.016.032.147.863.678.694.7110
2.4 仿真设置与分级参数定义
数值模拟求解采用软件ANSYS Fluent 2021R1。 通过DPM模型用于模拟颗粒运动和分级。 稳态气相流场计算完成后作为初始流场, 采用稳态(steady)方法追踪颗粒轨迹, 颗粒喷射方式为平面入射(face), 颗粒初速度大小设置为0。 研究颗粒运动时, 采取单变量法, 分别对8组不同粒径的单分散颗粒进行分级模拟, 最后进行综合分析。 研究颗粒分级效果时, 离散相颗粒尺寸分布根据试验物料测量, 粒径按Rosin-Rammler分布拟合, 最小粒径为1 μm, 最大粒径为110 μm, 平均粒径为58 μm, 分布指数为1.87, 在分级器的出口表面设置outlet-plane来记录和统计颗粒在此平面的位置和粒径分布。
模拟边界条件如图1所示,入口边界条件均设置为速度入口,出口边界设置为压力出口,分级器的固体壁面设置为无滑移边界条件。压力-速度耦合方程组采用半隐式方法求解(SIMPLE算法),控制方程对流项采用二阶迎风格式,设定当各个方程残差值小于10-4时收敛。
3 仿真结果及分析
3.1 颗粒运动轨迹
在重力分级的过程中,进入流场的气流速度是影响流场分布特性的一个重要因素,而流场的分布决定了海泡石颗粒的运动状态。为了研究不同粒径海泡石颗粒的运动轨迹,采取控制变量法,分别对粒径为1、 15、 30、 50、 65、 80、 95、 110 μm的海泡石颗粒进行颗粒分级仿真模拟。设定颗粒初速度为0、 分级器颗粒入口处的加速气流速度为15 m/s, 分级气流的速度为3 m/s, 出口处压强为1.01×105 Pa(即相对压强为0),不同粒径的海泡石颗粒的运动轨迹如图6所示。
颗粒在流场中的颗粒轨迹主要受到斯托克斯数的影响, 而斯托克斯数与颗粒的直径有关[17],斯托克斯数表征颗粒惯性作用和扩散作用的比值, 可定义为颗粒松弛时间与系统响应时间之比, 计算方法如下:
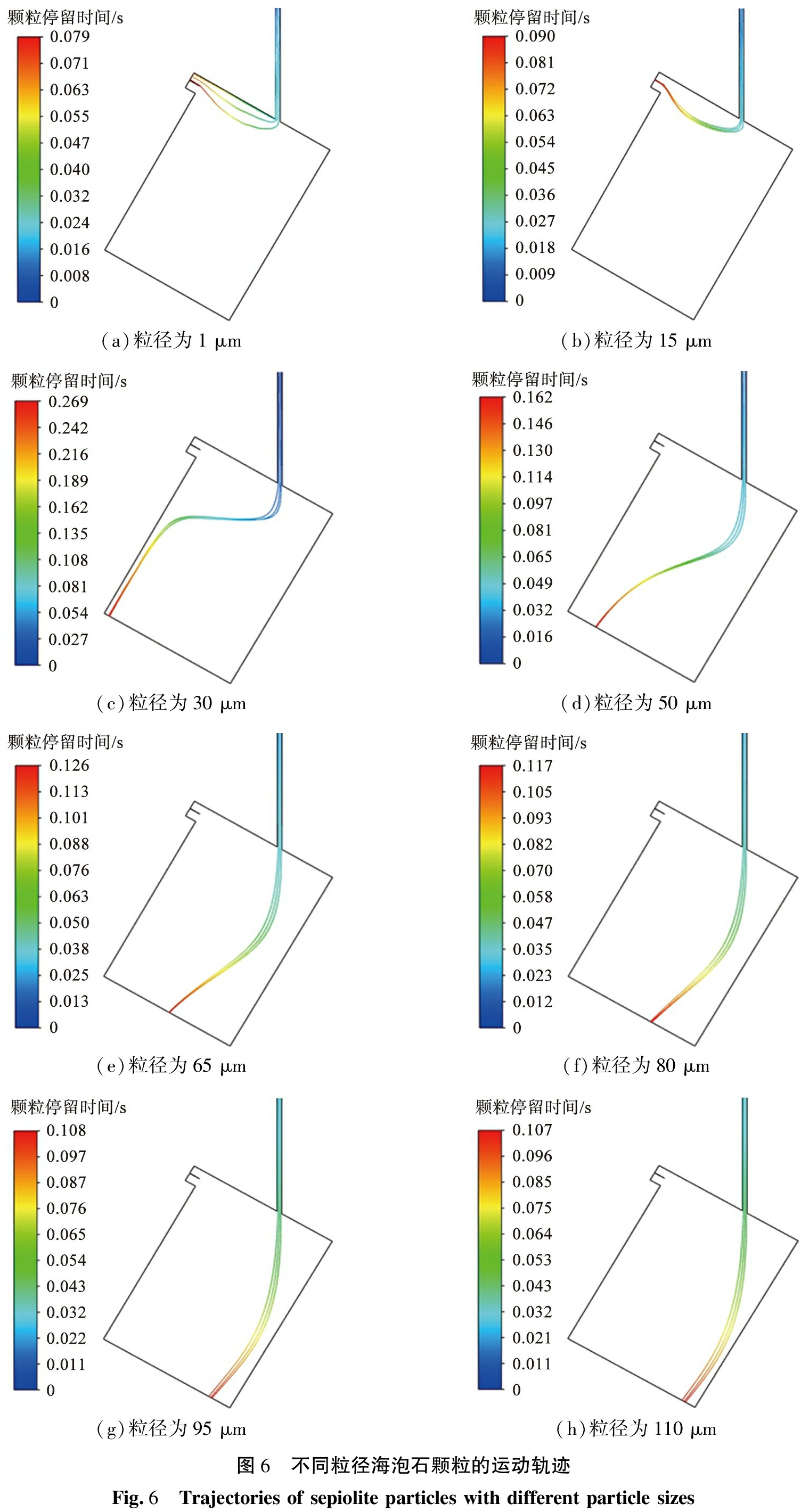
(a)粒径为1 μm(b)粒径为15 μm(c)粒径为30 μm(d)粒径为50 μm(e)粒径为65 μm(f)粒径为80 μm(g)粒径为95 μm(h)粒径为110 μm图6 不同粒径海泡石颗粒的运动轨迹Fig.6 Trajectories of sepiolite particles with different particle sizes
(6)
式中: CC为坎宁安系数; U0为流体平均流速; LC为特征长度; dp为颗粒直径。
图6所示为不同粒径海泡石颗粒的位置随时间的变化图。 由图可知, 不同粒径的海泡石颗粒在不同时刻水平和竖直方向的具体位置, 为划分海泡石颗粒重力分级器的分级区间提供数据参考。 从图6中可以看出, 不同粒径的海泡石颗粒具有不同的运动轨迹。 粒径为1、 15 μm的海泡石颗粒从左上侧的出口流出, 其余粒径的海泡石颗粒的出口位置随着粒径的增大距离颗粒入口处越近。 对于粒径为1、 15 μm的颗粒, 其斯托克斯数值小, 表明颗粒受流体曳力作用影响大, 颗粒缺乏从流体中分离的能力, 颗粒紧随流体运动, 使得细颗粒相比粗颗粒受分级气流的影响较大, 因此, 粒径为1、 15 μm的海泡石颗粒从左上侧出口流出。
随着颗粒粒径的增加,斯托克斯数值增大,颗粒的质量与惯性力增大,湍流扩散对颗粒的控制能力减弱,颗粒会更加倾向于沿原流线轨迹运动,最终导致粒径为30、 50、 65、 80、 95、 110 μm的海泡石颗粒在分级器下侧出口流出。由于粒径越大的颗粒受分级气流的影响越小,颗粒的水平运动距离也就越小,因此较细的颗粒的出口位置偏左,较粗的颗粒的出口位置偏右。表明该重力分级器既可以用来提取粒径为1~15 μm的海泡石超细颗粒,也可以对粒径为110 μm以内的海泡石颗粒进行简单分级。
3.2 颗粒位置
图7所示为不同粒径海泡石颗粒的位置随时间的变化。 从图7可以看出, 粒径为1、 15 μm的颗粒在水平方向的终点位置相等, 在竖直方向的终点位置不同, 因为这2种粒径的颗粒是在超细粉出口流出, 其水平方向的出口位置一样。 其余不同粒径的海泡石颗粒在水平方向的终点值随粒径的增大而增大。
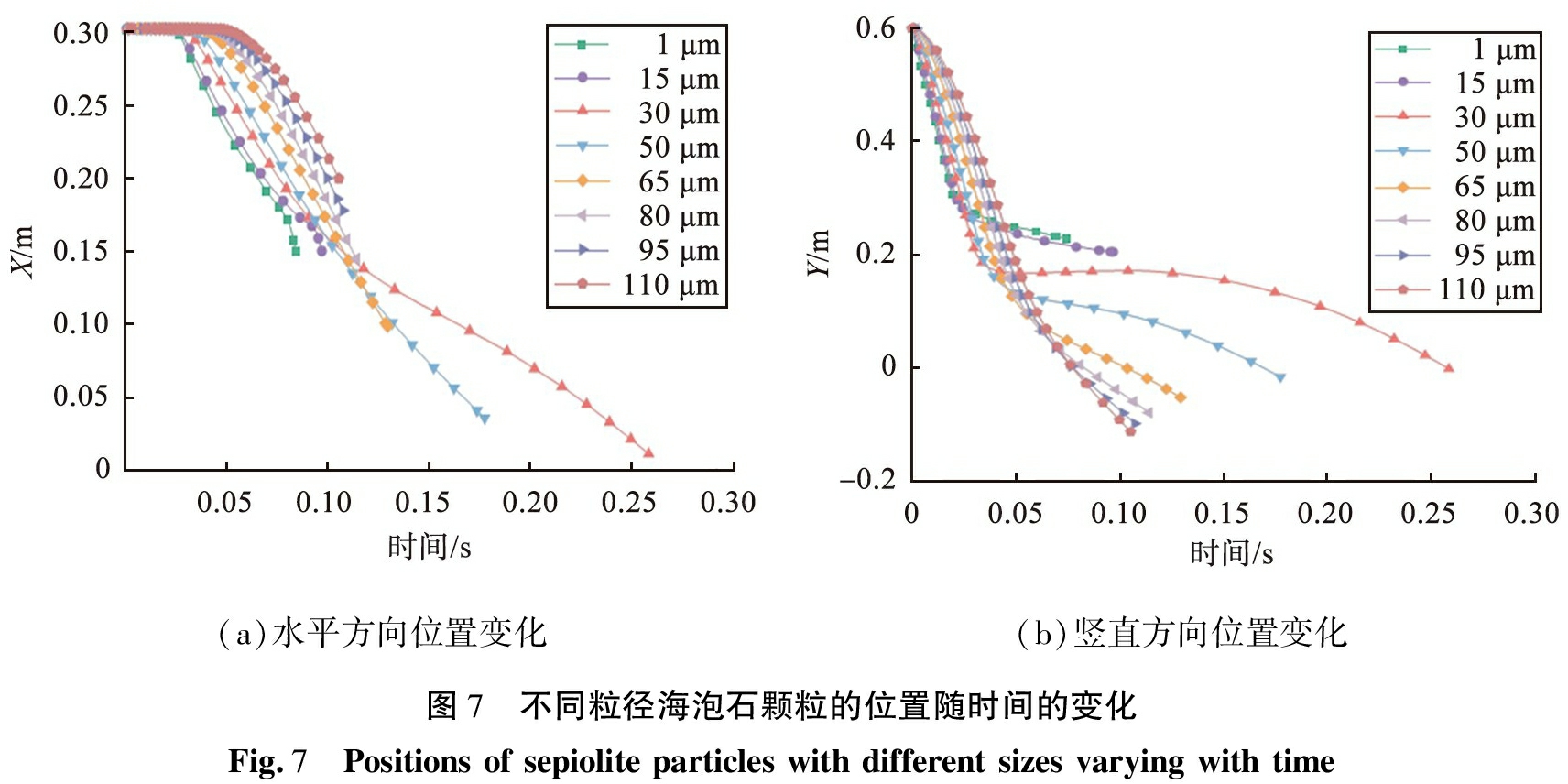
(a)水平方向位置变化(b)竖直方向位置变化图7 不同粒径海泡石颗粒的位置随时间的变化Fig.7 Positions of sepiolite particles with different sizes varying with time
3.3 颗粒分级区间
综上, 在颗粒初速度为0、 出口处压强为1.01×105 Pa( 即相对压强为 0)的前提下, 当分级器颗粒入口处的加速气流速度为15 m/s、 分级气流的速度为3 m/s时,粒径分别为1、 15、 30、 50、 65、 80、 95、 110 μm 的颗粒在水平方向上和竖直方向上的分级区间如表6所示。
表6 不同粒径海泡石颗粒在水平方向和竖直方向上的分级区间
Tab.6 Grading interval of seafoam particles with different particle sizes in horizontal and vertical directions

粒径/μm1153050658095110水平方向距离/m0.1550.1550.0110.0380.0980.1430.1760.200竖直方向距离/m0.3120.300-0.004-0.017-0.051-0.079-0.099-0.113
参考表6的数据,对分级区间进行划分,共分成7个分级区,分别为Ⅰ—Ⅶ,分级器各级出口对应的颗粒粒径范围如表7所示,分级区间对应的各级出口位置如图8所示。
表7 各级出口对应的颗粒粒径范围
Tab.7 Particle size range corresponding to each grade of outlet

出口编号ⅠⅡⅢⅣⅤⅥⅦ粒径范围/μm1~1515~3030~5050~6565~8080~9595~110
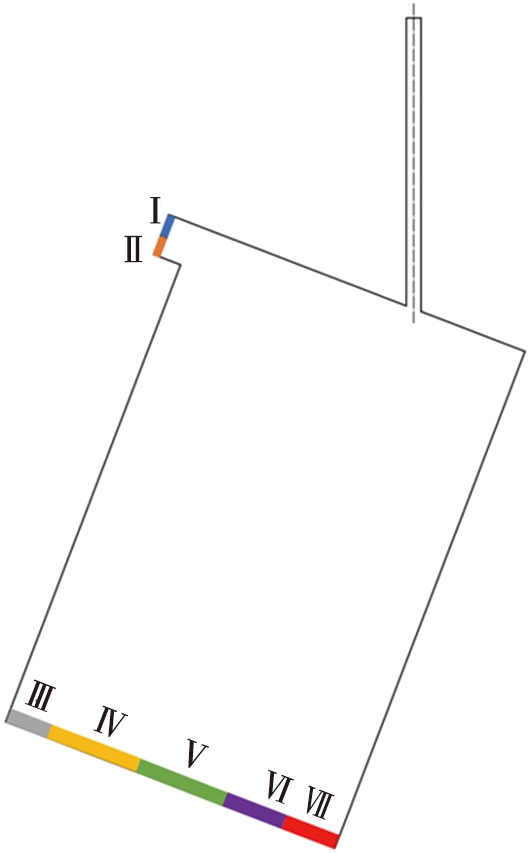
图8 各级粉体的出口位置
Fig.8 Exit position of all levels of powder
3.4 颗粒分级区间的颗粒粒径分布
为了探究划分后的分级区间的合理性, 对颗粒的分级效果进行研究。 对混合多粒径的海泡石颗粒进行仿真模拟, 根据试验物料测量值对粒径按Rosin-Rammler分布拟合, 最小粒径为1 μm, 最大粒径为110 μm, 平均粒径58 μm,分布指数设置为1.87,进行仿真模拟并收集各出口的颗粒数据,通过分析各出口的颗粒粒径分布来反应分级效果,各级出口的粒径分布如图9所示。从图中可知,分级器能获得多种不同粒径分布的颗粒。出口Ⅱ的粒径分布范围较广,且与出口Ⅰ的粒径分布范围重合较多。因为较细颗粒的分离时间较短,容易出现夹带现象,所以部分较粗的颗粒夹带着较细的颗粒从出口Ⅱ流出。随着粒径的增加,分离时间越长,夹带影响越小,所以出口Ⅲ、 Ⅳ、 Ⅴ的粒径分布范围情况较好。出口Ⅵ与出口Ⅶ的粒径分布范围有部分重合,由于出口Ⅶ靠近右边壁面,部分颗粒碰到右壁面有反弹,因此导致小部分颗粒从出口Ⅵ流出。
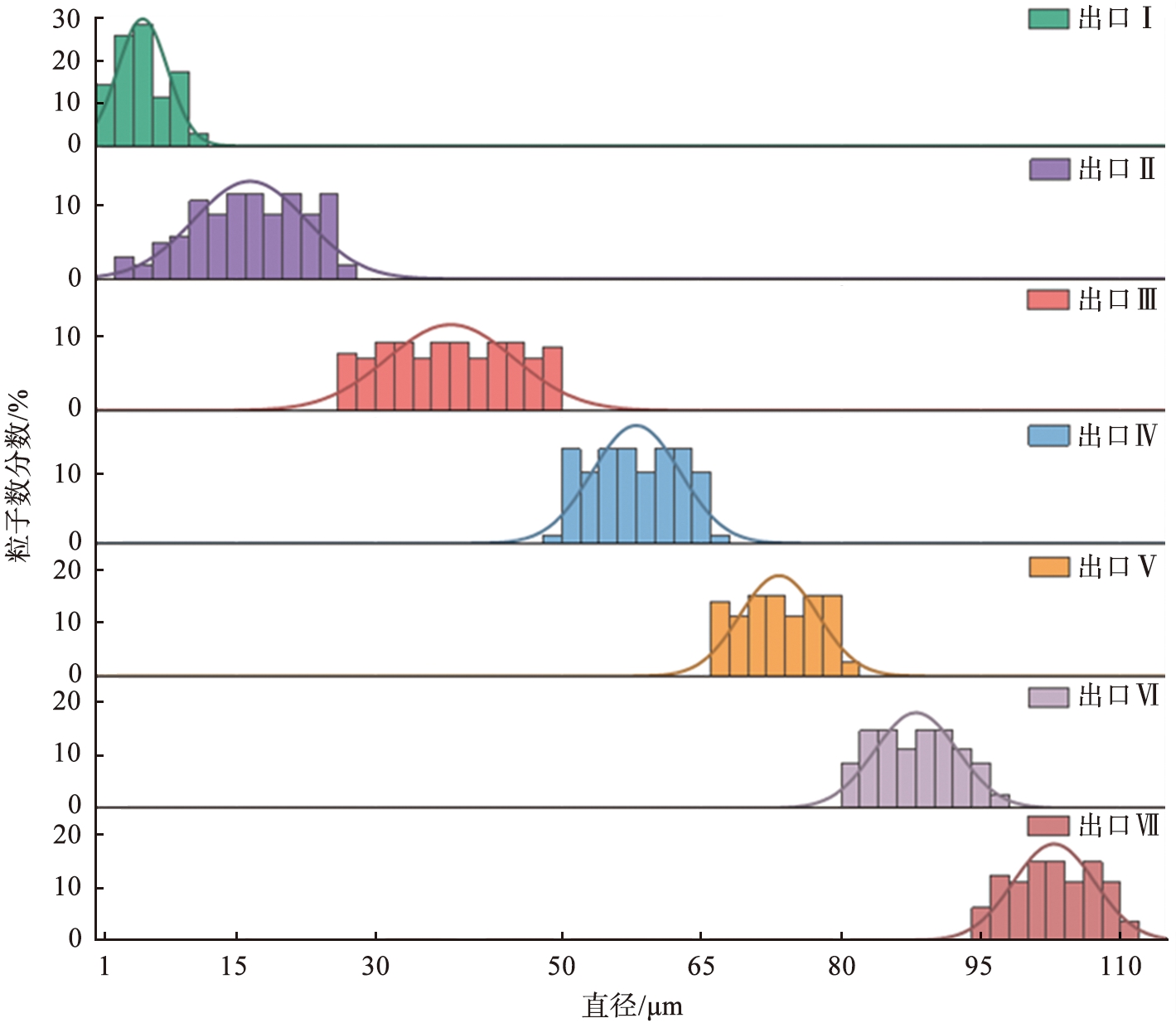
图9 各级出口的颗粒粒径分布直方图
Fig.9 Histogram of particle size distribution at all levels of outlets
出口Ⅰ处的粒度分布明显窄于其他出口处的粒度分布,表明分级后粒径范围为1~10 μm的超细海泡石颗粒表现出更集中的分布和更好的单分散性。同时可以看出,出口Ⅰ处的大部分颗粒粒径范围为1~10 μm,出口Ⅱ流出的大部分颗粒粒径范围为10~30 μm。通过分析各分级区间的颗粒粒径分布,将出口I修改为粒径为110 μm的海泡石颗粒出口,出口Ⅱ修改为粒径为10~30 μm的海泡石颗粒出口,从而更好地对海泡石颗粒进行分级,其中出口Ⅰ可以筛选出超细海泡石颗粒。
4 结论
1)海泡石颗粒的粒径越小,颗粒受分级气流的影响越大,出口位置距离分级器左侧壁面处越近。
2)通过模拟分析不同粒径海泡石颗粒在不同时刻的位置,划分颗粒的分级区间,在分级器设置了7个出口,并且研究了各级出口的颗粒粒径分布,结果表明分级器能获得多种不同粒径分布的颗粒。
3)总体上,该重力分级器能获得多种不同粒径分布的颗粒产品,通过构建横流域和顺流域叠加的分级流场,以流体对颗粒的作用力为主动力,并将出口设置在2个不同侧面上,有效地将细颗粒与粗颗粒分离,并能筛选出粒径为1~10 μm的超细海泡石颗粒产品。
[1]郑锡瀚, 马忻狄, 蓝丽红. 糖类物质改性海泡石复合材料制备方法及应用研究进展[J]. 化工矿物与加工, 2021, 50(1): 43-50.
ZHENG X H, MA X D, LAN L H. Research progress on the preparation and application of seafoam composites modified with sugars[J]. Chemical Minerals and Processing, 2021, 50(1): 43-50.
[2]RIENER K, ALBRECHT N, ZIEGELMEIER S, et al. Influence of particle size distribution and morphology on the properties of the powder feedstock as well as of AlSi10Mg parts produced by laser powder bed fusion (LPBF)[J]. Additive Manufacturing, 2020, 34: 101286.
[3]FATAHIAN H, FATAHIAN E, ESHAGH N M, et al. Novel designs for square cyclone using rounded corner and double-inverted cones shapes[J]. Powder Technology, 2021, 380: 67-79.
[4]孙占朋, 孙国刚, 独岩. 进料位置与风速对旋风分级器颗粒分级效果的影响[J]. 化工学报, 2018, 69(4): 1324-1331.
SUN Z P, SUN G G, DU Y. Effect of feed position and wind speed on particle classification effect of cyclone classifier[J]. Journal of Chemical Engineering, 2018, 69(4): 1324-1331.
[5]孙占朋, 孙国刚, 晁继阳, 等. 新型旋风分级器流场特性及颗粒分级性能[J]. 化工进展, 2019, 38(11): 4873-4879.
SUN Z P, SUN G G, CHAO J Y, et al. Flow field characteristics and particle classification performance of a new cyclone classifier[J]. Chemical Progress, 2019, 38(11): 4873-4879.
[6]SAFIKHANI H, ZAMANI J, MUSA M. Numerical study of flow field in new design cyclone separators with one, two and three tangential inlets[J]. Advanced Powder Technology ,2018, 29(3): 611-622.
[7]SHASTRI R, BRAR L S. Numerical investigations of the flow-field inside cyclone separators with different cylinder-to-cone ratios using large-eddy simulation[J]. Separation and Purification Technology, 2020, 249: 117-149.
[8]WANG S Y, LI H L, WANG R, et al. Effect of the inlet angle on the performance of a cyclone separator using CFD-DEM[J]. Advanced Powder Technology, 2019, 30(2): 227-239.
[9]WADENPOHL DR.ING.C. Production of powder coatings with defined particle size distribution by grinding and inline classification[J]. International Journal of Mineral Processing, 2004, 74: S155-S164.
[10]WANG Q P, MELAAEN M C, SILVA S R D. Investigation and simulation of a cross-flow air classifier[J]. Powder Technology, 2001, 120(3): 273-280.
[11]LAI W, LU W, CHOU M. Sorting of fine powder by gravitational classification chambers[J]. Advanced Powder Technology, 2009,20(2): 177-184.
[12]BANJAC V, PEZO L, PEZO M, et al. Optimization of the classification process in the Zigzag air classifier for obtaining a high protein sunflower meal-chemometric and CFD approach[J]. Advanced Powder Technology, 2017, 28(3): 1069-1078.
[13]周友行, 李昱泽, 徐长锋, 等. 海泡石颗粒气固两相射流分级的数值模拟[J]. 中国粉体技术, 2020, 26(4): 15-20.
ZHOU Y H, LI Y Z, XU C F, et al. Numerical simulation of gas-solid two-phase jet classification of seafoam particles[J]. China Powder Science and Technology, 2020, 26(4): 15-20.
[14]JOHANSSON R, EVERTSSON M. CFD simulation of a gravitational air classifier[J]. Minerals Engineering, 2012, 33(3): 20-26.
[15]袁竹林, 朱立平, 耿凡, 等. 气固两相流动与数值模拟[M]. 南京: 东南大学出版社, 2013.
YUAN Z L, ZHU L P, GENG F, et al. Gas solid two phase flow and numerical simulation[M]. Nanjing: Southeast University Press,2013.
[16]ZHOU Y, SHEN W. Numerical simulation of particle classification in new multi-product classifier[J]. Chemical Engineering Research and Design, 2022, 177: 484-492.
[17]伍赫, 郝子晗, 杨星, 等. 颗粒物沉积与平板气膜冷却耦合效应的数值研究[J]. 航空动力学报, 2023, 12(1): 5-24.
WU H, HAO Z H, YANG X, et al. Numerical study of the coupling effect of particle deposition and flat plate air film cooling[J]. Journal of Aerodynamics, 2023, 12(1): 5-24.