物料碎磨在矿业、 建材、 化工等行业有着广泛的应用, 在基础工业领域中占据着重要的地位。 对辊破碎机具有结构简单、 运行稳定等优势, 是物料碎磨常用的设备[1-2]。 随着矿产资源的贫化、 工业耗材用量的增加, 物料碎磨的总量逐年增加[3-4], 因此, 提高破碎机的破碎效率具有重要意义, 国内外学者通过分析影响破碎效率的因素以及探究其破碎规律开展了相关研究。 Mütze[5-6]通过数学建模分析了颗粒床挤压破碎过程中颗粒排列、 压实、 破碎的能量耗散。 张子龙[7]研究圆锥破碎机破碎腔内散体物料层压破碎行为, 建立了散体物料双粒形循环层压破碎操作模型。 破碎机的试验研究普遍存在腔内物料不可视、 破碎数据难采集等问题, 随着计算机技术发展, 数值模拟成为可供科研工作人员选择的研究手段[8-9]。 Zhou等[10]通过耦合有限元法与离散元法进行颗粒材料多尺度力学的建模和计算, 发现颗粒材料不同部位在细观尺度上差异较大, 但宏观尺度材料的应力、 应变演化关系密切。 蔡改贫等[11-12]通过建立符合真实岩石内部特征的多尺度内聚力颗粒模型和矿石破碎演化模型, 分析矿石破碎过程中颗粒间细观粘结键的承载力大小、 断裂顺序及宏观裂纹的拓展机制。 Barrios等[13]比较了使用颗粒替换模型建立的数值模拟与小型颚式破碎机的破碎结果, 发现建立的模型吻合度较高。 André等[14]建立多面体破碎模型, 并用于模拟圆锥破碎机破碎硬度不同的混合物料, 发现破碎产物不会随待碎矿石的硬度增加而呈比例减小。 程加远等[15]通过建立圆锥破碎机的离散元法(discrete element method,DEM)与多体动力学(multibody dynamics,MBD)耦合仿真模型,为圆锥破碎机的结构和参数优化提供新的思路。 Li等[16]建立了齿状双辊破碎机破碎过程的DEM模型,其数值模拟结果与实验数据有较好的一致性。
综上所述,相关研究较少分析不同入料粒径配比时矿石物料的孔隙率对破碎效率的影响,而不同的入料参数对破碎效率的影响差异显著,因此,本研究中基于对辊破碎机层压破碎过程的DEM-MBD联合仿真模拟及其试验,探究对辊破碎机层压破碎过程中物料破碎规律和破碎机受力运动情况,研究不同入料粒径配比时物料的孔隙率对破碎效率的影响,对比分析模拟与试验结果验证联合仿真模型的可靠性,为提高对辊破碎机的破碎效率以及研究碎磨设备的物料破碎规律提供参考思路。
1 对辊破碎机的层压破碎机理
Schönert[17]通过侧限压碎装置研究散体物料挤压破碎特性,提出区别于单颗粒破碎的层压破碎概念。当散体物料多层分布且相互作用发生破碎时,能量可以得到高效利用,但物料属性、 物料孔隙率、 入料参数、 料层高度对层压破碎效率均有影响。散体物料的层压破碎过程通常经历3个阶段:料层密实、 物料破碎和结团排料,对辊破碎机层压破碎示意图如图1所示。
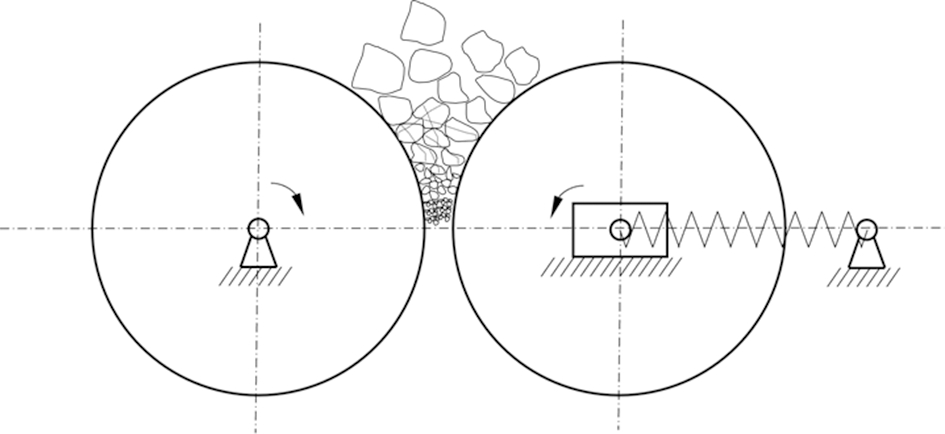
图1 对辊破碎机层压破碎示意图
Fig.1 Schematic diagram of laminating crushing process of roll crusher
在料层密实阶段,进入破碎腔的松散物料在重力、 挤压力作用下物料的孔隙率减小,邻近物料相互作用,但并未达到物料破碎强度;物料破碎阶段,随着破碎腔空间减小,料层进一步压缩,物料间受力达到破碎强度,物料出现群体性破碎;结团排料阶段,破碎后的物料受到挤压,其孔隙率继续减小,物料出现压实的情况,并排出破碎腔。
2 DEM-MBD联合仿真
2.1 联合仿真模型的建立
对辊破碎机的结构主要由机架、 固定辊、 移动辊、 滑块和弹簧构成,利用Pro/E建模软件创建其三维简化模型。将三维模型导入多体动力学软件Recurdyn中,设置各部件之间的接触模式、辊子转动速度和弹簧力。根据对辊破碎机的工作机制,辊子的接触为转动副,其转动速度为2.25 r/s;移动滑块与机架之间为弹簧接触;其他接触为固定接触。其中弹簧力为
Fs=-K(l-lf)m-Cin+F,
(1)
式中: K为弹簧劲度系数; C为弹簧阻尼系数; m为劲度系数指数; n为阻尼系数指数; l、 lf分别为弹簧现有长度和自由长度; i为弹簧长度的变化速率; F为弹簧预载荷。各参数的数值如表1所示。
表1 弹簧参数
Tab.1 Spring parameters

劲度系数阻尼系数劲度系数指数阻尼系数指数自由长度/mm现有长度/mm预载荷/N1.2×104111255215-4.5×105
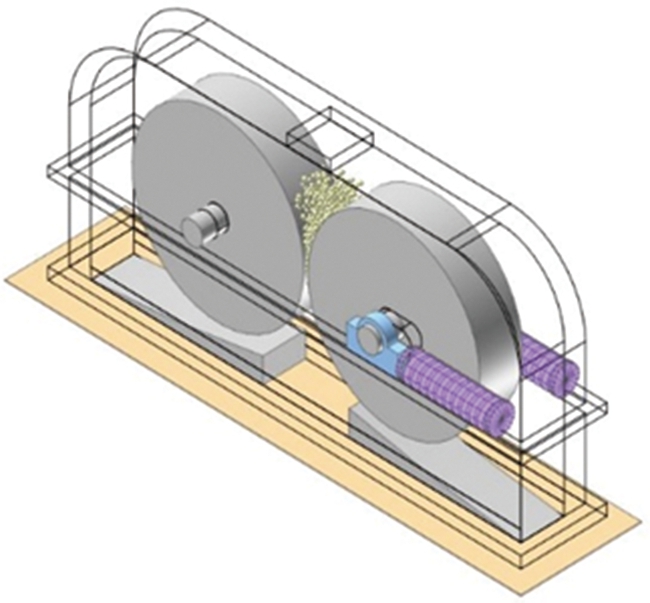
图2 DEM-MBD联合仿真模型
Fig.2 DEM-MBD co-simulation model
为了实现对辊破碎机的DEM-MBD联合仿真,需要将配置文件添加至Recurdyn软件根目录下,勾选EDEM软件中Recurdyn耦合选项,在EDEM软件的几何模型中添加从Recurdyn软件中导出的WALL格式模型文件,设置模型参数与仿真时步。对辊破碎机的辊缝在启动前可以根据破碎要求进行调节,在破碎过程中,当破碎力超过弹簧提供的弹簧力时,辊缝也会随受力大小变化,建立DEM-MBD联合仿真可以模拟破碎辊子与弹簧在破碎过程中的运动规律并记录其相互作用力。在Recurdyn软件中能够观察到颗粒破碎模型,相比于其他动力学软件具备优势。通过EDEM软件与Recurdyn软件耦合建立的DEM-MBD联合仿真模型如图2所示。
2.2 离散元破碎模型
本研究中采用的破碎模型为Tavares破碎模型,该模型描述了当脆性材料满足临界失效条件时,由一组碎后颗粒替换原颗粒。模型中包括一组函数表达式,其中有描述破碎概率的断裂能分布函数、解释损伤破坏的损伤破碎函数和描述碎后粒径分布的t10函数[18-20], 其中t10指碎后产物的粒径小于原颗粒粒径1/10的质量分数。
该破碎模型的临界失效条件为破碎能大于断裂能,其中破碎能由法向能和切向能组成,表达式为
Ek=En+ctEt,
(2)
式中: En、 Et为颗粒的法向能和切向能; ct为切向能的系数。
颗粒的断裂能是服从对数正态分布的函数,其误差函数为
(3)
(4)
(5)
式中: E50为断裂能分布的中位数; Emax为断裂能分布的上截断值; σ为断裂能分布的标准偏差; E∞为颗粒残余断裂能; φ为根据试验数据拟合的模型参数; d0、 dp分别为颗粒特征尺寸和颗粒粒径; kp、 kst分别为颗粒模量和颗粒接触物体的模量。
相关研究表明,脆性材料不仅在单次外力作用下发生破碎,也会在重复低能外力作用下发生损伤破碎[19-20]。Tavares破碎模型引入损伤累积效应描述这种损伤破碎,描述颗粒单次损伤破坏的表达式为
(6)
(7)
(8)
式中:![]() 分别为损伤前后的颗粒断裂能; D为损伤值; γ为损伤累积系数; e为破碎能比例系数。
分别为损伤前后的颗粒断裂能; D为损伤值; γ为损伤累积系数; e为破碎能比例系数。
Tavares[20]通过一系列破碎试验,得出颗粒受力破碎后,碎后粒径分布与颗粒的有效破碎能和断裂能有关,具体表达式为
(9)
式中: A、 b分别为待拟合的模型参数。
为了解决破碎模型替换前后颗粒的质量和体积损失的问题,原颗粒破碎替换成小颗粒时有一定的重叠量,同时避免重叠产生爆炸现象,通过添加阻尼力来减小因颗粒间初始重叠而产生的排斥力。
2.3 模型参数设置
联合仿真模型需要设置的参数包括材料的本征参数、 接触参数和破碎模型参数。其中材料的本征参数为材料本身固有属性和外部条件无关,包括泊松比、 剪切模量和密度,材料本征参数如表2所示。接触参数通过比较物料堆积仿真与试验结果,获取最佳接触参数值,包括碰撞恢复系数、 静摩擦因数和滚动摩擦因数,接触参数如表3所示。损伤累积破碎模型参数通过单颗粒破碎试验与料层破碎试验进行拟合,包括剪切能系数、 断裂能对数正态分布的上截断值、 标准偏差、 模型拟合参数、 损伤累积系数以及t10函数的拟合参数,破碎模型参数设置如表4所示。
表2 材料的本征参数
Tab.2 The intrinsic parameters of the material

材料泊松比剪切模量/GPa密度/(kg·m-3)钨矿石0.35252 830钢0.31212785 0
表3 材料的接触参数
Tab.3 Contact parameters of material
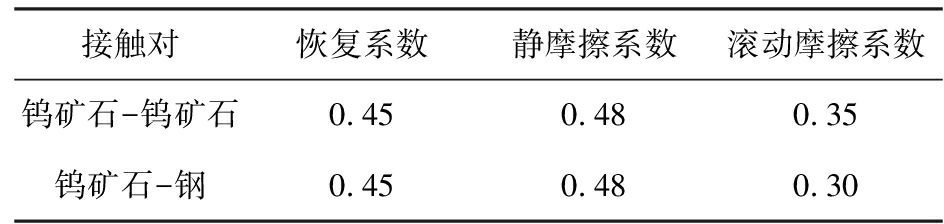
接触对恢复系数静摩擦系数滚动摩擦系数钨矿石-钨矿石0.450.480.35钨矿石-钢0.450.480.30
表4 破碎模型参数
Tab.4 Crushing model parameter

颗粒特征尺寸/mm颗粒残余断裂能/(J·kg-1)断裂能拟合参数断裂能标准偏差损伤累积系数t10拟合参数At10拟合参数b切向能系数断裂能上截断值/J20.116.80.840.405.044.20.0290.5100
3 试验
3.1 材料与装置
试验选用的矿石材料为赣南地区典型的黑钨矿石,破碎设备为2PG400*250型号对辊破碎机,频率为5.5 kW的变频器、振动分选筛、电子秤所组成。其中,振动分选筛用于将碎后不同粒径的混料振动分离并筛分,电子秤用于统计筛选后物料的质量。
3.2 试验过程
在对辊破碎机辊隙一定的情况下,为了研究待碎矿石的粒径分布和孔隙率对层压破碎效率的影响。进行如下破碎试验。
1)调节破碎机辊隙为10 mm,称取和筛选试验所需的粒径为10 mm以下的矿石,通过不同粒径配比控制矿石的孔隙率。将所需矿石平铺至桶中,再往筒中加入水至刚好漫过上层表面,测量所用矿石和水的质量。利用孔隙率计算公式获得矿石在破碎腔中的孔隙率,孔隙率的计算公式为
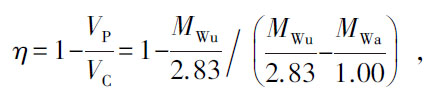
(10)
式中: VP、 VC分别为矿石所占体积和破碎腔体积,m3; MWu、 MWa分别为矿石和水的质量,kg。
在保证试验数据可靠、 减轻破碎试验工作量的前提下,进行10组对辊破碎机层压破碎试验,入料矿石的粒径配比如表5所示。
表5 入料矿石的粒径配比
Tab.5 Particle size ratio of incoming ore
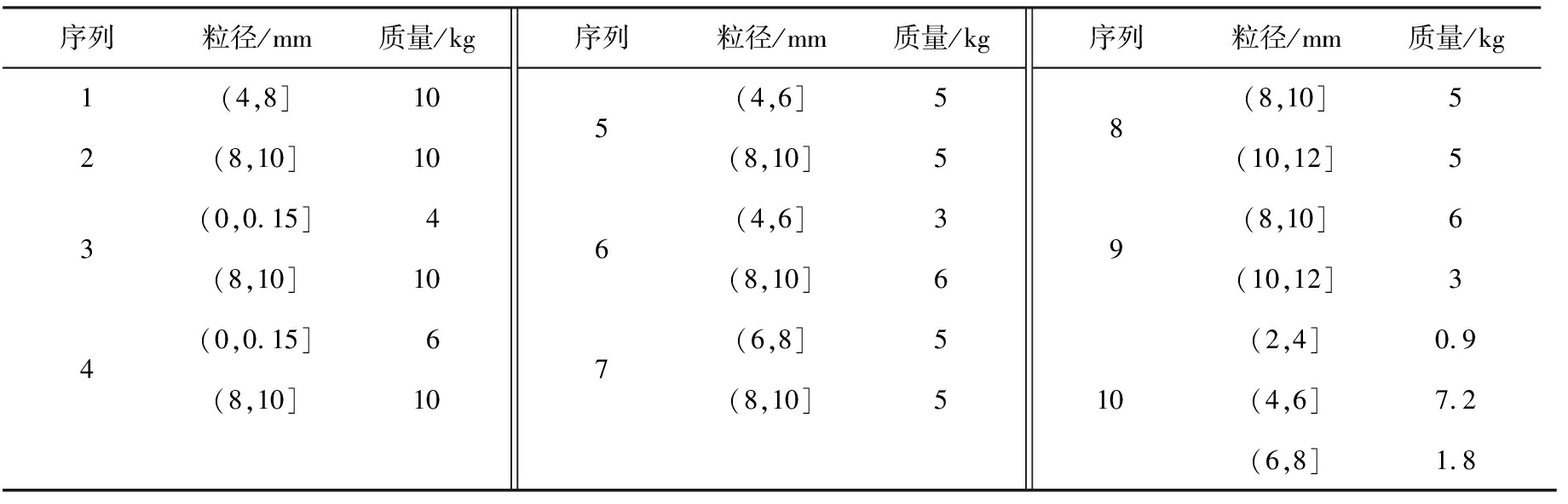
序列粒径/mm质量/kg序列粒径/mm质量/kg序列粒径/mm质量/kg1234(4,8]10(8,10]10(0,0.15]4(8,10]10(0,0.15]6(8,10]10567(4,6]5(8,10]5(4,6]3(8,10]6(6,8]5(8,10]58910 (8,10]5(10,12]5(8,10]6(10,12]3(2,4]0.9(4,6]7.2(6,8]1.8
2)启动机器,待其空载运行平稳后,一次性快速将矿石倒入破碎腔。此时入料粒度均小于辊隙,且物料迅速填满破碎腔,可以认为试验过程中物料的破碎完全符合层压破碎。为了减小误差,每组入料矿石重复进行3次破碎试验。
3)对碎后矿石进行缩分取样,将矿石倒入分选筛进行筛分,用电子秤测量各粒径范围碎后矿石质量,计算各粒径碎后矿石的质量分数。
4 结果与讨论
4.1 对辊破碎机层压破碎过程的特征分析
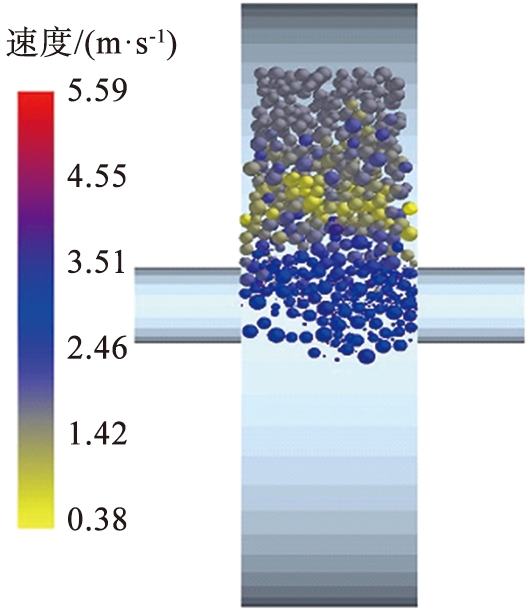
(a)速度分布
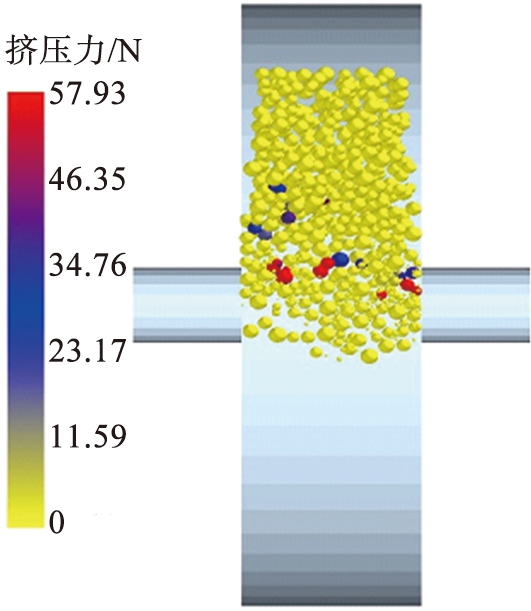
(b)受力分布
图3 联合仿真的对辊破碎机破碎腔内物料状态
Fig.3 Material state of co-simulation cavity of roll crusher
通过DEM-MBD联合仿真可以获取丰富的物料破碎信息,利用EDEM软件的后处理功能得到联合仿真对辊破碎机破碎腔内物料状态,如图3所示。从图3(a)中可以看出,对辊破碎机破碎腔内的物料速度从上至下先减小后增大,且有明显的分层现象;上层物料在重力作用下进入破碎腔,速度逐渐增大;中间层物料受到两侧辊子的挤压,物料速度降低;排料层物料在两侧辊子的切向摩擦力作用下,排出破碎腔,物料速度较大。从图3(b)中可以看出,破碎腔内上层物料较为松散,其受力较小,没有出现物料破碎的现象;中间层物料受到挤压较为密实,受力较大,同时物料出现群体性破碎现象;靠近排料口的物料层为碎后的细小物料,该层物料经密实后排出破碎腔。
对辊破碎机在整个联合仿真破碎过程中,矿石物料与移动辊子的时间-挤压力曲线如图4所示。由图可知,0.15 s之前移动辊子与矿石物料没有受到挤压力;0.15~0.27 s矿石物料、移动辊子的挤压力先增大后减小, 且移动辊子的挤压力大于矿石物料; 0.27 s之后矿石物料和移动辊子受力基本为0。移动辊子的时间-位移曲线如图5所示。
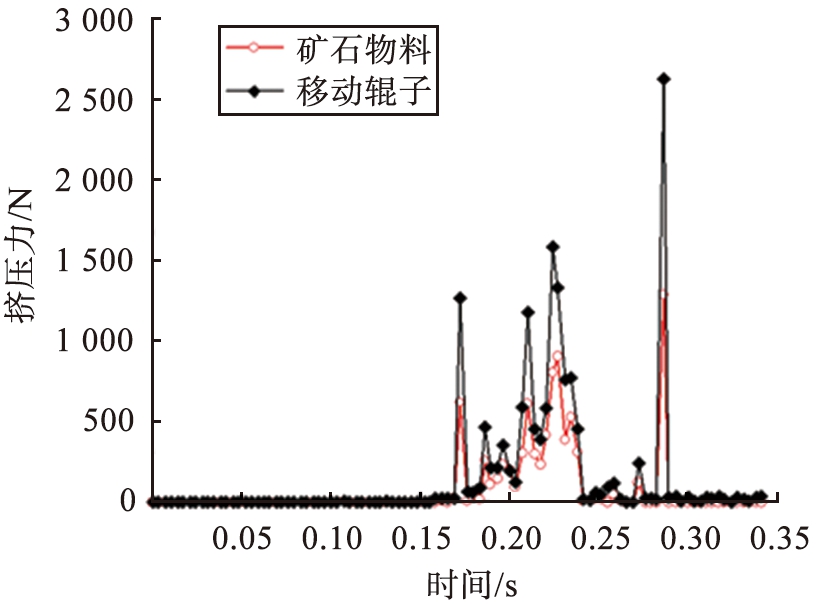
图4 矿石物料与移动辊子的时间-挤压力曲线
Fig.4 Time-extrusion curve of ore material and moving roller
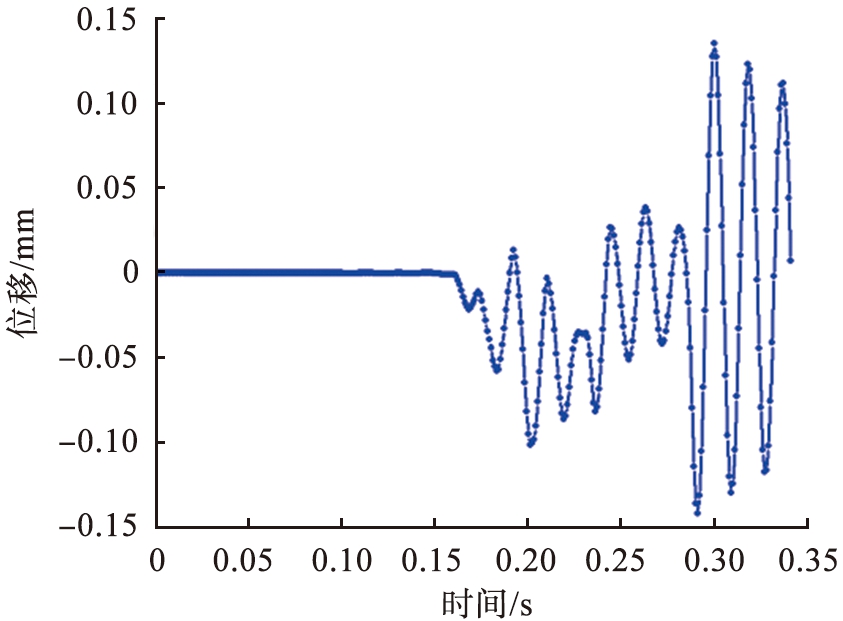
图5 移动辊子的时间-位移曲线
Fig.5 Time-displacement curve of moving roller
由图可知,辊位移在0.15 s开始增大;0.15~0.27 s移动辊子的位移在-0.15~0.15 mm范围内波动,0.27 s时达到位移的最大值;0.27 s之后,移动辊子的位移呈减小的趋势。综上所述,在对辊破碎机的破碎过程中,矿石物料首先在两侧辊子的作用下受到挤压,料层开始密实,部分矿石物料受力达到破碎强度发生破碎,移动辊子的挤压力与辊子位移开始增大。随后破碎腔内矿石物料维持料层密实、物料破碎、结团排料的平衡状态,最后矿石物料基本排出破碎腔,矿石物料的挤压力与位移和辊子位移均逐渐减小。依据矿石物料的破碎特征可以对破碎腔内空间进行分层,即对辊破碎机的层压破碎过程中存在料层密实、物料破碎和结团排料3个阶段。
4.2 物料孔隙率对破碎效率的影响
由式(10)计算得到10组试验的入料矿石孔隙率如表6所示。对辊破碎机层压破碎试验后,统计10组试验碎后矿石质量并计算其质量分数,碎后矿石中小于最小入料粒径的质量分数为该组试验的矿石破碎率。碎后矿石的粒径分布如图6所示。
表6 入料矿石的孔隙率
Tab.6 Porosity of incoming ore

试验编号12345678910孔隙率/%34.1648.5429.8519.3641.4445.9237.3033.7532.0233.30
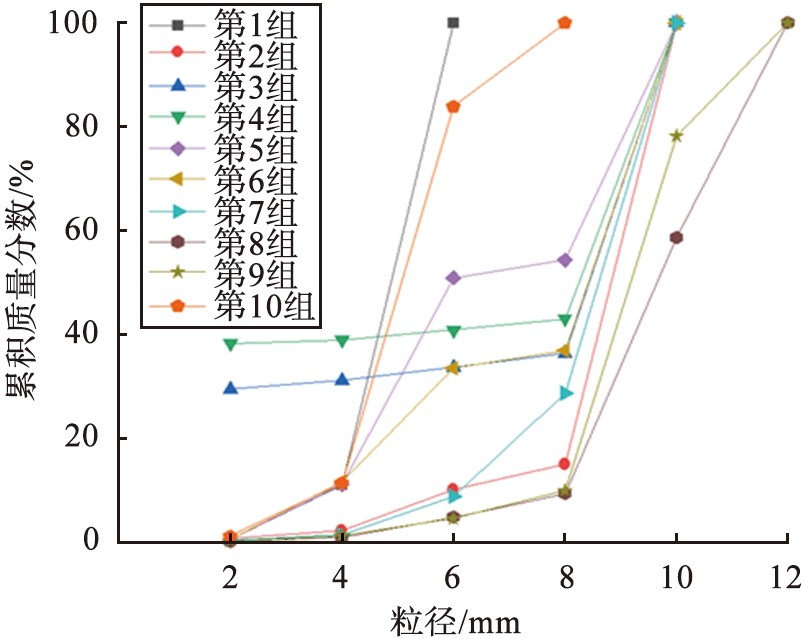
图6 碎后矿石的粒径分布
Fig.6 Particle size distribution of ore after crushing test
对比分析第1、 2组试验,孔隙率分别为34.16%、 48.54%,破碎率分别为11.17%、 7.23%。第2组试验孔隙率较高而破碎率却较低, 原因是第1组试验中入料粒径为8~10 mm, 第2组试验中入料粒级为4~6 mm,试验时对辊破碎机的辊间隙调节为10 mm, 第2组试验中较小的矿石颗粒容易在未破碎的情况下就滑出破碎腔。
对比分析第2、 3、 4组试验, 孔隙率分别为48.54%、 29.85%、 19.36%, 破碎率分别为15.11%、 7.94%、 5.56%。第3、 4组试验在入料粒径为8~10 mm中分别混入了40%、 60%粒径为0~0.15 mm的细颗粒。结果表明,通过混入细颗粒减小孔隙率,不能提高破碎率,反而降低了破碎率。原因是在破碎过程中细颗粒会填充矿石间的孔隙,且细颗粒形状多为球状,使破碎腔内的矿石之间无法稳定接触,未被破碎就排出了破碎腔。
对比分析第5、 6、 7组试验,孔隙率分别为41.44%、 45.92%、 37.30%,破碎率分别为15.64%、 15.41%、 17.83%。第5、 6组试验在入料粒径为8~10 mm中分别混入100%、 50%粒径为4~6 mm矿石,第7组试验在入料粒径8~10 mm中混入100%粒径为6~8mm矿石。结果表明,通过混入尺寸大小为入料粒径50%~100%的矿石降低孔隙率,有利于提高破碎率。
第8、 9组试验在入料粒径为10~12 mm中分别混入100%、 200%粒径为8~10 mm矿石,孔隙率分布为33.75%、 32.02%,破碎率分别为18.24%、 21.64%。第9组试验的破碎率明显升高,符合在矿石中混入尺寸为50%~100%入料粒径的矿石减小孔隙率,有利于提高破碎效率的结论。第10组试验在入料粒径为4~8 mm中添加9%粒径为2~4mm的矿石,与第1组试验相比孔隙率减小,但破碎效率从11.17%下降到5.73%,说明2~4 mm矿石在破碎腔内会降低矿石间的摩擦,不利于矿石之间相互咬合,使矿石未被破碎就排出破碎腔。综上所述,为提高对辊破碎机破碎效率,在满足入料粒径大于40%辊隙的条件下,通过混入尺寸大小为50%~100%入料粒径的矿石降低孔隙率,可以提高对辊破碎机破碎效率;而混入细颗粒减小孔隙率会降低对辊破碎机的破碎效率。
4.3 联合仿真模型的可靠性分析
为验证建立的DEM-MBD联合仿真模型的可靠性, 对比分析第7、 8组试验与仿真的破碎情况。 7、 8组试验的入料粒径分布均匀, 矿石尺寸介于6~12 mm与破碎机辊隙10 mm接近, 试验破碎效果较为明显, 便于统计仿真与试验误差。第7、 8组仿真与试验碎后矿石的粒径分布如图7所示。 由图可知, 在入料粒径分布相同的情况下, 仿真与试验碎后粒径分布曲线相一致。 由均方根公式计算仿真与试验碎后粒径累积质量分数的偏差, 其中第7、 8组仿真结果与试验结果的均方根误差分别为1.816、 1.404。 从碎后物料粒径分布曲线和碎后物料粒径累积质量分数偏差可知, 仿真与试验结果虽存在误差; 但一致性较高, 因此可认为通过Tavares破碎模型建立的DEM-MBD联合仿真参数设置较准确, 仿真结果具有一定的可靠性。
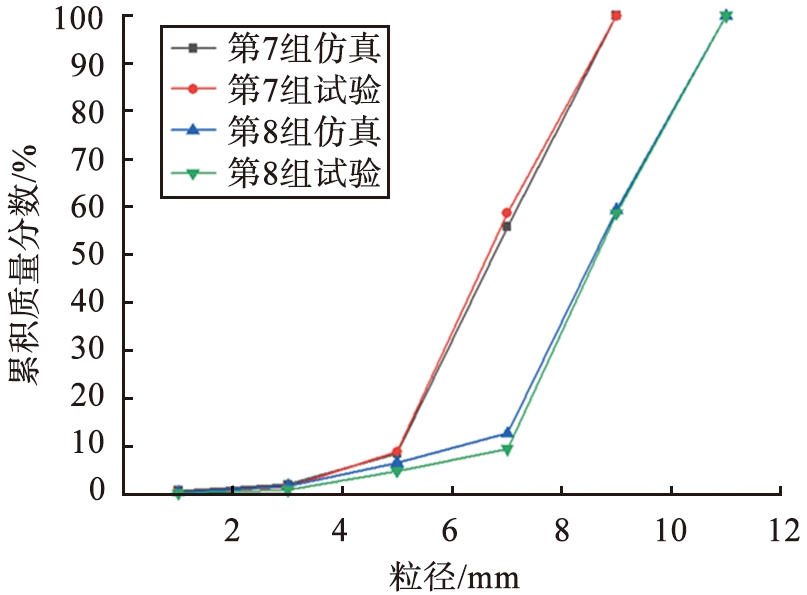
图7 仿真与试验碎后矿石的粒径分布
Fig.7 Particle size distribution of crushed ore in simulation and test
5 结论
1)对辊破碎机腔内物料的破碎由单颗粒破碎和料层破碎组成,而在对辊破碎机层压破碎过程中,物料层可分为料层密实、物料破碎和结团排料3个阶段。
2)在满足入料粒径大于40%辊隙的条件下,通过混入尺寸为入料粒径50%~100%的矿石降低孔隙率可以提高对辊破碎机破碎效率,而混入细颗粒降低孔隙率会减小对辊破碎机破碎效率。
3)通过联合仿真模拟与对辊破碎机层压破碎试验对比验证了模型的可靠性,说明利用Tavares破碎模型建立的对辊破碎机DEM-MBD联合仿真结果与实际工况接近,联合仿真模型可为后续深入研究矿石破碎机制提供参考。
[1]段希祥, 肖庆飞. 碎矿与磨矿[M]. 北京: 冶金工业出版社, 2012: 1-5.
DUAN X X, XIAO Q F. Crushing and grinding[M]. Beijing: Metallurgical Industry Press, 2012: 1-5.
[2]夏晓鸥, 沈政昌, 史帅星, 等. 选矿装备[M]. 北京: 冶金工业出版社, 2019: 4-6.
XIA X O, SHEN Z C, SHI S X, et al. Mineral processing equipment[M].Beijing: Metallurgical Industry Press, 2019: 4-6.
[3]JIANG H, ZHOU Y D, ZHANG C H. Interpretation of breakage characteristics of particle beds from confined compression tests[J]. Powder Technology, 2021, 378: 317-326.
[4]刘建远, 应平. 颗粒床压载粉碎对某硫化铜矿石矿物解离的影响[J]. 有色金属(选矿部分), 2018(5): 81-87.
LIU J Y, YING P. Impact of comminution by particle-bed compressive stressing on mineral liberation of a copper sulfide ore[J].Nonferrous Metals(Mineral Processing Section), 2018(5): 81-87.
[5]MÜTZE T. Energy dissipation in particle bed comminution[J]. International Journal of Mineral Processing, 2015, 136: 15-19.
[6]MÜTZE T. Modelling the stress behaviour in particle bed comminution[J]. International Journal of Mineral Processing, 2016, 156: 14-23.
[7]张子龙. 圆锥破碎机层压破碎腔形优化及工艺参数研究[D]. 秦皇岛: 燕山大学, 2019.
ZHANG Z L. Research on optimization of inter-particle breakage crushing chamber and process parameters of cone crusher[D]. Qinhuangdao: Yanshan University, 2019.
[8]WEERASEKARA N S, POWELL M S, CLEARY P W, et al. The contribution of DEM to the science of comminution[J]. Powder Technology, 2013, 248: 3-24.
[9]LISJAK A, GRASSELLI G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(4): 301-314.
[10]ZHOU Q, XU W J, LUBBE R. Multi-scale mechanics of sand based on FEM-DEM coupling method[J]. Powder Technology, 2021, 380: 394-407.
[11]蔡改贫, 宣律伟, 张雪涛, 等. 多尺度内聚颗粒模型破碎过程研究[J]. 岩土力学, 2020, 41(6): 1809-1817.
CAI G P, XUAN L W, ZHANG X T, et al. Investigation into the crushing process in multi-scale cohesive particle model[J]. Rock and Soil Mechanics, 2020, 41(6): 1809-1817.
[12]蔡改贫, 郭晋, 李臣, 等. 异形多级颗粒模型的数值模拟试验与破碎实验[J]. 中国粉体技术, 2019, 25(3): 65-71.
CAI G P, GUO J, LI C, et al. Numerical simulation test and crushing experiment of multi-stage particle models with deferent shape[J]. China Powder Science and Technology, 2019, 25(3):65-71.
[13]BARRIOS G K, HERRERA N J, TORRES S N F, et al. DEM simulation of laboratory-scale jaw crushing of a gold-bearing ore using a particle replacement model[J]. Minerals, 2020, 10(8): 717-733.
[14]ANDRÉ F P, TAVARES L M. Simulating a laboratory-scale cone crusher in DEM using polyhedral particles[J]. Powder Technology, 2020, 372:362-371.
[15]程加远, 任廷志, 张子龙, 等. 基于多体动力学与离散元耦合的惯性圆锥破碎机动态性能研究[J]. 振动与冲击, 2021, 40(8): 98-109.
CHENG J Y, REN T Z, ZHANG Z L, et al. A study on dynamic performance of an inertia cone crusher based on multi-body dynamics and discrete element coupling method[J].Journal of Vibration and Shock, 2021, 40(8): 98-109.
[16]LI Y W, ZHAO L L,HU E Y, et al. Laboratory-scale validation of a DEM model of a toothed double-roll crusher and numerical studies[J]. Powder Technology, 2019, 356: 60-72.
[17]SCHÖNERT K. Modelling of interparticle breakage[J]. International Journal of Mineral Processing,1996, 44(3): 101-115.
[18]TAVARES L M, RODRIGUEZ V A, SOUSANI M, et al. An effective sphere-based model for breakage simulation in DEM[J]. Powder Technology, 2021, 392: 473-488.
[19]BARRIOS G K P, JIMENEZ H N, TAVARES L M. Simulation of particle bed breakage by slow compression and impact using a DEM particle replacement model[J]. Advanced Powder Technology, 2020, 31(7): 2749-2758.
[20]TAVARES L M, CHAGAS A D. A stochastic particle replacement strategy for simulating breakage in DEM[J]. Powder Technology, 2021, 377: 222-232.