矿产资源主要是通过破碎或研磨之后才能得到充分利用,在全球范围内能源和劳动力变得越来越昂贵的情况下,采矿系统的发展更加依赖于矿石粉碎机械的效率以及可靠性能 [1-2]。目前我国的一些常规粉碎设备虽然暂时能满足国内生产的需要,但随着时代发展和经济转型,只有更低能耗、 产能稳定的设备才能适应市场的新需求[3]。
传热广泛应用于冶金、石油、化工、矿业等工业部门。以提高能源利用率和传热效率、 改进传热技术为目标,传热在业内广受好评,取得了非常迅速的发展。先进的强化传热工艺可分为3类:导热工艺强化、对流工艺强化和辐射工艺强化。其中,最常应用于工业生产中的是对流工艺。对流传热促进技术的强化可分为有源强化和无源强化2种。其中有源强化包括机械搅拌法、电磁场作用法、流体脉动法、喷射或吸出等[4-8];无源强化主要包括表面处理法、粗糙表面法、扩展表面法等[9-15]。另外还有将多种强化技术复合的传热技术[16]。
百叶窗翅片被认为是最有效的先进传热片之一。翅片作为二次传热的延伸,对散热器的整体传热性能起着重要作用。由于百叶窗翅片的结构复杂,因此研究主要集中在翅片的传热和阻力性能方面。一是对不同参数下的散热器实物进行实验,以获得在不同条件下的空气侧传热数据,并将所记录的最佳参数作为今后设计的依据;二是进行流体力学仿真分析,获取流场和温度场的相关情况,对散热器翅片的空气流动特性进行改进。
Cowell等[17]的研究发现,具有大水力直径的翅片拥有最佳的散热器传热面。Chang等[18]为了研究散热器的传热性能,对具有不同结构参数的原型管状散热器进行了91次实验,其中89%的实验结果表明,管带式散热器的传热性能检测误差为±15%,平均绝对值误差为7.6%。 后来,Chang等[19]在原始测试数据的基础上,使用1 109个数据点,拟合阻力性能关联式,结果显示,83.1%的数据点的相关度为±15%,算术平均误差为9.2%。之后Chang等[20]对阻抗相关性进行了修订,以提高匹配的准确性,避免以前匹配结果的不连续性。
综上所述,对于管带式散热器而言,振动强化传热和百叶窗翅片是具有潜力的研究方向,可以进一步提高散热器的工作效率和性能。为了探究振动对散热器传热性能的影响,先利用计算流体动力学方法(CFD)仿真,并对振动带来的传热问题进行模拟研究和数值分析,建立建立管带式散热器的数值模型,并通过采用振动壁和网格的方法确定模型的振动。
1 管带式散热器振动强化传热数值模型的建立
1.1 几何模型
本文中采用计算流体动力学方法研究散热器振动传热问题。为了建立管状散热器的数值模型,通过引入振动壁的方法和网格划分方法,纳入振动模型的边界条件。
管带式散热器工作时会跟随矿山粉碎机发生3个方向的振动,即上下(竖直方向)、 左右和前后方向上的振动。图1为管带式散热器工作过程中振动状态示意图。由图可知, 管带散热片的几何形状比较复杂,所以在模拟时,不能将管带散热片作为整体来考虑,需要进行简化。通过建立三维数学模型,能够更精确地预测百叶的换热特性,从而对百叶的结构进行优化。
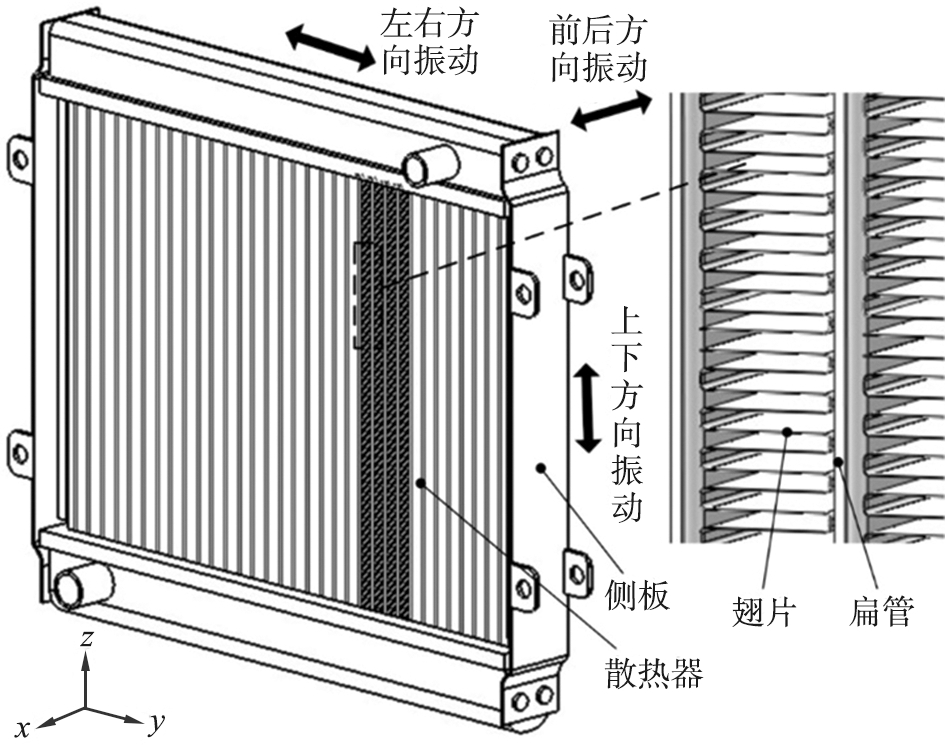
图1 管带式散热器工作过程中振动状态示意图
Fig.1 Schematic diagram of vibration state of tube-belt radiator during operation
在垂直于扁管传热面的平面上切割散热器, 形成一系列平行的、 周期性排列的扁管的二维截面。 为了减少计算负荷, 且考虑到管子之间的相互作用, 以解决垂直于扁管方向的模拟中的振动传热问题(见图2)。

图2 扁管二维模型
Fig.2 Two-dimensional model of flat tube
在与翅片垂直的情况下,建立3个相邻翅片的数学模型,以翅片为中心,重点研究翅片的传热特性,产生的几何模型如图3所示。

图3 翅片二维模型
Fig.3 Two-dimensional model of fins
1.2 数学模型
在现实中,散热器翅片中的流动不是层状的,因为流场受到振动的干扰,为了更好地模拟实际的流场分布,采用了湍流模型。关于这项工作的研究,鲜有文献报道。由于对流换热过程,散热器内的空气速度较小,因此假定空气为不可压缩流体;此外,空气温度较低,进出口温度相差很小,所以假定空气的黏度、密度和热导率以及其他物理参数为常数。
1)质量守恒方程
对于不可压缩的流量,密度是恒定的,则质量守恒方程[6-8]为
(1)
式中: u、 v和w是速度矢量在x、 y和z方向上的分量。
2)动量守恒方程
动量守恒方程表达如下:在任何参考微观元素中,流体动量随时间的变化率等于作用在微观元素上的各种外力的总和;对于不可压缩的、 通常是黏性的流体,数学表述如下:
(2)
(3)
(4)
式中: ρ为流体密度; t为时间; μ为空气动力黏度; p为压力; Su、 Sv、 Sw分别为x、 y、 z方向上的动量方程中的广义源项。
3)能量守恒方程
液体的能量通常由内能、动能和势能组成,为了方便,可以从中减去动能的变化,得到能量守恒方程(其中的变量是温度)。
(5)
式中: cp为空气定压比热; T为温度; λ为流体热导率。
上面的公式是一个控制方程,而在这个平面模型中,可以根据扁管和翅片的特性,把它们转换成对应的平面模型控制方程。
1.3 数值模型的边界条件和网格划分
1.3.1 边界条件
本文中使用的二维模拟模型中,入口边界被视为速度入口边界,速度在入口管的横截面上均匀分布。为了确保流体在到达换热器壁时得到充分发展,须在进口管和平管或翅片之间保持足够的距离。除了确定进口边界的对流传热率问题外,进口边界的温度也是给定的,并假定为常数。叶片和扁管都被定义为等温的壁面。为了模拟振动对传热的影响,必须确定平管和叶片的振动。在真实的破碎机驱动过程中,每次振动都可以看作是许多简谐振动的叠加,振动模式可以描述为
VA=2πfAcos(2πft)×10-3,
(6)
式中: VA为振动速度; A为振幅; f为频率。
1.3.2 网格划分

(a)扁管模型

(b)翅片模型
图4 管带式模型的网格划分
Fig.4 Grid division of tube-belt radiator
在进口和出口2个截面上, 网格点布设更粗的网格, 从中间扁管和翅片开始, 网格点布点在垂直于其表面的方向上, 网格点布点是逐渐变细的, 超出振幅范围的区域则是变稀的。 网格划分结果如图4所示。
2 管带式散热器振动强化传热仿真
基于上述的数值模型,利用计算流体力学软件Fluent进行模拟,得到的温度场和速度场的信息以及对流传热特性的结果。因为振动方向不同,所以对增强传热起作用的传热面也不同。
2.1 扁管振动强化传热仿真研究
根据图2的几何模型,在Fluent软件建立了如图5的仿真计算区域。具体数值的选取应考虑以下几点。
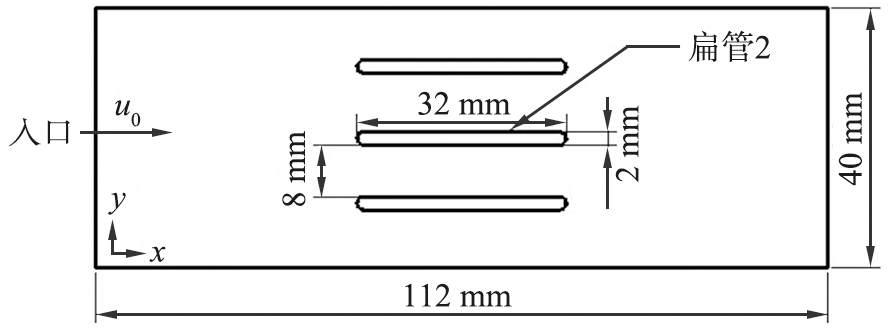
图5 扁管仿真计算区域
Fig.5 Flat tube simulation calculation area
1)入口风速u0,仿真采用的层流模型,根据雷诺数计算公式可推得层流时入口风速临界值uc为
uc=νRec/L,
(7)
式中: Rec为临界雷诺数; ν为空气运动黏度; L为特征长度,可由下式求得
(8)
式中: d为散热带波距; H为散热带波高。
取Rec为1 900,求得uc=20.7 m/s,因此风速要小于uc=20.7 m/s。考虑计算机的运算能力,综合上述几点,u0取为2、 5、 8、 11 m/s。
2)考虑到安装空间的限制和模拟的计算能力,选取振幅A分别为1、 2、 4、 6 mm。
散热器传热研究中通常用努塞尔数Nu来描述对流换热的强弱,定义为
(9)
式中: Tw为壁面温度; Tf为流体温度;下标y=0为函数在壁面处的取值。
相对于对流传热系数而言, Nu数更能反映传热过程中流体的热导率、 特征长度等因素, 对平板管道进行模拟分析时, Nu可以表达为
Nu=![]() ,
,
(10)
式中: q为热流密度; λ为流体热导率; T∞为来流温度,即流体入口温度。
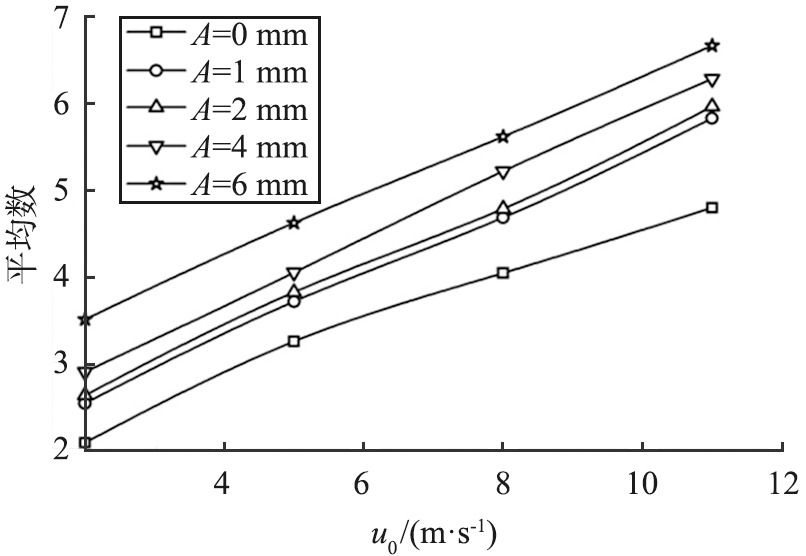
(a)不同振幅
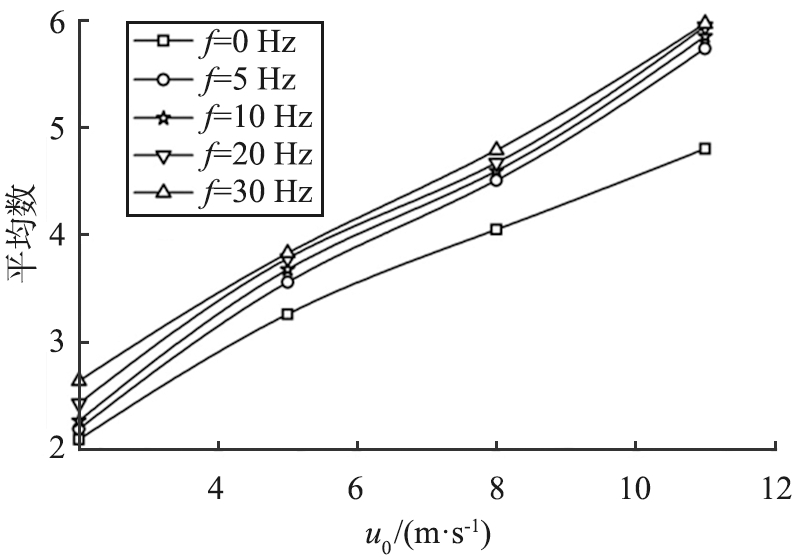
(b)不同频率
图6 Nu——随入口风速的变化
Fig.6 Nu—— changes with inlet wind speed
图6所示为振幅与频率之间的关系,![]() 为扁管2在一个振动周期中的平均值。从图中可以看到,
为扁管2在一个振动周期中的平均值。从图中可以看到,![]() 随着振幅和频率的增大而增大, 但是对
随着振幅和频率的增大而增大, 但是对![]() 的影响是不同, 当振幅和频率都相同时,
的影响是不同, 当振幅和频率都相同时,![]() 的变化会更大,但是振幅越大,
的变化会更大,但是振幅越大,![]() 的变化就越大。计算结果表明,当振幅增大时,
的变化就越大。计算结果表明,当振幅增大时,![]() 可增加14%~68%;增大频率时
可增加14%~68%;增大频率时![]() 可提高4.64%~26.03%,即强化传热方面振幅的作用大于频率。
可提高4.64%~26.03%,即强化传热方面振幅的作用大于频率。
随着风速的增加,按照强化传热理论,振动的强化传热作用会减弱,但是从图6中可以看出,效果相反,能确保振动可以发挥出最大的扰流效果。随着风速的增强,尽管扰流减弱,但对Nu的流场变化更为敏感,即湍流的增大会引起Nu的显著升高,而Nu的增量百分比则会随风速的增大而减少。
2.2 翅片振动强化传热仿真
散热器在垂直于翅片(z轴)方向振动过程中时, 翅片在空气侧传热中占有较大比例且起关键作用。 区域左边的壁面对应着速度入口, 入流速度为u0, 温度为300 K。 右边的壁面正对着出口的应力场, 而压力p=0, 将3种翅片模拟为移动壁, 使其按照式(6)的速度振动。 假定翅片的温度在管道中是均匀的, 并且比管道中的温度低。 模拟时, 将翅片的温度设置在358 K左右, 网格划分单元是四面体, 在翅片附近和移动区域中, 对其进行更密集的网格划分, 并确定为: u0=2~5 m/s时, 网格大小为0.1 mm; u0=6.5~9.5 m/s时, 网格大小0.04 mm, 见图7。
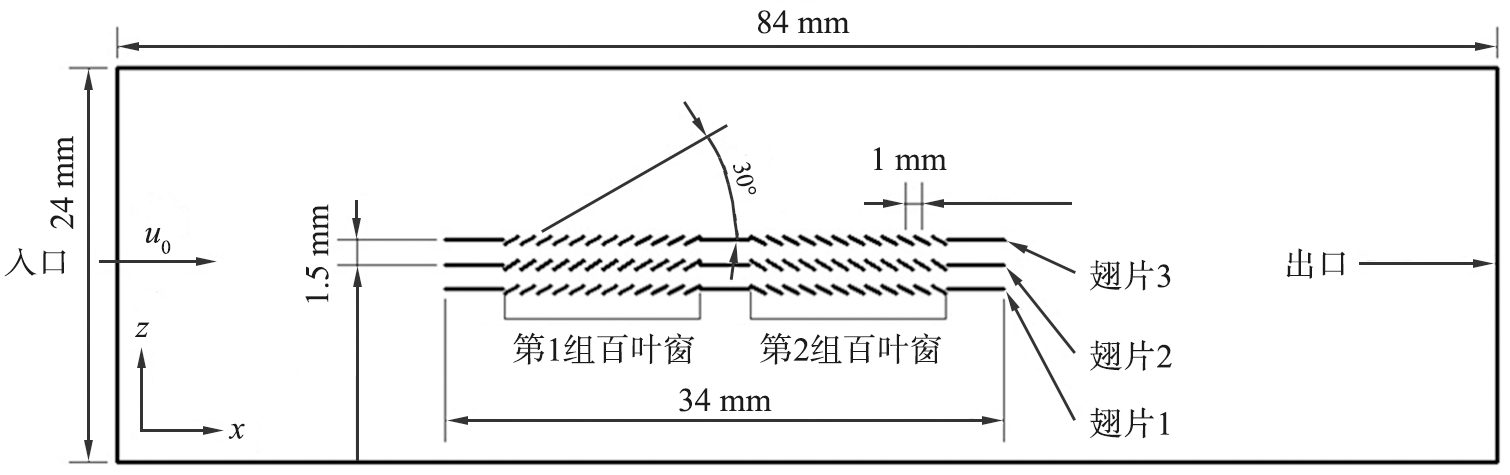
图7 翅片计算区域及边界条件
Fig.7 Fin calculation area and boundary conditions
2.2.1 温度场
图8所示为u0=2 m/s时不同振动参数下的温度分布云图。由图可知,当没有振动且振动率低时,第1组百叶窗的温度会迅速地升高,从而接近翅片的温度,然而,第2组的百叶窗的温度的平均温度比较高,可减少散热器的热饱和度,减少散热器的热量传递。在此情况下,翅片对提高流阻的影响更为显著。在振动频率高的情况下,翅片后半部的平均空气温度显著下降,换热性能提高。
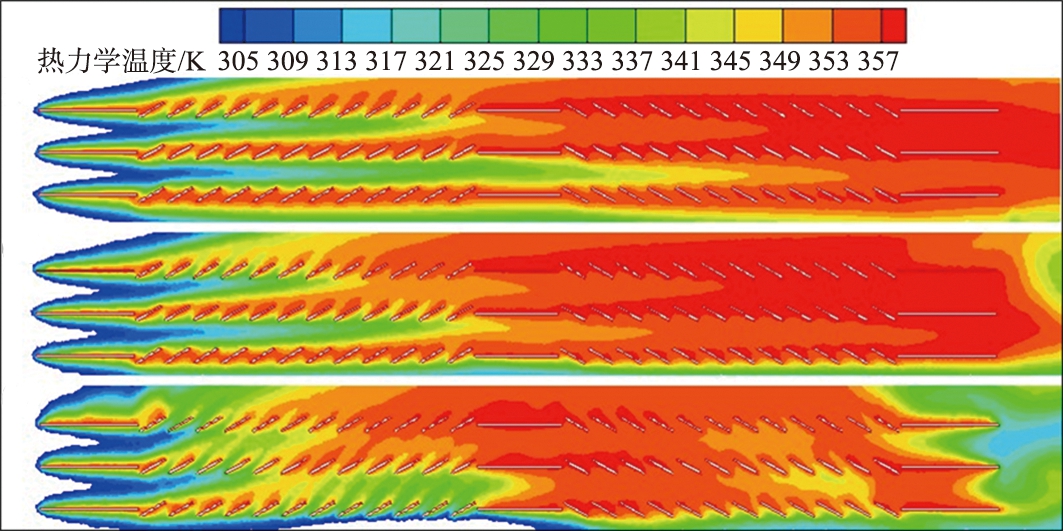
a—无振动; b—VA=0.13 m/s; c—VA=0.5 m/s。
图8 u0=2 m/s时翅片模型温度云图
Fig.8 u0=2 m/s when fin model temperature cloud
图9所示的u0=9.5 m/s时的温度分布云图。由图可知,与图8相比,翅片区域的平均温度大大降低,百叶窗散热效果明显提高,与振动和振动相关的温度范围变化不明显。从热痕迹看,第1组百叶窗是典型的翅片间干扰类型,第2组百叶窗是一种内干扰型,但上游热尾迹在到达下游百叶窗时越来越弱,对散热的影响相对较小。
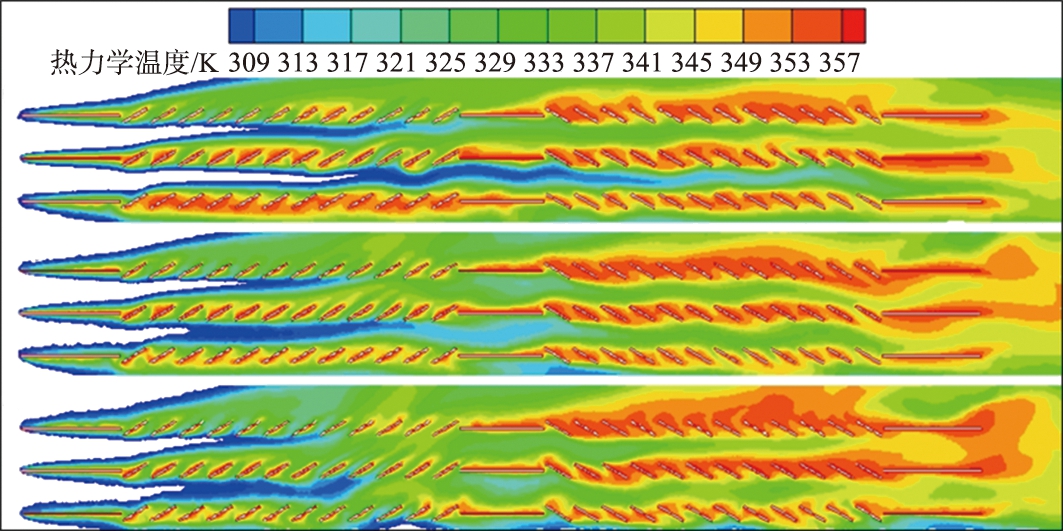
a—无振动; b—VA=0.13 m/s; c—VA=0.5 m/s。
图9 u0=9.5 m/s时翅片模型温度云图
Fig.9 u0=9.5 m/s when fin model temperature cloud
由以上分析可知,在低速时,振动能使空气中的平均温度下降,并产生一种热尾流加速了空气中的热量散失,从而有效地改善空气中的换热状况。
2.2.2 振动强化传热效果分析
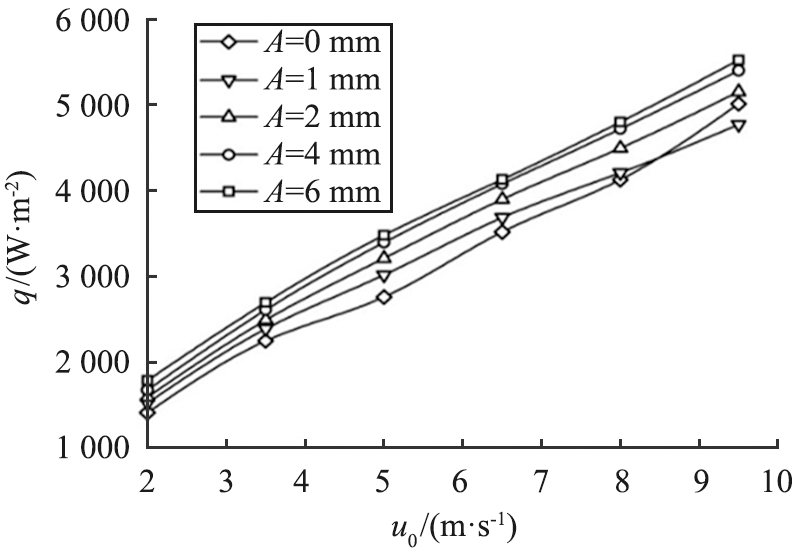
(a)振幅
(b)频率
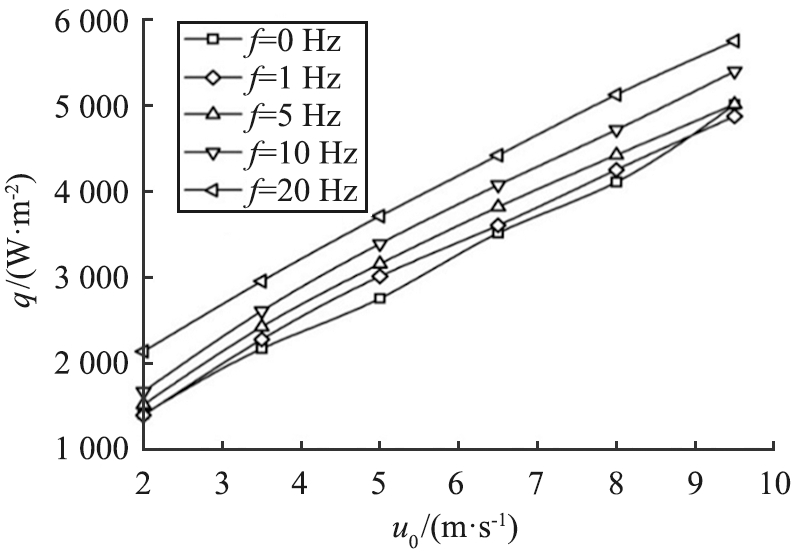
图10 振动参数对翅片热流密度的影响
Fig.10 Effect of vibration parameters on fin heat flux
图10所示为振幅和频率对热流密度的影响。从图中可以看出,振幅和频率对热流密度的影响是热流密度q随振幅、频率和风速的增大而增大,振动增强的传热效果会随着风速的增大表现出先增大后减小的情况。当u0=5 m/s时强化传热效果最好,在高风速及较小振幅和频率下,甚至出现热流密度降低的情况。
图11所示为在各种振幅下热通量和风速的关系。由图可知,当振幅增大时,q也随之增大,当振幅增大或频率增大时,会增大振动速度,从而进一步改善热传递性能,但是,这2种方法对传热的影响是不一样的。此外,从图10(a)中可以看出,在振幅A>4 mm的情况下,随着A的增大,温度的升高,热通量的增加,振幅的改变不显著;而从图10(b)可以看出,随着频率的持续增大, q明显增大,表明在振动过程中频率对换热的影响要比振幅大得多。
3 讨论
利用Fluent仿真软件,对扁管和翅片模型进行仿真分析,用努赛尔数Nu和壁面热流密度q分别描述对流换热强弱。
1)扁管的仿真研究表明, 振动对换热的增强作用随着振幅的增大而增强, 但与频率的关系不大。 随着风速的增大, Nu对振幅的敏感性逐渐下降, 说明在较高的风速时, 振动对换热的作用逐渐减弱。
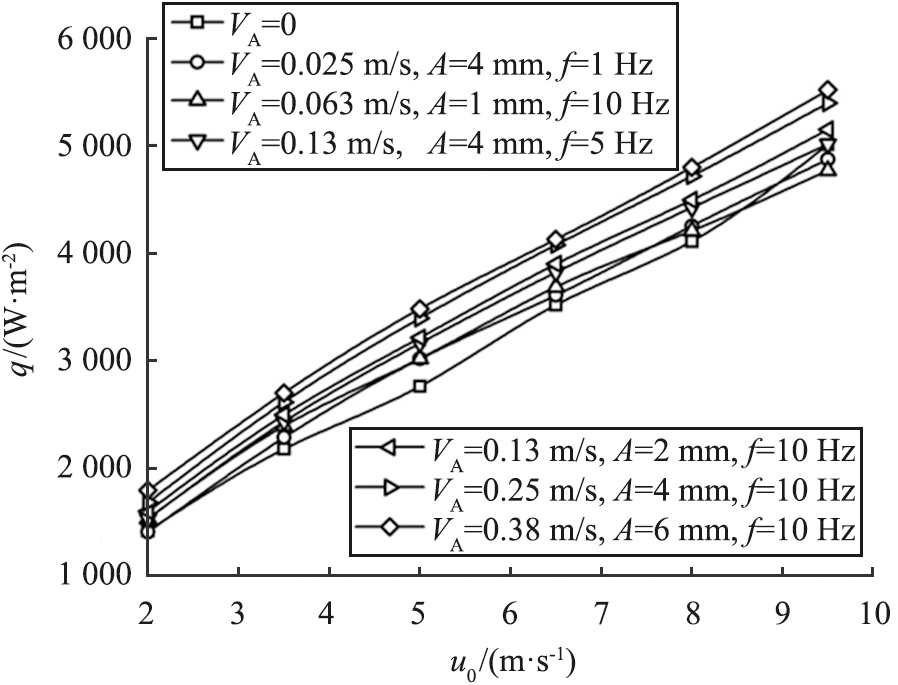
图11 不同振动速度VA时热流密度随风速的变化
Fig.11 Variation of heat flux with wind speed under different vibration velocity amplitude
2)振动作用打破了流场、 温度场, 改变了粒子的移动轨迹, 使气流沿着百叶窗流动, 增强了换热效果。 另外振动将导致翅片的平均热流量q增加, 频率对翅片的影响随振动强度和入口风速的增加而显著。
3)可利用振动破坏散热器翅片的温度场和流场,使得气流可以沿散热器百叶窗流动,从而使得百叶窗的边界层变薄,进而降低翅片的平均温度,提升散热器的换热效率。
[1]蔡改贫, 郝书灏, 黄金若, 等. 振动慢剪破碎机内锥动力学分析[J]. 中国粉体技术, 2022, 28(3): 9-15.
CAI G P, HAO S H, HUANG J R, et al. Dynamic analysis of inner cone of vibration slow shear crusher[J]. China Powder Science and Technology, 2022, 28(3): 9-15.
[2]韩跃新, 朱一民, 印万忠, 等. 低品位铝土矿在振动磨机中的选择性磨矿研究[J]. 中国粉体技术, 2009, 15(5): 16-20.
HAN Y X, ZHU Y M, YIN W Z, et al. Research on selective grinding of lowgrade bauxite in vibration mill[J]. China Powder Science and Technology, 2009, 15(5): 16-20.
[3]袁凤宇, 崔啸宇, 迟源. “立式磨+互联网”在非金属矿行业中的应用[J]. 中国粉体技术, 2016, 22(2): 108-111.
YUAN F Y, CHI Y, CUl X Y. Application of “vertical roller mill+Internet” in non-metallic minerals industry[J]. China Powder Science and Technology, 2016, 22(2): 108-111.
[4]METCALFE G, LESTER D. Mixing and heat transfer of highly viscous food products with a continuous chaotic duct flow[J]. Journal of Food Engineering, 2009, 95(1): 21-29.
[5]UDA N, YAMAOKA N, HORIIKE H, et al. Heat transfer enhancement in lithium annular flow under transverse magnetic field[J]. Energy Conversion and Management, 2002, 43(3): 441-447.
[6]YANG L J, REN J X, SONG Y Z. Convection heat transfer enhancement of air in a rectangular duct by application of a magnetic quadrupole field[J]. International Journal of Engineering Science, 2004, 42(5/6): 491-507.
[7]HABIB M A, ATTYA A M, SAID S A M, et al. Heat transfer characteristics and Nusselt number correlation of turbulent pulsating pipe air flows[J]. Heat and Mass Transfer, 2004, 40(4): 307-318.
[8]ROY S, SAIKRISHNAN P, RAVINDRAN R. Role of non-uniform slot injection (suction) model on the separation of a laminar boundary layer flow[J]. Mathematical and Computer Modelling, 2009, 50(1/2): 45-52.
[9]ARIK M, COHEN A B, YOU S M. Enhancement of pool boiling critical heat flux in dielectric liquids by microporous coatings[J]. International Journal of Heat and Mass Transfer, 2007, 50(5/6): 997-1009.
[10]TURNER A B, HUBBE-WALKER S E, BAYLEY F J. Fluid flow and heat transfer over straight and curved rough surfaces[J]. International Journal of Heat and Mass Transfer, 2000, 43(2): 251-262.
[11]POSEW K, LAOHALERTDECHA S, WONGWISES S. Evaporation heat transfer enhancement of R-134a flowing inside smooth and micro-fin tubes using the electrohydrodynamic technique[J]. Energy Conversion and Management, 2009, 50(7): 1851-1861.
[12]JOARDAR A, JACOBI A M. Heat transfer enhancement by winglet-type vortex generator arrays in compact plain-fin-and-tube heat exchangers[J]. International Journal of Refrigeration, 2008, 31(1): 87-97.
[13]VAJJHA R S, DAS D K, NAMBURU P K. Numerical study of fluid dynamic and heat transfer performance of Al2O3 and CuO nanofluids in the flat tubes of a radiator[J]. International Journal of Heat and Fluid Flow, 2010, 31(4): 613-621.
[14]KATTI V, PRABHU S V. Heat transfer enhancement on a flat surface with axisymmetric detached ribs by normal impingement of circular air jet[J]. International Journal of Heat and Fluid Flow, 2008, 29(5): 1279-1294.
[15]ZHOU J W, WANG Y G. Unsteady jet impingement: heat transfer on smooth and non-smooth surfaces[J]. International Communications in Heat and Mass Transfer, 2009, 36(2): 103-110.
[16]BHARADWAJ P, KHONDGE A D, DATE A W. Heat transfer and pressure drop in a spirally grooved tube with twisted tape insert[J]. International Journal of Heat and Mass Transfer, 2009, 52(7/8): 938-1944.
[17]COWELL T A, HEIKAL M R, ACHAICHIA A. Flow and heat transfer in compact louvered fin surfaces[J]. Experimental Thermal and Fluid Science, 1995, 10(2) :192-199.
[18]CHANG Y J, WANG C C. A generalized heat transfer correlation for louver fin geometry[J]. International Journal of Heat and Mass Transfer, 1997, 40(3): 533-544.
[19]CHANG Y J, HSU K C, LIN Y T, et al. Generalized friction correlation for louver fin geometry[J]. International Journal of Heat and Mass Transfer, 2000, 43(12): 2237-2243.
[20]CHANG Y J, CHANG W J, LI M C, et al. An amendment of the generalized friction correlation for louver fin geometry[J]. International Journal of Heat and Mass Transfer, 2006, 49(21/22): 4250-4253.