颗粒物质广泛存在于自然界、日常生活与工业生产中,颗粒材料动力学知识的研究对于筒仓以及旋转滚筒的工业设计有着十分重要的意义[1-4]。由于旋转滚筒中颗粒流动的控制和测量相对容易,因此已成为研究颗粒流动动力学的主要模型系统[5-6]。旋转滚筒中存在2个颗粒行为差异较大的区域,即主动层与被动层。被动层中的颗粒动力学的研究对提高颗粒物料的混合效率、揭示自然界中泥石流和崩塌的规律有指导意义。当较低转速下的滚筒内颗粒发生周期性离散崩塌时,主动层颗粒在重力作用下沿表面向下快速流动,被动层颗粒在主动层颗粒流剪切以及滚筒旋转作用下会在粒径尺度发生细微的位移,使原有的颗粒结构发生变化,即颗粒重排,从而带来颗粒系统的剪胀与压实。颗粒重排也会反过来对崩塌的触发与传播产生影响,目前对于整体崩塌机制与被动层局部颗粒重排之间联系的理解还不够明确[7-9]。
多年来,人们对旋转滚筒中颗粒材料的运动进行了大量的研究。Gray等[10]提出一种缓慢旋转滚筒中颗粒离散崩塌的理论框架,将颗粒系统划分为主动层的类流体区域和被动层的类固体区域,其中固相区域视为刚性旋转体,仅为表面崩塌流提供颗粒。Amon等[11]发现崩塌休止角的分布存在历史依赖性,主动层崩塌颗粒在进入被动层后形成的堆积结构可以在一定程度上影响崩塌的触发,表明被动层颗粒在崩塌系统中具有比单纯的质量传输更重要的作用。Dubé等[12]利用放射性粒子跟踪研究了非球形颗粒的动力学性质,发现崩塌前被动层中颗粒的重新排列会导致颗粒堆积结构的膨胀。Salinas等[13]研究了小尺度扰动在旋转滚筒崩塌发生中的作用,发现对于旋转滚筒内未达到休止角的颗粒系统,很小的扰动就可以触发崩塌,这表明颗粒局部重排在颗粒介质崩塌宏观响应中扮演着重要角色。
颗粒重排总是伴随着颗粒原有堆积结构的破坏以及个别颗粒的局部不规则运动,之前的学者对准静态剪切下颗粒重排的动力学及统计特点进行了深入研究,但对崩塌过程中的颗粒重排的研究还不够充分。Richter等[14]对缓慢倾斜的三维颗粒填料系统进行实验,发现在较大的倾斜角度下自由表面的颗粒重排更容易发生崩塌,且表面事件的细节强烈依赖于颗粒间相互作用的微观细节。Wang等[15]研究了二维滚筒中圆盘的崩塌,观察到崩塌过程中的力链重排。Li等[16]通过对旋转滚筒中的球形颗粒的主动层和被动层进行同步测量,确定被动层中的颗粒重排是由主动层中的崩塌触发的,并且总是从被动层上部区域开始沿平行于自由表面方向向下传播。Li等[17]通过同步测量旋转滚筒中不规则颗粒系统的主动层和被动层,观察到被动层不规则颗粒的重排存在2种不同的形式,分别处于崩塌间隔与崩塌期间。其中前者在球形颗粒的离散崩塌实验中并不能被观察到,出现这一现象的原因还不是很明确。
基于离散元法(discrete element method, DEM)的数值模拟为被动层的动力学研究提供了很多实验难以观测到的数据[18]。Stanifer等[19]对施加切应变下的颗粒系统进行数值模拟,发现崩塌可以分解为局部变形的爆发,并且使用持久同源性方法对其进行识别。Sanz等[20]的模拟结果指出崩塌的发生很大程度上是一个随机过程,在模拟过程中的任何时候随机化颗粒的速度都会导致不同的后续崩塌发生。冯靖禹等[21]通过对旋转滚筒中球形颗粒离散崩塌的数值模拟,统计崩塌开始时主动层表面率先发生大范围移动的颗粒的位置,发现崩塌起始位置在整个主动层表面上是随机分布的,然而之前对旋转滚筒的研究表明,崩塌总是从距离斜面顶部不远处开始,这与仿真结果之间存在分歧的原因有待进一步研究,需要对仿真系统中表现出的随机性进行进一步的统计分析。
本文中搭建旋转滚筒中球形颗粒离散崩塌的离散元法仿真系统,通过修正的颗粒温度计算方法识别被动层颗粒重排,分析颗粒重排的分布与传播特性,为崩塌的机制以及仿真与实验中的分歧做出可能的解释。
1 仿真方法
1.1 仿真系统
在本文中,利用Hertz-Mindlin接触力的软球DEM模型研究旋转滚筒中球形颗粒的离散崩塌,DEM跟踪所有颗粒,同时考虑颗粒之间和颗粒与边界的相互作用[22],通过牛顿第二运动定律描述颗粒的平移运动和旋转运动。对于颗粒i、 j相互作用的控制方程为
(1)
(2)
式中: ui和ωi分别表示颗粒i的平移速度和角速度; Fcn,ij、 Fct,ij分别为颗粒i与颗粒j之间的法向和切向接触力; Fdn,ij、 Fdt,ij分别为颗粒i与颗粒j之间的法向和切向阻尼力; Gi为颗粒i所受到的重力; Tt,ij为颗粒i与颗粒j之间的切向力; Tr,ij为颗粒i与颗粒j之间的滚动摩擦力,这2个力带来了作用在颗粒i上的颗粒j的转矩。这些力和转矩在与颗粒i接触的n个颗粒上求和。
仿真模型的几何形状如图1所示。x轴为滚筒轴向,y、 z轴分别指向水平与竖直方向。沿轴向x施加周期性边界条件。这种处理可以生成足够的数据进行分析,同时使用少量的颗粒(152 000个颗粒)以最大程度地减少计算时间。模拟的时间步长设置为4×10-7 s。本文中所用的滚筒和颗粒材料是干燥无黏性的玻璃,在参考文献[23]中已有报道。表1所示为离散元仿真参数。
表1 离散元仿真参数
Tab.1 DEM parameters

参数滚筒直径/mm滚筒长度/mm滚筒旋转速度/(r·min-1)填充率/%颗粒直径/mm颗粒密度/(kg·m-3)杨氏模量/Pa泊松比静摩擦系数滚动摩擦系数恢复系数数值140200.194612 4566.89×1090.290.450.020.65

图1 仿真系统示意图
Fig.1 Schematic diagram of simulation system
本文中通过比较实验与仿真中崩塌的上下休止角的变化来验证仿真系统的可靠性。 实验和仿真都是在相同的系统配置下进行的, 滚筒的转速为0.19 r/min。 对于此旋转速度, 实验和仿真中颗粒都表现为离散的崩塌。 我们通过在颗粒床表面拟合一条直线来研究在模拟和实验中表面角θ的变化。 图2所示为θ随时间t的变化, 其中蓝线表示仿真结果, 红点表示实验数据。 显然, 2条曲线显示出几乎相同的变化趋势, 这意味着所提出的仿真系统可以有效地模拟崩塌周期。 通过平均实验中的50个连续崩塌, 休止的上角为(30.51±0.5)°, 休止的下角为(27.45±0.5)°。 仿真结果表明, 休止角上角为(30.37±0.5)°, 休止角下角为(27.37±0.5)°, 平均值差异在0.5°以内, 因此, 仿真结果与实验数据吻合良好。
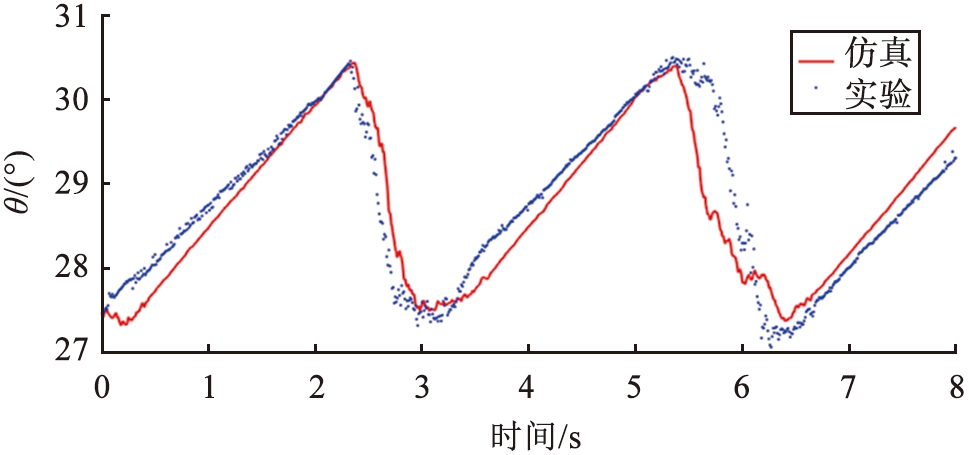
图2 模拟结果与实验数据的表面角度随时间的变化
Fig.2 Temporal variations of surface angles from simulation results and experimental data
1.2 颗粒温度计算方法
由于传统的以单个颗粒相对位移大小为指标的方法只能识别出单个重排颗粒,无法考察其邻域堆积结构的细微变化,因此本文中使用颗粒温度来捕捉颗粒系统内部颗粒重排引起的颗粒结构的变化。颗粒温度是衡量一个区域内颗粒非仿射运动剧烈程度的指标,能很好地识别出颗粒重排带来的颗粒非仿射位移。根据文献[24],DEM模拟中颗粒温度δv2的计算过程为
(3)
(4)
式中: p、 q表示x、 y、 z中的任意2个方向; 〈CpCq〉为单位体积内颗粒应力; n为单位体积的颗粒数; vp,k为颗粒k在方向p上的瞬时速度; cp为区域瞬时流体力学速度。颗粒温度定义为颗粒在3个方向上的正应力的均值。
对于本文中旋转滚筒中的颗粒系统,所有颗粒都会具有一个随着滚筒旋转的速度。在滚筒转速较低的情况下(0.19 r/min),该速度值较小(最大1.39 mm/s),对于主动层运动较为剧烈的区域的颗粒温度的计算不会产生影响,但是对于被动层测量点来说,即便测量点内颗粒全部相对静止,滚筒的旋转会给测量点内不同位置的颗粒带来不同的线速度,从而导致计算出的颗粒温度值偏高。为了消除滚筒旋转给颗粒温度计算值带来的背景颗粒温度,本文中对式(3)中的颗粒瞬时速度做出修正,将颗粒瞬时速度减去颗粒所在位置对应的滚筒旋转线速度,得到修正后的〈CpCq〉为
(5)
Vp,k=vp,k-vp,kro,
(6)
式中vp,kro为颗粒k所在位置对应的滚筒旋转线速度在方向p上的分量。
由于仿真中使用了周期性边界,因此着重研究位于颗粒床中间区域的颗粒的特性,以消除壁在实验中的影响。对于每个测点,选择直径为4 mm、长度为10 mm,与滚筒平行的小圆柱体进行颗粒温度的计算,每个计算区域内包含大约150个颗粒。
本文中试图使用颗粒温度来捕捉旋转滚筒的颗粒崩塌体系中被动层颗粒重排,利用颗粒局部不规则运动带来的颗粒温度波动来捕捉被动层中颗粒原有堆积结构的变化,但在这样一个重力作用下自然堆积而成的颗粒系统中颗粒的堆积并不是完全致密。孙其成等在文献[25]中将配位数小于等于3的颗粒划分为相对自由的颗粒,这种颗粒不参与颗粒系统的主力链,并且在主力链颗粒组成的“颗粒牢笼”中具有一定的运动自由度,可以在不影响主力链的情况下产生小范围的位移。这种单个相对自由的颗粒的不规则运动会产生较高的颗粒温度,给颗粒重排的识别带来很大的干扰。针对这种情况,在计算颗粒温度时去除了配位数小于等于3的颗粒,只考虑主力链颗粒的不规则运动情况。
图3(a)所示为由式(3)计算得到的滚筒侧面颗粒温度分布图, 被动层颗粒温度集中分布在10-4 mm2/s2左右; 图3(b)、 3(c)是由式(5)得到的结果,分别对应崩塌间隔与崩塌期间,图像针对被动层区域进行了对数增强,不难看出在去除滚筒旋转带来的影响后被动层颗粒温度得到更宽的分布范围,可以展现出更多细节。在崩塌间隔时,被动层颗粒温度近似水平分层,水平高度越低的区域具有越低的颗粒温度,随着崩塌的发生,被动层靠下方的区域颗粒温度在剪切与冲击作用下升高,被动层颗粒温度分布演变为平行于流动方向分层,这与文献[26]中实验测量得到的滚筒侧面颗粒温度具有相似的分布,进一步验证了本文中仿真系统的可靠性。图3(d)、 3(e)给出了去除配位数≤3的颗粒后计算得到的颗粒温度空间分布,有效去除了相对自由的颗粒不影响主力链的微小位移带来的速度波动,对该图像进行二值化,去除主动层区域以及被动层区域的细小亮点(半径<4 mm),剩下的亮点即可认为是颗粒重排区域。
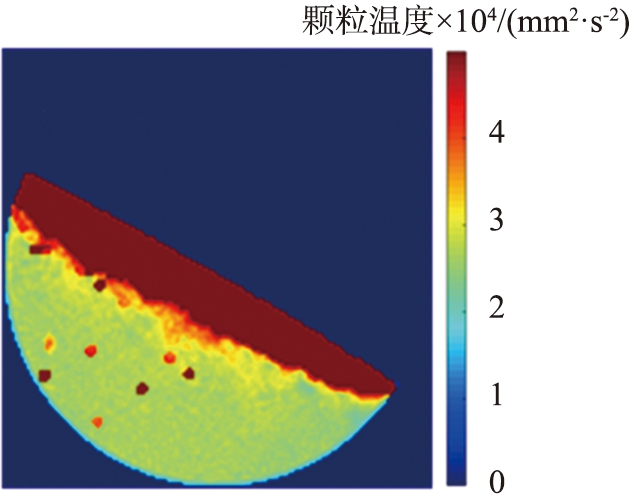
(a)以地面参考系下颗粒速度计算颗粒温度
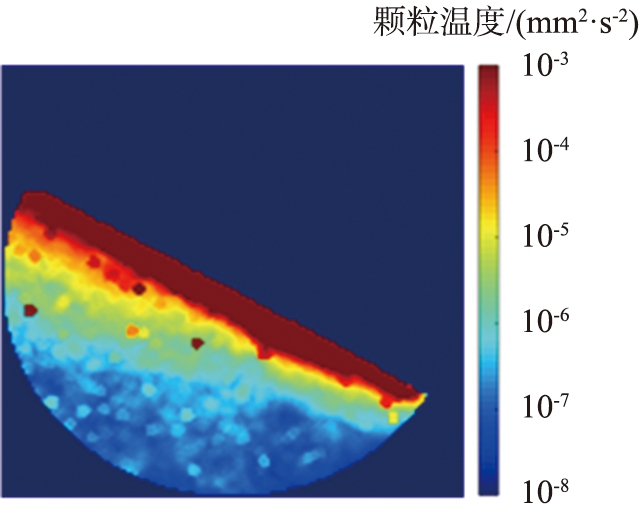
(b)以滚筒参考系下颗粒速度计算颗粒温度(崩塌间隔)
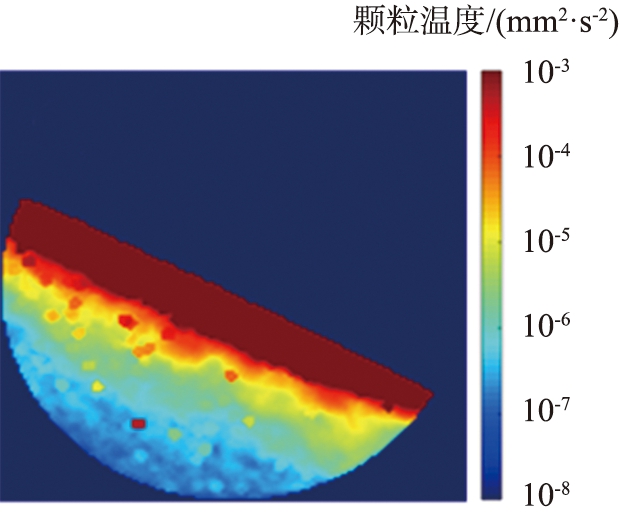
(c)以滚筒参考系下颗粒速度计算颗粒温度(崩塌期间)
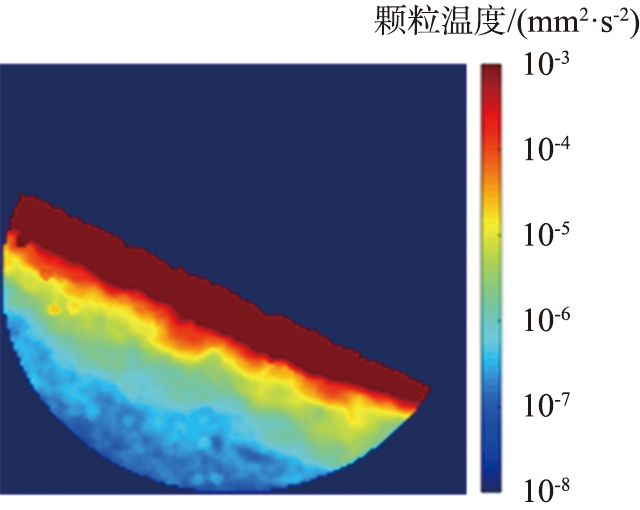
(d)去除配位数小于等于3的颗粒计算颗粒温度
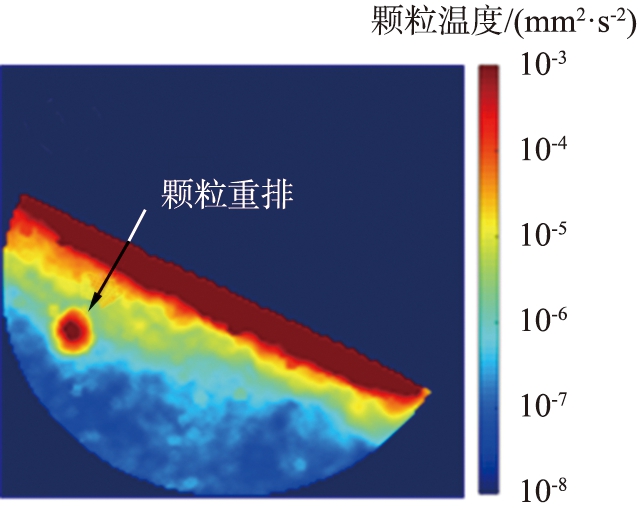
(e)一个典型的颗粒重排
图3 不同计算方法得到的颗粒温度的空间分布
Fig.3 Spatial distribution of granular temperature obtained using different computational methods
2 结果与讨论
2.1 颗粒重排的传播
颗粒温度计算方法通过计算颗粒重排带来的局部速度波动可以有效地识别出颗粒重排的触发、传播过程及其影响范围。图4所示为典型的被动层颗粒重排引起的动能波动的传播过程,重排由被动层一点开始(0.17 ms),重排区域直径大概为2个粒径,随后由该重排中心点向周围传播,在0.25 ms大致传播到最远距离。
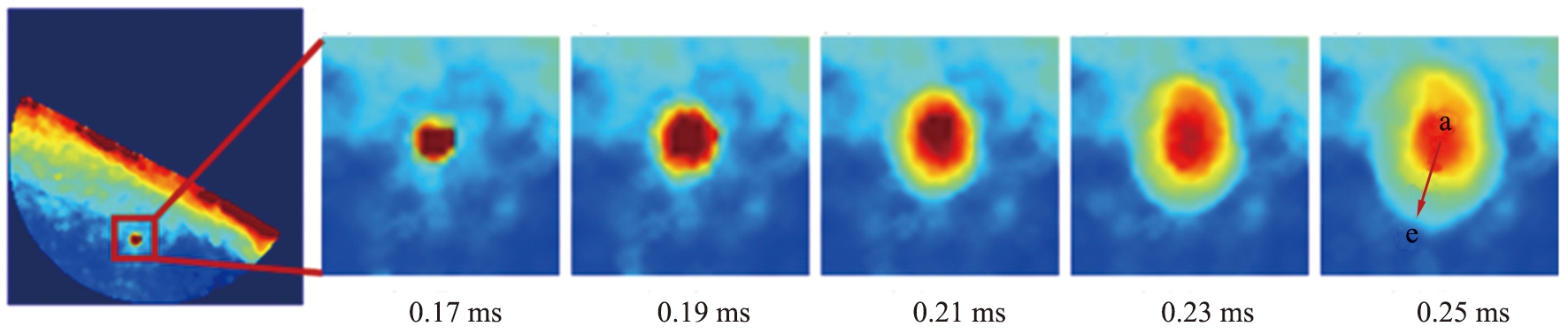
图4 不同时间颗粒重排传播的空间示意图
Fig.4 Spatial schematic diagram of particle rearrangement propagation at different time
图5所示为中心点a向边缘点e的连线上选取5个点计算颗粒温度。根据5个点颗粒温度脉冲之间的时序关系可以计算出此处动能波动传播速度为114 m/s。该速度与Lemrich[27]在沙堆中实验测量出的剪切波传播速度相一致,即(130±20) m/s。
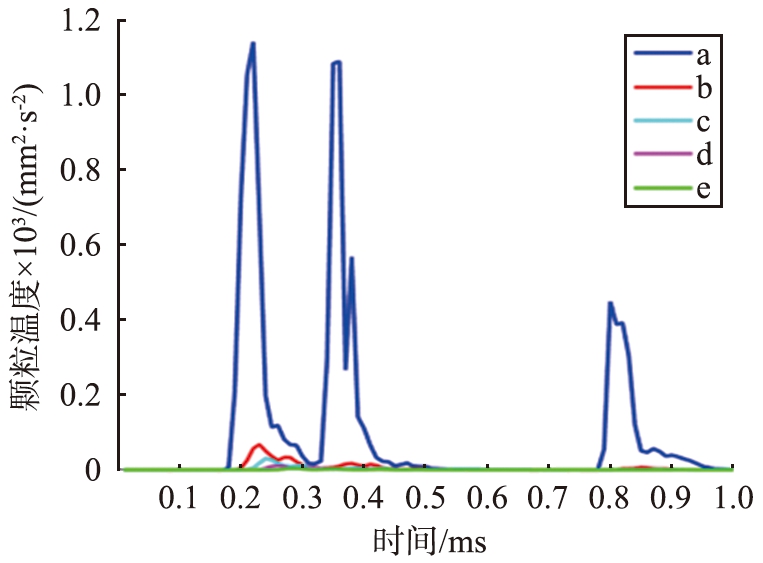
(a)整个重排过程
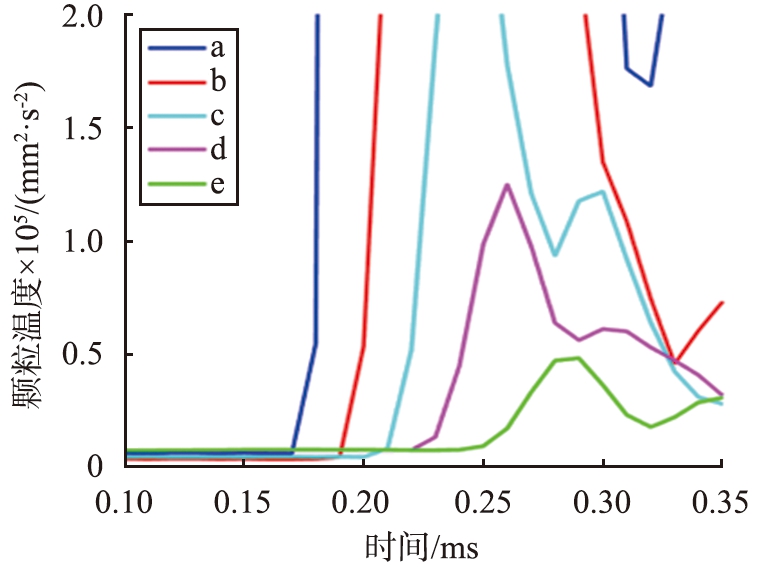
(b)重排刚触发时不同位置的颗粒温度
图5 由颗粒重排中心点到边缘颗粒温度
Fig.5 Propagation of velocity fluctuations induced by particle rearrangement
图6所示为颗粒温度峰值随离重排中心点距离的变化,由颗粒重排中心点到边缘等间隔1 mm选取12个颗粒温度计算点(蓝色的点),并对结果进行指数拟合(红线)。颗粒重排带来的动能波动以弹性波的形式由触发点向四周传播,并且波动幅度随着传播距离的增加呈指数下降形式,4 mm外的颗粒温度峰值显著降低。
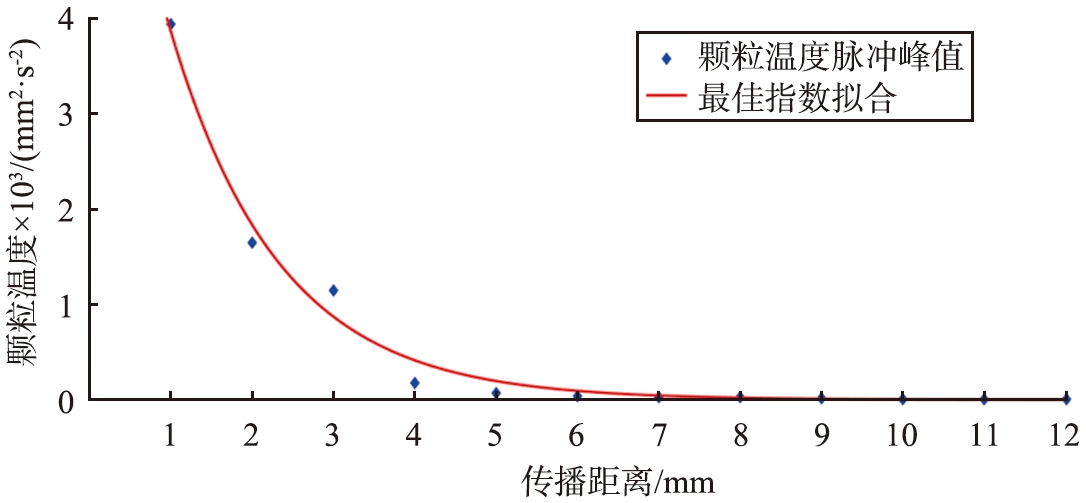
图6 颗粒温度脉冲峰值随距离颗粒重排中心点的变化
Fig.6 Granular temperature pulse peak with distance from rearrangement center
2.2 颗粒重排点的空间分布
图7所示为颗粒重排点的空间分布。对仿真系统中15个连续的崩塌周期进行统计,发现颗粒重排的传播过程在整个崩塌周期的被动层中都广泛存在。定义有任一颗粒在时间为0.1 s内位移超过1个粒径时崩塌开始,没有颗粒在0.1 s内位移超过1个粒径时崩塌结束,以此划分出崩塌期间与崩塌间隔2个阶段。图7(a)、 (c)分别展示了连续15个崩塌周期中崩塌与崩塌间隔阶段颗粒重排点的空间分布。沿着主动层表面方向将滚筒侧面划分为边长为10 mm的正方形网格,统计每个网格中颗粒重排点出现次数,绘制出归一化后伪彩色图如图7(b)、 (d)所示。可以看出,无论是崩塌间隔还是崩塌期间,颗粒重排发生最频繁的位置都位于被动层靠上的位置,颗粒重排发生的越频繁就意味着该区域相比之下结构更加脆弱,更容易在外力扰动下发生重排。
图7(b)所示为处于崩塌间隔期间的颗粒系统中被动层最脆弱的区域位于被动层最顶部,这可以解释文献[21]中观察到的仿真系统中崩塌起始位置与在实验中观察得到的结果不一致的现象。冯靖禹等[21]的DEM仿真仿真结果显示旋转滚筒中颗粒离散崩塌的起始位置是在自由表面上自由分布的,而实验观察到颗粒崩塌的起始位置总是位于距离斜坡顶部不远处,这可能是由实验与仿真系统之间的差异导致的。在仿真系统中颗粒重排的发生是相对局部的,崩塌间隔期间颗粒重排大部分是由相对自由颗粒撞击直接导致的,颗粒温度脉冲则由该点出发向四周辐射传播;在实验中,由于电机的振动、滚筒形状不够理想等因素,因此整个颗粒系统都处于微小扰动下,这种整体、持续的扰动会导致上述被动层最脆弱的区域率先发生大规模的重排,从而导致该区域上方即主动层上部区域颗粒率先发生崩塌。
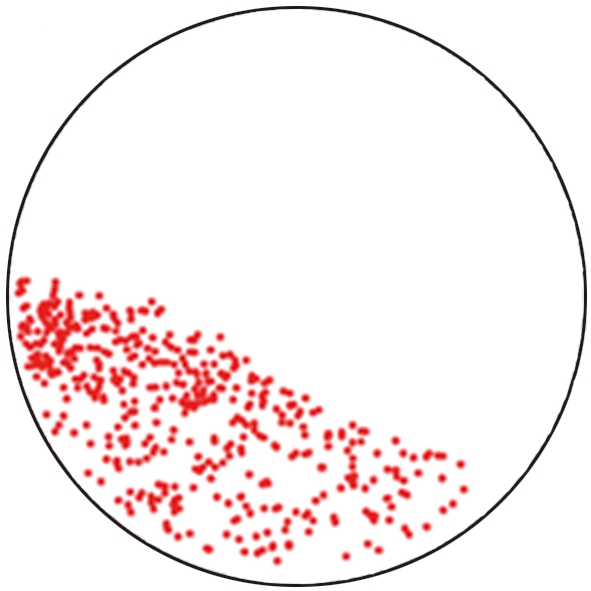
(a)崩塌间隔颗粒重排点空间分布
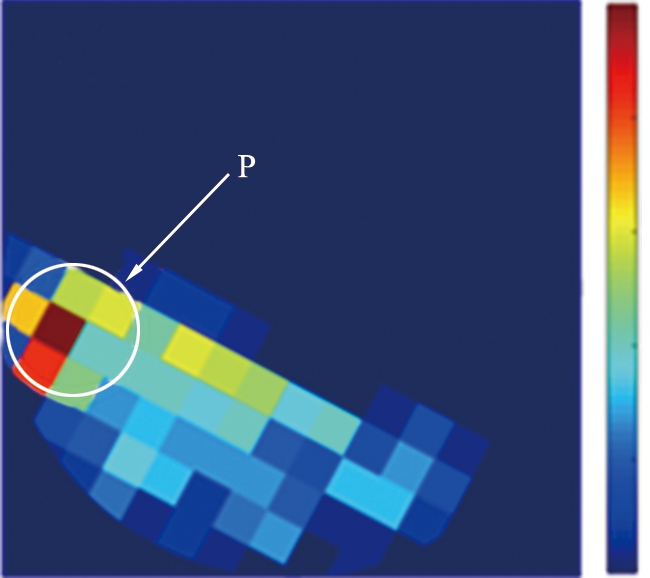
(b)崩塌间隔不同位置颗粒重排频率
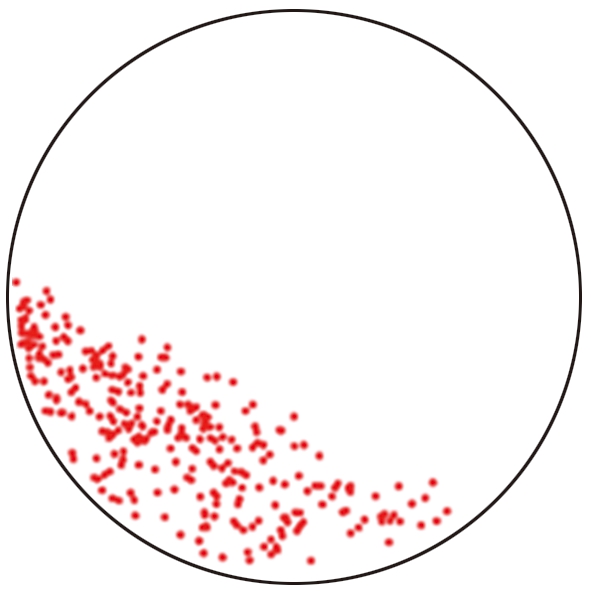
(c)崩塌期间颗粒重排点空间分布
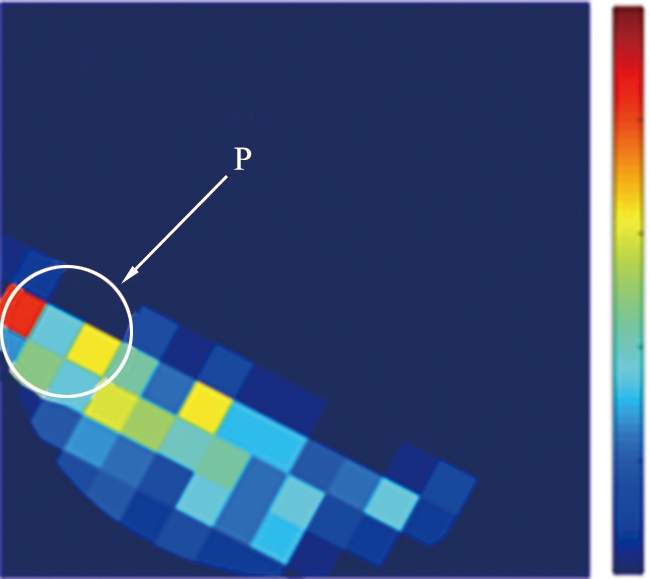
(d)崩塌期间不同位置颗粒重排频率
图7 15个崩塌周期中颗粒重排点的空间分布
Fig.7 Spatial distribution of particle rearrangement points during 15 avalanche periods
图7(d)所示为崩塌期间滚筒侧面各个位置颗粒重排发生次数,与图7(b)进行了相同的归一化。比较二者不难发现,被动层靠上部位置在崩塌间隔期间发生重排的频率更高,即P位置的颗粒重排更倾向于发生在崩塌间隔期间。由于崩塌期间主动层颗粒流的剪切作用,被动层颗粒在崩塌期间受到的扰动显然是要大于崩塌间隔期间,因此P区域颗粒在崩塌期间具有更加紧密的堆积结构,使其在更大的扰动下反而不容易发生颗粒重排,说明球形颗粒与不规则颗粒一样,在崩塌前颗粒系统上游区域会先发生颗粒压实。
选取深度为20~30 mm、平行于自由表面的区域,统计距离斜面顶部不同距离的区域颗粒重排点出现的频率。在15个崩塌周期中,崩塌期间出现的颗粒重排点有225个,崩塌间隔期间出现的颗粒重排点有437个,显著多于崩塌期间。图8所示为到斜面顶部不同距离的区域颗粒重排点出现次数统计结果。图8(a)、 (b)所示分别为崩塌间隔期间与崩塌期间重排点出现的次数以及最佳的伽马分布拟合(αrest=2.8, βrest=19.4; αava=2.4, βava=21.4)。这与文献[28]中给出的颗粒系统体积分数普遍服从的伽马分布具有一致性,但在滚筒被动层中球形颗粒体积分数变化不明显,具体重排概率与体积之间的关系还有待进一步研究。
由图4展示出的颗粒温度空间分布的变化过程可以看出, 颗粒重排引起的颗粒温度波动是由被动层中一点开始向四周传播, 且有时在传播速度上具有各向异性。 为了研究传播速度产生差异的原因, 本文中对颗粒重排区域的几何各向异性进行研究。 考察颗粒重排区域内所有颗粒与颗粒的接触点, 可以认为法向接触力大于区域平均法向接触力的接触点参与主力链的形成, 将参与主力链的2个颗粒之间接触向量在yOz平面上投影的角度定义为主力链接触角, 图9(b)给出了主力链接触角的分布, 区域表现出比较明显的各向异性, 大量触点沿力链方向排列, 少量触点沿垂直于力链的方向排列。 比较图9(a)、 (b)不难看出, 速度波动在力链方向上具有相对更高的传播速度。
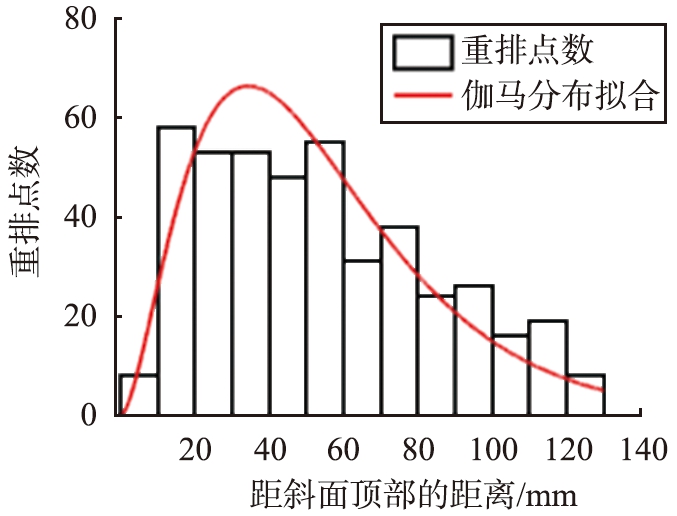
(a)崩塌间隔期间
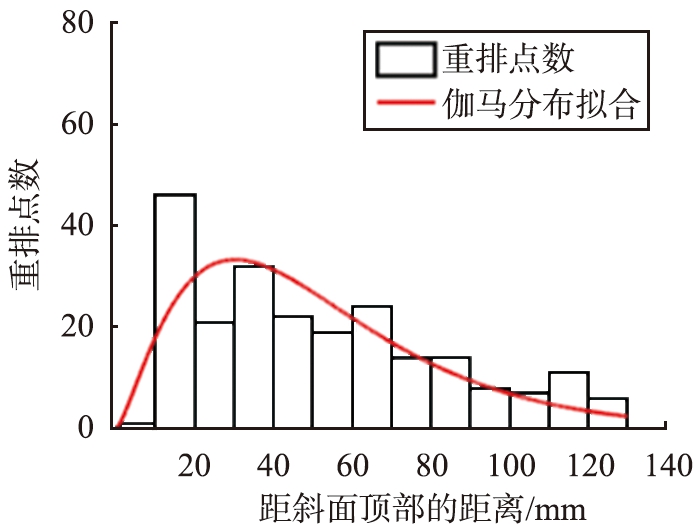
(b)崩塌期间
图8 离斜面顶部不同距离颗粒重排点的分布及最佳分布函数拟合
Fig.8 Distribution of particle rearrangement at different distances from top of surface and best-fit distribution function
为了进一步考察被动层区域几何各向异性在跟随滚筒旋转过程中的变化,图10给出了一个与滚筒相对位置保持不变的区域在其旋转到不同位置时主力链接触角分布的变化。计算区域为与滚筒平行、距离滚筒中心50 mm、半径为5 mm、长度为10 mm的小圆柱体,选取与y轴负方向夹角分别为60°、 90°、 120°、 150°的位置。可以看出颗粒从自由表面下部进入被动层时就具有较强的各向异性,且主要力链的方向大致指向滚筒的中心。图10(a)—(c)显示出在该区域随着滚筒旋转的过程中力链方向相对于滚筒大致不变,可以认为在这个过程中颗粒的相对堆积结构变化不大。当该区域随着滚筒继续上升至图10(d)位置时,颗粒原先的堆积结构的几何各向异性变弱,随着该区域原有力链方向逐渐趋于水平,在重力作用下原有力链不能支撑某些部位的几何结构,该位置颗粒堆积结构较之被动层其他位置更容易发生更大的变化,这也给图7所示的颗粒重排发生最频繁的位置位于被动层靠上的位置这一现象提供了解释。
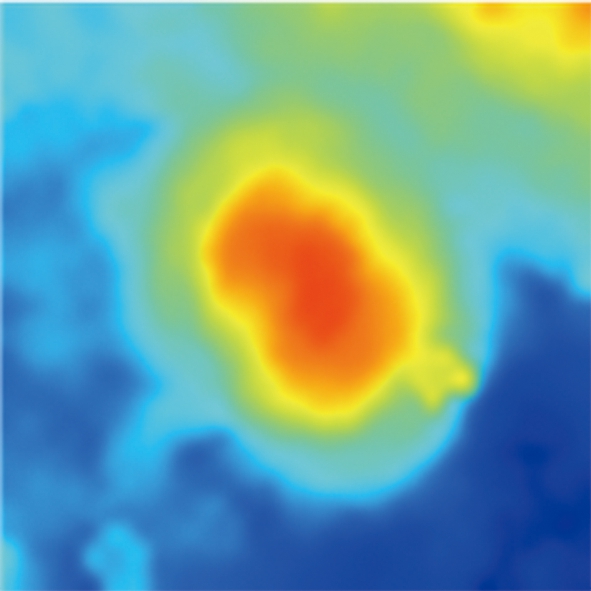
(a)颗粒温度空间分布
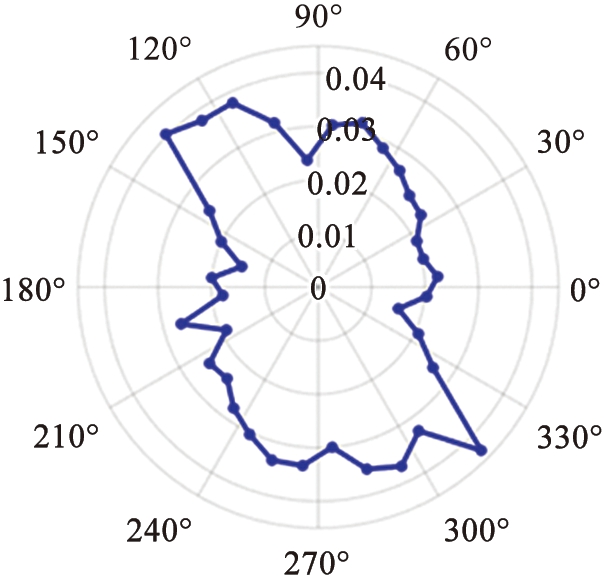
(b)主力链接触角的分布
图9 颗粒重排传播速度的各向异性与堆积结构几何各向异性
Fig.9 Anisotropy of particle rearrangement propagation velocity and particle contact network
2.3 重排的力学特征
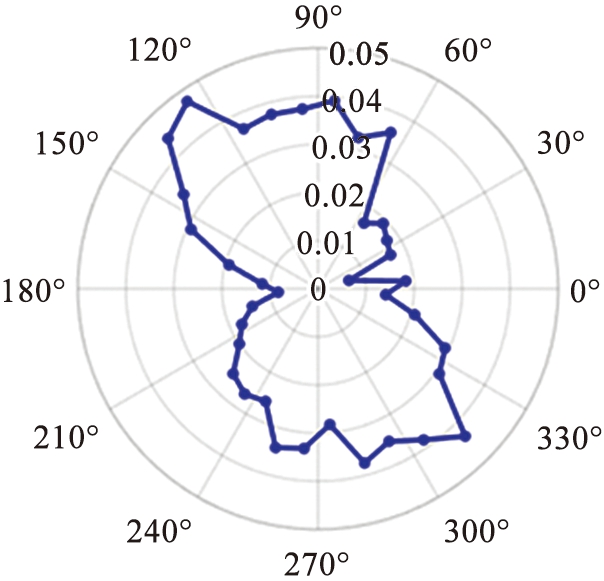
(a)计算区域-O-y轴负方向夹角60°
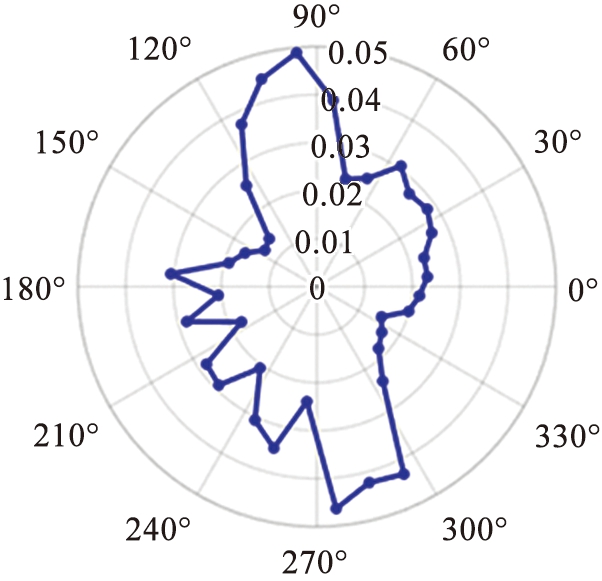
(b)计算区域-O-y轴负方向夹角90°
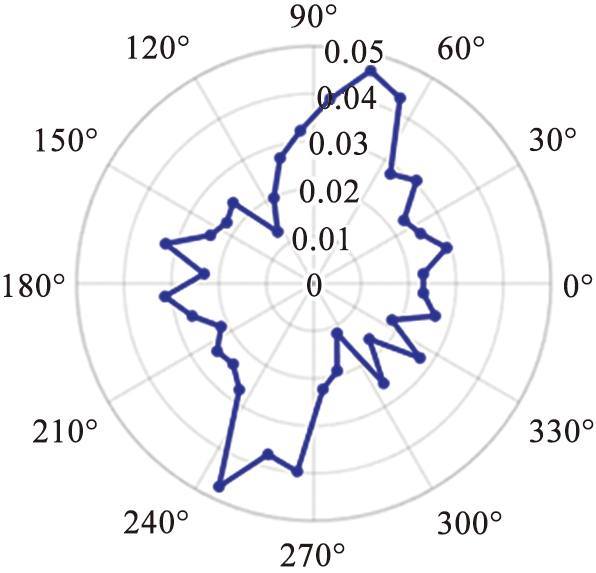
(c)计算区域-O-y轴负方向夹角120°
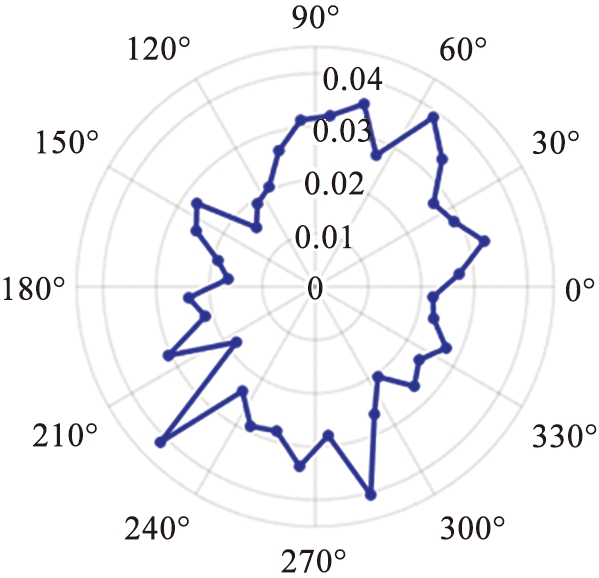
(d)计算区域-O-y轴负方向夹角150°
图10 被动层固定区域旋转到不同位置时接触点角度分布
Fig.10 Contact orientation distribution of fixed region in passive layer upon rotation to different positions
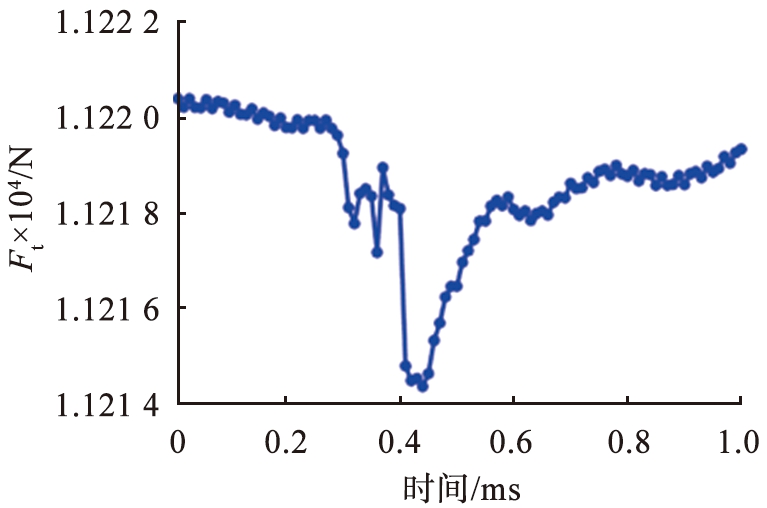
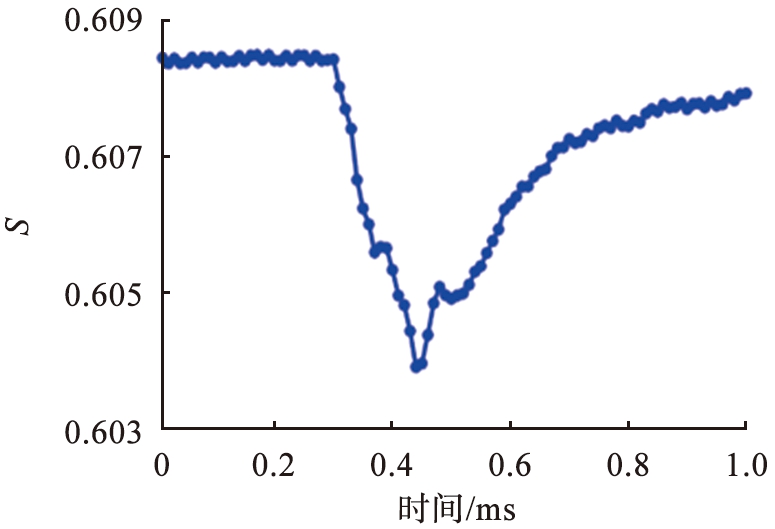
图11(b)、 (c)所示为颗粒重排点重排过程中平均法向力与切向力的变化。 由图可知, 0.3~0.37 ms颗粒间平均法向接触力迅速增加, 达到最大值, 平均切向力小幅度减小;0.37~0.42 ms平均法向力、切向力同时迅速减小到最小值。法向接触力在重排刚开始时的增加以及图4给出的颗粒重排引起的速度波动的传播模式说明了这种颗粒重排是由重力直接触发,即原有的力链在随着滚筒旋转一定角度后不能继续支撑原有的颗粒堆积结构,颗粒在重力作用下形成新的力链。被动层紧密堆积的颗粒是否能够发生颗粒重排主要受系统中摩擦力影响,为了研究摩擦力在系统中的作用,定义变量S=|Ft|/μFn,其中μ为静摩擦系数, Ft为切向力, Fn为法向力。变量S也可称作组织摩擦力,给出了接触点距离库仑失效准则有多远的信息,S越小说明接触点距离库伦失效准则越远, 如果触点处于库仑失效
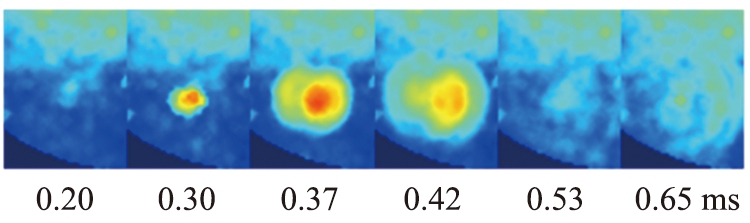
(a)典型的被动层颗粒重排过程
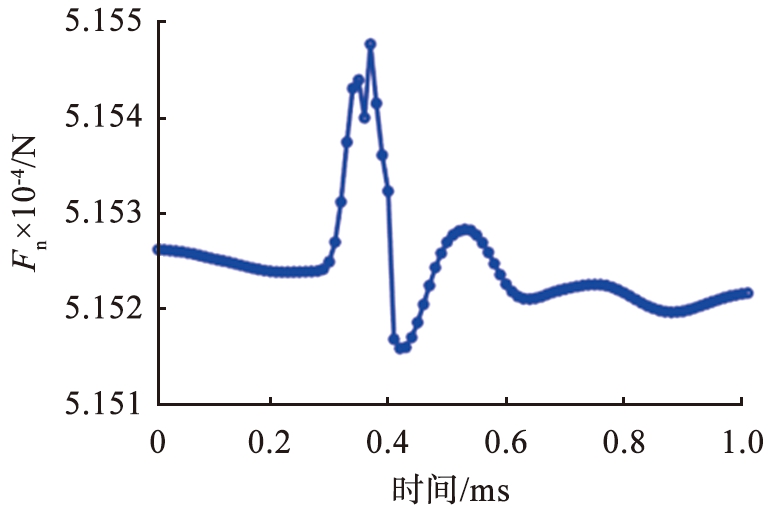
(b)平均法向力随时间的变化
(c)平均切向力随时间的变化
(d)变量S平均值随时间的变化
图11 颗粒重排前后颗粒间接触力的变化
Fig.11 Change in interparticle contact forces during particle rearrangement
准则,则S为1。图11(d)所示为颗粒重排过程中整个区域S平均值的变化,可以看到随着颗粒重排的发生,S的平均值先持续减小,在0.43 ms达到最小值,随后再逐渐增大,且重排后的S均值略微小于重排前的,说明在重排过程中颗粒体系先压实再膨胀,且整个重排过程使该区域的颗粒系统更加远离库伦失效准则。
(a)法向力与切向力分布
(b)组织摩擦力的分布
注: F为颗粒间接触力(红:切向力,蓝:法向力);
图12 被动层上部区域接触力及组织摩擦力的概率分布
Fig.12 Probability distribution of contact force and mobilized friction on upper region of passive layer
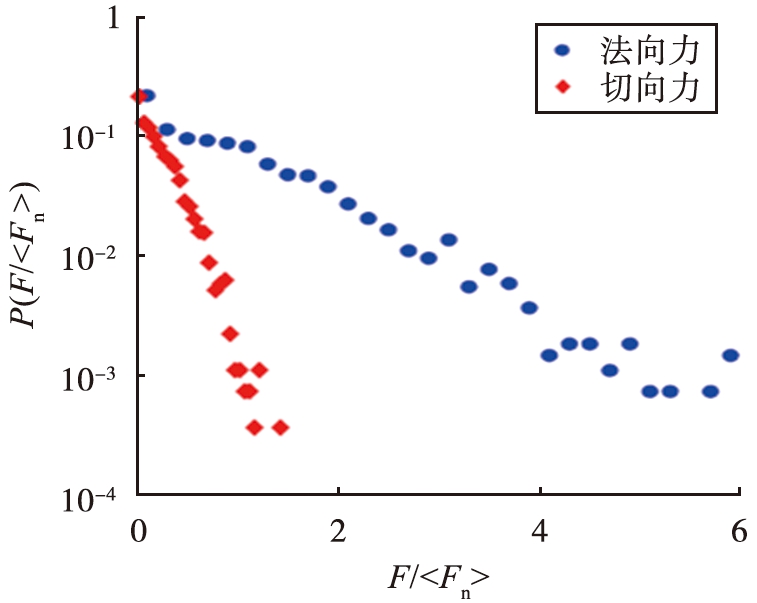
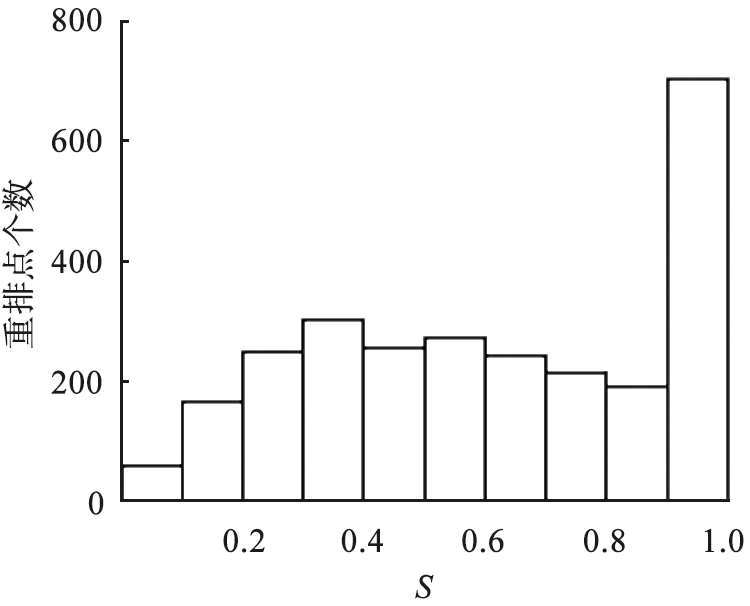
图12(a)所示为被动层上部区域的法向力、 切向力和切向力与法向力之比的分布。 法向力和切向力用平均法向力归一化。 与文献[29]中给出的剪切系统的分布相比, 法向力的分布具有相似的指数尾, 但在法向力低于平均值时具有不同的分布: 文献[29]给出的剪切系统由于受到更大的外部加载, 其法向力分布在力小于平均值时向0倾斜, 整个分布的峰值在平均值附近; 而在本文中给出的旋转滚筒中的颗粒系统中, 法向接触力小于平均值的颗粒数量占比更高, 在靠近0处达到分布的峰值。 图12(b)给出了变量S的分布,大量接触点处于库伦临界附近,对应于颗粒系统中相对自由的颗粒, 使得该颗粒系统中的颗粒重排与外部加载的剪切或压缩系统相比更易触发、 重排后带来的速度波动更小。
3 结论
使用DEM对旋转滚筒中的被动层颗粒重排进行研究,从被动层颗粒动力学及堆积结构的角度研究了旋转滚筒离散崩塌中被动层的颗粒重排机制。
1)颗粒重排在整个离散崩塌周期中广泛存在,颗粒重排带来的动能波动以弹性波的形式由触发点向四周传播,并且波动幅度随着传播距离的增加以指数形式衰减。
2)在整个离散崩塌周期中,被动层颗粒重排在靠近顶部的区域发生最为频繁;而相较于崩塌期间,崩塌间隔阶段的被动层顶部区域更容易发生重排。
3)颗粒重排传播速度的各向异性与重排点区域的几何各向异性相关,在主力链的方向上具有更高的传播速度。被动层颗粒堆积结构的几何各向异性在崩塌由主动层进入被动层后产生,且在其随滚筒旋转到被动层靠上部位时减弱。
根据颗粒重排点的空间与时间分布可知,在整个离散崩塌周期中被动层中最顶部的位置颗粒结构最脆弱,最容易发生颗粒重排,导致在实验系统的崩塌起始位置总是在离斜面顶部不远处。被动层颗粒堆积结构的几何各向异性在随滚筒旋转到被动层靠上部位时减弱,解释了为什么该区域是颗粒重排发生最频繁的区域,而崩塌间隔比崩塌期间更高的重排频率,说明球形颗粒与不规则颗粒一样,被动层上部区域会在崩塌前发生颗粒体系的压实,这一现象可能在滚筒中的颗粒离散崩塌中普遍存在。从颗粒重排点的力学特征分析可以看出,每一个颗粒重排都是一个细微的压实过程,重排区域在重排后离库伦失效准则更远,更不易发生进一步位移。而颗粒系统中本身包含了大量接近库伦失效准则的相对自由颗粒,使该系统中颗粒重排更易触发,带来的速度、体积分数等宏观响应更小。
[1]孙其诚, 金峰, 王光谦. 颗粒物质中的多尺度问题[J]. 力学与实践, 2010, 32(1): 10-15.
SUN Q C, JIN F, WANG G Q. The multiscale structure of dense granular matter[J]. Mechanics in Engineering, 2010, 32(1): 10-15
[2]杨猛,胡志超, 张延化, 等. 农业颗粒物料气力清选装置研究现状与展望[J]. 中国农机化学报, 2020, 41(3): 121-127.
YANG M, HU Z C, ZHANG Y H, et al. Research status and prospect of pneumatic cleaning device for agricultural granular materials[J]. Journal of Chinese Agricultural Mechanization, 2020, 41(3): 121-127.
[3]侯英伟, 曹东. 基于EDEM的混凝土板桩静压贯入过程三维颗粒流数值模拟[J]. 水利水电技术, 2020, 51(4): 123-131.
HOU Y W, CAO D. EDEM-based 3-D numerical simulation of particle flow during static-pressure penetration of concrete sheet pile[J]. Water Resources and Hydropower Engineering, 2020, 51(4): 123-131.
[4]周益娴. 基于连续数值模拟的筒仓卸载过程中颗粒物压强及其速度场分析[J]. 物理学报, 2019, 68(13): 230-238.
ZHOU Y X. Pressure and velocity field analysis of particulate matter in silo unloading process based on continuous numerical simulation[J]. Acta Physica Sinica, 2019, 68(13): 230-238.
[5]王昆, 凡凤仙. 滚筒装备内颗粒混合与粉磨研究进展[J]. 中国粉体技术, 2020, 26(4):38-45.
WANG K, FAN F X. Research progress on granular mixing and grinding in rotating equipments[J]. China Powder Science and Technology, 2020, 26(4):38-45.
[6]杨晖, 张国华, 王宇杰, 等. 密集颗粒体系的颗粒运动及结构测量技术[J]. 力学进展, 2018, 48(1): 541-590.
YANG H, ZHANG G H, WANG Y J, et al. Measurement techniques of grain motion and inter-grain structures in dense granular materials[J]. Advances in Mechanics, 2018, 48(1): 541-590.
[7]LÜKEN A, STÜWE L, LOHAUS J, et al. Particle movements provoke avalanche-like compaction in soft colloid filter cakes[J]. Scientific Reports, 2021, 11(1): 12836.
[8]ZHANG G, RIDOUT S A, LIU A J. Interplay of rearrangements, strain, and local structure during avalanche propagation[J]. Physical Review X, 2021, 11(4): 041019.
[9]MEI J, MA G, TANG L, et al. Spatial clustering of microscopic dynamics governs the slip avalanche of sheared granular materials[J]. International Journal of Plasticity, 2023, 163: 103570.
[10]GRAY J M N T. Granular flow in partially filled slowly rotating drums[J]. Journal of Fluid Mechanics, 2001, 441: 1-29.
[11]AMON D L, NICULESCU T, UTTER B C. Granular avalanches in a two-dimensional rotating drum with imposed vertical vibration[J]. Physical Review E, 2013, 88(1): 012203.
[12]DUBÉ O, ALIZADEH E, CHAOUKI J, et al. Dynamics of non-spherical particles in a rotating drum[J]. Chemical Engineering Science, 2013, 101: 486-502.
[13]SALINAS V, QUI INAO C, GONZ
INAO C, GONZ LEZ S, et al. Triggering avalanches by transverse perturbations in a rotating drum[J]. Scientific Reports, 2021, 11(1): 1-7.
LEZ S, et al. Triggering avalanches by transverse perturbations in a rotating drum[J]. Scientific Reports, 2021, 11(1): 1-7.
[14]DE RICHTER S K, LE CAЁR G, DELANNAY R. Dynamics of rearrangements during inclination of granular packings: the avalanche precursor regime[J]. Journal of Statistical Mechanics: Theory and Experiment, 2012, 2012(4): P04013.
[15]WANG Z, ZHANG J. Fluctuations of particle motion in granular avalanches-from the microscopic to the macroscopic scales[J]. Soft Matter, 2015, 11(27): 5408-5416.
[16]LI R, YANG H, ZHENG G, et al. Double speckle-visibility spectroscopy for the dynamics of a passive layer in a rotating drum[J]. Powder Technology, 2016, 295: 167-174.
[17]LI R, ZHENG G, CHEN Q, et al. Two types of particle dynamics in the passive layer of a granular bed composed of irregular particles[J]. Powder Technology, 2020, 362: 231-237.
[18]周池楼, 赵永志. 离散单元法及其在流态化领域的应用[J]. 化工学报, 2014, 65(7): 2520-2534.
ZHOU C L,ZHAO Y Z. Discrete element method and its applications in fluidization[J]. CIESC Journal, 2014, 65(7): 2520-2534.
[19]STANIFER E, MANNING M L. Avalanche dynamics in sheared athermal particle packings occurs via localized bursts predicted by unstable linear response[J]. Soft Matter, 2022, 18(12): 2394-2406.
[20]SANZ E, VALERIANI C, ZACCARELLI E, et al. Avalanches mediate crystallization in a hard-sphere glass[J]. Proceedings of the National Academy of Sciences, 2014, 111(1): 75-80.
[21]冯靖禹, 韩韧, 张宇峰, 等. 基于离散元法的雪崩效应的仿真研究[J]. 软件, 2020, 41(7): 264-268.
FENG J Y, HAN R, ZHANG Y F,et al. Simulation of avalanche effect based on discrete element method[J]. Computer Engineering &Software, 2020, 41(7): 264-268.
[22]XIA Y, STICKEL J J, JIN W, et al. A review of computational models for the flow of milled biomass part I: discrete-particle models[J]. ACS Sustainable Chemistry &Engineering, 2020, 8(16): 6142-6156.
[23]YANG H, ZHU Y, LI R, et al. Kinetic granular temperature and its measurement using speckle visibility spectroscopy[J]. Particuology, 2020, 48: 160-169.
[24]JUNG J, GIDASPOW D, GAMWO I K. Measurement of two kinds of granular temperatures, stresses, and dispersion in bubbling beds[J]. Industrial &Engineering Chemistry Research, 2005, 44(5): 1329-1341.
[25]孙其诚,刘晓星,张国华,等.密集颗粒物质的介观结构[J].力学进展.2017,47(1): 263-308.
SUN Q C, LIU X X, ZHANG G H, et al. The mesoscopic structures of dense granular materials[J]. Advances in Mechanics, 2017, 47(1): 263-308.
[26]MOU S, YANG H, LI R, et al. An improved wavelet analytical method for studying particle dynamics of the passive layer within a granular drum[C]//Journal of Physics: Conference Series. IOP Publishing, 2019, 1237(4): 042071.
[27]LEMRICH L. Discrete element modeling of acoustic wave propagation in granular media: nonlinearity and material softening[D]. Zurich:ETH Zurich, 2019.
[28]ASTE T, DI MATTEO T. Emergence of gamma distributions in granular materials and packing models[J]. Physical Review E, 2008, 77(2): 021309.
[29]MAJMUDAR T S, BEHRINGER R P. Contact force measurements and stress-induced anisotropy in granular materials[J]. Nature, 2005, 435(7045): 1079-1082.