颗粒系统是远离平衡态的复杂耗散体系[1],当颗粒系统内部颗粒足够稀疏,外加能量足够大导致颗粒间相互作用以2个颗粒碰撞为主时,这样的颗粒系统被定义为颗粒气体[2]。由于颗粒间非弹性碰撞和摩擦等能量耗散,由宏观粒子形成的颗粒气体体系会发生局部凝聚现象[3],颗粒系统从稀疏的均匀分布类气体状态转变到局部聚集的类液体状态,这一类似于分子气体液化的过程被称为颗粒系统的气液相变。理解和预测颗粒气体体系的气液相变的发生有助于人们对远离平衡态体系中存在的复杂现象,如颗粒自由冷却现象[4]、 麦克斯韦妖[5]现象的认知。
分子气体体系的速度分布服从麦克斯韦-玻尔兹曼分布,颗粒气体体系是否存在类似的速度分布,一直是研究人员关注的重点。大量实验研究观察到颗粒气体体系的速度分布P(v)与分子气体体系的速度分布有明显的不同,表现为一种指数分布形式[6-8],即
P(v)=C exp[-β(|v|∕σ)α],
(1)
式中: v为颗粒速度; C为常数; σ=<v2>1/2为颗粒温度, 表示颗粒系统内颗粒的运动激烈程度; β为拟合系数; α为拟合指数。
颗粒气体体系的速度分布一直是研究热门,研究者们尝试从颗粒速度分布的角度研究颗粒系统相变的动力学特征。Rouyer等[9]采用了视频跟踪的方法来测量垂直振动系统中颗粒运动的矢量速度,发现二维非弹性颗粒气体的速度分布函数形式符合指数分布函数,且速度分布指数(α)约为1.55。Shah等[10]在微重力环境条件下获得的颗粒气体体系运动时间为2 h的录像数据,通过设置不同颗粒数目的对照组实验,发现随着颗粒气体体系中颗粒数目的增多,颗粒气体的速度指数函数中的α逐渐由1.8减小至1.35。李睿等[11]通过分子动力学模拟建立颗粒气体体系,研究了受到边界加热机制作用的粒径呈幂律分布的颗粒气体中速度分布函数的特性,发现α会随着模拟系统中参数改变而呈现α<2的一系列值。Noirhomme等[12]在准二维振动驱动的颗粒气体体系中,通过图像跟踪的方法,增加颗粒数改变颗粒系统的密度,研究颗粒系统中局部密度变化的特征,得到了振动台中的颗粒系统开始由气态发生相变的临界颗粒密度。
目前,对于颗粒系统相变过程的研究大部分从颗粒动力学角度出发, 探究相变过程中速度分布的变化;但是对于颗粒系统相变时的临界特征还没得到统一的结论,因此,本文中提出了结合颗粒系统动力学特征以及颗粒系统结构特征的方法,通过测量垂直振动颗粒系统内颗粒的密度分布与矢量速度分布,探究颗粒系统气液相变的临界特征,为研究垂直振动颗粒系统相变过程中颗粒系统状态提供了判断依据。
1 实验
1.1 装置
图1(a)是颗粒振动实验装置示意图,实验装置系统由圆盘容器、 LED光源、 高速相机和垂直振动台4个部分组成。圆盘容器采用合金钢材料为底盘,透明玻璃为上表面加工制成,内径D为120.0 mm, 高度H为2.5 mm。 Godox SL30型LED光源(深圳市神牛摄影器材有限公司)产生平行光透过圆盘容器的上表面玻璃, 均匀照射到圆盘容器的颗粒上。 采用均匀填充方式将实验颗粒加载到圆盘容器中。 实验颗粒为聚苯乙烯颗粒, 粒径d1为2 mm。 圆盘容器由垂直振动台驱动, 垂直振动台采用电动式振动系统, 系统由SA-SG030型扫频发生器(无锡世敖科技有限公司)产生的正弦信号, 利用SA-PA080型功率放大器(无锡世敖科技有限公司)来调整SA-JZ050型激振器(无锡世敖科技有限公司)的振动参数, 在振动过程中通过高速相机记录圆盘容器内颗粒的运动信息,实验中采集的实验快照如图1(b)所示。在图像采集前, 调节振动台振动频率, 使得振动频率与相机采样频率一致, 从而减弱振动对图像采集的影响。圆盘容器的高度H比颗粒粒径d1大0.5 mm,颗粒间无法相互跳跃,以确保颗粒系统在振动过程中保持准二维状态。
1.2 粒子图像测速法
图2所示为粒子图像测速法(particle image velocimetry,PIV)的测量系统。PIV的原理是通过光源照亮所测颗粒流场区域,使用高速相机连续记录颗粒流场图像,再利用互相关方法分析所拍摄的图像,计算整个测量区域内离散颗粒的矢量速度[13-14]。
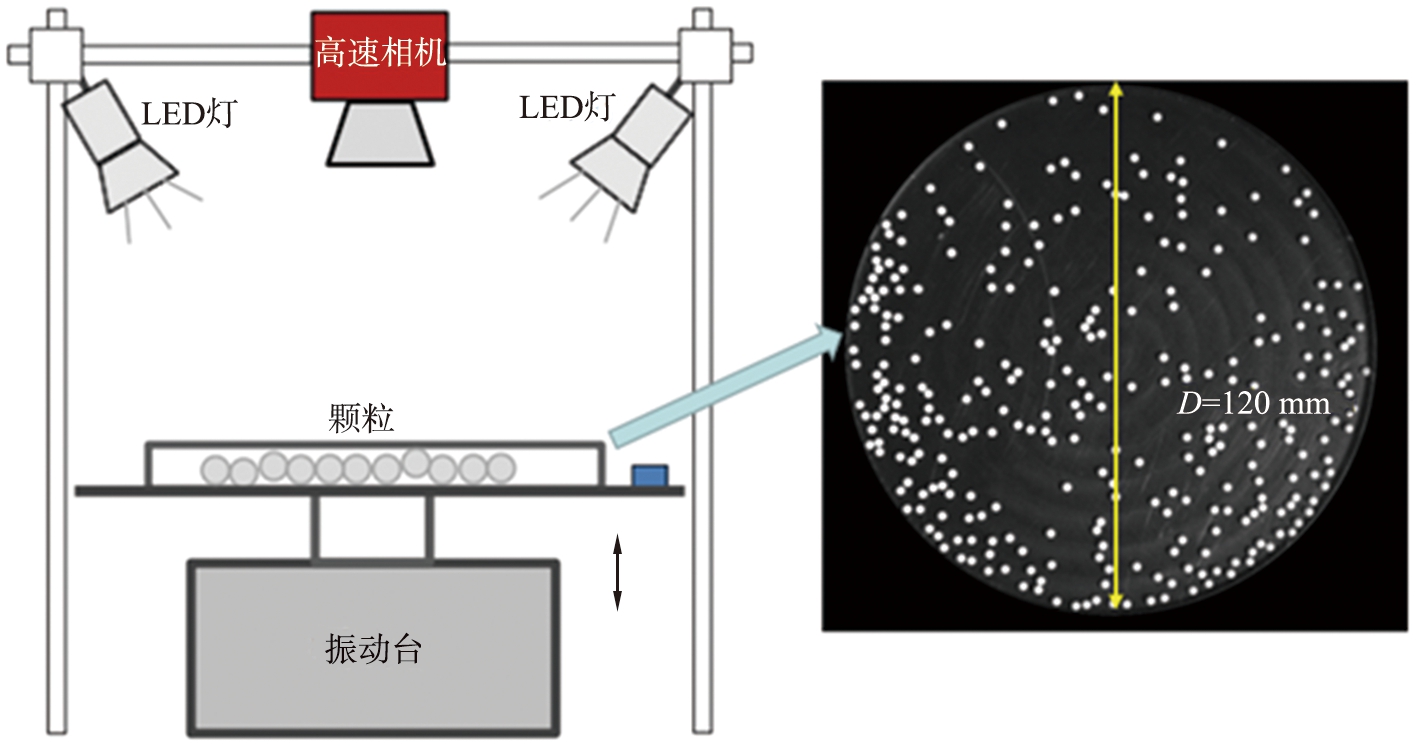
(a)振动实验系统示意图 (b)实验对振动台中颗粒的快照
图1 实验装置示意图
Fig.1 Schematic of experimental setup
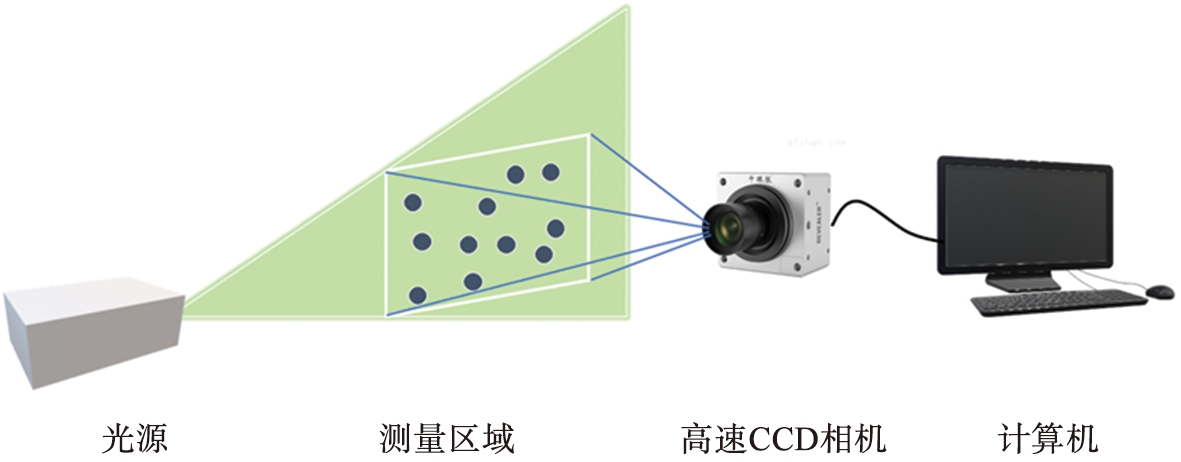
图2 PIV测量系统示意图
Fig.2 Schematic diagram of PIV measurement system
在时间间隔为Δt的2张图片中,流场中的颗粒在x、 y方向上的位移都是时间t的函数,颗粒的速度vx、 vy可以表示为
(2)
(3)
式中![]() 是颗粒沿x、 y方向的平均速度。当Δt趋向于0时,平均速度等于瞬时速度。
是颗粒沿x、 y方向的平均速度。当Δt趋向于0时,平均速度等于瞬时速度。
采用互相关法对2幅图像中离散颗粒的空间位置进行匹配。 首先, 对拍摄照片进行图片预处理, 采用高斯滤波的方法, 减小图像噪声, 然后计算图像中颗粒的相点的像素灰度分布函数[15], 得到颗粒相点光强分布为I(x, y), 将t1时刻的流场图像表示为I1(x, y)=I(x,y), 将t2时刻的流场图像表示为I2(x, y)= I(x+Δx, y+Δy), 计算I1(x, y)与I2(x, y)的互相关函数, 可得
r12=∬I1(x, y)I2(x+τx, y+τy )dxdy=∬I(x, y)I(x+Δx+τx, y+Δy+τy)dxdy,
(4)
式中: τx、 τy是图像中任意一点的位置; Δx、 Δy表示经过Δt时间间隔后相点在x, y方向上的位移。
函数I(x, y)的自相关函数r(τx,τy)为
r(τx,τy)=∬I(x, y)I(x+τx, y+τy)dxdy,
(5)
互相关函数可以化为
r12=r(τx+Δx,τy+Δy)。
(6)
由于自相关函数是偶函数且在原点取最大值, 因此根据式(6), 当τx=-Δx, τy=-Δy时, 互相关函数r12取得最大值,即2幅图像之间关联性最大。根据互相关法获得的颗粒位移Δx、 Δy,结合已知的图像采集间隔Δt,代入公式(2)可以获得颗粒流场的矢量速度信息。
1.3 局部密度判断法
颗粒气体体系是一个能量耗散的体系,维持系统的平衡态需要外力驱动, 例如振动驱动、 重力驱动、 剪切驱动或撞击等[16-18]。当系统从外界获取的能量不足以维持颗粒系统的平衡态时,离散颗粒会形成局部的高密度聚集,使得颗粒系统中发生凝聚现象,这种类似于气体中液化的现象,被称为团簇,通常采用局部密度判断进行描述。
图3为颗粒系统的网格分图。对圆盘容器最大内接正方形区域进行测量,正方形区域的边长S约为84.84 mm。首先将测量区域均匀划分成n个边长S1=S/M的小正方形区域,为了能够准确描述颗粒系统的局部密度变化,M取值为6[19],那么圆盘内颗粒系统的均值密度φ和局部密度φloc可以表示为
(7)
(8)
式中: N是系统内颗粒的总数量, Sloc是小正方形区域内离散颗粒的投影面积。
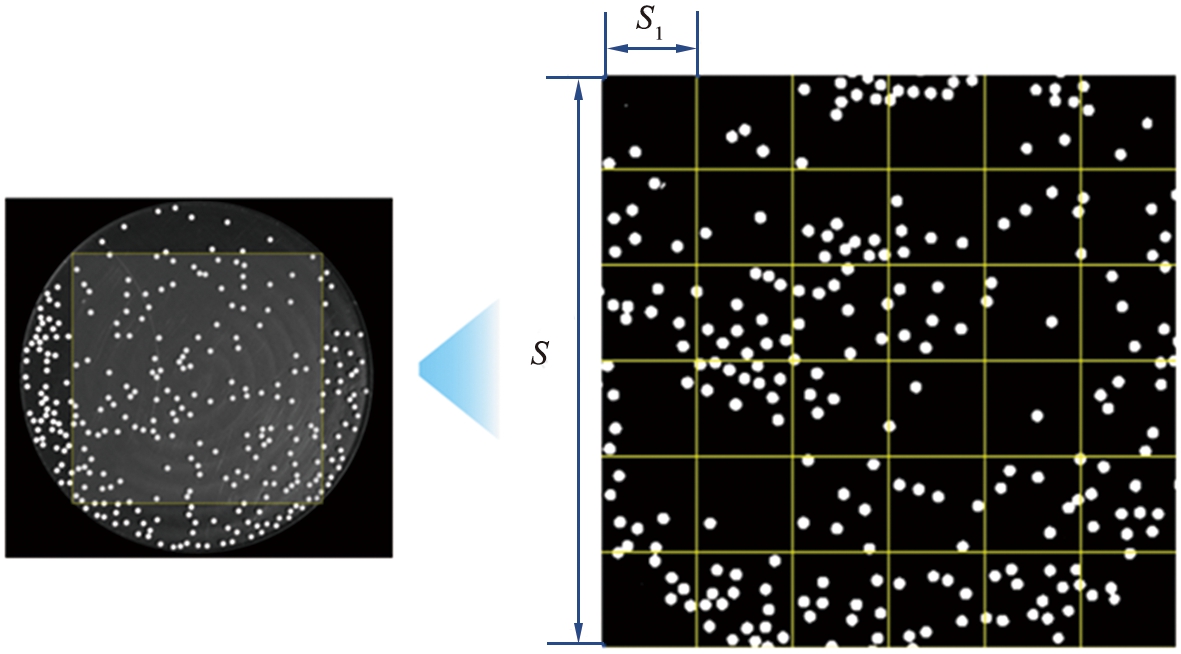
S—圆盘内接正方形边长; S1—划分的小正方形区域边长。
图3 圆盘内颗粒系统的网格划分
Fig.3 Meshing of particle system
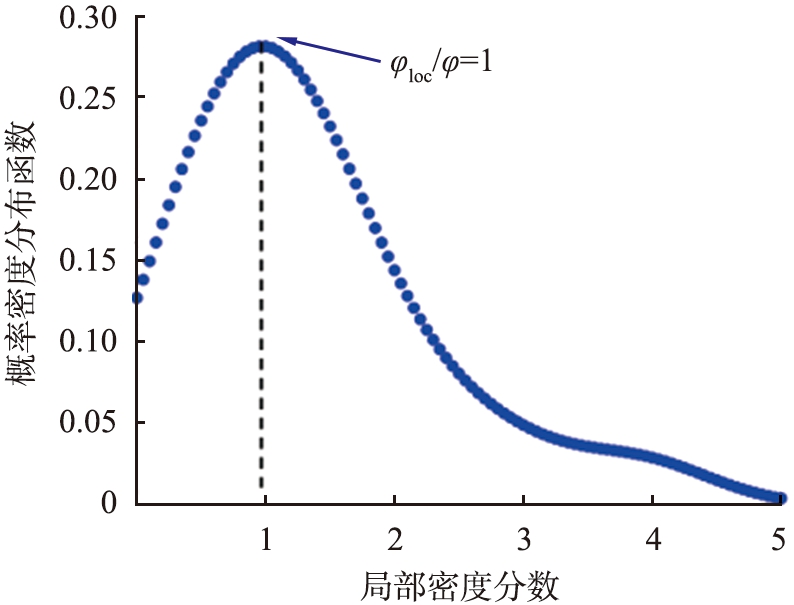
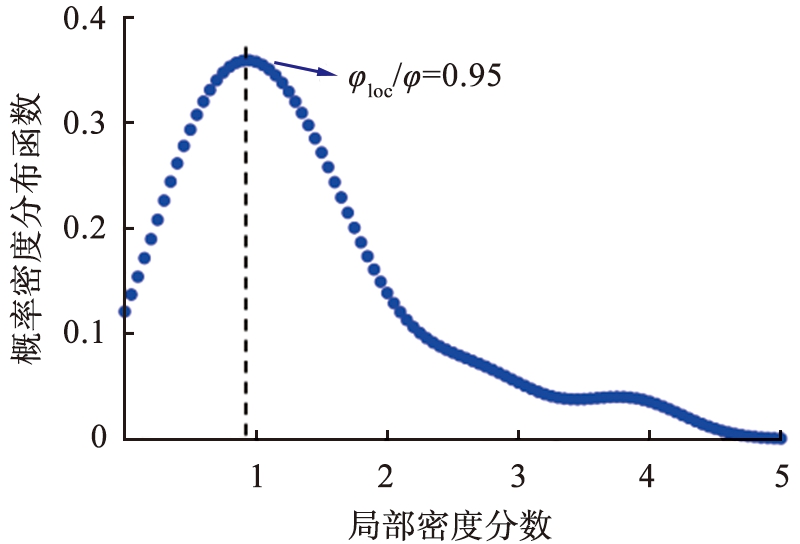
图4为颗粒系统局部密度的概率密度分布函数图。首先计算采集的每张图片中n个小正方形区域的局部密度φloc,然后进行缩放处理,将局部密度除以全局密度分数获得φloc/φ。另一方面,在【0,max{φloc/φ}】范围内,平均划分100个区间。同时,将计算得到的φloc/φ投影到该区间范围内,统计局部密度分数φloc/φ对应的出现次数F(φloc/φ),从而获得概率密度分布函数f(φloc/φ)[19-20]。
局部密度判断法就是通过概率密度分布函数f(φloc/φ)的分布确定颗粒系统是否发生团簇的方法。一般来说,颗粒系统的概率密度分布函数fφ由瑞利分布fg和高斯分布fl两部分组成[12]。
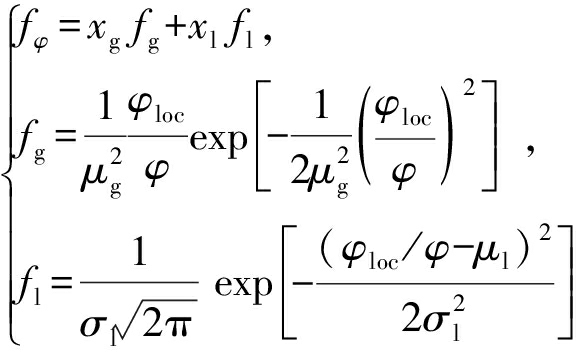
(9)
(a)φ=4%
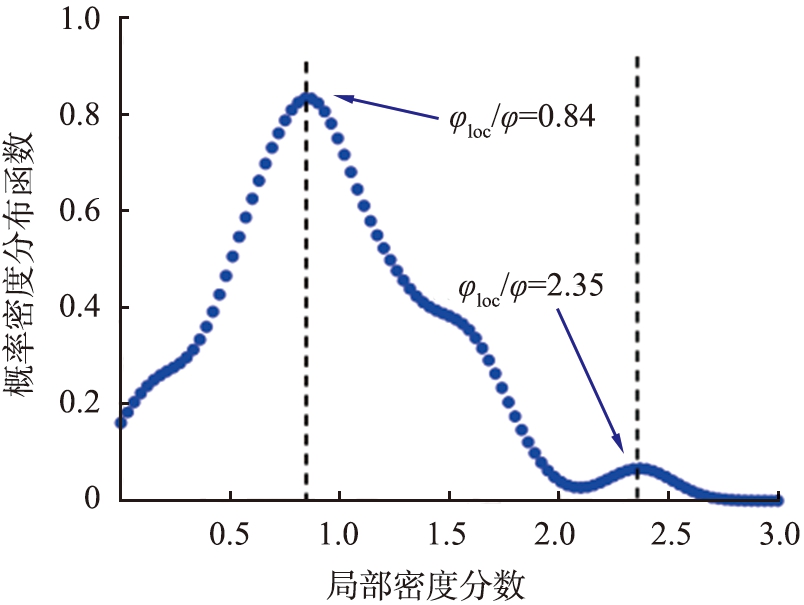
(b)φ=12%
图4 颗粒系统局部密度的概率密度分布
Fig.4 Probability density distribution function plot of local density of particle system
式中: μl和μg分别为颗粒系统中液相和气相的密度均值; xl和xg分别为液相和气相的体积分数, 即xl+xg=1。
根据Noirhomme等[12]的研究结论,振动驱动的准二维圆盘颗粒系统中,气态颗粒的概率密度分布满足瑞利分布;而液态颗粒的概率密度分布满足高斯分布。当颗粒系统处于气态时,xg=0,概率密度分布函数fφ满足瑞利分布,其峰值对应的横坐标φloc/φ=1,如图4(a)所示。当颗粒系统发生聚集时,概率密度分布函数fφ主峰值对应的横坐标φloc/φ<1,如图4(b)所示。值得注意的是,此时概率密度分布函数fφ存在第二个极值点。
2 结果与讨论
2.1 颗粒气体的特征
在不同的振动加速度和填充密度条件下,圆盘内离散颗粒的速度分布和概率密度分布具有相似性。选取Γ=20,φ=8%条件下进行实验。在Γ=20,φ=8%条件下,采用粒子图像测速法测量振动开始后第2 s到24 s时间段内圆盘中离散颗粒的矢量速度,观察到速度分布均满足指数函数。图5(a)所示为振动开始后第6 s时刻,圆盘内离散颗粒的速度分布图。将颗粒的速度v除以v0=<v2>1/2进行无标度化,并且在误差小于5%的条件下,采用最小二乘法拟合测量数据,如图中蓝色虚线所示。由图可以看出,离散颗粒的速度分布满足指数函数,指数α=1.31。
图5(b)所示为α与t的变化曲线。由图可以看出,在振动开始后12 s时间内,圆盘内离散颗粒的速度分布指数α随t增加而增大。这是由于颗粒系统在振动驱动条件下能量的传播是不均匀性造成的[21]。在12 s之后,α达到最大值,α=1.52 ±0.01,颗粒系统开始到达均匀“受热”状态。
通过局部密度判断法测量t=12 s时刻圆盘内颗粒概率密度分布,如图5(c)所示。为了方便讨论,记概率密度分布函数的第1个峰值对应的横坐标为K值。可以看出,离散颗粒的概率密度分布函数满足瑞利分布。在K=0.96时, f(φloc/φ)达到最大值,表明颗粒系统中大部分区域的密度都与全局密度大致相同,即颗粒均匀分布在颗粒系统的每一块局域中,颗粒系统中未出现团簇现象。
特征参数K和α可以准确描述颗粒系统的结构特征和动力学特征,因此在接下来的实验测量中,仅关注振动12 s后稳态颗粒系统的参数α和K的变化规律。
2.2 不同填充密度条件下颗粒系统气液相变的临界条件
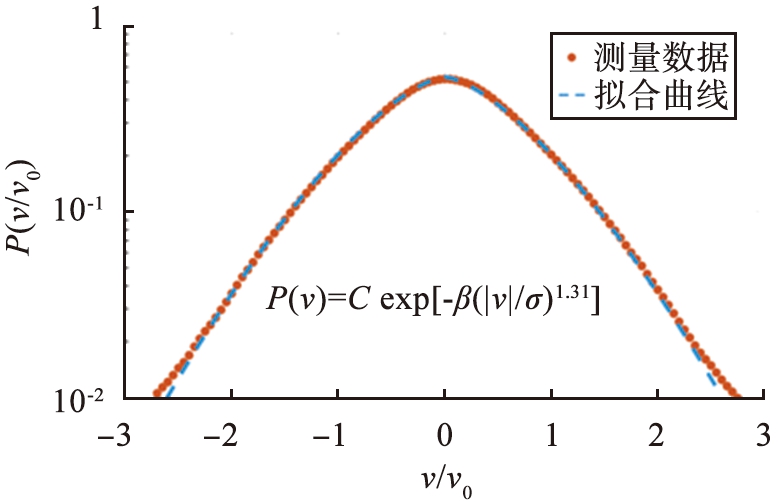
(a)离散颗粒的速度分布,t=6 s
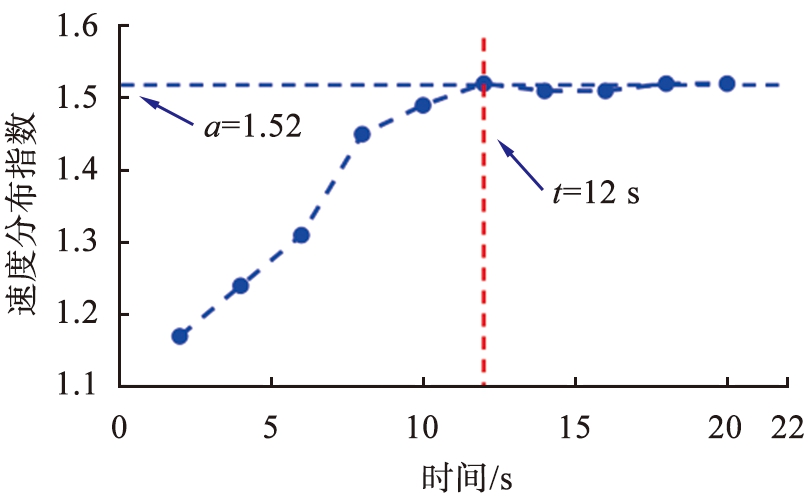
(b)速度分布指数α随时间t的变化曲线
(c)概率密度分布,t=12 s
图5 垂直振动颗粒系统的速度分布和密度分布特征
Fig.5 Velocity distribution and density distribution characteristics of vertical vibrating particle systems
为了探究颗粒系统相变的临界条件, 通过控制颗粒系统的φ来改变圆盘内颗粒系统的运动状态, 实验中φ每组增加2%, 以便于观察密度对颗粒系统运动的影响, 直到实验结果趋于稳定。 当φ∈[2%, 24%]时, 取Γ=20, 测量颗粒系统的速度分布和概率密度分布, 记录不同φ条件下α和K的变化。
图6所示为K与φ的变化曲线。在误差小于5%的条件下,采用最小二乘法拟合测量数据,如图中红色虚线所示。K与φ满足函数
(10)
式中: 拟合参数P1=0.529, P2=-14.88, P3=147.7, Q1=-18.95, Q2=154.1。
从图6中可以看出,在2%≤φ≤6%时,0.95≤K≤1.05,表明低密度条件下颗粒系统从振动台获得的能量能够维持颗粒间的非弹性碰撞产生的能量,颗粒完全处于自由运动的状态,颗粒系统内颗粒近似均匀分布,即颗粒系统表现为类气态。当6%<φ≤16%时,0.44≤K<0.95,K值随着均值密度增加而减小,这是由于颗粒数目的增多使得振动提供的的能量难以维持体系中颗粒间非弹性碰撞产生的耗散,这表明圆盘内离散颗粒开始出现颗粒分布不均匀现象。随着均值密度的进一步增大,当16%<φ≤24%时,K=0.34 ±0.01,此时,振动驱动提供的能量不足以维持圆盘内离散非弹性碰撞中的能量耗散,大量颗粒发生团簇现象,颗粒系统表现出液态的特征。
图7所示为dK(φ)/dφ和α与φ的变化曲线。为了准确描述颗粒系统气液相变的临界特征,对公式(10)进行微分处理,如图中红色实线所示。α随着φ的增大而减小,从最大值2附近慢慢减小,表明颗粒气体体系的速度分布随着均值密度的增大从高斯分布向非高斯分布转变,这与前人的结论一致[22]。当颗粒系统开始从气态向液态转变时,圆盘内离散颗粒发生团簇现象,使得颗粒系统概率密度函数对应的K值发生突变,取变化率最大K值点对应于颗粒气液相变的临界条件。由图7可以看出,dK(φ)/dφ的最大值对应的横坐标φ=9.40 %,即在φ=9.40 %时,K的变化率最大,对应的速度分布指数αc1=1.44±0.03,因此认为αc1=1.44±0.03为圆盘内离散颗粒气液相变的临界值。
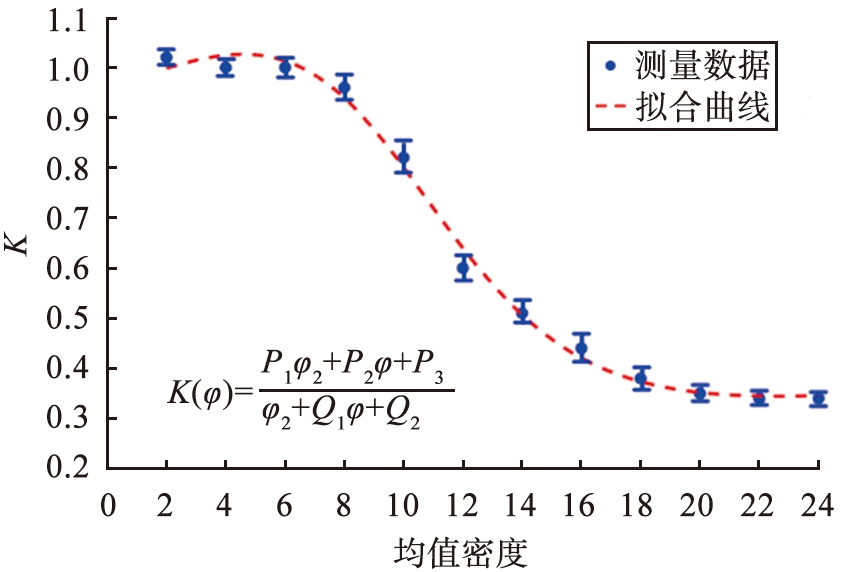
图6 特征参数K随均值密度φ的变化曲线
Fig.6 Curve of characteristic parameter K with mean density φ
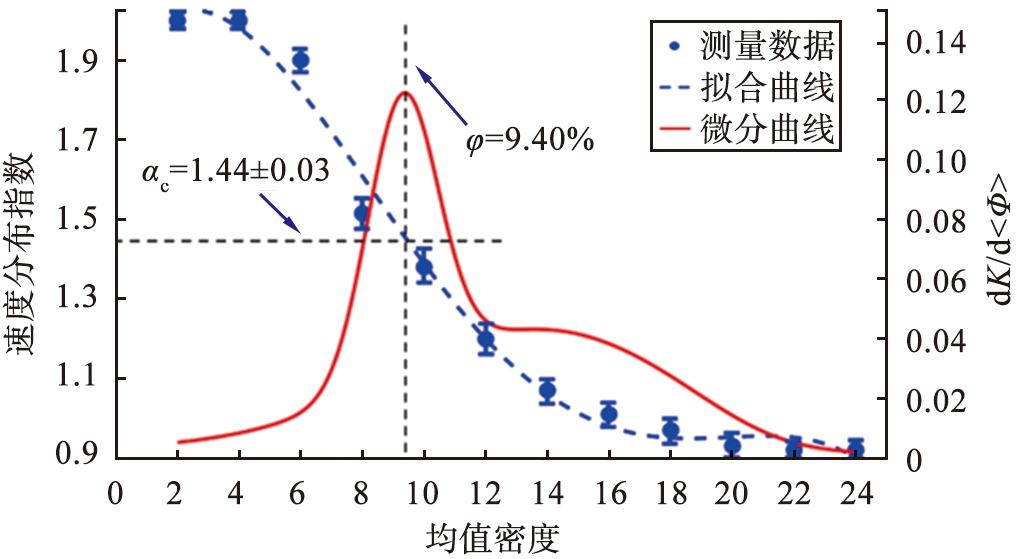
图7 速度分布指数α和特征参数K的微分随均值密度φ的变化曲线
Fig.7 Curves of velocity distribution index α and characteristic
parameter K with mean density φ
2.3 不同振动条件下颗粒系统气液相变的临界条件
为了进一步探究颗粒系统相变的临界条件,通过控制振动加速度Γ来改变圆盘内颗粒系统的运动状态。设置实验中Γ的增加梯度为5,以便于观察振动加速度对颗粒系统运动的影响,直到实验结果趋于稳定。选取φ=10 %,Γ∈[5,40]时,记录不同Γ条件下K值和α值的变化。
图8所示为K与Γ的变化曲线。在误差小于5%的条件下,采用最小二乘法拟合测量数据,如图中红色虚线所示。K与Γ满足函数
(11)
式中:拟合参数P1=0.780 8, P2=-15.05, P3=131.5, Q1=-29.31, Q2=362.6。
从图8可以看到,在5≤Γ<25时,0.29≤K<0.95,K值与Γ呈正相关关系。这是因为Γ的增大导致颗粒系统中的输入能量增加,表明Γ较小时,离散颗粒因振动驱动的能量不足以维持颗粒的非弹性碰撞的能量消耗,颗粒系统表现出类液态,随着Γ的增大,颗粒系统发生从类液态向类气态转变的过程。随着振动加速度的继续增大,当25≤Γ≤45时,0.95≤K≤1.05,K值位于1附近并稳定,表明强振动条件下颗粒系统从振动台获得的能量能够维持颗粒间的非弹性碰撞,即颗粒处于气体状态。图9所示为dK(Γ)/dΓ和α与Γ的变化曲线。由图可以看出,在Γ=19.60时,K的变化率最大,对应的速度分布指数αc2=1.42±0.02,因此认为αc2=1.42±0.02为圆盘内离散颗粒气液相变的临界值。
由图7、 9可知,在改变外驱动力和颗粒填充密度条件下,均观察到颗粒系统的气液相变,圆盘内离散颗粒气液相变的临界条件是一致的,即当αc=1.40时,颗粒系统开始从气态向液态发生转变,表明通过对K进行微分处理,可以准确判断颗粒系统气液相变过程中速度分布指数的临界值。
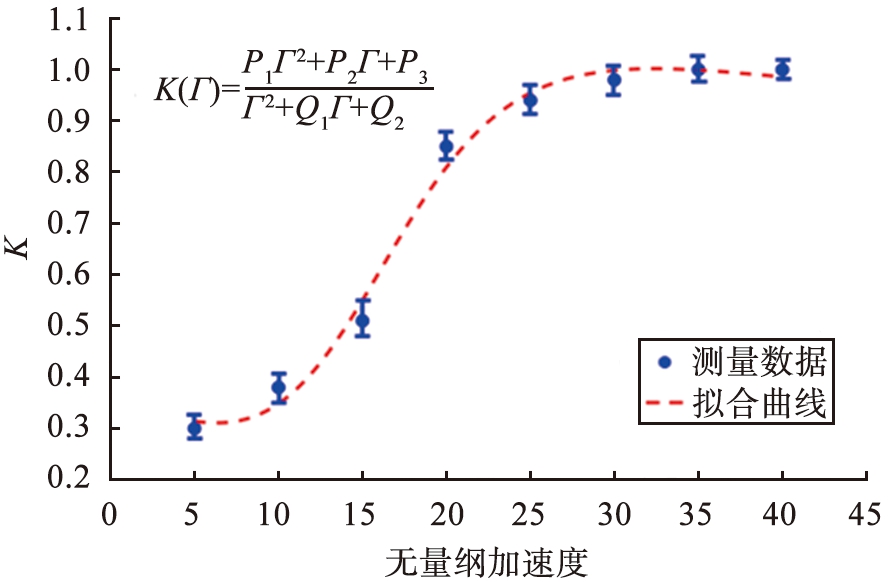
图8 特征参数K随加速度Γ的变化曲线
Fig.8 Curve of local density peak K with acceleration Γ
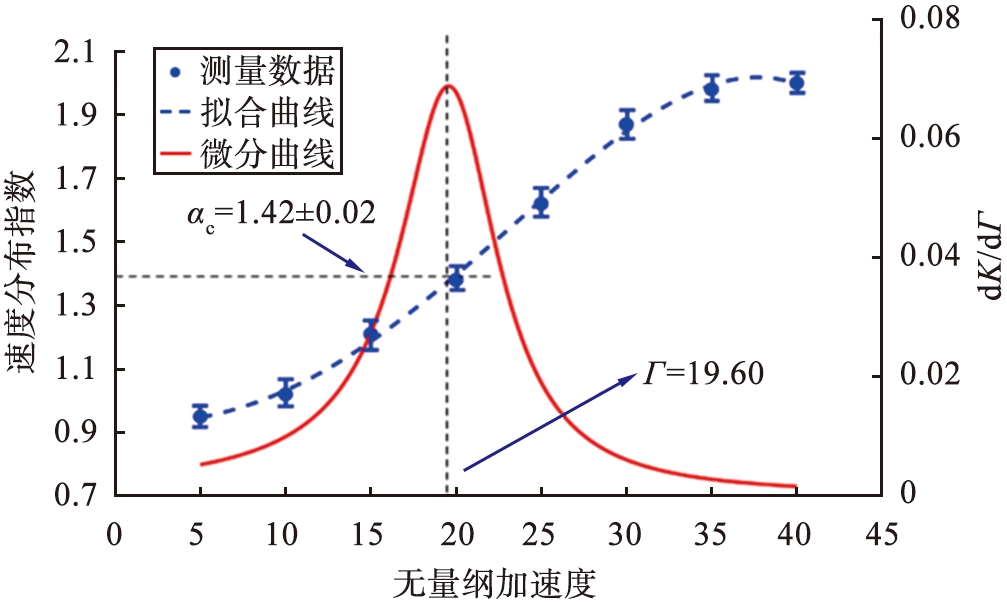
图9 速度分布指数α和特征参数K的微分随加速度Γ的变化曲线
Fig.9 Velocity distribution exponential α and characteristic parameter K with acceleration Γ
3 结论
在垂直振动的颗粒系统中,通过改变颗粒系统自身的颗粒密度以及颗粒系统外界能量输入,建立了局部概率密度分布的特征参数K、 φ和Γ的关系模型。
1) 在改变颗粒系统的φ和Γ时,都观察到颗粒系统的速度分布满足指数分布P(v)=Cexp[-β(|v|/σ)α,并且随着系统颗粒数的增多和输入能量的减小,α持续减小。
2) 通过增加颗粒系统的颗粒数和减小颗粒系统的能量输入来创造颗粒气液相变的过程。在改变φ时,K的变化率最大时对应的αc1=1.44±0.03。在改变Γ时,K的变化率最大时对应的αc2=1.42±0.02。2个过程中的相变点具有一致性,即当αc=1.40时,颗粒系统处于气态向液态发生转变的临界点。本文中实验结果描述颗粒系统相变特征,为研究垂直振动颗粒系统相变过程中颗粒系统状态提供了判断依据。
[1]NOIRHOMMME M, LUDEWIG F, VANDEWALLE N, et al. Cluster growth in driven granular gases[J]. Physical Review: E, 2017, 95(2): 022905.
[2]BRILLIANTOV N, POSCHEL T. Kinetic theory of granular gases[M]. New York: Oxford University Press, 2004: 35-49.
[3]WANG W G, HOU M Y, CHEN K, et al. Experimental and numerical study on energy dissipation in the freely cooling granular gases under microgravity[J]. Chinese Physics B, 2018, 27(8): 084501.
[4]BREY J J, DE SORIA M I G, MAYNER P. Inhomogeneous cooling state of a strongly confined granular gas at low density[J]. Physical Review: E, 2019, 100(5): 052901.
[5]FREITAS N, ESPOSITO M. Information flows in macroscopic Maxwell’s demons[J]. Physical Review: E, 2023, 107(1): 014136.
[6]LUDING S, CLEMENT E, BLUMEN A. Studies of columns of beads under external vibrations[J]. Physical Review: E, 1994, 49(2): 1634.
[7]LOSERT W, COOPER D G, DLOUR J. Velocity statistics in excited granular media[J]. Chaos, 1999, 9(1): 682-690.
[8]王文广. 微重力下颗粒气体自由冷却及相转变现象的研究[D]. 北京: 中国科学院大学, 2018.
WANG W G. Study on free cooling and phase transition phenomenon of particulate gas under microgravity[D]. Beijing: University of Chinese Academy of Sciences, 2018.
[9]ROUYER F, MENON N. Velocity fluctuations in a homogeneous 2D granular gas in steady state[J]. Physical Review Letters, 2000, 85(17): 3676.
[10]SHAH S H, LIN Y C, HOU M Y. Effect of number density on velocity distributions in a driven quasi-two-dimensional granular gas[J]. Chinese Physics: B, 2010, 19(10): 108203.
[11]李睿, 戴伟, 张端明. 加热机制对粒径呈幂律分布的颗粒气体中能量均分失效行为的影响[J]. 四川大学学报(自然科学版), 2017, 54(5): 1073-1076.
LI R, DAI W, ZHANG D M. Effect of heating mechanism on energy equalization failure behavior in particle size power-law distribution of granular gases [J]. Journal of Sichuan University(Natural Science Edition), 2017, 54(5): 1073-1076.
[12]NOIRHOMMME M, CAZAUBIEL A, FALCON E, et al. Particle dynamics at the onset of the granular gas-liquid transition[J]. Physical Review Letters, 2021, 126(12): 128002.
[13]吴麒麟. 微重力下颗粒物质运动行为基础研究[D]. 北京: 中国科学院大学, 2020.
WU Q L. Basic research on motion behavior of particulate matter under microgravity[D]. Beijing: University of Chinese Academy of Sciences, 2020.
[14]KNIGHT C, O’SULLIVAN C, VAN WACHEM B. Computing drag and interactions between fluid and polydisperse particles in saturated granular materials[J]. Computers and Geotechnics, 2020, 117: 103210.
[15]XU M B. Background interference removal algorithm for PIV preprocessing based on improved local Otsu thresholding[J]. Chinese Journal of Biomedical Engineering, 2022, 31(4): 147-159.
[16]MEER D, REIMANN P. Temperature anisotropy in a driven granular gas[J]. Europhysics Letters, 2019, 74(3): 384-386.
[17]HOU M, LIU R, ZHAI G. Velocity distribution of vibration-driven granular gas in Knudsen regime in microgravity[J]. Microgravity Science and Technology, 2008, 20(2): 73-80.
[18]PRASADV V, DAS D, SABHAPANDIT S, et al. Velocity distribution of driven granular gases[J]. Journal of Statistical Mechanics: Theory and Experiment, 2019, 2019(6): 063201.
[19]ROVERE M, HEERMANN D W, BINDER K. Block density distribution function analysis of two-dimensional Lennard-Jones fluids[J]. Europhysics Letters, 1988, 6(7): 585-588.
[20]ROVERE M, HEERMANND W, BINDER K. The gas-liquid transition of the two-dimensional Lennard-Jones fluid[J]. Journal of Physics: Condensed Matter, 1990, 2(33): 709-714.
[21]HARTH K, TRITTEL T, WEGNER S, et al. Free cooling of a granular gas of rodlike particles in microgravity[J]. Physical Review Letters, 2018, 120(21): 214301.
[22]KAWARADA A, HAYAKAWA H. Non-Gaussian velocity distribution function in a vibrating granular bed[J]. Journal of the Physical Society of Japan, 2004, 73(8): 2037-2040.