离散单元法(discrete element method,DEM)是一种处理非连续介质问题的数值模拟方法,广泛用于散体物料的过程模拟和强度分析,如粉末流动、粉末混合和散装压缩的过程分析,是模拟粉体处理过程的一个很好的预测工具[1]。在DEM中,为满足模拟的精度要求,需要首先获取反映颗粒真实性能的物理量的离散元仿真参数值,离散元仿真参数的标定是DEM在工程应用中的主要难点。
离散元仿真参数标定主要有直接测量法和间接标定法[2]。直接测量法测得的参数值有较高的准确性,该方法不依赖于软件和所使用的接触模型,但缺点在于部分参数难以直接测量,只适用于毫米级及以上尺度的颗粒,对于微米或纳米级别尺度的颗粒并不适用。间接标定法是工程中最常用的方法,通过将宏观层面的物料参数测量值作为响应,再批量改变离散元仿真参数值的组合,使颗粒的整体宏观响应值与离散元仿真参数值相匹配。目前,已有诸多学者通过间接标定法对染料[3]、 黏土[4]、 植物基质[5]、 药粉[6]等不同物料进行了离散元仿真参数的标定。
在离散元仿真参数标定中,计算效率是工程应用中必须考虑的问题。影响DEM计算效率最关键的2个物理量为颗粒数量[7]和颗粒接触刚度[8]。在实际应用中,细粉体中的颗粒数量通常会达到百万级甚至上亿级,为了减少计算量可以将颗粒放大,从而有效减少影响计算效率的颗粒数量。任建莉等[9]基于颗粒缩放理论将煤粉颗粒放大,在DEM中模拟了颗粒在垂直螺旋输送过程中的运动,验证了颗粒缩放法的准确性。Hu等[10]通过对颗粒床的单轴压缩实验,发现原始颗粒与放大颗粒有着几乎相同的应力-应变曲线,验证了放大后的颗粒可用于模拟原始颗粒。减小颗粒接触刚度可以增大仿真的时间步长,减少计算迭代次数,从而提高计算效率。Lommen等[11]进行了渗透测试和休止角实验,验证了在一定范围内减小刚度后的颗粒不会对整体行为产生较大的影响。Chen等[12]通过模拟填充试验验证了引入减小刚度的颗粒与原始颗粒的填充效果保持一致。上述2种对颗粒的简化方法不可避免地会改变颗粒的运动状态和接触力,但简化颗粒与实际颗粒的宏观响应必须尽可能地相同[13],因此,需要通过离散元仿真参数标定过程来修正参数值,减小简化颗粒带来的负面影响。
目前,对离散元仿真参数标定多采用单一的静态休止角(static angle of repose)作为宏观响应指标,并不能充分反映粉体颗粒的真实性能。在实际情况中,粉末颗粒具有静态和动态的双重特性,同时使用静态和动态休止角(dynamic angle of repose)作为响应指标可以在DEM模拟中更好地反映颗粒真实的性能。基于此,本文中以钛白粉的静态休止角和动态休止角作为宏观响应指标,对进行颗粒简化后的钛白粉进行离散元仿真参数标定,通过单因素试验和Box-Behnken试验获得最优的离散元仿真参数组合,最后对离散元仿真参数进行实验验证。所得最优的离散元仿真参数值组合可为后续模拟研究钛白粉的输送、包装问题提供数据,同时也为其他黏性细粉体的离散元仿真参数标定提供参考。
1 建立离散元仿真模型的理论依据
1.1 JKR接触模型
离散单元法的基本原理是把整个散体系统分解为每一个单元体元素,求解单个元素的牛顿第二定律来计算颗粒的运动和相互作用力[14]。颗粒的运动特征和所受接触力与所用的颗粒接触模型密切相关,模型的选取决定了离散元模拟的准确性。对于钛白粉这种黏性细粉物料,选择采用JKR(Johnson-Kendall-Roberts cohesion)接触模型对颗粒进行计算,该模型认为黏附力作用在颗粒的接触区域内并有助于接触表面变形,因此获得了比Hertz-Mindlin理论预测的更大的接触面积[15]。在JKR模型中,颗粒的法向弹性接触力FJKR[14]表示为
(1)
(2)
式中: E*为等效弹性模量; R*为等效颗粒半径; α为法向重叠量; γ为颗粒表面能; δ为切向重叠量。式(1)中的第1项为基于Hertz-Mindlin理论的法向接触力,第2项为基于JKR理论的颗粒黏附力;当颗粒表面能γ=0时,JKR模型将退化为Hertz-Mindlin模型。
1.2 颗粒缩放原则
Feng等[16]基于颗粒间的相互作用,引入了颗粒缩放应遵守的3个相似原则,分别为几何相似、运动相似和动力相似原则。几何相似原则表示在原始模型和缩放模型中颗粒尺寸与颗粒域特征长度均选用恒定的比例因子,同时2个模型应有相同的颗粒堆积形态。运动相似原则表示2个模型中对应点处的速度方向相同,大小成一定比例。动力相似原则指的是当颗粒的惯性力不能被忽略时,2个模型作用在颗粒上的所有力应具有相同的比例。上述3种相似原则,若满足几何相似,则缩放模型中也必须使用与物理模型中相同的颗粒数,这将等同于对未缩放模型的计算量;若满足运动相似,则需要颗粒间的相互作用定律不随比例变化;若满足动态相似,则要求2个模型所用颗粒的密度成比例,而这样却很难保证接触力的相似,大多数分析中2个模型的密度均取相同值。在实际应用中很难同时满足以上3个相似原则。
为了实现缩放后的颗粒与原模型有相同的物理特性,本文中颗粒选用相同的密度,并遵循几何相似原则,将颗粒的尺寸进行放大,通过标定过程对相关离散元仿真参数进行修正,以满足颗粒的运动和动力的相似性。
1.3 减小颗粒刚度原理
瑞利时间步长指的是颗粒之间2次碰撞运算的时间长度,是影响DEM模拟计算效率的重要因素。瑞利时间步长的计算公式为
(3)
式中: tR为瑞利时间步长; r为颗粒半径; ν为颗粒泊松比; ρ为颗粒密度; G为颗粒切变模量。为保证仿真的效率及准确性,通常选用瑞利时间步长的10%~30%作为计算时间步长。由式(3)可知,颗粒的切变模量是影响时间步长的主要因素,减小颗粒刚度可允许在模拟中使用更大的时间步长,减少计算迭代次数,从而提高计算速度。
在JKR模型中引入减小刚度的颗粒后,颗粒在运动碰撞过程中会发生更多重叠。若颗粒的表面能保持不变,则碰撞损失的动能会增加。为保证颗粒碰撞后的运动结果保持不变,使发生接触的2个颗粒所需的分离能量保持恒定,减小颗粒刚度必须通过减小颗粒的表面能来平衡,需满足的条件[17]为
(4)
式中, γmod、 Gmod分别为修正后的颗粒的表面能和切变模量。
随着颗粒刚度的减小和时间步长增加,计算速度得到提高,但颗粒刚度减小范围应有一定的限制。为防止颗粒刚度减小过多而造成过大的重叠量,减小刚度后的颗粒切变模量须保持在107 Pa以上[11]。
2 测定实验
2.1 粉体颗粒的粒径
本文中选取的研究对象钛白粉属于一种黏性细粉,实验测定前需要对钛白粉进行干燥处理,使用激光粒度分布仪(BT-9300ST型,丹东百特仪器有限公司)测定钛白粉样品的粒径分布,钛白粉颗粒粒径分布如图1所示。由图可知,d10为0.35 μm, d50为0.74 μm,d90为3.03 μm,分别表示颗粒累积体积分数达10%、 50%、 90%所对应的粒径值。本文中将钛白粉颗粒放大为粒径为1 mm的球型颗粒进行后续的模拟试验。
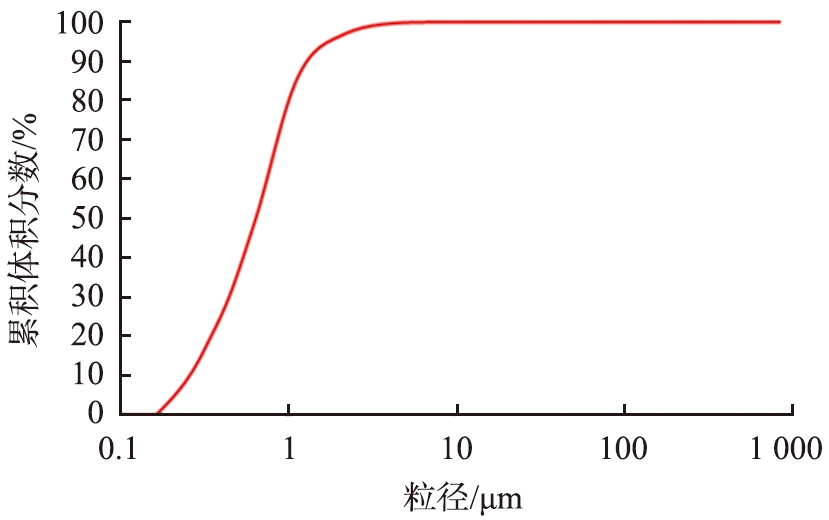
图1 钛白粉颗粒粒径分布
Fig.1 Particle size distribution diagram of titanium dioxide particles
2.2 静态休止角
静态休止角第一次出现时为粉体物料自由堆积体形成的堆积坡面与水平面之间的最大夹角。参照注入法进行静态休止角的测定,自制的测定钛白粉静态休止角的装置如图2所示。

图2 静态休止角的测定装置
Fig.2 Measuring device for static angle of repose
静态休止角的测定步骤为:用烧杯盛取一定量的钛白粉,将钛白粉缓慢倒入漏斗中,同时使用玻璃棒缓慢搅动以防止钛白粉堵住漏斗出口,钛白粉经漏斗下落在底部不锈钢垫片上形成锥体,待钛白粉堆积高度不再发生变化后测定钛白粉的堆积高度,计算出相应的静态休止角。静态休止角及其平均值的计算公式为
θi=arctan![]() ,
,
(5)
![]() ,
,
(6)
式中: θi(i=1,2,…,5)为静态休止角; Hi为钛白粉堆积高度; L为不锈钢垫片直径; θ为静态休止角的平均值。重复5次实验后,计算得到钛白粉静态休止角的平均值为40.9°。

图3 动态休止角的测定装置
Fig.3 Measuring device for dynamic angle of repose
2.3 动态休止角
动态休止角第一次出现时是指在粉末随着圆筒的转动而上升过程中,当粉末间的作用力不能与重力保持平衡时,粉末崩塌前堆积坡面与水平面之间的最大倾斜角度。动态休止角是一种可以用来表征粉末动态流动特性的参数[18]。基于旋转鼓法进行动态休止角的测定,自制的钛白粉动态休止角的测定装置如图3所示。由图可见,装置由旋转圆筒(直径为100 mm,长度为100 mm,内壁贴附不锈钢铁片)、联轴器、电机和调速器组成。动态休止角的测定步骤为:将一定量的钛白粉装入圆筒中,圆筒中的钛白粉填充率达到25%后,启动电机使圆筒开始旋转,设置恒定转速为50 r/min,通过旋转圆筒正前方摆设的摄像机实时记录钛白粉的动态休止角。重复5次实验后,得到钛白粉动态休止角α的平均值为65.5°。
3 离散元仿真参数标定
3.1 离散元仿真模型的建立
在Solidworks软件中,参照测定装置的尺寸,按照比例为1∶1建立了静态和动态休止角测定装置的三维几何模型,保存为STL格式后导入EDEM软件中,测定装置的三维几何模型如图4所示。
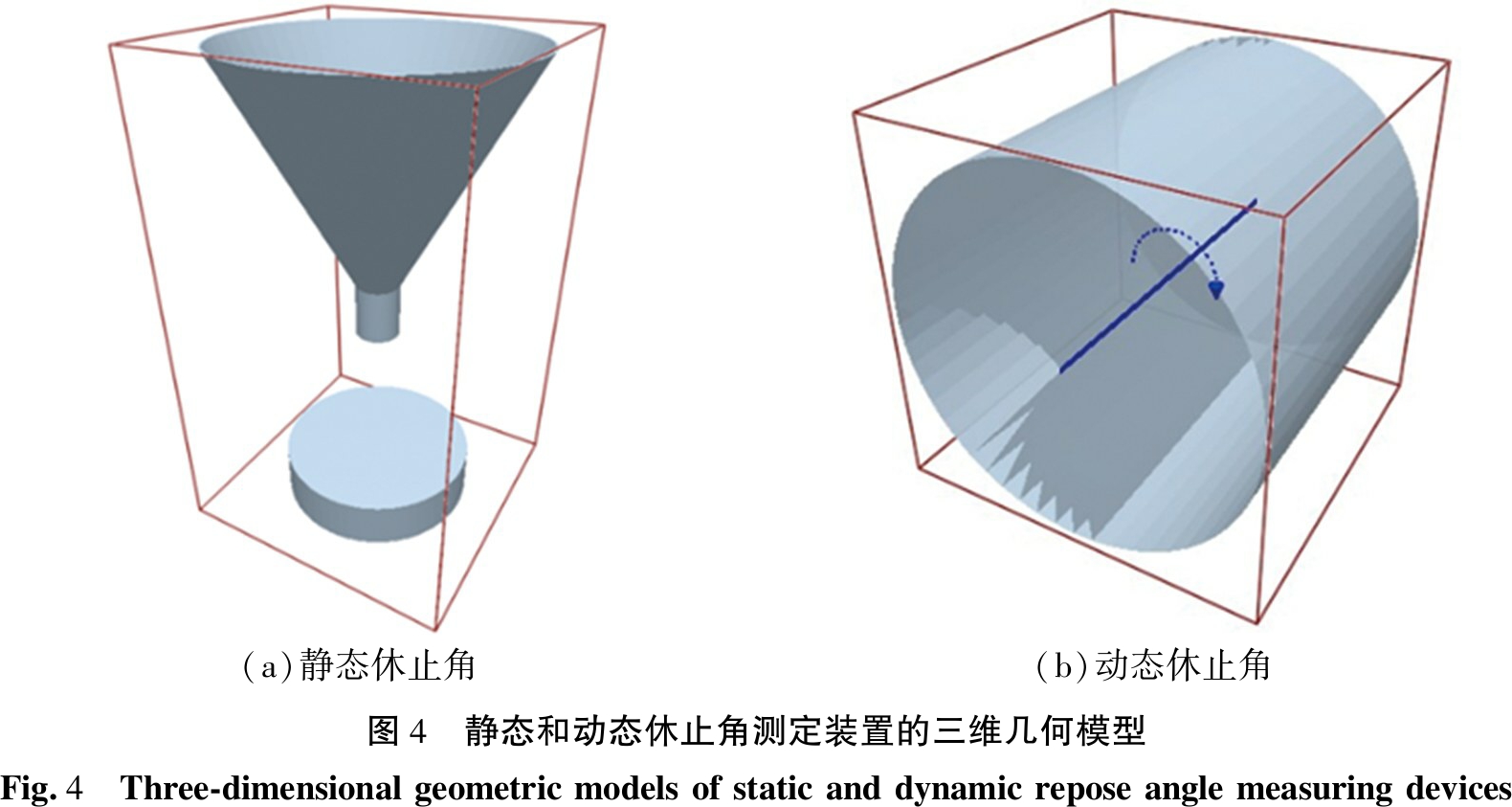
(a)静态休止角(b)动态休止角图4 静态和动态休止角测定装置的三维几何模型Fig.4 Three-dimensional geometric models of static and dynamic repose angle measuring devices
仿真的初始条件设置为:放大后球型颗粒的粒径设为1 mm,生成方式为动态生成。静态休止角模型在漏斗顶部建立颗粒工厂,颗粒总个数为20 000,生成速率设定每秒颗粒个数为5 000。动态休止角模型在圆筒内部建立颗粒工厂,生成颗粒的总个数达到5 000,即填充率达到静态休止角的25%;颗粒静止后在模型中心添加旋转轴,转速设定为50 r/min。2个模型的计算时间步长均取瑞利时间步长的20%,网格尺寸选取最小球形单元尺寸的3倍。当仿真结果达到稳定后,通过EDEM的测量工具对休止角进行测量。
离散元仿真参数主要包括颗粒与三维几何模型的本征参数、 颗粒与颗粒间的接触参数以及颗粒与几何体的接触参数。 由文献[19-20]可知, 钛白粉的密度为4 200 kg/m3, 泊松比为0.27, 切变模量为9×1010 Pa,JKR表面能为0.83 J/m2。初步设定切变模量减小为1×107~9×107 Pa,根据式(4)修正得到的JKR表面能为0.021 7~0.052 4 J/m2。三维几何模型采用不锈钢材料,接触参数的变化范围通过预实验测定。离散元仿真参数如表1所示。
表1 离散元仿真参数
Tab.1 Discrete element simulation parameters
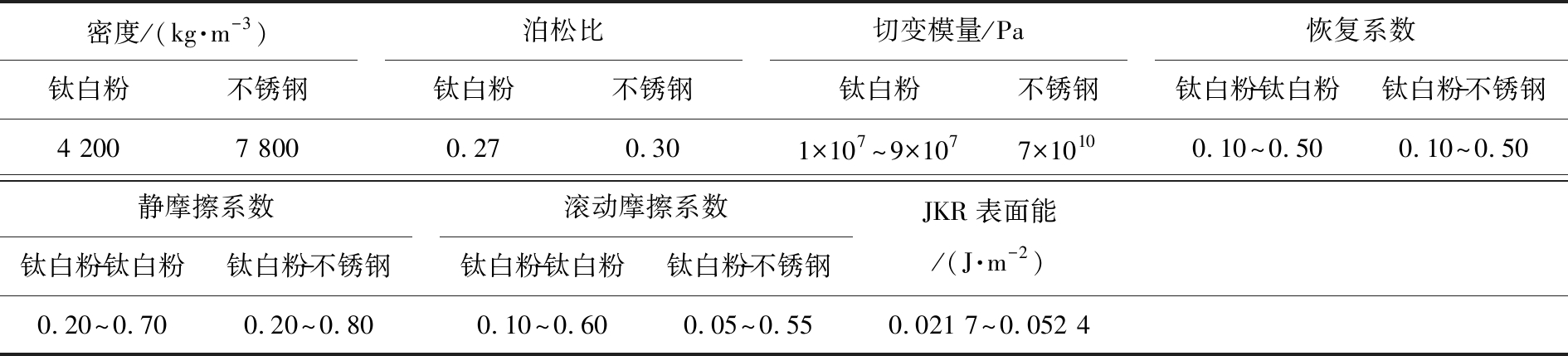
密度/(kg·m-3)钛白粉不锈钢泊松比钛白粉不锈钢切变模量/Pa钛白粉不锈钢恢复系数钛白粉-钛白粉钛白粉-不锈钢4 2007 8000.270.301×107~9×1077×10100.10~0.500.10~0.50静摩擦系数钛白粉-钛白粉钛白粉-不锈钢滚动摩擦系数钛白粉-钛白粉钛白粉-不锈钢JKR表面能/(J·m-2)0.20~0.700.20~0.800.10~0.600.05~0.550.021 7~0.052 4
3.2 离散元仿真参数单因素试验
由于待标定的离散元仿真参数过多,因此,为降低工作量、提高计算效率,需要通过单因素试验排除部分对颗粒整体性能影响较小的参数。文献[21-23]指出,颗粒的切变模量、恢复系数和JKR表面能对颗粒的整体性能影响较小,因此,分别以钛白粉颗粒的切变模量、钛白粉-钛白粉恢复系数、钛白粉-不锈钢恢复系数、钛白粉的JKR表面能共4个离散元仿真参数做单因素试验。以静态和动态休止角作为响应指标,验证4个离散元仿真参数各自的影响。
离散元仿真参数各单因素试验的结果如图5所示。由图可知,钛白粉-钛白粉恢复系数、 钛白粉-不锈钢恢复系数对休止角几乎无影响;静态休止角随着钛白粉颗粒的切变模量呈现略微增大,切变模量达到5×107 Pa后静态休止角逐渐稳定;随着JKR表面能的增加,静态休止角和动态休止角的数值存在上下波动,但波动范围较小,均在可接受范围内,表明根据式(4)修正后的JKR表面能可以基本满足缩放要求。在后续的标定试验中对上述4个离散元仿真参数均取中位数值。

(a)颗粒切变模量(b)钛白粉-钛白粉恢复系数(c)钛白粉-不锈钢恢复系数(d)JKR(Johnson-Kendall-Roberts cohesion)表面能图5离散元仿真参数各单因素试验的结果Fig.5 Results of each single factor test for discrete element simulation parameters
3.3 Box-Behnken试验及回归分析
进行Box-Behnken试验,采用响应面分析法寻求离散元仿真参数的最优解。以静态和动态休止角为试验响应指标,以钛白粉-钛白粉静摩擦系数A、 钛白粉-钛白粉滚动摩擦系数B、 钛白粉-不锈钢静摩擦系数C、 钛白粉-不锈钢滚动摩擦系数D为试验因素,Box-Behnken试验的因素编码如表2所示。共设置26组试验,Box-Behnken试验的设计与结果如表3所示。
表2 Box-Behnken试验的因素编码
Tab.2 Factor coding for Box-Behnken tests

编码因素钛白粉-钛白粉静摩擦系数A钛白粉-钛白粉滚动摩擦系数B钛白粉-不锈钢静摩擦系数C钛白粉-不锈钢滚动摩擦系数D-10.200.100.200.05 00.450.350.500.30 10.700.600.800.55
表3 Box-Behnken试验的设计与结果
Tab.3 Design and results of Box-Behnken test
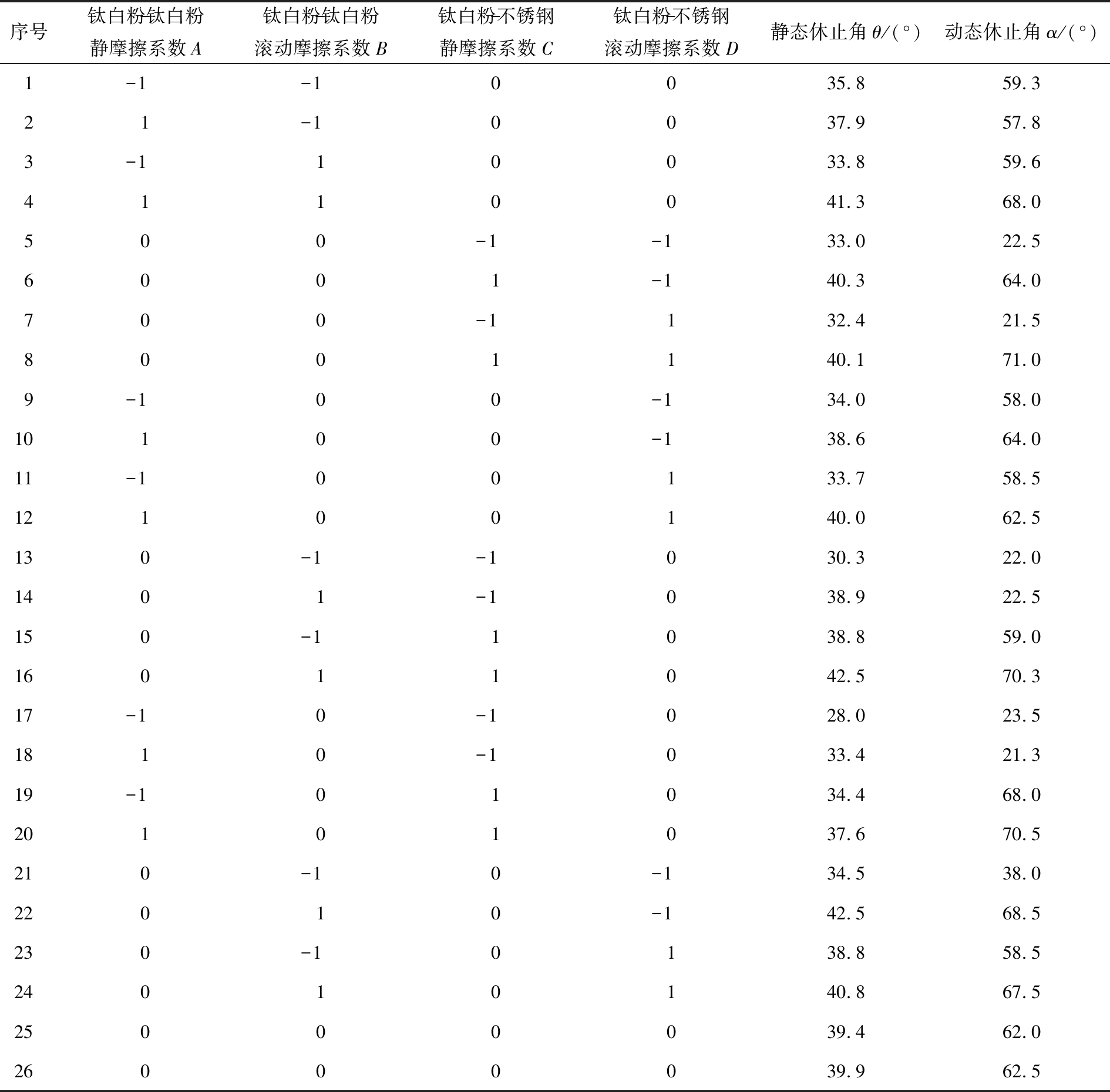
序号钛白粉-钛白粉静摩擦系数A钛白粉-钛白粉滚动摩擦系数B钛白粉-不锈钢静摩擦系数C钛白粉-不锈钢滚动摩擦系数D静态休止角θ/(°)动态休止角α/(°)1-1 -1 0035.859.321-1 0037.957.83-1 10033.859.64110041.368.0500-1 -1 33.022.56001-1 40.364.0700-1 132.421.58001140.171.09-1 00-1 34.058.010 100-1 38.664.011 -1 00133.758.512 100140.062.513 0-1 -1 030.322.014 01-1 038.922.515 0-1 1038.859.016 011042.570.317 -1 0-1 028.023.518 10-1 033.421.319 -1 01034.468.020 101037.670.521 0-1 0-1 34.538.022 010-1 42.568.523 0-1 0138.858.524 010140.867.525 000039.462.026 000039.962.5
表4、 5分别为Box-Behnken试验中静态和动态休止角的方差分析。 由表可知, 2个拟合模型的p值 (p值为在原假设为真时, 获得检验统计量的观测值及更不支持原假设的其他值的概率)均小于0.01, 表明休止角与所得回归方程关系呈极为显著; 失拟项的p值均大于0.05, 表明回归方程不失拟, 具有预测意义;静态休止角决定系数为0.9 347,动态休止角决定系数为0.9 745,表明拟合效果较好。对于静态休止角,钛白粉-钛白粉静摩擦系数A、 钛白粉-钛白粉滚动摩擦系数B、 钛白粉-不锈钢静摩擦系数C、 二次项A2和C2的p值均小于0.01,对静态休止角的影响极其显著;钛白粉-不锈钢滚动摩擦系数D的p值大于0.05,说明该因素对静态休止角影响不显著;各交互项的p值均大于0.05,说明各因素的交互作用对静态休止角的影响也不显著。对于动态休止角,钛白粉-钛白粉滚动摩擦系数B、 钛白粉-不锈钢静摩擦系数C、 二次项C2的p值小于0.01,对动态休止角的影响极其显著,交互项BD的p值为0.033 6,小于0.05,对动态休止角的影响较显著。
表4 Box-Behnken试验中静态休止角的方差分析
Tab.4 Analysis of variance of staticangle of repose in Box-Behnken test

方差来源平方和自由度均方值F值p值模型347.19 14 24.80 11.25 0.000 1A70.57 170.57 32.00 0.000 3B46.81 146.81 21.22 0.000 8C118.44 1118.44 53.71 <0.000 1 D0.7010.700.320.584 2AB7.2917.293.310.096 3AC1.2111.210.550.474 4AD0.7210.720.330.578 6BC6.0016.002.720.127 2BD9.0019.004.080.068 4CD0.0410.040.020.895 3A238.95 138.95 17.66 0.001 5B20.8410.840.380.550 8C235.13 135.13 15.93 0.002 1D20.9310.930.420.528 7残差24.26 11 2.21失拟项24.13 10 2.4119.31 0.175 4纯误差0.1310.13总和371.44 25 注: A为钛白粉-钛白粉静摩擦系数; B为钛白粉-钛白粉滚动摩擦系数; C为钛白粉-不锈钢静摩擦系数; D为钛白粉-不锈钢滚动摩擦系数;F值为统计量; p值为在原假设为真时,获得检验统计量的观测值及更不支持原假设的其他值的概率。
建立的接触参数与静态休止角θ、 动态休止角α的二阶回归方程分别为
θ=39.65+2.42A+1.97B+3.14C+0.24D+1.35AB-0.55AC+0.42AD-1.22BC-1.50BD+
0.10CD-2.99A2+0.44B2-2.84C2-0.46D2,
(7)
α=62.25+1.43A+5.15B+22.46C+2.04D+2.48AB+1.17AC-0.50AD+2.70BC-5.38BD+
2.00CD+0.40A2-2.10B2-16.46C2-1.66D2 。
(8)
表5 Box-Behnken试验中动态休止角的方差分析
Tab.5 Analysis of variance of dynamic angle of repose in Box-Behnken test
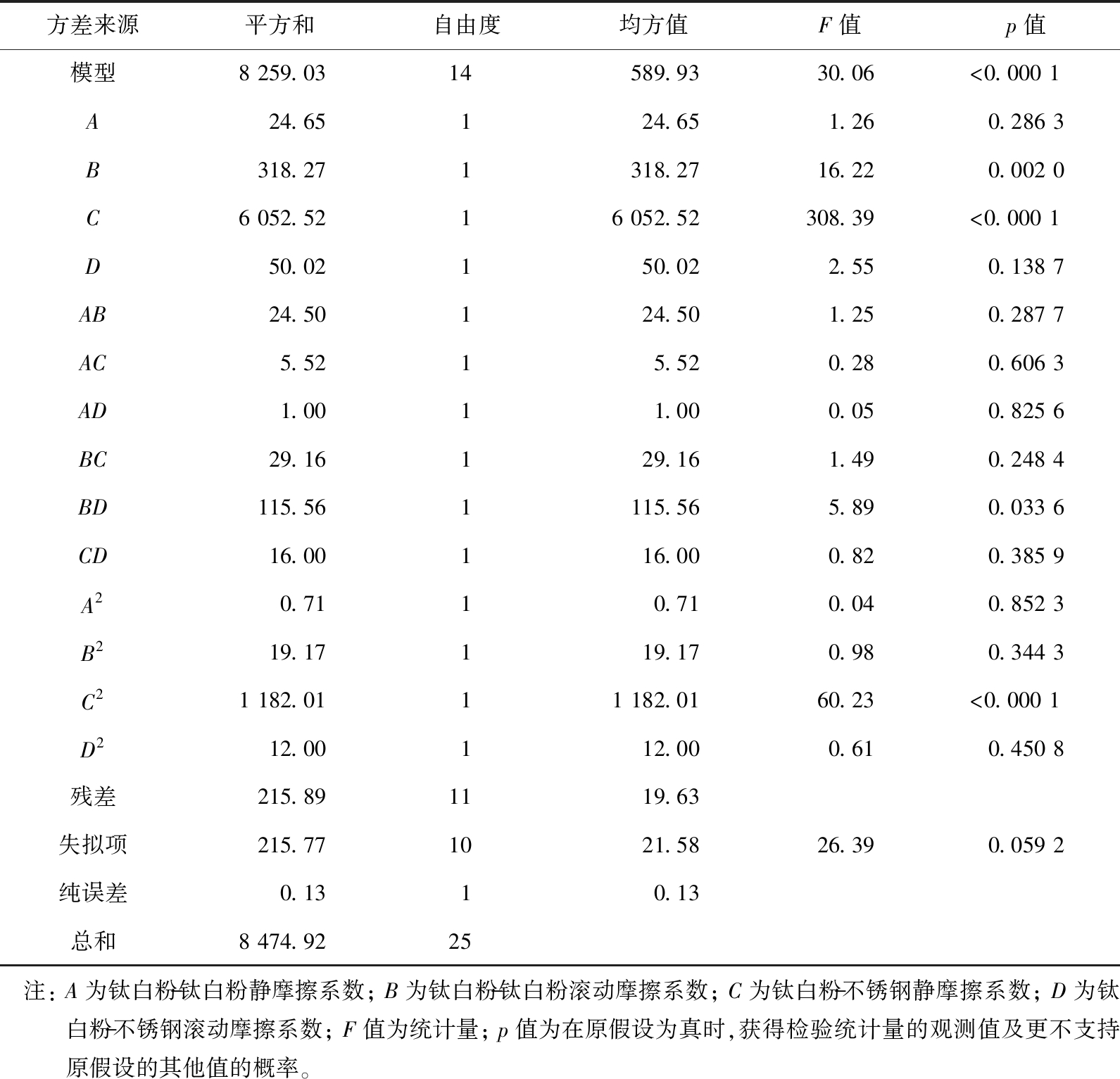
方差来源平方和自由度均方值F值p值模型8 259.0314 589.9330.06<0.000 1 A24.65124.651.260.286 3B318.271318.2716.220.002 0C6 052.5216 052.52308.39<0.000 1 D50.02150.022.550.138 7AB24.50124.501.250.287 7AC5.5215.520.280.606 3AD1.0011.000.050.825 6BC29.16129.161.490.248 4BD115.561115.565.890.033 6CD16.00116.000.820.385 9A20.7110.710.040.852 3B219.17119.170.980.344 3C21 182.0111 182.0160.23<0.000 1 D212.00112.000.610.450 8残差215.8911 19.63失拟项215.7710 21.5826.390.059 2纯误差0.1310.13总和8 474.9225 注: A为钛白粉-钛白粉静摩擦系数; B为钛白粉-钛白粉滚动摩擦系数; C为钛白粉-不锈钢静摩擦系数; D为钛白粉-不锈钢滚动摩擦系数; F值为统计量; p值为在原假设为真时,获得检验统计量的观测值及更不支持原假设的其他值的概率。
3.4 离散元仿真参数的确定及验证
为了验证回归方程的准确性,对方程进行随机求解离散元仿真参数组合值,通过比较回归方程的预测值和模拟值,验证回归方程的可靠性和准确性。分别进行8次随机预测和模拟,离散元仿真参数回归方程的随机预测值与模拟值如图6所示,预测值和模拟值几乎重合。计算预测值和模拟值得到静态休止角和动态休止角的平均相对误差分别为2.93%和2.75%,误差在可接受范围内,表明回归方程有较好的预测性,可对实际值进行预测。

(a)静态休止角(b)动态休止角图6 离散元仿真参数回归方程的随机预测值与模拟值Fig.6 Random predicted value and simulated value of regression equation for discrete element simulation parameters
分别以实验测得的钛白粉休止角为响应目标, 对回归方程进行寻优求解, 将得到的各离散元仿真参数值组合输入EDEM软件中进行仿真。 图7所示为各寻优离散元仿真参数值组合的模拟值与实验值, 计算得到平均相对误差分别为1.37%、 1.10%, 休止角模拟值与实验值无明显差异。 虽然各组的休止角相近; 但由于不同的离散元仿真参数值组合会导致颗粒不同的接触效果和力链分布, 从而会使得颗粒群呈现不同的堆积形态, 因此对所求得的5组离散元仿真参数值组合选取堆积形态与实际最为相近的作为最终优选离散元仿真参数值组合, 即钛白粉-钛白粉静摩擦系数A为0.51,钛白粉-钛白粉滚动摩擦系数B为0.29, 钛白粉-不锈钢静摩擦系数C为0.62, 钛白粉-不锈钢滚动摩擦系数D为0.17。
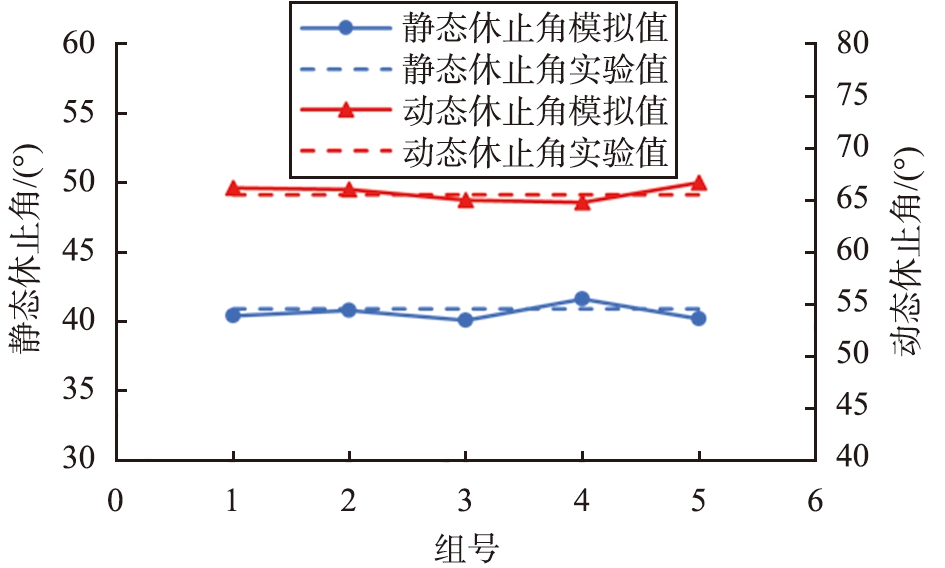
图7 寻优离散元仿真参数组合的模拟值与实验值
Fig.7 Simulated value and experimental value of optimization parameter combination
钛白粉的静态和动态休止角如图8、 9所示。由图8、 9可见,仿真结果图像与实物无明显差异,实物的静态休止角为40.9°,动态休止角为65.5°;仿真的静态休止角为40.4°, 动态休止角为66.2°; 静态和动态休止角的相对误差分别为1.22%、 1.07%,误差较小,因此所得离散元仿真参数值组合可用于后续模拟过程。

(a)实物(b)仿真图像图8 钛白粉的静态休止角Fig.8 Static angle of repose of titanium dioxide

(a)实物(b)仿真图像图9 钛白粉的动态休止角Fig.9 Dynamic angle of repose of titanium dioxide
4 结论
颗粒通过尺寸缩放和减小刚度后,极大地提高了离散元仿真的计算速度。单因素试验结果表明,在一定数值范围内,颗粒的切变模量、恢复系数和JKR表面能均对休止角无明显影响。在Box-Behnken响应面试验中,以钛白粉的静态和动态休止角作为双重响应指标,可以得到更加精确的离散元仿真参数,使模拟的颗粒更加逼近真实状态。本文中以钛白粉的静态休止角和动态休止角作为宏观响应指标,对简化后的钛白粉颗粒进行了离散元仿真参数标定。通过单因素试验和Box-Behnken试验获得最优的离散元仿真参数组合,最后对离散元仿真参数进行了实验验证。相关结论如下:
1)使用自制的测定装置测得钛白粉的静态和动态休止角的平均值分别为40.9°和65.5°。
2)根据颗粒的几何相似原则和减小刚度原理,对钛白粉颗粒的粒径和切变模量进行简化,计算得到修正后的JKR表面能为0.0 217~0.0 524 J/m2。
3)应用Box-Behnken试验分别建立了钛白粉的静态和动态休止角的二阶回归方程, 以实际测定的休止角为目标值对2个回归方程进行寻优求解, 实验验证后得到了最优离散元仿真参数值组合: 钛白粉-钛白粉静摩擦系数为0.51, 滚动摩擦系数为0.29, 钛白粉-不锈钢静摩擦系数为0.62, 滚动摩擦系数为0.17。
4)仿真的静态休止角为40.4°, 动态休止角为66.2°, 静态和动态休止角的相对误差分别为1.22%、 1.07%,误差较小,所得离散元仿真参数值较为可靠,可用于后续离散元仿真模拟。
[1]El-KASSEM B, SALLOUM N, BRINZ T, et al. A multivariate regression parametric study on DEM input parameters of free-flowing and cohesive powders with experimental data-based validation[J]. Computational Particle Mechanics, 2021, 8(1): 87-111.
[2]COETZEE C J. Review:calibration of the discrete element method[J]. Powder Technology, 2017, 310: 104-142.
[3]韩伟, 王绍宗, 张倩, 等. 基于JKR接触模型的微米级颗粒离散元参数标定[J]. 中国粉体技术, 2021, 27(6): 60-69.
HAN W, WANG S Z, ZHANG Q, et al. Discrete element parameter calibration of micron sized powder particles based on JKR contact model[J]. China Powder Science and Technology, 2021, 27(6): 60-69.
[4]孙景彬, 刘琪, 杨福增, 等. 黄土高原坡地土壤与旋耕部件互作离散元仿真参数标定[J]. 农业机械学报, 2022, 53(1): 63-73.
SUN J B, LIU Q, YANG F Z, et al. Calibration of discrete element simulation parameters of sloping soil on loess plateau and its interaction with rotary tillage components[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(1): 63-73.
[5]ZHAO L, ZHOU H P, XU L Y, et al. Parameter calibration of coconut bran substrate simulation model based on discrete element and response surface methodology[J]. Powder Technology, 2022, 395: 183-194.
[6]石辰风, 杨茂蕊, 唐正馨, 等. 中药浸膏粉离散元模拟参数标定方法研究[J]. 中草药, 2020, 51(24): 6205-6212.
SHI C F, YANG M R, TANG Z X, et al. Calibration of discrete element simulation parameters of Chinese medicine extractpowders[J]. Chinese Traditional and Herbal Drugs,2020, 51(24): 6205-6512.
[7]ALIZADEH M, ASACHI M, GHADIRI M, et al. A methodology for calibration of DEM input parameters in simulation of segregation of powder mixtures: a special focus on adhesion[J]. Powder Technology, 2018, 339: 789-800.
[8]KETTERHAGEN W, WASSGREN C. A perspective on calibration and application of DEM models for simulation of industrial bulk powder processes[J]. Powder Technology, 2022, 402: 117301.
[9]任建莉, 周龙海, 韩龙, 等. 基于颗粒缩放理论的垂直螺旋输送离散模拟[J]. 过程工程学报, 2017, 17(5): 936-943.
REN J L, ZHOU L H, HAN L, et al. Discrete simulation of vertical screw conveyor based on particle scaling theory[J]. The Chinese Journal of Process Engineering, 2017, 17(5): 936-943.
[10]HU Y Z, CHAN E L, TSUJI T, et al. Geometric similarity on interparticle force evaluation for scaled-up DEM particles[J]. Powder Technology, 2022, 404: 117483.
[11]LOMMEN S, SCHOTT D, LODEWIJKS G. DEM speedup:stiffness effects on behavior of bulk material[J]. Particuology, 2014, 12: 107-112.
[12]CHEN S, LIU W W, LI S Q. A fast adhesive discrete element method for random packings of fine particles[J]. Chemical Engineering Science, 2019, 193: 336-345.
[13]ROESSLER T, KATTERFELD A. Scaling of the angle of repose test and its influence on the calibration of DEM parameters using upscaled particles[J]. Powder Technology, 2018, 330: 58-66.
[14]HOSHISHIMA C, OHSAKI S, NAKAMURA H, et al. Parameter calibration of discrete element method modelling for cohesive and non-spherical particles of powder[J]. Powder Technology, 2021, 386: 199-208.
[15]CHEN X Z, ELLIOTT J A. On the scaling law of JKR contact model for coarse-grained cohesive particles[J]. Chemical Engineering Science, 2020, 227: 115906.
[16]FENG Y T, HAN K, OWEN D R J, et al. On upscaling of discrete element models: similarity principles[J]. Engineering Computations, 2009, 26(6): 599-609.
[17]H☞RVIG J, KLEINHANS U, WIELAND C, et al. On the adhesive JKR contact and rolling models for reduced particle stiffness discrete element simulations[J]. Powder Technology, 2017, 319: 472-482.
[18]TISCAR J M, ESCRIG A, MALLOL G, et al. DEM-based modelling framework for spray-dried powders in ceramic tiles industry: part I: calibration procedure[J]. Powder Technology, 2019, 356(C): 818-831.
[19]魏志钢, 张红星, 李前树, 等. 二氧化钛(TiO2)表面能的理论研究[J]. 高等学校化学学报, 2008(4): 824-826.
WEI Z G, ZHANG H X, LI Q S, et al. Theoretical study on the surface energy of TiO2 rutile[J]. Chemical Journal of Chinese Universities, 2008(4): 824-826.
[20]WANG Y J, CHANG J, TAN L N, et al. Elastic properties of rutile TiO2 at high temperature[J]. Chinese Physics Letters, 2007,24(9): 2642-2645.
[21]YAN Z, WILKINSON S K, STITT E H, et al. Discrete element modelling (DEM) input parameters: understanding their impact on model predictions using statistical analysis[J]. Computational Particle Mechanics,2015,2(3): 283-299.
[22]El-KASSEM B, SALLOUM N, BRINZ T, et al. A semi-automated DEM parameter calibration technique of powders based on different bulk responses extracted from auger dosing experiments[J]. KONA Powder and Particle Journal, 2021, 38: 235-250.
[23]MASSAH J, KHAZAEI J. Simultaneous measurement of rice grain friction coefficient and angle of repose using rotating cylinders[J]. Journal of Applied Botany and Food Quality, 2022, 95: 60-66.