在国内外大力发展太阳能作为新能源的背景下,硅料的产量连年增长,清洗、筛选硅料变得尤为重要,特别是硅料的清洗和烘干工艺[1]。多晶硅料超声波清洗装置可高效去除多晶硅料表面的污染物,使表面色泽光亮、均衡统一[2]。硅料烘干是全自动硅料超声波清洗装置的重要工艺过程之一,直接影响到产品的性能、 形态、 质量以及过程的能耗等。在硅料颗粒烘干加工中,不同粒径颗粒间的混合效果和颗粒床内颗粒的传热过程对硅料烘干效率有很大的影响。
在工装篮烘干筒中, 硅料颗粒的混合是非常重要的环节, 混合速率和混合均匀性直接影响着烘干筒的干燥速率和干燥品质。 随着计算机技术的快速发展, 研究颗粒运动和混合主要采用数值模拟的方法, 分别是欧拉多相流模型和离散元模型(discrete element model, DEM)[3]。 DEM不仅可以对任何颗粒运动轨迹展开精准跟踪, 还可以将不同区域中的颗粒分布精准地显示出来。 由于考虑到各个粒径颗粒间存在的作用力, 因此DEM也普遍使用在颗粒物料混合和运动分析工作中。
各国学者在分析滚筒颗粒混合方面也选择采用DEM。李沐沅等[4]在开展研究工作时借助数值模拟对颗粒物料传热性和运动特性受到列板填充率、结构、转速等影响规律展开分析。徐颖等[5]在对滚筒内颗粒混合过程展开分析时采用DEM,将各种高度以及数量的抄板设置在滚筒之中,同时确保颗粒粒径统一,在此基础上模拟混合过程。刘义伦等[6]在研究过程中借助DEM针对不同转速与倾角时颗粒的混合过程进行数值模拟。Zou等[7]采用DEM模拟了强化混合器中的颗粒混合过程,研究了混合器的结构和工艺参数对颗粒混合性能和功耗的影响。Xu等[8]研究了转鼓内颗粒的运动和混合。通过分析颗粒与壁面的接触数、颗粒速度分布、活性层厚度、颗粒交换系数、颗粒浓度分布和混合指数,对转鼓结构进行优化和选择较为合适的操作参数。
另外,国内外学者大多针对圆形滚筒研究了转速、填充率、抄板长度和形状以及数量等影响因素对颗粒运动与混合特性的影响,但对六棱柱工装篮烘干筒内颗粒运动混合的研究较少,对其内搅棒的形状和数量对颗粒混合特性的研究更少。
本文中基于离散元素法,对工装篮烘干筒内不同粒径的颗粒状硅料混合特性进行分析,研究不同操作参数与搅棒结构对硅料颗粒在工装篮烘干筒中运动与混合的影响;通过对比分析2种粒径固体单球型硅料颗粒运动轨迹与混合分布以及颗粒床中的Lacey指数随时间的变化, 选取较合理的操作参数与搅棒的结构,以改善硅料颗粒混合的均匀性,从而使烘干性能得以改善,提高烘干筒的工作效率。

图1 SGSI28-10CD全自动硅料清洗机
Fig.1 SGSI28-10CD automatic silicon cleaning machine
1 研究对象及相关参数
选择SGSI28-10CD全自动硅料清洗机(如图1所示), 其工作流程(如图2所示)包括颗粒状硅料经过上料、 超声波清洗、 碱洗、 超声波清洗、 漂洗、 酸洗、 超声波清洗、 烘干、 下料等工艺, 获得光伏产业所需的硅料。 烘干在全自动硅料清洗机中处于重要位置, 决定了最后获得物料的质量, 因此, 本文中对全自动硅料清洗机中的烘干工艺进行研究, 对参数与结构进行优化, 从而使硅料具有较好的形态和质量。
图3所示为新型六棱柱工装篮烘干筒的基本结构和尺寸,传输通道的外径为50 mm,内径为40 mm,传输通道入口与气泵直接相连,传输通道支撑4根长度为85 mm的圆柱搅棒和边长为181.5 mm的六边形烘干筒,喷气孔分布在传输通道上,是用来对烘干筒中的颗粒进行干燥。
如图3所示,烘干筒内2种不同粒径硅料颗粒都集中在下部,中部主要为来自传输通道喷口的流化热风(热空气),上部为颗粒中的水分经过蒸发后的水蒸气,硅料颗粒与热空气进行对流换热,与此同时颗粒与颗粒间也很会发生热传导,热量从温度高的颗粒传向温度较低的颗粒。在烘干筒外框的转动下,硅料颗粒在烘干筒中运动,再经过搅棒的作用,颗粒的运动更加剧烈,混合程度得到提高,从而提高传热效率,减少了能源的浪费。
图2 全自动硅料清洗机的工作流程
Fig.2 Work process of automatic silicon cleaning machine
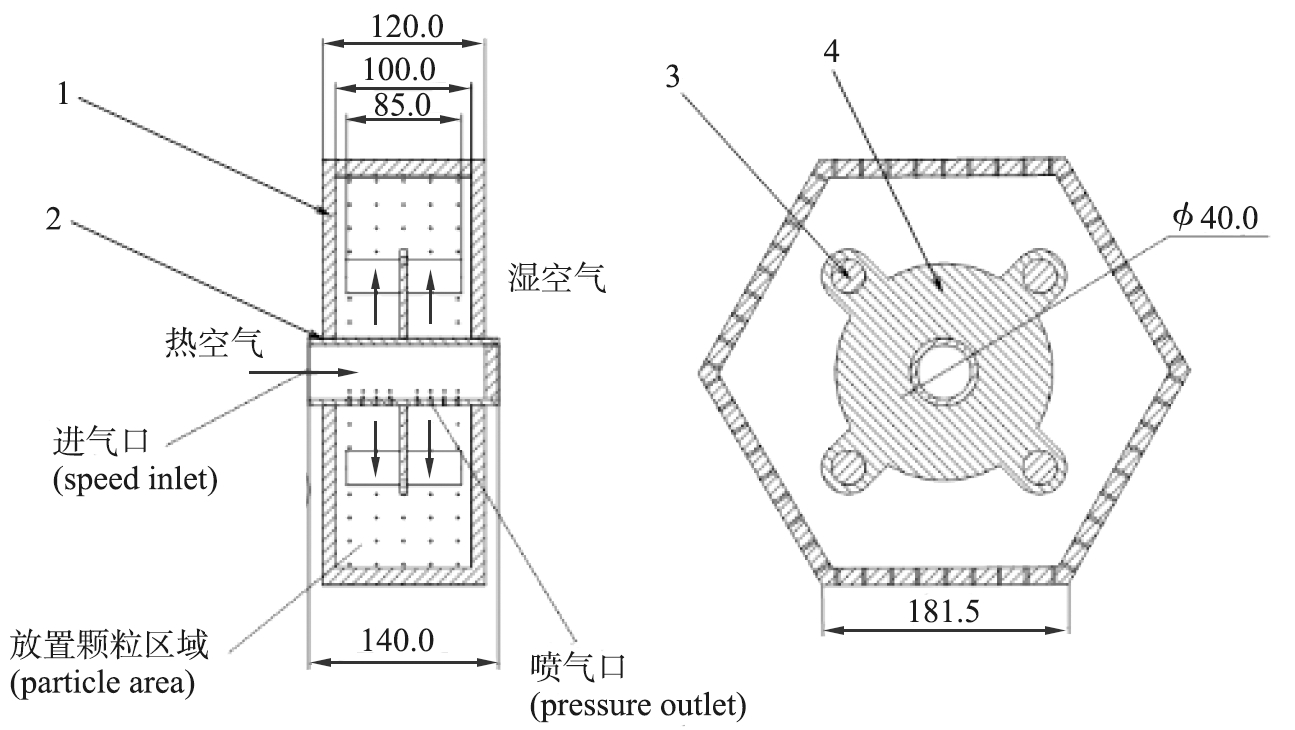
1—烘干筒; 2—传输通道; 3—搅棒; 4—支撑件。
图3 工装篮烘干筒的基本结构和尺寸
Fig.3 Basic structure and size of tooling basket drying cylinder
2 数值模型
2.1 颗粒运动方程
在DEM软件中,研究旋转工装篮烘干筒中的球形硅料颗粒,通过计算作用在颗粒上的合力,采用牛顿第二定律求解每个球形颗粒的位移、 速度及加速度,从而跟踪每个硅料颗粒的运动轨迹[9],最终得到硅料颗粒整体的宏观运动规律。法向接触力的合力Fn和切向接触力Ft可由线性黏弹性模型求得,分别表示为
Fn=-knδn-ηnvn,
(1)
Ft=-ktδt-ηtvt,
(2)
式中: kn、 kt为颗粒法线和切线方向的弹性系数; δn、 δt为法向和切向的质点位移; ηn、 ηt为法线方向和切线方向阻尼系数; vn、 vt为颗粒间的相对法线方向和切线方向速度,用于计算颗粒间发生滑动时的切向接触力。
扭矩T表示为
T=L×(Ft+Fn),
(3)
式中: L为从粒子中心到接触点的距离矢量。
在EDEM模型中,采用硅料颗粒的各种力平衡来预测、计算离散相的运动轨迹。使用牛顿第二定律,控制硅料颗粒运动的常微分方程见式(4)、 (5),即
(4)
(5)
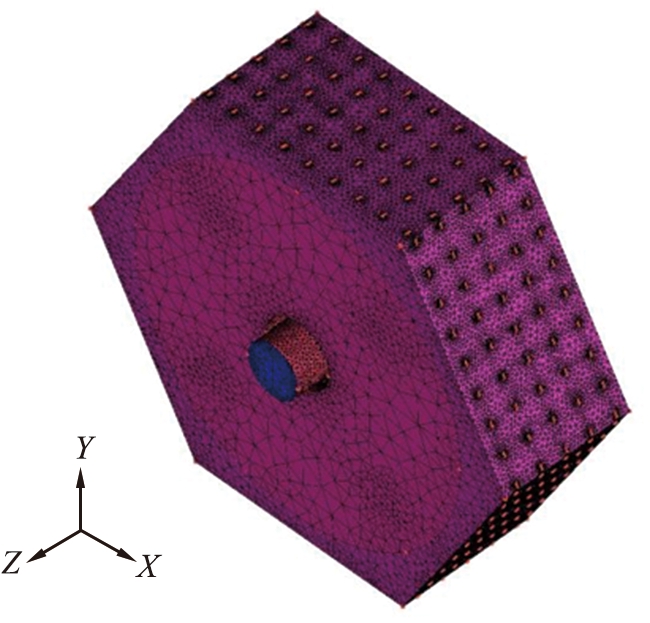
图4 工装篮烘干筒有限元网格模型
Fig.4 Finite element mesh model of work basket drying cylinder
式中: mi为颗粒的质量; vi为颗粒的速度; ωi为颗粒的角速度; Ii为颗粒的转动惯量; di为颗粒的直径; N为碰撞颗粒的数量; Fnij为颗粒i、 j之间的法向力; Ftij为颗粒i、 j之间的切向力; Mrij为颗粒i、 j之间的滚动摩擦力矩。
2.2 划分网格
由于EDEM软件中的网格划分相对比较粗糙,因此为了更好地模拟工装篮烘干筒内颗粒的运动混合,需要对工装篮进行网格细化。本文中采ICEM CFD软件对工装篮的网格进行划分,网格数量为113 467 5,细化后的网格模型如图4所示。
2.3 颗粒模型
设定2种颗粒为EDEM中默认的圆球颗粒,如图5所示。2种颗粒的直径分别为3、 5 mm,2种颗粒的泊松比、 剪切模量和密度等物理属性相同。

(a)3 mm(b) 5 mm图5 不同粒径颗粒模型Fig.5 Particle models with different particle sizes

图6 工装篮烘干筒内颗粒混合的模型验证装置
Fig.6 A verification device for particle mixing effect model in drying barrel of tooling basket
2.4 边界条件
本文中选取球接触模型,颗粒和搅拌器之间选取Standard Rolling Friction和Hertz-Mindlin (no slip)模型。工装篮顶部设定为仿真的虚拟颗粒工厂,颗粒创建速率设为2 000 s-1。综合考虑仿真速度和计算精度后,时间步长为瑞利时间步长的33%,仿真时间为100 s,网格边长为5.25 mm。
2.5 验证模型
图6所示为工装篮烘干筒内颗粒混合的模型验证装置。六棱柱工装篮烘干筒外框部分用聚丙烯建造,两端板一侧为齿轮聚丙烯板,另一侧用透明聚氯乙烯材料制成,以方便观察。该装置中工装篮烘干筒是由带有调速器的电机驱动齿轮传动的。通过对粒径约为3、 5 mm的2种硅料颗粒进行混合实验,采用示踪颗粒观察颗粒的运动轨迹,验证示踪颗粒运动轨迹的观察结果与模拟计算结果基本一致,验证模型模拟的正确性。
2.6 DEM参数
本文中研究的烘干筒形状为正六边形(如图3), 边长为181.5 mm, 筒外部长度为140 mm, 筒的内部长度为120 mm, 其他DEM参数取值如表1所示。 模拟工况如下: 1)在填充率为31.73%和转速为4.08 rad/s时, 模拟烘干筒在无搅棒、 使用圆柱形搅棒、 长方体形搅棒和三棱柱形搅棒下颗粒的混合分布; 2)模拟烘干筒分别在搅棒数为2、 4和6时的颗粒混合分布; 3)模拟烘干筒分别在填充率为23.60%、 31.73%、 41.40%时的颗粒混合分布; 4)模拟烘干筒分别在转速为4.08、 8.91、 16.4 rad/s时的颗粒混合分布。为了更好地表示颗粒混合分布,以蓝、 绿2种颜色标记表示分布状态。
表1 DEM参数取值
Tab.1 DEM parameter values
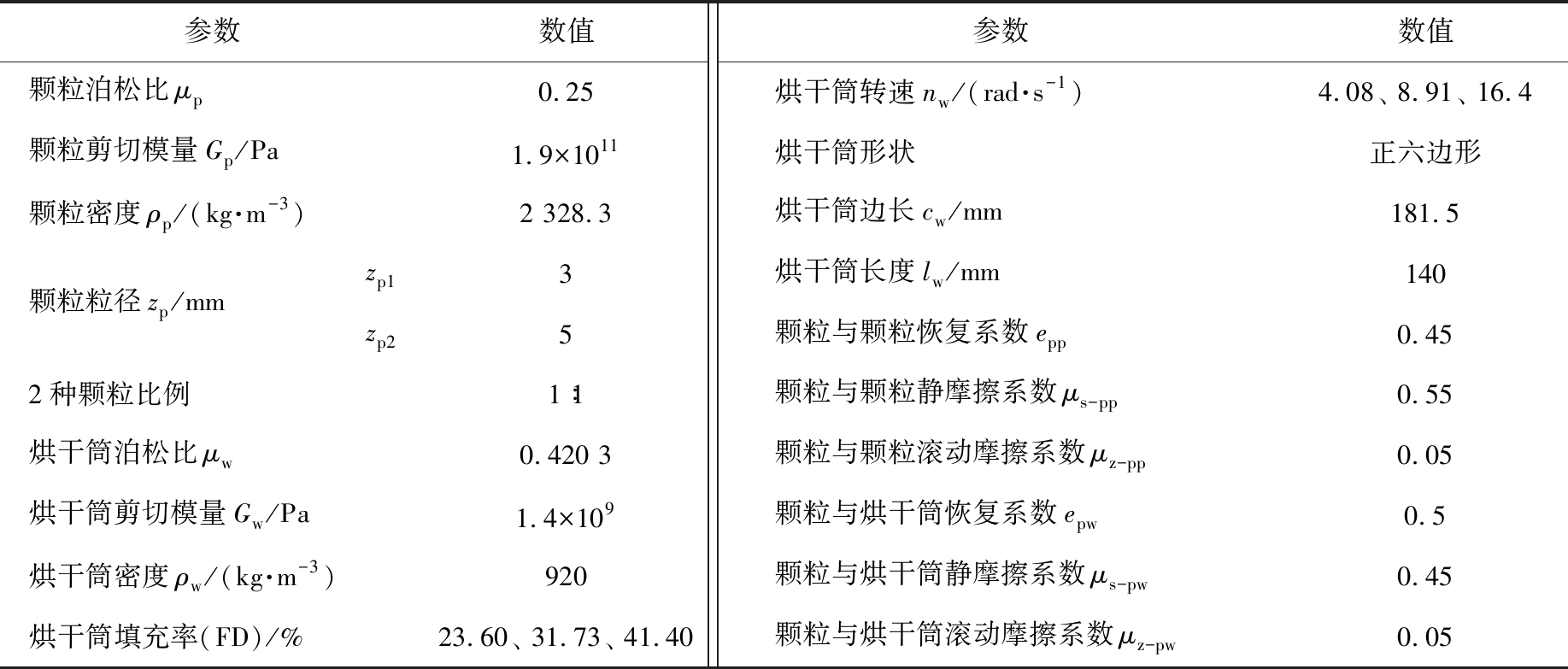
参数数值颗粒泊松比μp0.25颗粒剪切模量Gp/Pa1.9×1011颗粒密度ρp/(kg·m-3)2 328.3颗粒粒径zp/mmzp13zp252种颗粒比例1∶1烘干筒泊松比μw0.420 3烘干筒剪切模量Gw/Pa1.4×109烘干筒密度ρw/(kg·m-3)920烘干筒填充率(FD)/%23.60、 31.73、 41.40参数数值烘干筒转速nw/(rad·s-1)4.08、 8.91、 16.4烘干筒形状正六边形烘干筒边长cw/mm181.5烘干筒长度lw/mm140颗粒与颗粒恢复系数epp0.45颗粒与颗粒静摩擦系数μs-pp0.55颗粒与颗粒滚动摩擦系数μz-pp0.05颗粒与烘干筒恢复系数epw0.5颗粒与烘干筒静摩擦系数μs-pw0.45颗粒与烘干筒滚动摩擦系数μz-pw0.05
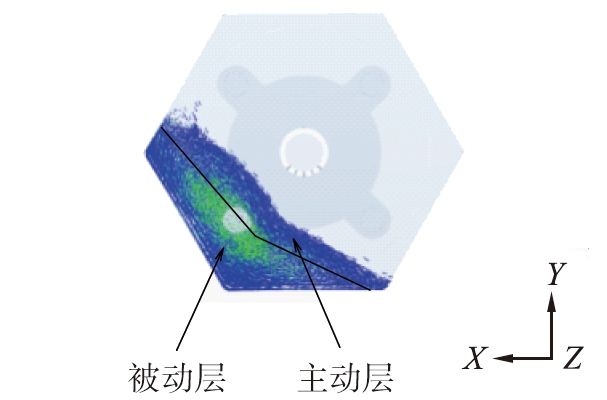
图7 烘干筒内颗粒速度矢量图
Fig.7 Vector illustration of particle velocity in drying drum
3 模拟结果与分析
3.1 颗粒的混合机理
通常情况下,通过对工装篮烘干筒中颗粒的混合研究可以发现,颗粒混合机制具体包含3种,分别是剪切混合、对流混合以及扩散混合。混合开始阶段主要是剪切和对流混合为主,之后混合作用便持续提升,一直到彻底混合。由于受到对流混合模式的影响,颗粒床能够被细分成2个不同区域,主要有被动层和主动层[10],如图7所示。主动层的颗粒持续由高端向下滑落,被动层的颗粒伴随烘干筒开始转动,在运动过程中当颗达到相应高度时,颗粒间摩擦力与重力相比较小,此时颗粒顺着主动层迅速下滑。颗粒在烘干筒的带动下实现转动,方向是逆时针。
为了对时间与颗粒混合程度变化关系进行定量分析,在统计分析烘干筒中颗粒混合状况时采用Lacey指数评价法[11-13]。该方法是基于统计学分析方法提出的针对颗粒混合度定量描述2种物料颗粒整体混合程度评价的理论方法。为了顺利获取Lacey指数,首先要将烘干筒细分成相应的样本,随后进行统计分析。
选择广泛使用的Lacey混合指数M[14]对旋转烘干筒中颗粒混合状况展开分析。M能够作为最大方差与瞬时方差间的比值。将直径分别为5、 3 mm的颗粒分别设为颗粒p1与颗粒p2。
(6)
式中:![]() 为初始时刻(完全分离时)的混合方差;
为初始时刻(完全分离时)的混合方差;![]() 为2种颗粒混合均匀时刻的方差; S2为任意时刻颗粒的混合方差。
为2种颗粒混合均匀时刻的方差; S2为任意时刻颗粒的混合方差。
(7)
(8)
(9)
(10)
式中: P为颗粒p1所占比例;Np1和Np2分别为所有样本中p1颗粒数的总和与p2颗粒数的总和。
(11)
式中: Pi为每个样品中p1颗粒所占比例,其中i为样品序号;![]() 和
和![]() 分别为单个样本中p1颗粒数与p2颗粒数。
分别为单个样本中p1颗粒数与p2颗粒数。
3.2 单因素分析
为了更好地研究每个影响因素的变化对颗粒混合特性的影响,本文中通过单因素分析法,对工装篮烘干筒内硅料颗粒的运动混合进行模拟,具体的模拟情况如表2所示。
表2 单因素分析法的所有模拟情况
Tab.2 All simulations of single factor analysis
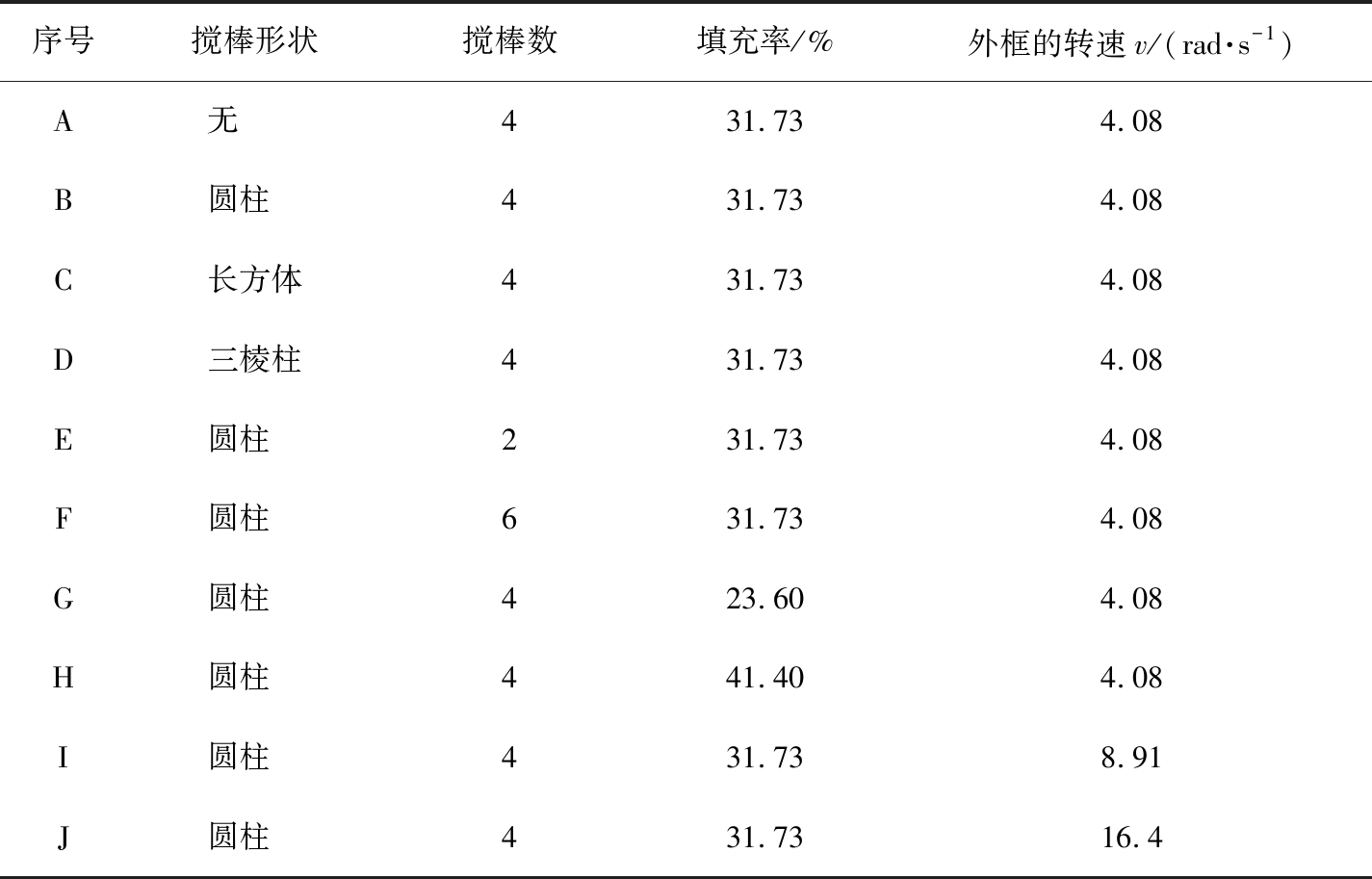
序号搅棒形状搅棒数填充率/%外框的转速v/(rad·s-1)A无 431.734.08B圆柱 431.734.08C长方体431.734.08D三棱柱431.734.08E圆柱 231.734.08F圆柱 631.734.08G圆柱 423.604.08H圆柱 441.404.08I圆柱 431.738.91J圆柱 431.7316.4
3.2.1 不同形状的搅棒对混合特性的影响
图8所示为颗粒混合时间为50 s时无搅棒和不同形状的搅棒情况下硅料颗粒床的混合分布图。由图8(a)可知, 在没有搅棒的情况下, 颗粒的运动路径相对随机, 颗粒床内存在明显的未混合颗粒团, 表明无搅棒时混合效果较差。 由图8(b)可知, 在圆柱形搅棒的搅动下, 促进了鼓内颗粒之间的接触和碰撞。 对于长方体形的搅棒(图8(c)), 颗粒床内未混合颗粒团明显减少, 表明搅棒为长方体板时能充分搅拌颗粒床。 由图8(d)可知, 在使用三棱柱形的搅棒时, 颗粒床中的颗粒仍存在为混合的颗粒团。 搅棒不转动时, 只有烘干筒的外框转动, 在此速度下, 颗粒的运动全都靠外框的转动带动, 而颗粒与搅棒之间的运动幅度与频率相对较低, 因此, 颗粒在搅棒上的停留时间较短, 导致颗粒落入床内的速度和动能降低, 削弱了硅料颗粒在床内的流动性, 所以选择合适形状的搅棒可以有效地改善硅料物料的混合。
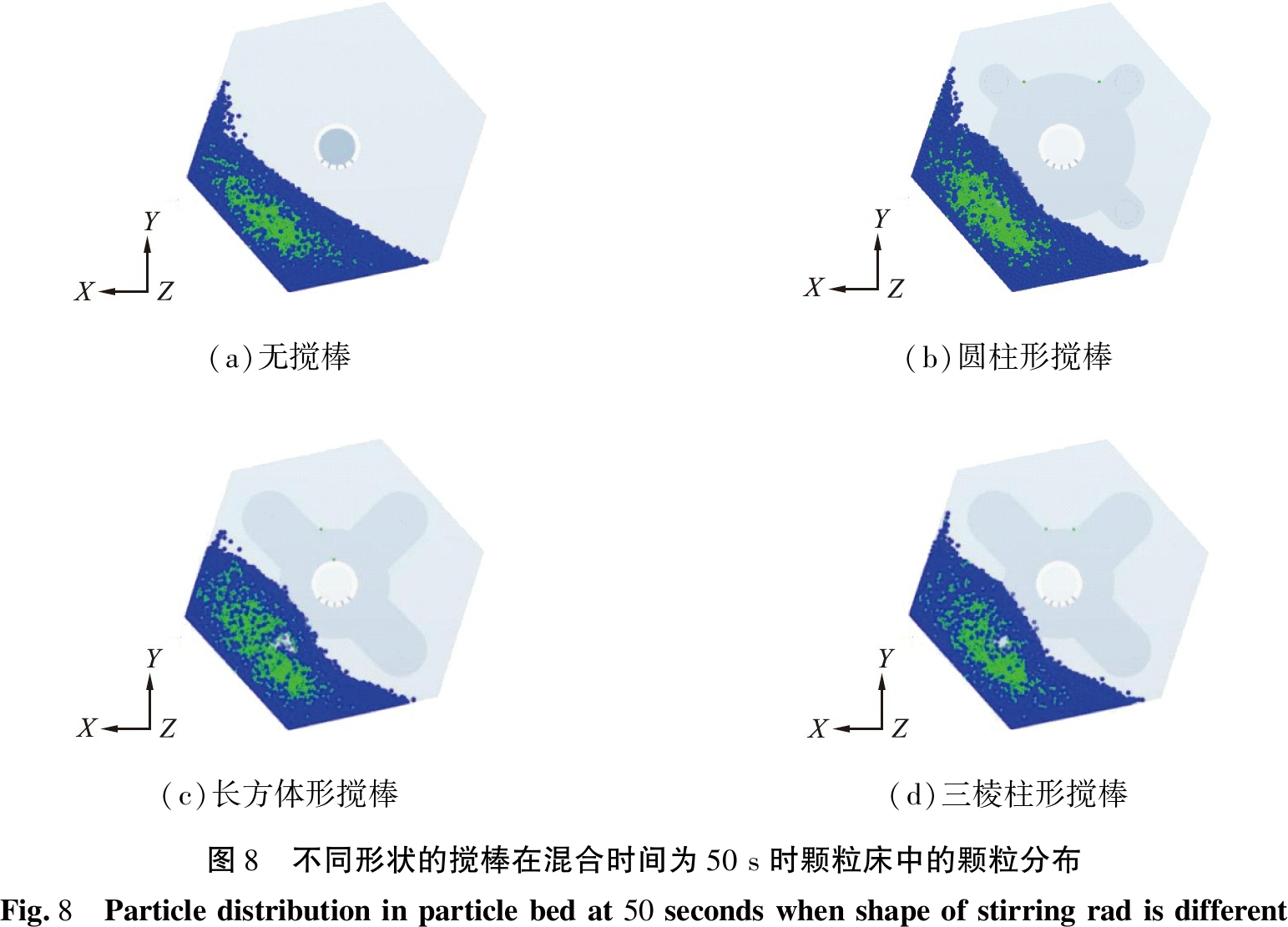
(a)无搅棒(b)圆柱形搅棒(c)长方体形搅棒(d)三棱柱形搅棒图8 不同形状的搅棒在混合时间为50 s时颗粒床中的颗粒分布Fig.8 Particle distribution in particle bed at 50 seconds when shape of stirring rad is different
使用Lacey指数对颗粒的混合程度进行定量分析,图9所示为不同形状的搅棒在烘干筒内颗粒的M随时间的具体变化图。由图可知,当没有搅棒时颗粒混合程度较低,M约为0.5。前10 s混合较为剧烈,在之后的90 s中依旧未达到稳定状态,M具有小幅度的波动,但对混合结果没有大的影响,且混合程度不高。当搅棒为圆柱时,曲线基本与无搅棒时重合,圆柱形状形状并不会增加对流作用。随着搅棒变为三棱柱时,混合程度得到增加,同时在前10 s中的混合速率也得到了相应的提高,尤其是当搅棒变为长方体时混合速率增加最快,M大于0.6,混合程度也得到了提高,因此,当搅棒为长方体时可以有效地改善颗粒的混合。
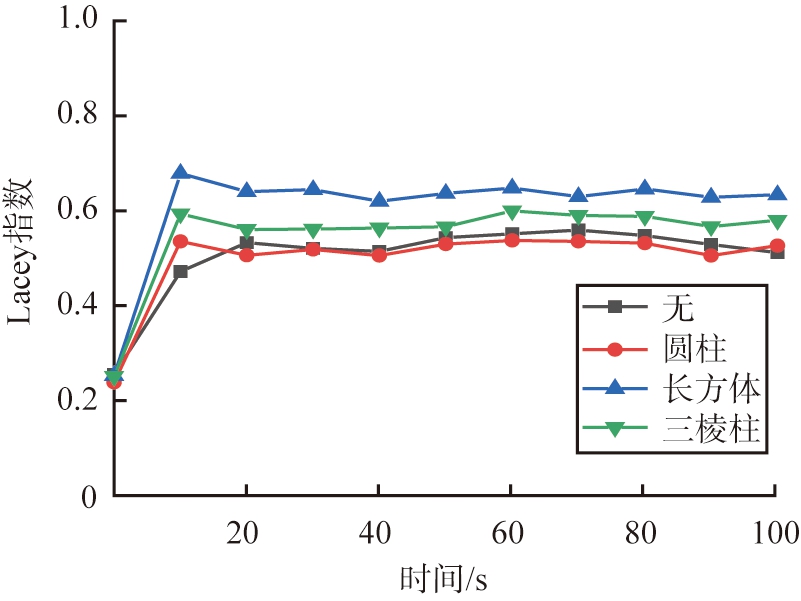
图9 搅棒形状不同时烘干筒内颗粒的Lacey指数随时间的变化
Fig.9 Change of Lacey index of particles in drying cylinder with time when shape of stirring rod is different
3.2.2 不同数量的搅棒对混合特性的影响
图10、 11所示分别为不同搅棒数量下颗粒床中的混合分布和Lacey指数随时间变化的分布曲线图。实验设置3种不同数量的圆形搅棒:2, 4和6,其余参数保持不变。由图11可知:当搅棒数为2时,绿色颗粒在烘干筒内不能充分混合,M约为0.5。当搅棒数为4时,曲线走势大致与搅棒数为2时的类似,这是由于搅棒是不转动的,而是外框在转动,在颗粒运动过程中真正起作用的只有1个,这与搅棒数为2时的作用效果一致,但颗粒最终的混合指数比搅棒数为2时略大。当搅棒数为6时,曲线最终达到的稳定的值明显比其他数目的值要大,M约为0.6,这是由于当搅棒数为6时,由于搅棒增多,使得在运动区域内对颗粒的搅拌作用较大,增加了颗粒与颗粒之间接触次数,从而提高了颗粒的混合度。综上所述,当搅棒为数6时,Lacey混合指数较大,颗粒混合效果更明显。
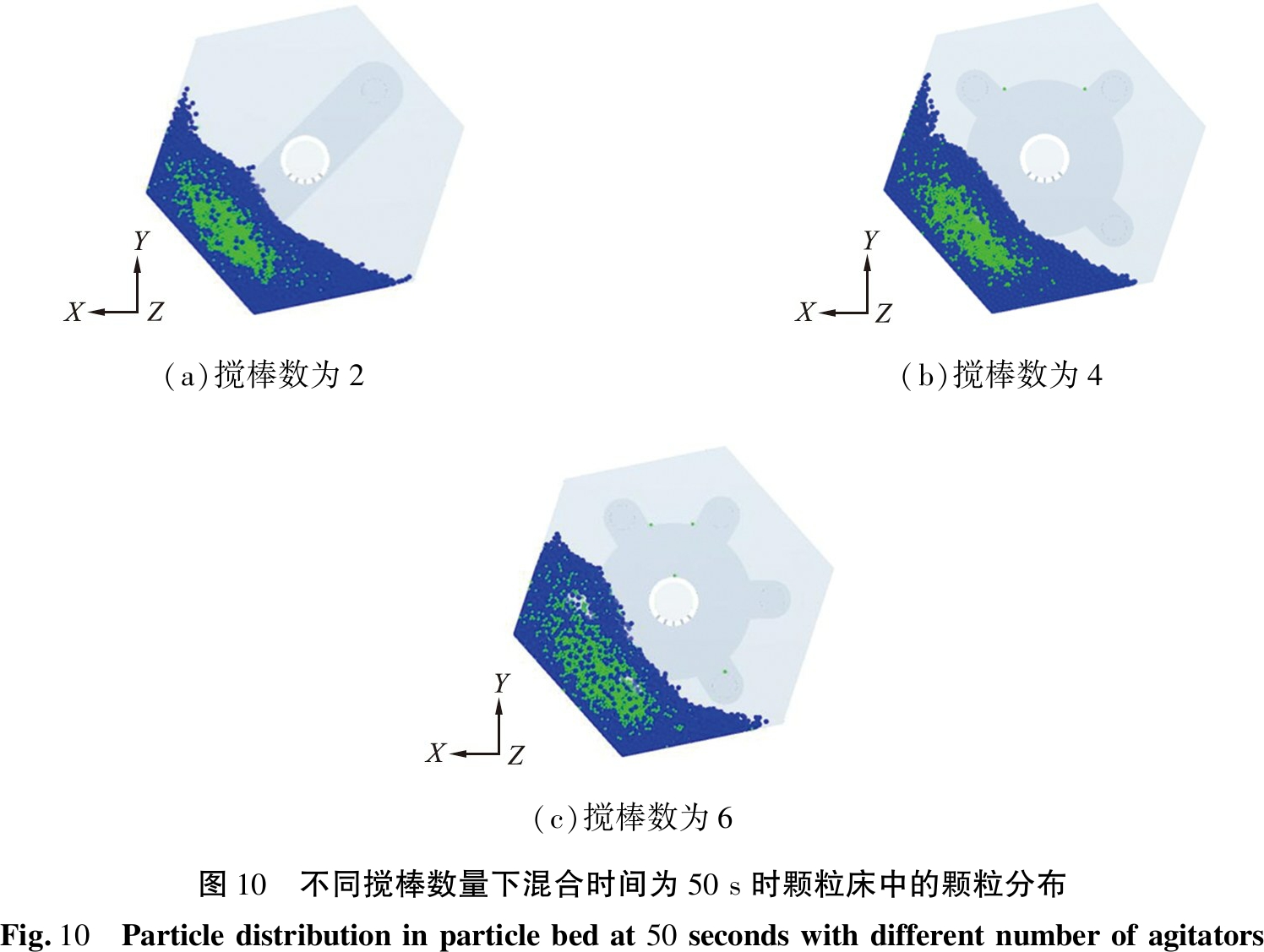
(a)搅棒数为2(b)搅棒数为4(c)搅棒数为6图10 不同搅棒数量下混合时间为50 s时颗粒床中的颗粒分布Fig.10 Particle distribution in particle bed at 50 seconds with different number of agitators
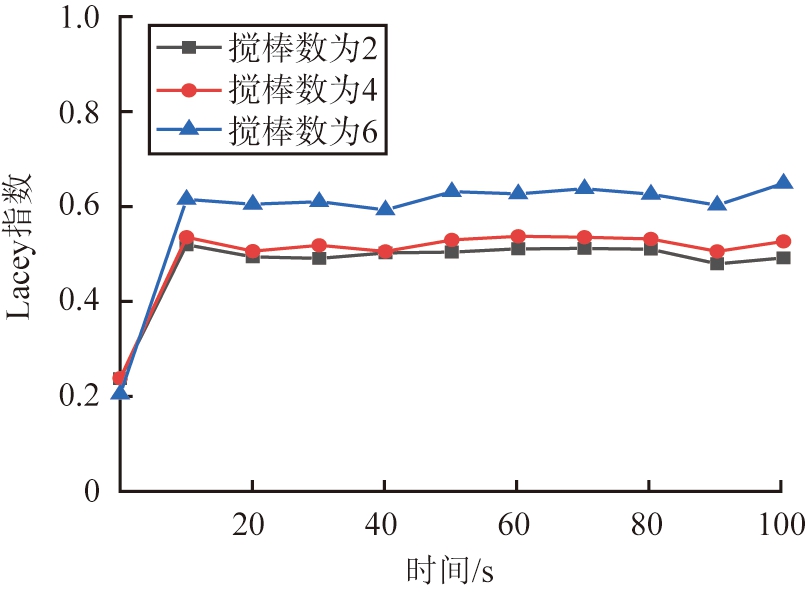
图11 搅棒数量不同时烘干筒内颗粒随时间Lacey指数的变化
Fig.11 Variation of Lacey index of particles in drying cylinder with different number of agitators over time
3.2.3 不同颗粒填充率对混合特性的影响
图12所示为颗粒填充率不同时的颗粒混合实验结果。通过分析图12可知,填充率为23.60%时颗粒群混合效率比前者的更快。对比图12(a)、 (b)、 (c)后发现,在填充率为23.60%时,颗粒受对流混合和局部混合的共同作用更加显著,蓝、 绿色颗粒团的相对运动接触也更加充分。由图12(b)可知,蓝、 绿色颗粒群在搅拌器强制作用下具有不太明显的分层,混合效果不佳。分析图12(c)可知,颗粒群局部绿色颗粒聚集在中间,处于上层的颗粒运动较快,由于颗粒数量较多,颗粒群中端颗粒受搅拌器作用较小,所以该中间区域颗粒运动速度较慢,混合效果不佳,因此,当填充率为23.60%时,蓝、 绿色颗粒群对流混合效果也最为显著。
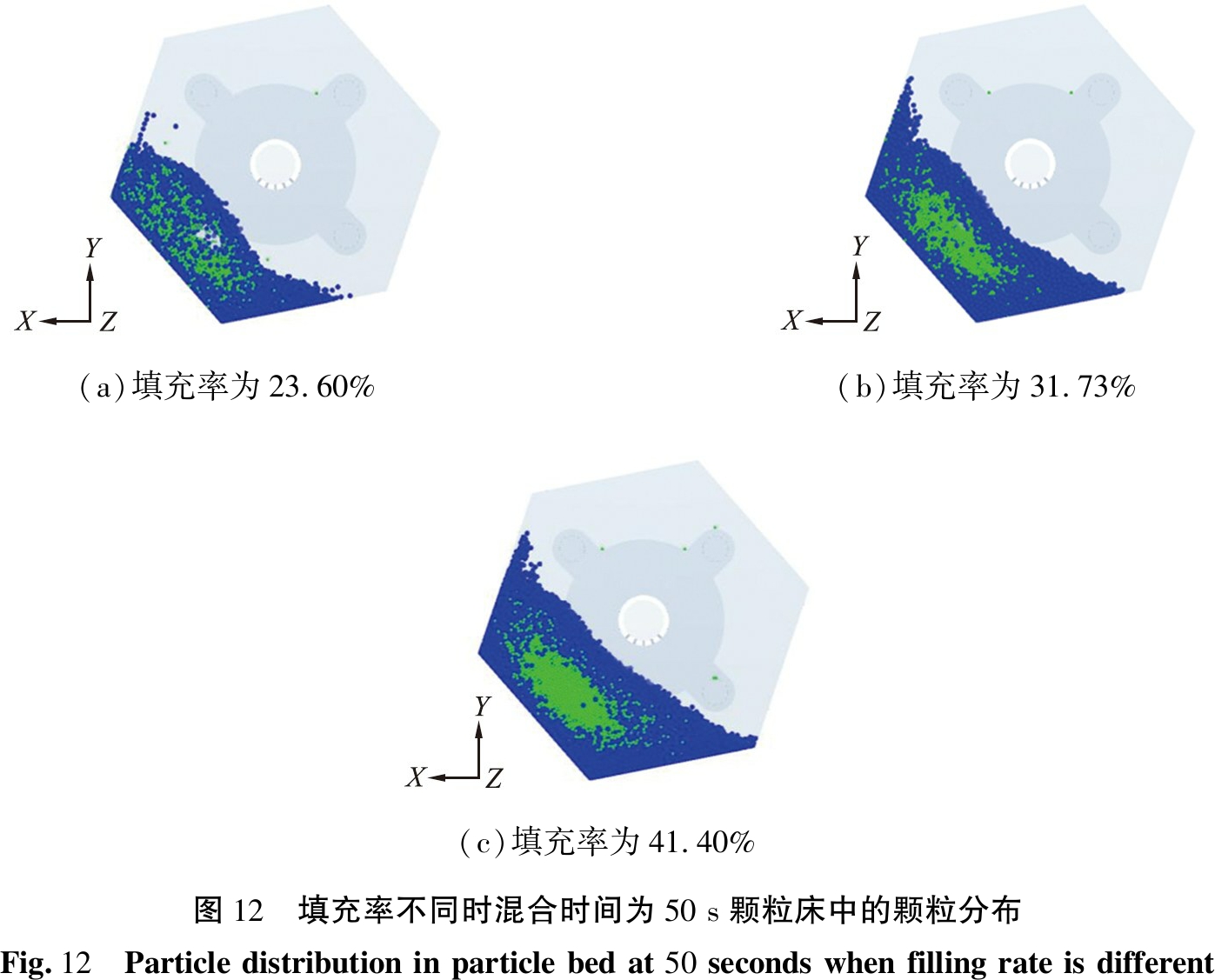
(a)填充率为23.60%(b)填充率为31.73%(c)填充率为41.40%图12 填充率不同时混合时间为50 s颗粒床中的颗粒分布Fig.12 Particle distribution in particle bed at 50 seconds when filling rate is different
当填充率不同时,造成混合指数变化的原因也不尽相同。如图13所示,填充率为23.60%时,颗粒群在最终的Lacey混合指数最大能达到0.7~0.8,且混合效果最好。与填充率为31.73%和41.40%的相比,混合指数上升更快,最终的均匀混合程度也更好。原因在于颗粒数量的增加影响了颗粒群的宏观运动,降低了颗粒运动的速度。综上所述,填充率为23.60%时具有均匀混合速率和混合效果。
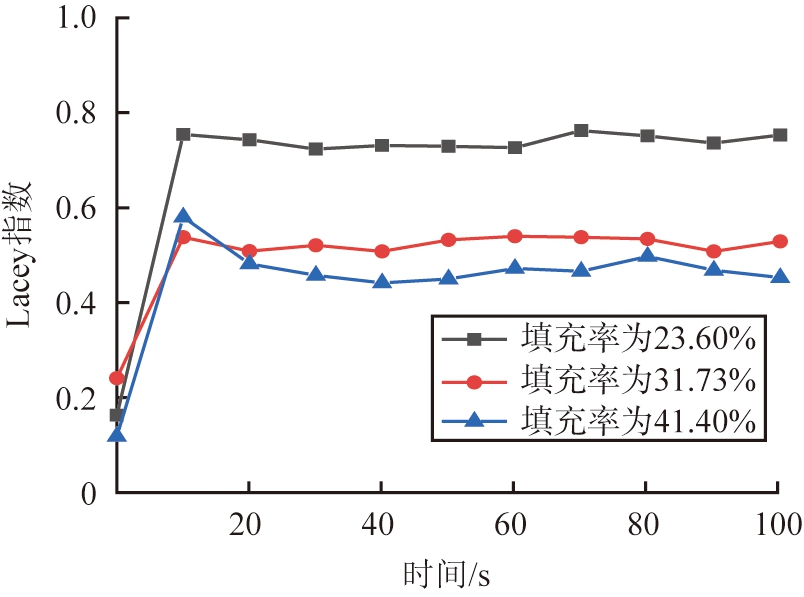
图13 填充率不同时烘干筒内颗粒随时间Lacey指数的变化
Fig.13 Variation of Lacey index of particles in drying cylinder with time when filling rate is different
3.2.4 不同外框转速对混合特性的影响
图14、 15定性地显示了粒径为3、 5 mm的2种硅料颗粒在不同外框转速下颗粒的运动轨迹和混合物的分布。实验设置3种不同外框转速: 4.08、 8.91、 16.4 rad/s,其余参数保持不变。
从粒子床中随机选择2个粒子,直径分别为3、 5 mm,如图14(a)、 15(a)所示,当烘干筒的外框的旋转转速为4.08 rad/s时,较大的颗粒逐渐下沉到床层中心形成明显的偏析核心,而较小的颗粒逐渐向床层外围移动。颗粒物料的运动形态主要为滑移、塌落和滚落。在这种运动形态下,颗粒床的大部分颗粒通过烘干筒壁的旋转向上旋转,颗粒层均匀静态流动。颗粒运动主要表现为对流运动和剪切运动,因此颗粒混合发生区域主要在主动层。
如图14(b)、 15(b)所示, 在较高的外框转速下, 粒径分别为3、 5 mm的颗粒偏离了原来滚动滑移的运动路径, 并且在混合过程中在床的中心没有形成偏析核心。 颗粒物料的运动形态主要为泻落和抛落。 随着旋转速度的进一步增加(8.91 rad/s), 抛出的粒子数量增加, 颗粒从床分离并被抛入筒内的自由空间, 粒子在筒内的自由空间内得到充分的混合。
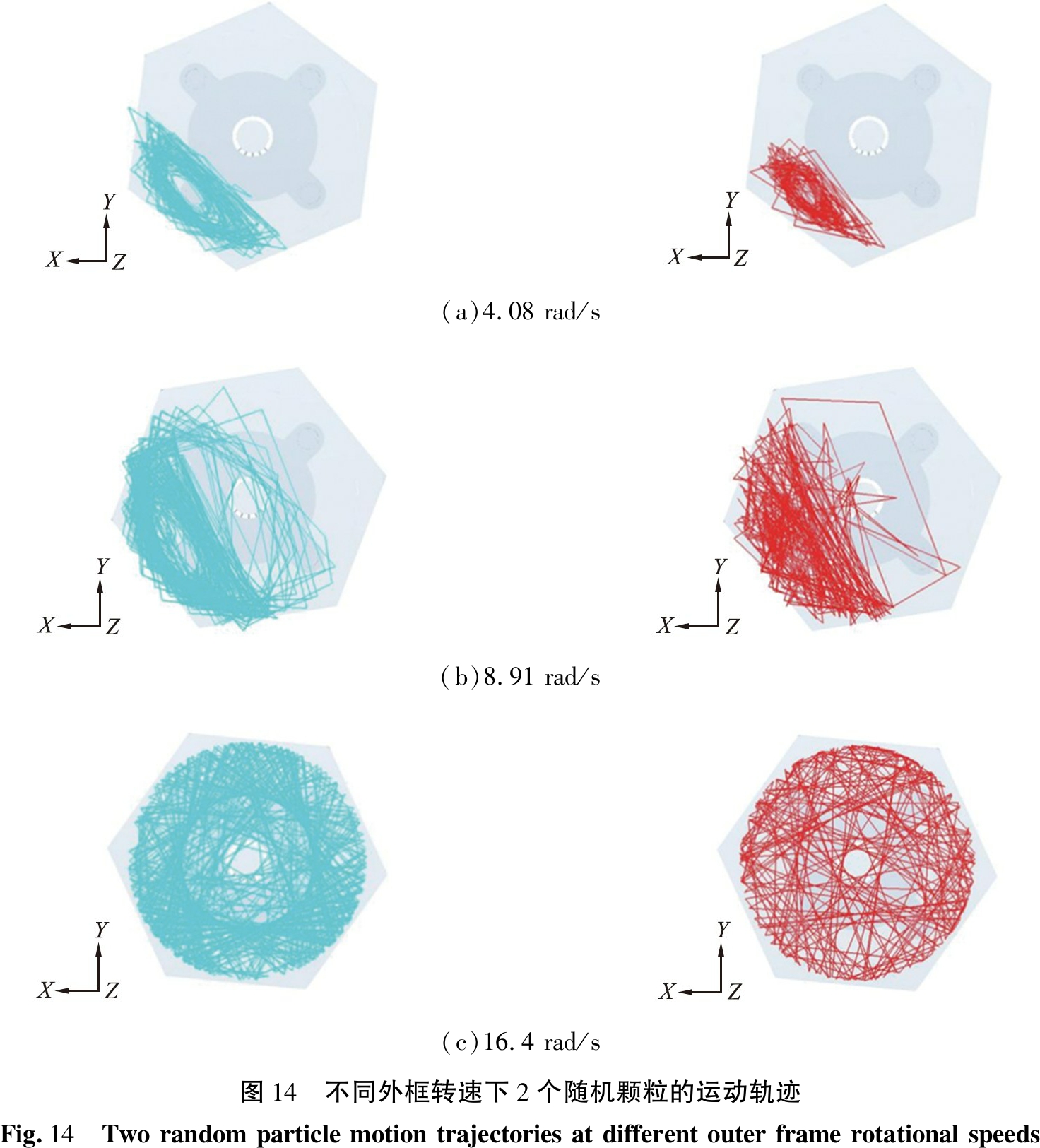
(a)4.08 rad/s(b)8.91 rad/s(c)16.4 rad/s图14 不同外框转速下2个随机颗粒的运动轨迹Fig.14 Two random particle motion trajectories at different outer frame rotational speeds
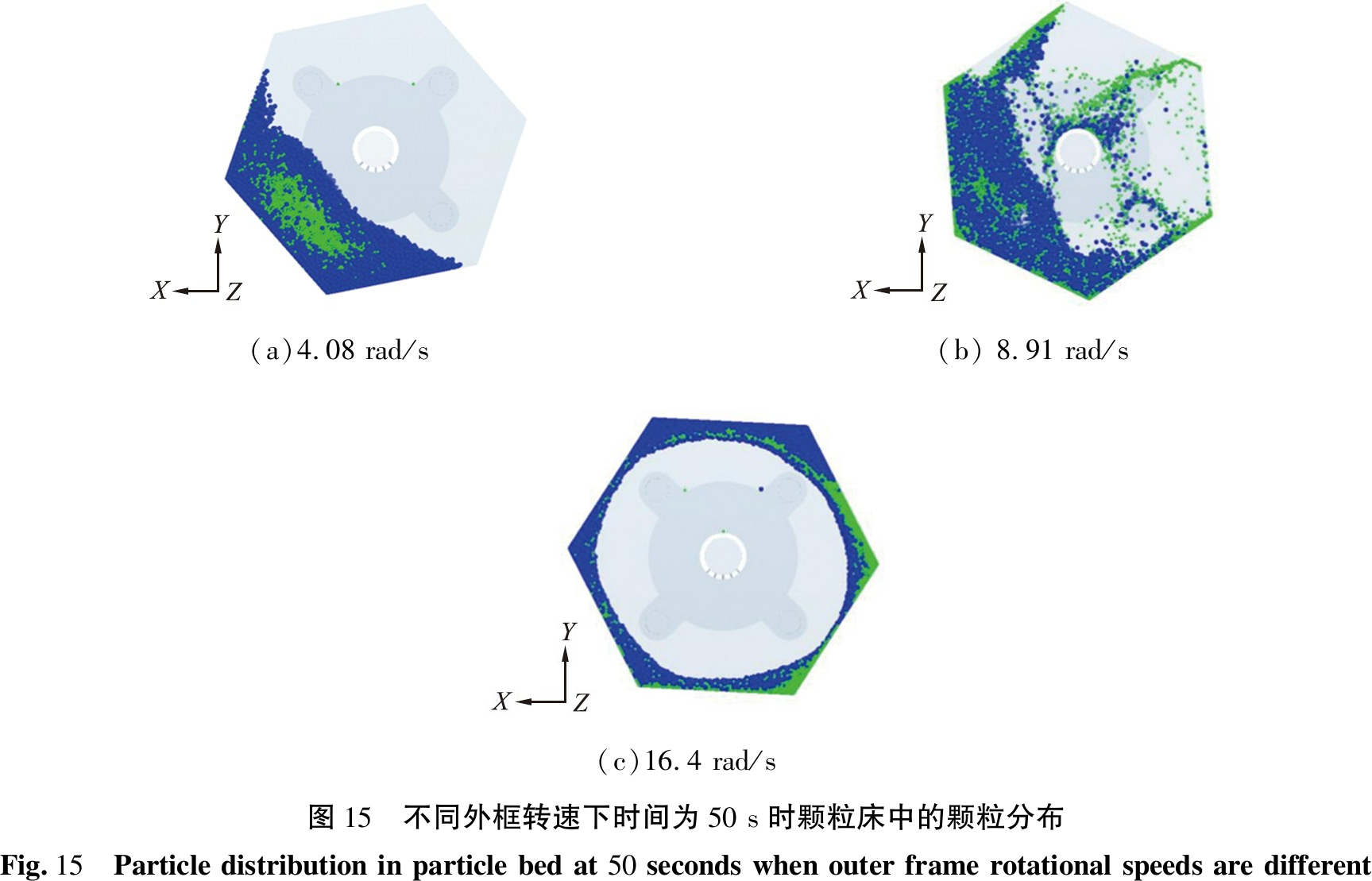
(a)4.08 rad/s(b) 8.91 rad/s(c)16.4 rad/s图15 不同外框转速下时间为50 s时颗粒床中的颗粒分布Fig.15 Particle distribution in particle bed at 50 seconds when outer frame rotational speeds are different
图14(c)、 15(c)显示了外框转速为16.4 rad/s时的混合效果。 颗粒物料的运动形态主要为离心。 随着转速的增加, 颗粒的离心力越来越大, 颗粒物料紧贴烘干筒壁获得动能也越来越大。 当转速过大时, 颗粒物料会一直紧贴外框壁面, 此时为离心模式。 由于转速不断提升, 离心现象会变得特别显著, 在回转滚筒内大小颗粒受到了不同的离心力, 所以在转动时, 大小颗粒产生类似“偏析”的现象。
从图14、 15可以看出,随着旋转速度的增加,旋转滚筒中固体运动的不同状态已被确定,如滚动、滑移、泻落、抛落和离心。颗粒物料受到滚落以及泻落等模式而能够均匀且较快的混合,从混合效率提升的层面进行分析,烘干筒的最佳转速为8.91 rad/s。
由于烘干筒转速增大后, 在重力作用下的颗粒会缓慢掉到底床, 促使颗粒之间的碰撞以及接触进一步加大, 使颗粒更加具备活跃性, 而且颗粒物料的混合效率以及整体混合指数显著增大, 如果转速大到一定程度, 转速再进行增加, 也会逐步减少对混合的影响。 如图16所示, 当转速为16.4 rad/s时的M比转速为8.91 rad/s时的要小。 但颗粒物料混合所需稳定时间相差不大, 都在10 s左右。 当转速增加到一定程度后, 对混合的影响逐渐变小, 出现不增反降的情况, 因此, 为了能增加其混合效果, 转速为8.91 rad/s比较合适。
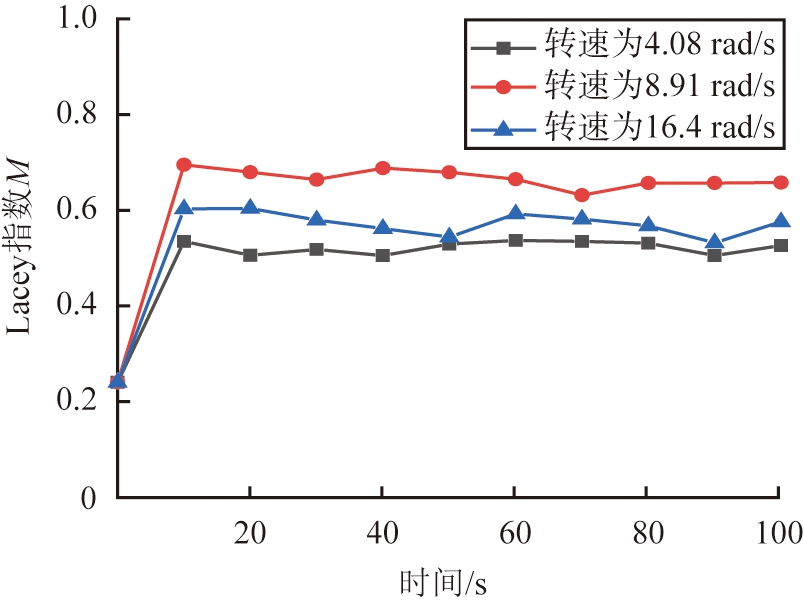
图16 转速不同时烘干筒内颗粒随时间Lacey指数的变化
Fig.16 Variation of Lacey index of particles in drying cylinder with time at different rotational speeds
3.3 影响因素的正交分析
在旋转烘干筒设备对颗粒混合效果的影响因素中,烘干筒外框转速、颗粒填充率、搅棒数、搅棒形状是4个互不影响的因素。根据Santos等[15]对不同操作条件下转鼓内颗粒的动力学行为的研究,确定了烘干筒外框转速与颗粒填充率的3个水平;根据实际工况,确定了搅棒的数量与形状的3个水平。在p1和p2数量相同的工况下,设计四因素三水平的正交表,对影响因素的主次效果进行分析,表3所示为设计实验因素和水平。
表3 正交实验水平
Tab.3 Orthogonal test level

水平烘干筒外框转速v/(rad·s-1)颗粒填充率/%搅棒数搅棒形状14.0823.602圆柱 28.9131.734长方体316.441.406三棱柱
由于本实验为四因素三水平正交实验,故通过SPSS软件选择L9(34)正交表进行实验设计。正交实验方案的设计如表4所示。
由图9、 11、 13和16可知,在前20 s中混合基本稳定,但在20 s之后Lacey指数会发生小幅度波动,对最后的混合结果造成的影响较小。考虑到计算机的计算力与最终的混合效果,将时间步长设为20 s。将以上单因素分析的各个最优结果组成第10组,与正交分析的各组进行对比分析,从而得到最优的一组。
表4 L9(34)正交实验表
Tab.4 L9(34) Orthogonal tables
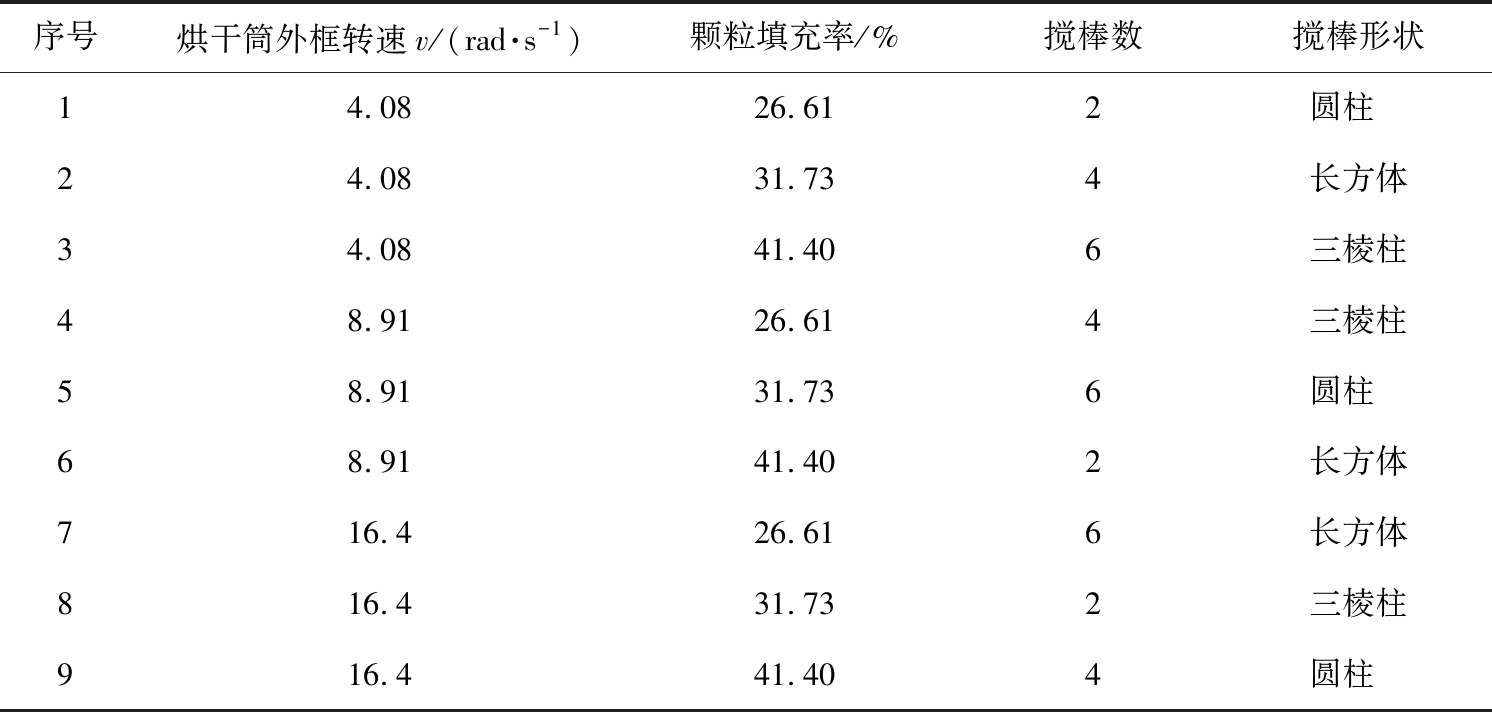
序号烘干筒外框转速v/(rad·s-1)颗粒填充率/%搅棒数搅棒形状14.0826.612圆柱 24.0831.734长方体34.0841.406三棱柱48.9126.614三棱柱58.9131.736圆柱 68.9141.402长方体716.426.616长方体816.431.732三棱柱916.441.404圆柱
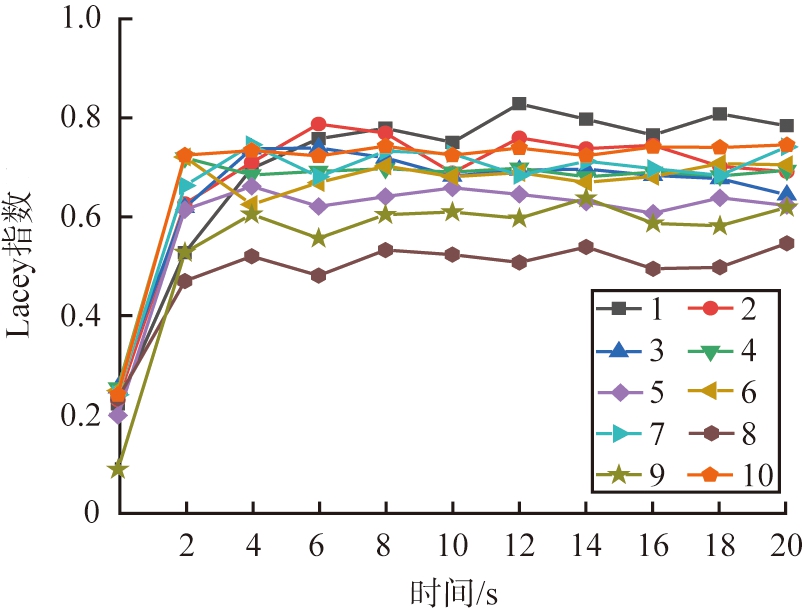
图17 烘干筒内颗粒随时间变化的Lacey指数
Fig.17 Lacey index of particles in drying tube with time
将各因素中影响最大的水平组合(为编号10)与正交组进行对比分析, 从而得到最优组合。 从图17可以看出, 第1组在混合时间为2~4 s时, 混合指数远远低于第10组, 从第4 s之后, 混合指数得到大大提升, 说明第1组在前4 s的混合效率较低; 而第10组在混合时间为2 s时混合指数就达到了0.722 7, 具有较高的混合效率。 第1组与第10组相比, 第1组的混合指数具有较大的波动, 而第10组则具有较好的稳定性, 混合指数始终稳定在约0.73。
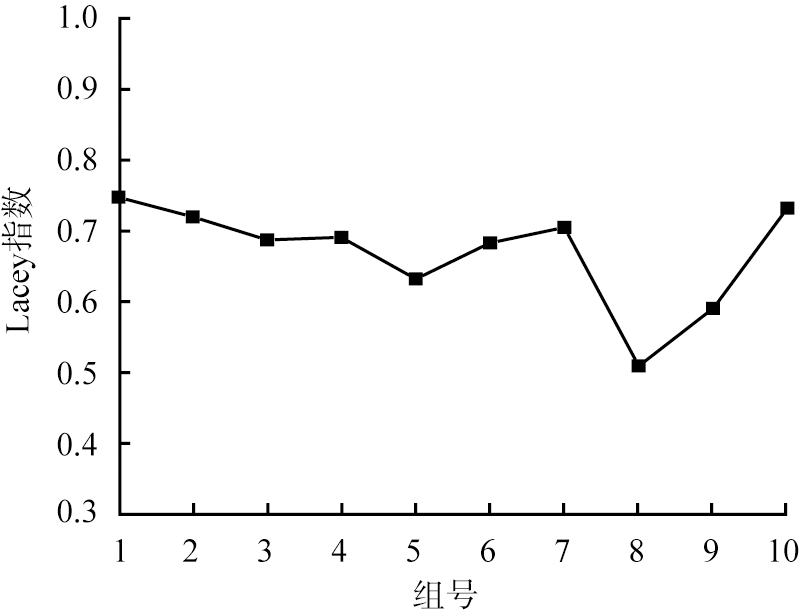
图18 不同组别的Lacey指数平均值
Fig.18 Average Lacey index for different groups
如图18所示,混合指数最高的是第1组,平均混合指数达到0.747 52;其次是影响因素最大的水平组(第10组),平均混合指数达到0.7319 1。通过对整个时间段的混合指数、混合效率以及混合稳定性的综合考虑,最终确定最优方案组合是影响因素最大的水平组(第10组)。各自的影响因素水平为:烘干筒外框转速为8.91 rad/s,颗粒填充率为23.60%,搅棒数为6,搅棒形状为长方体。
4 结论
1)烘干筒内有无搅棒和搅棒的形状影响着表观混合效果,无搅棒与圆柱形搅棒的混合速率和混合程度基本一致,而三棱柱形搅棒与长方体形搅棒的混合效果要好于前2种的,这是因为搅棒与颗粒之间的接触面增加了,促进了颗粒间对流,提高了混合效果,其中长方体的混合最好。
2)增加搅棒的数量后,发现搅棒在搅拌的过程中增加了中间内部颗粒从被动层进入主动层的数量,从而提高了对流作用,加速了2种颗粒的混合过程。通过模拟发现,当搅棒数为6时混合程度最佳。
3)颗粒群混合效果随着填充率的增加而下降。 与填充率为31.73%和41.40%相比, 填充率为23.60%时对流混合作用影响最强, 混合效果更好。
4)转速对工装篮烘干筒内2种不同粒径颗粒的混合影响较大,当转速为8.91 rad/s时混合效果及效率最高,均匀性最好。选择合适的烘干筒转速不仅可以提高硅料颗粒混合的均匀性和质量,从而提高混合效率。
5)通过单因素分析可以看出,烘干筒外框转速对混合效果的影响最大,其次为颗粒填充率、搅棒数、搅棒形状。
6)通过单因素得到的组合与正交组进行对比, 考虑到混合效率及混合效果, 烘干筒外框转速为8.91 rad/s, 颗粒填充率为23.60%,搅棒数为6,搅棒形状为长方体时是较优的一组。
[1]申燕, 贾艳飞, 姚旭, 等. 太阳能硅料化学清洗研究进展[J]. 中国洗涤用品工业, 2016(3): 50-53.
SHEN Y, JIA Y F, YAO X, et al. Research progress on chemical cleaning of solar silicon materials[J]. China Detergent Industry, 2016(3): 50-53.
[2]李璐, 李家成, 王佳豪, 等. 超声波清洗技术在工业领域的应用研究进展[J]. 应用化工, 2021, 50(3): 759-764.
LI L, LI J C, WANG J H, et al. Research progress in the application of ultrasonic cleaning technology in industry[J]. Applied Chemistry, 2021, 50(3): 759-764.
[3]李斌, 于洋, 马梦祥, 等. 三维喷动床内异径干湿颗粒混合特性数值模拟[J]. 化工学报, 2017, 68(12): 4545-4555.
LI B, YU Y, MA M X, et al. Numerical simulation of mixing characteristics of anisotropic dry and wet particles in a three-dimensional spray-actuated bed[J]. Journal of Chemical Engineering, 2017, 68(12): 4545-4555.
[4]李沐沅, 凌祥, 彭浩, 等. 板式回转干燥机的颗粒流动传热特性研究[J]. 压力容器, 2016, 33(3): 21-31, 68.
LI M Y, LING X, PENG H, et al. Study on the heat transfer characteristics of particle flow in a plate rotary dryer[J]. Pressure Vessels, 2016, 33(3): 21-31, 68.
[5]徐颖, 吴家正, 张亨伟, 等. 红外滚筒干燥机内颗粒混合的模拟研究[J]. 节能技术, 2018, 36(2): 125-129.
XU Y, WU J Z, ZHANG H W, et al. Simulation study of particle mixing in an infrared drum dryer[J]. Energy Saving Technology, 2018, 36(2): 125-129.
[6]刘义伦, 伍天翔, 赵先琼, 等. 颗粒物料在半封闭式回转鼓内的混合特性[J]. 化工进展, 2018, 37(5): 1687-1691.
LIU Y L, WU T X, ZHAO X Q, et al. Mixing characteristics of granular materials in a semi-enclosed rotary drum[J]. Chemical Progress, 2018, 37(5): 1687-1691.
[7]ZOU Z J, GONG S G, XIE G L, et al. Numerical investigation of granular mixing in an intensive mixer: effect of process and structural parameters on mixing performance and power consumption[J]. Chinese Journal of Chemical Engineering, 2021, 32(4): 241-252.
[8]XU G G, ZHANG Y, YANG X G, et al. Effect of drum structure on particle mixing behavior based on DEM method[J]. Particuology, 2023, 74: 74-91.
[9]何涛, 王佳, 何庆中, 等. 翅片结构对灰渣颗粒混合效应的影响[J]. 中国粉体技术, 2022, 28(1): 138-146.
HE T, WANG J, HE Q C, et al. Effect of fin structure on the mixing effect of ash particles[J]. China Powder Technology, 2022, 28(1): 138-146.
[10]何庆中, 赖镜安, 王佳, 等. 基于EDEM-FLUENT耦合的滚筒冷渣机颗粒轴向扩散运动[J]. 科学技术与工程, 2022, 22(3): 1004-1010.
HE Q C, LAI J A, WANG J, et al. Axial diffusive motion of particles in drum chillers based on EDEM-FLUENT coupling[J]. Science Technology and Engineering, 2022, 22(3): 1004-1010.
[11]ZHOU Y C, YU A B, STEWART R L, et al. Microdynamic analysis of the particle flow in a cylindrical bladed mixer[J]. Chemical Engineering Science, 2004, 59(6): 1343-1364.
[12]CHANDRATILLEKE G R, YU A B, STEWART R L, et al. Effects of blade rake angle and gap on particle mixing in a cylindrical mixer[J]. Powder Technology, 2009, 193: 303-311.
[13]桂泽东. 基于DEM法对V型混合机性能分析及结构优化[D]. 乌鲁木齐: 新疆大学, 2019.
GUI Z D. Performance analysis and structural optimization of V-mixer based on DEM method[D]. Urumqi: Xinjiang University, 2019.
[14]李天驰. 颗粒搅拌反应釜混合特性的实验研究及DEM模拟[D]. 北京: 北京化工大学, 2019.
LI T C. Experimental study and DEM simulation of mixing characteristics of particle stirred reactor[D]. Beijing: Beijing University of Chemical Technology, 2019.
[15]SANTOS D A, PETRI I J, DUARTE C R, et al. Experimental and CFD study of the hydrodynamic behavior in a rotating drum[J]. Powder Technology, 2013, 250: 52-62.