土壤是植物生长繁育和农业生产的基础,是人类得以生存和发展的重要自然资源之一,然而近年来,随着工业和农业生产中所用化学产品种类和数量的不断增加,土壤的酸化和重金属污染愈发严重,已成为我国重大环境问题[1]。实践表明,在酸性土壤中施用生石灰粉是改善耕地质量最有效、最经济的方法之一。传统人工撒施生石灰粉效率低下,且具有2大危害:一是人工撒施不均匀,容易造成扬尘污染;二是生石灰粉具有腐蚀性,会对人体皮肤造成伤害。为减轻生石灰撒施带来的环境污染,并降低对农民身体造成危害的可能性,课题组研发了螺旋循环式石灰撒施机[2],但该机器在设计时主要依据传统的经验和试验,缺乏完整的优化理论体系。通过离散单元法(DEM)研究生石灰粉撒施过程,是一种优于传统经验和试验设计方法的新手段,能更好地对机器进行数字化的设计与优化[3]。
由于农用生石灰粉粒径较小,若对整机进行模拟仿真,则颗粒数量会达到数千万甚至过亿,普通计算机难以完成模拟计算。解决该问题有3种较常用的方法:计算机并行计算、均质化处理和颗粒缩放法[4],其中颗粒缩放法是目前应用较为广泛的处理方法。Sakai等[5]提出一种用于大规模DEM模拟的粗颗粒模型,并在气力输送系统的水平管道中对模型进行数值模拟,验证了该模型的准确性和优越性;Thakur等[6]在对模型进行放大的同时将刚度和粘附力也进行了线性缩放,得出缩放模型能表现出与原系统相同特性的结论。此外,目前已有学者对小麦粉[7]、煤粉[8]等物料进行了基于颗粒缩放理论的离散元仿真参数虚拟标定,而关于生石灰粉离散元参数标定的研究鲜有报道。基于此,通过相似理论和量纲分析对生石灰粉颗粒进行放大处理,借助离散元仿真软件EDEM对生石灰粉进行堆积模拟,并以生石灰粉的休止角为响应值,通过Plackett-Burman试验、最陡爬坡试验和Box-Benhnken试验对模型接触参数进行虚拟标定,得到最优接触参数组合,可为与生石灰粉相关的离散元仿真模型的参数选取提供参考。
1 材料与方法
1.1 材料
高纯度生石灰粉,购于上高县腾顺钙业有限公司,白色粉末状,氧化钙(CaO)纯度高于90%(质量分数)。
1.2 生石灰粉的物理属性测试
为了获取生石灰粉的颗粒密度,参照JC/T 478.1—2013中关于粉状生石灰密度的测定方法:取量程250 mL的量筒,用药匙将生石灰粉加入量筒,每添加50 mL生石灰粉测算1次堆密度,最后得到生石灰粉的平均堆密度为1.127 g/cm3。由于颗粒粒径较小,忽略颗粒间空隙的影响,将测得的堆密度近似看作颗粒密度。
为了获取生石灰粉的平均粒径,采用筛孔尺寸分别为0.380、0.198、0.106、0.048 mm的标准检验筛进行筛分试验。试验时称取300 g生石灰粉置于顶筛,手持筛子往复水平摇动并不时拍打,最后称量每层筛网中生石灰粉的质量,得到生石灰的粒度分布如表1所示。由表中数据可知,所测生石灰粒度85%以上集中在0.049~0.198 mm,以质量为基准计算平均粒径[9]
(1)
式中:mi为第i级颗粒的质量分数,%;di为第i级颗粒粒径的中值,mm。将表1中的数据代入式(1)中,得到生石灰粉颗粒的平均粒径为0.126 mm。
表1 生石灰粉的粒度分布
Tab.1 Size distribution of quicklime powder
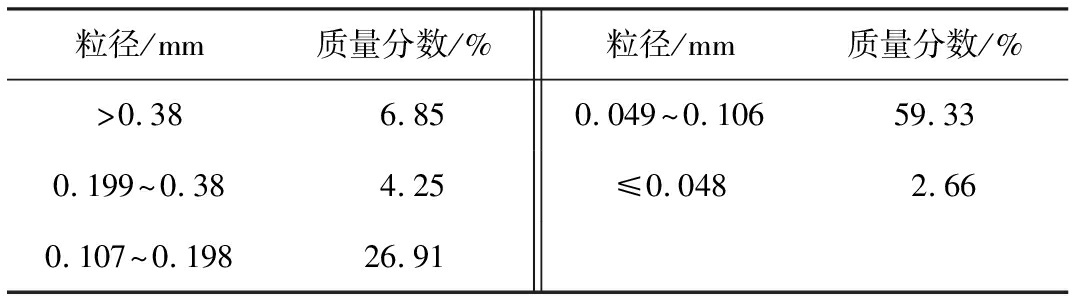
粒径/mm质量分数/%粒径/mm质量分数/%>0.386.850.049^0.10659.330.199^0.384.25≤0.0482.660.107^0.19826.91
2 颗粒缩放理论
2.1 相似理论
为了保证缩放后的数值模型能够准确地再现有关的物理现象,Feng等[10]借鉴传统流体力学的相似原理,提出一套适用于离散元建模的相似理论。该理论要求颗粒在缩放前后必须满足3个相似原则(几何相似、力学相似和动态相似),且颗粒间的相互作用关系应具有尺度不变性,即描述应力-应变关系的函数与颗粒尺寸无关。为了便于分析,将形状不规则的生石灰粉颗粒简化为软质球形颗粒,两颗粒的接触模型如图1所示。
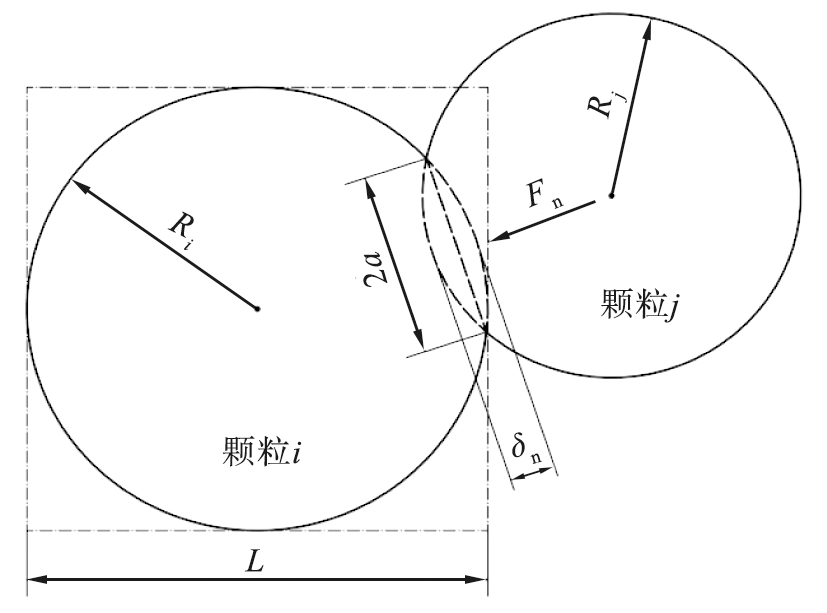
Ri、Rj—颗粒i、j的半径;δn—2个颗粒的法向重叠量;a—接触半径。
图1 球形颗粒的接触模型示意图
Fig.1 Schematic diagram of contact model of spherical particle
一对颗粒接触时的法向力Fn为
Fn=F(δn, R),
(2)
对于颗粒i,接触时的应变和应力可表示为
(3)
式中:ε为颗粒接触时的应变量,mm;L为颗粒的特征长度,L=2Ri,mm;σ为颗粒的接触应力,Pa;A为特征面积,A=L2,mm2。
接触颗粒间相互作用关系的应力-应变形式为
σ=σ(ε, R),
(4)
则颗粒的应变能E可表示为
(5)
对于模型中任意颗粒,其在一个主方向上的运动满足牛顿第二定律:
(6)
式中:M为颗粒的质量,kg;F(δ, R)为颗粒间的合接触力,N;Q(t)为颗粒的合外力,N;δ为颗粒的位移,m;![]() 为颗粒的加速度,m/s2。
为颗粒的加速度,m/s2。
几何相似是指物理模型和与缩放模型中颗粒的堆积形态相同、同时颗粒尺寸和颗粒域成比例[4];力学相似要求2个模型中的颗粒应变、应力和应变能函数相同;动态相似要求缩放前后作用于颗粒的力应有相同的比例关系。设缩放因数为h,用下标m表示缩放模型,下标p表示物理模型。根据相似理论,模型的各物理量需满足:
(7)
为了直观地表现出物理模型与缩放模型之间各物理量的比例关系,设q为原系统中任意物理量,则缩放模型中与之对应的变量![]() 可表示为
可表示为
(8)
式中,λq为物理量q的缩放因数,确定所有物理量的缩放因数,即确定了整个缩放模型。
2.2 量纲分析
通常系统中的物理量并不是相互独立的,当选定一组基本量后,其他物理量都可以从所选基本量中导出。若选择长度[L]、时间[T]、密度[ρ]作为基本量,根据量纲分析法[11],系统中任意物理量的量纲均可表示为
[q]=[L]a[T]b[ρ]c,
(9)
则物理量q的缩放因数![]() 其中a、b、c均为常数。
其中a、b、c均为常数。
若取λL=λT=h、λρ=1,对弹性模量、应力及应变的缩放因数进行推导:
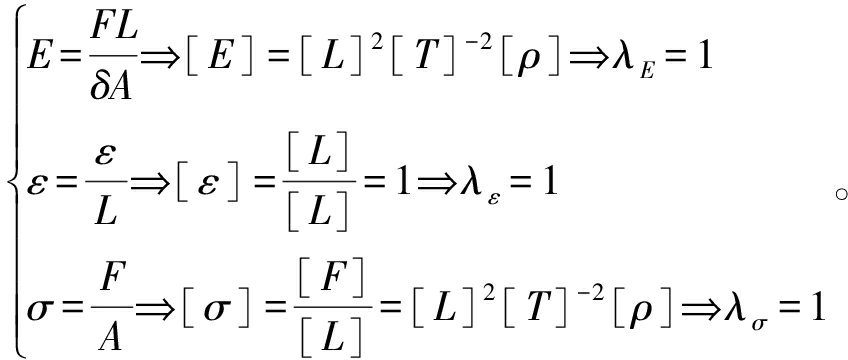
(10)
由量纲分析可知,对于任意的缩放因数h,若保持颗粒材料密度不变,则颗粒弹性模量、应力和应变均保持不变。由式(3)可知,颗粒的应变ε是无量纲量且与h无关,而应力与接触力相关,要保证应力σ也独立于h,则要求颗粒的应力-应变函数满足σ(ε, R)=σ(ε),即应力只与应变有关,与粒径无关。
描述黏弹性球形颗粒的接触力通常采用JKR(Johnson Kendall Roberts)模型或DMT(Derjaguin Muller Toporov)模型,前者适用于软粒子,后者更适合硬粒子[12]。本文中的研究对象为生石灰粉,具有一定粘附性,因此在计算颗粒法向接触力时还需考虑颗粒的粘附力。根据JKR接触理论[13],颗粒的法向接触力可表示为
(11)
式中:Fn为法向接触力,N;E*为颗粒的有效杨氏模量,Pa;R*为颗粒的有效半径,m;a为接触半径,m;Δγ为颗粒的表面自由能,J/m2。其中,有效杨氏模量E*和有效半径R*分别为
(12)
式中:Ei、vi、Ri和Ej、vj、Rj分别为接触颗粒的杨氏模量、泊松比和半径。
接触半径a与有效半径R*的关系满足:
(13)
将式(13)代入式(11)得:
(14)
将式(14)转换为应力-应变形式:
(15)
其中颗粒的特征面积A=L2=(R*)2,等式右边第1项完全符合Hertz接触理论[14],具有尺度不变性,而第2项明显不满足尺度不变的条件,所以JKR接触模型不具有尺度不变性。为实现模型的尺度不变性,要求Δγ/R*为常数,即颗粒的表面自由能要随着颗粒的缩放而变化。
上述相似理论与量纲分析表明,在采用颗粒缩放法进行离散元模拟时,为便于仿真结果与试验结果作对比,可以保持材料的本征参数不变,但需要对接触模型的相关参数进行标定以保证模拟的准确性。
3 参数标定
3.1 休止角的测定
根据相关国家标准GB/T 11986—1989、GB/T 16913.5—1997,并参考散体物料休止角测定相关研究[15-17],采用漏斗法测定生石灰粉的休止角,试验装置如图2所示。该装置主要由铁架台、玻璃漏斗和圆柱台组成,试验时用药匙将生石灰粉缓慢加入漏斗中,粉末沿漏斗落在圆柱台上形成堆积状态,待石灰堆布满整个圆柱台且堆积高度保持稳定,停止添加生石灰粉。休止角计算公式为

1—铁架台;2—铁圈;3—玻璃漏斗;4—夹子;5—圆柱台。
注:D为圆柱台的直径,mm;H为石灰粉的堆积高度,mm。
图2 休止角测定装置
Fig.2 Angle of repose measurement equipment
(16)
式中:H为堆积高度,mm;D为圆柱台直径,mm。
根据公式(16)计算出休止角的大小。更换不同直径的圆柱台进行多次试验,求得生石灰粉的平均休止角为48.76°。
3.2 离散元仿真试验
3.2.1 仿真模型的建立
接触模型是离散单元法的核心,其选取对仿真结果的准确性有较大的影响。本研究中采用的离散元软件EDEM内含多种接触模型可供选择,考虑到干燥的生石灰粉末在宏观上表现出一定的粘附性,因此选择适用于模拟粘性系统的“Hertz-Mindlin with JKR Cohesion”接触模型。
EDEM中需要的物性参数大致分为3类:本征参数、基本接触参数和接触模型参数[18]。目前国内外关于生石灰粉的研究较少,无法通过查阅文献获取相关的离散元仿真参数。本文中参考其他粉体物料的离散元仿真研究,并结合软件内置的GEMM数据库,得到模型的接触参数如表2所示。
表2 仿真模型的接触参数
Tab.2 Parameters of the simulation model
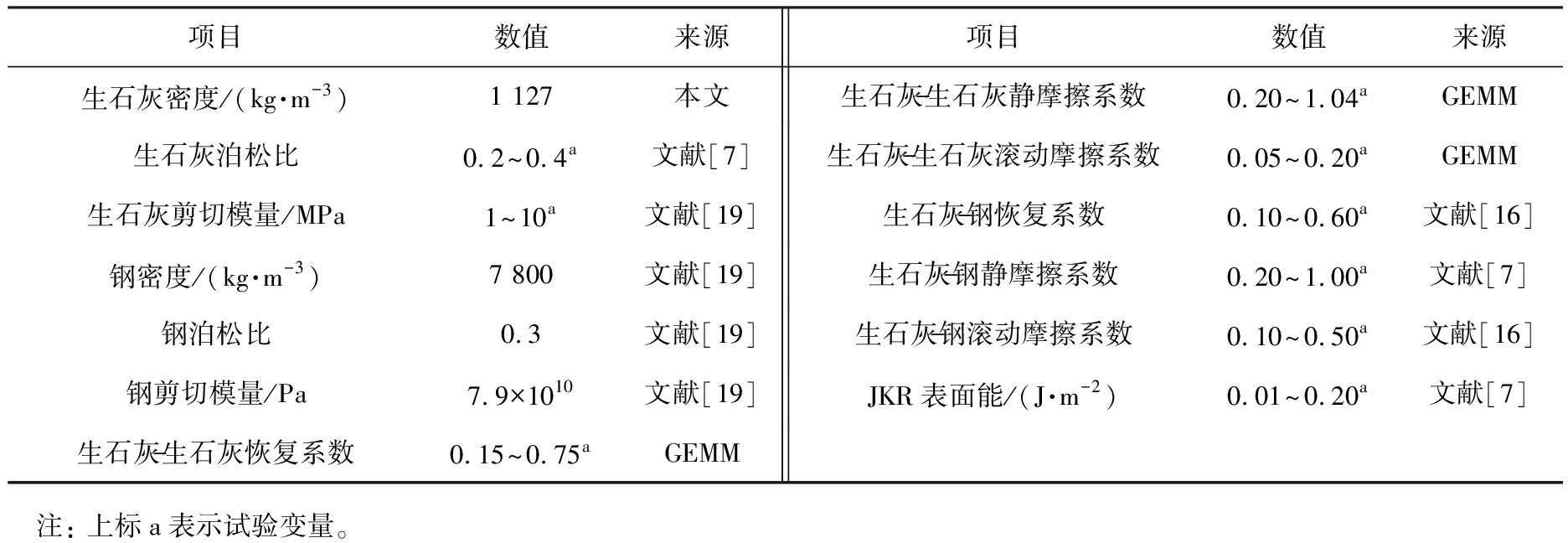
项目数值来源项目数值来源生石灰密度/(kg·m-3)1 127本文生石灰-生石灰静摩擦系数0.20^1.04aGEMM生石灰泊松比0.2^0.4a文献[7]生石灰-生石灰滚动摩擦系数0.05^0.20aGEMM生石灰剪切模量/MPa1^10a文献[19]生石灰-钢恢复系数0.10^0.60a文献[16]钢密度/(kg·m-3)7 800文献[19]生石灰-钢静摩擦系数0.20^1.00a文献[7]钢泊松比0.3文献[19]生石灰-钢滚动摩擦系数0.10^0.50a文献[16]钢剪切模量/Pa7.9×1010文献[19]JKR表面能/(J·m-2)0.01^0.20a文献[7]生石灰-生石灰恢复系数0.15^0.75aGEMM 注: 上标a表示试验变量。
根据图2所示的试验装置,在仿真软件中建立试验装置模型,接料台的直径为80 mm,顶部开有1 mm的凹槽以便于物料堆积;漏斗下方出口直径为15 mm,距接料盘上表面75 mm。生石灰颗粒的类型选择单球型,尺寸分布设置为正态分布。为了减少仿真计算时间,同时保证仿真结果的可靠性,将颗粒粒径放大至2 mm。设置颗粒数量为10 000个,生成速率为2 000个每秒,生成方式选择动态。时间积分方式选择Euler法,固定时间步长,取Rayleigh时间步长的20%~40%以保证仿真的连续性,仿真时间设置为6 s,网格尺寸取颗粒最小半径的3倍。参数设置完毕后开始仿真,待仿真完成后进行休止角的测量。
3.2.2 休止角的测定
为了更准确地测得堆积物料的休止角,采用基于Python开发的EDEMpy库对仿真结果文件进行分析。测量原理:首先定义一个径向圆柱形容器阵列;其次确定每个容器中最高的颗粒;再通过最小二乘法对这些颗粒的质心坐标进行线性拟合;最后得到拟合线与水平线的夹角即为休止角,休止角测定方法示意图如图3所示。为了得到较好的分析结果,应选取堆积较稳定的区域进行分析,本文中选取分析区域的下限值D1为10 mm,上限值D2为40 mm,定义容器的直径D3为6 mm。此外沿多个不同方向角进行测量,可得到平均休止角,休止角多次测量示意图如图4所示。

D1—分析域的下限值;D2—分析域的上限值;D3—定义容器的直径;θ—休止角;δ—切片方向角。
图3 休止角测定方法示意图
Fig.3 Schematic diagram of testing method of repose angle
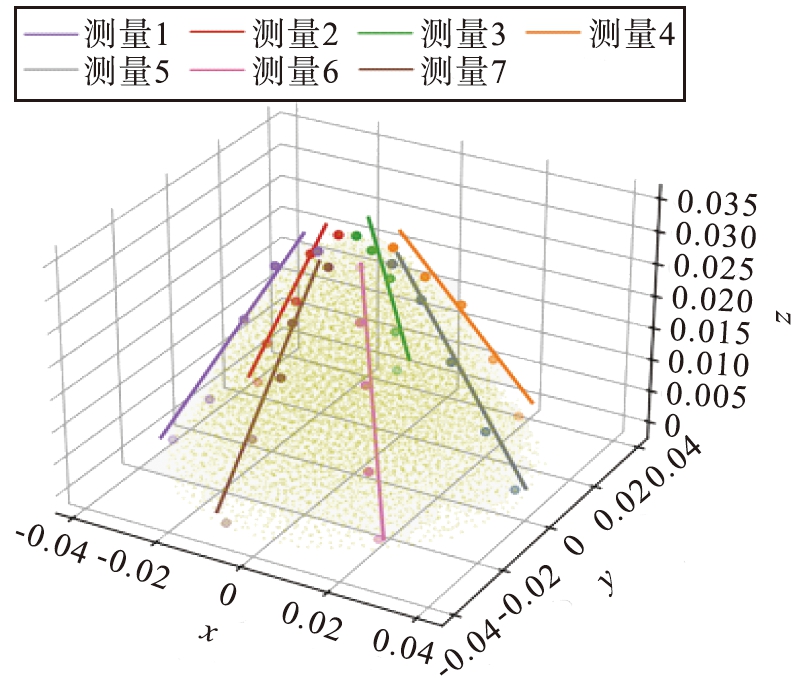
图4 休止角多次测量示意图
Fig.4 Schematic diagram of multiple measurements of angle of repose
3.3 仿真试验设计
3.3.1 Plackett-Burman试验
离散元仿真所设置的参数并非都对休止角有显著的影响,如Marigo等[20]已经证明了剪切模量对粉末颗粒堆积特性的影响不显著。此外,剪切模量与Rayleigh时间步长相关联,因此,剪切模量数值过高还会导致仿真时间大幅增加。为了确定表2中各试验变量对休止角的影响是否显著,以生石灰粉的休止角为响应值,表2中9个待确定参数和2个虚拟参数为试验因素,应用Design-Expert软件中的Plackett-Burman Design进行参数筛选试验,试验因素与水平见表3。试验因素低水平取各个参数取值范围的下限值,高水平设置为低水平的2倍,并设置1个中心点用于检测拟合函数曲率,共进行13次试验,试验方案及结果如表4所示。
表3 Plackett-Burman试验因素与水平
Tab.3 Factors and levels table of Plackett-Burman test
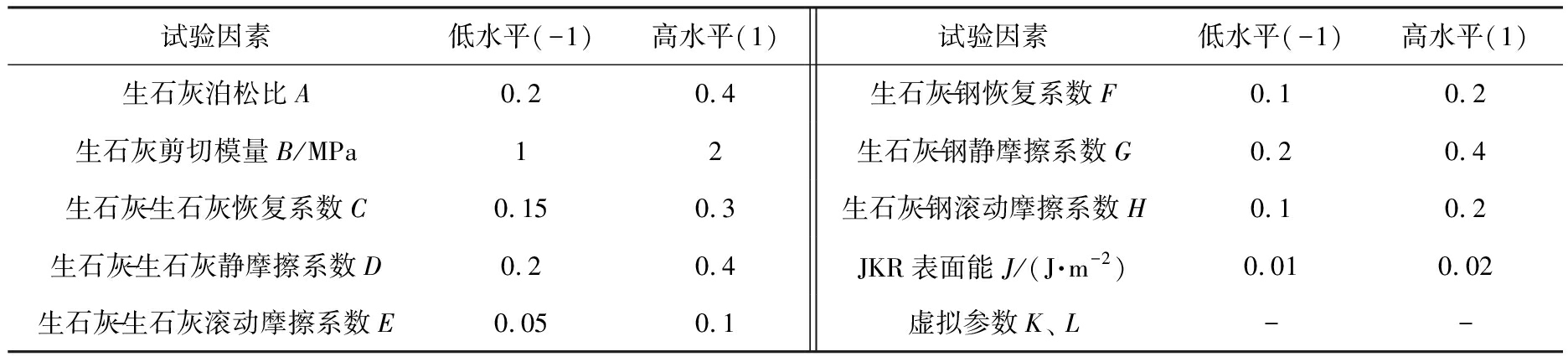
试验因素低水平(-1)高水平(1)试验因素低水平(-1)高水平(1)生石灰泊松比A0.20.4生石灰-钢恢复系数F0.10.2生石灰剪切模量B/MPa12生石灰-钢静摩擦系数G0.20.4生石灰-生石灰恢复系数C0.150.3生石灰-钢滚动摩擦系数H0.10.2生石灰-生石灰静摩擦系数D0.20.4JKR表面能J/(J·m-2)0.010.02生石灰-生石灰滚动摩擦系数E0.050.1虚拟参数K、 L--
表4 Plackett-Burman试验方案及结果
Tab.4 Scheme and results of Plackett-Burman test
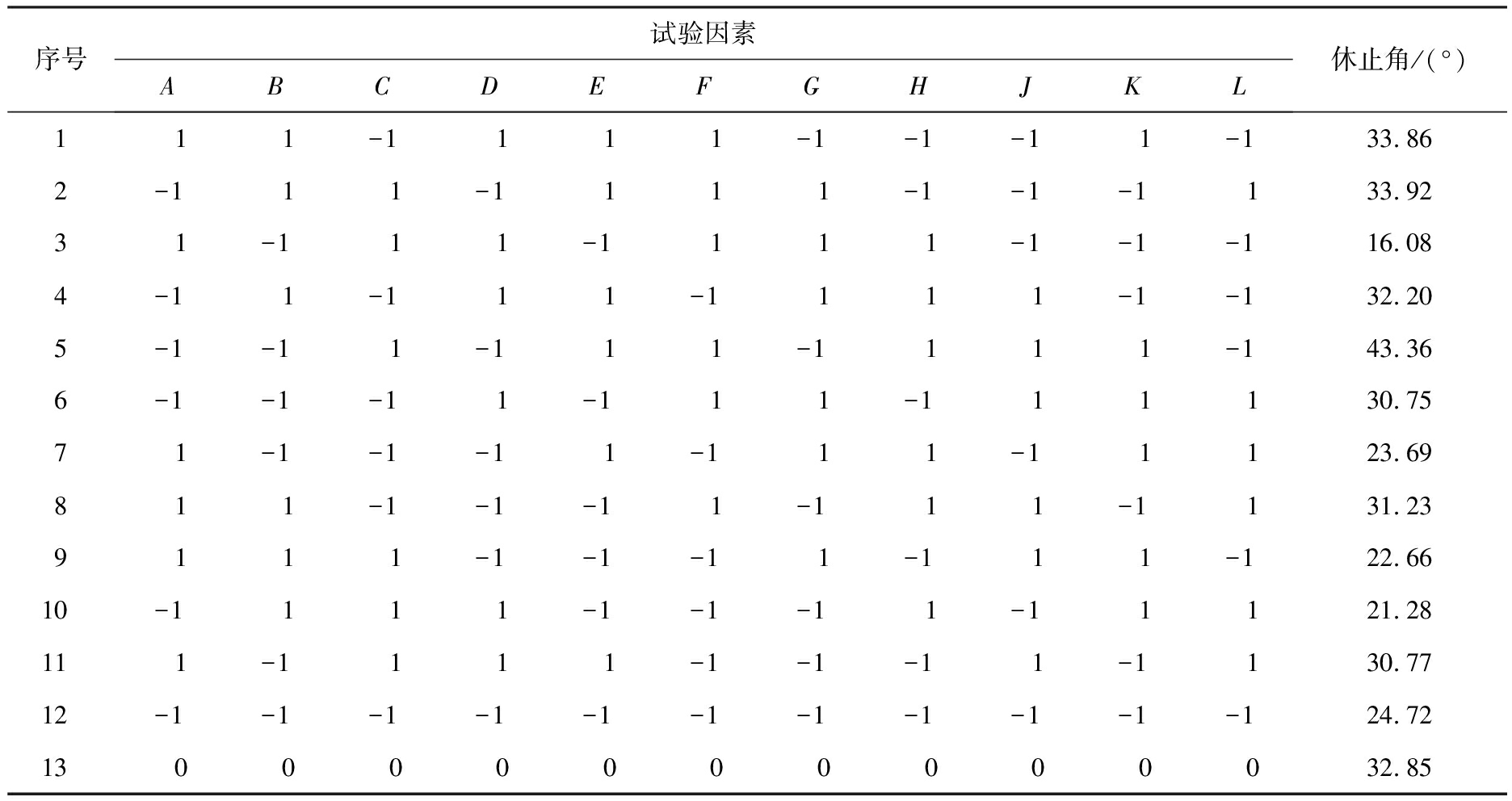
序号试验因素ABCDEFGHJKL休止角/(°)1 1 1-1 1 1 1-1-1-1 1-133.862-1 1 1-1 1 1 1-1-1-1 133.923 1-1 1 1-1 1 1 1-1-1-116.084-1 1-1 1 1-1 1 1 1-1-132.205-1-1 1-1 1 1-1 1 1 1-143.366-1-1-1 1-1 1 1-1 1 1 130.757 1-1-1-1 1-1 1 1-1 1 123.698 1 1-1-1-1 1-1 1 1-1 131.239 1 1 1-1-1-1 1-1 1 1-122.6610 -1 1 1 1-1-1-1 1-1 1 121.2811 1-1 1 1 1-1-1-1 1-1 130.7712 -1-1-1-1-1-1-1-1-1-1-124.7213 0 0 0 0 0 0 0 0 0 0 032.85
对表4中的试验结果进行方差分析,得到各试验参数的显著性如表5所示。由表可知,生石灰-生石灰滚动摩擦系数的P<0.01,对仿真结果的影响非常显著;JKR表面能、生石灰-钢恢复系数、生石灰泊松比及生石灰-钢静摩擦系数的P<0.05,对仿真结果的影响显著;其余参数P值均大于0.05,对仿真结果的影响极小。
表5 Plackett-Burman试验参数显著性分析
Tab.5 Significance analysis of Plackett-Burman test parameters
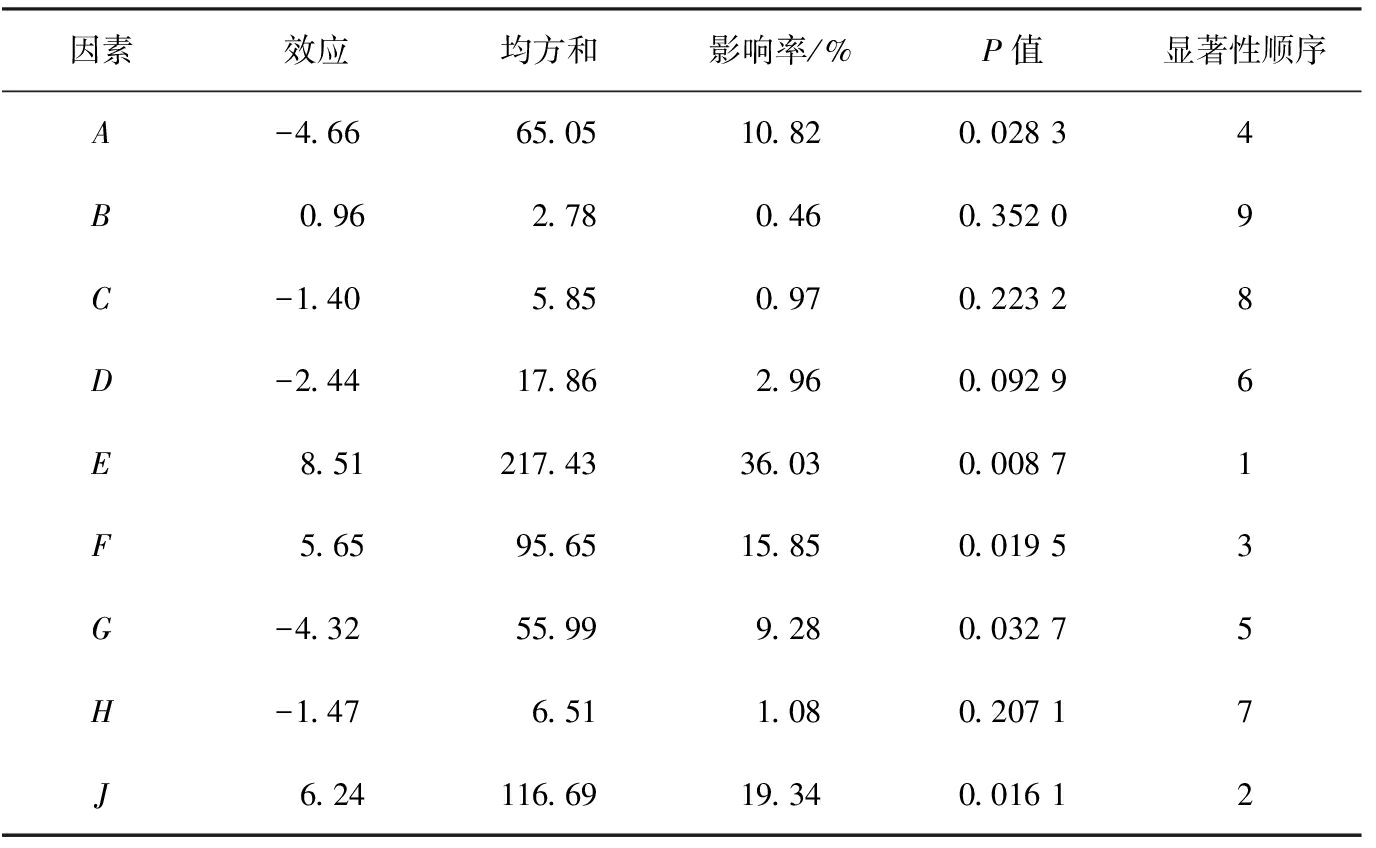
因素效应均方和影响率/%P值显著性顺序A-4.6665.0510.820.028 34B 0.962.780.460.352 09C-1.405.850.970.223 28D-2.4417.862.960.092 96E 8.51217.4336.030.008 71F 5.6595.6515.850.019 53G-4.3255.999.280.032 75H-1.476.511.080.207 17J 6.24116.6919.340.016 12
3.3.2 最陡爬坡试验
最陡爬坡试验能精准地确定试验因素水平中心值,使初始响应区域快速地接近最优响应区域。根据参数筛选试验的结果,选取表5中显著性排名前3的因素(E、F、J)进行最陡爬坡试验。所选试验参数按照选定的爬坡步长逐步增加,其余参数选择中间水平(生石灰泊松比0.3、生石灰剪切模量5.5×106、生石灰-生石灰恢复系数0.45、生石灰-生石灰静摩擦系数0.62、生石灰-钢静摩擦系数0.6、生石灰-钢滚动摩擦系数0.3),试验结果如表6所示。由表可知,休止角随着试验因素数值的增加逐渐增加,而相对误差呈现先减小后增大的趋势,其中3号试验的相对误差最小。
表6 最陡爬坡试验方案与结果
Tab.6 Scheme and results of steepest ascent test
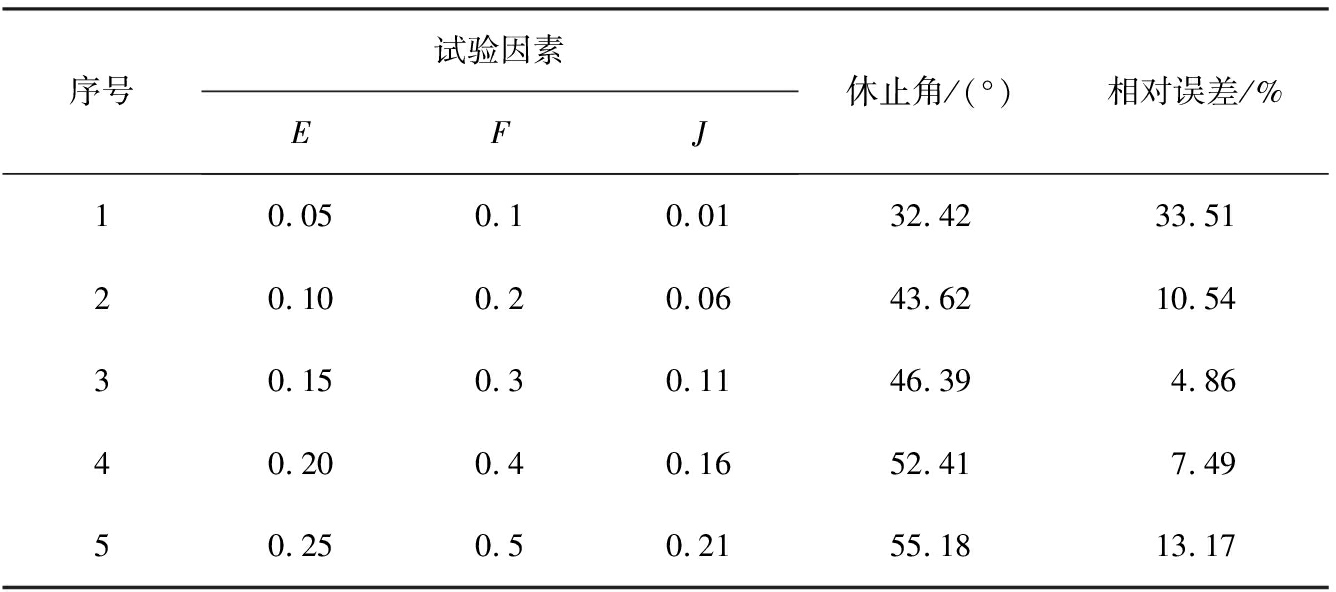
序号试验因素EFJ休止角/(°)相对误差/%10.050.10.0132.4233.5120.100.20.0643.6210.5430.150.30.1146.394.8640.200.40.1652.417.4950.250.50.2155.1813.17
3.3.3 Box-Behnken试验
为了得到休止角与显著影响因素(生石灰-生石灰滚动摩擦系数、生石灰-钢恢复系数和JKR表面能)的数学回归模型,采用Box-Behnken法进行响应面试验。根据最陡爬坡试验的结果,选取表6中3号试验参数值为中间水平,4号、5号的参数值分别为低水平和高水平进行试验设计,试验方案及结果如表7所示。
表7 Box-Behnken试验方案及结果
Tab.7 Scheme and results of Box-Behnken test

序号试验因素EFJ休止角θ/(°)序号试验因素EFJ休止角θ/(°)1 1(0.20)-1(0.2)0(0.11)49.8190-1 151.362 0(0.15) 1(0.4)1(0.16)52.8310-1 0-1 42.293-1(0.1) 0(0.3)150.0711-1 1047.28410152.531200048.4450-1 -1(0.06)44.6013-1 -1 043.87600048.231400049.08710-1 47.681501-1 45.23811049.33 注:括号内的数字为水平编码对应的真实值。
二次回归模型的方差分析结果如表8所示。由表可知,拟合模型的P<0.001,失拟项的P>0.05,表明模型极显著,且回归方程的拟合性较好;模型的决定系数R2=0.993 7,校正决定系数Ra2=0.982 3,表明模型预测实际数值的可靠性极高。
表8 二次回归模型的方差分析
Tab.8 Anova of quadratic regression model
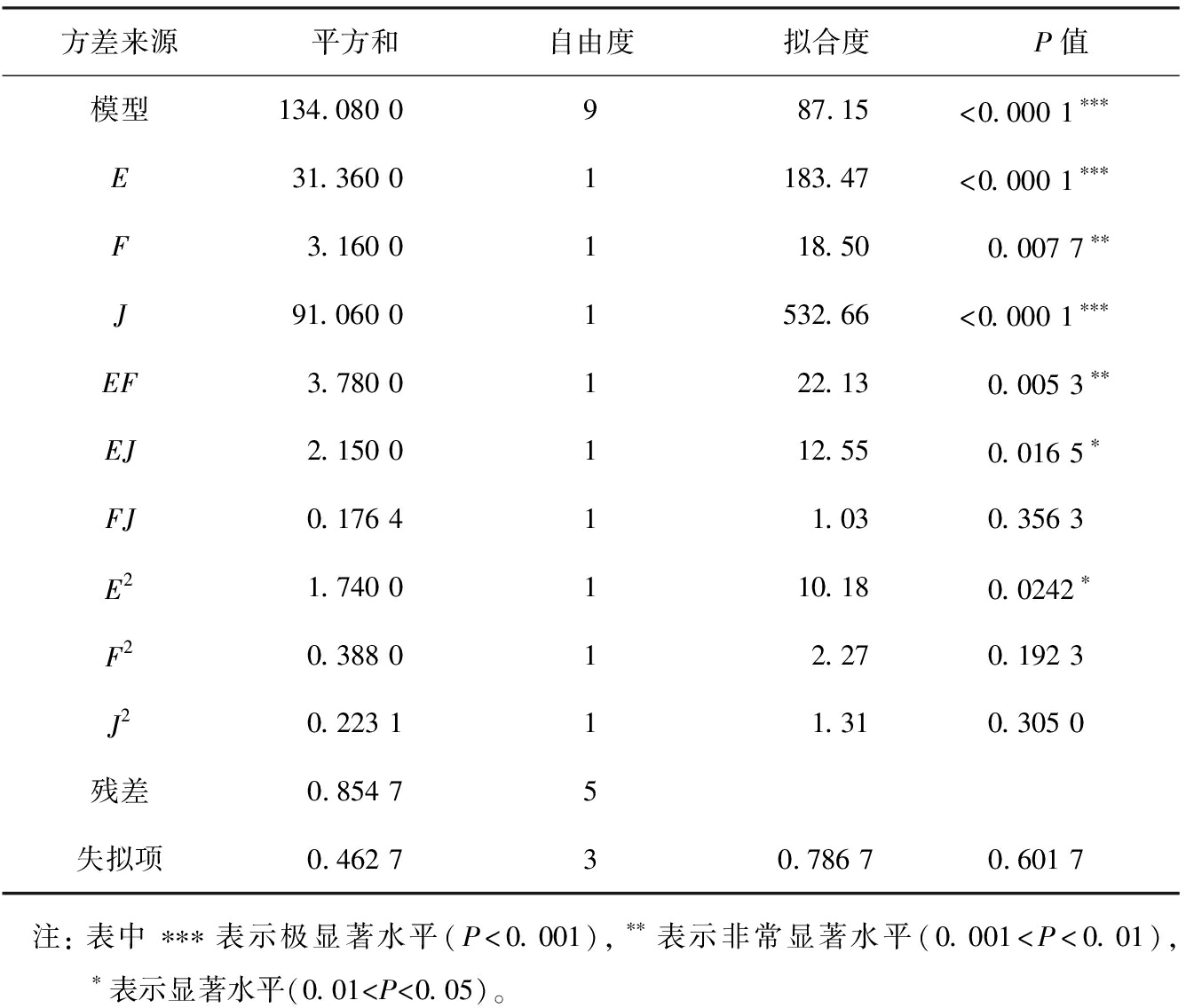
方差来源平方和自由度拟合度P值模型134.080 0 987.15<0.000 1∗∗∗E31.360 0 1183.47<0.000 1∗∗∗F3.160 0118.50 0.007 7∗∗J91.060 0 1532.66<0.000 1∗∗∗EF3.780 0122.13 0.005 3∗∗EJ2.150 0112.55 0.016 5∗FJ0.176 411.03 0.356 3E21.740 0110.18 0.0242∗F20.388 012.27 0.192 3J20.223 111.31 0.305 0残差0.854 75失拟项0.462 730.786 7 0.601 7 注: 表中∗∗∗表示极显著水平(P<0.001),∗∗表示非常显著水平(0.001
在保证模型显著、不失拟的前提下,忽略模型中的不显著项(FJ、F2、J2),得到数学回归模型的二次回归方程:
θ=13.57+211.91E+35.46F+111.43J-194.5EF-293EJ-272.43E2。
(17)
3.4 最优参数组合的确定与验证
以试验参数的高、低水平为约束条件,预测休止角与实测休止角相对误差最小为目标,寻优求解Box-Behnken试验获得的数学回归模型,得到最佳参数组合:生石灰-生石灰滚动摩擦系数为0.165、生石灰-钢恢复系数为0.215、JKR表面能为0.113 J/m2。采用最优参数组合进行仿真试验,得到休止角为48.39°,与实际休止角的相对误差仅为0.76%。图5为休止角仿真试验结果与物理试验结果的对比,从图中可以看出,二者堆积轮廓十分相似,表明所选接触参数能较好表现出生石灰粉的堆积特性。

(a)仿真试验结果(b)物理试验结果图5 休止角仿真试验与物理试验结果对比Fig.5 Results comparison of simulation test and physical test of repose angle
4 结论
1)为获得生石灰粉在离散元仿真中所需的材料本征参数,通过物理测试测得生石灰粉的堆积密度为1.127 g/cm3,平均粒径为0.126 mm,休止角为48.76°。以离散元仿真软件EDEM为载体,根据颗粒缩放原理将颗粒粒径放大至2 mm进行虚拟参数标定。
2)通过Plackett-Burman试验分析接触参数对生石灰粉休止角影响的显著性,并根据分析结果选取了3个显著性较强的参数进行最陡爬坡试验和Box-Behnken试验,建立休止角与生石灰-生石灰滚动摩擦系数、生石灰-钢恢复系数以及JKR表面能的数学回归模型。
3)以预测休止角与实际休止角相对误差最小为目标,对数学回归方程进行寻优求解,得到最优参数组合:生石灰-生石灰滚动摩擦系数为0.165、生石灰-钢恢复系数为0.215、JKR表面能为0.113 J/m2。以最优参数组合进行仿真试验得到休止角为48.39°,与物理试验所测休止角的相对误差仅为0.76%,表明通过虚拟标定得到的离散元仿真参数准确可靠。
[1]周建斌,陶静静,赵梦真,等.农业生产对石灰性土壤无机碳库损失的影响[J].土壤学报,2022,59(3): 593-602.
[2]高自成,李立君,阳涵疆,等.正反螺旋式土壤改良石灰撒施机设计与试验[J].农业工程学报,2015,31(10): 43-50.
[3]曾智伟,马旭,曹秀龙,等.离散元法在农业工程研究中的应用现状和展望[J].农业机械学报,2021,52(4): 1-20.
[4]周龙海.垂直螺旋输送的EDEM仿真与实验研究[D].杭州: 浙江工业大学,2017.
[5]SAKAI M,KOSHIZUKA S.Large-scale discrete element modeling in pneumatic conveying[J].Chemical Engineering Science,2009,64(3): 533-539.
[6]THAKUR S C,OOI J Y,AHMADIAN H.Scaling of discrete element model parameters for cohesionless and cohesive solid[J].Powder Technology,2016,293: 130-137.
[7]李永祥,李飞翔,徐雪萌,等.基于颗粒缩放的小麦粉离散元参数标定[J].农业工程学报,2019,35(16): 320-327.
[8]任建莉,周龙海,韩龙,等.基于颗粒缩放理论的垂直螺旋输送离散模拟[J].过程工程学报,2017,17(5): 936-943.
[9]曹林.旋耕机石灰撒施装置的设计与试验研究[D].长沙: 湖南农业大学,2016.
[10]FENG Y T,HAN K,OWEN D R J,et al.On upscaling of discrete element models: similarity principles[J].Engineering Computations: Int J for Computer-Aided Engineering,2009,26(6): 599-609.
[11]李郁,崔可源.基于量纲分析方法的水平螺旋输送机离散元仿真研究[J].起重运输机械,2021(17): 36-40,46.
[12]FENG Y T,OWEN D R J.Discrete element modelling of large scale particle systems-I: exact scaling laws[J].Computational Particle Mechanics,2014,1(2): 159-168.
[13]JOHNSON K L,KENDALL K,ROBERTS A D.Surface energy and the contact of elastic solids[J].Proceedings of the Royal Society of London:Series A,Mathematical and Physical Sciences,1971,324(1558): 301-313.
[14]YANG F,DU Y,FU Q,et al.Design and testing of seed maize ear peeling roller based on Hertz theory[J].Biosystems Engineering,2021,202(7): 165-178.
[15]宋占华,李浩,闫银发,等.桑园土壤非等径颗粒离散元仿真模型参数标定与试验[J].农业机械学报,2022,53(6): 21-33.
[16]罗帅,袁巧霞,GOUDA Shaban,等.基于JKR粘结模型的蚯蚓粪基质离散元法参数标定[J].农业机械学报,2018,49(4): 343-350.
[17]王志鹏,李永祥,徐雪萌.基于堆积实验的小米离散元参数标定[J].中国粮油学报,2021,36(2): 115-120.
[18]韩伟,王绍宗,张倩,等.基于JKR接触模型的微米级颗粒离散元参数标定[J].中国粉体技术,2021,27(6): 60-69.
[19]王黎明,范盛远,程红胜,等.基于EDEM的猪粪接触参数标定[J].农业工程学报,2020,36(15): 95-102.
[20]MARIGO M,STITT E H.Discrete element method(DEM)for industrial applications: comments on calibration and validation for the modelling of cylindrical pellets[J].KONA Powder and Particle Journal,2015,32: 236-252.