近年来,随着我国经济迅速增长,由颗粒组成的高密度纤维板、玻镁板等木质板材在市面上层出不穷,给从事相关行业的人员及企业带了巨大的研究价值和经济效益。颗粒混合的工艺大多数与搅拌工艺结合,在相应的搅拌设备中进行,如立轴式搅拌机、卧轴式搅拌机等搅拌设备都得到了广泛的应用。例如,董玉刚等[1]通过利用EDEM对双卧轴搅拌机搅拌工艺进行试验对比分析,得到了不同的搅拌工艺对物料搅拌均匀性有很大的影响的结论。施进发等[2]通过研究分析了不同的转速对物料混合度的影响。孔鲜宁等[3]通过对双卧轴搅拌机上进行模拟试验,对比得到了比较适合双卧轴搅拌机的物料填充率。郭良等[4]对搅拌机叶片的安装角度进行分析,得到了叶片的最佳安装角度。Alian等[5]通过离散元法分析犁头混合器中固体颗粒的混合,研究了叶轮转速、颗粒填充水平和粒度等参数对搅拌质量的影响。
市面上立轴式搅拌机对混凝土的搅拌研究有很多,但是应用于新型木质板材加工制备方面的研究却寥寥无几。目前市面上常见的合成板材的各方面性能都比不上新型木质板材,除了所加原材料的物理性能、化学性质存在差异性,还需在生产木质板材过程中,根据实际情况优化和改进原有的搅拌机构装置。为了更加明了新型木质板材的各种物料混合过程,使物料混合更加均匀,以得到更好的搅拌效果,本文中以木屑、氯化镁、氧化镁、卤水为搅拌原料,以聚氯乙烯树脂粉、尿素为添加剂,基于离散元分析软件研究物料在不同参数情况下搅拌的混合情况,由此对搅拌机构进行优化设计。
1 搅拌混合机理
当搅拌物料时,物料颗粒不仅会受重力影响,还会受到搅拌机构的推动以及物料之间的相互碰撞,产生分散、融合,实现物料颗粒的混合。物料颗粒的整个搅拌过程可大致分为3个阶段[6-8]:对流、剪切和扩散。对流阶段,物料颗粒受外力作用从一个区域运动到另一个区域,物料颗粒之间产生大规模、大尺度的相对流动,颗粒在空间中快速交错混合,这一阶段主要发生在搅拌初期;剪切阶段,由于前面的对流过程,物料颗粒之间相互运动过程中产生碰撞,颗粒之间相互摩擦滑动,大的颗粒团被打散与其他物料颗粒混合,这一阶段发生在搅拌中期;扩散阶段,单个小颗粒物料在搅拌过程中处于某一个小区域范围内自由运动,与其他的物料颗粒进行混合,此阶段主要是发生在搅拌后期。在实际搅拌过程中,以上3个阶段几乎是同时进行,从而达到物料之间充分搅拌均匀的效果。
2 EDEM仿真分析
2.1 三维模型的建立
利用三维建模软件Solidworks创建立轴行星式搅拌机简化模型[9]。简化后的实体模型主要由搅拌筒、2根行星搅拌轴、6根搅拌臂、2个侧刮板和多个叶片组成。每根搅拌臂上各有1个叶片。在叶片上任取一点,画出其运动模型如图1所示。
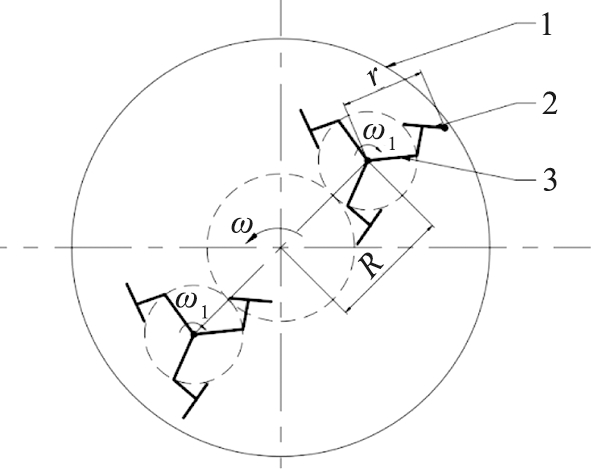
1—搅拌筒;2—叶片;3—搅拌臂。
图1 叶片运动模型
Fig.1 Leaf motion model
可建立该点的运动参数方程为
(1)
对时间求导可得
![]()
(2)
式中:以搅拌桶的中心为原点建立坐标系,R为行星搅拌轴中心到搅拌桶中心的距离,mm;r为叶片上的动点到行星搅拌轴中心的距离,mm;ω为公转的角速度,rad/s;ω1为自转角速度,rad/s。设M=r/R, C=ω1/ω,将建立好的模型导入到EDEM中,如图2所示。

图2 导入模型
Fig.2 Into model
2.2 颗粒接触模型
物料颗粒在离散元研究方法中被看成单独的颗粒单元,运动产生的相互作用力使物料颗粒互相接触碰撞。当物料颗粒发生接触时会在接触点产生相互作用,由于物料颗粒具有离散性,因此在受载或者不受载的情况下都会有很复杂的运动产生,但目前为止还未建立很好的接触模型[10],故颗粒模型往往被简化成硬质球模型以及软质球模型。在实际生产中氯化镁、木屑等物料颗粒之间的碰撞将持续一段时间,故接触过程中颗粒运动可以近似采用振动方程进行模拟,如图3所示。
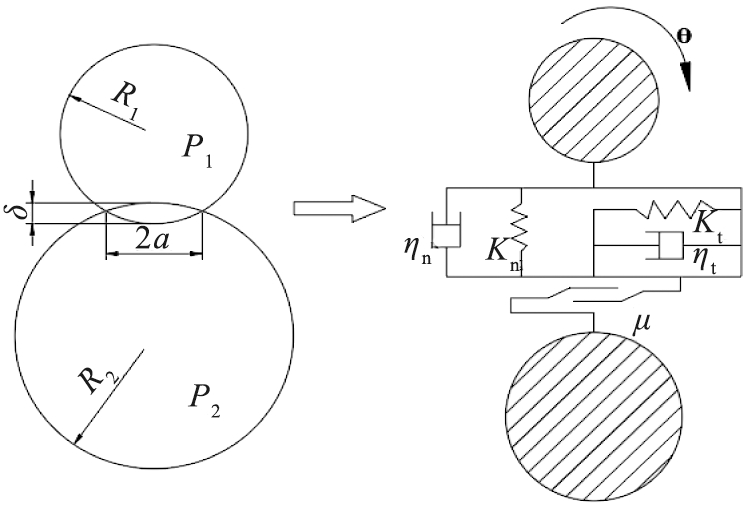
图3 接触模型
Fig.3 Contact model
将物料颗粒接触过程中发生的振动运动分为法向运动和切向运动,法向振动运动方程为
(3)
在接触过程中切向运动方程为
(4)
(5)
式中:m0,1为颗粒等效质量,kg;I0,1为颗粒等效转动惯量,kg·m2;ηn、ηt为颗粒法向及切向阻尼系数;Kn、Kt为法向及切向弹性系数;Fn、Ft为颗粒法向力及切向力,N;θ为颗粒自身旋转角度,rad;un、ut为颗粒法向和切向相对位移,mm;t为旋转半径,mm;M为颗粒所受外力矩,N·m。
2.3 设置仿真参数
本文中所运用的立轴行星式搅拌机是根据某工厂实际生产情况下对其原型进行了缩放的设备。当物料在搅拌时,物料颗粒之间会发生相互碰撞等作用,具有相互作用的剪切力、碰撞力以及黏性力等,故物料颗粒之间采用Hertz-Mindlin with bonding接触模型[11-12],为了尽可能与实际情况相符合,选择4种物料颗粒模型进行仿真。为了简化运算,假定物料颗粒为单个球形颗粒(如图4所示),粒径为10~15 mm;其中氯化镁、氧化镁、木屑、添加剂的颗粒数分别为8 000、4 000、40 000、6 000。为了方便观察搅拌结果,人为设定仿真过程的物料颗粒,颗粒数目并非实际搅拌过程中的真实值。
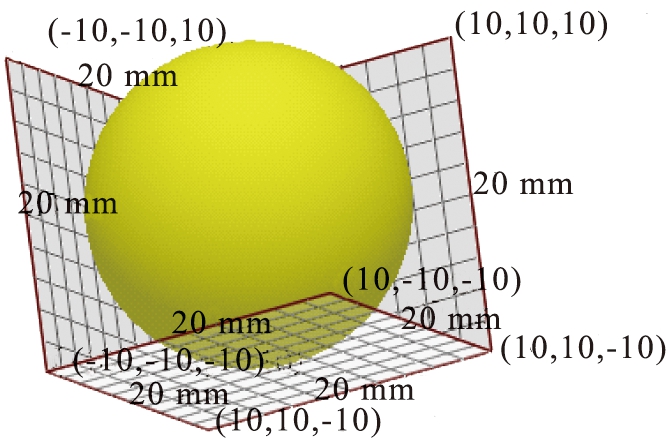
图4 颗粒模型
Fig.4 Particle model
为模拟物料颗粒在运动过程中会出现相互碰撞、颗粒之间会产生相互作用力的实际情况,需要设置各物料颗粒的材料属性和相互之间的接触参数,如表1、2所示。
表1 材料属性
Tab.1 Material properties

材料密度/(kg·m-3)剪切模量/109 Pa泊松比材料密度/(kg·m-3)剪切模量/109 Pa泊松比氧化镁3 5805.770.30其他2 5000.100.25氯化镁2 3450.130.25钢7 85080.000.30木屑6000.530.33
表2 接触参数设置
Tab.2 Contact parameters
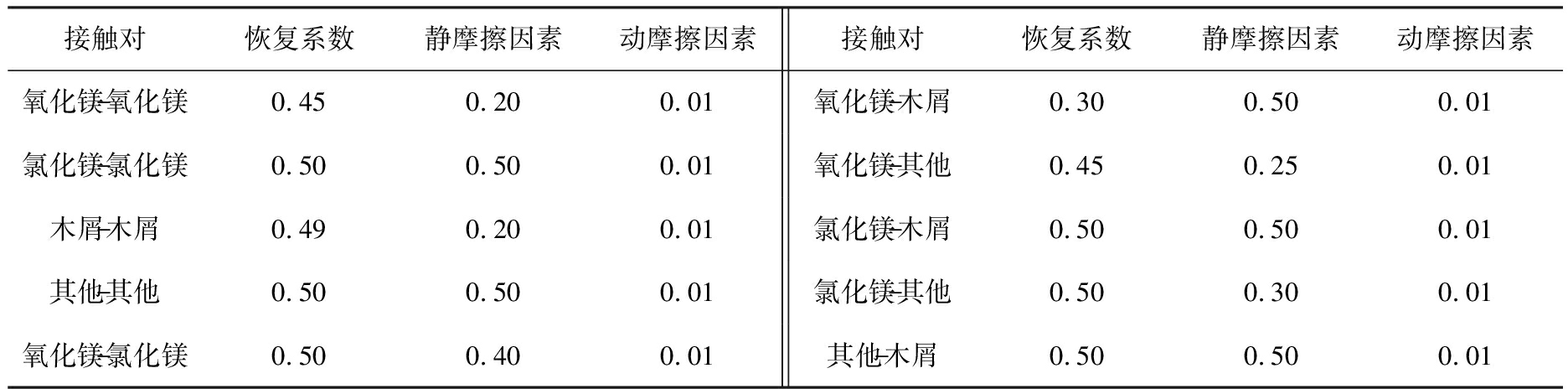
接触对恢复系数静摩擦因素动摩擦因素接触对恢复系数静摩擦因素动摩擦因素氧化镁-氧化镁0.450.200.01氧化镁-木屑0.300.500.01氯化镁-氯化镁0.500.500.01氧化镁-其他0.450.250.01木屑-木屑0.490.200.01氯化镁-木屑0.500.500.01其他-其他0.500.500.01氯化镁-其他0.500.300.01氧化镁-氯化镁0.500.400.01其他-木屑0.500.500.01
3 搅拌可变参数设置与仿真结果分析
3.1 混合度分析
为了能够清晰分析改变搅拌参数后搅拌效果好坏,物料颗粒的混合度是一个重要的评判指标。在EDEM应用中进行网格划分,将搅拌筒的空间划分成4×4×4的空间网格,某一时刻的网格划分如图5所示,为提高结果准确性,将导出数据表格中剔除颗粒数少于100的网格数据。
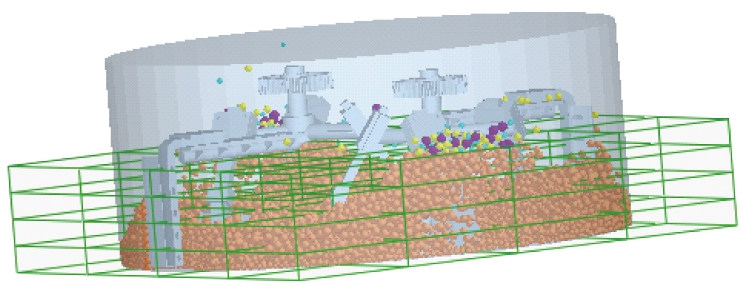
图5 网格划分
Fig.5 Meshing
颗粒均匀度是衡量物料颗粒搅拌质量的重要评判指标。在评价混合物混合效果时,一般通过测量某一特定物料颗粒的离散系数来衡量物料的混合效果。本文中以氯化镁颗粒为例,经过搅拌混合的物料,在搅拌区域内取组数据样本,样本i中氯化镁颗粒的数为ni,总颗粒数为Ni,则该颗粒在样本i中所占比例pi
(6)
该数据样本的最佳混合度p
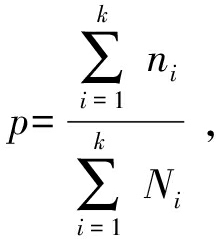
(7)
则样本的离差Xi
(8)
计算其平均值![]() 及标准差S,
及标准差S,
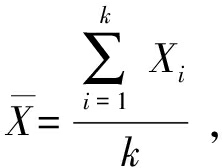
(9)
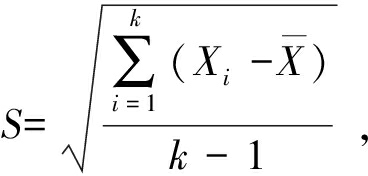
(10)
则该颗粒的离散系数Cv为
(11)
离散系数反映了搅拌机内物料颗粒的混合程度,其值越小,则表明混合度越高,搅拌质量越好[13]。
3.2 搅拌叶片角度变化对搅拌效果的影响
由叶片安装角的定义[14]可知,它是指搅拌臂的法向平面与叶片法相平面的夹角,如图6中角度α。取α的角度分别为35°、40°、45°、50°、55°等5个角度作为实验对象。为了得到更为准确的分析结果,在搅拌时间为35 s内,每隔5 s取1次数据,求出各时间点颗粒的平均速度,如图7所示。
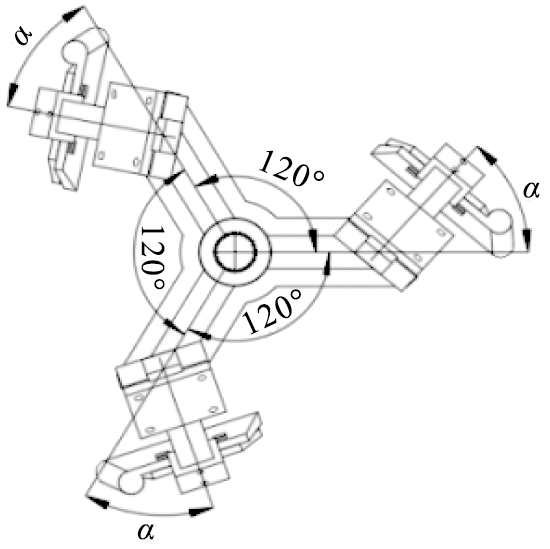
图6 叶片安装角所示α
Fig.6 Blade mounting angle α
在一定的搅拌时间内,物料颗粒的平均速度反映了搅拌桶内物料颗粒的运动情况,速度越大,表明流动性越好。从图中可以看出,当搅拌叶片安装角度为45°时,搅拌筒内物料颗粒的流动性更好,故初步判定搅拌效果也可能会更好。同时,为了准确的分析物料搅拌后的效果,选取氯化镁颗粒作为所测颗粒样本,从求得离散系数来衡量物料的混合效果,将数据导出至表格3并绘制其折线图,如图8所示。
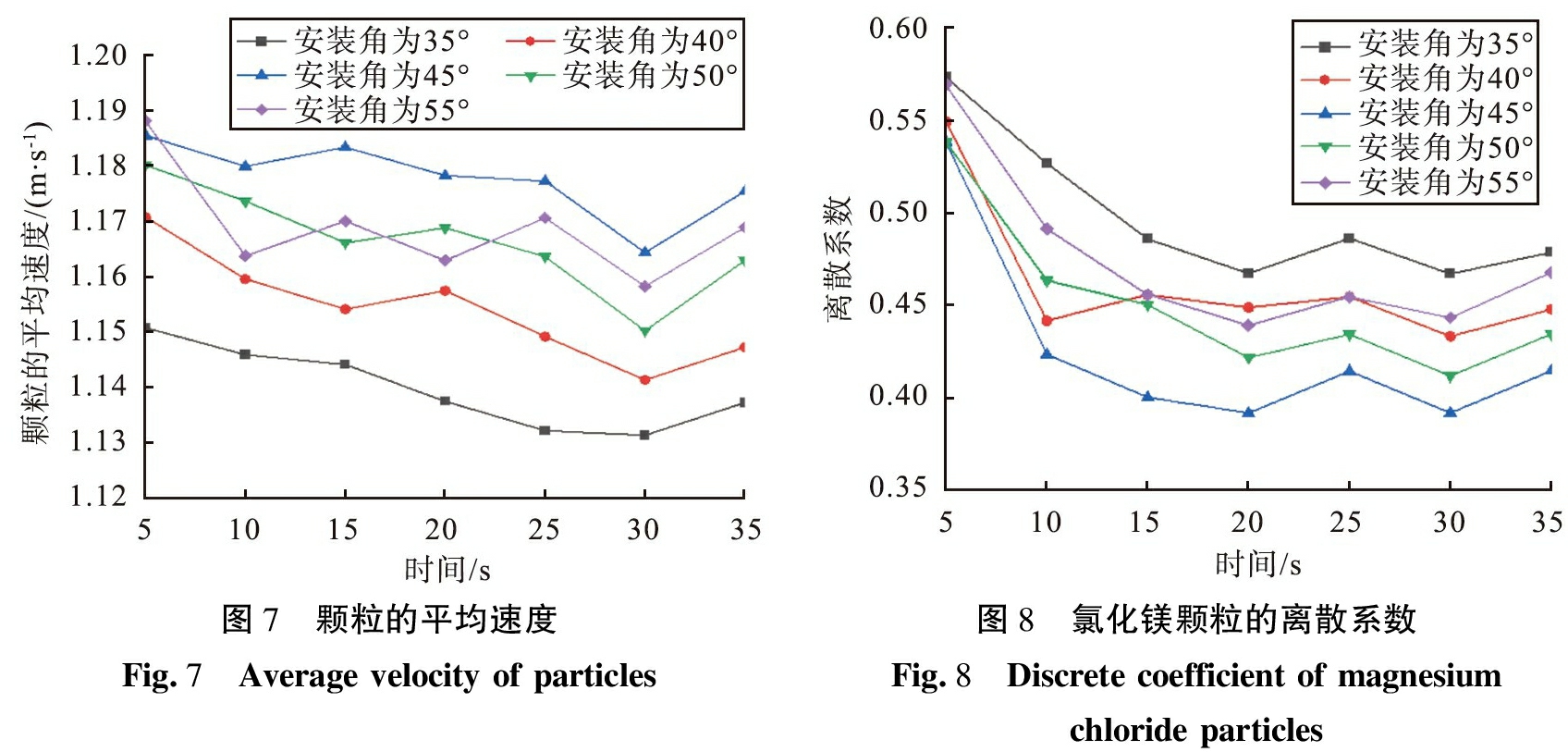
图7 颗粒的平均速度Fig.7 Average velocity of particles图8 氯化镁颗粒的离散系数Fig.8 Discrete coefficient of magnesium chloride particles
表3 氯化镁的离散系数
Tab.3 Discrete coefficient of magnesium chloride particles
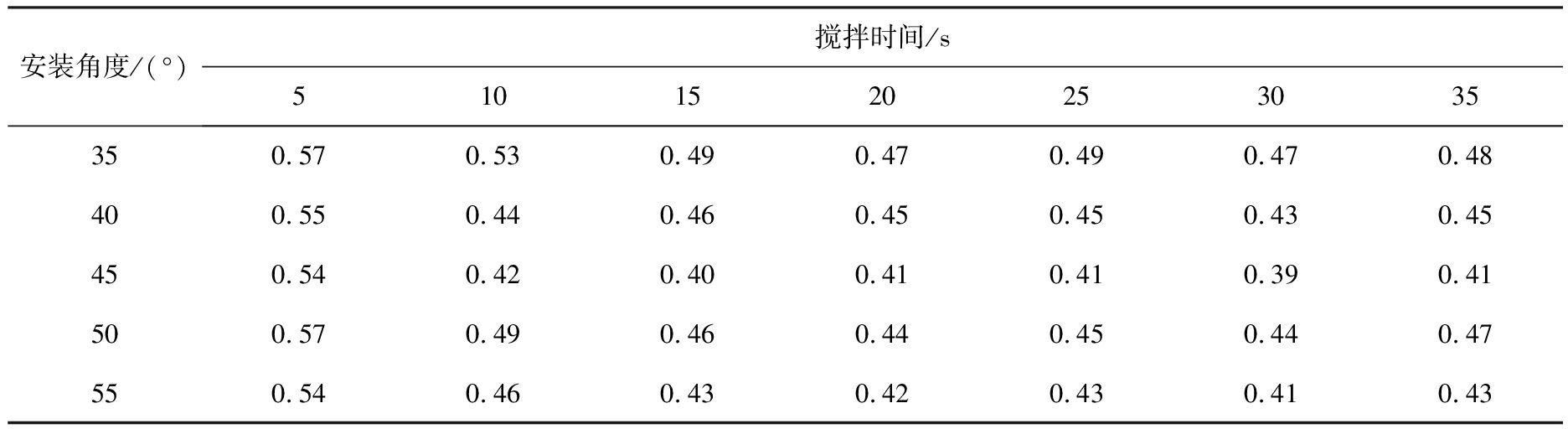
安装角度/(°)搅拌时间/s5101520253035350.570.530.490.470.490.470.48400.550.440.460.450.450.430.45450.540.420.400.410.410.390.41500.570.490.460.440.450.440.47550.540.460.430.420.430.410.43
由图8可知,随着搅拌时间的增加,物料混合均匀过程可分为3个阶段:5~10 s为第1阶段,物料颗粒混合非常迅速,颗粒在外力作用下进行急速相对运动,形成强力的对流混合,氯化镁颗粒的离散系数急速下降;10~20 s为第2阶段,物料颗粒运动形成剪切流,在剪切的作用下进行混合,同时还进行第1阶段的对流混合,剧烈程度与第1阶段相比下降;20~35 s为第3阶段,物料颗粒的运动逐渐变得缓慢,这个阶段主要依靠小颗粒之间的相互渗透和扩散发生混合,氯化镁颗粒的离散系数则出现平缓波动,离散系数减小是因为物料颗粒之间开始混合,符合实际生产中的混合情况。当叶片安装角度从35°逐渐增大到45°时,物料颗粒混合过程所受到叶片剪切的作用逐渐增大,所产生的剪切力驱使物料颗粒之间相互运动,混合程度越好,氯化镁颗粒的离散系数小;当安装角度从45°增大为55°时,颗粒所受到叶片的剪切作用力减小,物料颗粒不能在搅拌筒内有效地运动,无法与其他颗粒发生混合作用,混合程度不好,氯化镁的离散系数大。由于离散系数反映搅拌混合的程度,其值越小,说明混合效果越好,因此当叶片安装角度为45°时,搅拌效果最佳。
3.3 搅拌轴转速不同对搅拌效果的影响
根据实际调查结果以及大量试验证明,立轴行星式搅拌机的搅拌叶片最佳搅拌线速度在1.4~1.7 m/s之间浮动[15],搅拌轴转速的最佳范围在20~40 r/min。根据搅拌臂旋转半径大小,为了准确比较物料颗粒的混合程度,以搅拌轴转速为20、30、40 r/min进行仿真实验,选取氯化镁物料颗粒作为研究对象,求得离散系数来衡量物料的搅拌效果,将数据绘制成折线图,如图9所示。
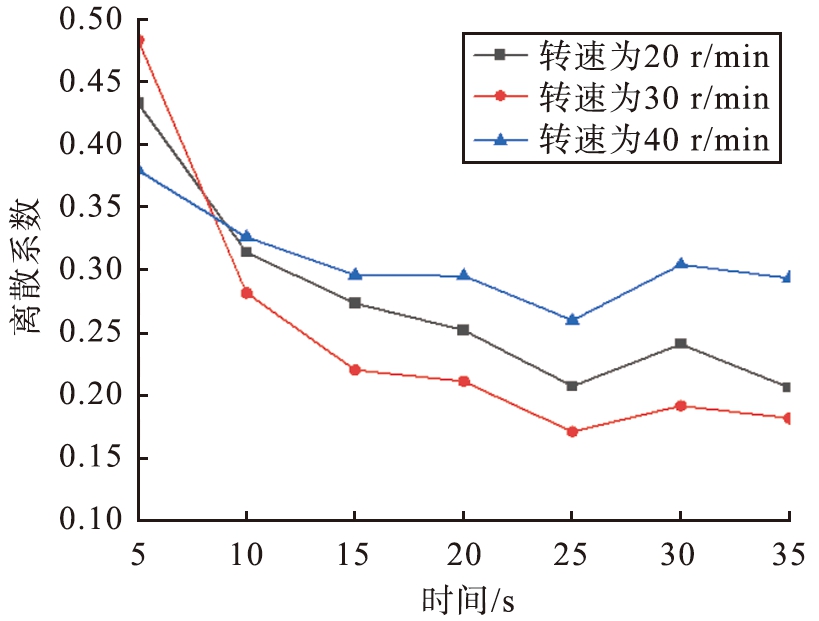
图9 氯化镁颗粒的离散系数
Fig.9 Discrete coefficients of magnesium chioride particles
在生产效率不变的条件下,要增加物料颗粒之间的碰撞次数和相互摩擦次数,提高物料颗粒参与运动的次数以及运动轨迹交叉的频率,就应该考虑提高搅拌轴的转速,使物料颗粒的流动性增加,从而提高混合度。从图9中可以看出,当搅拌轴转速为30 r/min时,氯化镁颗粒的离散系数最小,说明其搅拌效果最好。当转速为20 r/min时,搅拌桶内物料颗粒之间交叉运动的次数减少,导致混合程度不高。当转速为40 r/min时,由于转速过大,导致混合物料颗粒的离心力大,不同粒径的物料颗粒惯性力不同且大于和叶片之间的摩擦力时,会以不同的速度抛离叶片,造成物料颗粒之间的离析,反而使物料之间混合度下降。通过比较3组转速情况下氯化镁颗粒的离散系数可知,当搅拌轴转速为30 r/min时,混合程度最好。
4 木质板材性能试验与结果分析
4.1 试验条件
很多学者为了研究搅拌机的参数特性,试验对象多采用以混凝土为原材料进行研究,宏观均匀度多用拌合物中砂浆密度的相对误差以及粗骨料质量的相对误差进行评价;由于本实验所用的氯化镁、氧化镁等材料不同,因此检测衡量的标准也不同,使用如图10所示微机控制人造板万能试验机进行力学试验,对最终木质板材的静曲强度、弹性模量及内结合强度进行测量。

图10 微机控制人造板万能力学试验机
Fig.10 Microcomputer control universal mechanical testing machine of wood-based panel
4.2 试验原理
依照国家标准《人造板及饰面人造板理化性能试验方法(2013版)》,木质板材的静曲强度和弹性模量的测量方法是在2个点支撑的板材中间部位施加载荷,在最大载荷作用下板材所受弯矩的值除以抗弯截面模量的值即为所测静曲强度;在弹性极限允许的范围施加载荷后木质板材产生的应力与应变之比为弹性模量;内结合强度是试件表面承受均匀分布的拉力,直至破坏时的抗拉能力的测定,内结合强度是垂直于试件表面的最大破坏拉力和试件面积之比。
4.3 试验板材
由于成品板材尺寸过大,为方便测量及万能力学试验机试验,裁剪成长为210 mm、宽为50 mm的矩形板材,如图11所示。

图11 试样板材
Fig.11 Sample plate
4.4 试验方法
图12为测定装置示意简图。
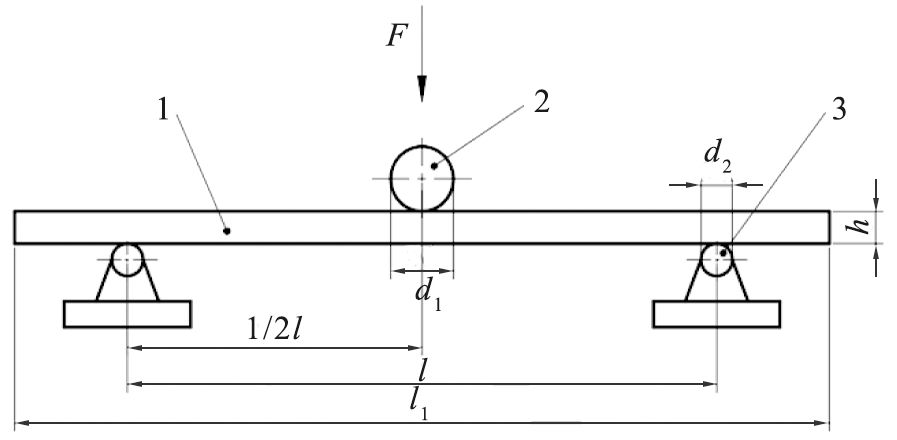
1—试件;2—加荷辊;3—支承辊;F—载荷;h—试件厚度。
图12 测定试验简图
Fig.12 Schematic diagram of measuring device
测量板材的长度为210 mm,宽度为50 mm,厚度为8 mm;调整2个支座之间的跨距至少为板材厚度的20倍,至少大于100 mm,不超过1 000 mm,测量支座间的中心距;板材平放在支座上,板材长轴与支撑辊垂直,板材中心点在加荷辊下方;试验过程中恒速加载,在木质板材的中心处测量挠曲变形,精确至0.1 mm;记录最大载荷,精确至1%;根据板材的横纵向,取2组板材进行试验,一组测试板材正面朝上,另一组背面朝上。
木质板材的静曲强度σb计算公式为
(12)
式中:Fm表示板材被破坏时的最大载荷,N;l表示支座间的距离,mm;b表示板材的宽度,mm;h表示板材厚度,mm;每张板材在每组试件的静曲强度是同组全部试件的算术平均值。
木质板材的弹性模量E计算公式为
(13)
式中:ΔF表示板材被破坏时的最大载荷,N;l表示支座间的距离,mm;b表示板材的宽度,mm;h表示板材厚度,mm;Δt表示板材变形量,mm;每张板材在每组试件的静曲强度是同组全部试件的算术平均值。
木质板材的内结合强度σ┴计算公式为
(14)
式中:Fmax表示试件破坏时最大载荷,N;l1表示试件长度,mm;b为试件宽度,mm;每张板的内结合强度是同一张板内全部试件内结合强度的算术平均值。
4.5 结果分析
由仿真结果可知,搅拌叶片的安装角度、搅拌轴的转速都会对搅拌质量产生影响,控制其他参数不变,在安装角度及转速不同情况下进行试验,测出不同情况下多功能木质板材的静曲强度、弹性模量及内结合强度,测量结果如表4所示。
图13所示为安装角度不同得到的板材的应力-应变曲线图,图14所示为转速不同得到的板材应力-应变曲线图。从图13、14、表4中可知,随着应力地增加应变随之增加,相同应变情况下,安装角为45°时,所对应的弯曲应力最大;当转速为30 r/min时,所对应的弯曲应力最大,静曲强度、弹性模量及内结合强度最大,说明板材的力学性能明显提升,与前面仿真得到的结论符合。
表4 不同参数情况下板材力学性能
Tab.4 Mechanical properties of plates with different parameters
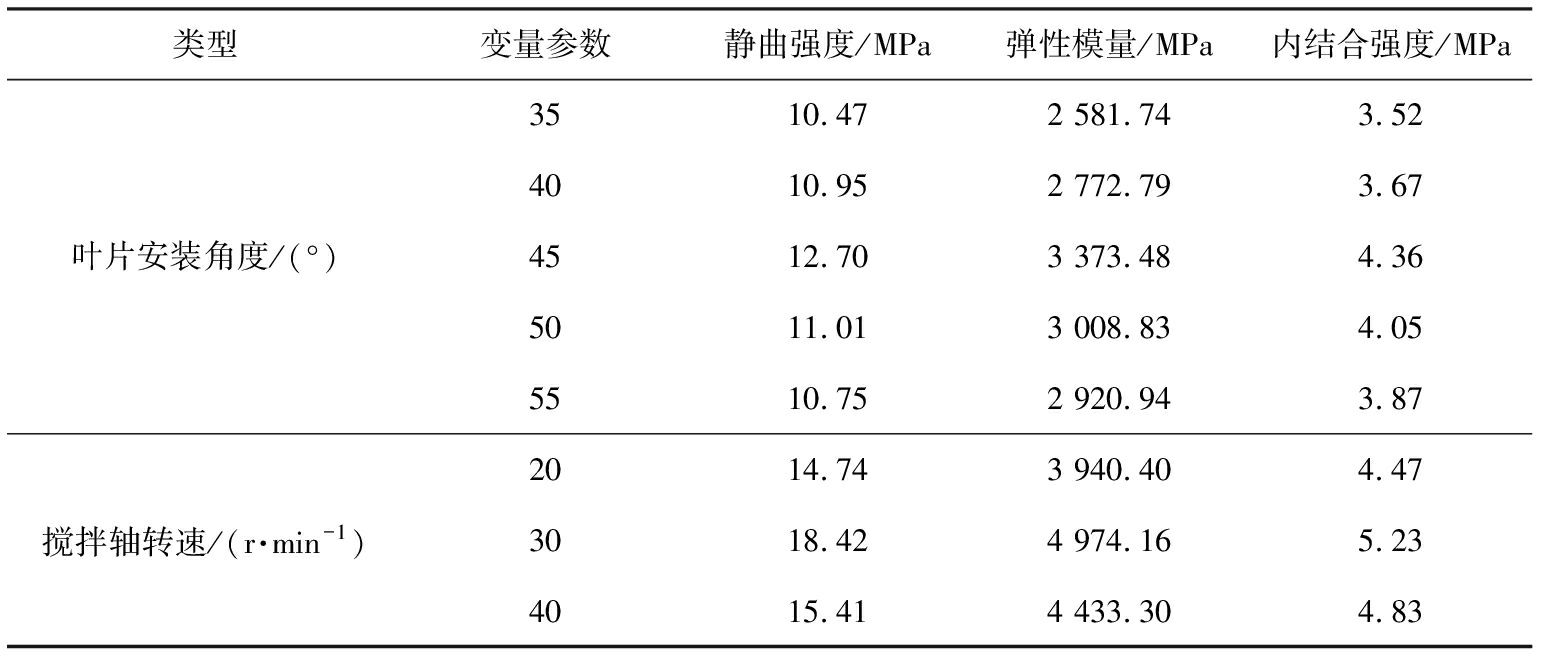
类型变量参数静曲强度/MPa弹性模量/MPa内结合强度/MPa叶片安装角度/(°)3510.472 581.743.524010.952 772.793.674512.703 373.484.365011.013 008.834.055510.752 920.943.87搅拌轴转速/(r·min-1)2014.743 940.404.473018.424 974.165.234015.414 433.304.83
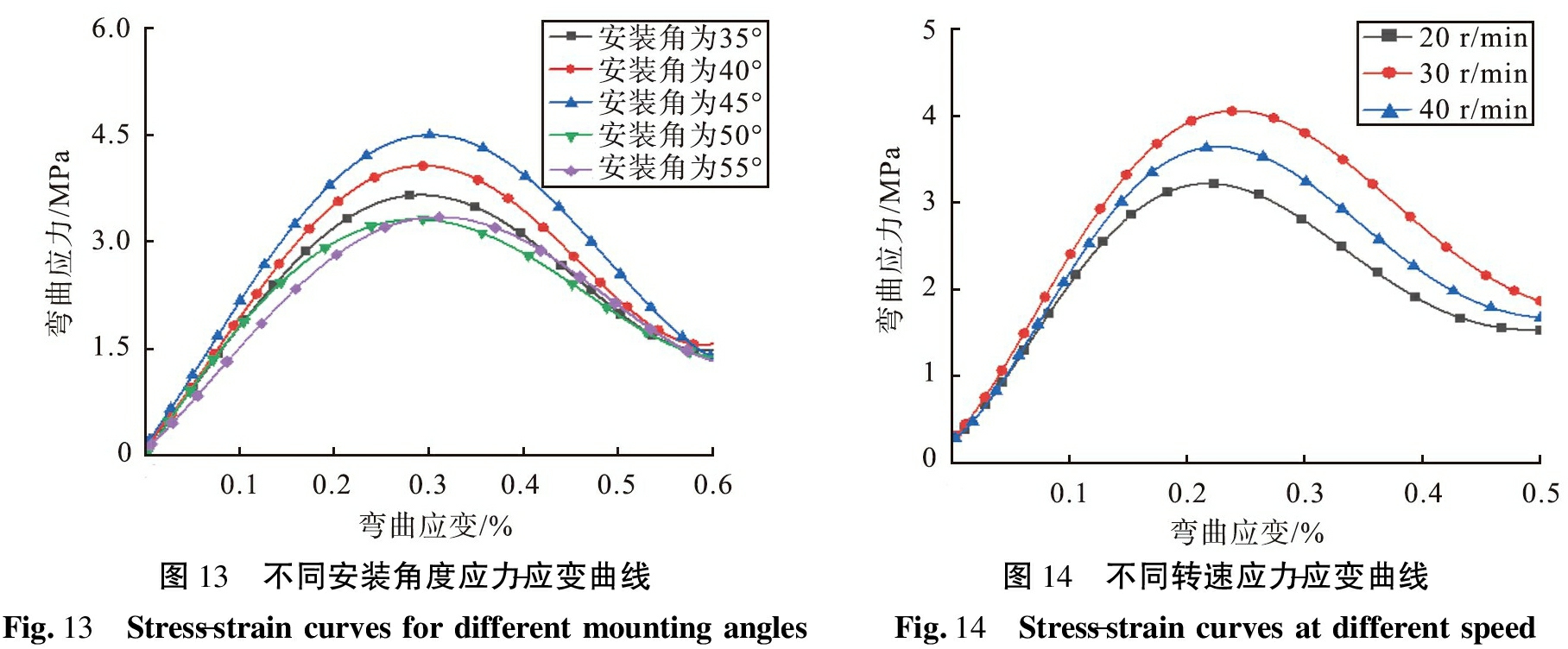
图13 不同安装角度应力-应变曲线Fig.13 Stress-strain curves for different mounting angles图14 不同转速应力-应变曲线Fig.14 Stress-strain curves at different speed
5 结论
利用Unigraphics NX软件建立了立轴行星式搅拌机模型,并导入EDEM软件中,在其他参数不变的情况下,通过改变搅拌叶片安装角度以及搅拌轴转速,研究对搅拌质量的影响,最后通过试验验证木质板材的力学性能,得到以下结论。
1)在其他参数不变的情况下,根据EDEM软件模拟搅拌过程的结果以及通过对改变搅拌叶片安装角度的搅拌效果的试验验证,得到当叶片安装角度为45°时,搅拌效果最佳。
2)在其他参数不变的情况下,根据EDEM软件模拟搅拌过程的结果以及通过对改变搅拌轴转速的搅拌效果的试验验证,得到当搅拌轴转速在30 r/min时,其搅拌效果最佳。
[1]董玉刚, 林亮亮, 孔鲜宁,等.基于EDEM的双卧轴搅拌机搅拌工艺对比研究[J].水泥工程, 2016(2): 87-90.
[2]施进发, 高志龙, 杨杰,等.基于EDEM的双卧轴搅拌机混合度研究[J].筑路机械与施工机械化, 2020, 37(增1): 126-129.
[3]孔鲜宁, 杨宏晓, 李耀.基于EDEM的双卧轴搅拌机合理充盈率探究[J].水泥工程, 2015(5): 9-12.
[4]郭良, 赵悟, 王敬,等.基于EDEM双立轴振动搅拌机叶片安装角度仿真分析及试验研究[J].现代制造技术与装备, 2018(11): 3-6.
[5]ALIAN M, EIN-MOZAFFARI F, UPRETI S R.Analysis of the mixing of solid particles in a plowshare mixer via discrete element method(DEM)[J].Powder Technology, 2015, 274: 77-87.
[6]毛娅, 范雄, 江智.基于EDEM的连续性立式搅拌机混合特性研究[J].计算机仿真, 2018, 35(12): 181-184,415.
[7]SAKAI M, SHIGETO Y, BASINSKAS G, et al.Discrete element simulation for the evaluation of solid mixing in an industrial blender[J].Chemical Engineering Journal, 2015, 279: 821-839.
[8]RADL S, KALVODA E, GLASSER B J, et al.Mixing characteristics of wet granular matter in a bladed mixer[J].Powder Technology, 2010, 200(3): 171-189.
[9]陈勇棠, 蒲明辉.基于UGNX的外啮合行星搅拌机运动特性研究[J].柳州职业技术学院学报, 2017, 17(4): 114-120.
[10]胡国明.颗粒系统的离散元素法分析仿真: 离散元素法的工业应用与Edem软件简介[M].武汉: 武汉理工大学出版社, 2010.
[11]周志勇.基于DEM的强力混合机混匀过程模拟及结构优化[D].湘潭:湘潭大学, 2014.
[12]CHAO J W, XIE H X, LIU X D, et al.Analysis of the mixing of solid particles in a vertical cylindrical mixer via discrete element method(DEM)[J].Journal of Simulation, 2017, 5(4):47-51.
[13]李少华, 朱明亮, 张立栋,等.回转装置内三组元颗粒径向混合评价方法分析[J].化工进展, 2013, 32(6): 1224-1229.
[14]赵利军, 冯忠绪, 姚运仕,等.搅拌机叶片安装角的确定方法[J].长安大学学报(自然科学版), 2006(5): 99-102.
[15]冯忠绪, 王卫中, 姚运仕,等.搅拌机合理转速研究[J].中国公路学报, 2006(2): 116-120.