流化床换热器是一种引入了流态化技术的新型换热器,在换热管内加入了固体颗粒并在换热管内形成循环运动,固体颗粒刮擦换热管的内壁从而实现在线防除垢。流化床换热器可以应用于污垢检测[1]、 热回收[2]和太阳能发电[3-4]等领域。Kollbach等[5]、 Rautenbach等[6]在20世纪80年代研究发现,添加惰性颗粒可以增强流化床换热器管壁的传热性能,并能起到防垢、 除垢的作用。Pronk等[7-8]比较了固定床和循环流化床的传热效果和除垢能力,发现液-固两相流化床换热器能够有效防止和去除水垢的因素主要有2个,即颗粒对壁面的冲击和颗粒间的碰撞。
在流化床的所有参数中,最小流化速度是反映液体动力特性的一个关键参数[9]。影响最小流化速度的因素较多,主要有流体黏度、 流体密度、 颗粒大小、 颗粒分布、 初始床层以及实验环境(温度、 压力)等。采用实验法研究颗粒特性需要购买和维护实验设备,成本较高,并且实验中测量颗粒的数量有限,数据采集和处理较为困难,而数值模拟方法可以有效避免上述缺点,提高研究效率。Mawatari等[10]基于Ergun方程对振动流化床进行了模拟研究,预测了颗粒的最小流化速度。Shao等[11]模拟了高温高压下气-固流化床中颗粒的最小流化速度,并与实验结果进行了对比,验证了仿真结果的准确性。Fu等[12-13]对磁铁矿颗粒和磁铁矿与砂、 矸石、 煤粉的二元颗粒混合物进行初始流动模拟试验, 研究初始床层颗粒对初始流动特性的影响,发现单颗粒和双颗粒混合物的最小流化速度都随着床层质量的增大而增大。 目前, 以气-固流化床为模型对最小流化速度进行数值模拟研究的较多[14-16], 以液-固流化床为模型的较少。 Mehran等[17]对液-固两相流化床的主要传热参数进行了数值模拟和实验研究, 发现保持合适的颗粒粒径可以实现最大的传热效率。 张仪等[18]则对液-固流态化动态过程中相间作用力进行了数值模拟及实验验证,确定了最佳操作条件。 综上, 液-固两相流的流动规律较为复杂, 纯粹的理论研究存在许多困难,而大量实验测量耗费过多资源, 因此, 数值模拟方法较为适合研究最小流化速度问题。
计算颗粒流体力学(computational particle fluid dynamics, CPFD)是一种新的应用欧拉-拉格朗日法的计算流体力学(computational fluid dynamics, CFD), 采用了粒子包裹算法和多相质点网格模型(multiphase particle-in-cell, MP-PIC)[19],在一定的时间内可以模拟大规模工业多相流系统。在密集流动中,很难计算每个粒子的应力梯度,而MP-PIC利用网格上的梯度将每个粒子的应力梯度插值到离散粒子上,不需要计算每一个粒子及其粒子间的相互作用,大大降低了计算成本。
本文中首先建立液-固两相流化床实验系统,测量5种不同颗粒的最小流化速度;然后使用CPFD方法对单管液-固流化床模型进行数值模拟,将5种颗粒的最小流态化速度的实验值与模拟值对比并进行误差分析,从而验证数值模拟方法的正确性。
1 测试实验
1.1 测试系统
液-固流化床实验系统用于颗粒的流化实验和数据采集,以便获取颗粒的最小流化速度。液-固流化床实验测试系统示意图如图1所示。由图可见,实验装置采用的是内径为60 mm、 高度为1.45 m的单管液-固流化床,流化床管道为圆柱形有机玻璃立管。实验系统中的流化介质为液态水,颗粒加入到流化床底部,在流体的携带作用下沿流化床向上移动,形成颗粒流化状态。实验过程中采用浮子流量计调节入口流量,采用压力计测量入口和出口压力,实验数据实时传输至计算机。

1—水箱; 2—水泵; 3—电磁阀; 4、 5—球阀; 6、 7、 8—调节阀; 9、 10、 11—浮子流量计;
12、 14—丝网; 13—单管液-固流化床; 15—压力计; 16—计算机。
图1 液-固流化床实验测试系统示意图
Fig.1 Schematic diagram of liquid-solid fluidized bed experimental test system
1.2 测试原理
实验过程中,流体从底部流入,通过颗粒床层时,流体对颗粒产生曳力,流体通过床层时所受到的摩擦阻力导致流体压力上升,床层入口和出口处的压降增大。实验中采用降低流速法,在床层由流态化缓慢返回到固定床过程中,记录下相对应的流体流速和床层压降,取固定床压降差拟合线和流化床压降差拟合线的交点的横坐标数值为颗粒的最小流化速度。计算机记录每个流速下的床层压力,绘制床层压降随液体流速的变化曲线。
1.3 颗粒参数
实验过程中,初始加入颗粒的体积分数为30%。选择5种不同材料和粒径的颗粒进行液-固两相流化床实验。5种实验颗粒参数如表1所示。由表可见,5种实验颗粒的代号分别记为E1、 E2、 E3、 E4、 E5; E1、 E2的材料分别为氧化铝、氧化锆,E3、 E4和E5的材料为轴承钢,氧化铝、 氧化锆和轴承钢的密度分别为2 364、 4 123、 7 729 kg/m3; E1、 E2和E4的粒径为2 mm,E3、 E5粒径分别为1、 3 mm。
表1 实验颗粒参数
Tab.1 Parameters of experimental particle

实验颗粒代号粒径/mm材料密度/(kg·m-3)实验颗粒代号粒径/mm材料密度/(kg·m-3)E12氧化铝2 364E42轴承钢7 729E22氧化锆4 123E53轴承钢7 729E31轴承钢7 729
2 数值模拟试验
2.1 模型网格划分与边界条件
使用单管液-固流化床作为模拟装置,网格数设为81 000,进口压力设为118 000 Pa,出口压力设为101 325 Pa,温度设为300 K,初始入口速度设为0.01 m/s。在初始状态下,固体颗粒被添加到单管的下部,其余部分充满液体,所有管壁都采用无滑动边界条件,边界选在入、 出口边界的第1层网格。单管液-固流化床三维模型图如图2所示。

(a)单管液-固流化床(b)出口端网格划分(c)入口边界条件(d)出口边界条件图2 单管液-固流化床模型图Fig.2 Model diagram of single-tube liquid-solid fluidized bed
2.2 仿真参数设置
液相为水,密度为1 000 kg/m3。固相设为5种模拟颗粒,代号分别记为S1、 S2、 S3、 S4、 S5; S1、 S2的材料分别为氧化铝、氧化锆,S3、 S4、 S5的材料为轴承钢,氧化铝、 氧化锆和轴承钢的密度分别为2 300、 4 100、 7 700 kg/m3; S1、 S2、 S4的粒径为2 mm,S3、 S5的粒径分别为1、 3 mm。模拟颗粒参数见表2。
表2 模拟颗粒参数
Tab.2 Parameters of simulated particles

代号粒径/mm材料密度/(kg·m-3)代号粒径/mm材料密度/(kg·m-3)S12氧化铝2 300S42轴承钢7 700S22氧化锆4 100S53轴承钢7 700S31轴承钢7 700
根据使用CPFD软件的经验[20],小的时间步长并不能提高仿真结果的准确性,因此,在仿真阶段的初始时间步长设置为0.001 s。CPFD模拟主要参数设置如表3所示。
表3 CPFD模拟的主要参数设置
Tab.3 Main parameter settings for CPFD simulation

曳力模型初始时间步长/s模拟总时长/s初始床层高度/m堆积体积分数初始颗粒体积分数/%法向动量保留系数切向动量保留系数收敛条件判断数Wen-Yu0.00120 s0.3,0.45,0.60.5520,30,400.30.991.2~1.5
3 结果和讨论
3.1 最小流态化速度的实验值
3.1.1 根据压降-流体速度的求解
实验测得的不同颗粒的压降差随流体速度的变化曲线如图3所示。由图可见,颗粒的最小流化速度所在的位置为固定床和流化床的分界点,固定床的压降随流体速度的增大快速上升,而流化床的压降随流化速度变化的曲线较为平缓,固定床压降差拟合线和流化床压降差拟合线为压降-流体速度曲线的斜率,2条拟合线交点的横坐标数值即为颗粒的最小流态化速度,因此,颗粒E1, E2, …, E5的最小流态化速度实验值分别为0.021 6、 0.036 7、 0.029 3、 0.055 5、 0.084 5 m/s。
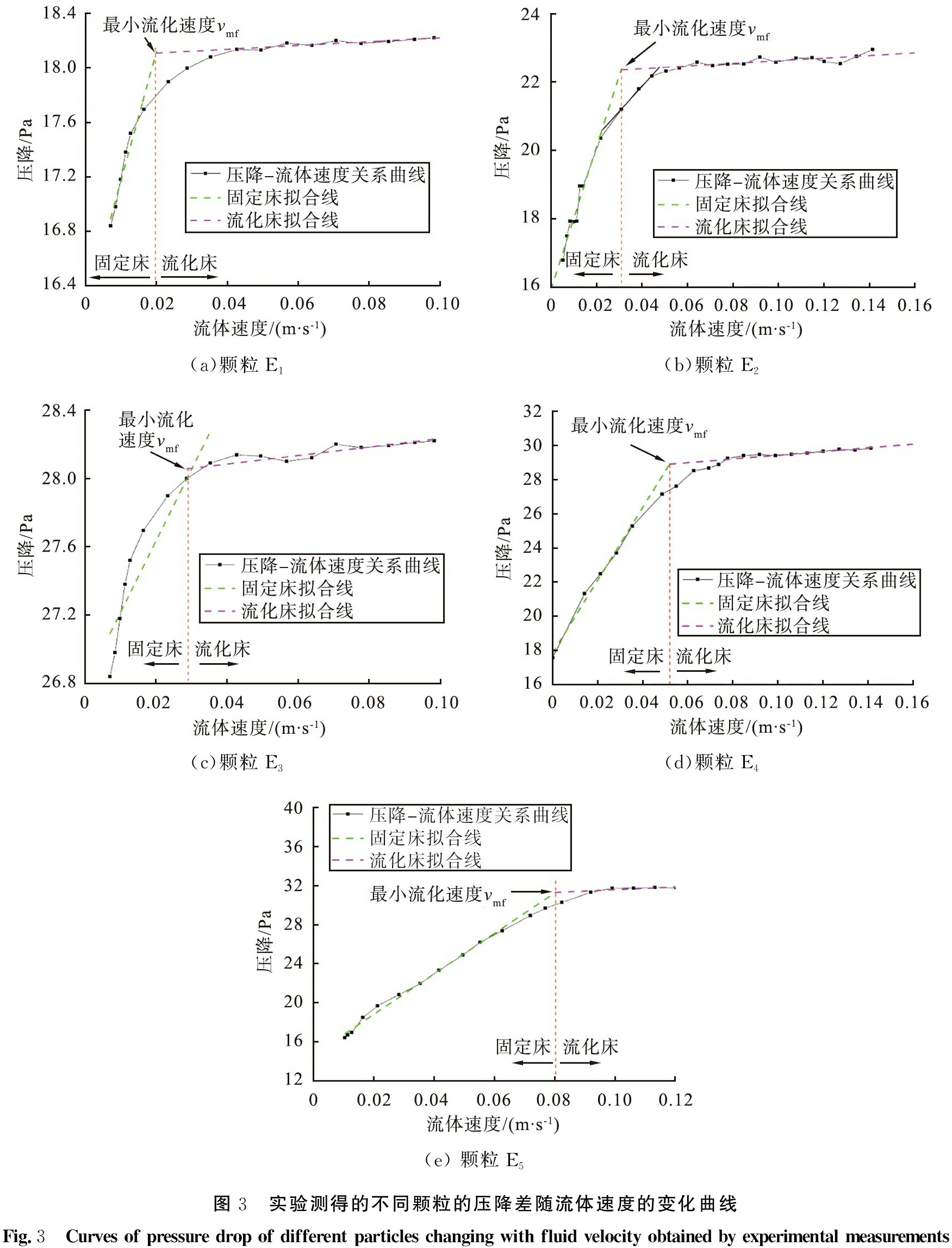
(a)颗粒E1(b)颗粒E2(c)颗粒E3(d)颗粒E4(e) 颗粒E5图3 实验测得的不同颗粒的压降差随流体速度的变化曲线Fig.3 Curves of pressure drop of different particles changing with fluid velocity obtained by experimental measurements
3.1.2 计算公式验证
使用Wen-Yu公式以及优化后的经验公式[21]对最小流化速度的实验结果进行验证。阿基米德数Ar、 雷诺数Remf以及最小流态化速度vmf的计算公式分别为
(1)
(2)
vmf=![]() ,
,
(3)
式中: 在Wen-Yu公式中, 常数C1为33.67, C2为0.040 8;在优化公式中,常数C1为33.8, C2为0.038; Ar为阿基米德数,无量纲; μf 为流体黏度, Pa; ρf为流体密度, kg/m3; ρs为颗粒密度, kg/m3; d为颗粒直径, mm; g为重力加速度,取值为9.81 m/s2。颗粒E1, E2, …, E5的最小流态化速度的Wen-Yu公式计算值分别为0.021 6、 0.037 6、 0.030 6、 0.060 4、 0.080 8 m/s,颗粒E1, E2, …, E5的最小流态化速度的优化公式计算值分别为0.020 7、 0.036 1、 0.029 1、 0.058 1、 0.078 0 m/s。
床层达到稳定流化状态时,实验测量值和计算值如表4所示。由表可见,颗粒E1, E2, …,E5的最小流态化速度的2个公式计算值都与实验值较为吻合,最大相对误差小于10%,平均相对误差小于5%,实验结果是可靠的。
表4 最小流态化速度的实验值验证
Tab.4 Verification of experimental values of the minimum fluidization velocity
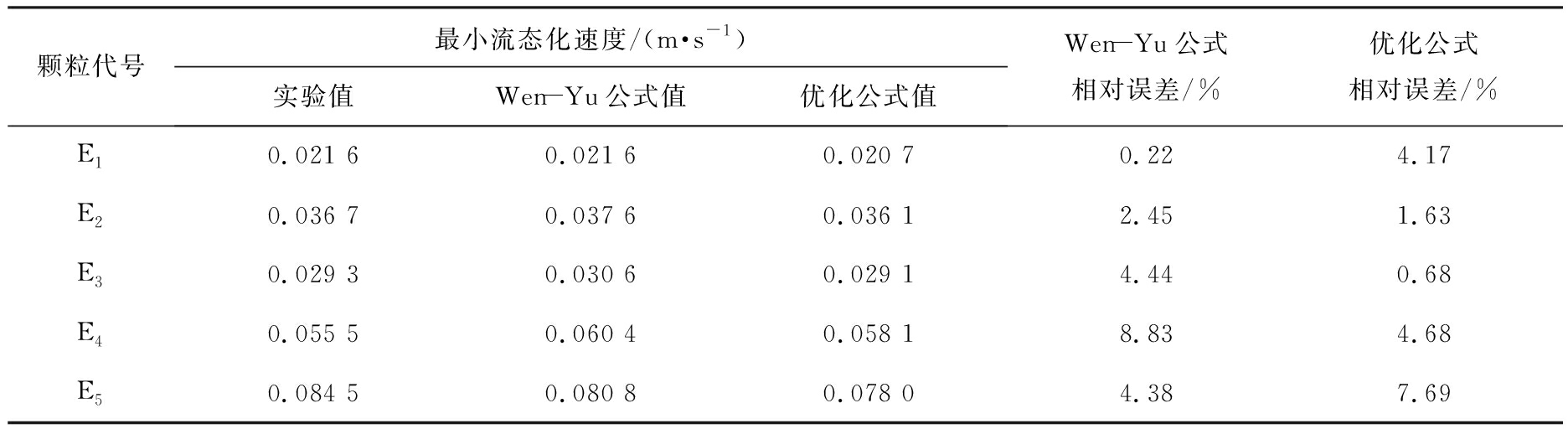
颗粒代号最小流态化速度/(m·s-1)实验值Wen-Yu公式值优化公式值Wen-Yu公式相对误差/%优化公式相对误差/%E10.021 60.021 60.020 70.224.17E20.036 70.037 60.036 12.451.63E30.029 30.030 60.029 14.440.68E40.055 50.060 40.058 18.834.68E50.084 50.080 80.078 04.387.69
3.2 最小流态化速度的模拟值
3.2.1 求解
以S1颗粒在液体流速为0.14 m/s时床层压降分布仿真结果如图4所示。由图可以看出,取最大压降为131 603.8 Pa,最小压降为101 343.8 Pa,计算压降差为30 260 Pa。
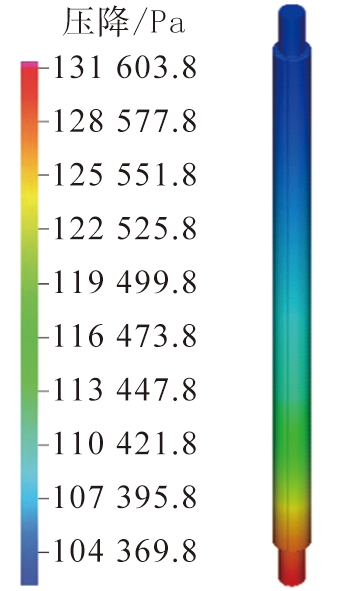
图4 颗粒S1在液体流速为0.14 m/s时
床层压降分布的仿真结果
Fig.4 Simulation results of bed pressure drop
distribution of particle S1 at liquid flow rate of 0.14 m/s
将颗粒S1, S2, …, S5处于各个流速下的床层压降按照上述方法处理,得到5种模拟颗粒在不同流速下的压降差,如表5所示。
表5 5种模拟颗粒在不同流速下的压降差
Tab.5 Pressure drop difference of five kinds of simulated particles at different flow velocity
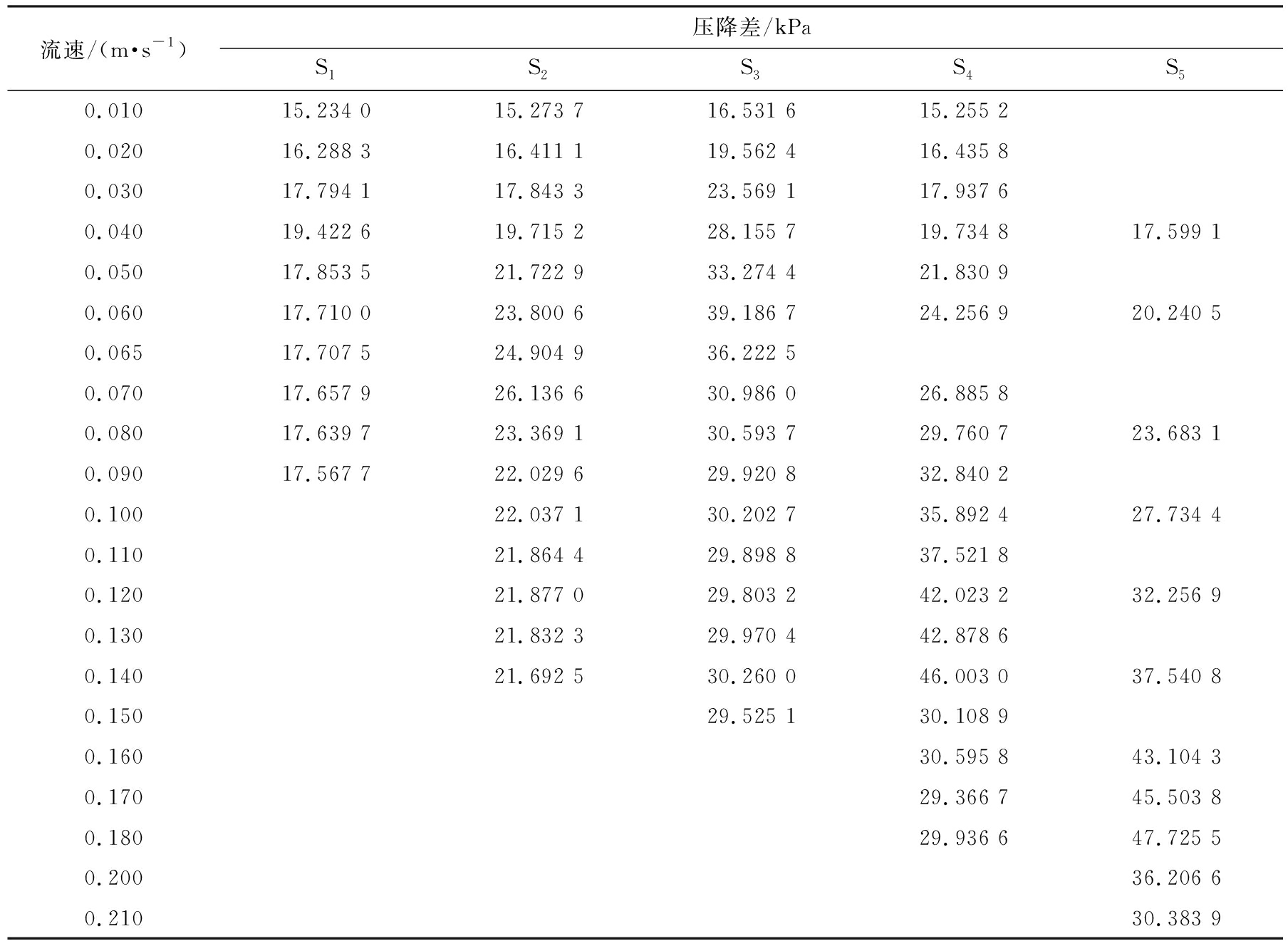
流速/(m·s-1)压降差/kPaS1S2S3S4S50.01015.234 015.273 716.531 615.255 20.02016.288 316.411 119.562 416.435 80.03017.794 117.843 323.569 117.937 60.04019.422 619.715 228.155 719.734 817.599 10.05017.853 521.722 933.274 421.830 90.06017.710 023.800 639.186 724.256 920.240 50.06517.707 524.904 936.222 50.07017.657 926.136 630.986 026.885 80.08017.639 723.369 130.593 729.760 723.683 10.09017.567 722.029 629.920 832.840 20.10022.037 130.202 735.892 427.734 40.11021.864 429.898 837.521 80.12021.877 029.803 242.023 232.256 90.13021.832 329.970 442.878 60.14021.692 530.260 046.003 037.540 80.15029.525 130.108 90.16030.595 843.104 30.17029.366 745.503 80.18029.936 647.725 50.20036.206 60.21030.383 9
模拟获得的不同颗粒的压降差随流体速度的变化曲线如图5所示。由图可见,在固定床阶段,床层的压降差与流体速度成正比。在流化床阶段,床层达到流化床状态,压降差随流速增加先增大后减少,符合数值模拟中增加流速时的特征[9]。取固定床压降差拟合线和流化床压降差拟合线的交点横坐标数值为颗粒的最小流化速度vmf,颗粒S1, S2, …, S5的最小流态化速度模拟值分别为0.031、 0.052、 0.045、 0.085、 0.112 m/s。
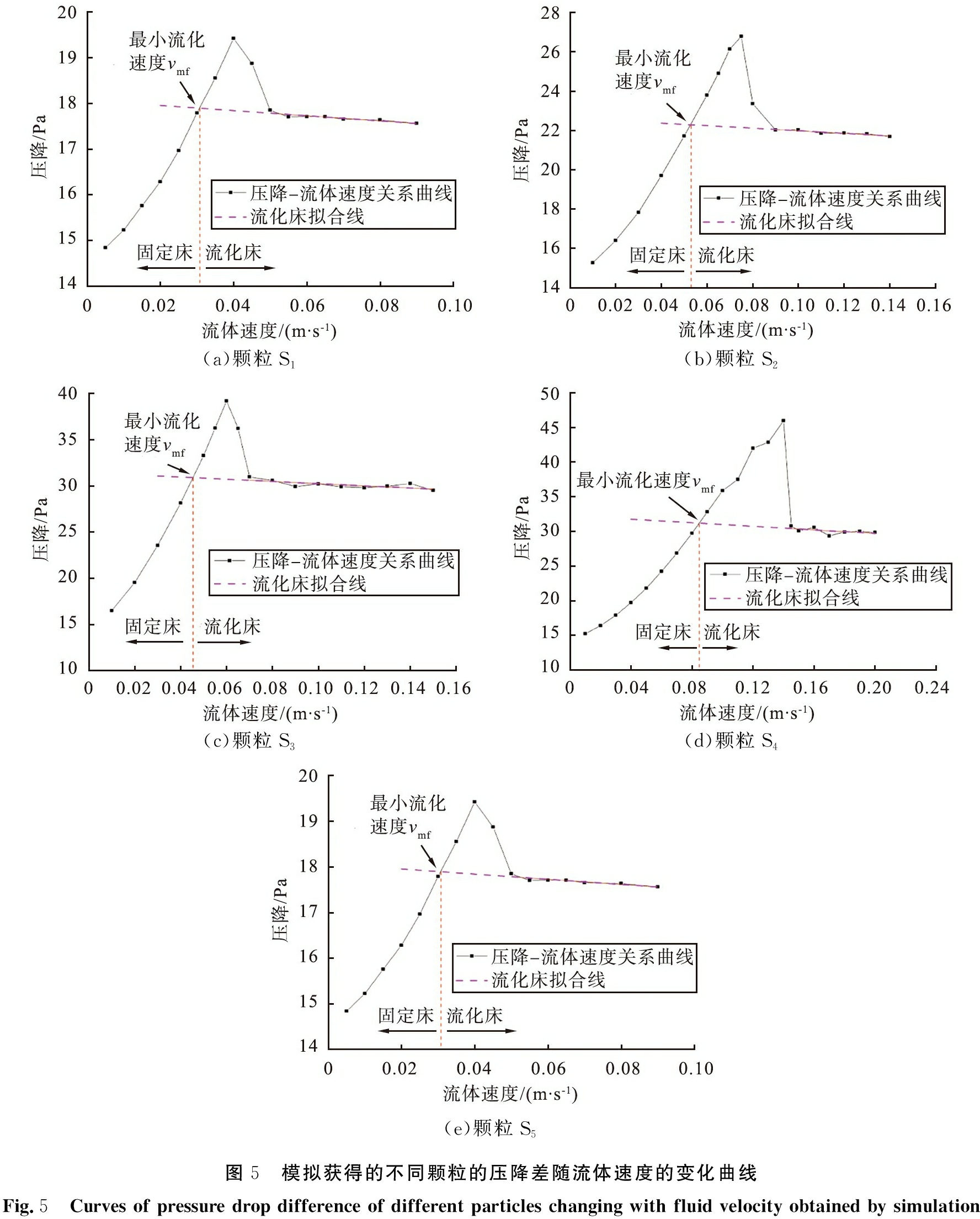
(a)颗粒S1(b)颗粒S2(c)颗粒S3(d)颗粒S4(e)颗粒S5图5 模拟获得的不同颗粒的压降差随流体速度的变化曲线Fig.5 Curves of pressure drop difference of different particles changing with fluid velocity obtained by simulation
3.2.2 最小流态化速度模拟值的修正与误差验证
由于在实际测量过程中,流化床上、下部分别设置了370 μm的丝网分布器,分布器存在阻力损失,而在模拟模型中并未对丝网分布器进行建模,因此需要对模拟结果进行修正。丝网阻力损失的压降差ΔP的经验公式[22]为
ΔP=1.469v+808.3v2,
(4)
式中: v为液体流速, m/s; ΔP为压降差,Pa。根据式(4)可以修正模拟压降。
最小流态化速度实验值和模拟值的修正及误差如表6所示。由表可知,颗粒S1、 S2、 S4、 S5的模拟修正值与颗粒E1、 E2、 E4、 E5的实验值之间的最小流态化速度的误差分别为11.1%、 19.9%、 24.3%、 26.6%,均为正向偏差且在工程允许范围内。这是因为,模拟过程中进行了理想化处理,忽略了实验过程中的复杂因素,比如,没有考虑管壁材质表面粗糙度的影响等。
表6 最小流态化速度实验值和模拟值的修正及误差
Tab.6 Correction and error of experimental and simulated values of the minimum fluidization velocity
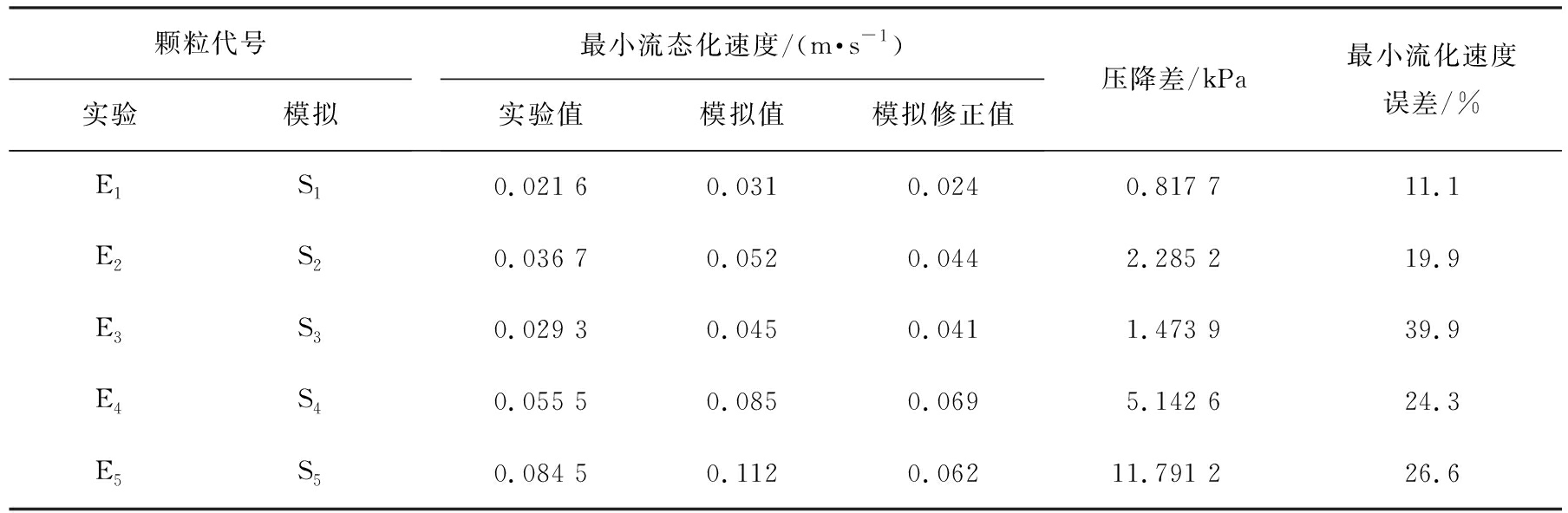
颗粒代号实验模拟最小流态化速度/(m·s-1)实验值模拟值模拟修正值压降差/kPa最小流化速度误差/%E1S10.021 60.0310.0240.817 711.1E2S20.036 70.0520.0442.285 219.9E3S30.029 30.0450.0411.473 939.9E4S40.055 50.0850.0695.142 624.3E5S50.084 50.1120.06211.791 2 26.6
3.3 颗粒粒径和密度对最小流态化速度的影响
不同粒径条件下最小流态化速度的测量值与模拟值如图6所示。由图6可以获得实验颗粒E3、 E4、 E5的最小流态化速度分别为0.029 3、 0.055 5、 0.084 5 m/s,模拟颗粒S3、 S4、 S5的最小流态化速度分别为0.045、 0.085、 0.112 m/s,可见,最小流态化速度随着颗粒的粒径的增大而增大。
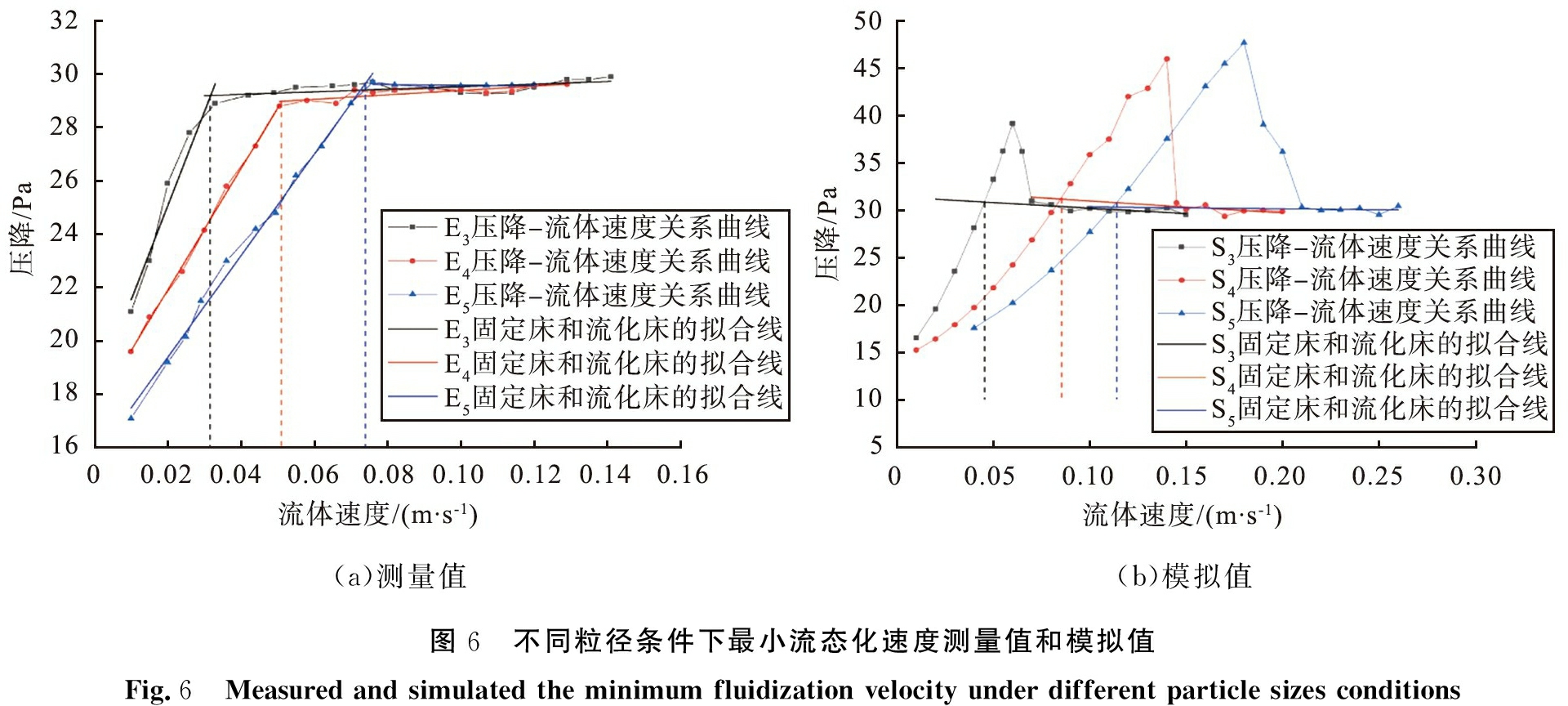
(a)测量值(b)模拟值图6 不同粒径条件下最小流态化速度测量值和模拟值Fig.6 Measured and simulated the minimum fluidization velocity under different particle sizes conditions
不同颗粒密度条件下的测量值与模拟值如图7所示。由图可以获得实验颗粒E1、 E2、 E4的最小流态化速度分别为0.021 6、 0.036 7、 0.055 5 m/s,模拟颗粒S1、 S2、 S4的最小流态化速度分别为0.031、 0.052、 0.085 m/s,可见,最小流态化速度随着颗粒的密度的增大而增大。
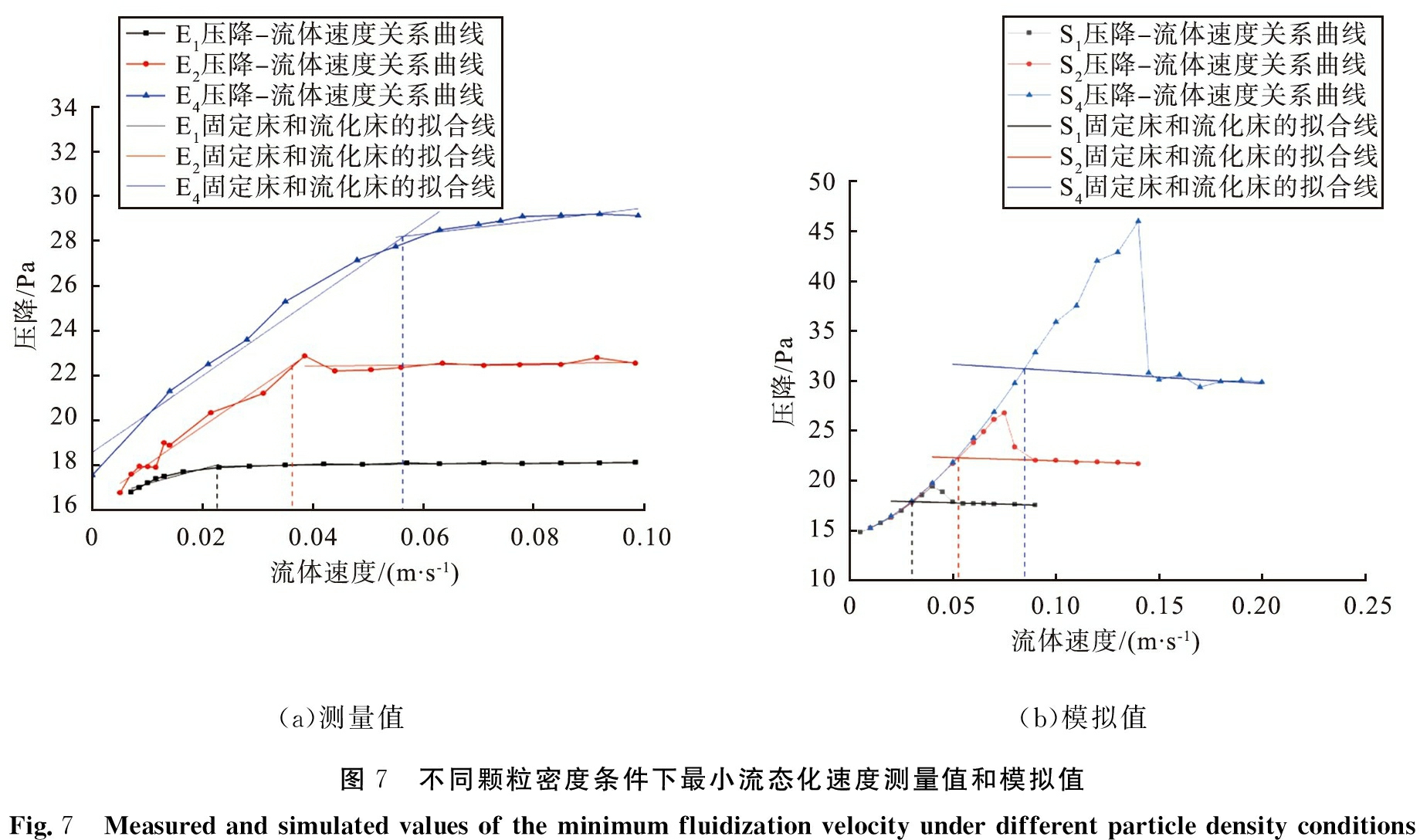
(a)测量值(b)模拟值图7 不同颗粒密度条件下最小流态化速度测量值和模拟值Fig.7 Measured and simulated values of the minimum fluidization velocity under different particle density conditions
由图6、 7还可以看到,在数值模拟结果中,压降-流体速度关系曲线在固定床和流化床的临界处先从逐渐升高转变为快速下降;而在实验测试结果中,关系曲线在临界处之后趋于水平。实验测试时使用的是降低流速法,即通过降低流化床中的初始流速使床层缓慢脱流来记录压降曲线;而在数值模拟中是通过重复改变流体速度值来记录压降曲线,曲线特征符合升高流速法,2种方法获得的曲线特征虽然不一致,但根据拟合线交点的横坐标取得的最小流态化速度却是相同的[9]。
4 结论
本文中建立了单管的液-固两相流化床实验系统,测量出5种颗粒的最小流化速度;应用CPFD方法对单管液-固流化床模型进行数值模拟,比较了5种颗粒的最小流态化速度的实验值与模拟值,并进行误差分析,验证了数值模拟方法的正确性。
1)颗粒的最小流化速度所在的位置为固定床和流化床的分界点,固定床的压降随流体速度的增大快速上升,而流化床的压降随流化速度变化的曲线较为平缓,固定床压降差拟合线和流化床压降差拟合线交点的横坐标数值即为颗粒的最小流态化速度。
2)5种实验颗粒的最小流态化速度实验值分别为0.021 6、 0.036 7、 0.029 3、 0.055 5、 0.084 5 m/s,2种公式验算值与实验值的最大相对误差均小于10%, 平均相对误差小于5%, 因此, 实验结果是可靠的。
3)5种模拟颗粒的最小流态化速度模拟修正值分别为0.024、 0.044、 0.041、 0.069、 0.062 m/s; 颗粒S1、 S2、 S4、 S5的模拟修正值与颗粒E1、 E2、 E4、 E5的实验值之间的最小流态化速度的误差分别为11.1%、 19.9%、 24.3%、 26.6%,均为正向偏差且在工程允许范围内,验证了CPFD数值模拟方法的可靠性。
4)最小流态化速度随固体颗粒的密度和粒径的增大而增大。
[1]JAE W C, SEOKHEE S, SOO Y P, et al. Temperature difference-bed fouling detection in the heat exchanger of gas-solid fluidized beds[J]. Chemical Engineering and Technology, 2022, 45(9): 1623-1630.
[2]CHOKPHOEMPHUN S, EIAMSA-ARD S, PROMVONGE P, et al. Heat transfer of a coil-tube heat exchanger in the freeboard zone of a rice husk fluidized-bed combustor[J]. International Communications in Heat and Mass Transfer, 2021, 127: 1-7.
[3]MA Z W, JANNA M. Analysis of a fluidized-bed particle/supercritical-CO2 heat exchanger in a concentrating solar power system[J]. Journal of Solar Energy Engineering, 2021, 143(3): 1-12.
[4]AIDA F, IBRAHIM D. Thermodynamic assessment of a hybrid particle-based concentrated solar power plant using fluidized bed heat exchanger[J]. Solar Energy, 2019, 179: 236-248.
[5]KOLLBACH J, DAHM W, RAUTENBACH R. Continuous cleaning of heat exchanger with recirculating fluidized bed[J]. Heat Transfer Engineering, 1987, 8(4): 26-32.
[6]RAUTENBACH R, ERDMANN C, KOLBACH J. The fluidized bed technique in the evaporation of wastewaters with severe fouling/scaling potential-latest developments, applications, limitations[J]. Desalination, 1991, 81(1/2/3): 285-298.
[7]PRONK P, CAI F, WITKAMP G J. Prevention of fouling and scaling in stationary and circulating liquid-solid fluidized bed heat exchangers: particle impact measurements and analysis[J]. International Journal of Heat and Mass Transfer, 2009, 52(15/16): 3857-3868.
[8]PRONK P, CAI F, WITKAMP G J. Mitigation of ice crystallization fouling in stationary and circulating liquid-solid fluidized bed heat exchangers[J]. International Journal of Heat and Mass Transfer, 2010, 53(1/2/3): 403-411.
[9]MOHAMMAD A, AHMED A I. Minimum fluidization velocity and defluidization behavior of binary-solid liquid-fluidized beds[J]. Powder Technology, 2002, 126(3): 241-254.
[10]MAWATARI Y, TATEMOTO Y, NODA K. Prediction of minimum fluidization velocity for vibrated fluidized bed[J]. Powder Technology, 2003, 131(1): 66-70.
[11]SHAO Y J, GU J R, ZHONG W Q, et al. Determination of minimum fluidization velocity in fluidized bed at elevated pressures and temperatures using CFD simulations[J]. Powder Technology, 2019, 350: 81-90.
[12]FU Z J, ZHU J, BARGHI S, et al. Minimum fluidization velocity growth due to bed inventory increase in an air dense medium fluidized bed[J]. Chemical Engineering Journal, 2019, 359: 1372-1378.
[13]FU Z J, ZHU J, BARGHI S, et al. Minimum fluidization velocity of binary mixtures of medium particles in the air dense medium fluidized bed[J]. Chemical Engineering Science, 2019, 207: 194-201.
[14]MCLAREN C P, METZGER J P, BOYCE C M,et al. Reduction in minimum fluidization velocity and minimum bubbling velocity in gas-solid fluidized beds due to vibration[J]. Powder Technology, 2021, 382: 566-572.
[15]KRITTIN K, CHAIWAT S, PORNPOTE P, et al. Effect of particle size distributions on minimum fluidization velocity with varying gas temperature[J]. International Journal of Environmental Science and Development,2020,11(11): 524-529.
[16]WU G P, CHEN W, HE Y. Investigation on gas-solid flow behavior in a multistage fluidized bed by using numerical simulation[J]. Powder Technology, 2020, 364: 251-263.
[17]MEHRAN E, SALMAN M, SHAHROKH S. The effect of particle properties on the heat transfer characteristics of a liquid-solid fluidized bed heat exchanger[J]. International Journal of Thermal Sciences, 2016, 102: 111-121.
[18]张仪, 李兵, 白玉龙, 等. 液固流态化动态过程中相间作用力的数值模拟及实验验证[J]. 化工学报, 2020, 71(11): 5129-5139.
[19]姜勇. 基于MP-PIC方法的流态化反应器快速模拟研究[D]. 北京: 中国科学院大学(中国科学院过程工程研究所), 2020.
[20]LIANG Y S, ZHANG Y, LI T, et al. A critical validation study on CPFD model in simulating gas-solid bubbling fluidized beds[J]. Powder Technology, 2014: 1-57.
[21]陈罕, 周昆颖, 张卫义. 液-固流态化系统固体颗粒特性研究(1): 颗粒的初始流态化速度vmf[J]. 北京化工大学学报(自然科学版), 2006(1): 94-97.
[22]侯宗宗, 王宾宾, 王要伟, 等. 金属丝网的流场数值模拟分析[J]. 过滤与分离, 2017, 27(2): 20-24.