粉体通常指的是粒径不超过1 000 μm的、由大量固体颗粒及颗粒间的空隙组成的集合体[1]。料仓用于各种粉体的贮存与流通，是粉体工艺过程中必不可少的设备[2]。料仓系统的工作稳定性和准确性关系到整个生产工作效率， 因此料仓设计备受化工、 能源、 冶金、 包装、 食品与制药等相关工业领域的关注[3]。由于粉体的特殊性质和流动过程的复杂性，粉体在料仓内的卸料过程一直是研究的热点与难点[4]。料仓中粉体的流动不同于流体流动，而是在重力及外力作用下的滚动、 滑动和沉降，粉体在料仓中需要保持连续、 平稳、 顺畅地卸料以保证后续工艺过程的安全及稳定运行，同时粉体在卸料时对料仓壁面造成的应力影响也是导致料仓损坏坍塌的主要原因，因此对粉体在料仓中卸料过程的研究具有较高的科研和工业应用意义，国内外已有诸多学者通过实验及数值模拟等方法解释了料仓中粉体流动的现象[5-6]。基于此，本文中首先总结了整体流料仓设计方法及料仓的材料与结构，然后重点阐述了料仓重力卸料中粉体的卸料流率、 压力分布以及改流体的影响，并介绍了一些其他卸料助流方式，为粉体料仓设计的应用及卸料特性的进一步研究提供参考。
1 粉体料仓设计
1.1 粉体料仓的流型
20世纪60年代，美国学者Jenike[7]首次对料仓内物料的流动特性进行研究，将料仓流型分为2种基本流型：整体流和中心流。整体流料仓(见图1a)的特点为卸料时所有粉体均向卸料口流动，仓内基本无静止的区域，符合“先进先出”的卸料顺序。中心流料仓(见图1b)在卸料时只有中心部分的粉体产生流动，在中心流动区域外存在着流动“死区”。因为流动区域呈漏斗状，又被称为漏斗流，卸料顺序为“先进后出”。整体流料仓相较于中心流料仓具有卸料速率稳定、 仓储时间一致、 仓内压力波动小等优点[8]，但由于料仓内壁长期受到粉体冲刷，导致料仓寿命较短，且针对某一粉体设计的整体流料仓并不适用于其他粉体，导致通用性和经济性较差。虽然整体流料仓是料仓设计中的首选流型，但也各有利弊，应综合考虑实际工况需要和经济性来选择合适的料仓流型[9]。
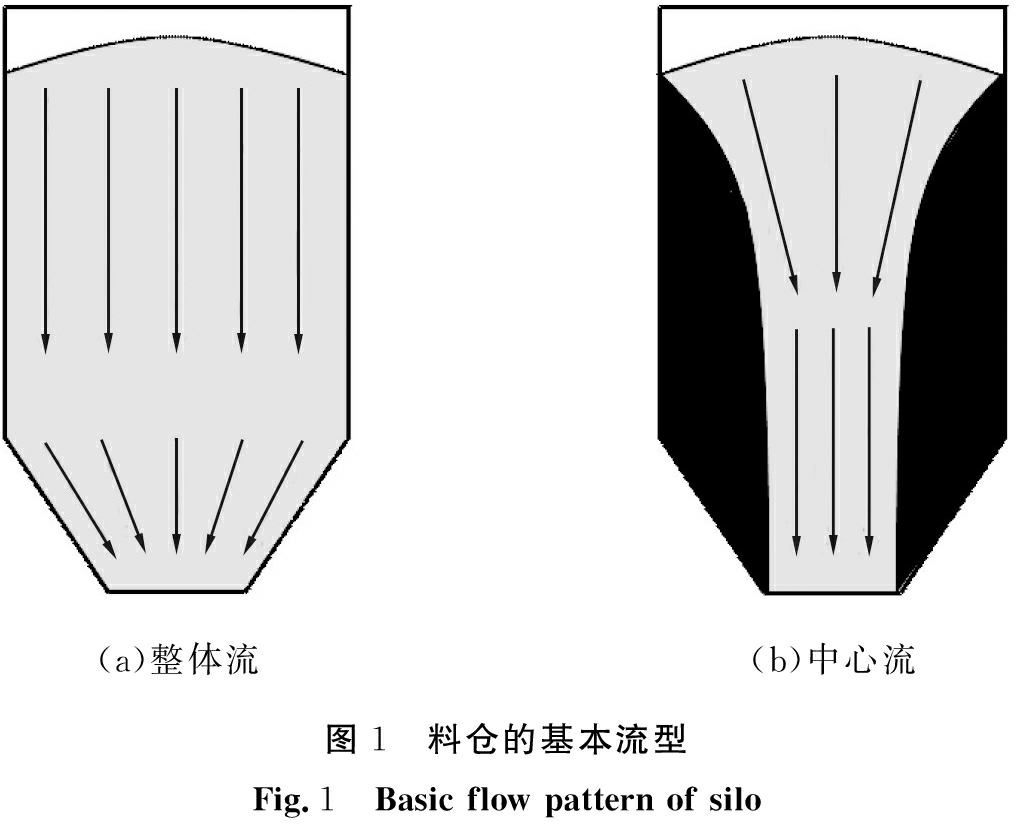
(a)整体流(b)中心流图1 料仓的基本流型Fig.1 Basic flow pattern of silo
1.2 基于Jenike理论的整体流料仓设计
Jenike以土壤力学理论为基础，创建了一套用于表征粉体流动性的参数和料仓设计理论，形成了Jenike理论[10]。粉体流动性表征参数主要包括：粉体的内摩擦角φ和有效内摩擦角δ、 粉体与壁面的内摩擦角φw、 无约束屈服强度fc、 最大主应力σ1以及粉体的密度γ。
剪切实验法通过定量测定粉体力学特性来评价粉体的流动性， Jenike剪切试验原理[10]如图2所示， 具体实验操作见文献[11]。 通过剪切试验， 共得到1个预剪切点P(σ,τ)、 4个剪切点Si(σi,τi), i=1～4。通过4个剪切点拟合得到一条位于预剪切点P上方的直线，定义为屈服轨迹YL，屈服轨迹与横轴的夹角为粉体的内摩擦角φ。通过原点作莫尔圆与屈服轨迹相切，圆心位于横轴，取右边与横轴相交点为无约束屈服强度fc。过预剪切点P作一个与屈服轨迹YL相切的半圆，称为主摩尔半圆，圆心位于横轴，取右边与横轴相交点位最大主应力σ1。再过原点作主莫尔圆的切线，即为有效屈服轨迹EYL，有效屈服轨迹与横轴的夹角为粉体的有效内摩擦角δ。粉体剪切试验屈服轨迹如图3所示。
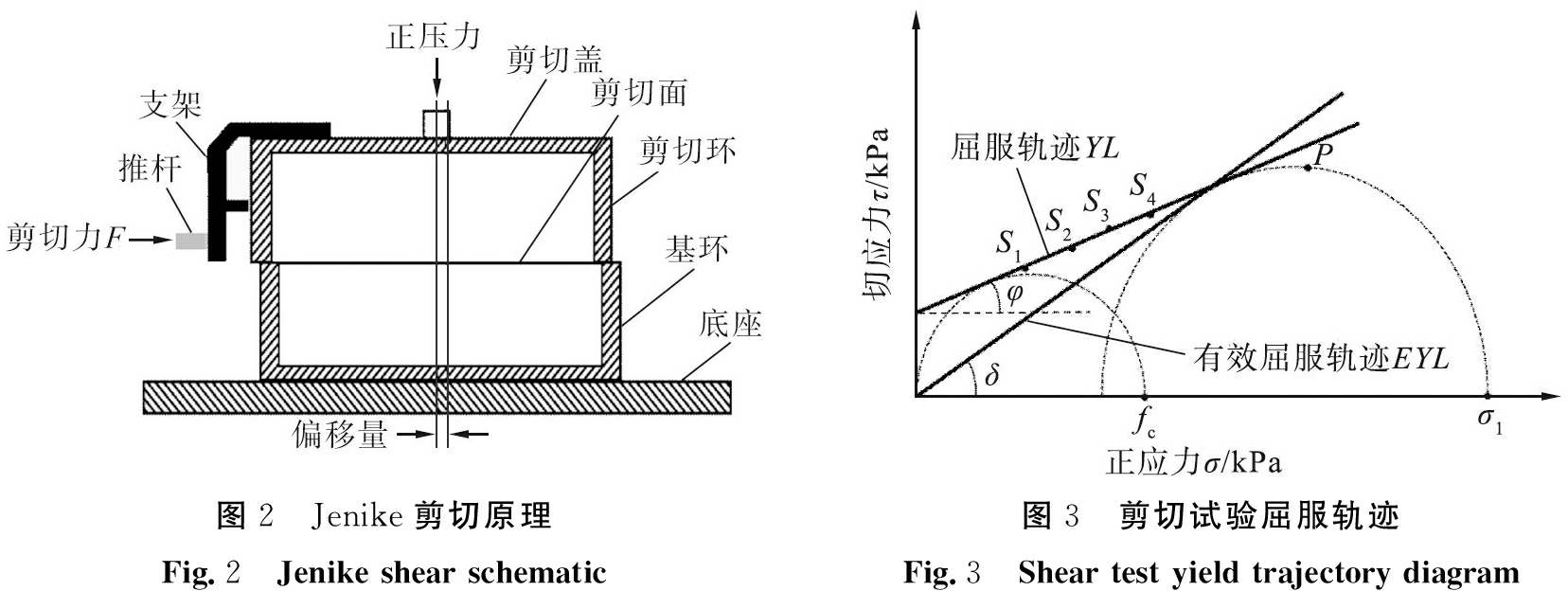
图2 Jenike剪切原理Fig.2 Jenike shear schematic图3 剪切试验屈服轨迹Fig.3 Shear test yield trajectory diagram
另取4个不同的预剪切正压力做剪切试验， 可以得到4组相对应的最大主应力和无约束屈服强度， 将4组数据进行拟合可以得到无约束屈服强度fc与最大主应力σ1的函数关系式， 定义为流动函数。
对于圆锥型料仓，若料斗的半顶角较小，粉料流动形态主要为整体流；若半顶角较大，粉料流动形态主要为中心流。保持整体流所需的最大半顶角α为
(1)
式中： α为料斗半顶角， (°)； φw为壁面摩擦角，(°)； δ为粉料的有效内摩擦角， (°)。
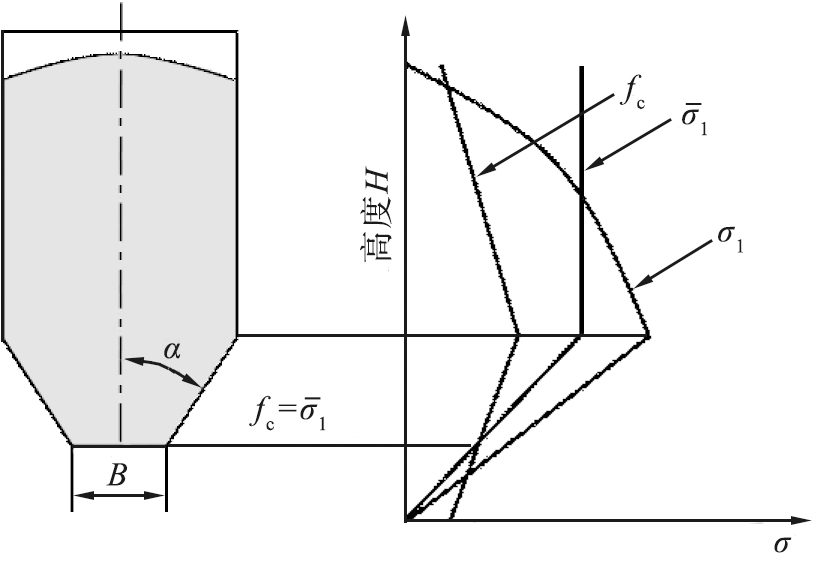
图4 整体流料仓应力变化图
Fig.4 Mass flow silo stress change diagram
在整体流料仓中，若卸料口尺寸过小，则会在卸料口处形成料拱，在料拱上存在着主应力
它与料仓的卸料口尺寸B成正比，见式(2)。整体流料仓内的应力随高度变化如图4所示。由图可知，无约束屈服强度fc与料拱主应力
相交于一个临界值，从而可以确定最小卸料口尺寸B。
(2)
式中：
为料拱主应力， Pa； B为卸料口尺寸， m； γ为粉体密度， kg/m3； H(θ)为料仓半顶角的函数， H(θ)=(1+m)+0.01×(0.5+m)α， m为料仓的形状系数，对于轴对称圆锥料斗，m取1，对于平面对称楔形，m取0。
根据Jenike理论的流动-不流动准则，形成整体流料仓的临界条件为
对于圆锥形料斗，料拱主应力与最大主应力σ1的关系可由式(3)表示。通过联立式(3)和流动函数即可求出该临界屈服强度,用
表示。将带入式(2)中即可得到整体流料仓最小卸料口尺寸，见式(4)。
(3)
(4)
Jenike剪切原理及料仓设计理论被广泛用于各类粉体料仓设计，已被证明为较为可靠的料仓设计方法。惠顺利等[12]以流动函数为指标，研究了不同粒径以及不同配合比的干混砂浆流动性能，通过计算得到一组干混砂浆的料仓结构参数。鲁磊明等[13]对3种超细含能粉料进行流动性测试，得到不同的料仓结构参数，通过对料仓的加料实验，发现在螺杆口的出料质量与料仓的加料质量误差较小，料仓内无明显“死区”停滞现象，实现了整体流料仓的稳定卸料。对于同类粉末，不同的粒径、 含水量[14]、 温度及贮藏时间[15]等因素均会对粉末的流动性能产生影响，因此在对同类粉末料仓设计中还应充分考虑粉体在实际工况条件下的性能。
1.3 料仓大小与形状
料仓的大小决定了料仓的容积，料仓的容积越大，储存的物料也就越多，工作周期长，但同时粉料堆积时间长、仓压大，易造成粉料成团和堵塞，形成漏斗流式卸料[16]。料仓的容积小则存储粉料少，仓压小，更容易以整体流方式卸料，但工作周期短，料位变化过快，会造成卸料不稳定。实际操作中要根据生产规模，科学合理的确定料仓大小。
料仓的中间仓部分，最常见的结构为圆筒形和矩形[16]。矩形料仓造价高，四角处易产生物料死角，影响卸料，一般仅会在设备空间有限的情况下使用，圆筒型料仓则相比矩形适用性更广。仓底料斗部分一般可分为锥形料斗、 曲线形料斗和平底形料斗。锥形料斗可细分为圆锥形料斗和楔形料斗；曲线形料斗[9]可细分为双曲线料斗和部分曲线料斗。一般大型料仓多采用平底形料斗，而中小型料仓多采用锥形和曲线型料斗。
对于圆筒料仓，以高径比H/D=1.5为界限被区分为深仓和浅仓[17]，其中H为料仓的高度，D为圆筒料仓的内径。即≥1.5为深仓；H/D<1.5为浅仓。粉体在深仓与浅仓中压力以及接触状态各不相同[18]。
1.4 料仓材料
根据Jenike理论，料仓能否处于整体流，不仅与粉体材料本身有关，还与料仓的材料有关。Borg[19]对77种常用粉体的壁面摩擦角进行了测定，壁面材料选用常用的4种料斗材料：不锈钢、 铝合金、 碳钢以及聚四氟乙烯。其中聚四氟乙烯和不锈钢的平均壁面摩擦角较小，铝合金的次之，碳钢的最大。聚四氟乙烯和不锈钢在料仓设计中更易形成整体流，但聚四氟乙烯的耐磨性较差，使用寿命较短，所以选用不锈钢作为料斗材料是较为理想的[20]。在实际设计中，需综合考虑料仓的整体质量、 安全、 经济等因素来合理选材。
2 粉体料仓卸料特性
2.1 重力卸料
2.1.1 卸料流率特性
20世纪50年代，Brown[21]在研究料仓重力卸料时，发现料仓卸料口附近存在一个环形的“卸料死区”，死区现象减小了颗粒的流通质量，Brown将它称之为“空环效应”。Beverloo[22]基于此效应，提出了一种预测平底料仓圆形孔口处卸料流率的模型。随后U
ac等[23]通过实验证明该模型同样适用于圆锥形料仓。Myers 等[24]又将该模型推广至具有平底和矩形孔口的矩形料仓。Oldal等[25]在Beverloo模型中引入了一个与粉体成拱有关的参数，基于新的方程不再需要通过经验常数来确定卸料流率。Brown[26]根据最小能量理论在Beverloo模型中添加了对锥形料仓半顶角的修正，建立了针对锥形料仓预测卸料流率认可度最高的Brown and Richards模型。上述模型均被证明为只适用于粒径较大的颗粒卸料预测，而对于粒径小于500 μm的细颗粒卸料，预测模型则会产生较大的误差。Crewdson等[27]认为对于粒径较小细颗粒，需要考虑颗粒间隙中气体对卸料过程的影响。当颗粒在重力作用下移动时，颗粒床层的孔隙率发生变化，这就导致颗粒与间隙中的气体产生相对速度，形成了逆压力梯度。通过对Beverloo模型中重力作用项进行修正，考虑了逆压力梯度对颗粒重力卸料的影响，得到Crewdson模型。由Crewdson模型可知，出料口的空环效应和逆压力梯度是影响卸料流率的2个重要因素。空环效应项(D0-kdp)与颗粒的粒径dp成反比，即颗粒粒径越大，则有效出口直径越小，空环效应的影响越显著；而逆压力梯度项与颗粒粒径的平方成负相关，即颗粒粒径越大，颗粒与空气间产生的相对速度越小，逆压力梯度的影响就越小。钟佳等[28]在Crewdson模型的基础上进一步对逆压力梯度项进行了修正，基于半球形自由下落拱架假定对颗粒的滑移速度进行了分析，得到的预测模型均适用于锥形和平底料仓。Zheng等[29]借助有限元法，忽略空环效应，考虑了颗粒的内摩擦角、膨胀角等参数的影响，建立了一个描述下料流率相对精确的模型。陆海峰等[30]基于细颗粒间的相互作用对Brown and Richards模型进行了修正，通过剪切测试得到颗粒床层的拉伸应力，引入Rumpf方程和无量纲Bond数对粉体床层的孔隙率进行修正，建立了预测粉体卸料流率模型。总结上述预测方程如表1所示。
表1 料仓质量流量预测方程
Tab.1 Silo mass flow prediction equation
研究者质量流率预测方程标注适用情况Beverloo等[22]Q=Cρbg(D0-kdp)5/2 C为与颗粒流动相关的经验常数,一般取0.55～0.65; ρb为颗粒的堆积密度; g为重力加速度; D0为卸料口直径; k为与颗粒形状有关的系数,球型颗粒取1.5; dp为颗粒的粒径 粒径大于500 μm的颗粒;锥形和平底料仓Myers等[24]Q=C ρbg(L0-kdp)(W0-kdp)3/2L0为孔口的长度; W0为孔口的宽度 粒径大于500 μm的颗粒;具有平底和矩形孔口的矩形料仓Oldal等[25]Q=π2δg6 ρb(D0-dp)5/2δ为材料的拱形系数中心流的锥形料仓Brown[26]Q=C ρbg(D0-kdp)5/21-cos3/2αsin5/2α α为料斗的半顶角 粒径大于100 μm的颗粒;锥形料仓Crewdson等[27]Q=C ρbg+1ρb×dpdr(D0-kdp)5/2 ,其中-dpdr=Kη(1-ε)2usd2pε2 dp/dr为压力梯度项; p为压力; r为颗粒流动的径向半径; K为CARMAN-KOZENY常数; η为空气动力黏度; us为气固滑移速度 粒径小于500 μm的细颗粒;锥形和平底料仓钟佳等[28]Q=C1 ρp(1-ε)g-C2(1-ε)gD0d2p ρpε21/2(D0-kdp)5/2 C1、 C2为非线性拟合参数; ρp为颗粒的真实密度; ε为颗粒床层的孔隙率 粒径小于500 μm的细颗粒;锥形和平底料仓Zheng等[29]Q=0.581-cosmαsin5/2α (1.08-0.016 4ψ)ρbgD5/20 ,其中m=4.25e(-0.1φ)+0.44e(-8.5μw+1.31) φ为颗粒的内摩擦角;ψ为颗粒的膨胀角; μw为壁面摩擦系数锥形料仓陆海峰等[30]Q=C ρpHg(D0-kdp)5/21-cos3/2αsin5/2α ,其中H=1-ε0-(1-ε0)e(-mB-n0) ε0为颗粒自然堆积时的孔隙率; m、 n为关于孔隙率的拟合参数; B0为无量纲Bond数,表示为颗粒黏附力与体积力的比值 粒径小于100 μm的细颗粒;锥形料仓
2.1.2 仓内压力特性
料仓内的壁面压力是仓内粉体所受应力的宏观表现，也是料仓设计与防护的重要依据。早在1895年，Janseen[31]就根据静态平衡原理，得到了粉体处于静置时颗粒对料仓壁面的压力变化规律，推导了深筒仓的静态压力公式。Janseen模型在工程界被广泛使用，也是目前大多数分析模型的基础[32]。通常对于仓内压力可根据工作状态的不同分为静态压力和动态压力[33]。
静态压力是指料仓在储料期间，由静止的物料对仓体产生的作用力，主要包括料仓壁上的侧压力以及仓底的竖向压力。对于静置的无限深度的料仓，Janseen模型提供了水平应力σh及垂直应力σv的分布估计：
(5)
式中: ρb为粉体堆积密度， kg/m3； g为重力加速度， 9.8 m/s2； A为筒仓直径, m； μw为壁面摩擦系数； h为料位深度， m； k为侧压力系数。
Rankine公式根据土压力理论来预测浅筒仓的静态侧压力[34]：
(6)
动态压力是指料仓在进料和卸料过程中， 动态物料对仓体产生的作用力。 物料在流动过程中壁面所受作用力在空间与时间上分布与静态相比有较大差异[35]， 这种差异在料斗段尤为显著， 存在应力场的不连续性。 料仓事故多发生在动态卸料过程中， 因此料仓的动态压力问题成为工程中重点的研究内容。 Walkers[36]和Walters[37]通过在料斗部分应用Janseen的元素切片法建立了一个描述动态压力的模型：
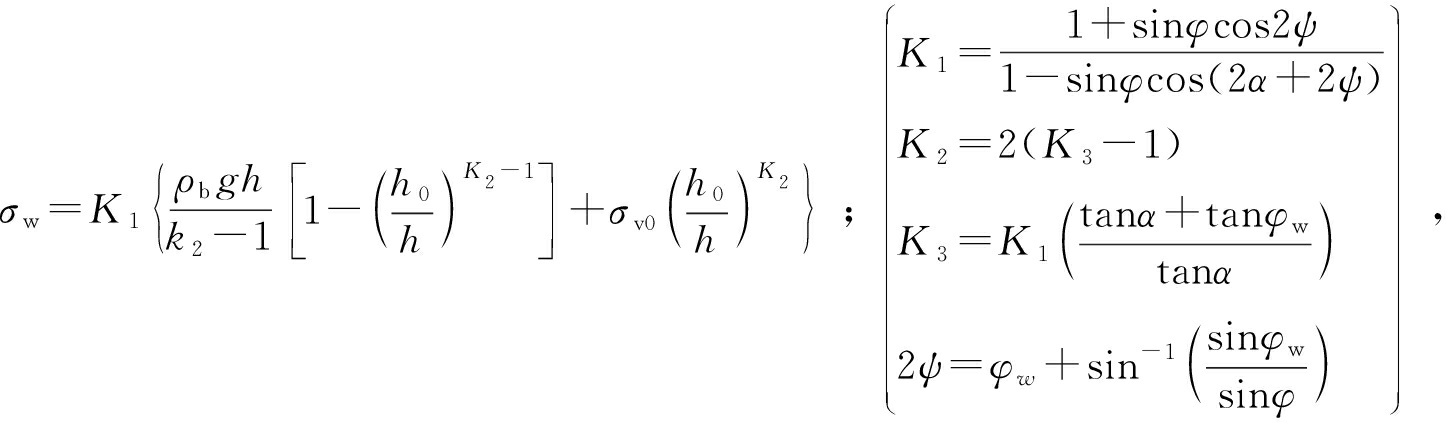
(7)
式中： K1、 K2、 K3均为系数； σv0为料斗顶部的垂直应力， Pa； h0为筒仓的装料高度， m； ψ为斗段斜面与水平面的夹角, (°)。
Jenike[38-39]在Janssen理论的基础上，通过引入动态侧压力系数kh来反映料斗动态应力状态和静态应力状态:
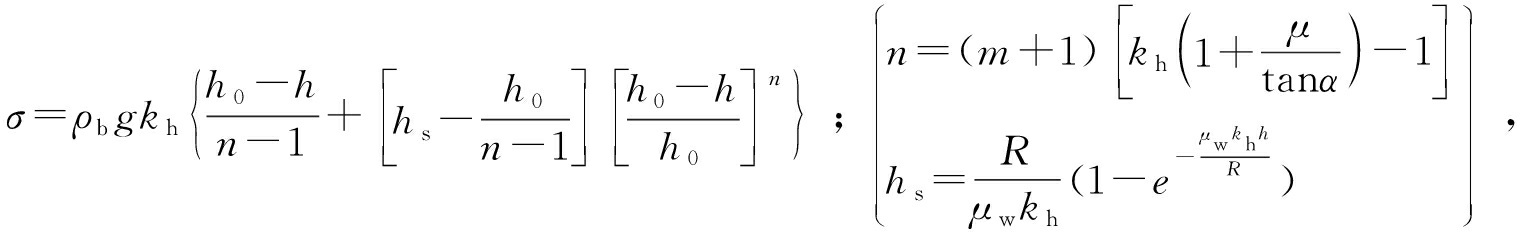
(8)
式中： n、 hs为系数； μ为粉体的内摩擦系数； m为对称系数， 物料平面流动时， m=0， 轴对称流动时， m=1。当物料处于静止堆积状态时，侧压力系数kh为：
(9)
当物料处于卸料状态时，侧压力系数kh为：
;
。
(10)
综上所述，诸多学者从理论分析及实验中对料仓内压力特性做了不同程度的研究，并得到了相应的预测模型，但料仓内粉体的运动和应力影响因素很多，在不同情况下粉体的流动特性和应力分布之间的关系仍没有被完全掌握。
陈阳阳等[40]分析了粉体在料仓中静态水平应力与垂直应力的分布特性。结果表明，随着距离出口高度的增加，壁面水平应力逐渐增加，内部水平应力基本不变；对于垂直应力，从料仓中心至仓壁，垂直应力呈逐渐减小的趋势。在靠近壁面处，侧压力系数(水平压应力与垂直压应力之比)随着距出口高度的增加出现先增大后减小的趋势，在筒锥结合处大于1。原方等[41]对6个不同高径比的料仓卸料进行了模拟研究，发现相同高度下，随着直径增大，料仓的最大动压力整体呈上升趋势；无论是深仓或者浅仓，仓侧壁附近的力链会随着料仓深度的增加而变得密集。直径越大的料仓，颗粒在卸料时结拱所需的时间也越长，原因是颗粒还未调整结拱的最佳位置时已经下沉，降低了结拱的可能性，这也是造成深浅仓卸料压力不同的重要原因。Xu等[42]对于高径比为1.0～1.5的圆锥浅仓，考虑了筒仓壁和储存材料的变形，提出一种改进的筒仓壁侧压力的计算方法。实验与数值模拟结果表明，新的计算方法对比Janssen公式和Rankine公式预测更为精准。
2.1.3 仓内改流体的影响
改流体作为一种最简单有效的料仓结构调整方法，常被用来改善料仓内粉体的流动[43]。1966年，Johanson[44-45]首次提出引入改流体来改善粉体下料。通过实验研究发现，改流体能够实现粉体流动模式的改变，可以有效防止料仓内出现穿孔、 结拱等现象。针对在流动过程中仓内可能出现的不安全现象,可以根据不同需要设计、 安装不同类型的改流体，常用的改流体形式主要有垂直挡板、 倾斜挡板、 空心圆柱、 Binsert、 倒锥体、 双锥体等，结构如图5所示。
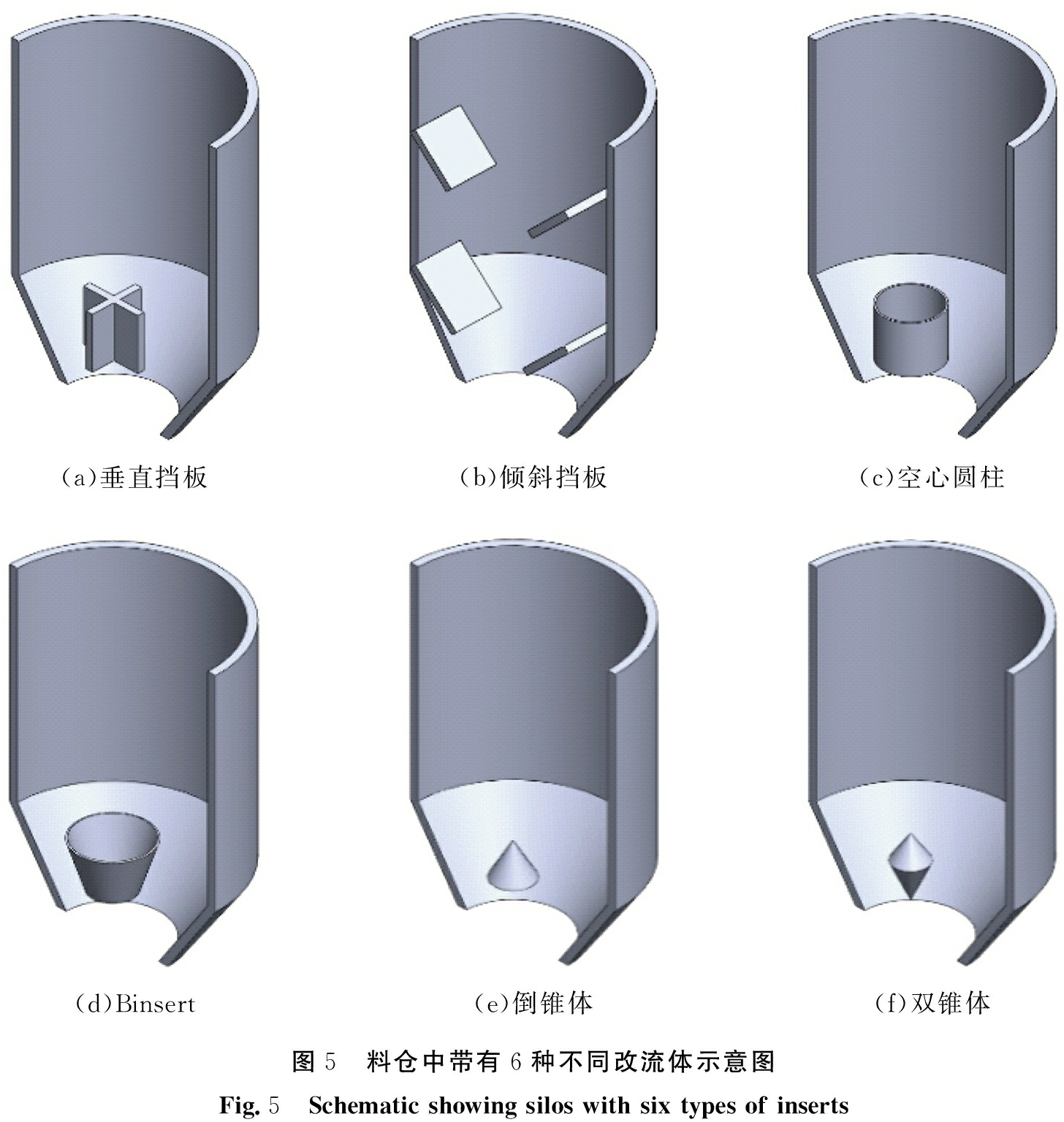
(a)垂直挡板(b)倾斜挡板(c)空心圆柱(d)Binsert(e)倒锥体(f)双锥体图5 料仓中带有6种不同改流体示意图Fig.5 Schematic showing silos with six types of inserts
改流体对提高工艺过程以及改善仓内物料流动形态有着较高的应用价值和广泛的应用前景[46]。依据作用可主要分为以下3类[47]：改善粉体在料仓的流动环境及流动区域；增大粉体的流动速率以及降低卸料时的过载压力。
1)改善粉体在料仓内的流动环境及流动区域。谭援强等[48]对锥形改流体下部孔径的影响进行了离散元模拟研究，结果表明，减小锥形改流体下部孔径可以使料仓的整体流系数增大，物料流态跟容易从中心流转变为整体流。Ding等[49-50]研究了双锥形改流体的对料仓流动的影响。结果表明，双锥改流体锥角较小的一端朝向出口对料仓中心流的改善最佳，粉体的流动区域最大，流型分布更均匀；改流体的不对称布置则会导致流型的不对称性。
2)改变粉体的流动速率。Sun等[51]对无改流体、封闭式改流体以及开放式改流体对锥形料仓卸料流率进行了研究。相比无改流体，封闭式及开放式改流体均能提升粉体流速，且封闭式改流体的提升效果最好。在不同的粉体中，流动性较弱的粉体会表现出较大的流率增量。Chung等[52]分析了5种不同的改流体对Fe2O3颗粒在料仓中的卸料速率的影响。结果显示，与无改流体料仓相比带有锥形、 圆盘、 空心筒仓以及Binsert改流体的料仓，颗粒的质量流率下降，而空心圆柱改流体料仓的质量流率显著增加。此外带有锥形、圆盘及Binsert改流体中料仓的颗粒流显示出更均匀的垂直和径向速度分布。
3)降低卸料时的过载压力。翟志轩等[53]通过DEM-FEM耦合的方法对有无改流体的料仓进行了对比分析。得出改流体可以缓冲颗粒间的碰撞，使内部静态、动态压力均小于无改流体的料仓；耦合分析表明改流体降低了卸料频率的波动，减缓了物料对料仓内壁的冲刷。Wójcik等[54]在全尺寸料仓中锥形改流体对料仓卸料时所受压力进行了实验。结果表明，料仓内的应力分布取决于改流体的位置和形状，相比无改流体的料仓，有改流体的料仓料斗上部的壁面法向应力增加，而由于改流体承担了一部分压力，料斗下部的壁面法向应力大大降低。
2.2 振动卸料
振动卸料是一种较为普遍的料仓助流方式， 常见的振动设备有仓壁振动器、 空气锤、 振动料斗[55]。 仓壁振动器安置在料仓易结拱处对应的仓壁外侧， 通过电磁、 气动或振动电机产生振动， 经过仓壁或振动壁传递给粉料， 破坏料拱使物料松动卸料。 安徽攀登重工股份有限公司[56]设计的对称式仓壁振动器， 振动器支座与料仓外壁通过销轴连接， 同时设置橡胶密封板， 便于安装的同时也降低了振动对料仓的损伤。 李振等[57]设计的新型仓壁振动装置， 将振动电机与振动器通过传动轴连接， 工作时振动电机将动力通过传动轴传输给振动器， 电机本身并不参与振动， 有效解决了电机长时间振动容易烧毁的问题。
空气锤通过压缩空气对料仓底部实施间歇性锤击循环，在撞击瞬间机械能传递到料仓外壁来实现破拱助流。谢屹[58]针对黏性潮湿物料粘接在下料仓内壁，使用气动空气锤对锥形料斗进行垂直锤击，相比使用原有振动电机，振动频率更大，下料更加流畅。
振动料斗主要适用于非黏性的干松散物料，安装时需与贮存料仓及支撑结构相隔开。上海博隆装备技术股份有限公司[59]设计了一种新型旋转式振动料斗，料仓与底部料斗通过上下法兰盘橡胶密封连接，底部激励电机通过旋转座与下法兰盘转动连接，工作时可根据不同物料的卸料情况来改变激振方向使物料均匀流出。
除了以上几种振动设备，一些新型的振动助流器逐渐得到开发与应用。Zhang等[60]设计了一种新型悬垂式助流振动器，料仓顶部有延伸至角落的振动棒，振动棒内部设有振动子，在电机驱动下，振动子使振动棒产生高频微幅机械振动实现助流。优点在于维修方便，且当一个振动棒出现故障时，其余的振动棒仍可以正常工作，保证了振动助流的连续性。对于所有的振动设备，在振动部位均需加强料仓连接处的强度以防振裂，同时也应避免发生共振情况。在实际应用中应根据不同的物料特性来选择合适的振动助流方式，以及考虑是否需要连续振动或是间歇振动等。
振动卸料的运动过程复杂，且影响因素较多，目前诸多国内外学者通过实验及计算机模拟等方法对不同情况下振动卸料过程进行了研究。Kollmann等[61]通过谐波振动对石灰石和二氧化钛粉末的流动特性进行了研究。发现应用振动导致粉末的剪切强度显著降低，使无约束屈服强度及与壁面摩擦角降低，但内摩擦角几乎不变，因此在对有应用振动的料仓设计中，满足整体质量流的要求可以降低最小出料口直径，提高料斗的最大半顶角。武永桥等[62]使用EDEM软件对粉末振动下料过程进行了分析。仿真显示随着振动频率的增大，粉末所获得的动能增大，下料速度也增大，但同时下料的稳定性会变差。Hunt等[63]研究了水平振动对圆锥形料仓卸料速率的影响，结果表明，对料仓整体的水平振动可以提高卸料速率，减少料斗中的停滞区域。在一定的振动范围内可以有效解决漏斗流料仓的“先进后出”的问题。Kumar等[64]基于上述研究，进行一步使用离散元方法对圆锥形料仓多组分混合物料的流动行为进行了研究，发现随着振动强度的增加，质量流率也增加，但超过一定幅值后，物料的偏析会占主导作用；在相同的振动条件下，不同的混合物料也会产生不同的偏析行为。Jafari等[65]研究了局部振动对楔形料仓卸料的影响。观察到在料仓质量流无堵塞卸料时，振动不会对料仓卸料产生显著影响。在料仓产生堵塞时，振动器在料斗靠近出口最低位置其助流效果最好，随着振动器位置上升，总卸料时间和卸料断流都会增加。 通过正交实验对比振动器位置、 振动频率以及无量纲振动强度对卸料的影响， 得出振动器位置是影响振动料仓卸料的最主要因素。 Pascot等[66]探讨了垂直振动对二维平底料仓中颗粒卸料及出口速度的影响。 通过实验和DEM模拟表明， 振动条件下颗粒的流动表现出2种不同的状态， 通过引入弗劳德数和相对频率可以界定二者的经验公式。 在第1种情况下， 振动会导致死区流动从而加大颗粒碰撞的能量耗散， 流速降低； 在第2种情况下， 随着振动强度的增加， 振动能量引起的扰动会超过颗粒的重力驱动， 使得流速增加。 Du等[67]研究了垂直振动对倾斜料仓卸料的影响。 实验表明无论是否振动， 料位深度对卸料速率几乎没有影响。 振动对卸料速率的影响主要受振动参数的影响， 在低振幅下， 卸料速率随振频的增加而增加； 在高振幅下， 当振频高于某个值时， 继续增加频率则会抑制卸料。
2.3 气力卸料
气力卸料是一种实用效果较好，应用较为广泛的料仓助流方式。基本特点是利用空气喷吹原理[55]，将压缩空气通过吹气管或者流化板吹入到易结拱部位, 减弱物料间的内摩擦力及与料仓内壁间的壁面摩擦力，使粉体流态化，这种方法对水含量很低的粉体尤为适用。赵敏[68]设计了一种气力清仓装置料斗，特点是输气管在料仓外壁成螺旋状设置，并在靠近料仓一侧均匀分布了高压喷头。工作时，高压气流在料仓内形成旋风式气流使粉料脱离料仓内壁而均匀下落，同时气流产生的剪力也会破坏料拱，达到了对黏性粉体的破黏、 破拱效果。吴佑俭等[69]开发了一种粉矿仓气力清堵助流系统，在垂直方向上设置为6层进行分段式喷吹，随布置高度升高，喷嘴数量也相应递增，并且上下2层的喷嘴相互错位以发挥最佳喷吹效果，系统在实际运行后有效降低了料仓内的滞留料，提高了生产效率。
Lu等[70]对不同气流速率下碳钢料仓的煤粉卸料进行了研究。将不同速率气流对煤粉卸料的影响划分为4个不同的流动区域。实验证明了气流可以促进料仓出口处的良好压力梯度，使粉末流态化。同时气流也提供能量减少粉末的团聚现象以产生平滑的粉体流。Zhu等[71]设计了一种方波脉冲气流料斗，研究了脉冲气流对黏性和非黏性粉末的卸料影响。结果表明，脉冲气流对非黏性粉末卸料有恶化的影响；而对黏性粉末，脉冲气流可以提高卸料的速率和稳定性，同时所需的气流量相比连续气流降低了一半。基于脉冲气流料斗，Zhu等[72]又研究了强黏性纳米粉末的料仓卸料特性，发现在卸料过程中料仓上部会出现黏性拱，而下部会出现自由落体拱，单脉冲气流可以破坏下部的自由落体拱，但无法继续向上破坏黏性拱，因此提出了一种双脉冲气流的方法，通过实验确定了最佳双脉冲的位置及气流速率，消除了多级拱的影响，对比单脉冲气流，大大提高了卸料效率。
2.4 机械搅动卸料
仓内机械搅动一般采用桨叶式或螺旋式搅动器[53]，通过在传动轴上安装桨叶或者螺旋进行搅拌松动物料和破坏结拱，促使料仓稳定卸料，结构如图6所示。这种方法相比气力卸料和振动卸料，无需压缩空气，也不会对整体结构产生振动，但设备内部结构相对复杂，安装和维护成本较高，且容易对料仓内壁造成损伤，多适用于小型料仓。
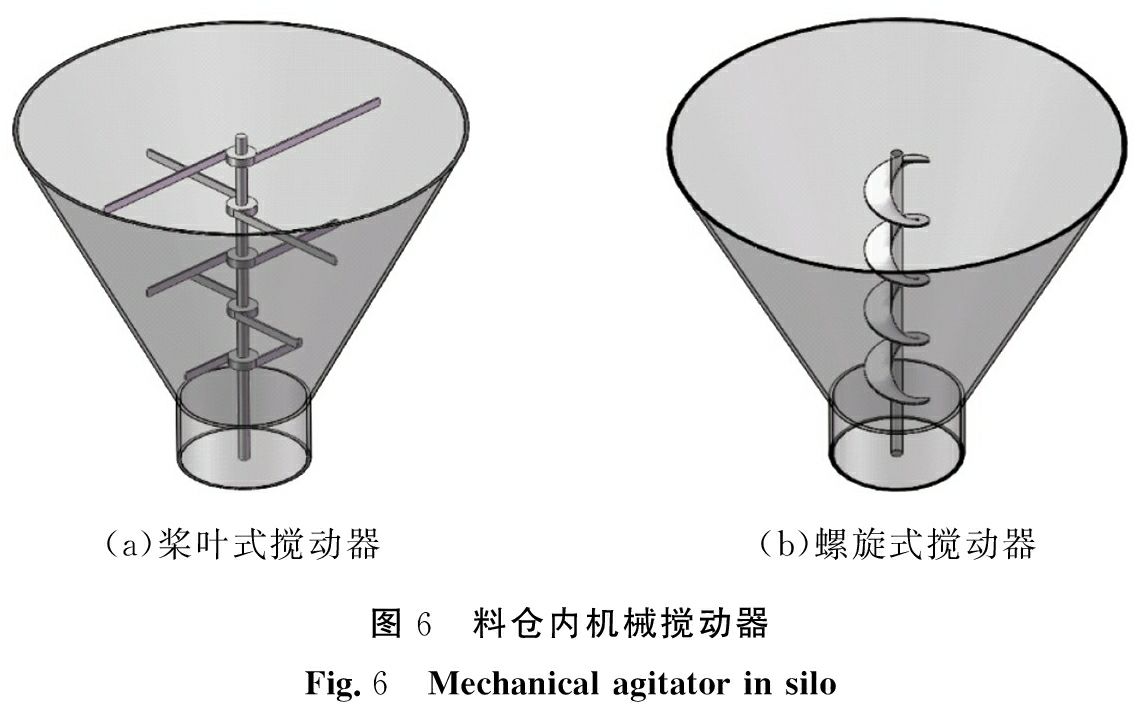
(a)桨叶式搅动器(b)螺旋式搅动器图6 料仓内机械搅动器Fig.6 Mechanical agitator in silo
3 结论
料仓作为储运粉体的重要设备，以其简单的结构备受工业界的青睐。粉体从料仓流出的卸料特性直接影响到后续工艺过程的安全及稳定，因此对料仓卸料过程的研究具有很高的科研价值与应用意义。
1)料仓设计中主要考虑料仓的流型、大小形状以及材料，其中料仓的流型是首要考虑的因素。整体流因其可实现粉体的稳定卸料而作为设计者所首选的流型，在基于Jenike理论可对不同粉体的流动性能进行试验，从而对料仓结构参数进行设计计算。
2)重力卸料是最常见的料仓卸料方式，同时也是其它卸料方式的理论和实验的基础。粉体颗粒在料仓的卸料流率以及压力分布已有大量的学者进行了研究，不同粉末在不同料仓中会产生不同的流动形式，而随着实验和数值模拟技术的推进将更好地解释粉体颗粒在重力作用下的运动状态，预测方程也会更加精确。
3)仓内改流体作为一种常用的改善粉体流动的结构，具有广泛的应用前景，其主要作用为：改善粉体在料仓的流动环境及流动区域；增大粉体的流动速率以及降低卸料时的过载压力。
4)振动卸料、 气力卸料、 机械搅动卸料是常见的3种料仓外力助流装置。每种助流方式所基于的原理不同，对所选用的粉体也有所限制，应综合考虑工况要求、 经济性、 安全性等因素来选择合适的助流方式。同时料仓内因外力的加入，粉体颗粒的运动将会变得更为复杂，对于复杂料仓颗粒运动的研究将会成为未来工程界主要的热点与难点。
[1]邹佳兴. 基于压差推动的粉体料仓下料过程强化研究[D]. 上海： 华东理工大学, 2020.
[2]李忠毅, 李勇, 姜开忠. 粉体料仓存在的问题及解决方法[J]. 起重运输机械, 2022(6): 29-35.
[3]惠顺利, 钱静, 李东阳. 一种粉粒料包装机料仓的设计研究[J]. 包装与食品机械, 2015, 33(2): 35-38.
[4]陆海峰, 阮琥, 曹嘉琨, 等. 细粉下料过程的气固流体动力学作用分析[J]. 化工学报, 2021, 72(11): 5533-5542.
[5]RAM
REZ-G
MEZ
. The discrete element method in silo/bin research：recent advances and future trends[J]. Particulate Science and Technology, 2020, 38(2): 210-227.
[6]孙珊珊, 袁竹林. 料仓内稠密粉体卸料流动特性研究[J]. 热能动力工程, 2019, 34(6): 91.
[7]GARG V, MALLICK S S, GARCA-TRINANES P, et al. An investigation into the flowability of fine powders used in pharmaceutical industries[J]. Powder Technology, 2018, 336: 375-382.
[8]陆海峰. 煤粉在通气料仓中的下料及其影响因素研究[D]. 上海: 华东理工大学, 2012.
[9]陈长冰. 基于整体流型的粉体料仓设计分析[J]. 化工设备与管道, 2006(3): 34-38.
[10] CARSON J W, WILMS H. Development of an international standard for shear testing[J]. Powder technology, 2006, 167(1): 1-9.
[11]廖荣福, 邱生祥, 潘仁湖. Jenike型剪切测试仪在颗粒物料流动性测试中的应用[J]. 硫磷设计与粉体工程, 2011(6): 23-29.
[12]惠顺利, 钱静, 李东阳. 基于Jenike理论的粉粒料流动性测试及料仓设计[J]. 包装工程, 2014, 35(23): 37-42.
[13]鲁磊明, 邓国栋, 汪庆华, 等. 超细含能固体粉料流动性测试及加料仓设计[J]. 中国粉体技术, 2016, 22(6): 26-31.
[14]OGINNI O, FASINA O. Theoretical estimation of silo design parameters for fractionated loblolly pine grinds-moisture content and particle size effects[J]. Industrial Crops and Products, 2018, 123: 379-385.
[15]SALEHI H, BERRY R, FARNISH R, et al. Temperature and time consolidation effect on the bulk flow properties and arching tendency of a detergent powder[J]. Chemical Engineering & Technology, 2020, 43(1): 150-156.
[16]孙秉礼. 粉体料仓的卸料问题[J]. 水泥, 2014(3): 53-56.
[17]原方, 王辉, 胡玉霞, 等. 筒仓分类方法评价[J]. 东南大学学报: 英文版, 2009, 25(3): 381-384.
[18]王学文, QIN Y, 李娟莉, 等. 散料在锥仓中的静压接触状态与影响因素[J]. 农业工程学报, 2015, 31(16): 65-70.
[19]BORG L T. Erfahrungen aus scherversuchen mit schüttgütern der chemie[J]. Chemie Ingenieur Technik, 1981, 53(8): 662-663.
[20]李志义, 王淑兰, 丁信伟. 粉体物料和料斗材料对料仓流型的影响[J]. 化学工业与工程技术, 2000(1): 12-14，1.
[21]BROWN R L. Exploratory study of the flow of granules through apertures[J]. Transactions of the Insitution of Chemical Engineers, 1959, 37: 108-119.
[22]BEVERLOO W A, LENIGER H A, VAN DE VELDE J. The flow of granular solids through orifices[J]. Chemical engineering science, 1961, 15(3/4): 260-269.
[23]U
AC R O, VIDALES A M, BENEGAS O A, et al. Experimental study of discharge rate fluctuations in a silo with different hopper geometries[J]. Powder technology, 2012, 225: 214-220.
[24]MYERS M E, SELLERS M. Chemical engineering tripos, part 2, research project report[J]. University of Cambridge, Cambridge, 1978.
[25]OLDAL I, KEPPLER I, CSIZMADIA B, et al. Outflow properties of silos: the effect of arching[J]. Advanced Powder Technology, 2012, 23(3): 290-297.
[26]BROWN R L. Minimum energy theorem for flow of dry granules through apertures[J]. Nature, 1961, 191: 458-461.
[27]CREWDSON B J, ORMOND A L, NEDDERMAN R M. Air-impeded discharge of fine particles from a hopper[J]. Powder Technology, 1977, 16(2): 197-207.
[28]钟佳, 吕慧, 曹贵平, 等. 细颗粒在锥形和平底料仓中的重力卸料特性[J]. 化工进展, 2017, 36(11): 3940-3946.
[29]ZHENG Q J, XIA B S, PAN R H, et al. Prediction of mass discharge rate in conical hoppers using elastoplastic model[J]. Powder technology, 2017, 307: 63-72.
[30]陆海峰, 曹嘉琨, 郭晓镭, 等. 基于颗粒间相互作用的细颗粒粉体料仓下料过程分析[J]. 化工学报, 2021, 72(8): 4047-4054.
[31]MORGENEYER M, RAMíREZ-GMEZ A, POLETTO M, et al. Particle technology as a uniform discipline? Towards a holistic approach to particles, their creation, characterisation, handling and processing[J]. Chemical Engineering Research and Design, 2019, 146: 162-165.
[32]SALEH K, GOLSHAN S, ZARGHAMI R. A review on gravity flow of free-flowing granular solids in silos-basics and practical aspects[J]. Chemical Engineering Science, 2018, 192: 1011-1035.
[33]赵光明, 石鑫, 丁圣潇, 等. 筒仓散体物料压力研究现状与新进展[J]. 河南建材, 2021(4): 38-41.
[34]XU Z, LIANG P, CHENG Y, et al. Reduction mechanism of the normal stress exerted on silo wall with chutes during eccentric discharge[J]. Powder Technology, 2022, 407: 117659.
[35]郭秀琦. 料仓粉体出料过程中应力分布及流动特性研究[D]. 南京： 东南大学, 2019.
[36]WALKER D M. An approximate theory for pressures and arching in hoppers[J]. Chemical Engineering Science, 1966, 21(11): 975-997.
[37]WALTERS J K. A theoretical analysis of stresses in silos with vertical walls[J]. Chemical Engineering Science, 1973, 28(1): 13-21.
[38]JENIKE A W. Bin loads-part 2: Concepts ASME[J]. Journal of Engineering for Industry, 1973, 95(1): 1-5.
[39]JENIKE A W. A theory of flow of particulate solids in converging and diverging channels based on a conical yield function[J]. Powder technology, 1987, 50(3): 229-236.
[40]陈阳阳, 郭秀琦, 梁财, 等. 料仓内粉体静态应力分布特性[J]. 化工进展, 2019, 38(4): 1681-1687.
[41]原方, 刘海林, 程远浩, 等. 深浅仓卸料压力离散元数值模拟研究[J]. 河南工业大学学报 (自然科学版), 2020, 41(1): 117-123.
[42]XU Z, LIANG P. Modified lateral pressure formula of shallow and circular silo considering the elasticities of silo wall and storage materials[J]. Scientific Reports, 2022, 12(1): 1-10.
[43]孙栋. 料仓改流体对粉体下料影响的研究[D]. 上海： 华东理工大学, 2020.
[44]JOHANSON J R. The placement of inserts to correct flow in bins[J]. Powder Technology, 1968, 1(6): 328-333.
[45]JOHANSON J R. The use of flow-corrective inserts in bins[J]. Journal of Manufacturing Science and Engineering, 1966, 88(2): 224-230.
[46]肖国先, 徐德龙, 陈延信, 等. 料仓中仓型改流体作用的数值模拟[J]. 计算机与应用化学, 2005(7): 12-16.
[47]陈延信, 徐德龙, 肖国先. 仓内粉体流动现象与改流体的作用效果分析[J]. 中国粉体技术, 2000(增1): 174-176.
[48]谭援强, 肖湘武, 郑军辉, 等. 锥形改流体下部孔径对筒仓卸料流态的影响[J]. 农业工程学报, 2016, 32(19): 82-87.
[49]DING S, DYRØY A, KARLSEN M, et al. Experimental investigation of load exerted on a double-cone insert and effect of the insert on pressure along walls of a large-scale axisymmetrical silo[J]. Particulate Science and Technology, 2011, 29(2): 127-138.
[50]DING S, LI H, OOI J Y, et al. Prediction of flow patterns during silo discharges using a finite element approach and its preliminary experimental verification[J]. Particuology, 2015, 18: 42-49.
[51]SUN D, LU H, CAO J, et al. Flow mechanisms and solid flow rate prediction of powders discharged from hoppers with an insert[J]. Powder Technology, 2020, 367: 277-284.
[52]CHUNG Y C, KUO T C, HSIAU S S. Effect of various inserts on flow behavior of Fe2O3 beads in a three-dimensional silo subjected to cyclic discharge: part I: exploration of transport properties[J]. Powder Technology, 2022, 400: 117220.
[53]翟志轩, 熊丽敏, 苏文献. 料仓卸料流动特性及结构强度数值模拟研究[J]. 化工设备与管道, 2021, 58(2): 35-42.
[54]WJCIK M, TEJCHMAN J, ENSTAD G G. Confined granular flow in silos with inserts: full-scale experiments[J]. Powder Technology, 2012, 222: 15-36.
[55]刘茼, 刘桂林. 浅谈粉体料仓防架桥装置的应用[J]. 轻工科技, 2019, 35(10): 50-51.
[56]操江, 程冬林. 207141942U： 一种仓壁振动装置[P]. 2018-03-27.
[57]李振, 徐成. 213263865U： 一种新型仓壁振动器[P]. 2021-05-25.
[58]谢屹. 211002806U： 一种具有空气锤的下料仓[P]. 2020-07-14.
[59]金泽荣, 陈俊, 孟碧琼, 等. 213976162U： 一种振动料仓下料器[P]. 2021-08-17.
[60]ZHANG C, QIU C, PU C, et al. The mechanism of vibrations-aided gravitational flow with overhanging style in hopper[J]. Powder technology, 2018, 327: 291-302.
[61]KOLLMANN T, TOMAS J. Effect of applied vibration on silo hopper design[J]. Particulate science and technology, 2002, 20(1): 15-31.
[62]武永桥, 管声启, 柴彩彩. 基于EDEM的固体粉末物料振动下料过程分析[J]. 西安工程大学学报, 2017, 31(2): 278-282, 288.
[63]HUNT M L, WEATHERS R C, LEE A T, et al. Effects of horizontal vibration on hopper flows of granular materials[J]. Physics of fluids, 1999, 11(1): 68-75.
[64]KUMAR R, JANA A K, GOPIREDDY S R, et al. Effect of horizontal vibrations on mass flow rate and segregation during hopper discharge: discrete element method approach[J]. Sādhanā, 2020, 45(1): 1-13.
[65]JAFARI A, ABOLGHANDI A, GHARIBI A, et al. Effects of local vibration on silo discharge and jamming: Employing an experimental approach[J]. Journal of Particle Science & Technology, 2018, 4(2): 91-100.
[66]PASCOT A, MOREL J Y, ANTONYUK S, et al. Discharge of vibrated granular silo: a grain scale approach[J]. Powder Technology, 2022, 397: 116998.
[67]DU J, LIU C, TONG L, et al. Effects of vibrations on tilted silo discharge[J]. Chemical Engineering Research and Design, 2021, 171: 247-253.
[68]赵敏. 215246998U： 气力清仓装置漏斗[P]. 2021-12-21.
[69]吴佑俭, 徐进军, 吉万健, 等. 高黏性物料粉矿仓气力清堵助流系统的设计与应用[J]. 金属矿山, 2021(7): 198-205.
[70]LU H, GUO X, GONG X, et al. Experimental study on aerated discharge of pulverized coal[J]. Chemical engineering science, 2012, 71: 438-448.
[71]ZHU L, LU H, POLETTO M, et al. Hopper discharge of cohesive powders using pulsated airflow[J]. AIChE Journal, 2020, 66(7): 16240.
[72]ZHU L, LU H, GUO X, et al. Multi-level arch characteristics and flow enhancement regulation of nano powders discharged from silo[J]. Chemical Engineering Science, 2022, 252: 117492.