近些年，针对水平井、大位移钻井、薄油层钻水平井等钻井技术需求的增加，旋转导向技术应运而生[1]。为了提高钻井效率、 控制钻井成本，准确的掌控井底流场信息对于旋转导向钻井工具的研制十分重要。在实际钻进时钻头切削岩石会产生大量岩屑颗粒，岩屑颗粒的增多会对钻头钻进效率产生影响，为了使钻井液带动井底岩屑颗粒快速的运移出井底，针对旋转导向钻具井底岩屑颗粒进行运动学分析，对提高旋转导向钻具的破岩效率与井眼清洁度是必不可少的。
井底岩屑运移所涉及的流体与岩屑颗粒运动的信息是复杂多变的，导致井底流场的试验难以复现真实工况。随着计算流体力学的数值模拟计算的发展，采用新型理论计算流体动力学（computational fluid dynamics，CFD）和离散单元法（discrete element method，DEM）耦合算法[2-4]对井底流场与岩屑颗粒的分析已成趋势，国内外学者相关文献主要关注于钻井工具[5]、钻头水力结构[6]、钻井液物性参数[7]对于岩屑颗粒运移的影响，采用的理论模型大多以分散相模型（discrete phase model，DPM）[8-9]与欧拉模型[10-12]为主，鲜见以岩屑颗粒动力学为基础对旋转导向钻具实际工况下关于井底流场与岩屑颗粒运移情况的研究。旋转导向钻具会产生的不规则井底流场计算域，示意图如图1所示。不规则的井底空间对整个流场信息产生影响，目前对于旋转导向钻具钻头导向钻进过程井底流场的研究很少。
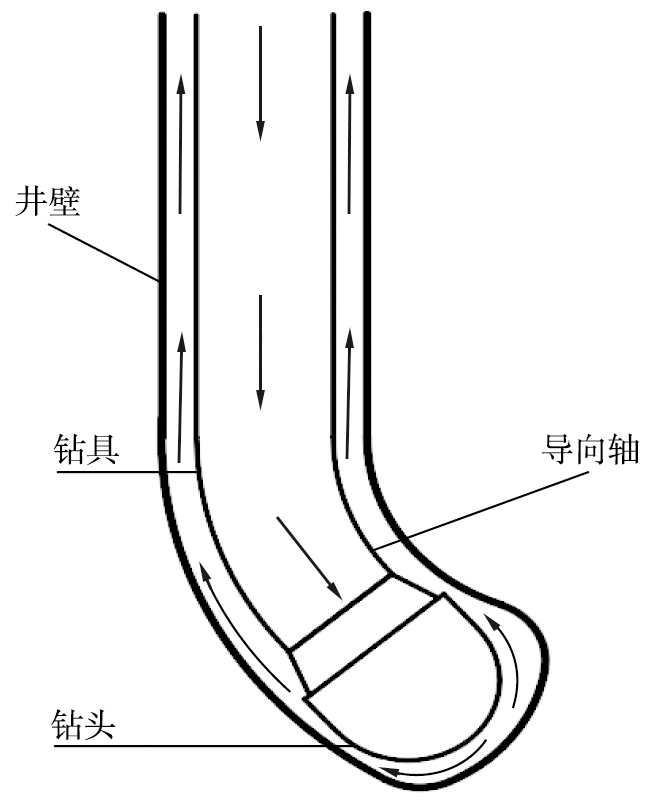
图1 旋转导向钻头偏置下的井底流场示意图
Fig.1 Flow field at bottom of well under offset of rotary guide bit
本文中采用 CFD和DEM建立描述井底钻井液与岩屑颗粒复杂两相流动的双向耦合算法，用来分析井底岩屑颗粒的运动学特性。使用有限元软件FLUENT与离散元软件EDEM耦合数值仿真模拟旋转导向钻头钻进时井底岩屑颗粒运移以及导向钻进过程中井底流场岩屑运动情况。通过数值仿真模拟分析钻头偏置角度，钻井液流速、钻头转速、岩屑颗粒粒径对井底岩屑颗粒运移速度的影响规律以及井底流场岩屑运动情况。
1 流体-颗粒耦合算法模型
旋转导向钻头井底的岩屑运移研究对提高井底清洁能力、机械钻速、钻井效率具有至关重要的作用[13]。简化的钻头模型如图2所示。
1.1 流体力学控制方程
流体力学计算方程采用Navier-Stokes方程并考虑到岩屑颗粒的相互作用，
（φuρ）+
·（φρuu）=-p+·T+φρg-Rp，
（1）
+·（φρu）=0，
（2）
图2 简化的钻头模型
Fig.2 Simplified drill model
T=μ[u+（u）T]，
（3）
式中： t为时间， s； φ为体积分数，即孔隙率； u为钻井液的速度， m/s； ρ为钻井液密度，g/cm3； p为孔隙压力， Pa； T为钻井液应力张量， Pa； g为重力加速度， m/s2； Rp为钻井液和颗粒之间的相互作用， N； μ为流体黏度，Pa·s； T为温度，℃。
1.2岩屑颗粒离散单元控制方程
为求得岩屑颗粒的运动速度以及所受到的力，采用离散单元中的岩屑颗粒运动由牛顿第二定律控制，即
（4）
（5）
式中： mi为岩屑颗粒i的质量， g； ui为岩屑颗粒i的线速度，
为岩屑接触数目；
为岩屑颗粒i受到其岩屑颗粒或者壁面的接触力，
为岩屑颗粒i受到钻井液的作用力，包括拖曳力、流体浮力等，N； Ii为转动惯量， kg·m2； ωi为岩屑颗粒i的线速度和角速度矢量， rad/s； 
分别为岩屑颗粒i受到其岩屑颗粒或者壁面的扭矩，N·s。
1.3颗粒碰撞模型
在流体力学控制方程中，岩屑颗粒与钻井液的相互作用是基于岩屑颗粒的曳力模型进行动量交换[14]。岩屑颗粒之间的碰撞接触模型采用Hertz-Mindlin非线性接触模型，并引入Di-Felice曳力模型[15]。岩屑颗粒受到的抗转动动力Nij矩可分为弹簧转矩
和黏性阻尼转矩
即
（6）
t时刻转矩为
则转矩增量
可表示为：
（7）
式中： θp为岩屑双颗粒的相对滚动角速度， rad/s； kr为滚动刚度， N/m。
t+Δt时刻弹簧扭矩
可表示为：
（8）
式中
为弹簧转矩极限，可表示为：
（9）
式中： μr为岩屑滚动阻力系数，无量纲； Fn为岩屑颗粒法向应力, N； Rr为岩屑颗粒滚动有效半径， m。
Rr表示为：
（10）
式中ri、 rj为双颗粒半径， m。
1.4 CFD-DEM耦合算法计算流程
CFD-DEM耦合分析计算的关键在于钻井液与岩屑颗粒数据交换， 基于FLUENT和EDEM软件， 采用编程二次开发耦合接口， 建立流体力学与离散元法耦合的动力学分析模型。 CFD数值求解采用SIMPLE算法， 对环空流动的钻井液进行流体力学连续性方程和动量方程进行求解， 数值求解迭代至收敛后得到岩屑颗粒与钻井液的相关速度， 以及岩屑颗粒在钻井液中所受力， 将求解数据传输到EDEM中并进行离散元求解， 并将颗粒运动方程代入， EDEM迭代计算完成得到离散相岩屑颗粒的空间位置、 速度、 受力等数据。 将数据再次传递回CFD求解器， 并更新计算域信息进入下一循环时间。 CFD-DEM耦合计算流程如图3所示。
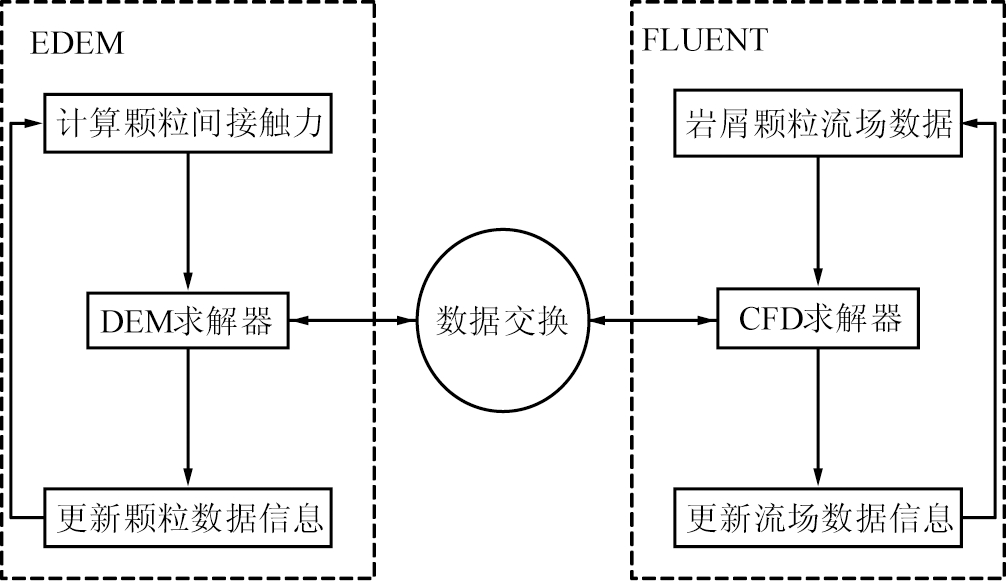
图3 CFD-DEM耦合算法模型
Fig.3 CFD-DEM coupling algorithm model
2 计算与模型参数
2.1 旋转导向钻具井底流场网格划分
选择半径为124 mm的PDC钻头，整个井底计算域长度为500 mm，流场域的厚度为6 mm。旋转导向钻头的井底流场模型如图4所示。在进行网格划分时，对切削齿与喷嘴结构进行简化，并且对井底部进行加密网格处理，网格示意图如图5所示。整个流场计算域只分析岩屑存在的外部流道、环空区、井底区，网格尺寸为岩屑颗粒尺寸的1.25～2.5倍。
图4 井底流场计算域
Fig.4 Flow field calculation domain at bottom of well
图5 计算域网格示意图
Fig.5 Schematic diagram of computational domain grid
2.2 计算参数与边界条件
计算模型为非定常计算，总体时间0.6 s，流体计算时间步长设置为5×10-4 s，CFD-DEM耦合计算中颗粒计算时间步长要求不能大于流体计算时间步长，参考瑞利时间步长大小，颗粒计算的时间步长控制在瑞利时间步长的60%以内，颗粒的计算步长为5×10-6 s。在进行数值模拟时，钻井液为连续介质，岩屑颗粒为离散介质，旋转导向钻具为运动无滑移边界，其他壁面为固定无滑移边界且壁面模型采用标准型，湍流模型为RNG k-ε模型。井底流场的复杂性使得重力影响较小，故忽略流体重力影响。湍流流场的计算采用二阶迎风格式，对钻井液的入口定义为速度入口边界条件，出口定义为自由出流边界；设置钻井液和岩屑颗粒从入口进入，钻井液设定为水，选择速度入口，方向与钻头的喷嘴方向一致，选择压力出口。钻头的旋转方向为顺时针，且旋转轴为钻头的中心轴线。为了能够更好地契合室内试验条件，钻井液设定为水，密度为1 000 kg/m3，黏度为0.002 98 Pa·s，选择能够更好地描述水基钻井液流变模式的赫谢尔-巴尔克莱模式; 岩屑颗粒粒径大小为1.5 mm，岩屑颗粒密度为2 600 kg/m3，泊松比为0.26，杨氏模量为15 000 MPa，选择井底的岩石面为岩屑颗粒产生面，模拟岩屑颗粒切削生成，颗粒工厂的颗粒生成速度为每秒5 000个。其中岩屑颗粒的物性参数如下表1所示。
表1 岩屑颗粒物性参数
Tab.1 Physical properties parameters of rock chip particles
类型静摩擦系数滚动摩擦系数碰撞恢复系数岩屑与岩屑0.600.010.45岩屑与壁面0.750.020.50
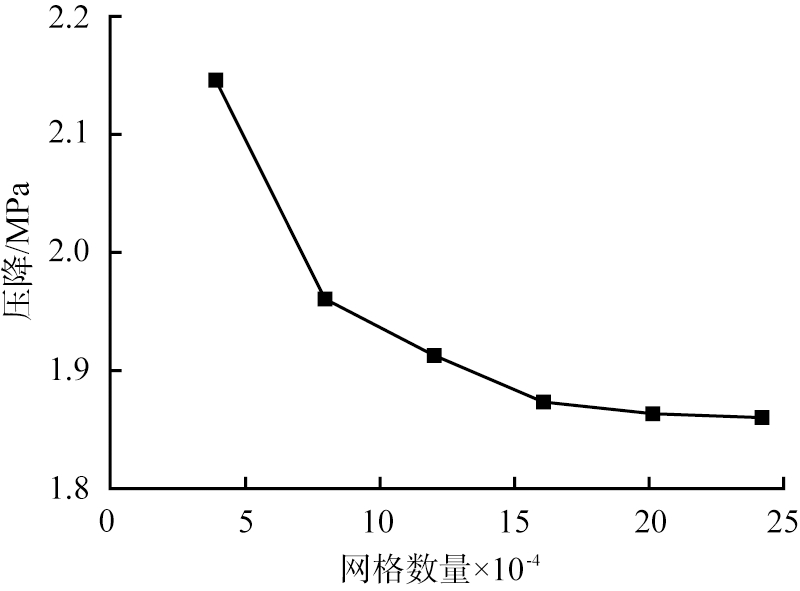
图6 网格无关性验证图
Fig.6 Grid-independent verification graph
2.3 网格无关性验证
以井底计算域中井底流场进出口压降为指标，进行网格无关性验证。以旋转导向钻头偏置的指向角度为5°的井底计算域为例，结果如图6所示。从图中可以看出，网格数量大于20万时，继续增加网格数量也不会对进出口压降产生影响。
3 模拟分析
3.1 岩屑颗粒在不同转速时的运移规律
在旋转导向钻头工作过程中，钻头的旋转会在井底流场产生漩涡流，钻头在切削岩石，并不断地碾磨较大的岩石颗粒，带动岩屑颗粒产生旋转，沿着排屑槽进入环空区域。为探究不同钻速下井底流场的岩屑颗粒运移规律，选择4种不同钻速下的工况，对旋转导向钻头的井底流场进行数值模拟。转速分别为6、 7、 8、 9 rad/s。旋转导向钻头井底流速如图7所示，岩屑颗粒在井底分布及运移速度如图8所示。从图中可以看出，在靠近喷嘴区域的钻井液流速较大，而远离喷嘴区域的钻井液流速较小，位于钻头中心区域的钻井液流速较小，在中心区域易产生岩屑聚集，当岩屑聚集较多时，则会产生泥包，进而影响到整个钻井的工作效率。随着钻头钻速的增大，各个区域的流速增大，空间区域中岩屑被快速携带，流速相对较小的区域面积逐渐减少。钻头的旋转可造成井底岩屑受力不均，能够有助于岩屑快速脱离井底上返。
由于喷嘴位置分布的不规则，钻头的旋转使得水力能量在规律性变化，形成高速与低速水流交错出现，有助于井底岩屑的清洗。岩屑颗粒运移平均速度如图9所示。由图可知，钻头旋转速度为6 rad/s时， 位于井底流场区域的钻井液流速最高仅为1.84 m/s， 岩屑颗粒运移速度在迭代时间t=0.6 s时仅为1.73 m/s， 随着钻头旋转速度逐渐增大至9 rad/s时， 岩屑运移平均速度高达2.12 m/s， 在迭代时间t=0.6 s时可达到1.98 m/s，在井底流场中的钻井液最大流速和岩屑颗粒的最大运移速度相近。综上所述，旋转导向钻具钻头旋转的转速增大，钻井液与岩屑颗粒的运动速度也增大，对于井底岩屑颗粒的运移起到正反馈的作用，提高了井底清洁度。
3.2 岩屑颗粒在不同钻井液流速时的运移规律
在钻井过程中，井底流场可能会出现水力能量不足够，岩屑颗粒不易被携带至环空，井底中心出现处低速区与中心漩涡[17]，钻井液流速对调节井底的水力能量起重要作用，同时对井底岩屑颗粒的运移也产生影响。选定4种不同的钻井液流速对旋转导向钻头井下岩屑颗粒运移进行数值模拟分析，钻井液流速分别为1.5、 2、 2.5、 3 m/s。井底钻井液流速如图10所示，不同钻井液流速时井底岩屑颗粒分布及运移速度如图11所示。由图10可得到，随着钻井液流速的增大，钻头中心部位的低流速区域明显变小，在每个流道以及排屑槽中的流速变大，整个钻头表面的钻井液流速大幅度提高。
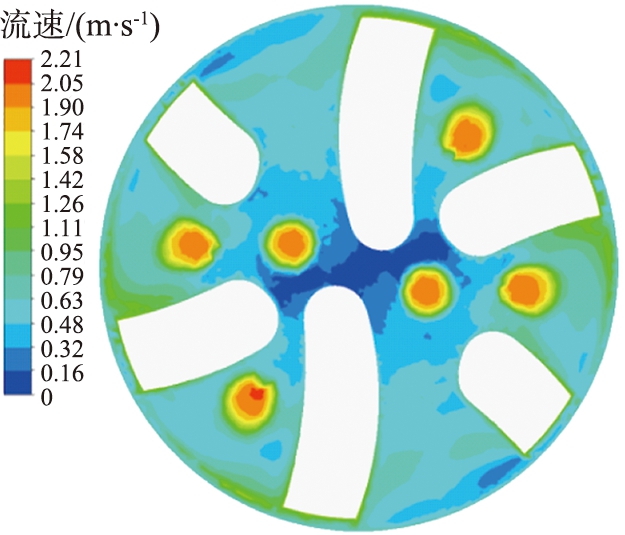
（a）6 rad/s
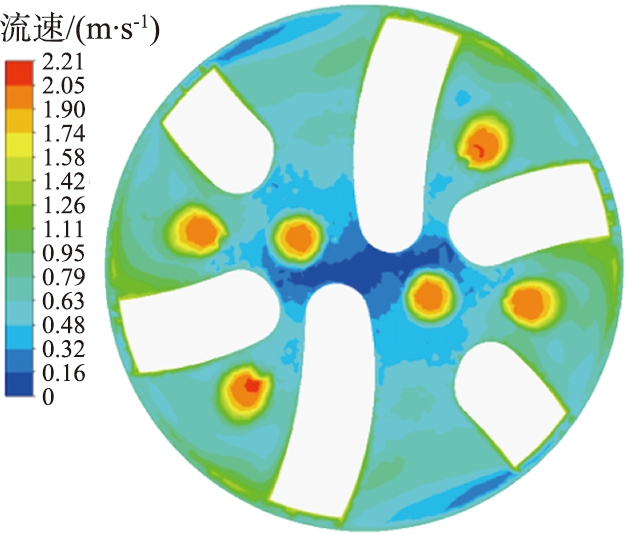
（b）7 rad/s
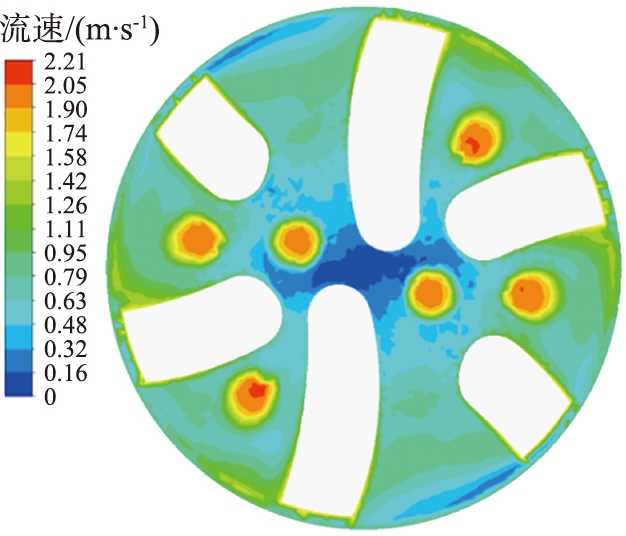
（c）8 rad/s
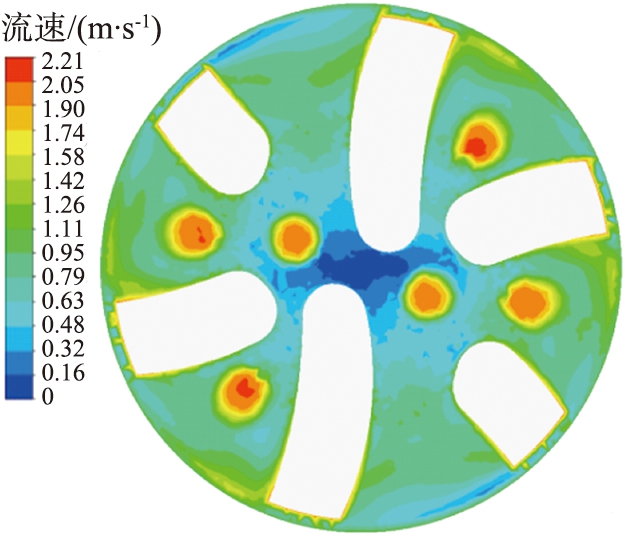
（d）9 rad/s
图7 不同转速时井底流场速度云图
Fig.7 Velocity clouds of flow field at bottom of well at different speeds
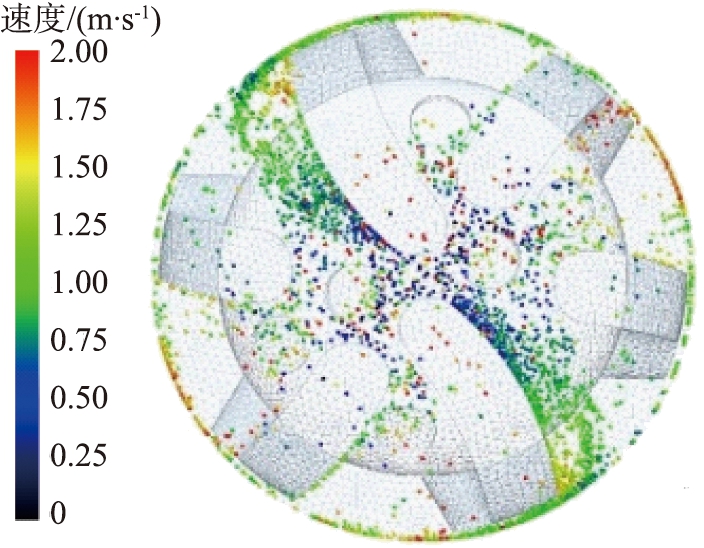
（a）6 rad/s
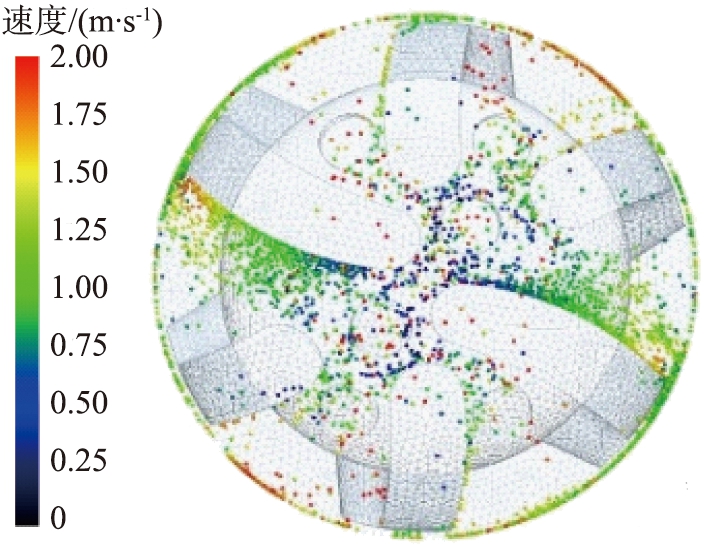
（b）7 rad/s
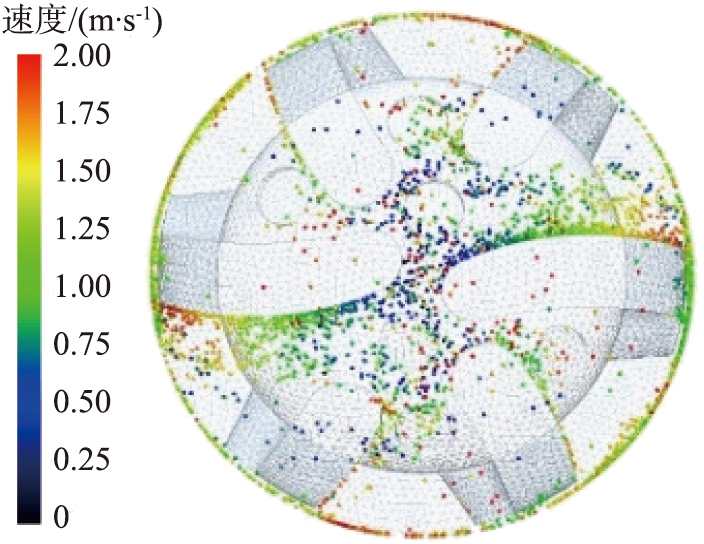
（c）8 rad/s
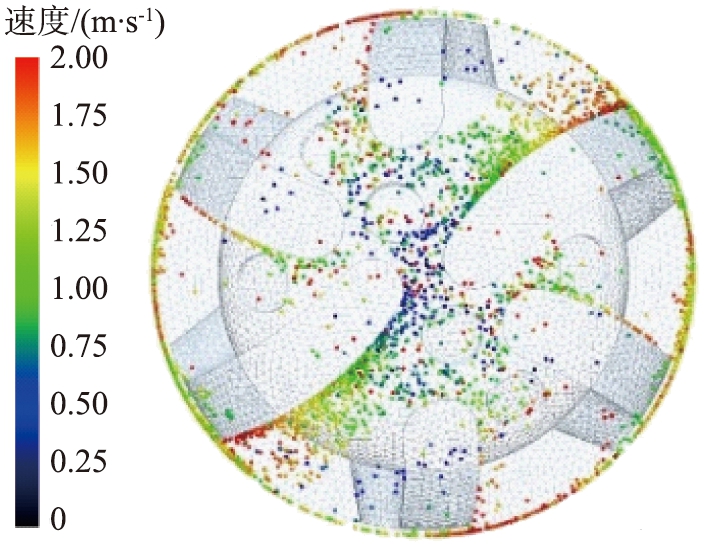
（d）9 rad/s
图8 不同转速时井底岩屑颗粒分布及运移速度图
Fig.8 Distribution and transport velocity of rock chip particles in bottom of well at different rotational speeds
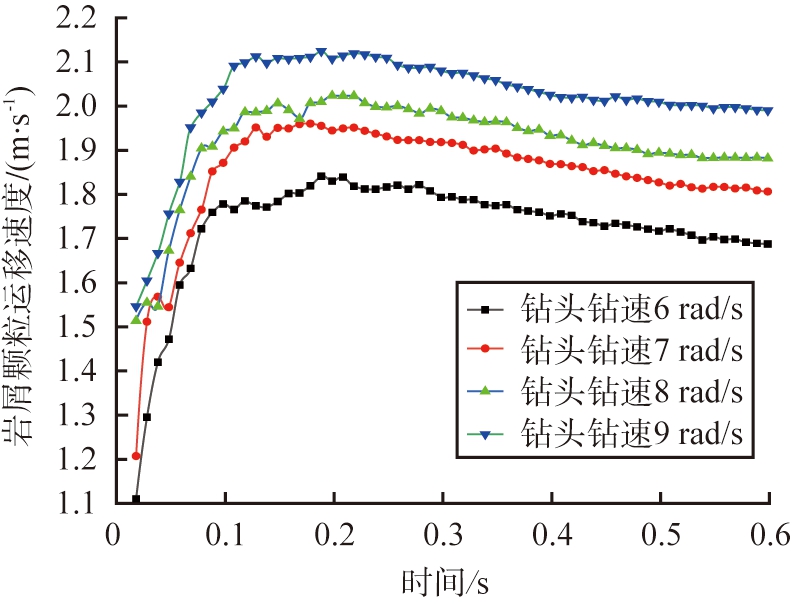
图9 不同转速时岩屑颗粒运移平均速度
Fig.9 Transport velocity of rock chip particles at different rotational speeds
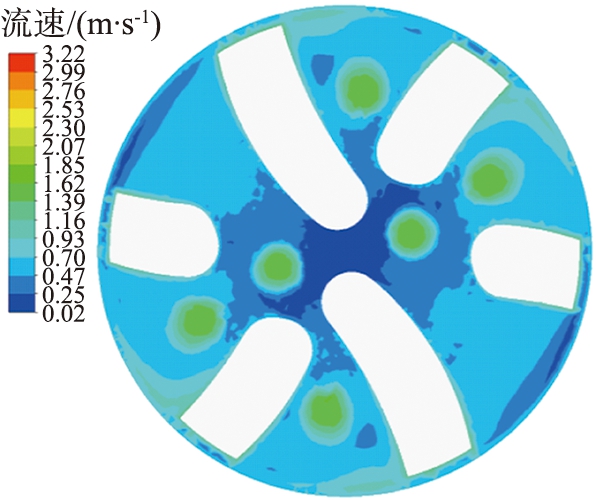
（a）1.5 m/s
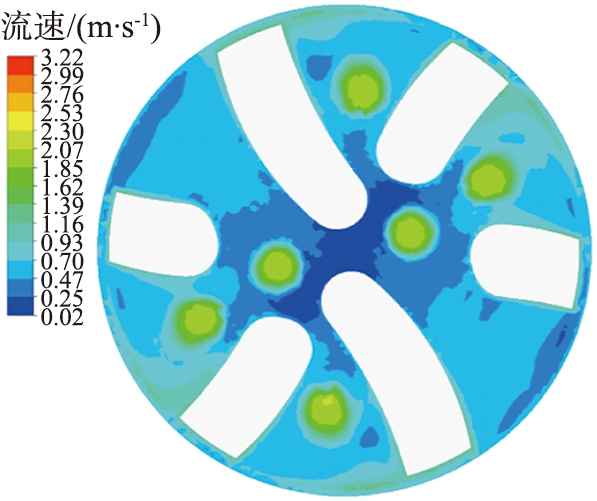
（b）2.0 m/s
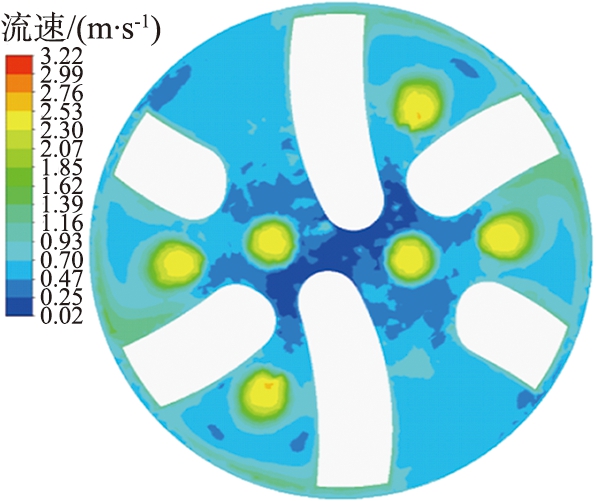
（c）2.5 m/s
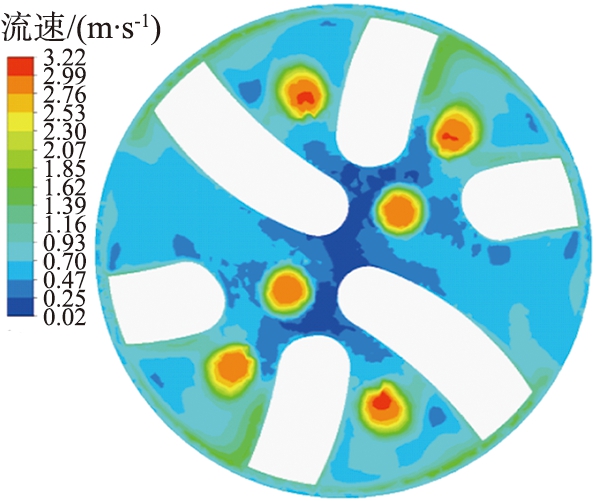
（d）3.0 m/s
图10 不同钻井液流速时井底流场速度云图
Fig.10 Velocity cloud of bottom hole flow field at different drilling fluid flow rates
图12所示为岩屑颗粒在不同流速时的平均运移速度。由图可知，随着钻井液流速的增大，岩屑颗粒所得到的动能增大，颗粒的运动轨迹更加复杂，获得更大的动能使得岩屑颗粒被快速通过流道运移至环空的概率增加，足够的水力能量作用于岩屑颗粒使得井底岩屑浓度大幅度的减小，岩屑颗粒在井底的聚集也大大减少。钻井液流速的提升使得最大岩屑颗粒运移速度从1.4 m/s增大至2.82 m/s，当迭代时间为0.6 s时，岩屑运移平均速度由最低的1.32 m/s提升至2.66 m/s。由此可知，增大流速可以使得井底水力能量增大，岩屑颗粒运移效率增加，提高了井眼清洁度。
3.3 不同粒径岩屑颗粒的运移规律
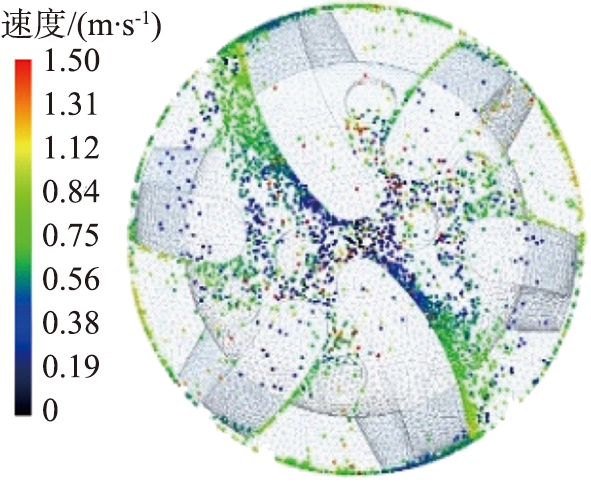
（a）1.5 m/s
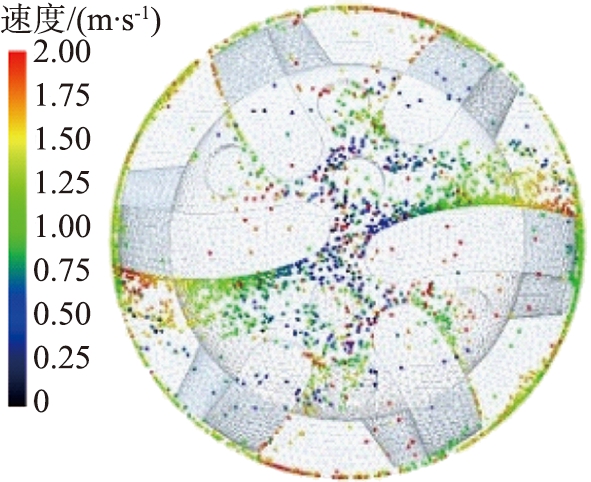
（b）2.0 m/s
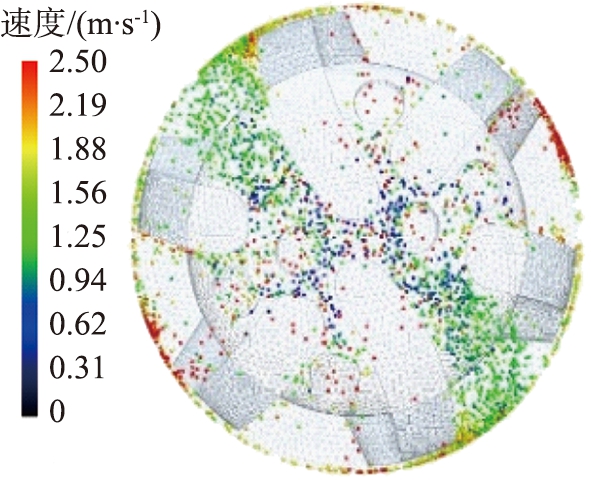
（c）2.5 m/s
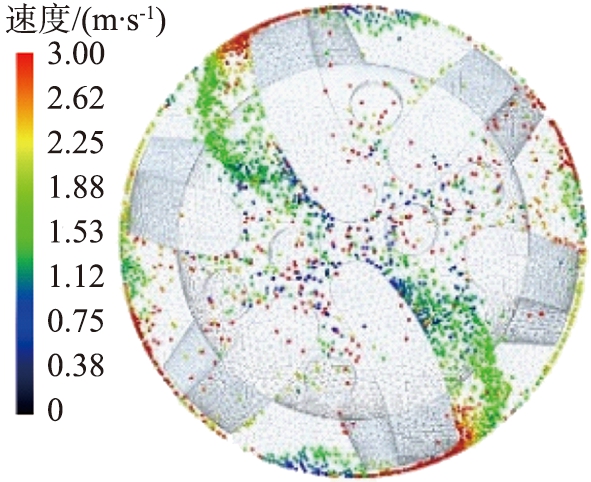
（d）3.0 m/s
图11 不同钻井液流速时井底岩屑颗粒分布及运移速度图
Fig.11 Distribution and transport velocity of rock chip particles at bottom of well under different drilling fluid flow rates
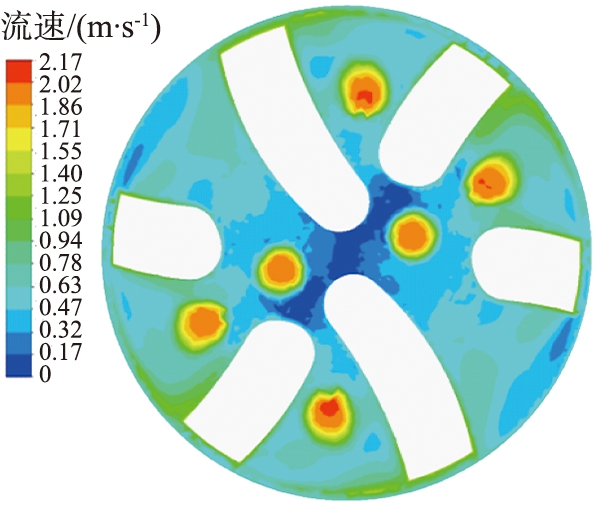
岩屑颗粒粒径也时刻影响着井底流场的变化， 当岩屑颗粒粒径过大时， 大块岩屑可能会堵塞排屑槽， 使得井底岩屑颗粒不能通过排屑槽运移至环空处， 排屑槽的堵塞会造成钻井液的回流， 钻井液回流会携带岩屑重新回到井底[18]，导致岩屑颗粒重复碾磨，不利于井底岩屑清理， 严重影响钻井效率。为探究岩屑颗粒粒径大小对井底岩屑颗粒运移规律的影响， 选定颗粒直径分别为1、 2、 2.5、 3 mm的球形颗粒进行数值仿真模拟， 在不同岩屑颗粒粒径条件下钻井液流速如图13所示， 不同岩屑颗粒粒径时井底岩屑颗粒分布及运移速度图如图14所示。 由图可知， 随着颗粒粒径的增大， 井底流场的流速变化明显， 在钻头边缘部的钻井液速度受到影响较为显著， 岩屑颗粒的增大会增加上返环空的难度。
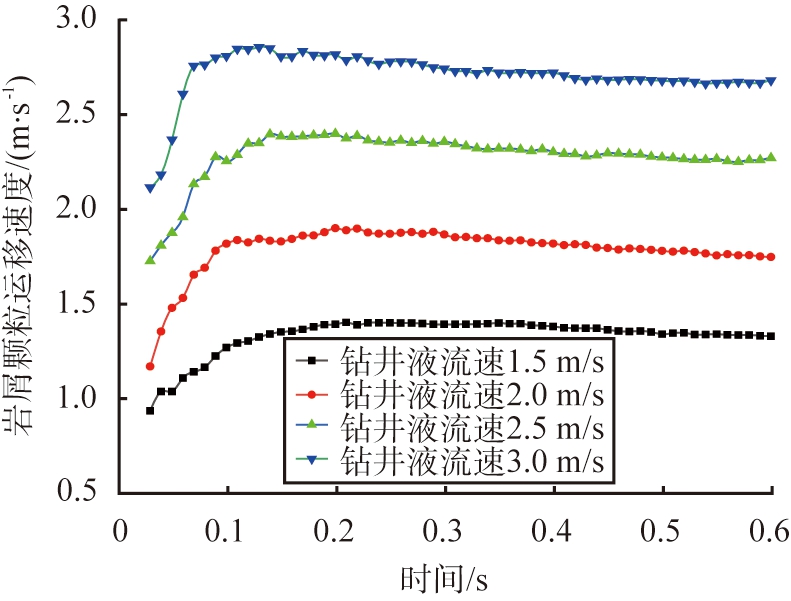
图12 不同钻井液流速时岩屑颗粒平均运移速度
Fig.12 Rock chip particle transport velocity under different drilling fluid flow rates
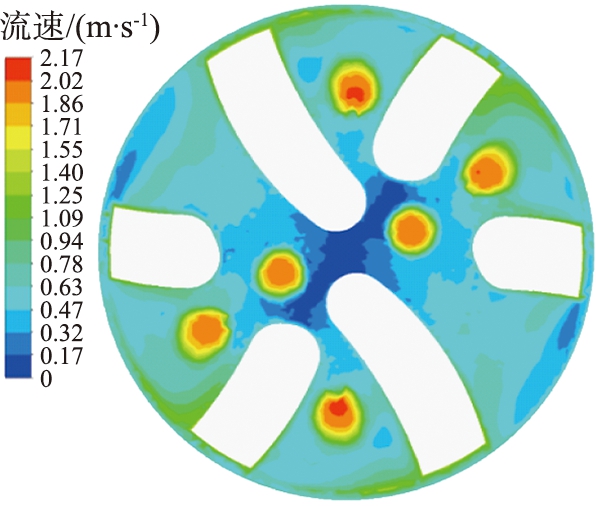
（a）1.0 mm
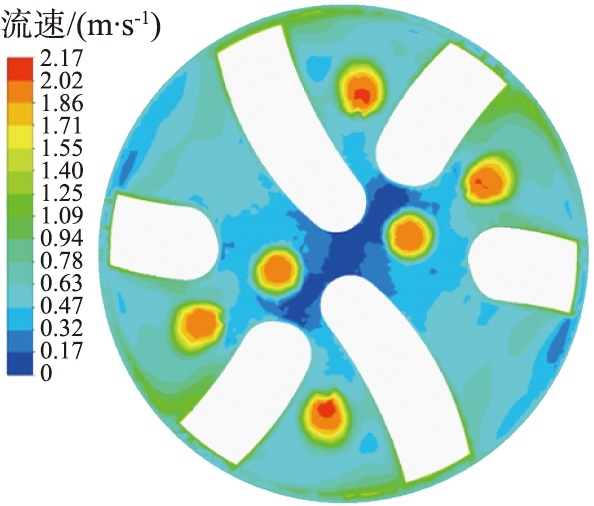
（b）2.0 mm
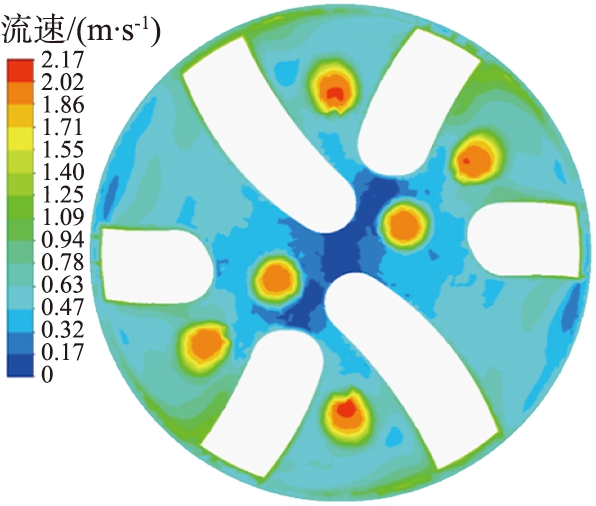
（c）2.5 mm
（d）3.0 mm
图13 不同岩屑颗粒粒径时井底流场速度云图
Fig.13 Velocity clouds of flow field at bottom of well for different particle sizes of rock chips
岩屑颗粒粒径的增大， 岩屑颗粒运移出井底所需的水力能量就会增大， 随着岩屑颗粒的产生增多， 岩屑颗粒就会因水力能量的缺乏而无法快速运移到上返环空， 最终导致井底岩屑颗粒聚集。 岩屑颗粒的运移平均速度如图15所示。 由图可知， 随着粒径的增大， 岩屑运移的速度降低，直径为1 mm的岩屑颗粒最大的运移平均速度可达到2.1 m/s，而直径为3 mm的岩屑颗粒最大的运移平均速度仅为1.71 m/s。由此可知，粒径较大的岩屑会大大影响岩屑颗粒的运移效果。岩屑颗粒粒径的增大导致岩屑颗粒自身的质量增大，钻头的旋转与钻井液的流动所产生的水力能量不足，不能够带动大颗粒岩屑至环空； 在狭窄的井底环境中， 岩屑的聚集减少了颗粒之间的碰撞， 导致更多的岩屑聚集， 从而产生钻头泥包， 导致钻井效率降低。
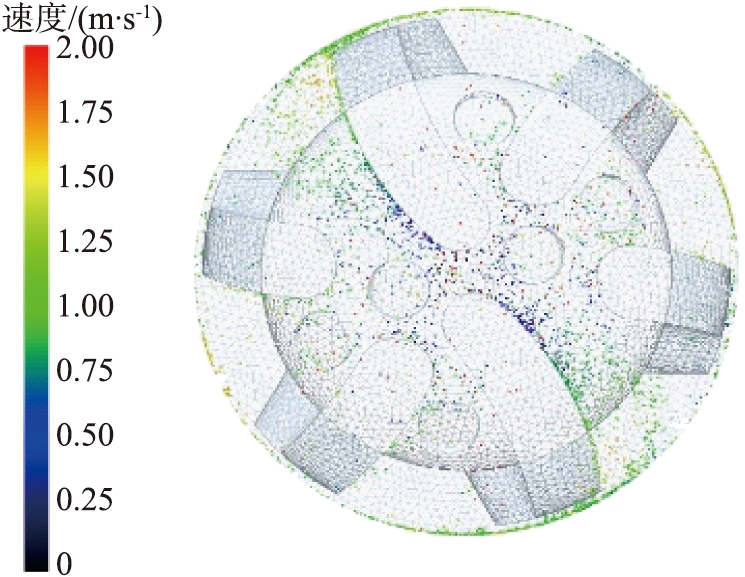
（a）1.0 mm
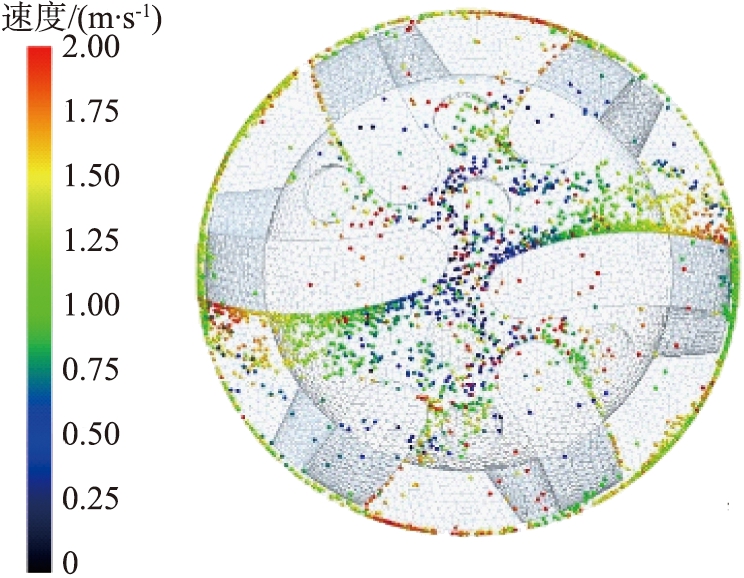
（b）2.0 mm
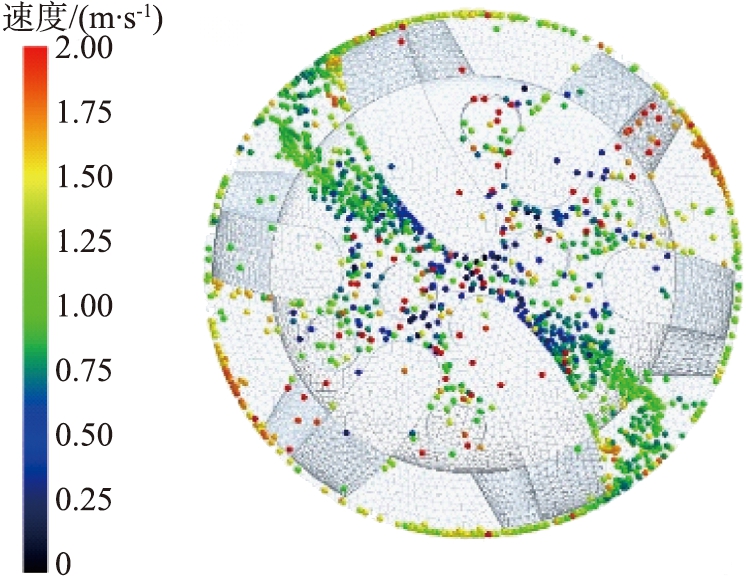
（c）2.5 mm
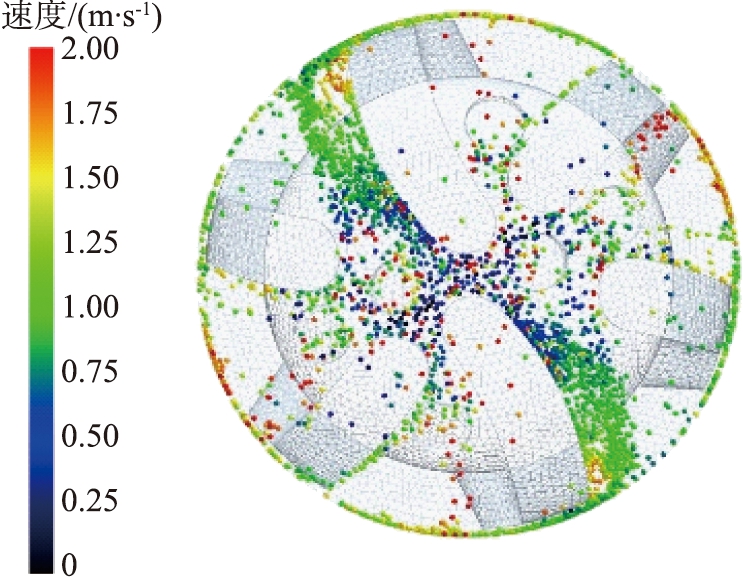
（d）3.0 mm
图14 不同岩屑颗粒粒径时井底岩屑颗粒分布及运移速度图
Fig.14 Distribution and transport velocity of rock chip particles in bottom of well with different particle size of rock chip
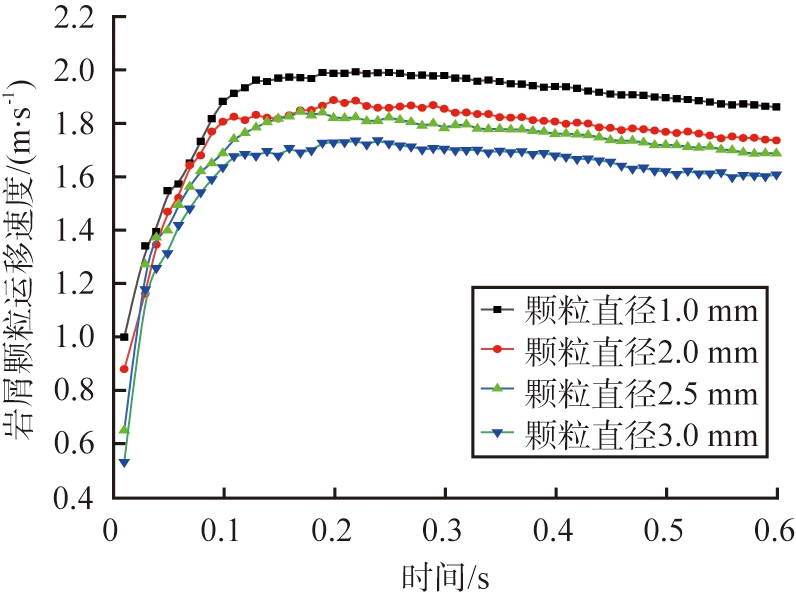
图15 不同岩屑颗粒粒径时岩屑运移平均速度
Fig.15 Rock chip transport velocity under different particle size of rock chip
3.4 岩屑颗粒在不同钻头偏置角度时的运移规律
旋转导向钻具在进行造斜时，钻头偏置一定角度会导致井底空间结构的改变，同时也影响着整个井底流场岩屑颗粒的运移效率。为了探究旋转导向钻头的不同指向角度对井底流场的影响，设定钻井液流速为3 m/s，选定旋转导向钻头偏置的指向角度分别为0°、 2.5°、 5°进行数值模拟分析，在不同钻头偏置角度时的井底钻井液流速云图如图16所示，不同钻头偏置角度时井底岩屑颗粒分布及运移速度图如图17所示。由图可知，钻头未发生偏置时，钻头两侧的速度分布均匀且呈轴对称分布，最小流速区域处于钻头中心部位。当钻头的偏置的指向角度发生改变时，偏置导致一侧与井壁的间隙变小，另一侧间隙增大，间隙大的钻井液流速因岩屑可快速通过；但是由于空间体积增大，钻井液的流动力量被削弱，因此岩屑颗粒所获得水力能量也被减弱。间隙小的钻井液流速虽然增大，但是较大颗粒可能会堵塞空隙，大大降低岩屑运移效率。钻头偏置的指向角度逐渐增大到最大5°时，整个流场分布呈现不均匀分布，间隙大的一侧钻井液流速低于间隙小的一侧的，井底流场空间内的低速区域增大。
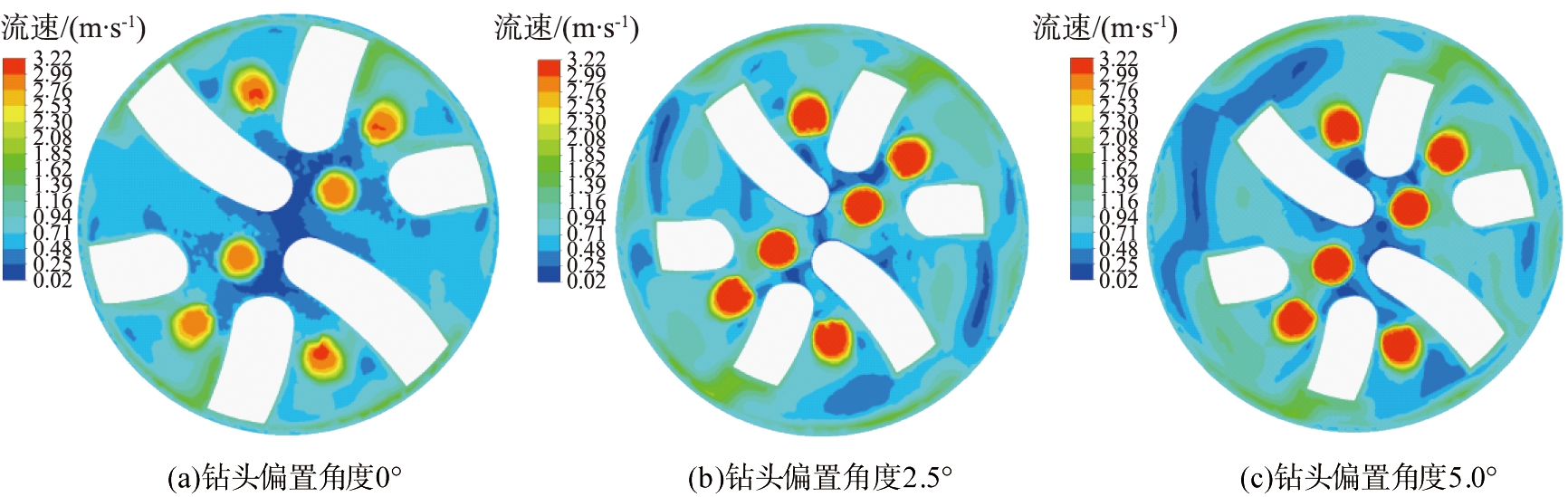
图16 不同钻头偏置角度时井底流场云图
Fig.16 Flow field clouds at bottom of well with different drill bit offset angles
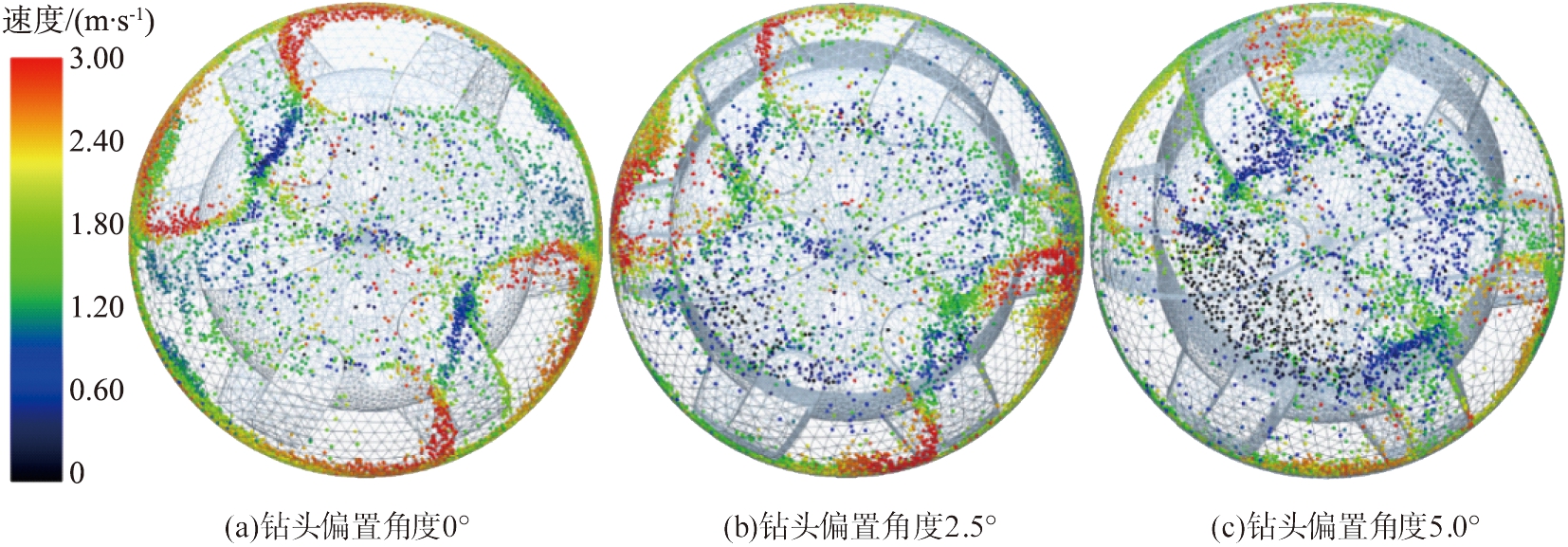
图17 不同钻头偏置角度时井底岩屑颗粒分布及运移速度
Fig.17 Distribution and transport rate of rock chip particles at bottom of well under different bit offset angles
旋转导向钻头的偏置会使得岩屑颗粒的运动变得更加复杂，空间结构的改变加剧了颗粒间的碰撞，大量无规则的碰撞与运动会消耗岩屑颗粒的动能，导致岩屑颗粒上返回运移至环空的运动速度不足。图18所示为不同钻头偏置角度时岩屑颗粒运移平均速度，随着钻头偏置的角度的增大，最大岩屑颗粒平均速度从2.95 m/s减小至2.41 m/s，在迭代时间为0.7 s时未发生钻头偏置的井底流场岩屑颗粒平均速度为2.75 m/s，而在钻头偏置角度为5°时，井底流场中岩屑颗粒的动能损耗较为明显，岩屑颗粒运移平均速度仅为2.34 m/s。由此可得，在进行导向钻进过程中，钻进时间不易过长，应进行间歇钻进以清理井底岩屑颗粒，也可在导向钻进时加大钻井液流速。旋转导向钻头的偏置会使得岩屑颗粒的运移效率降低，可能会加剧钻头磨损与泥包问题。
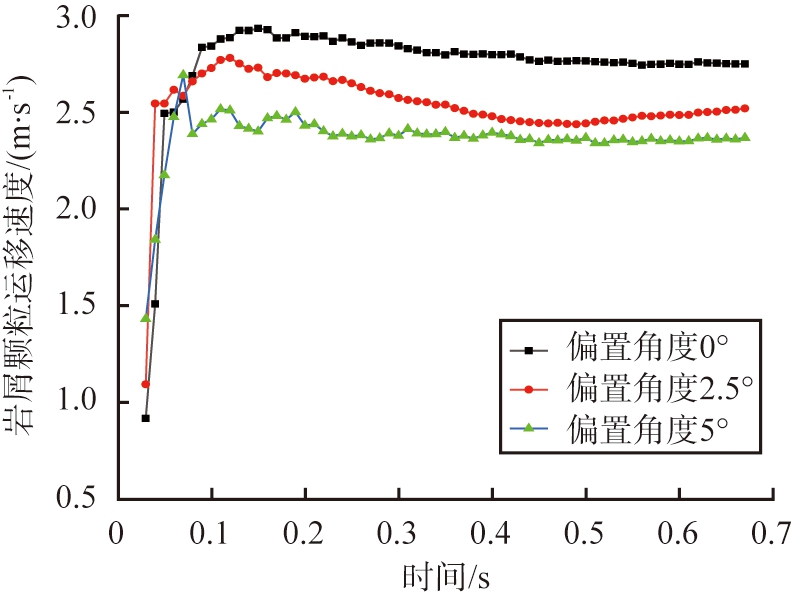
图18 不同钻头偏置角度时岩屑运移平均速度
Fig.18 Chip transport velocity at different bit offset angles
4 结论
1）CFD-DEM耦合算法考虑到钻井液与岩屑颗粒的相互作用，能够更加接近实际工况，为后续的理论研究和实验研究提供参考。
2）提高旋转导向钻头转速与钻井液流速，岩屑颗粒的运移动速度增大，对于井底岩屑颗粒的运移起到正反馈的作用，提高了井底清洁度；岩屑颗粒粒径的增大会减小岩屑颗粒的运移速度，降低岩屑运移效率。当岩屑颗粒直径大于3 mm时，岩屑运移速度降低更加明显。
3）旋转导向钻头偏置会导致井底空间结构的变化，同时也影响着整个井底流场岩屑颗粒的运移效率。导向钻进的流场是不规则的井底形状，加剧岩屑颗粒之间碰撞导致动能损耗，水力能量也因空间结构的改变而削弱，使得岩屑颗粒的运移速度降低，最终可能会加剧钻头磨损，并产生泥包问题。
[1]姜伟, 蒋世全, 付鑫生, 等. 旋转导向钻井技术应用研究及其进展[J]. 天然气工业, 2013, 33（4）: 75-79.
[2]王志亮, 赵莹, 丛成, 等. 基于CFD-DEM的新型铝合金钻杆携岩仿真分析[J]. 机床与液压, 2021, 49（20）: 130-136.
[3]邵兵, 闫怡飞, 毕朝峰, 等. 基于CFD-DEM耦合模型的大粒径非常规岩屑颗粒运移规律研究[J]. 科学技术与工程, 2017, 17（27）: 190-195.
[4]罗金武, 况雨春, 张锐, 等. 基于CFD-DEM耦合的水平井PDC钻头水力结构研究[J]. 工程设计学报, 2020, 27（5）: 636-644.
[5]豆旭谦, 王力. 煤矿井下硬岩定向钻进技术装备与应用[J]. 煤矿安全, 2021, 52（11）: 117-122.
[6]杜鹏, 张汶定. 自进式直旋混合射流钻头结构优化与钻孔能力分析[J/OL]. 煤田地质与勘探: 1-10[2022-04-10]. http://kns.cnki.net/kcms/detail/61.1155.P.20220316.0823.004.html.
[7]马腾飞, 周宇, 李志勇, 等. 新型低伤害高性能微泡沫钻井液性能评价与现场应用[J]. 油田化学, 2021, 38（4）: 571-579.
[8]李劲, 边晨阳, 刘忠, 等. 基于DPM模型的旋切式PDC钻头流场特性研究[J]. 石油机械, 2021, 49（9）: 24-32.
[9]闫炎, 管志川, 阎卫军, 等. 基于DPM模型的双级PDC钻头流场特性研究[J]. 石油机械, 2019, 47（9）: 1-9.
[10]张杰, 李荣鑫, 李鑫, 等. 泡沫钻水平井岩屑颗粒的运移规律研究[J]. 钻采工艺, 2022, 45（1）: 53-58.
[11]ZHANG F F， MISKA S， YU M J， et al. A unified transient solid-liquid two-phase flow model for cuttings transport-modelling part[J]. Journal of Petroleum Science and Engineering， 2018， 166： 146-156.
[12]SUN B J， XIANG H F， LI H， et al. Modeling of the critical deposition velocity of cuttings in an inclined-slimhole annulus[J]. SPE Journal, 2017， 22（4）： 1213-1224.
[13]陈修平， 邹德永. PDC钻头泥页岩地层钻进泥包机理及对策研究进展[J]. 天然气工业， 2014， 34（2）： 87-91.
[14]刘国强， 屈圣力， 李照. 煤层气水平井防砂泵井液携煤粉流动特性分析[J]. 特种油气藏， 2019， 26（4）： 165-169.
[15]王胤， 艾军， 杨庆. 考虑粒间滚动阻力的CFD-DEM流-固耦合数值模拟方法[J]. 岩土力学， 2017， 38（6）： 1771-1780.
[16]AKHSHIK S， BEHZAD M， RAJABI M. CFD-DEM simulation of the hole cleaning process in a deviated well drilling: the effects of particle shape[J]. Particuology， 2016， 25（2）： 72-82.
[17]赵健， 徐依吉， 孙宝京， 等. 粒子射流喷射钻塞流场特性及参数优化[J]. 中国石油大学学报（自然科学版）， 2020， 44（6）： 63-72.
[18]陈绪跃， 曹通， 高德利， 等. 射流磨钻头流场特性及其外排屑槽影响的数值模拟[J]. 石油钻采工艺， 2020， 42（2）： 162-166.