超细粉体技术发展至今已有50余年, 通常将粒径全部小于30 μm的粉体定义为超细粉体[1]。 超细粉因具有独特的性质被广泛的应用于能源、 化工、 生物、 制药等领域和行业。 粉碎法是目前工业制备超细粉的主流方法之一, 介质砂磨机作为采用粉碎法制备超细粉的重要设备, 被各行各业普遍使用[2]。 随着计算流体动力学(computational fluid dynamics, CFD)技术与计算机技术的快速发展, CFD技术早已拓展应用于冶金、 化工、 建筑等相关领域[3-5]。 传统砂磨机实验设计方法周期长, 设计成本高, 利用CFD技术可以直接对砂磨机内部流动进行模拟, 分析设计的合理性, 缩短设计周期与成本[6-7]。
张国旺等[8-9]运用CFD方法对不同类型砂磨机进行仿真数值模拟与对比试验, 结果表明, 棒销式砂磨机的研磨效果较好, 验证了数值模拟分析的正确可靠性。 龚曙光等[10]对介质搅拌磨机分散盘结构进行单相仿真优化, 后进行试验验证, 结果表明, 介质搅拌磨单相仿真可行, 仿真结果具有参考性。 赵艳平[11]利用流体力学仿真软件Fluent对不同转速下的卧式砂磨机进行了三维层流与湍流的数值模拟,对其速度场与切变率分布进行分析,找到了研磨破碎的主要区域, 得出了砂磨机的粉碎机理。 Fukui等[12]通过三维离散元方法(discrete element method, DEM)对介质搅拌磨机的搅拌轴方向进行了模拟研究, 认为在评价颗粒碰撞能大小的同时也要评价颗粒运动的均匀性。 Zheng等[13]对不同转速的叶轮式湍流磨机(impeller type turbulent mill, ITTM)进行数值模拟后得出, 流动湍流与研磨腔大尺度涡完成了研磨的初始阶段, 定子附近的小尺度涡进一步细化了材料。 Kwade[14]运用数值计算方法对颗粒滞留时间与磨机几何形状对产品颗粒分布产生的影响进行了讨论, 结论表明, 研磨首先发生在速度梯度较大的区域,并且产物细度与比能之间存在一定关系。 近些年的研究主要针对砂磨机内层流与湍流流场, 对某一类型砂磨机结构改变对内部速度场以及切变率带来的影响的研究较少。 本文中采用CFD方法对涡轮式砂磨机内部单相流场进行数值模拟, 对涡轮结构进行改进并分析探讨了涡轮转速对砂磨机内部流场与研磨特性的影响。
1 涡轮式磨砂机几何结构
本文中初始模型采用HHN系列90 L卧式涡轮式砂磨机作为研究对象,该砂磨机的涡轮组由3个涡轮组成,皆由镜像对称的涡轮装配在一起。涡轮叶片共16片,叶片型线为圆弧段的简单拼接,其出口角β=42°,图1所示为涡轮部件模型图。

图1 涡轮部件模型图
Fig.1 Model diagram of turbine components
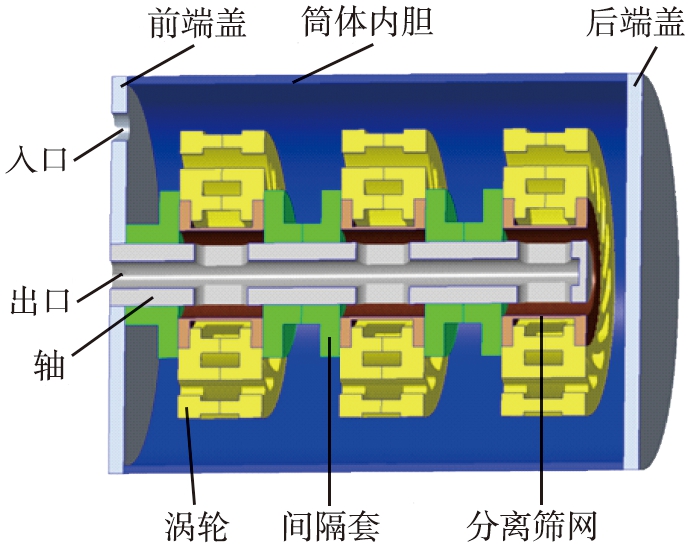
图2 主要部件装配图
Fig.2 Assembly drawing of main components
数值模拟所涉及的研究区域为砂磨机工作时内部充满流体的区域, 部件包括入口, 陶瓷罐内胆, 前、 后端盖板, 涡轮组, 主轴以及动态过滤筛网。 图2所示为各主要部件装配图, 各部件几何参数如表1所示。
表1 研磨腔内各部件主要几何尺寸
Tab.1 Main geometric dimensions of components in grinding chamber mm
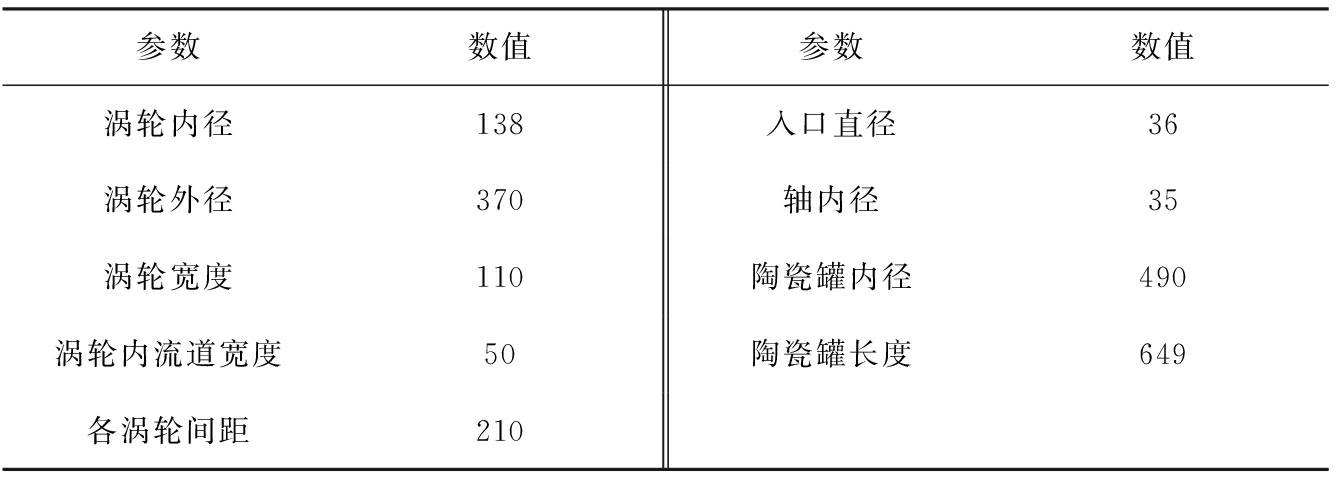
参数数值参数数值涡轮内径138入口直径36涡轮外径370轴内径35涡轮宽度110陶瓷罐内径490涡轮内流道宽度50陶瓷罐长度649各涡轮间距210
浆料从进口流入,流经研磨区域后通过动态分离筛网进行分离,后从出口流出完成研磨,筛网固定在轴上随之一起转动,从而可以减轻筛网受到研磨介质周向分速度带来的摩擦磨损。

(a)研磨腔内流体网格

(b)涡轮内流体网格

(c)主轴内流体网格
图3 砂磨机研磨腔内各部件流体网格图
Fig.3 Fluid grid diagram of each component in grinding chamber of sand mill
采用Ansys ICEM软件对计算流体域进行网格划分,以涡轮出口处流体速度作为网格无关性验证的指标,经过验证后选定网格数为1.187×107的水体模型进行数值模拟。图3所示为砂磨机各部件内部流体网格划分情况,表2所示为各部件内部流体网格数。
表2 各部件流体网格数
Tab.2 Number of fluid grids of each component

入口处流体涡轮处流体(3组)研磨腔内流体主轴内流体总计12×1042.49×1063.96×1064.1×1041.187×107
2 数值方法
2.1 控制方程与边界条件
本文中研究的两相混合介质由水、物料颗粒以及研磨介质(锆珠)构成,具有如下特点。
1)固相的颗粒直径小。物料颗粒粒径范围为1~1.5 μm,研磨介质粒径为0.4 mm。
2)固相的体积分数大,研磨介质的填充率(体积分数)高达75%。
3)研磨介质比物料颗粒大很多。由于固相颗粒小、体积分数大,使得固体颗粒之间距离小,相互碰撞频繁;同时研磨介质始终处于研磨区域中,物料在研磨机存续时间长,使得固相之间和固相与液相之间具有较强的相互约束作用。固相和液相之间的伴随性强,由于惯性和重力的作用,固相和液相之间存在一定的速度差,但这个差值微小,可以近似忽略,因此从宏观角度上,即使在边界层或者速度梯度大的区域,也可忽略研磨介质与流体之间的速度差。
Graeme[15]认为仅限于研究研磨介质与浆料混合, 可以忽略微观层面上各组分间存在着的相对运动, 并通过对比试验验证了单相模拟的正确性。 另外, Stehr等[16]通过实验观察发现了体积分数大的研磨介质对矿浆的流动几乎没有影响。 针对所研究的固相体积分数大的两相混合介质, 若构建两相流模型, 其计算量是难以达到的。 一些类似的研究工作中[8-11]也是采用和本文中相同的模型和处理方法。
综上所述,为减少计算量,将研磨腔内流体介质看作是均一的不可压缩流体介质是合理的、 现实的。采用某磷酸铁锂浆料作为研磨目标,经测量,黏度为3.8 Pa·s,换算密度为3 475 kg/m3。
经过以上假设,数值模拟过程需要对Navier-Stokes(N-S)方程与连续性方程进行求解。
N-S方程为
![]() ,
,
(1)
连续性方程为
![]() =0,
=0,
(2)
式中: xi、 xj(i, j=1, 2, 3)为笛卡尔坐标方向; ui、 uj为坐标上的速度分量; t为时间, s; ρ为密度, kg/m3; p为压强, Pa; ν为运动黏度,m2/s。
采用ANSYS CFX商业软件对N-S方程与连续性方程进行求解,运用High-resolution格式离散对流项,采用二阶欧拉向后差分格式离散瞬态项,运用标准k-ω湍流模型对砂磨机内部流场进行非定常计算,采用定常计算结果作为计算初场,设置时间步长为8.772×10-4 s,涡轮转速为760 r·min-1,模拟旋转6个周期,每个时间步长涡轮旋转4°,共模拟0.48 s。
所有壁面设置为无滑移壁面,涡轮内部流体区域设置为旋转坐标系,其余流体域设置为静止坐标系。采用压力为0.4 MPa的入口边界条件以及质量流量为0.6 kg·s-1的出口边界条件。
2.2 数值计算方案以及分析方法
针对HHN系列90 L涡轮式砂磨机,改进其涡轮结构,确定合适的涡轮转速,为后续的设计制造提供参考。首先对原结构下砂磨机进行数值模拟,分析原始流场内部流动规律,采用合理的方法对涡轮结构进行改进设计,通过一系列改进后,确定最终改进方案并对改进后的砂磨机内部流场进行分析,评价流场改进效果。
采用改进后的砂磨机模型,研究涡轮转速n对砂磨机内部流场以及研磨强度的影响,在合理的范围内采用不同的涡轮转速进行模拟,分别为560、 660、 760、 860、 960 r·min-1。
改进后的涡轮应使整个速度场有较大的提升,使得研磨物料中的颗粒发生碰撞的频率以及能量提升。当物料颗粒直径较小的时候,造成物料颗粒破碎的主要作用力为剪应力,而剪应力大小主要由流体的速度梯度大小而决定,速度梯度大的区域剪应力大,颗粒碰撞的频率与强度越大,即研磨效果越好,可以用平均速度梯度的函数切变率S来表示,公式如下:
![]() ,
,
(3)
式中: x、 y、 z为直角坐标方向; ∂vx、 ∂vy、 ∂vz为为坐标上的速度分量; S为切变率, s-1。
对研磨腔内流体切变率进行相对体积占比与累积体积占比统计,相对体积占比为研磨腔中切变率在某一区间范围内的所有体积占总体积的比例,累积体积占比为研磨腔中切变率从0开始向上累积到某一数值的区间范围内的所有体积占总体积的比例。统计累积体积占比为50%与95%的点,分别代表整体研磨强度与最大研磨强度,记作S50、 S95,来评价砂磨机研磨性能。
3 计算结果及分析
3.1 砂磨机原始流场分析
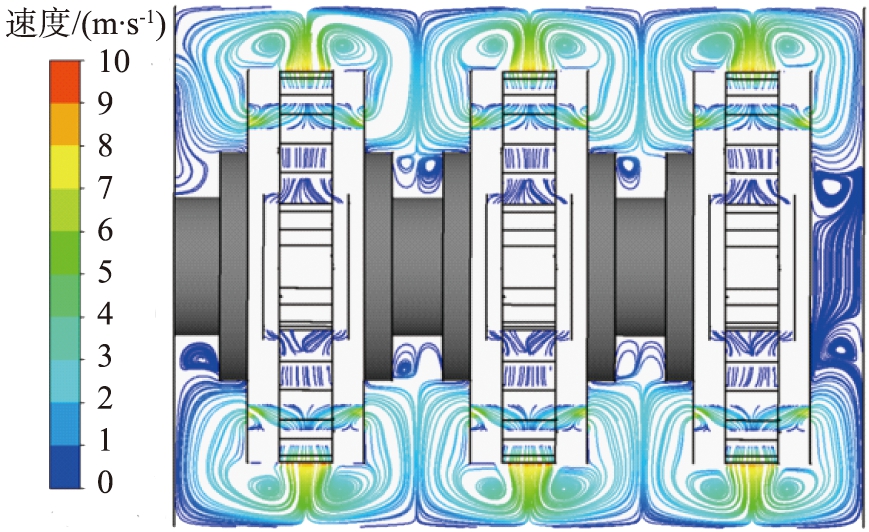
(a)研磨腔轴向截面
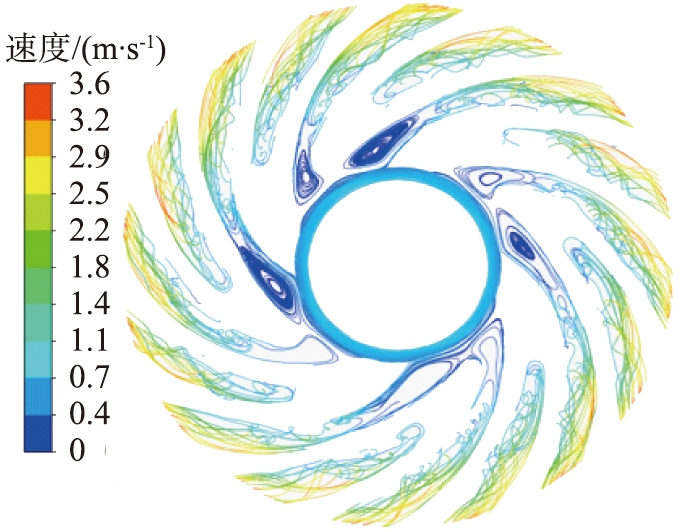
(b)涡轮内周向截面
图4 原始涡轮模型下流线图
Fig.4 Flow diagram of original turbine model
图4所示为原始涡轮模型下研磨腔轴向截面以及涡轮内周向截面流线图。由图4(a)可知,除涡轮侧面出口与陶瓷罐壁面附近流速较大外,其余部分流速较低,砂磨机内整体流速与涡轮外缘线速度相差较大,说明现有涡轮结构不能有效地对流体进行加速。由图4(b)可知,由于浆料黏性较大,因此受边界层的影响,涡轮壁面附近流速低,涡轮应当适当拓宽流道,以增强叶片对流体的加速能力。

图5 改进后的涡轮模型
Fig.5 Optimized turbine model
3.2 改进后砂磨机流场分析
对比不同设计方案数值模拟结果,最终选定以下涡轮结构改进设计:叶片减少到8片,并采用长短叶片;叶片出口角度β由原版42°改为47°;将原版圆弧段连接式叶片型线改为三次样条曲线;在涡轮背侧开槽,槽深为5 mm。改进后的涡轮结构如图5所示。
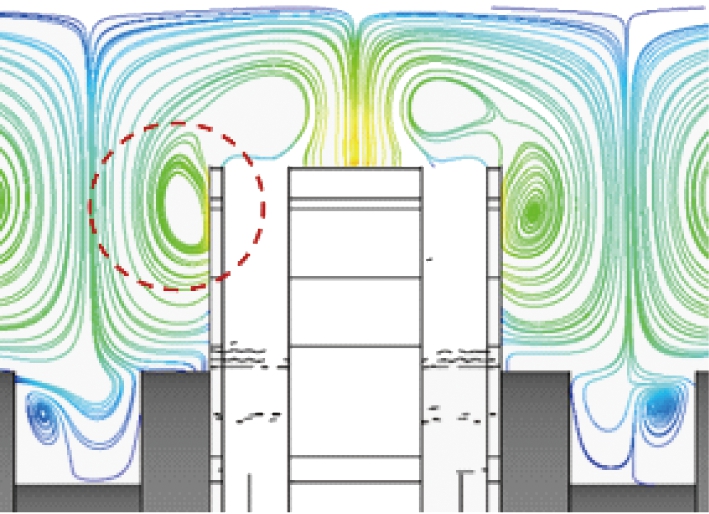
(a)改进后
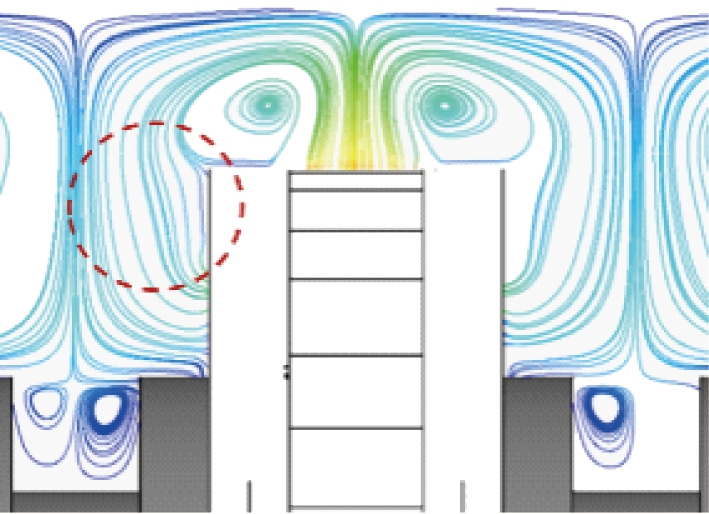
(b)改进前
图6 研磨腔局部轴向截面流线图对比
Fig.6 Comparison of flow chart of local axial section of grinding chamber
图6所示为涡轮改进前、后研磨腔轴向截面流线对比图。由图可知,改进后的研磨腔内的速度场变化明显,对比图6(a)、 (b)发现,原向下流动的流体受涡轮背面开槽的影响在涡轮两侧红色虚线标记的区域形成旋涡流动。除此之外,改进后的涡轮对应的研磨腔内的流体流速明显增大了,接下来对速度场进行更为详细的分析。
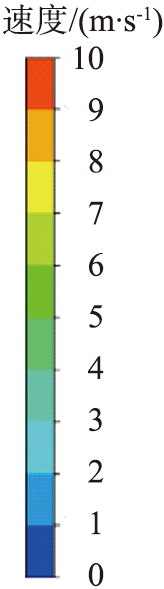

(a)改进后

(b)改进前
图7 涡轮中间局部周向截面速度云图
Fig.7 Velocity cloud of local circumferential section in middle of turbine
图7所示为涡轮改进前、后中间周向截面的速度对比云图。由图可知,改进后研磨腔内的流体流速提升明显,改进后的涡轮增强了对流体的加速能力,从而使得整个研磨腔的内部流速都有所提升。
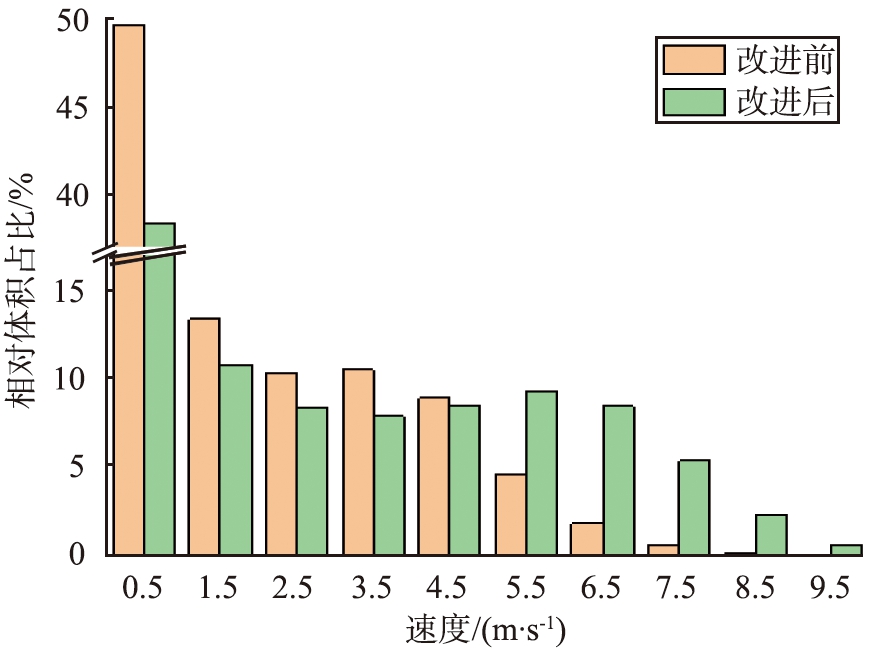
(a)涡轮

(b)研磨腔内
图8 涡轮改进前、 后速度分布
Fig.8 Velocity distribution before and after turbine improvement
对改进前、后的涡轮与研磨腔内的流体速度分布进行统计得到的数据如图8所示。由图8(a)可以发现,涡轮内流体速度小于5 m/s的区域有所减小,而流体流速大于5 m/s的区域明显增加,说明改进后的涡轮内高速流体所占区域的比例明显提升。流体经改进的涡轮后获得了更大的速度,图8(b)所示为研磨腔内的速度分布对比图,改进前研磨腔内的流体速度大部分小于3 m/s,改进后研磨腔内流速介于4~5 m/s的区域所占的比例最大,接近30%,并且流速大于3 m/s的区域所占的比例由15.9%显著增大到56.4%。
(a)轴截面,改进前

(b)轴截面,改进后

(c)中间截面,改进前

(d)中间截面,改进后
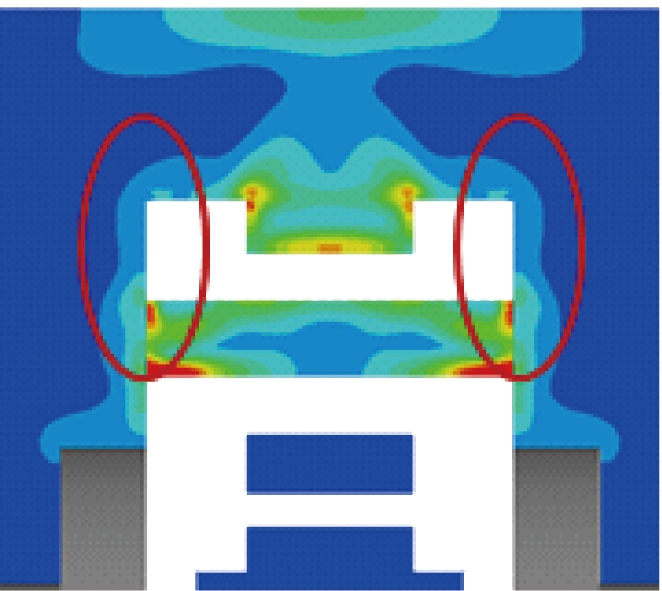
图9 涡轮改进前、后切变率云图对比
Fig.9 Cloud image comparison of turbine shear rate before and after turbine improvement
图9所示为涡轮改进前、后研磨腔轴向截面与涡轮周向截面的切变率云图。从图9(a)、(b)中可以发现,改进后切变率较大的红色与浅蓝色区域有所增加。 从图9(c)、(d)中可以发现, 涡轮内部流道中心以及叶片边缘区域切变率有所提升。当涡轮背后开槽后,附近区域(红圈标记处)的切变率有了明显的提升并且切变率数值较高,但受开槽深度仅有5 mm的影响,其所影响的区域并不大。
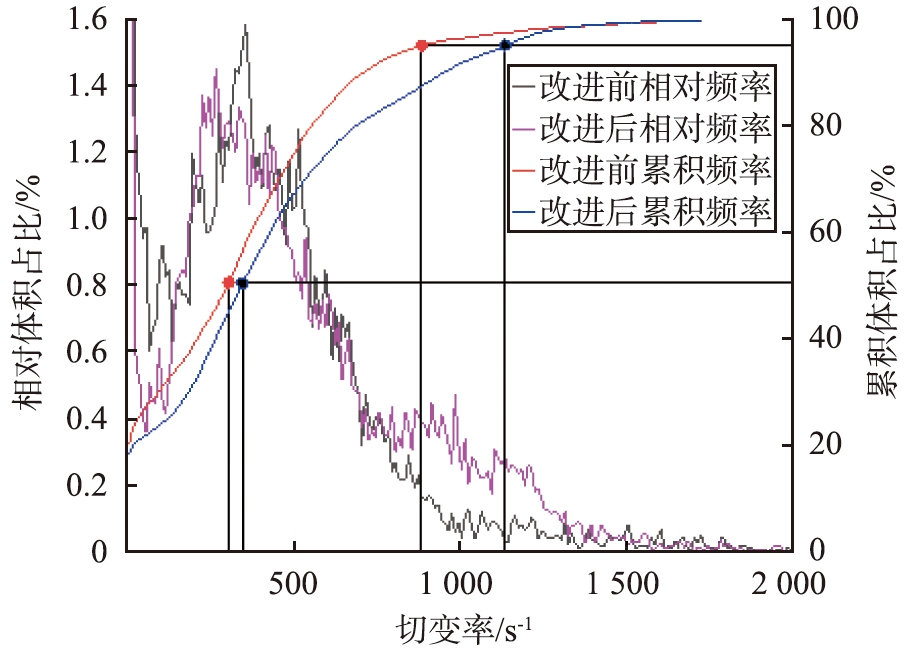
(a)涡轮
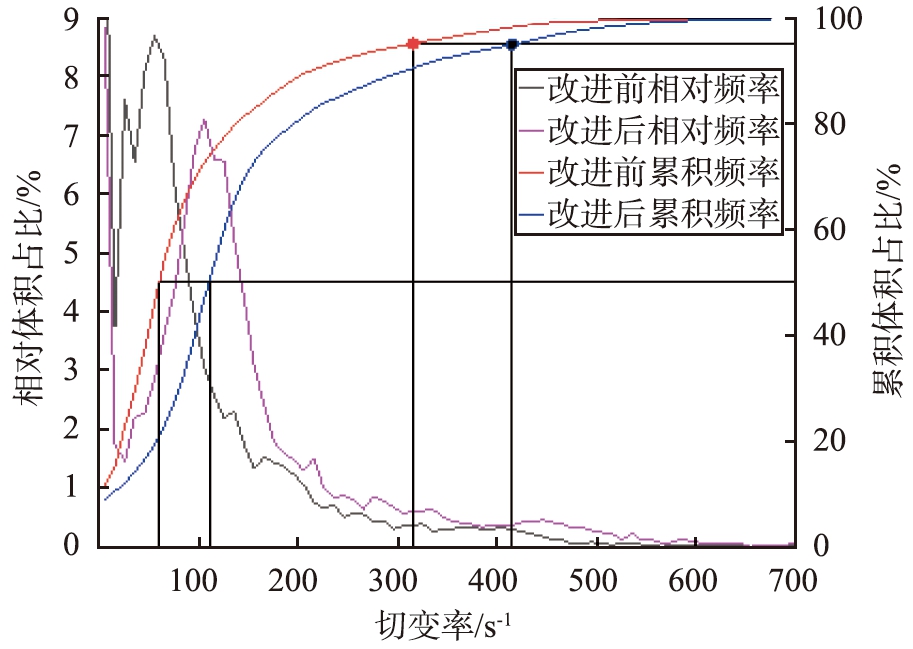
(b)研磨腔内
图10 涡轮改进前、后切变率分布体积占比对比
Fig.10 Comparison of shear rate distribution frequency before and after turbine improvement
图10所示为涡轮与研磨腔内流体在涡轮改进前、后切变率分布统计图。由图10(a)所示的涡轮内部情况可以看出,相对体积占比曲线主要差别在切变率为750~1 300 s-1的区间内,改进后的砂磨机在这一切变率区间内的相对体积占比有明显提升,改进后的累积体积占比曲线呈现出整体向右偏移的趋势,表明涡轮内高切变率区域增加。由图10(b)所示的研磨腔内情况可以看出,与涡轮内部的变化相似,相对与累积体积占比曲线整体呈现出向右偏移的趋势,这是由改进后研磨腔内部整体流速增加的原因引起的。
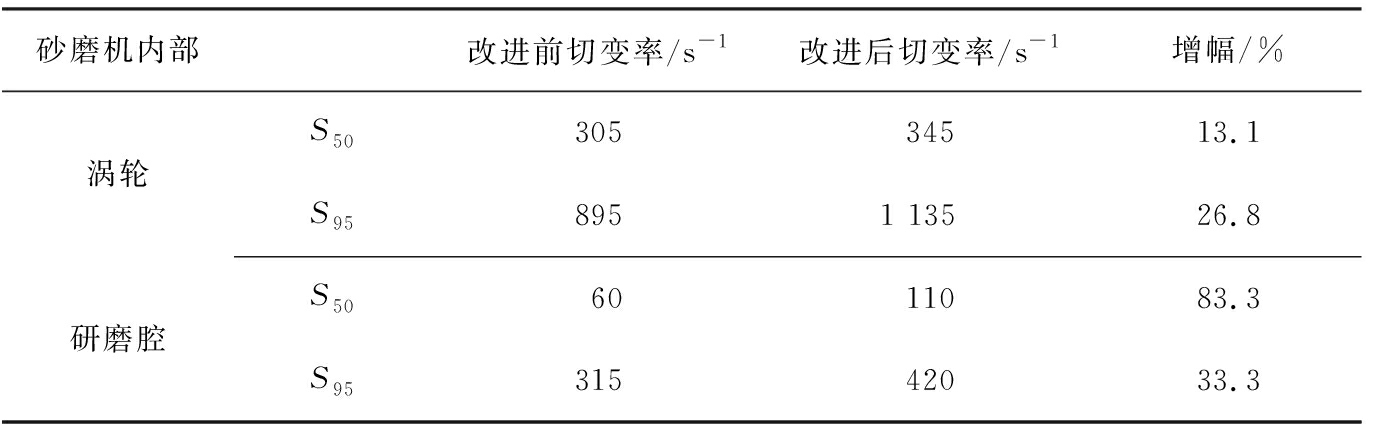
表3所示为涡轮内与研磨腔内S50与S95的数值变化以及改动前、后的增幅。从表中可以看出,在涡轮内与研磨腔内S50与S95都有较大的增幅,其中研磨腔内切变率的增幅要大于涡轮内部的,尤其S50的值增长了83.3%。
表3 涡轮改进前、后S50及S95变化
Tab.3 Changes of S50 and S95 before and after turbine improvement
砂磨机内部改进前切变率/s-1改进后切变率/s-1增幅/%涡轮S5030534513.1S958951 135 26.8研磨腔S506011083.3S9531542033.3
3.3 涡轮转速的影响
采用改进后涡轮模型对涡轮转速所带来的影响进行研究,在保持其他参数不变的情况下,对5组不同的涡轮转速n进行模拟,对比内部流场评价砂磨机研磨强度。
图11所示为不同转速下涡轮中心周向截面速度云图。涡轮内部流速随着离心半径增加而增加,在涡轮出口附近出现最大值。相同位置的流体速度同涡轮转速成正比,出口附近增长趋势最明显,这是因为转速增加后,涡轮内部离心力增大,流体获得的加速度更大造成的。
对不同转速的涡轮内流体速度分布体积占比进行统计,如图12所示。从图中可以发现,随着转速的增加,涡轮内部高速流体所占区域的比例增大,低速流体所占的区域比例减小,涡轮作为动力部件其转速不仅对涡轮内部流体产生影响而且影响研磨腔内的流体。


(a) 560 r·min-1

(b) 660 r·min-1

(c) 760 r·min-1

(d) 860 r·min-1

(e) 960 r·min-1
图11 不同转速下的涡轮中间截面速度云图
Fig.11 Velocity cloud of turbine middle section at different speeds
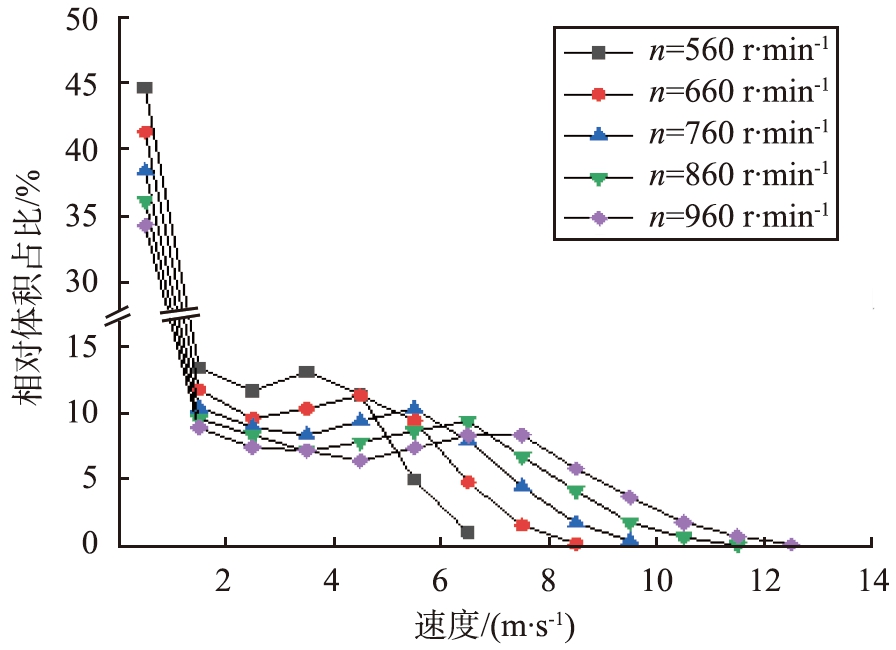
图12 不同转速下的涡轮内速度分布曲线
Fig.12 Frequency curves of velocity distribution in turbines at different speeds

(a) 560 r·min-1

(b) 660 r·min-1

(c) 760 r·min-1

(d) 860 r·min-1

(e) 960 r·min-1
图13 不同转速下的轴截面速度云图
Fig.13 Cloud image of axial section velocity at different speeds
图13所示为不同转速下的研磨腔内轴向截面速度云图。由图可知,随着转速增加研磨腔内除陶瓷罐边缘外的流速都有所提升, 并且随着转速增加影响的区域更广。 统计不同转速下的研磨腔内流体速度分布如图14所示。由图可知,速度分布曲线形状并没有发生改变,只是向右偏移,与涡轮内流体变化规律相同,即流速与转速成正比。
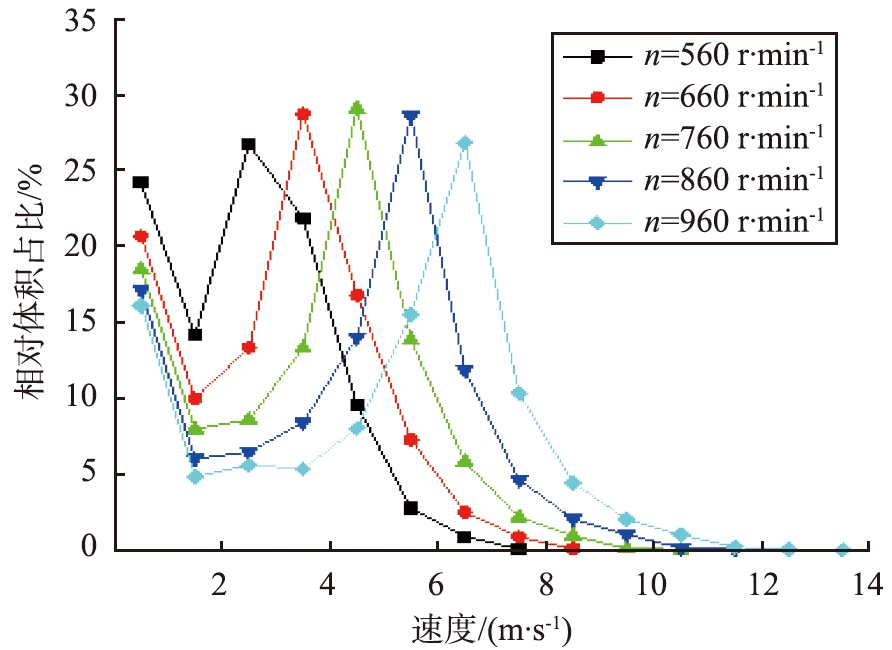
图14 不同转速下的研磨腔内速度分布曲线
Fig.14 Frequency curve of grinding chamber velocity distribution at different rotational speeds

(a) 560 r·min-1

(b) 660 r·min-1

(c) 760 r·min-1

(d) 860 r·min-1

(e) 960 r·min-1
图15 不同转速下的涡轮中间截面切变率云图
Fig.15 Cloud diagram of turbine mid-section shear rate at different speeds
图15所示为不同转速下涡轮内中间截面的切变率云图。从图中可以发现,随着转速的增加,涡轮内高切变率的区域逐渐增加,叶片表面与流道中心区域的切变率增长明显。图16所示为研磨腔轴向截面的切变率云图。从图中可以看出,随着转速的提升,研磨腔内的高切变率的区域也随之提升。切变率变化较大的区域主要包括涡轮外表面附近、涡轮出口附近、涡轮出口对应的陶瓷罐表面附近以及研磨腔端盖附近。

(a) 560 r·min-1

(b) 960 r·min-1
图16 不同转速下的轴截面切变率云图
Fig.16 Cloud diagram of axial section shear rate at different rotational speeds
为定量分析转速对研磨强度带来的影响,统计了涡轮内与研磨腔内S50和S95在不同涡轮转速下的数值,得到线性拟合图,如图17所示。结果表明,在研究转速范围内,S50和S95都与转速呈正比例线性关系,可以得到线性拟合公式:
S50=-79.12+0.552n,
(4)
S95=-134.76+1.611n,
(5)
![]() ,
,
(6)
![]() ,
,
(7)
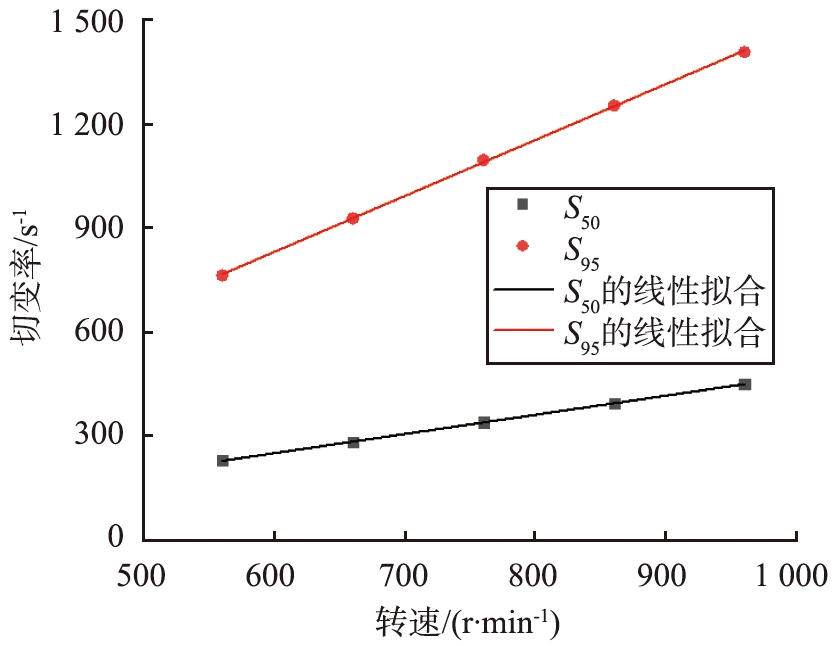
(a)涡轮
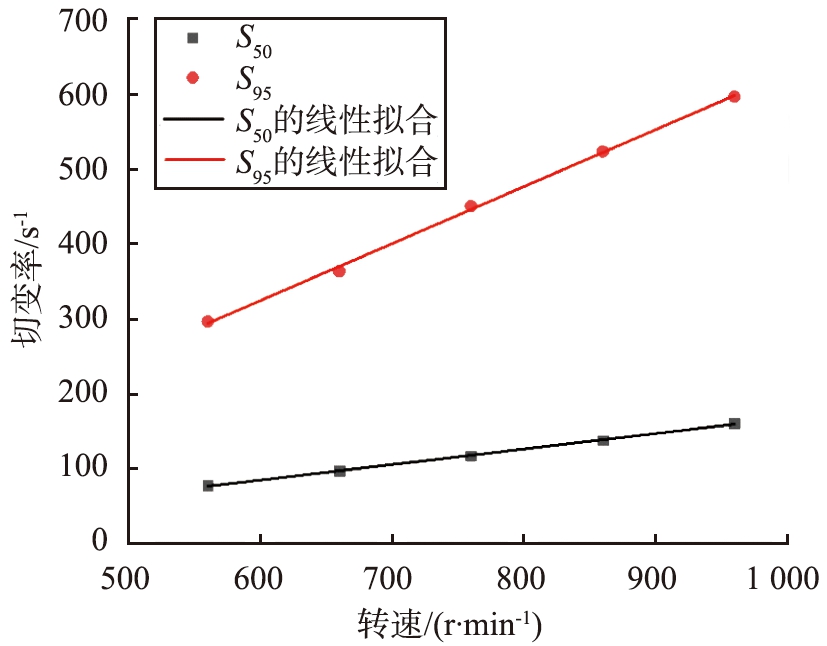
(b)研磨腔
图17 S50和S95随涡轮转速的变化
Fig.17 Changes of S50 and S95 with turbine speed
式中:![]() 为研磨腔内切变率累积体积占比为50%的值,
为研磨腔内切变率累积体积占比为50%的值,![]() 为研磨腔内切变率累积体积占比为95%的值, s-1; n为转速,r·min-1。
为研磨腔内切变率累积体积占比为95%的值, s-1; n为转速,r·min-1。
4 结论
1)涡轮经过改进后,内部流道更宽,流体受到的阻力减小,使得内部流体流速提升,进而使得整个研磨腔内的流体流速增大。流速的增加使研磨介质中颗粒间碰撞频率与能量都得到提高,同时增大了流体近壁侧的速度梯度。
2)改进后的砂磨机流场内整体切变率增大,流场内S50与S95的数值都显著增大,表明与研磨效率有关的整体研磨强度和与最小粒径有关的最大研磨强度都有提高,因此,改进后的砂磨机研磨效率更高,产品颗粒更细。
3)改变涡轮转速对涡轮式砂磨机流场特征并未产生较大影响,只是相关参数数值上的增加,随着涡轮转速增加,无论是整体研磨效率还是最大研磨强度都得到了一定提高,自定义参数S50、 S95与涡轮转速呈线性正相关。
[1]朱常龙, 任常兴, 许永胜. 超音速气流粉碎机生产超细粉体的安全问题探讨[J]. 安全与环境工程, 2003(3): 88-91.
[2]黄业豪, 李茂林, 姜兴科. 卧式搅拌磨机能量利用率的研究[J]. 中国粉体技术, 2016, 22(1): 44-47.
[3]姚征, 陈康民. CFD通用软件综述[J]. 上海理工大学学报, 2002, 24(2): 137-144.
[4]CHEN Y S, SHAN X W, CHEN H D. New direction of computational fluid dynamics and its applications in industry[J]. 中国科学E辑: 英文版, 2007, 50(5): 521-533.
[5]徐传福, 车永刚, 李大力, 等. 天河超级计算机上超大规模高精度计算流体力学并行计算研究进展[J]. 计算机工程与科学, 2020, 42(10): 1815-1826.
[6]曾桂忠, 段希祥. 立式球磨机在铝土矿选择性磨矿的试验研究[J]. 矿山机械, 2009, 37(17): 58-60.
[7]陈璟, 谢帮灵, 吴国勇, 等. 应用CFD技术改进研磨机结构[J]. 中国胶粘剂, 2017, 26(2): 29-34.
[8]张国旺. 超细搅拌磨机的流场模拟和应用研究[D]. 长沙: 中南大学, 2005.
[9]张国旺, 黄圣生. 超细搅拌磨机的流场模拟和应用[J]. 矿山机械, 2008, 36(21): 78-83.
[10]龚曙光, 刘剑, 谢桂兰, 等. 卧式超细搅拌磨机分散盘的结构改进及试验研究[J]. 矿山机械, 2017, 45(12): 36-42.
[11]赵艳平. 超细卧式搅拌磨的流场模拟及其粉碎机理研究[D]. 昆明: 昆明理工大学, 2009.
[12]FUKUI S, TSUNAZAWA Y, HISATOMI S, et al. Effect of agitator shaft direction on grinding performance in media stirred mill: investigation using DEM simulation[J]. Materials Transactions, 2018, 59(3): 488.
[13]ZHENG M, WU F, HUANG W, et al. Multiphysics design and analysis of an impeller-type superfine grinding turbulence mill driven by a high-speed permanent magnet machine[J]. Journal of Mechanical Science and Technology, 2021, 35(12): 5611-5620.
[14]KWADE A. Wet comminution in stirred media mills: research and its practical application[J]. Powder Technology, 1999, 105(1): 14-20.
[15]GRAEME L. CFD modelling of a stirred bead mill for fine grinding[C]//CSIOR Minerals. Proceedings of the Second International Conference on CFD in the Minerals and Process Industries: 1999. Melbourne: CSIOR, 1999: 449-454.
[16]STEHR N, SCHWEDES J. Investigation of the grinding behavior of a stirred ball mill[J]. German Chemical Engineering, 1983, 6(6): 337-343.