机械式粉体混合机是一种通过机械搅拌混合粉体物料的设备,目前已经在材料、化工等领域得到了广泛应用。搅拌功率能直接影响搅拌过程中的能量消耗,是研究粉体混合过程的重要参数。采用离散单元法(discrete element method,DEM)能够突破实验条件的限制,随时将运动过程暂停,对某一时刻出现的现象进行分析,不仅能够得到颗粒运动流的微观与宏观行为之间的联系,对粉体混合设备的混合效果和功耗情况进行简单快速的分析[1-3],还能够直观地观察颗粒运动学特性[4]。本文中使用EDEM软件模拟粉体颗粒的混合过程,通过对于颗粒运动规律的揭示和总结,对粉体运动过程进行全面分析。
国内外学者对于影响粉体混合过程中的搅拌功率、扭矩的参量进行了研究,总结了操作、结构参数对于搅拌过程和混合效果的实际影响。Nakamura等[5]运用三维离散元的方法模拟研究了不同的容器体积(2~112 L)对内部颗粒流、颗粒碰撞能量造成的影响;宣颖等[6]使用DEM模拟的方式,分析了搅拌转速、桨叶直径等参数对功率、扭矩的影响,并拟合总结得到了一种新的功率计算公式;Lekhal等[7]通过实验方法测量了立式圆筒混合机中的干、湿颗粒暴露表面的瞬时、平均、波动速度场;Remy等[8]采用数值模拟与实验验证相结合的方法,观测得到颗粒速度、温度分布,得到了叶片式混合机中颗粒的微观运动过程,获取物料运动速度与转速之间的关系;Remy等[9]对叶片式混合机中湿颗粒的流动特性进行粒子图像测速实验及验证;Chandratilleke等[10]采用离散元方法模拟细颗粒在垂直轴圆柱叶片混合器中的混合行为,检验了颗粒间的内聚力、倾角和颗粒内聚力对细颗粒流动、混合行为的影响和效果;Sebastian等[11]研究了黏性颗粒的表面能、直径等特性对颗粒混合行为过程的影响,并进行定量表征;Siraj等[12]通过数值模拟的方法分析桨叶形状对桨叶受力情况的影响,探究了桨叶各截面上的速度、力场的分布,总结分析桨叶叶片的形状、角度对于颗粒间接触力的影响。
综上所述,对于颗粒尺度、形状等参数对于功率、扭矩的影响情况,目前研究尚不深入。使用离散单元法探究颗粒尺度、形状对于搅拌扭矩和功率的影响规律,可以提高机械式粉体混合机使用寿命,为工业上的应用提供参考。
1 数值模拟的可靠性检验
1.1 DEM模拟
DEM是用来解决复杂运动问题的一种数值模拟方法[13]。该方法的核心思想是离散化所需要分析群体,研究离散化相对独立的个体,根据独立个体之间产生的作用力,通过牛顿第二定律以及个体受到的转矩来影响颗粒的运动,针对所有独立个体,在每一个对应的时间步内进行迭代计算,再及时刷新所有单元的位置,直到模拟过程的完成[14]。
分析颗粒的运动过程,作用于粒子上的力的计算公式为
(1)
(2)
式中:X为位置矢量,m;m为质量,kg;t为时间,s;Fc为接触力,N;g为重力加速度,m/s2;ωp为角速度,rad/s;τc为扭矩,N·m;I为惯性矩,N·m。
扭矩T计算公式为
(3)
式中:Fcx,i为粒子与桨叶间方向x轴方向的接触力,N;Fcy,i为y轴方向的接触力,N;rx,i为粒子到桨叶中心在x轴方向的位移,m;ry,i为y轴方向的位移,m;nc为发生接触粒子数。
1.2 模型建立
建立三维模型,模型筒体内径为180 mm,直叶平桨直径为d,模型的整体结构如图1(a)。在实验室搭建实验台,实验台由OS40-Pro LCD数控顶置式搅拌器、筒体、桨叶等各部分组成,整体结构如图1(b)所示。
1.3 DEM参数设置
在DEM中设置参数,颗粒的直径为4 mm,在搅拌筒的内部均匀填充2种颗粒,总数为20 000,在初始填充的方式上,选择上下填充,2种颗粒数各10 000,使得颗粒的装填容积达到整个搅拌筒的有效容积的35%,转速分别设置为100、200、300、400、500 r/min,时间为4 s。相关参数设置如表1、2所示。
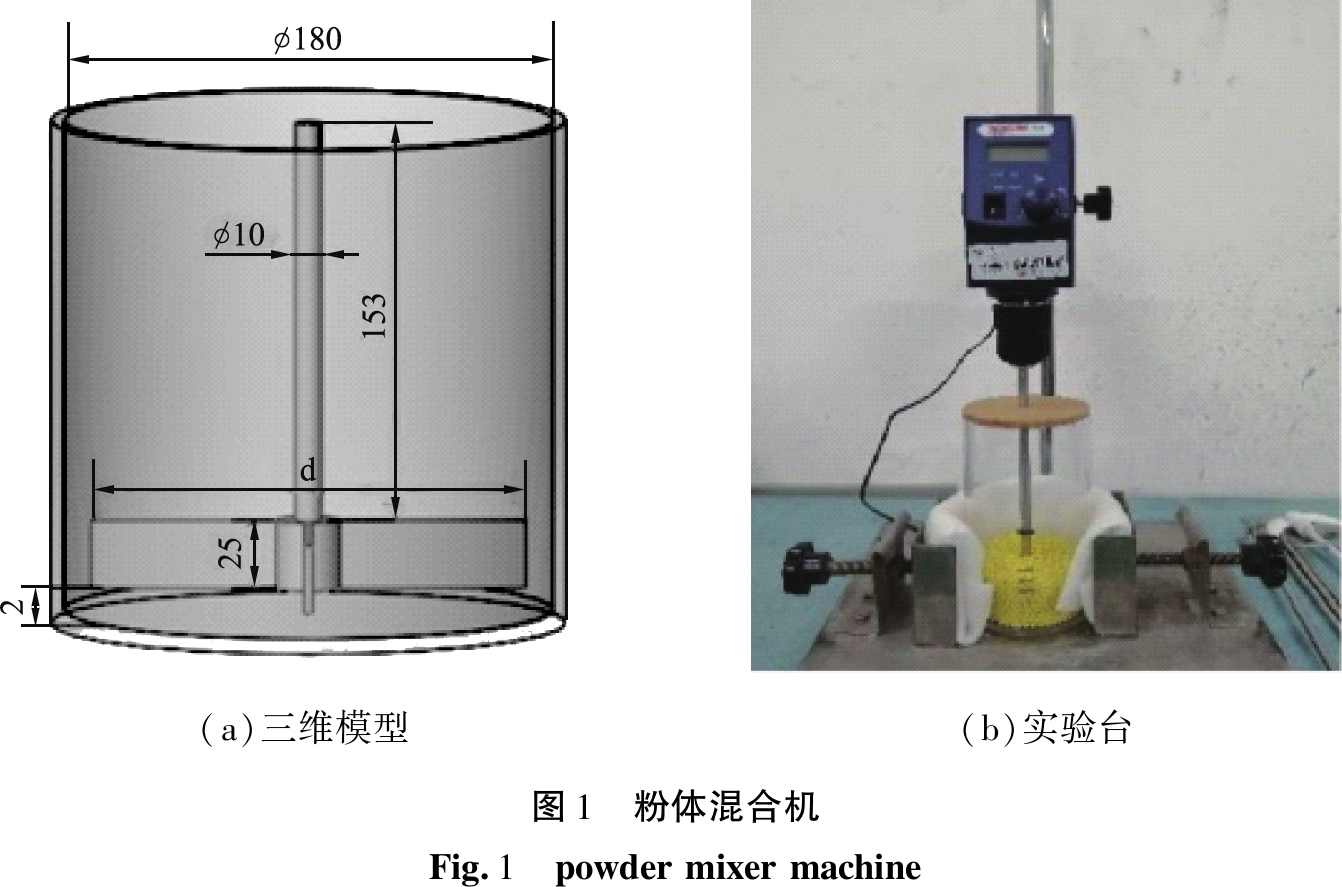
表1 DEM颗粒、壁面参数设置
Tab.1 Parameter setting of particle and wall in DEM

泊松比μ密度ρ/(kg·m-3)剪切模量G/Pa颗粒0.3512008.9×108壁面0.3712008.0×108
表2 DEM接触参数设置
Tab.2 Contact parameter setting in DEM

碰撞形式接触类型恢复系数E静摩擦系数fs动摩擦系数f颗粒与颗粒无滑移0.450.60.05颗粒与壁面无滑移0.450.40.05
1.4 实验验证
为验证数值模拟的可靠性,使用直径d为160 mm的四直叶平桨,改变搅拌转速,进行混合实验。图2所示为实验与模拟中的颗粒静止状态对比。
将顶面的图像分为26块等大的区域,进行AI图像分析识别每块区域中的红色颗粒所占面积,通过模拟和实验的搅拌筒内顶面颗粒分布情况的比对,对颗粒混合过程进行定量比较,计算模拟与实验之间的相对偏差,来判断模拟的准确程度[15]。相对偏差的公式为
(4)
式中:Eri为偏差;psi为红色仿真比例;pei为红色实验比例。
顶面图对比如图3所示。在实验过程中,观察到了与模拟过程类似的混合过程,通过实验结果表明,实验中红色颗粒的分布结果与模拟过程吻合情况较好。

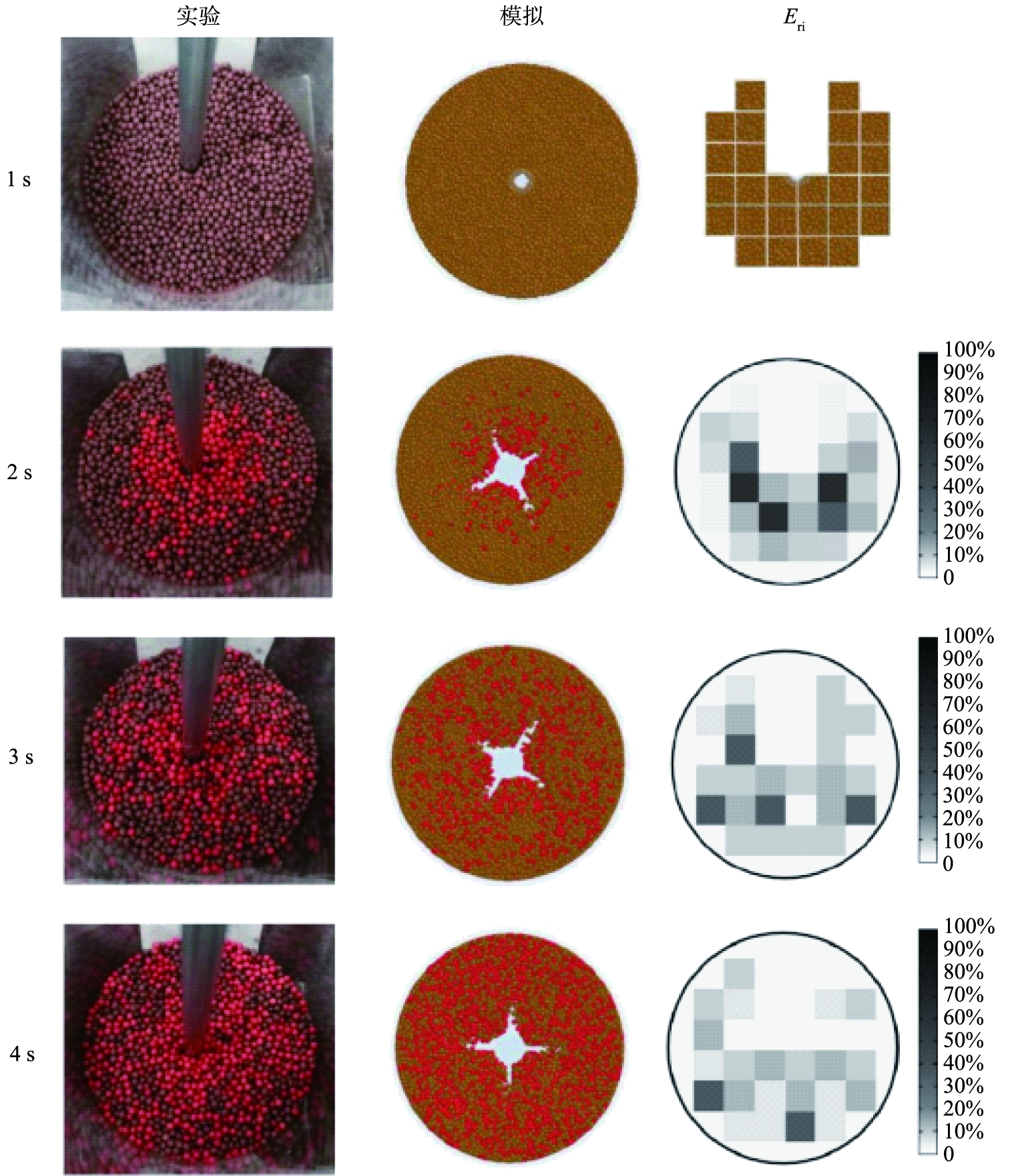
图3 实验与仿真上表面颗粒颜色分布对比
Fig.3 Comparison of color distribution of surface particle between experiment and simulation
模拟结果表明:当搅拌桨叶的直径固定为160 mm不变时,随着转速的增加,功率值持续增大,功率值与转速呈正相关的趋势。图4所示为扭矩和功率的结果对比,可知二者变化的走向趋势类似。
综合分析影响搅拌功率值的各种特性对于搅拌过程、混合效果的影响,总结推出搅拌功率公式为
(5)
式中:N为转速,r/min;n为桨叶数。
碰撞力作用在旋转轴方向的扭矩为搅拌扭矩,由EDEM软件计算后直接导出,功率由扭矩通过公式转化计算得出。对实验测得的功率值与公式所得的计算值进行对比,如图5所示,偏差小于10%,说明数值模拟具有一定的可靠性。
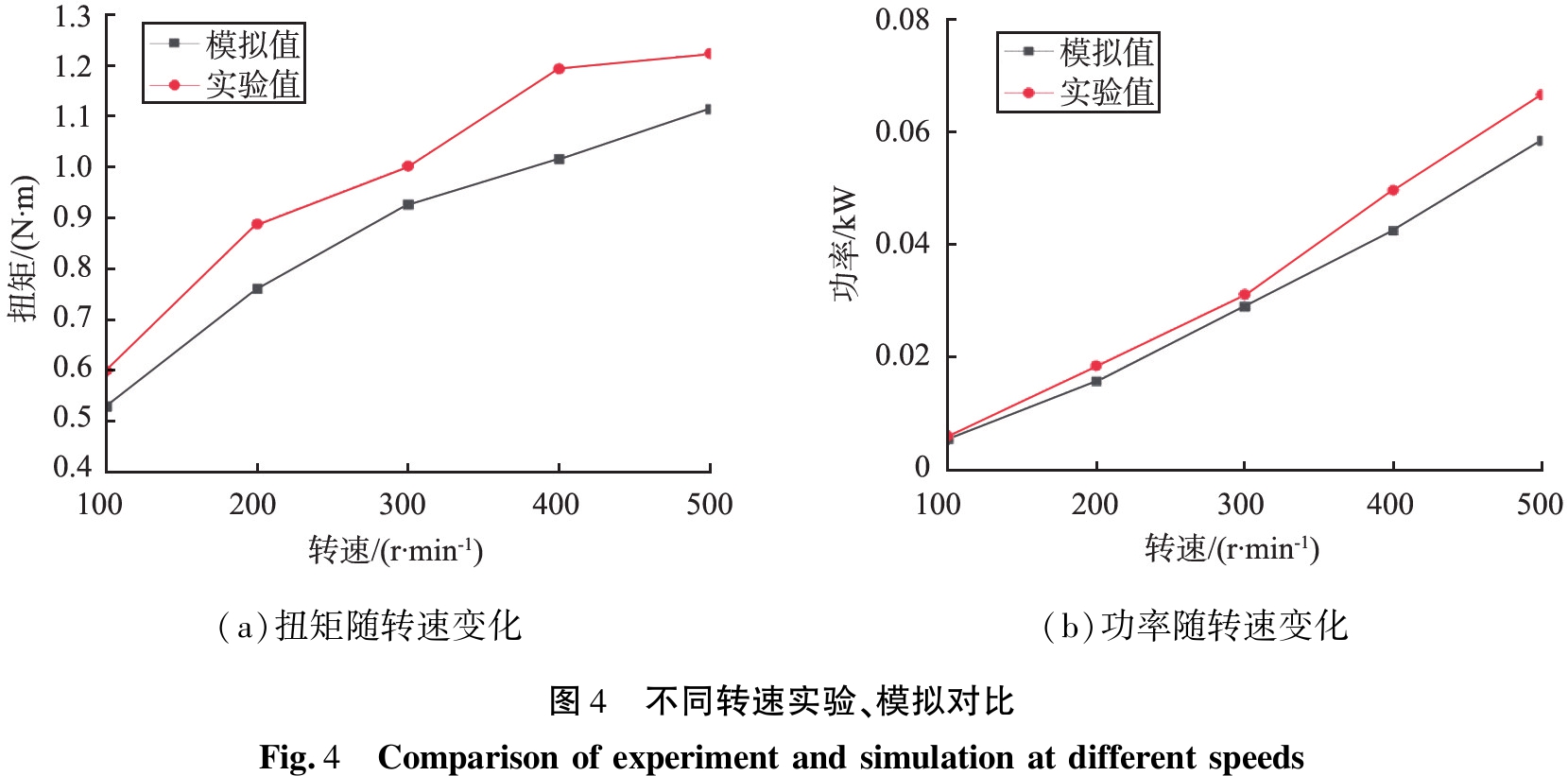
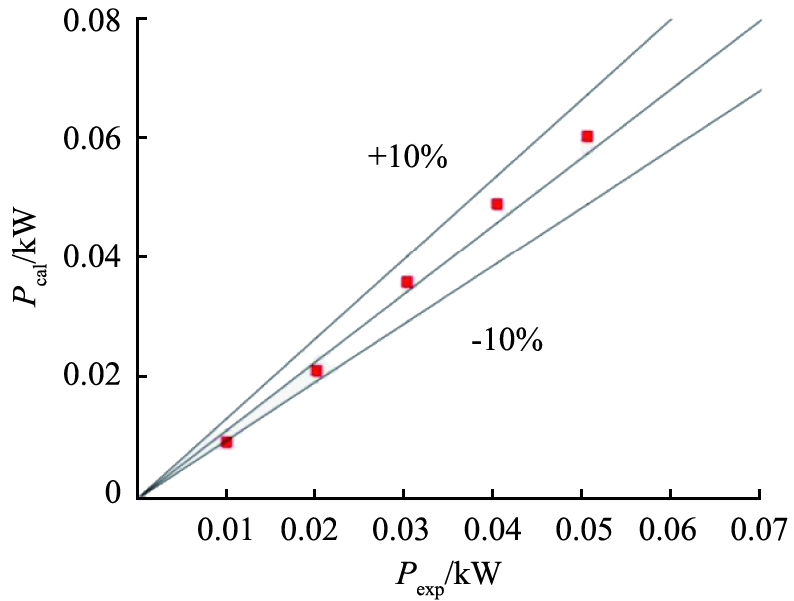
图5 不同转速下的实验测得值与模拟所得值的偏差
Fig.5 Deviation between experimental and simulated values at different speeds
2 颗粒尺度和形状对搅拌扭矩和功率的影响
2.1 颗粒粒径大小对扭矩和功率的影响
2.1.1 DEM参数设置
使用三维软件建立粉体混合机的模型,搅拌桨为四直叶平桨,保证搅拌筒内颗粒静止填充后的所占总体积35%不变,即完成装填后的初始状态下,颗粒堆积总高度一致,颗粒数分别为160 000、20 000、5 926 ,直径分别为 2、4、6 mm,相关参数设置如表1、2所示。
2.1.2 结果分析
图6为颗粒粒径为4 mm时,不同时刻粉体混合过程效果图。当颗粒粒径改变时,仿真效果相似,均在4 s时达到稳定混合状态。图7为颗粒粒径不同时,机械搅拌扭矩值随着搅拌转速的升高而持续变化的趋势图。从图中可以看出,在同一转速下,当颗粒填充量不变的时候,随着颗粒平均粒径的减小,扭矩值在不断增大。这是由于当颗粒直径越小的时候,颗粒间的孔隙率就越小,使得颗粒在下落时,堆积密度更大,对搅拌桨施加的力也更大。随着转速增加,搅拌过程中的扭矩值呈现增加的趋势。其中除了粒径为2 mm的颗粒外,粒径为4、6 mm的颗粒均表现出扭矩值线性增大的趋势。
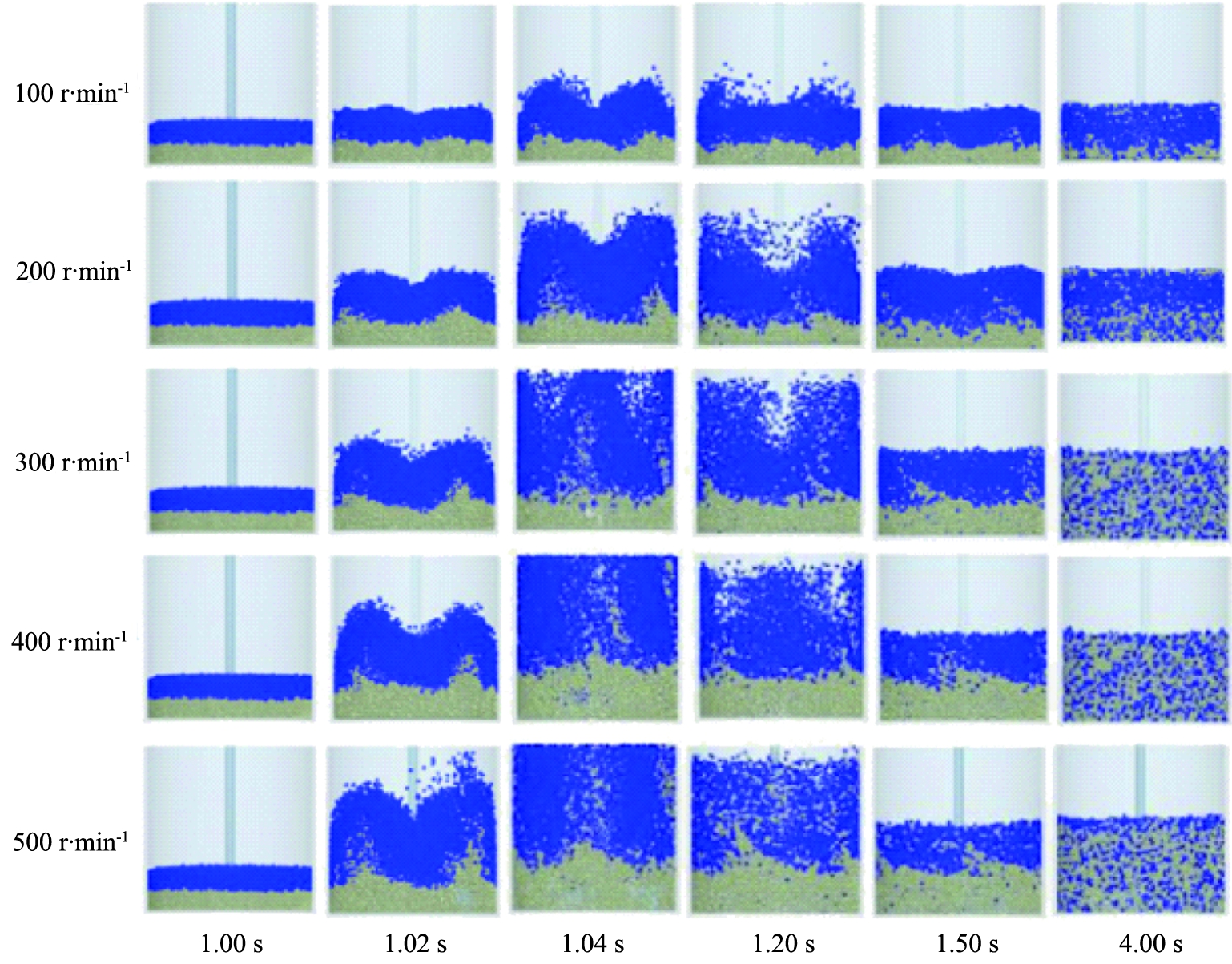
图6 不同时刻粉体混合状态图
Fig.6 Powder mixing state diagram at different times
在搅拌过程中,搅拌扭矩值波动最为明显的情况出现在颗粒直径为2 mm的时候,当转速达到300 r/min之后,扭矩值的增加速度开始放缓,且增幅变化为三者中最大。这是因为颗粒较细小,所以扬起度更大,在被抛起时的有效上升距离比其他2种颗粒都更高,且随后下落的速度为三者中最慢。
图8为颗粒粒径不同时,搅拌功率值随转速变化图。随着转速的增大,功率值呈线性增加的趋势,当转速相同且颗粒充填量保持不变的时候,随着粉体颗粒的粒径增大,功率值会逐渐减小。而当转速持续增大时,功率值随着颗粒粒径的减小波动会更加明显。
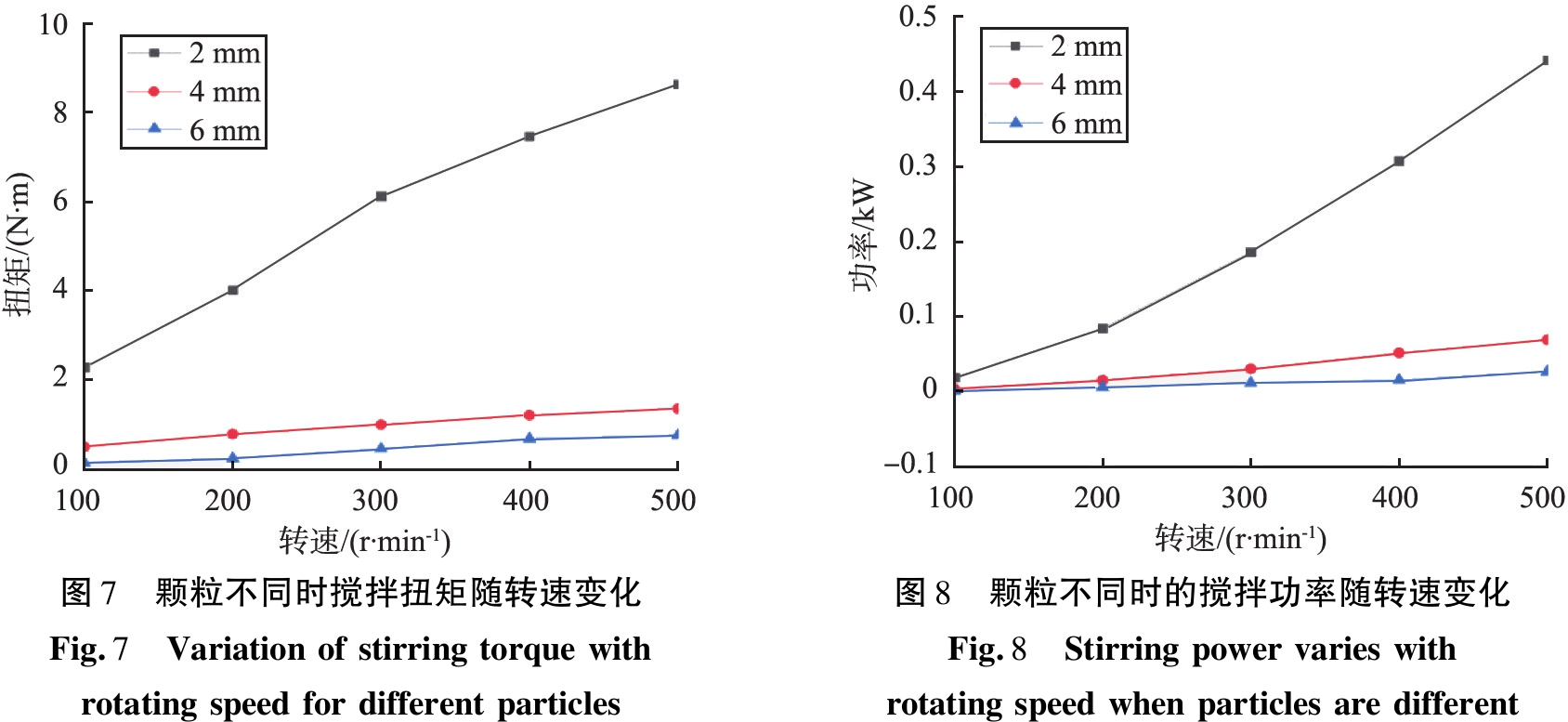
图7 颗粒不同时搅拌扭矩随转速变化Fig.7 Variationofstirringtorquewithrotatingspeedfordifferentparticles图8 颗粒不同时的搅拌功率随转速变化Fig.8 Stirringpowervarieswithrotatingspeedwhenparticlesaredifferent
2.1.3 单、多种颗粒对扭矩、功率的影响
选取2组颗粒,1组为直径4 mm的单种标准球形颗粒,另1组为粒径呈现正态分布的标准球形颗粒,也就是粒径不同的多种颗粒,对2组颗粒分别进行模拟。图9所示为颗粒不同时,机械搅拌扭矩值随着转速改变而不断变化的大小对比图。由图9可知,二者的扭矩值十分接近,但前者的较后者的略小。分析原因,由于受到重力应变影响,粒径较大颗粒之间的空隙可以轻易容许细小颗粒穿过,这使得当二者填充量完全相同的时候,后者的堆积会更加密实,在同样大小的区域内颗粒质量更大,搅拌桨的受力也更大,从而使扭矩值变大。同时,2种类型的颗粒其扭矩值的变化趋势都随转速升高而增加,当转速升到300 r/min的时候,后者的增速开始变缓。具体比较数值可以得知,二者的扭矩值虽有差异;但相差不大,所以单、多种颗粒之间的搅拌扭矩差距较小。
图10为2种颗粒的机械功率值对比图。由图可知,二者的功率值较为接近,随着功率升高而改变的变化趋势几乎相同,但直径为4 mm的球形颗粒的功率值略小。
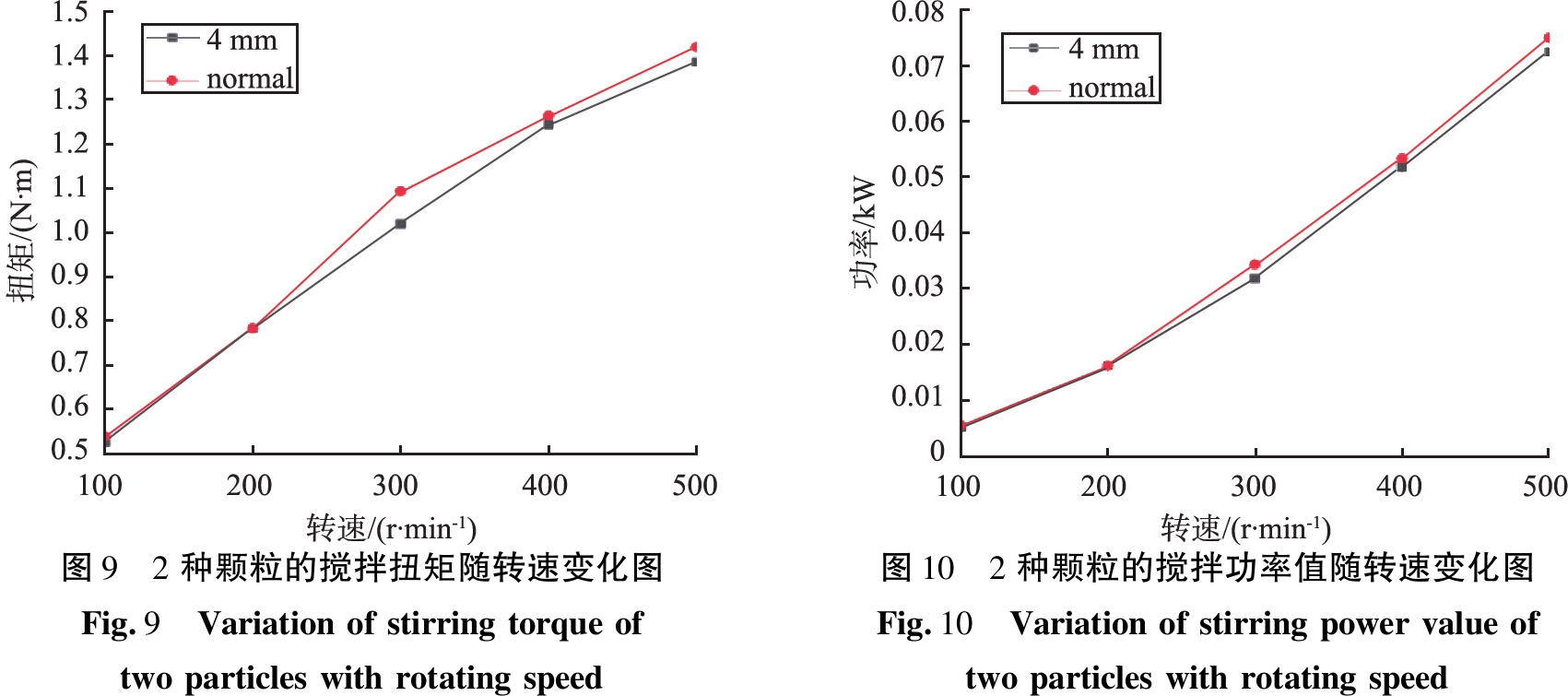
图9 2种颗粒的搅拌扭矩随转速变化图Fig.9 Variationofstirringtorqueoftwoparticleswithrotatingspeed图10 2种颗粒的搅拌功率值随转速变化图Fig.10 Variationofstirringpowervalueoftwoparticleswithrotatingspeed
2.2 颗粒形状对扭矩、功率的影响
表示颗粒的形状特征时通常使用形状因数[16]。本文中用球形度表征颗粒形状,探索研究颗粒形状对扭矩值和功率值的影响[17],对非球形颗粒特性与搅拌功率的关系进行定量分析。
2.2.1 不同球形度的颗粒模型
如图11所示,建立体积相同、球形度不同的3种颗粒模型,椭球型颗粒模型的球形度为0.955,圆柱形颗粒模型的球形度分别为0.86和0.69。当颗粒的形貌接近于球形时,球形度更接近于1,球形度计算公式为
(6)
式中:S1为颗粒表面积,m2;S0为等体积球体表面积,m2。

在建模方式上,采用球形颗粒叠放的方式完成对不同形状的3种椭球颗粒的建模[18]。保证单个颗粒的体积相同,椭球模型内部分别填充有5、3、9个球形颗粒,通过控制球形颗粒的尺寸、数量,保证体积相同而球形度不同,球形度分别为0.955、0.86、0.69,经组合调整后的颗粒模型如图11所示。
2.2.2 仿真条件设置
搅拌时控制变量,保证搅拌筒内颗粒静止填充后的所占总体积为35%不变,即装填后的高度一致,不同形状的颗粒堆积方式、堆积密度不同,填充颗粒的数量由软件自动计算。在搅拌筒内部分别填充球形度φ=1、0.955、0.86、0.69的颗粒,填充个数分别为20 000、40 000、30 000、16 000。
2.2.3 结果分析
图12所示为球形度φ=1、0.955、0.86、0.69时,各组搅拌扭矩随转速的变化。随着转速的增大,所有组别的搅拌扭矩值的变化都呈现上升趋势。在转速相同的情况下,随着球形度的减小,扭矩值也呈减小的趋势。这是由于随着球形度的减小,球形颗粒的堆积情况逐渐变得松散,流动性能逐渐减小,颗粒之间的相互渗透速度也在变慢,从而导致扭矩值更小。
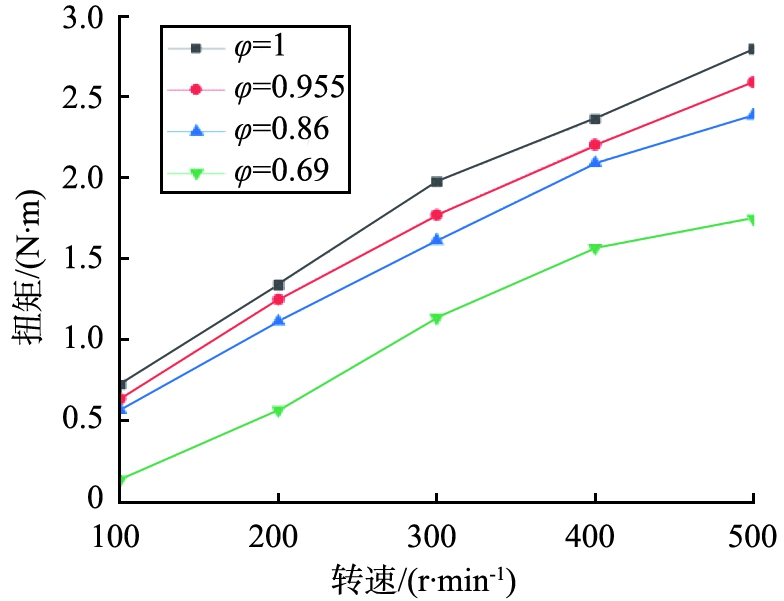
图12 不同颗粒下的机械扭矩随转速变化
Fig.12 Mechanical torque of different particles changes with speed
从结构来看,球形度φ=0.955的颗粒为椭球状,而φ=0.86的颗粒为短柱形,虽然二者形状不同,但长径比比较接近,扭矩值随着球形度变化而改变的趋势也大致相同,均始终呈现随球形度减小而降低的趋势。这是由于当粉体颗粒的形状相似时,球形度较小的颗粒堆积时会更加松散,堆积密度会更小,在同样的填料高度下,颗粒的总质量更小,施加在搅拌桨叶上的作用力也更小,因此,当粉体颗粒的外形较为接近时,混合时的扭矩值会随着球形度的减小而呈降低的趋势。
从形状上来看,球形度φ为0.86或0.69的粉体颗粒均为柱状颗粒,但前者的机械扭矩值明显要小于后者的。这是因为φ=0.86的粉体颗粒结构偏向于粗短柱状,而φ=0.69的粉体颗粒则偏向于细长条状,而扁长类颗粒即球形度φ=0.69的粉体颗粒在堆积的时候更容易形成架桥现象,在相同的填充高度之下,粉体的堆积情况更加松散,导致扭矩值更小;在颗粒的搅拌混合过程中,扁长类颗粒的扬起度会更高,架空现象更容易出现。
选取2种柱形颗粒,即球形度φ为0.86、0.69的柱状颗粒,图13为同一时刻同种条件下稳定混合时的模拟对比图。由图可知,球形度较大的粉体颗粒在混合时的颗粒床膨胀高度更高,更容易出现架空现象。在混合搅拌过程中,与搅拌桨叶的碰撞颗粒数量也相对较少,对搅拌桨叶所施加的压力也更小,因此,当形状相同时,随着粉体球形度的减小,粉体混合机内的搅拌扭矩值呈现减小的趋势。
图14所示为3组颗粒球形度不同时,搅拌功率随转速变化图。搅拌功率都随转速增大而呈增长趋势;当搅拌转速相同的时候,随着球形度的减小,功率值均不断减小。

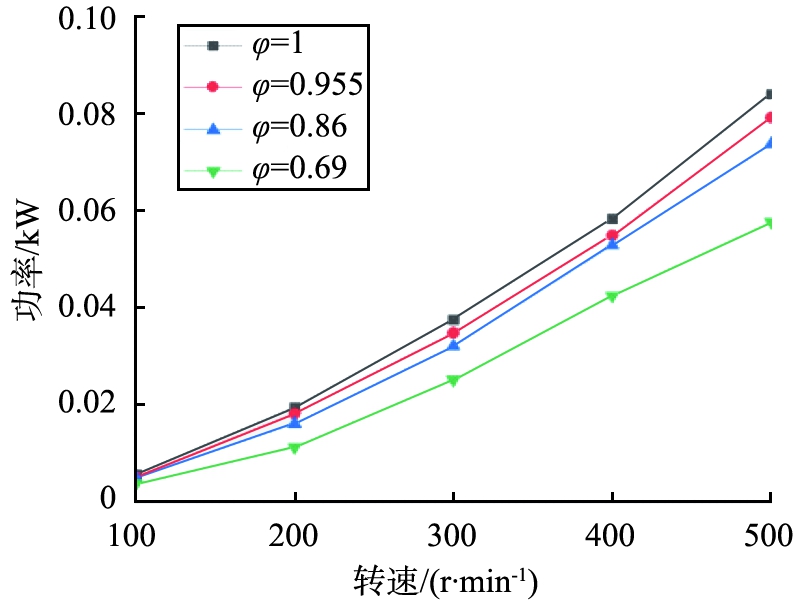
图14 不同颗粒下的机械功率随转速变化
Fig.14 Mechanical power of different particles varies with speed
3 结论
1)当颗粒充填量相同时,随着颗粒平均粒径的减小,同一转速下直叶桨式粉体混合机内扭矩值和功率值均逐渐增大。
2)当转速持续增大的时候,所有粒径的颗粒的搅拌功率值的变化都呈现线性增加的趋势,且随着颗粒粒径的减小,搅拌功率值的波动变得更加明显。
3)基于正态分布的颗粒,对搅拌扭矩值的影响略大于粒径4 mm标准直径的颗粒,2种类型的颗粒对搅拌扭矩值的影响都随转速增大呈增加,当转速达到300 r/min时,前者对搅拌扭矩值的影响随增速逐渐减缓,2组颗粒对搅拌扭矩值的影响较为接近。
4)在相同的填料高度下,无论何种颗粒,机械搅拌扭矩和功率值都随球形度的逐渐减小而呈现不断下降的趋势。对于外形接近或相同形状的粉体颗粒,随着球形度的减小,在粉体混合机内混合时的搅拌扭矩值都呈现减小的趋势。
[1]CLEARY P W.Industrial particle flow modelling using discrete element method[J].Engineering Computations,2009,26(6):698-743.
[2]HASSANPOUR A,TAN H,BAYLY A,et al.Analysis of particle motion in a paddle mixer using discrete element method (DEM)[J].Powder Technology,2010,206(1):189-194.
[3]曹鑫鑫,徐超.基于EDEM的稳定土搅拌机搅拌装置的优化研究[J].建设机械技术与管理,2016,29(3):62-64.
[4]ROJEK J,LABRA C,SU O,et al.Comparative study of different discrete element models and evaluation of equivalent micromechanical parameters[J].International Journal of Solids and Structures,2012,49(13):1497-1517.
[5]NAKAMURA H,FUJII H,WATANO S.Scale-up of high shear mixer-granulator based on discrete element analysis[J].Powder Technology,2013,236:149-156.
[6]宣颖,刘雪东,周成奇,等.粉体混合过程及搅拌功率的DEM数值模拟和实验[J].化工进展,2021,40(7):3598-3607.
[7]LEKHAL A,CONWAY S L,GLASSER B J,et al.Characterization of granular flow of wet solids in a bladed mixer[J].AICHE Journal,2006,52(8):2757-2766.
[8]REMY B,CANTY T M,KHINAST J G,et al.Experiments and simulations of cohesionless particles with varying roughness in a bladed mixer[J].Chemical Engineering Science,2010,65(16):4557-4571.
[9]REMY B,KHINAST J G,GLASSER B J.Wet granular flows in a bladed mixer:experiments and simulations of monodisperse spheres[J].AICHE Journal,2012,58(11):3354-3369.
[10]CHANDRATILLEKE R,YU A,BRIDGWATER J.Flow and mixing of cohesive particles in a vertical bladed mixer[J].Industrial &Engineering Chemistry Research,2014,53(10):4119-4130.
[11]ESCOTET-ESPINOZA M S,FOSTER C J,IERAPETRITOU M.Discrete element modeling (DEM) for mixing of cohesive solids in rotating cylinders[J].Powder Technology,2018,335:124-126.
[12]SIRAJ M S.Single-blade convective powder mixing:the effect of the blade shape and angle[J].Powder Technology,2014,267:289-301.
[13]张洪武,秦建敏.基于非线性接触本构的颗粒材料离散元数值模拟[J].岩土工程学报,2006,28(11):1964-1969.
[14]徐泳,孙其诚,张凌,等.颗粒离散元法研究进展[J].力学进展,2003,33(2):251-260.
[15]BAO Y Y,LI T C,WANG D F,et al.Discrete element method study of effects of the impeller configuration and operating conditions on particle mixing in a cylindrical mixer[J].Particuology,2020,49:146-158.
[16]孔亮,彭仁.颗粒形状对类砂土力学性质影响的颗粒流模拟[J].岩石力学与工程学报,2011,30(10):2112-2119.
[17]李远征,魏玉峰,雷壮,等.基于离散元法研究颗粒球度对粗粒土抗剪强度的影响[J].水资源与水工程学报,2019,30(4):225-232.
[18]陶贺,金保昇,钟文琪.非球形颗粒在移动床中流动特性的离散单元法直接数值模拟[J].中国电机工程学报,2010,30(23):78-83.