纳米颗粒悬浮液Zeta电位的调控与检测已在食品[1-2]、化工[3-4]、环境[5-6]、医学[7-8]等领域得到广泛应用。Zeta电位是衡量胶体溶液稳定程度的重要依据[9] ,目前市场测试方法主要有光学电泳法和声学电泳法2种检测分析技术[10]。电泳光散射(electrophoretic light scattering,ELS)是光学电泳法测量颗粒Zeta电位主要技术,其中相位分析技术(phase analysis light scattering,PALS)和相关法是使用较多的ELS信号解析手段[11-12]。在电泳光散射技术中,常用电极设计为U型毛细管电极,本文中定义为常用毛细管电极。测试过程中,在电极两端施加电压,胶体颗粒处于电场中,并在电场力作用进行电泳运动。检测点通常位于该电极底部中间位置,因此毛细管底部测试区域的电场分布的均匀性及激光入射位置对测试结果有重要影响。电场沿U型毛细管底部纵向分布不均匀会引发电泳速度的不均匀,从而导致信号中多普勒频移的分布变宽,增加测试结果的不确定性。当使用不同毛细管电极进行测试时,毛细管电极的制造公差也会导致不同电极间检测点位置具有一定偏差,此时探测点周围场强分布不均匀会导致不同电极测试结果的电极间差。黄桂琼等[13]和Huang等[14]通过有限元方法对毛细管电极设计进行电场模拟研究,发现底部场强不均对颗粒测试结果产生较大影响,并提出在传统U型毛细管电极两侧电场分布均匀的竖直区域设置测试点来减小测试误差,但是这种方式在实际实验过程中仍具有一定操作难度,同时设备设计复杂程度相对较高。
目前没有相关理论或成熟经验公式来对毛细管进行几何参数优化设计,但是利用优化算法及有限元软件相互耦合,不仅可得到复杂条件下的特定物理参数特性,如电场、热场等,还可以解决缺乏理论经验公式的复杂结构优化问题[15]。
在该研究中,为解决毛细管电极复杂非连续目标函数优化问题,提高测试结果的稳定性及电场的均匀度,使用有限元基本理论,对U型毛细管电极分布进行数值模拟,调用梯度自由优化(bound optimization by quadratic approximation,BOBYQA)算法,在无需对目标函数进行求导的情况下,对U型毛细管电极进行优化迭代求解。考虑内、外径比例因子K1、K2对毛细管底部场强的影响,提出一种新型毛细管电极结构,解决纳米颗粒Zeta电位测量过程中电场不均问题,为毛细管电极的设计优化提供新思路。
1 原理
1.1 几何模型构建
U型毛细管电极是较普遍使用的用于Zeta电位测试的电极结构,其示意图如图1所示。在该结构中,毛细管电极高为35 mm。为缩短计算时间,对该轴对称三维模型进行抽象简化,得到如图1(b)所示的二维简化示意图。U型毛细管电极的建模流程如下:首先利用三次贝赛尔曲线实现对弧线AB的构建,三次贝赛尔曲线比例因子为K2,初始值为0.53,且弧线上每点占比权重为1。A、B、C点坐标依次为(0,r2)、(r2,0)、(r1,0),其中,r1=2 000 μm,r2=4 000 μm;然后利用三次贝赛尔曲线构建弧线CD,比例因子为K1,初始值为0.53,弧线上每点权重也为1;确定D点坐标(0,r1);根据毛细管电极实际长度确定E、F点的坐标(-RL,r1)、(-RL,r2),RL=32 000 μm;连接各点完成1/2模型构建。根据二维镜像,实现毛细管电极二维结构整体绘制,该模型的初始值管径为2 mm,管长为33 mm,管宽为11 mm。
1.2 物理场设置
选取有限元软件内置电场模块对毛细管电极进行数值模拟,流体区域材料参数见表1。边界条件:毛细管电极左、右侧施加的电压分别为VL=150 V,VR=0。当给毛细管电极施加交变电压时,其电场分布由拉普拉斯方程控制。
表1 流体区域材料参数
Tab.1 Material parameters in fluid area

密度ρ/(kg·m-3)黏度η/(Pa·s)相对介电常数10310-378
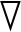 2V=0,
2V=0,
(1)
E=-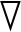 V,
V,
(2)
式中:V为电势,V;E为电场强度,V/m。
1.3 BOBYQA算法简介及优化函数的确定
BOBYQA是一种主要针对复杂函数且不需计算目标函数导数的优化算法。该算法通过在插值区间内用二次近似函数替代目标函数进行迭代求解,解决多维非线性优化问题[16-18]。BOBYQA算法的基本流程如下。
对于目标区间内最小值问题的求解问题,首先构建最小目标函数
min F=F(x),x∈Rn,
(3)
式中:F为目标函数;Rn为多变量可行域。
1)当初始迭代步数k=0时,给定初始向量x0∈Rn,给定初始、结束的可信赖域半径δc>δd>0,Δ1=δc。
2)构建初始区间的插值函数集{ym∶m=1,2,3,…,m},同时给定m取值范围。
y1=x0,
(4)
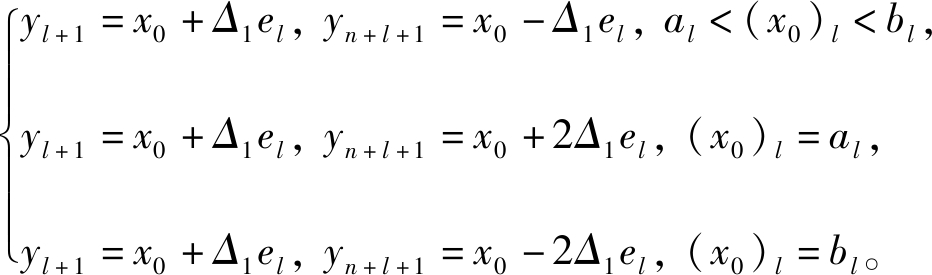
(5)
式中:el为多变量可行域内第l个坐标向量;al、bl为可行域变量的上、下限。
3)开始进行迭代运算,并记为k=k+1。
4)当收敛条件满足Δk≤ρe时,优化完成,如果未满足,进行步骤5操作。
5)从插值函数集ym存在点xk有最小值,即:
F(xk)=min{F(ym)∶j=1,2,…,m}。
(6)
6)通过求解可信赖域的子问题以确定试探步长,
dk=minQk(xk+d),d∈Rn,
(7)
式中:dk为试探步长;Qk为二次近似公式。
7)构造新的插值点:
(8)
8)构造新的插值点范围,然后构建新的二次近似公式及下一步迭代的可信赖区域半径。
在毛细管电极二维模型基础上,取内外径底部端点C、B上下场强差值为目标函数,场强差值越小,毛细管电极的精度越高。毛细管电极底部场强差主要受几何模型结构影响,内、外半径是影响几何模型的主要因素。表征内、外半径的贝赛尔曲线比例因子K1、K2描述内外径的弯曲程度,过大或过小会在优化过程造成单元反转或无法达成预期优化效果。如式(10),K1、K2被作为优化变量,并给定优化参数的取值范围。优化容差为0.001,最大迭代次数为1 000。
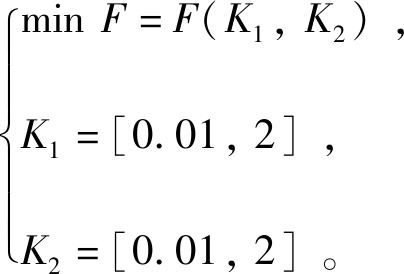
(9)
1.4 电泳光散射测量Zeta电位基本原理
1.4.1 颗粒电泳
在样品两端施加电压,颗粒在电场力的作用下进行电泳运动。颗粒的电泳速度v和电场场强E呈线性正比。
(10)
式中:q为颗粒上的电荷数量;r为颗粒半径,m;η为分散介质黏度,Pa·s。
1.4.2 电泳光散射法基本原理
激光器经过分束器分成2束激光,分别为入射光和参考光。入射光经过样品池照射在进行电泳运动的颗粒表面,发生散射,由于光学多普勒效应,其散射光的频率相对于入射光频率有所偏移;散射光与参考光经过合数器拍频,通过计算散射光信号与参考光信号之间的频率差得到颗粒的电泳迁移率μ[11-12]。
将电泳迁移率带入亨利方程,可以计算得到Zeta电位ζ结果,
(11)
式中:ε为绝对介电常数;f(ka)为亨利函数;ka为颗粒双电层厚度和颗粒半径的比值。
2 实验
2.1 仪器设备
BeNano 90 Zeta电位仪、Zeta电位标准样品(丹东百特仪器有限公司),标称Zeta电位为(-39±5) mV,主要成分为带电的聚苯乙烯球分散在蒸馏水为主的配方溶液中。
2.2 方法
分别采用优化设计前的U型毛细管电极和优化设计后毛细管电极进行Zeta电位测试,实验温度为25 ℃,每个数据测量5次,取平均值。
为了验证底部测试区域电场不均而引入的测量误差,采用升降台控制毛细管电极的高度,在毛细管电极底部测试区域沿纵向即图1(b)中的CB方向,设定若干探测点进行测试,其中CB方向中点设为坐标原点,B点为-1 mm,C点为1 mm。
3 结果与讨论
3.1 仿真优化路径
图2所示为内、外径比例因子K1、K2在管径d为2 mm时的优化迭代路径。在15个迭代步骤之前,该优化系统处于不断波动状态,K1、K2在不断增长。之后随着迭代次数增加逐渐趋于稳定,最终在第28个步骤满足优化条件得到收敛。K1、K2的比例因子初始值为0.55,经优化迭代后得到的最终值为1.30、1.39。图2(b)描述了优化目标值随迭代次数的变化过程。测试区域场强差在前期不断波动,执行第5个迭代步骤后场强差在逐渐呈现趋势性降低,最终稳定在0.04 V/m,可见引入优化算法可实现毛细管电极的快速优化。
3.2 仿真优化结果及电极选型
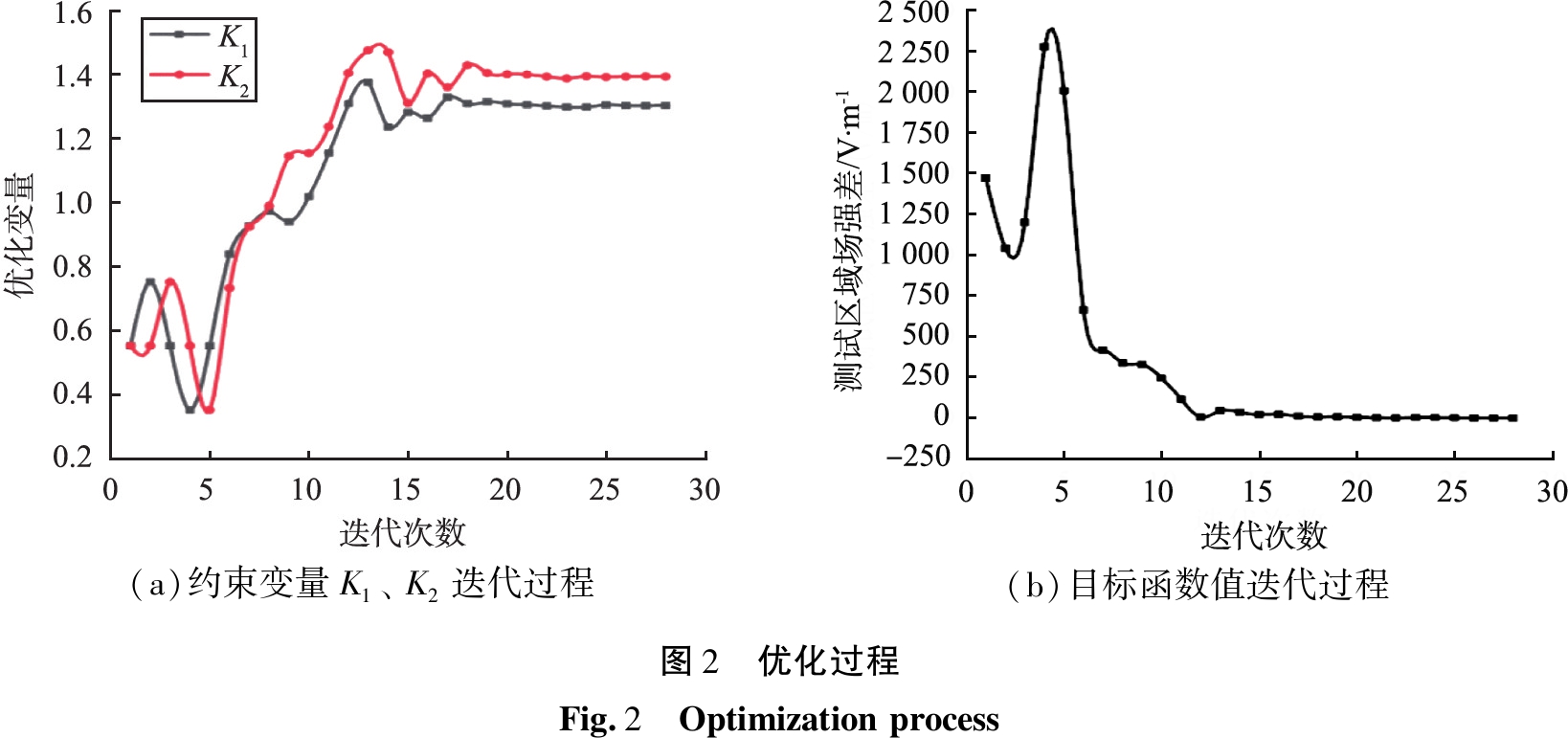
图3所示为优化前常用毛细管电极场强分布。由图可知,优化前常用毛细管电极的整体电场分布呈现两侧毛细管比较均匀的特点,底部靠近检测区域电场分布不均,存在较大的场强梯度。毛细管底部靠近检测点附近场强从内径到外径逐层递减并成环状分布,靠近内径拐点处场强最大,沿CB方向场强逐渐减小,这是由于常用毛细管电极底部电场线发生折叠造成的。黄桂琼等[13]提出将探测点位置选取在毛细管电极两侧,其目的是利用两侧较为均匀的电场形成的均匀电泳,从而得到稳定的测试结果,但是在实际测量应用场景中,颗粒Zeta电位检测范围一般在2~110 μm。当所测颗粒粒径较大,发生相对较强的沉降行为,当颗粒沉降运动与电泳运动相互作用时,此时探测点选取电极两侧将影响测试结果精度,因此常用毛细管电极探测点位置通常选取在底部。当颗粒所处区域电场越强,其在电场力作用下的电泳运动越强烈,均匀性较差的电场分布将增加检测区域电泳的不确定性。这是电泳光散射测试中引发结果偏差的不利因素之一。
当内、外径比例因子K1、K2为别为1.30、1.39时,基于BOBYQA算法优化得到的毛细管电极电场分布如图3(b)所示,此时场强极大点在底部两端内径尖角处出现,而测试区域场强整体分布较为均匀,但优化得到的电极结构内外径曲率变化较大,且底部距离毛细管电极外避较近,在外力作用下容易发生断裂,基于电极当前加工技术及机械强度等综合考虑,需对得到的电极结构进行优化预处理,得到如图3(c)所示的结构图。其基本结构成锥形构造,底部场强极大值远离检测点位置,且底部距离毛细管电极距离较远,强度加大。
图3(d)所示为优化前后毛细管底部测试区域沿CB方向场强分布。随着探测位置向上移动,常用U型毛细管电极场强中心截线场强从底部的-1.0 mm位置的1 471 V/m增大到顶端1.0 mm位置的3 000 V/m,场强增幅超过100%,该位置存在较大场强梯度。
算法优化后毛细管电极,截线场强从底部-1.0 mm位置的2 012.03 V/m增大到顶端1.0 mm位置2 012.3 V/m,场强变化率为0.01%。实际优化后毛细管电极场强从底部-1.0 mm位置1 926 V/m增大到顶端1.0 mm位置的1 994 V/m,增幅仅为0.35%,电场不均匀度减小,表明优化后的毛细管结构测试区域电场均匀性得到明显的改善。
4 实验验证
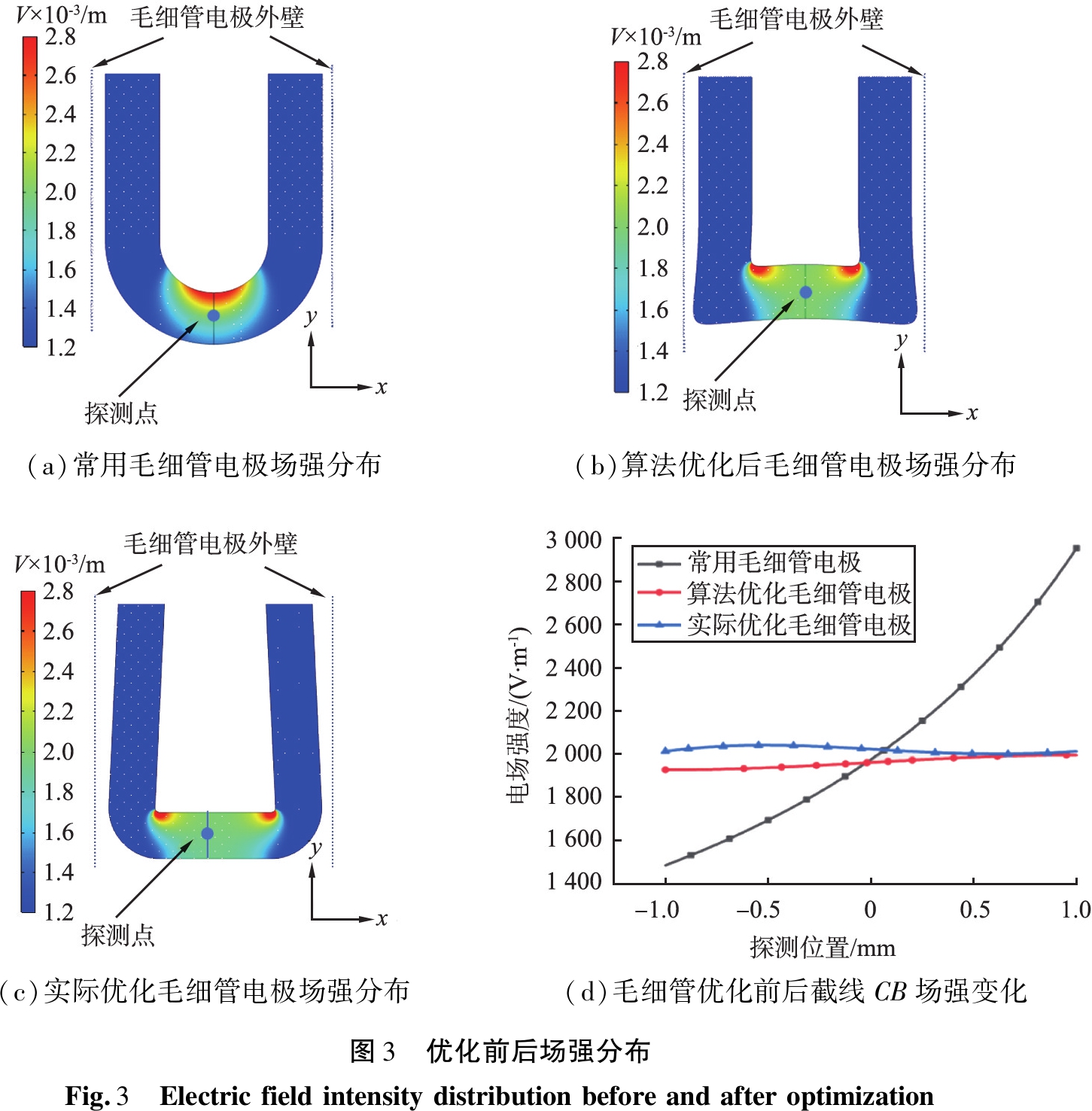
为验证颗粒电泳迁移率及Zeta电位对探测位置及场强的敏感性,进行了实际的样品测试,优化前、后毛细管电极所检测的Zeta电位和电泳迁移率对于检测点位置的依赖特性结果如图4所示。图4(a)所示为优化前后毛细管电极颗粒电泳迁移率随探测位置的变化情况。由图可知,随着检测点位置从测试区域底部向上移动过程中,常用U型毛细管电极所测电泳迁移率结果变化明显,在探测范围为-0.7~0.9 mm,电泳迁移率从1.2 μm·cm/(V·s)增大到3.6 μm·cm/(V·s),增大了200%。在使用实际优化后毛细管电极检测颗粒电泳迁移率时,随着随探测点向上移动,所检测的颗粒电泳迁移率也呈上升趋势,在探测范围-0.9~0.9 mm内,电泳迁移率从2.92 μm·cm/(V·s)增大到3.21 μm·cm/(V·s),增大了10%。优化后的毛细管电极的电场迁移率沿BC方向变化远小于优化前的常用U型毛细管电极的。由于颗粒的电泳速度正比于电场强度,因此证实了仿真计算得到的优化毛细管电极具有更加均匀的电场,极大地减小了检测结果对于沿BC方向检测点位置的依赖性。
颗粒表面Zeta电位可通过Herry方程计算得到。待测标样颗粒带负电,所测Zeta电位为负值,为便于讨论,此处选取Zeta电位取绝对值作为目标值。图4(b)所示为Zeta电位随检测点位置变化的测试结果。从图中可看出,常用U型毛细管电极所测得的Zeta电位绝对值在探测范围-0.7~0.9 mm内从16 mV增大到46 mV。考虑到标准样品的电位绝对值分布在34~44 mV,其靠近内径上壁和外径下壁区域的Zeta电位测量值已明显偏离了标准样品的标称区间,而优化后毛细管探测范围-0.9~0.9 mm内,颗粒Zeta电位绝对值从37.4 mV增大到41.5 mV,略有增加,但是测试结果均在标准样品的标称值范围内。
通过实验验证,基于BOBYQA算法优化后的新型毛细管电极的Zeta电位测试对探测位置的敏感度较低,该结构可有效优化测试区域场强不均造成的测试偏差及解决制造工艺偏差带来电极间差问题。
5 结论
1)基于有限元基本原理及BOBYQA算法可得到毛细管电极优化后结构,该模型可为同类型毛细管优化设计提供依据。
2)当管径d=2 mm,K1=1.30,K2=1.39时,优化后毛细管测试区域场强分布均匀度得到明显改善,其场强变化从常用的U型设计的100%降为4%,利于对探测点的选取及纳米颗粒表面Zeta电位测试。
[1]吕思瑶,朱登兆,鲍云翔,等.大豆分离蛋白与染料木素共价交联对蛋白表征和结构的影响[J/OL].食品科学:1-12[2021-12-15].https://kns-cnki-net.webvpn.wzu.edu.cn/kcms/detail/11.2206.TS.20211015.2005.002.html.
[2]陈雅琪,陈玲,雷芬芬,等.南瓜籽油Pickering乳液的制备及其稳定性研究[J].粮食与油脂,2021,34(11):52-56.
[3]童志明,李亚兵,黄茗,等.井下作业返排残液对原油破乳脱水的影响及破乳剂筛选[J].化学与生物工程,2021,38(11):43-49.
[4]王市委,杨光祥,石开仪.低阶煤浮选颗粒间黏附作用研究[J].矿业研究与开发,2021,41(10):142-146.
[5]王智巧,马杰,陈雅丽,等.不同环境条件下水铁矿和针铁矿纳米颗粒稳定性[J].环境科学,2020,41(5):2292-2300.
[6]杜晓丽,刘殿威,崔申申.径流入渗土壤胶体释放对重金属截留的影响[J].中国环境科学,2022,42(3):1278-1286.
[7]杨娟,尚曙玉,贾安,等.木犀草素固体脂质纳米粒的制备及其体内药动学研究[J].中成药,2021,43(9):2281-2286.
[8]汪琼卉,薛学鑫,刘芸雅,等.艾塞那肽温敏型凝胶纳米粒鼻喷剂研究[J].中国药学杂志,2021,56(17):1406-1413.
[9]刘伟,张珊珊,Thomas J C,等.基于频谱细化算法的电泳光散射Zeta电位测量方法[J].光学学报,2017,37(2):292-298.
[10]许任良.颗粒悬浊液的Zeta电位特性[C]//中国建筑材料联合会粉体技术分会.2008国际粉体技术与应用论坛暨全国粉体产品与设备应用技术交流大会论文集.北京:中国建筑材料联合会,2008:18-19.
[11]秦福元.基于相位分析光散射的Zeta电位测量研究[D].淄博:山东理工大学,2018.
[12]XU R.Particle characterization:light scattering methods[J].China Particuology,2003,1(6):271-271.
[13]黄桂琼,邱健,韩鹏,等.U型样品池中电场分布仿真及其对Zeta电位测量的影响[J].中国粉体技术,2019,25(4):26-32.
[14]HUANG G,XU B,QIU J,et al.Symmetric electrophoretic light scattering for determination of the zeta potential of colloidal systems[J].Colloids and Surfaces A:Physicochemical and Engineering Aspects,2020,587:124339.
[15]WANG C F,SONG Y X,PAN X X.Electrokinetic-vortex formation near a two-part cylinder with same-sign zeta potential in a straight microchannel[J].Electrophoresis,2020,41(10/11):793-801.
[16]吴新杰,许超,徐明达,等.基于BOBYQA算法的EMT传感器结构优化研究[C]//中共沈阳市委,沈阳市人民政府.第十八届沈阳科学学术年会论文集.沈阳:沈阳市科学技术协会,2021:425-430.
[17]POWELL M J D.The BOBYQA algorithm for bound constrained optimization without derivatives[J/OL].NA Report,2009(6):1-39[2022-02-01].http://www6.cityu.edu.hk/rcms/publications/preprint26.pdf.
[18]唐晟,赵耀华,刁彦华,等.基于BOBYQA算法的微小通道热沉优化设计[J].北京工业大学学报,2018,44(6):940-947.