粉末成型技术在冶金、化工、食品、药品、环保等行业得到了广泛应用[1]。在腔体填充过程中，移动的送料履带片将不同物理性质(大小、密度、形状等)的颗粒输送到固定的腔体(模具或床体)中。在此过程中，颗粒的流动行为会对其在腔体内的堆积效果产生很大影响，容易引起颗粒在空间分布上的不均匀[2-3]。
目前，用来研究腔体填充过程中粉末流动特性的实验手段很多，经常采用由固定模具和移动送料机构组成的模型系统对粉末流入封闭模具内的流动特性进行测试分析，影响模具内颗粒填充性能的因素很多，诸如送料速度、环境气流、颗粒性质和模具形状等等，掌握这些因素的影响规律需要进行大量系统性的实验研究与测试分析[4]，因此，采用实验法进行研究，不仅耗时耗力，而且受限于现有的测试手段和水平，难以作深层次的研究。
近年来，随着计算机技术的发展，数值模拟方法在气固流体运动研究中得到了广泛应用，为深入探究颗粒群的流动性与填充性能提供了可行的手段。计算流体力学-离散单元法(CFD-DEM)最初由Tsuji等[5]、Hoomans等[6]同时开发，后来发展为气固流动数值计算中的标准方法，所使用的数学模型将气相描述为连续体，将每个单独的粒子视为离散实体，同时考虑了气体与粒子、粒子与粒子之间的相互作用。
Nicolin等[7]模拟颗粒形状对混合过程的影响，发现球形颗粒的混合速度最快，多面体颗粒需要增加50%的混合时间才能达到与球形颗粒类似的混合效果；Zhou等[8]基于CFD-DEM方法研究了竖直管道中粗颗粒的水力输送过程，发现颗粒易在管道中部发生集聚，输送速度的提高会改善颗粒分散度但却提高了压降，而颗粒直径对流动状态影响很小；Gou等[9]发现颗粒致密化程度与冲击空气速度呈正相关性。迄今为止，有关模腔内颗粒填充过程的数值模拟研究大多局限于单一要素对颗粒输送行为的影响，对颗粒群运动分离行为的系统性研究不足。
本文中基于CFD-DEM方法，模拟分析高密度无黏性颗粒混合物在填充模具过程中的分离行为，研究送料速度、颗粒生成方式、送料机构壁面斜度、环境空气、模具形状与深度等多种因素对颗粒混合物分离行为的影响，为进一步探究模腔内颗粒的运动、转移及其填充特性提供理论依据。
1 CFD-DEM模型建立
1.1 流体相的控制方程
根据连续性方程和Navier-Stokes方程[10]，流体相的运动控制方程描述为
(1)
(2)
式中：αg为当地网格气相体积分数，%；ρg为流体密度，kg/m3；t为时间，
表示x、y、z方向的时均速度，m/s；xi、xj、xk为x、y、z方向距离，m；δij为系数，i=j时为1，i≠j时为0；p为流体平均压力，Pa；μ为动力黏度，Pa·s；
为控制体内平均颗粒流体阻力，N；g为重力加速度，取为9.81 m/s2。
1.2 颗粒相的运动模型
根据牛顿第二运动定律，颗粒i的平移和旋转运动的计算公式为
(3)
(4)
式中：mi为颗粒的质量，
为颗粒i的矢量速度，m/s；Vi为颗粒体积，m3；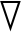
p为压力梯度，
为颗粒i受到的碰撞作用力(基于Hertz-Mindlin无滑移模型[11-12])，N；I为颗粒的惯性矩，m4；ω为角速度，rad/s；T为扭矩，N·m；其中，曳力
的计算公式为
(5)
式中：β为相间动量交换系数；ε为孔隙率，%。
1.3 几何模型的建立
颗粒填充机构示意图如图1所示，其由移动送料机构、固定模具、平板等组成，速度可调的移动送料机构装载着颗粒混合物直线移动至固定模具上方，颗粒混合物在重力作用下填充到固定模具中。
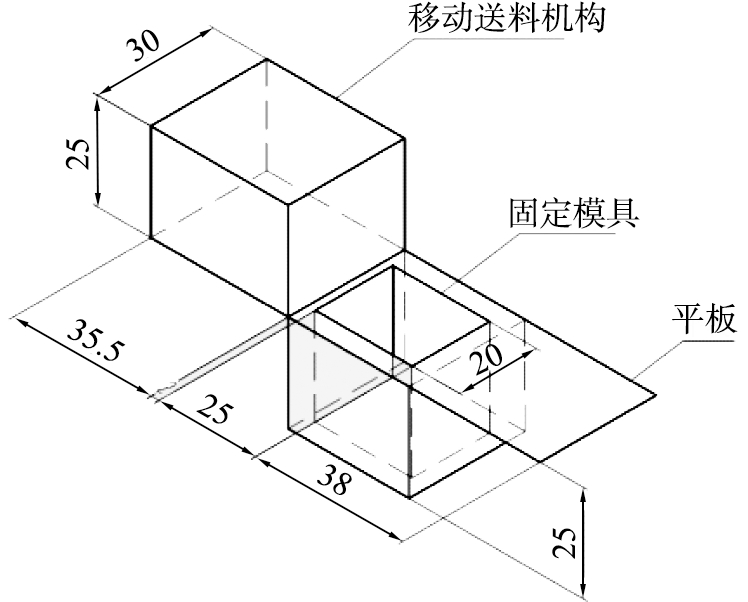
图1 颗粒填充机构示意图
Fig.1 Schematic diagram of particle filling mechanism
1.4 物理模型的建立
颗粒选用粉末冶金和环保领域常用的高密度颗粒，密度均为2 500 kg/m3；设置3种粒径分别为1.0、1.5、2.0 mm的颗粒(编号分别为a、b、c)组成三元混合物，颗粒与其填充机构的材料性质及碰撞特性[13-15]分别见表1、2。
表1 材料性质
Tab.1 Properties of materials
材料质量/g密度/(kg·m-3)杨氏模量/GPa泊松比颗粒122500880.2填充机构12002.30.4
表2 碰撞参数
Tab.2 Parameters of particle collision
弹性恢复系数静摩擦系数滚动摩擦系数颗粒-颗粒0.90.20.05颗粒-填充机构0.70.30.10
颗粒的2种生成方式分别为工业生成、分层生成[16]。工业生成方式是将每种粒径的颗粒在三元混合物中均匀混合分布生成，将工业生成方式设置为标准对照组，送料速度设为100 mm/s、送料机构壁面斜度设为90°、长方体模具系统的深度设为25 mm，试验编号为1。分层生成指每种粒径的颗粒按既定顺序在送料机构内分别生成后覆盖叠加，混合物中不同颗粒完全分离，颗粒按粒径由小到大编号后，在送料机构内3种分层生成方式由下至上依次为颗粒a—b—c、b—c—a、c—a—b。在标准对照组试验1基础上，改变送料速度(试验编号为1、2、3)、生成方式(试验编号为4、5、6)、倾斜角度(试验编号为7、8)、模具形状和深度的参数值(试验编号为9、10、11)，观测颗粒的填充过程。各试验编号的参数值见表3。
表3 试验参数值
Tab.3 Parameter values for each experiment
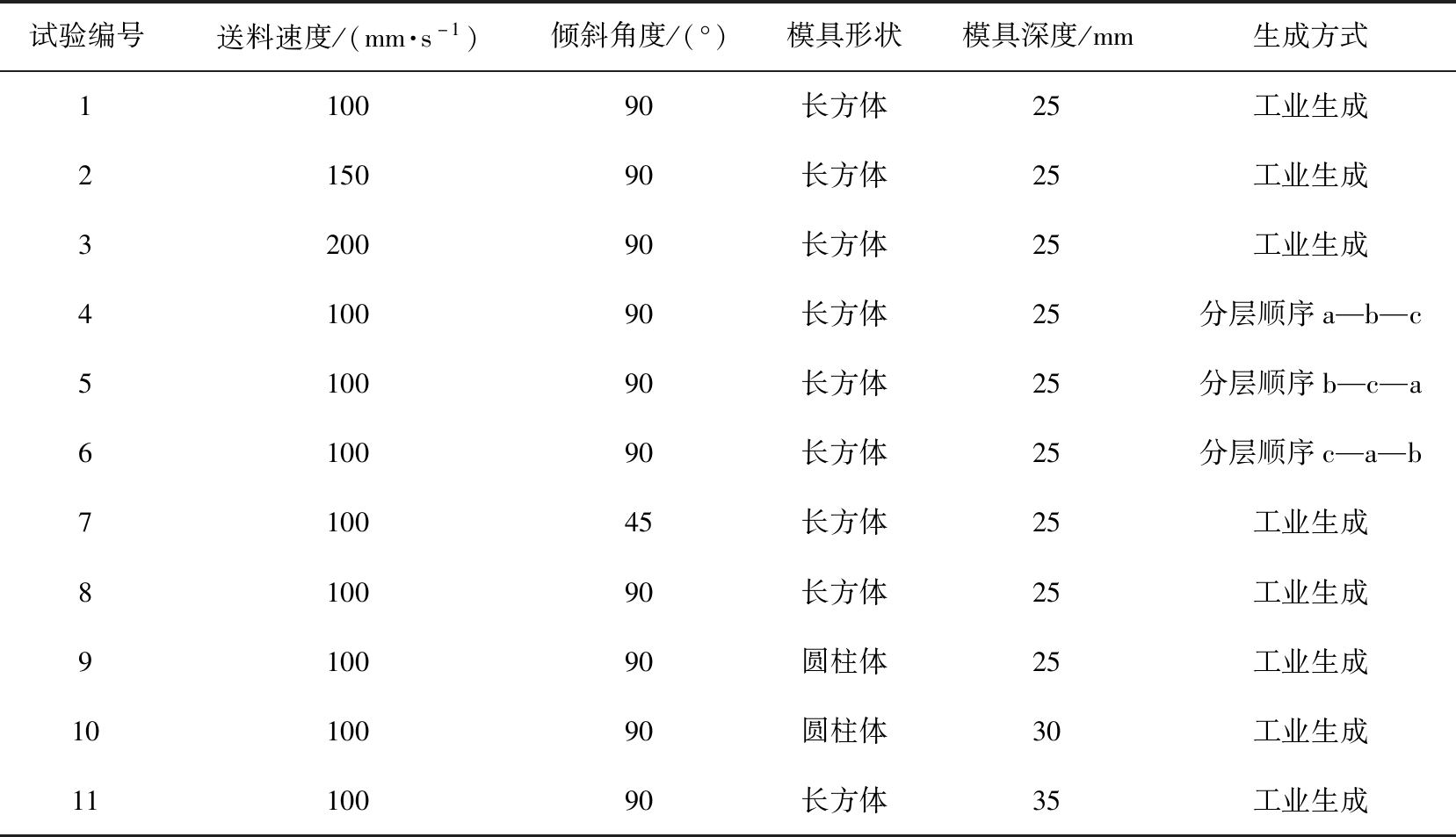
试验编号送料速度/(mm·s-1)倾斜角度/(°)模具形状模具深度/mm生成方式110090长方体25工业生成215090长方体25工业生成320090长方体25工业生成410090长方体25分层顺序a—b—c510090长方体25分层顺序b—c—a610090长方体25分层顺序c—a—b710045长方体25工业生成810090长方体25工业生成910090圆柱体25工业生成1010090圆柱体30工业生成1110090长方体35工业生成
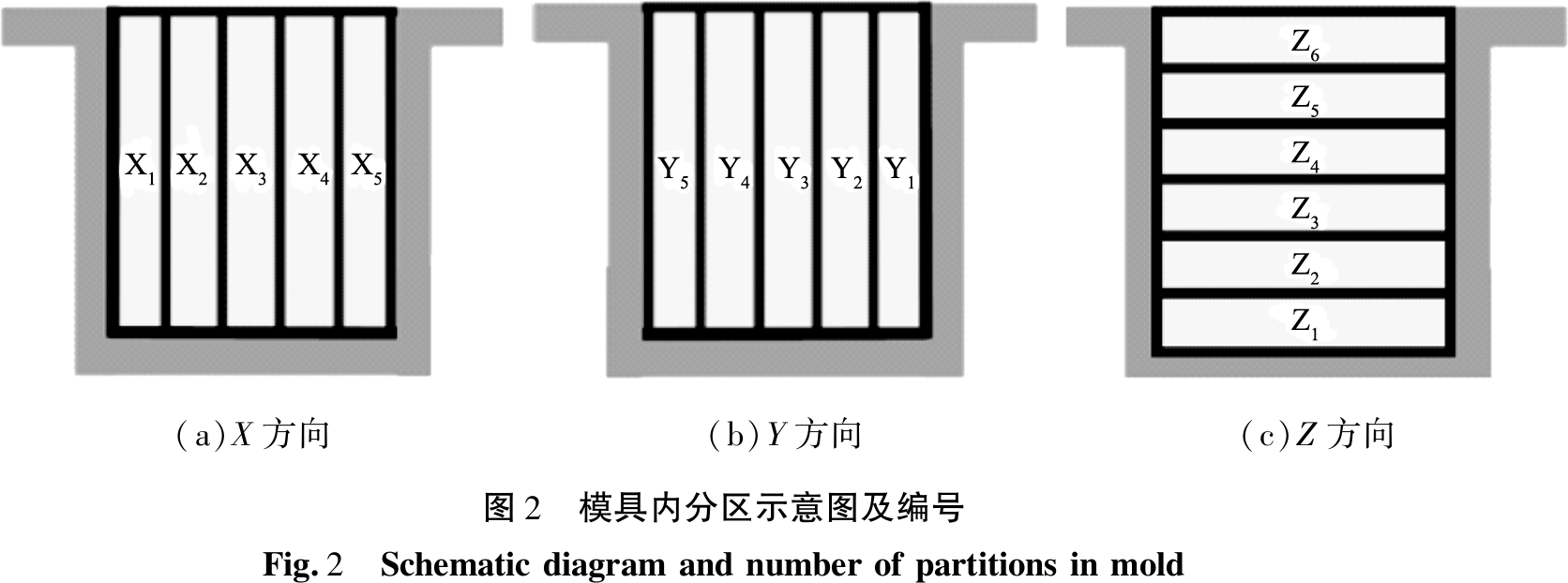
颗粒混合物在模具内的分布均匀程度通常由不同方向上颗粒的质量分布来反映[17-18]，将模具在X方向平均划分为5个子区域X1、X2、X3、X4、X5，在Y方向平均划分为5个子区域Y1、Y2、Y3、Y4、Y5，在Z方向平均划分为6个子区域Z1、Z2、Z3、Z4、Z5、Z6，模具内分区示意及编号如图2所示。
那么，分离指数(segregation index，Is)根据不同分区直接反映颗粒在不同变量条件下的分布特性，可以评价颗粒混合物填充模腔时的分离行为。分离指数的计算公式[15]为
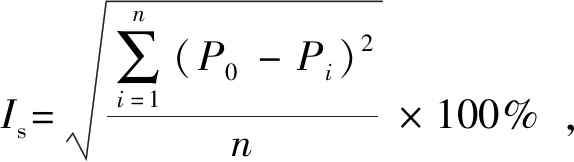
(6)
式中：n为分区数；P0为标准分布指数，%；Pi为某粒径颗粒实际的分区质量分数，%。
1.5 可靠性验证
为了验证模拟结果的准确性，对有关球形玻璃珠填充模腔的流动特性试验[1]进行了数值模拟，通过对比实验和模拟得出的模腔填充率数值，验证模拟计算的可靠性。在送料速度分别为400、500、600、1 000 mm/s时采用玻璃珠填充模具。不同送料速度条件下，模腔填充率的实验值和模拟值如图3所示。由图3可见，模拟得到的模腔填充率随送料速度的变化规律与实验结果基本吻合，且两者的最大相差0.07，在一定程度上说明了数值模拟结果的准确性。
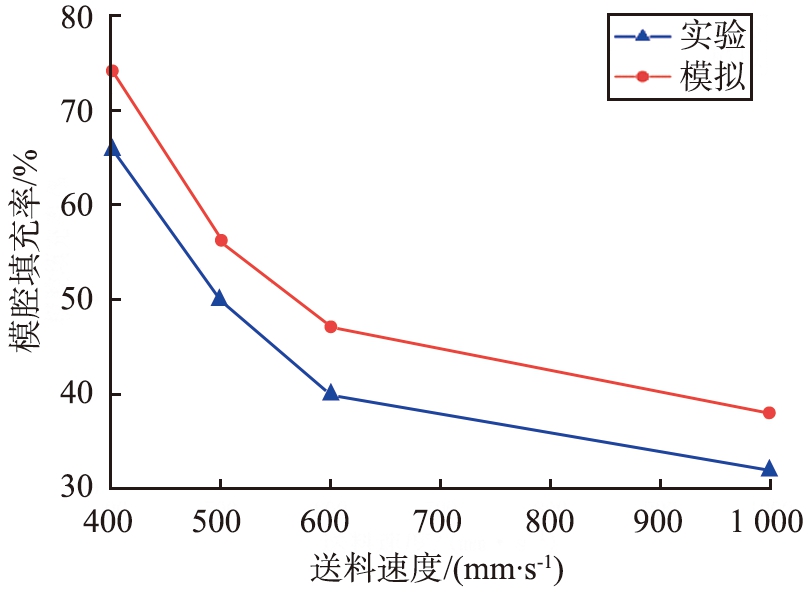
图3 不同送料速度下模腔填充率实验值和模拟值
Fig.3 Experimental and simulated values of cavity filling rate at different feeding speeds
2 结果与分析
2.1 颗粒初始状态的影响
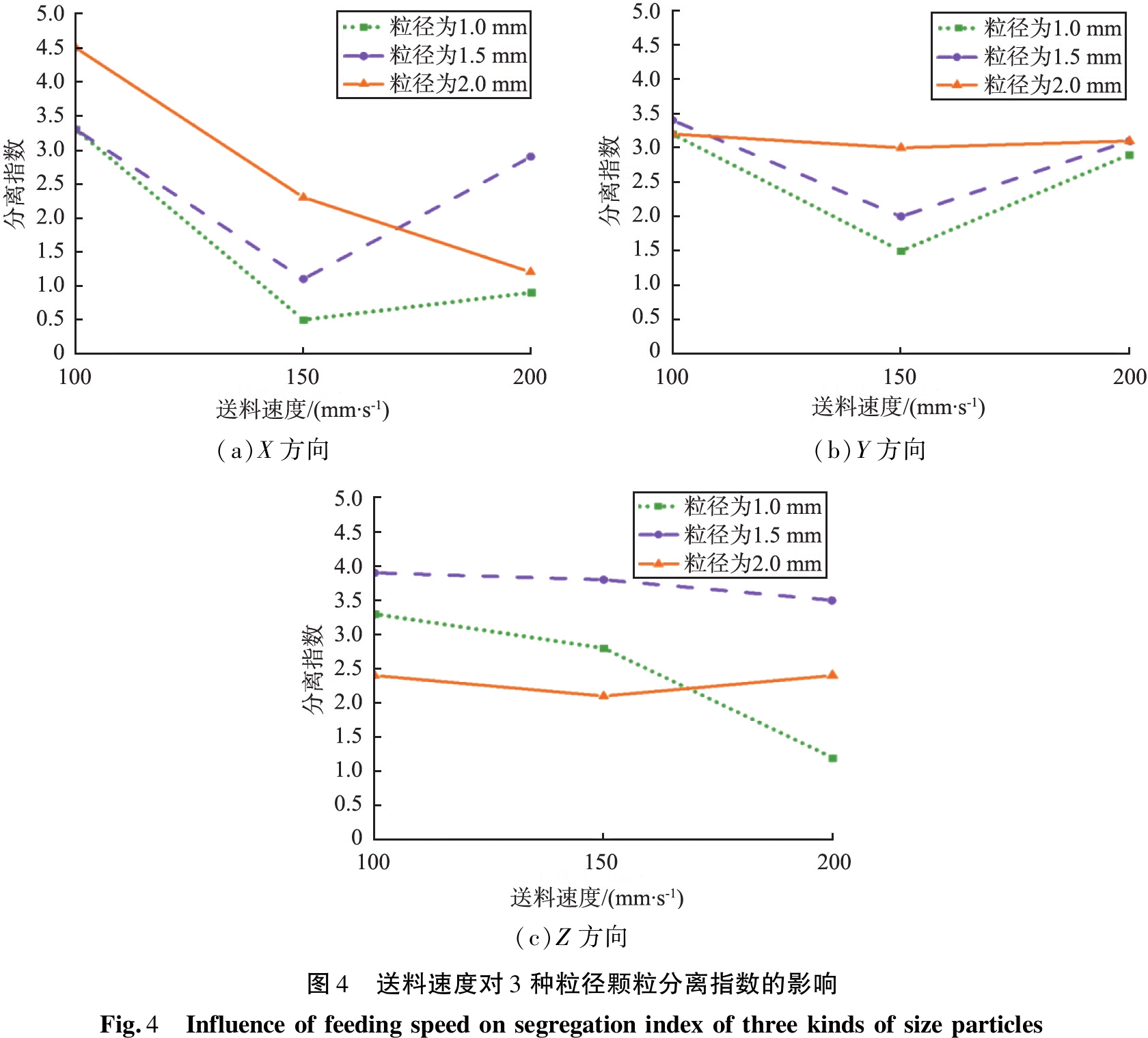
在试验1、2、3中，模具形状为长方形、模具深度为25 mm、送料机构壁面斜度为90°、颗粒为工业生成方式时，送料速度对3种粒径颗粒分离指数的影响见图4。由图4可见，当送料速度由100 mm/s提高到150 mm/s时，各个方向不同大小颗粒的分离指数均有不同程度的降低，其中X方向(送料方向)上的下降最明显，但当送料速度由150 mm/s提高到200 mm/s时，不同方向、不同尺寸颗粒的分离指数随送料速度呈不同的变化趋势。在X方向，粒径为2.0 mm的较大颗粒的分离指数由4.5下降到1.2，粒径为1.5 mm的中等尺寸颗粒的分离指数则由1.1提高到2.9，而粒径为1.0 mm的小颗粒的分离指数略有增加；在Y、Z方向，粒径为2.0 mm的较大颗粒的分离指数随速度增加变化不大，但粒径为1.0、1.5 mm的较小颗粒的分离指数在上述2个方向则呈相反的变化趋势，即在Y方向逐渐增加而在Z方向则有不同程度的下降。
在试验1、4、5、6中，模具形状为长方形、模具深度为25 mm、送料机构壁面斜度为90°、送料速度为100 m/s时，颗粒生成方式和分层顺序对3种粒径颗粒在各方向的分离指数的影响如图5所示，为便于比较，图中同时标明了分离指数值。由图5可见，在工业生成方式下(试验1)，由于颗粒混合物填充前就已在送料机构内充分混合，因此在不同方向上的分离指数相差不大，且数值很小(4.5以下)；在分层生成方式下(试验4、5、6)，送料机构行进方向为X方向的各粒径分离指数明显大于Y、Z方向的，这是由于颗粒混合物填充模腔时呈现鼻流现象[19]，导致在X方向上不同颗粒的流动存在明显的先后顺序；此外，在分层生成方式下，颗粒在送料机构内的初始位置不同也会对颗粒的分离行为产生影响，表现为不同粒径的颗粒按不同的顺序分层生成后进行填充时，位于中间层颗粒群的分离指数相比于上、下2层始终更小。由填充过程可知，送料机构内下层颗粒进入模腔后，中层颗粒随之进入，沿着X正方向产生堆积，挤压下层颗粒，使之向X负方向及Y方向两侧堆积，造成下层颗粒群的分离。上层颗粒最后进入模腔，由于填充区域受限，因此与中层颗粒相挤压，在模具上部中央位置大量堆积，造成颗粒间Y方向上的分离，而中层颗粒群填充时受到上、下区域颗粒的共同挤压作用，分离行为受到抑制。
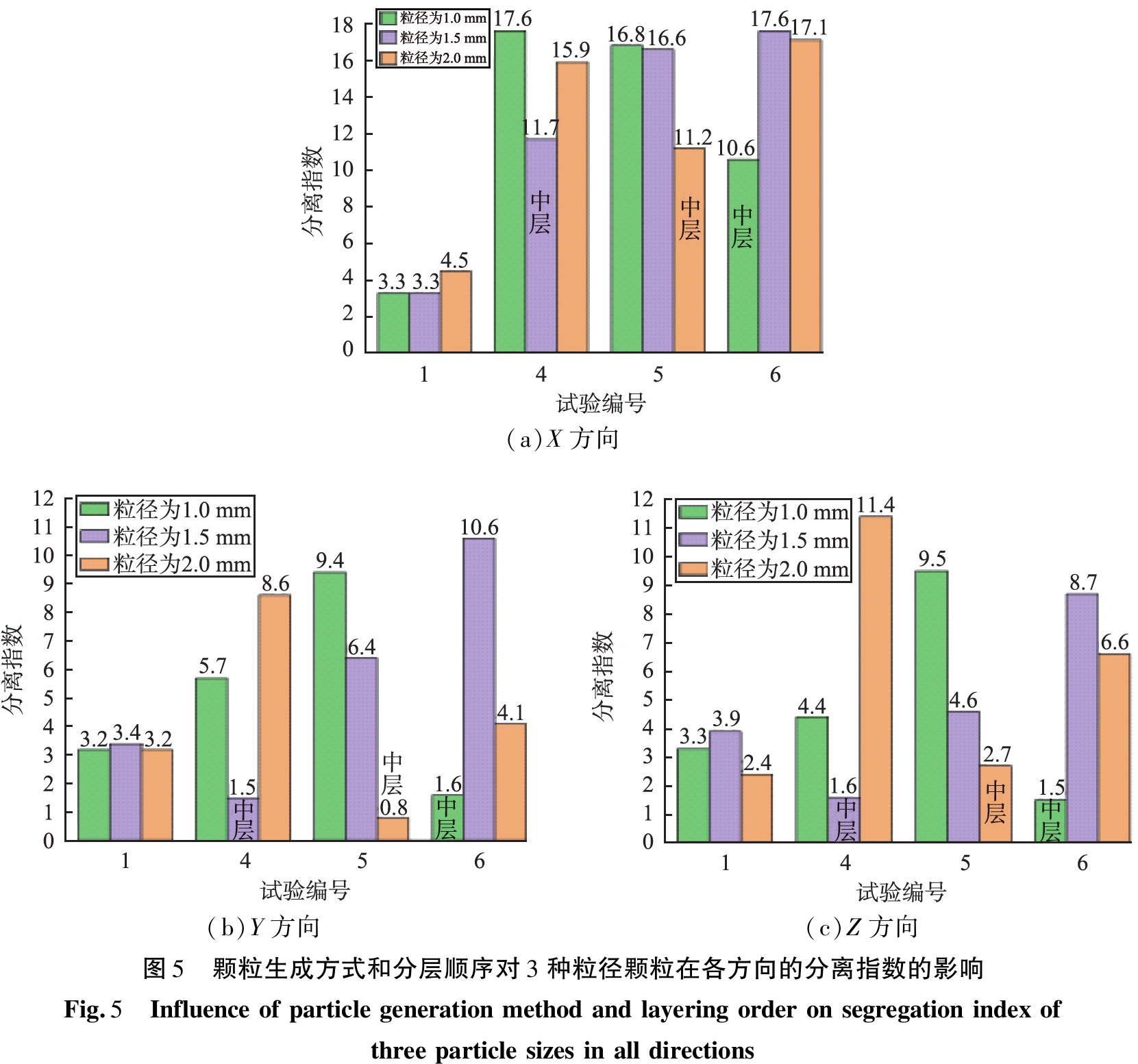
综上，增大送料速度能显著降低运动方向上大粒径颗粒的分离指数，降幅达到71%，在其他方向的颗粒分离指数仅略有下降；相较于分层生成方式，工业生成方式各颗粒群的分离指数均较小，最大仅为4.5，且各方向上分离指数相接近，而分层生成方式时位于中层的颗粒群受到上、下颗粒群的挤压，其分离指数小于工业生成方式的，在X方向上因受鼻流影响而分离指数普遍更大。
2.2 送料机构和模具形状尺寸的影响
试验7、8中，颗粒为工业生成方式、送料速度为100 m/s、模具形状为长方形、模具深度为25 mm时，送料机构壁面斜度对填充过程的颗粒流动行为的影响如图6所示。由图6可见，送料机构壁面斜度为90°时，颗粒填充时有明显的先后顺序，形成一个斜坡面，造成模腔内颗粒的局部堆积；送料机构壁面斜度为45°时，颗粒混合物填充时会先向送料机构中间聚集，然后再进入模腔，避免了直接填充，流动呈现漏斗状，没有明显的填充顺序，颗粒分布更均匀。减小送料机构壁面斜度对颗粒混合物分离行为的抑制，主要是通过改变送料机构内可填充颗粒区域，减弱颗粒流斜坡面的影响。如将长方体模具替换为底面积相同的圆柱体模具，同样可通过减小送料机构壁面斜度改变机构内可填充区域，抑制颗粒混合物分离。所不同的是，前者模腔内部存在边角，易引发颗粒局部堆积，后者内壁与颗粒一样为圆弧，颗粒与壁面间的碰撞反弹，利于颗粒混合物的均匀分布[20]。
在试验9、10、11中，送料速度为100 m/s、模具形状为长方形、送料机构壁面斜度为90°、颗粒为工业生成方式时，模具深度对3种粒径在Z方向上的颗粒分离指数的影响如图7所示。从图7中可以发现，模具深度由25 mm增加到30 mm会显著抑制不同粒径颗粒间的分离行为，继续增加到35 mm后，分离指数无显著变化，原因在于增加模具深度后颗粒触底时速度提高，碰撞反弹加剧，与后续颗粒流相挤压，使颗粒向模具四周扩散，颗粒与颗粒、内壁间作用力随之增大，空隙减小，分离指数减小，而颗粒间空隙有限且不存在细颗粒的渗流，继续增加深度对颗粒分离行为的影响有限。
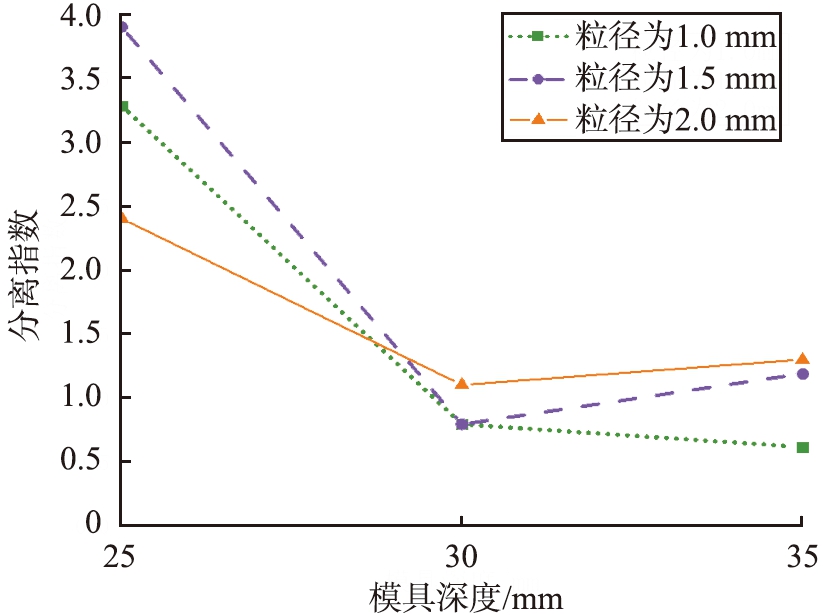
图7 模具深度对3种粒径在Z方向上的颗粒分离指数的影响
Fig.7 Effect of die depth on particle separation index of three particle sizes in Z-direction
综上，替换方形模具为圆形以及加深模具均能抑制颗粒混合物分离，前者减少了颗粒的局部堆积，后者通过加剧触底反弹使颗粒分布更为紧密而减小分离指数，对细颗粒影响明显，分离指数降幅最高达79%，但是在深度达到30 mm后继续增大深度效果有限。
2.3 环境空气的影响
颗粒运动受环境空气的影响程度通常取决于颗粒自身属性，一般用空气敏感指数[10]来判断，选用的颗粒密度为2 500 kg/m3，其敏感指数临界值为9.6×106，对应的颗粒直径为0.37 mm。直径大于0.37 mm的颗粒受环境空气的影响较小，而直径为0.37 mm以下的小颗粒则对环境空气流动比较敏感。选择以直径为0.25 mm的细颗粒为例进行模拟试验。
2.3.1 固定式送料机构
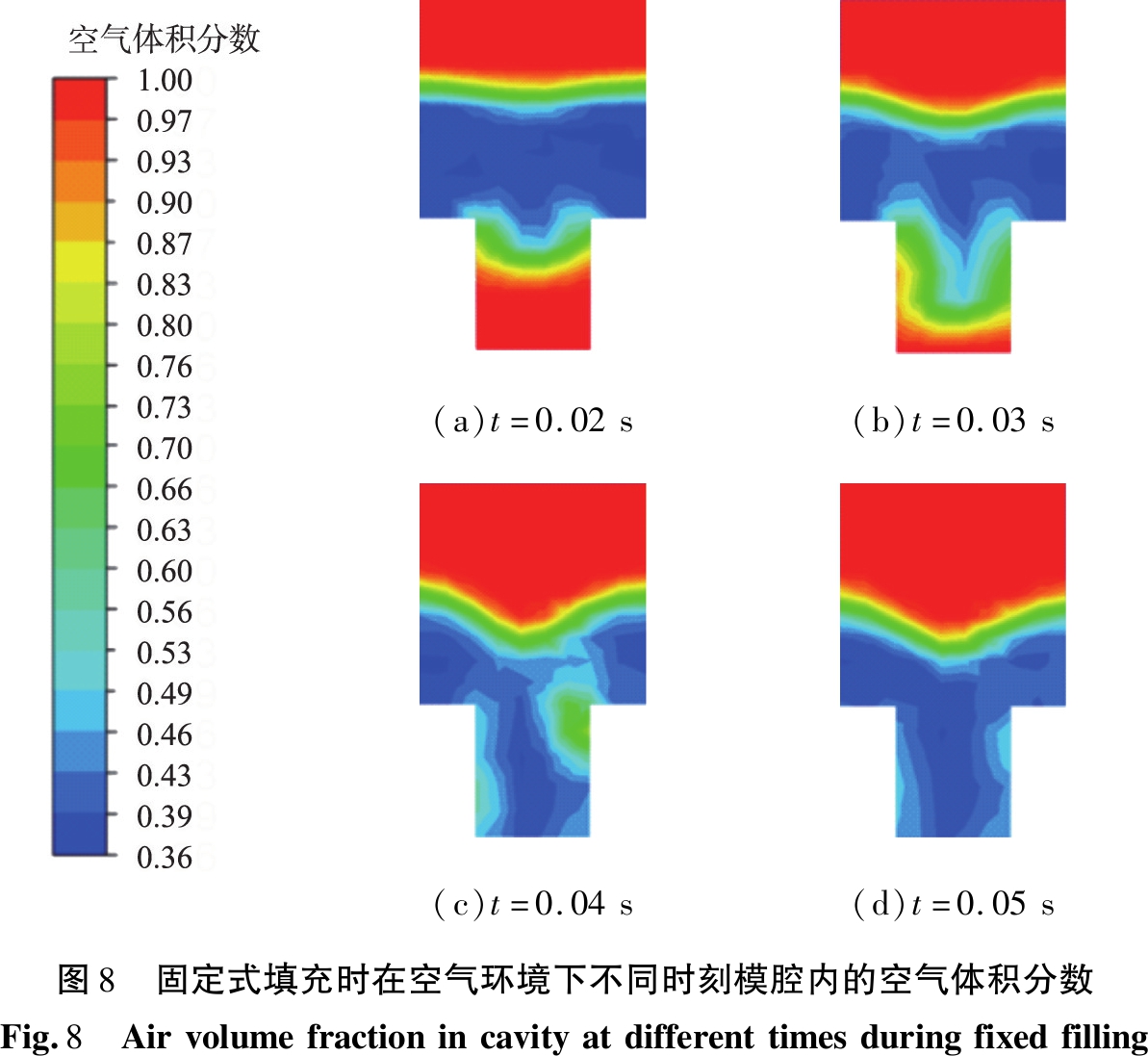
以固定式送料机构填充模具过程，在空气环境下不同时刻模腔内的空气体积分数如图8所示。由图8可见，在颗粒填充过程中，模腔中间区域内空气体积分数总是小于两侧区域内的，说明颗粒混合物直接排入模腔后，受挤压的空气向模腔边缘运动并从四周向上排出。密集填充的颗粒受到空气流的冲击作用而产生局部稀疏，同时空气的逸散阻碍迟滞颗粒运动，使颗粒流端部形成中间低四周高的下凹式分布。
固定式填充时，真空和空气环境下细颗粒在Z方向上的质量分数如图9所示。由图9可见，直径为0.25 mm的细颗粒在真空中填充时，颗粒分布比较均匀，但在空气环境填充时，由于上升气流对其沉积有明显的阻碍作用，因此细颗粒大量集聚在模具顶部，而中、下部质量分数较小。
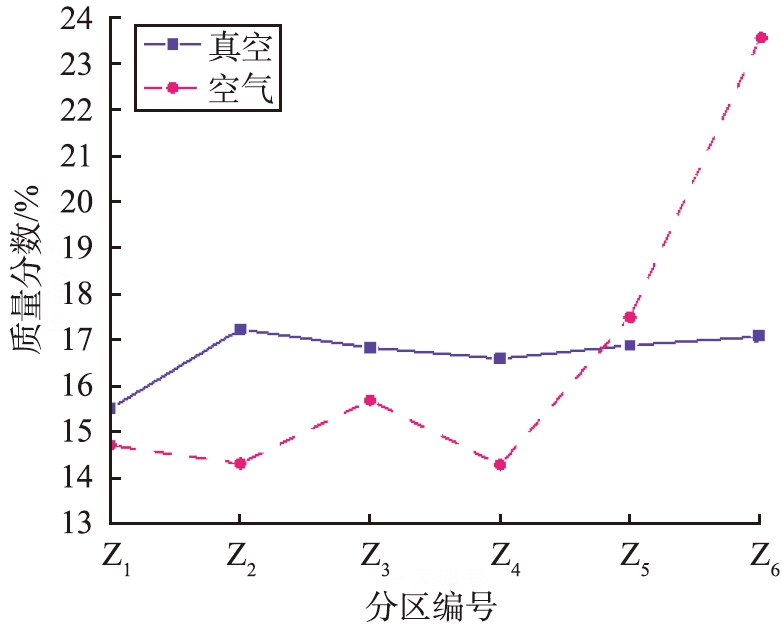
图9 固定式填充时真空和空气环境下细颗粒在Z方向上的质量分数
Fig.9 Mass fraction of fine particles in Z direction in vacuum and air environment during fixed filling
2.3.2 直线式移动送料机构
直线式移动送料机构以50 mm/s匀速移动时，在空气环境下将细颗粒填充模具，不同时刻模腔内的空气体积分数如图10所示。由图10可见，颗粒流动呈现鼻流，模腔空间沿X方向被分隔成2个区域，右侧区域空气自由逸出，另一侧空气受颗粒流挤压向左侧团聚，颗粒混合物受重力作用流向该区域，被挤压的空气从颗粒缝隙中向右上方逸出，期间密集的颗粒流受到逸出空气在X方向上的阻力作用发生迟滞产生局部稀疏，沿运动方向产生弧形偏折。
直线移动式填充时，在真空和空气环境下细颗粒在X方向上的质量分数如图11所示。直线移动式填充模具过程中细颗粒在Z方向上的分布与固定式填充时相似，均受到空气作用影响，多集中分布在模具上部，而由图11可见不同在于直线移动式填充时细颗粒在X方向上会受到气流阻碍，填充时颗粒流在惯性作用下优先填充模腔中X正方向的一侧，另一侧的空气受到挤压后则斜向上逸出，颗粒流与气流在模腔X3、X4分区发生密集交汇，细颗粒的运动发生停滞，导致其在X3、X4分区内的聚集。
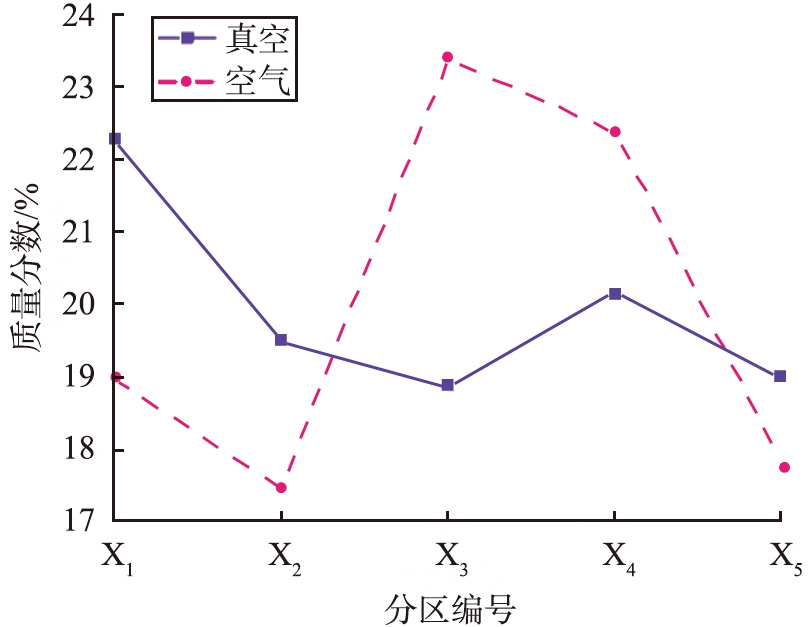
图11 直线移动式填充时在真空和空气环境下细颗粒在X方向上的质量分数
Fig.11 Mass fraction of fine particles in X direction in vacuum and air environment during linear moving filling
综上，颗粒混合物在空气环境中填充模具时会受到气流影响，流动形态发生变化。在固定式送料机构填充时，颗粒流挤压空气形成下凹式分布，同时逸散的空气迟滞细颗粒运动，导致约40%的颗粒堆积在模具Z方向的Z5、Z6分区，粗颗粒则几乎不受影响；在移动式机构送料过程中，细颗粒与空气在模具X方向的X3、X4分区发生密集交汇，颗粒流动发生偏折，导致约44%的细颗粒在该分区集聚。
3 结论
针对直线式移动机构和固定模具填充系统，基于CFD-DEM方法，三元颗粒混合物填充模具时，分析不同参数条件下的颗粒流动分离特性。
1)增加送料机构行进速度，可在行进方向(X方向)上显著抑制大粒径颗粒的分离行为，分离指数最大降幅达71%，而在Y和Z方向上对其的影响较小。对于工业生成方式产生的颗粒混合物填充前就已在送料机构内充分混合，故在不同方向上，各粒径颗粒物的分离指数均小于4.5且差距不大。分层生成方式产生的颗粒混合物，填充模腔时呈现鼻流现象，在送料机构行进方向(X方向)各粒径颗粒的分离指数明显高于其他方向(Y和Z方向)；颗粒在送料机构内的初始位置不同也会对颗粒的分离行为产生影响，而中层颗粒群受到上下区域颗粒的共同挤压作用，分离行为受到显著抑制，分离指数最小，仅为0.8。
2)送料机构的倾斜壁面可以使颗粒群产生漏斗状流动，从而抑制其分离，促进模腔内颗粒混合物的均匀分布。适当增加模具深度有利于颗粒混合物均匀分布，在模具深度由25 mm增加到30 mm时，分离指数下降79%，但当深度达到35 mm时，继续增加对颗粒混合物分离行为的影响不大。
3)空气流与颗粒流相互挤压，改变了颗粒混合物的运动形态，填充时形成凹陷偏折流动，逸散气流对细颗粒的运动有明显的迟滞作用，导致约40%的细颗粒在模腔内部分区域聚集，而对空气不敏感的粗颗粒几乎不受影响。
[1]钟文镇,昃向博,李国平,等.球形玻璃珠填充模腔的流动特性试验[J].中国粉体技术,2019,25(6):32-37.
[2]HUAQIN Y,YUKI M,KAZUYA T,et al.Numerical investigation on the influence of air flow in a die filling process[J].Journal of the Taiwan Institute of Chemical Engineers,2018,90:9-17.
[3]XU Z B,YOSHINAGA S,TSUNAZAWA Y,et al.Numerical investigation of segregation behavior of multi-sized particles during pharmaceutical mini-tablet die filling[J].Journal of Drug Delivery Science and Technology,2020,61:102301.
[4]WIDARTININGSIH P M,MORI Y,TAKABATAKE K,et al.Coarse graining DEM simulations of a powder die-filling system[J].Powder Technology,2020,371:83-95.
[5]TSUJI Y,KAWAGUCHI T,TANAKA T.Discrete particle simulation of twodimensional fluidized bed[J].Powder Technology,1993,77(1):79-87.
[6]HOOMANS B P B,KUIPERS J A M,BRIELS W J,et al.Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidised bed:a hard-sphere approach[J].Chemical Engineering Science,1996,51(1):99-118.
[7]NICOLIN N,WILKE D N,WU C Y,et al.Large-scale GPU based DEM modeling of mixing using irregularly shaped particles[J].Advanced Powder Technology,2018,29(10):2476-2490.
[8]ZHOU M M,WANG S,KUANG S B,et al.CFD-DEM modelling of hydraulic conveying of solid particles in a vertical pipe[J].Powder Technology,2019,354:893-905.
[9]GOU D,AN X,YANG X,et al.CFD-DEM modeling on air impact densification of equal spheres:structure evolution,dynamics and mechanism[J].Powder Technology,2017,322:177-184.
[10]CHEN J L,LI X F,HUAI X L,et al.Numerical study of collection efficiency and heat-transfer characteristics of packed granular filter[J].Particuology,2019,46:75-82.
[11]HERTZ H Z.On the contact of elastic solids[J].Journal Für Die Reine und Angewandte Mathematik (Crelles Journal),1880,92:156-171.
[12]MINDLIN RD,DERESIEWICZ H.Elastic spheres in contact under varying oblique force[J].Journal of Applied Mechanics,1953,20(3):327-344.
[13]YUKI T,YUSUKE S,CHIHARU T,et al.Numerical simulation of industrial die filling using the discrete element method[J].Chemical Engineering Science,2015,138:791-809.
[14]DANIEL M,FERNANDO J M,RAFAEL M.Particle size segregation promoted by powder flow in confined space:the die filling process case[J].Powder Technology,2014,262:215-222.
[15]GUO Y,WU C Y,THORNTON C.The effects of air and particle density difference on segregation of powder mixtures during die filling[J].Chemical Engineering Science,2011,66(4):661-673.
[16]CRISTINA R A,FERNANDO A E,ANA G M,et al.Segregation in the tank of a rotary tablet press machine using experimental and discrete element methods[J].Powder Technology,2018,328:452-469.
[17]GUO Y,KAFUI K D,WU C Y,et al.A coupled DEM/CFD analysis of the effect of air on powder flow during die filling[J].AICHE Journal,2010,55(1):49-62.
[18]RYOICHI F,YUKI S,KAZUNORI K,et al.Size-induced segregation during pharmaceutical particle die filling assessed by response surface methodology using discrete element method[J].Journal of Drug Delivery Science and Technology,2016,35:284-293.
[19]江帆,肖纳,黄春曼.粉末冶金装粉过程的充型均匀性研究[J].特种铸造及有色合金,2017,37(8):820-823.
[20]SAED S R,VIRENDRA M P.Uniformity differentiation analysis of powder deposition characteristics in circular and rectangular shallow dies using feed shoe with square cross-section[J].Particulate Science and Technology,2011,29(3):260-271.