催化裂化再生烟气中的SOx和NOx是主要的大气污染物,不仅直接危害人体健康,也是形成光化学烟雾和酸雨的主要原因[1-2]。相对于传统的湿法及半干法烟气处理工艺,干法烟气净化技术由于不耗水、无废液排放等特点越来越受到关注[3]。中国石化石油化工科学研究院研发的吸附法吸附催化裂化再生烟气中SOx和NOx技术[4-5]属于干法烟气净化技术的一种,吸附剂能够通过高温再生和还原处理恢复吸附性能而被循环利用。已有研究表明,再生温度越高,再生吸附剂的吸附性能恢复得越好[6]。
吸附剂高温再生的释放热量不能满足再生温度需求,因此再生过程需要补充部分热量。在重油或渣油催化裂化过程中,由于原料偏重,催化裂化反应与再生系统的热量是过剩的,需要通过外设取热器吸取多余的热量来维持系统热平衡[7]。由于吸附剂和催化裂化的再生剂物性相似,因此不能采用直接混合换热方式实现这2个过程的热量互供。姚秀颖等[8]提出了一种流化床间壁换热再生耦合装置设计方案,壁面两侧的高温催化裂化再生催化剂与低温吸附剂通过设置在壁面上的高效传热元件——热管进行换热,热管内相变介质的导热系数是铝、紫铜、银等金属的几百甚至上千倍,最高可达105 W/(m·℃)[9],因此,控制性热阻为流化颗粒与热管壁间的对流传热。
为了保证待生吸附剂的高效再生和换热,吸附剂操作于湍流床状态[10-11],热管与水平方向成20°布置。Lechner等[12]实验测量发现,单根水平管的传热系数随着管径的增加逐渐减小。Abid等[13]研究发现换热管表面不同周向位置的传热系数分布不同,受操作条件和换热管倾斜角度的影响:在较高气速时,换热管顶部的传热系数最大,两侧的传热系数次之,底部的最小;在较低气速时,换热管两侧的传热系数最大,底部次之,顶部最小;同时,换热管的布置越接近水平,不同周向位置的传热系数差异越大。Kim等[14]在水平管流化床内,测得低气速时的传热系数分布与Abid等[13]的研究结果一致,同时发现在水平管的顶部存在固含率(即颗粒相体积分数)较高的颗粒垫,底部存在固含率较低的气泡垫,换热管两侧的固含率中等,且颗粒的更新频率较高。姚秀颖等[15]通过数值模拟获得高气速时热管表面的固含率分布规律,在换热管下部固含率最高,上部最小,两侧固含率中等。同时,换热管的存在会将大气泡劈裂为小气泡,从而改变流化床内颗粒速度分布[16],因此,水平换热管表面不同周向位置的速度分布存在差异[17]。
在工业过程中,换热管通常需要排布多根管束。Lechner等[12]发现换热管水平和轴向间距越大,单根换热管的传热系数越高。对于三角形布置的3层管束,上层换热管表面的颗粒速度、固含率和传热系数均受到下层换热管的影响,但各层换热管不同周向位置的分布状况相同[18]。
近年来,研究者们开始采用数值模拟方法考察湍流床内床层与内浸表面间的传热特性,以及内浸物体对气固流动特性的影响。Lee等[19]在双流体模型框架下采用Gidaspow曳力模型模拟了毫米级颗粒脉动流化床内床层与浸没管之间的固含率和传热系数分布,发现鼓泡床的传热效果优于湍流床,这是由于湍流床内换热管上部存在较大的气泡垫和颗粒滞留层。Bisognin等[20]在Lee等[19]所用模型基础上优选出RNG k-ε湍流模型,能够用于模拟湍流床内粒径为500 μm的玻璃珠颗粒与浸没圆柱体表面间的换热系数,结果表明,圆柱体的直径越大,其换热系数越小,且圆柱体直径对床层动力学有明显影响。Wang等[21]采用DEM-LES模型研究了循环流化床内管束布置方式对气固流动和传热特性的影响,发现管束的存在会使颗粒分布更加均匀,而且交错布置的管束可使传热系数更大,然而,上述研究所模拟的湍流床内颗粒直径均较大。姚秀颖等[15]采用双流体模型耦合EMMS曳力模型模拟了Geldart A类颗粒湍流床内倾斜热管表面及热管所在区域的固含率分布特性,发现换热管仅对其末端区域的固含率有明显影响,并且明确了主换热区的存在。
颗粒团更新理论[22]表明,换热表面的颗粒团时间分率和更新频率是影响颗粒与壁面间换热系数的2个关键参数。颗粒团时间分率直接与固含率相关[19],更新频率除了与颗粒在换热表面的停留时间相关外,还与颗粒速度相关[16]。在气固流化床内,由于颗粒的比热远大于气体的,因此颗粒对流传热过程起主要作用[23]。
本文中采用双流体模型耦合EMMS曳力模型对倾斜热管间壁式换热器湍流床一侧进行模拟研究。首先进行几何建模、网格划分和模型验证;然后研究颗粒轴向速度的轴向分布,明确热管的存在对颗粒轴向运动的影响;接着详细分析热管之间和热管所在区域的颗粒轴向速度的径向分布,明确热管、轴向高度和表观气速对颗粒轴向速度的径向分布的影响,综合分析气泡在热管区的运动状态及速度分布;之后研究热管相对位置对热管表面的颗粒轴向速度分布的影响,理清热管表面不同区域的颗粒运动状态;最后,结合固含率在换热表面的分布特性[15],分析热管表面不同周向位置的颗粒运动对换热过程的影响,并考察操作条件和换热管位置对换热性能的影响,以期获得颗粒流动与换热过程的影响规律。
1 模拟对象及模型验证
1.1 换热器几何建模与网格划分
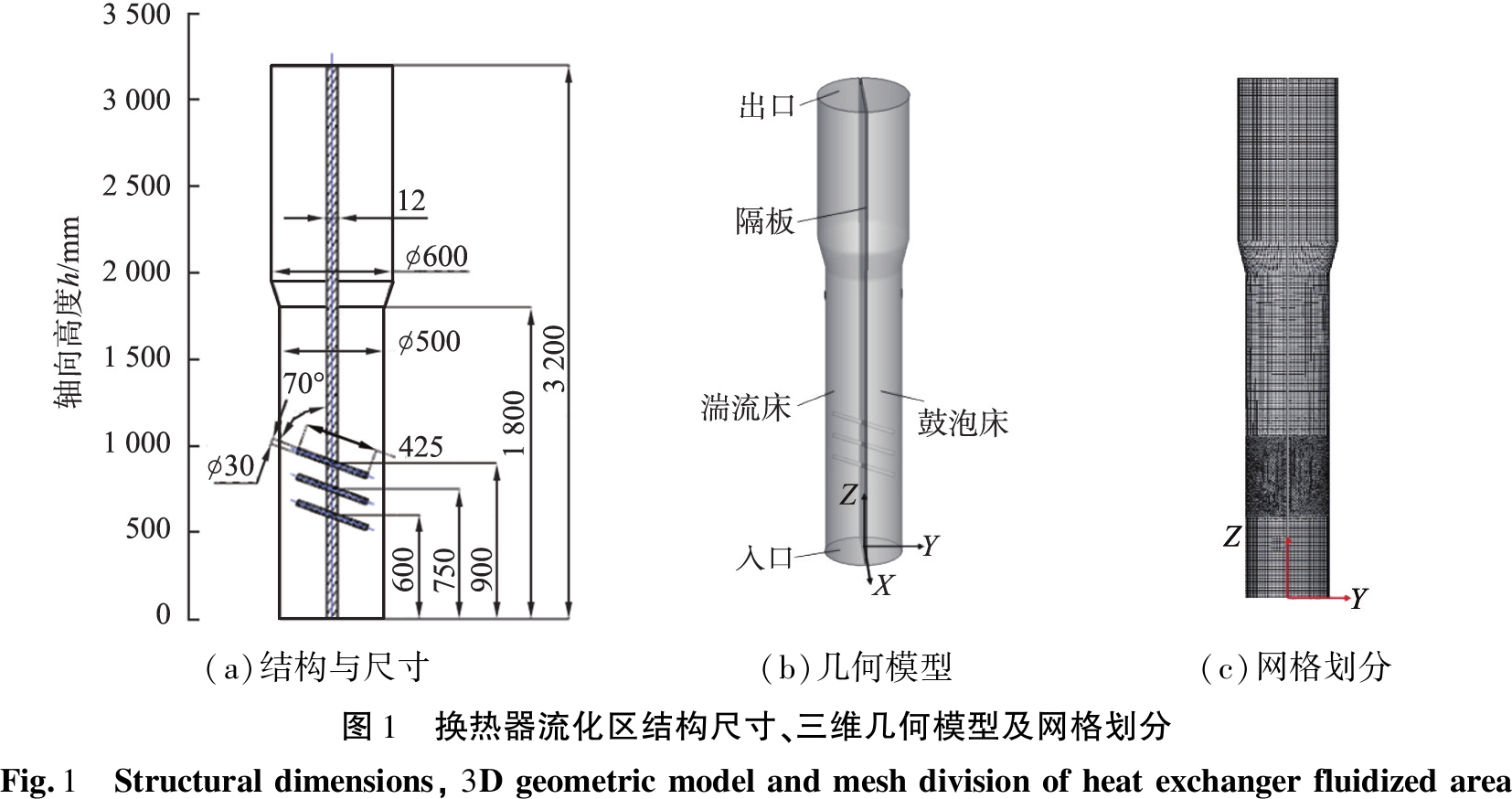
换热器流化区结构尺寸、三维几何模型及其网格划分如图1所示。由图1(a)可见,为节省计算资源,换热器流化区总高设为3 200 mm,圆柱形筒体内径为500 mm,上部1 800 mm高的筒体直径增大到600 mm以减小颗粒夹带量;筒体内设厚度为12 mm的隔板,隔板上布置3根热管用于将隔板一侧高温颗粒的热量传递给隔板另一侧的低温颗粒。为减小分布器小孔射流的影响,热管距底部入口的高度分别为600、750、900 mm,热管直径为30 mm,长度为425 mm,与垂直方向夹角为70°。由图1(b)可知,热管在湍流床一侧向上倾斜,以保证热管内换热介质的自循环;旋风分离器的颗粒收集过程采用用户自定义子程序实现,以保证物料守恒。由图1(c)可知,换热器三维几何模型采用全尺寸建模,除热管所在区域采用四面体非结构化网格外,其余部分均采用六面体结构化网格;网格无关性验证表明,选用12 mm的网格能够很好地重构流化床内固含率分布情况[15];在底部气体入口,气固两相均设为速度入口边界条件,上部出口均设为压力出口边界条件;对于气相,壁面采用无滑移边界条件,颗粒相采用部分滑移边界条件,镜面系数为0.1[24]。
1.2 研究对象与初始条件
研究对象为流化床间壁式换热器湍流床一侧的气固流动状态,操作气速为0.6~1.0 m/s。流化介质为常温常压空气,密度和黏度分别为1.225 kg/m3和1.782×10-5 Pa·s,固体颗粒为催化裂化平衡催化剂,颗粒密度和平均粒径分别为1 500 kg/m3和70 μm。为保证热管所在区域为稳定流化区,将初始床高设为0.8 m,初始固含率为0.6,初始速度为0.003 5 m/s。采用Fluent 6.2进行求解,颗粒-壁面间碰撞恢复系数es为0.9,时间步长为0.001 s。模拟结果表明,床层在25 s后达到稳定流化状态,故取25~40 s之间的数据进行统计平均,用于分析不同区域的流动状态。
1.3 数学模型及模型验证
在湍动流化床内,因为颗粒相呈连续状态而气泡呈离散状态,所以采用双流体模型对其进行模拟研究,气固相间相互作用采用EMMS曳力模型。本文中所用模型与文献[15]相同,这里不再赘述。
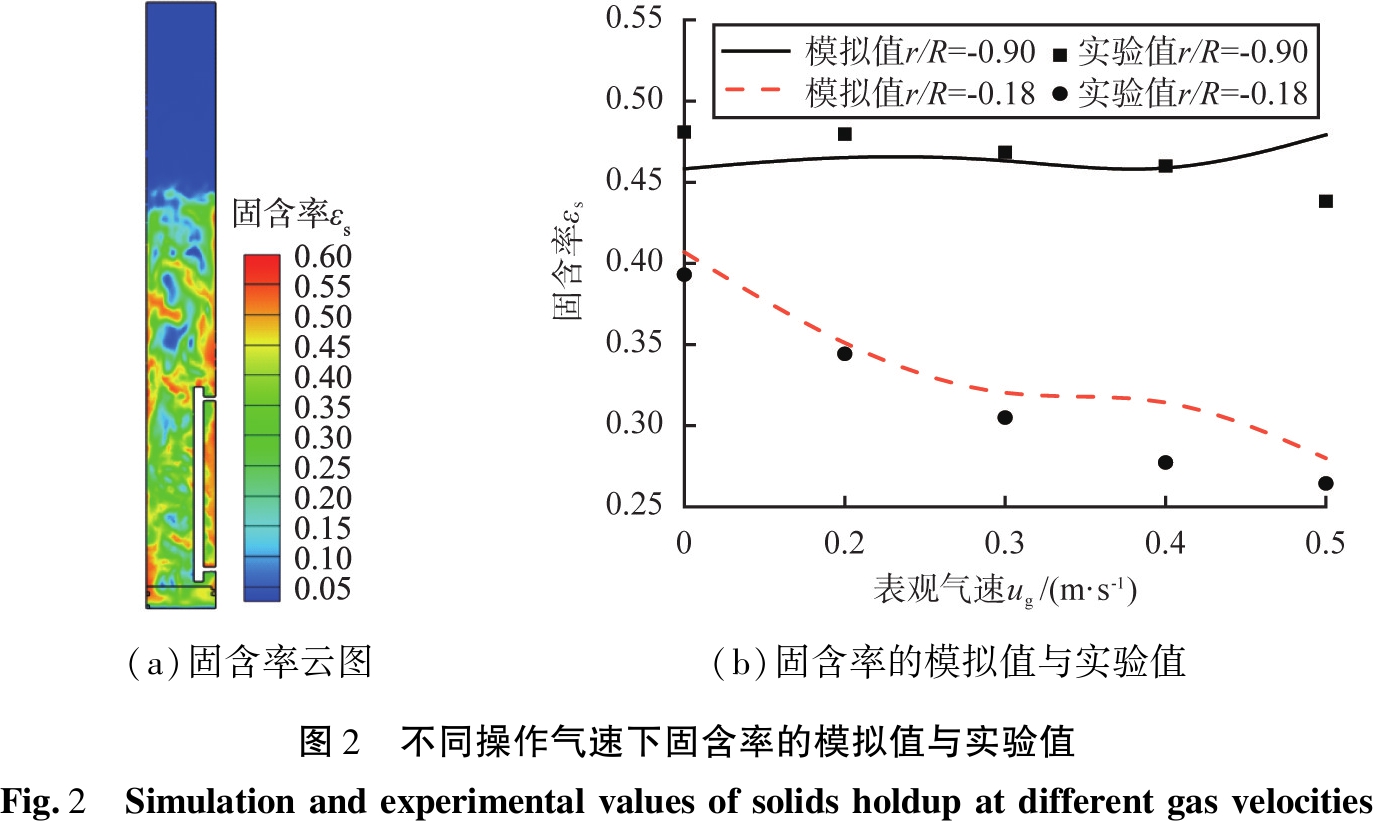
模型验证采用垂直管流化床换热器的实验结果[25]进行比较,不同操作气速下固含率的模拟值与实验值如图2所示。由图2(a)可知,床内存在尺寸不均匀的气泡,固含率分布较均匀,呈典型的湍流床流动状态;由图2(b)可知,模拟结果能够很好地描述固含率中心低、边壁高的分布特征,且随着表观气速的增加,中心位置(r/R=-0.18,其中r为任意径向位置,R为换热器半径)固含率逐渐减小,床壁附近(r/R=-0.18)固含率几乎不变。模拟结果与实验数据吻合较好,表明该模型能够很好地描述湍流床内气固两相的流动和分布特征。
2 结果与讨论
2.1 颗粒轴向速度的轴向分布
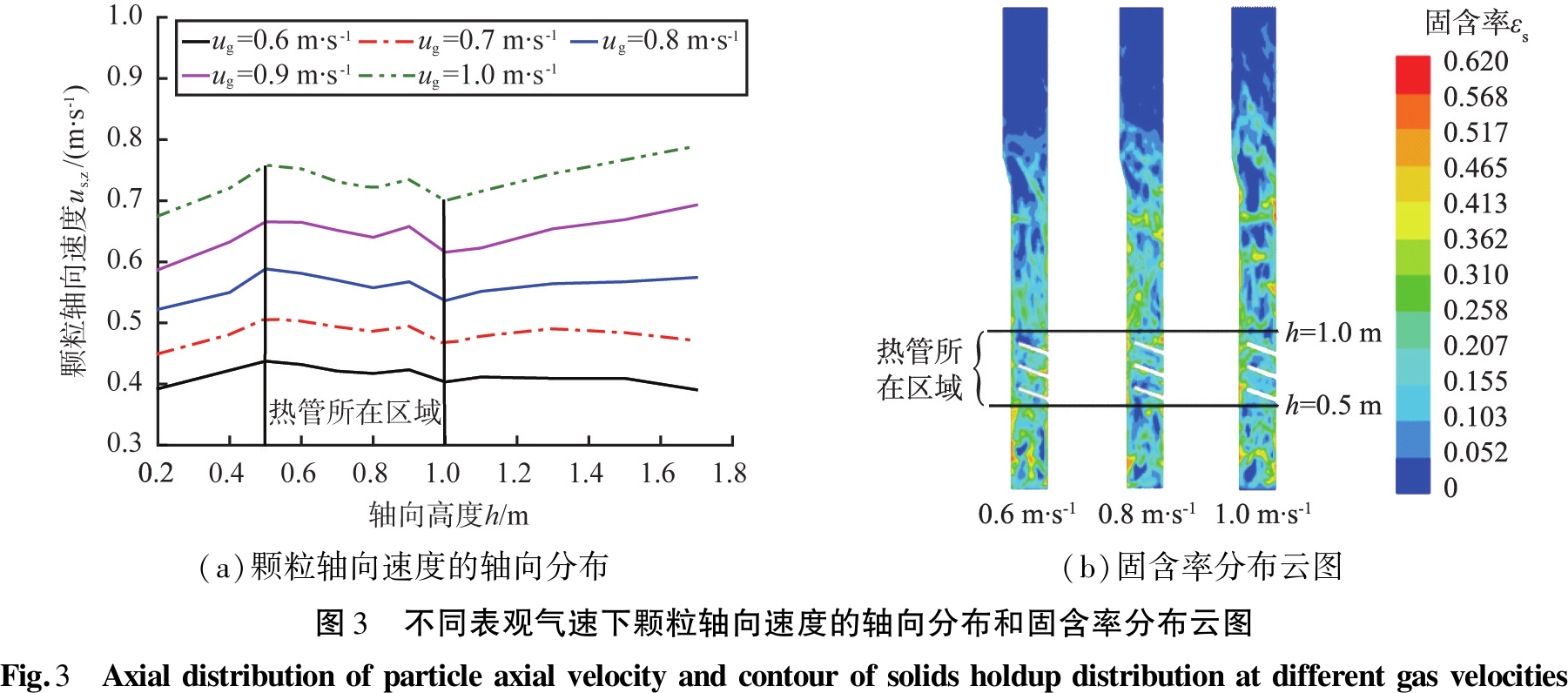
在不同表观气速下,颗粒轴向速度的轴向分布和固含率分布云图如图3所示。由图3(a)可知,在不同高度处,颗粒轴向速度呈现出不同的分布状态;在床层下部区域(h<0.5 m),气体由分布器进入床层,随着颗粒的向上运动,其轴向速度逐渐增大,这是由于气泡尺寸随轴向高度的增大而逐渐增大,导致气泡带动颗粒上升速度增加;当上升的气泡遇到热管后,气泡被热管劈裂为较小的气泡,进入热管所在区域(0.5 m<h<0.8 m)的颗粒轴向速度随轴向高度有所减小,因此,颗粒轴向速度的极大值出现在热管区域的下部;在热管所在区域(0.8 m<h<1.0 m),颗粒轴向速度稍有增大后迅速减小,这是由于该区域内颗粒受热管的限制作用减弱,致使颗粒轴向速度增大,而流过该区域后颗粒的动能逐渐减小,且流通面积增大,导致颗粒轴向速度迅速降低。由图3(b)可知,颗粒进入热管区域上部(h>1.0 m)后,气速较低时,由于受床层膨胀高度所限,颗粒轴向速度几乎不随轴向高度而变化;气速较高时,颗粒轴向速度随轴向高度逐渐增大,这是由于气泡尺寸随轴向高度逐渐增大;随着表观气速的增加,相同截面高度的颗粒轴向速度显著增大;在热管所在区域及其下部区域,颗粒轴向速度与表观气速的增幅相当,而在热管区域上部,不同表观气速下颗粒轴向速度的增幅随轴向高度的增大而增大。综上,热管的存在使湍流床内颗粒平均速度增大,颗粒的聚集和返混现象减弱;增大气速,热管所在区域的颗粒运动更加剧烈,热管对湍流床内颗粒轴向速度的影响也增强。
2.2 颗粒轴向速度的径向分布
2.2.1 热管之间区域
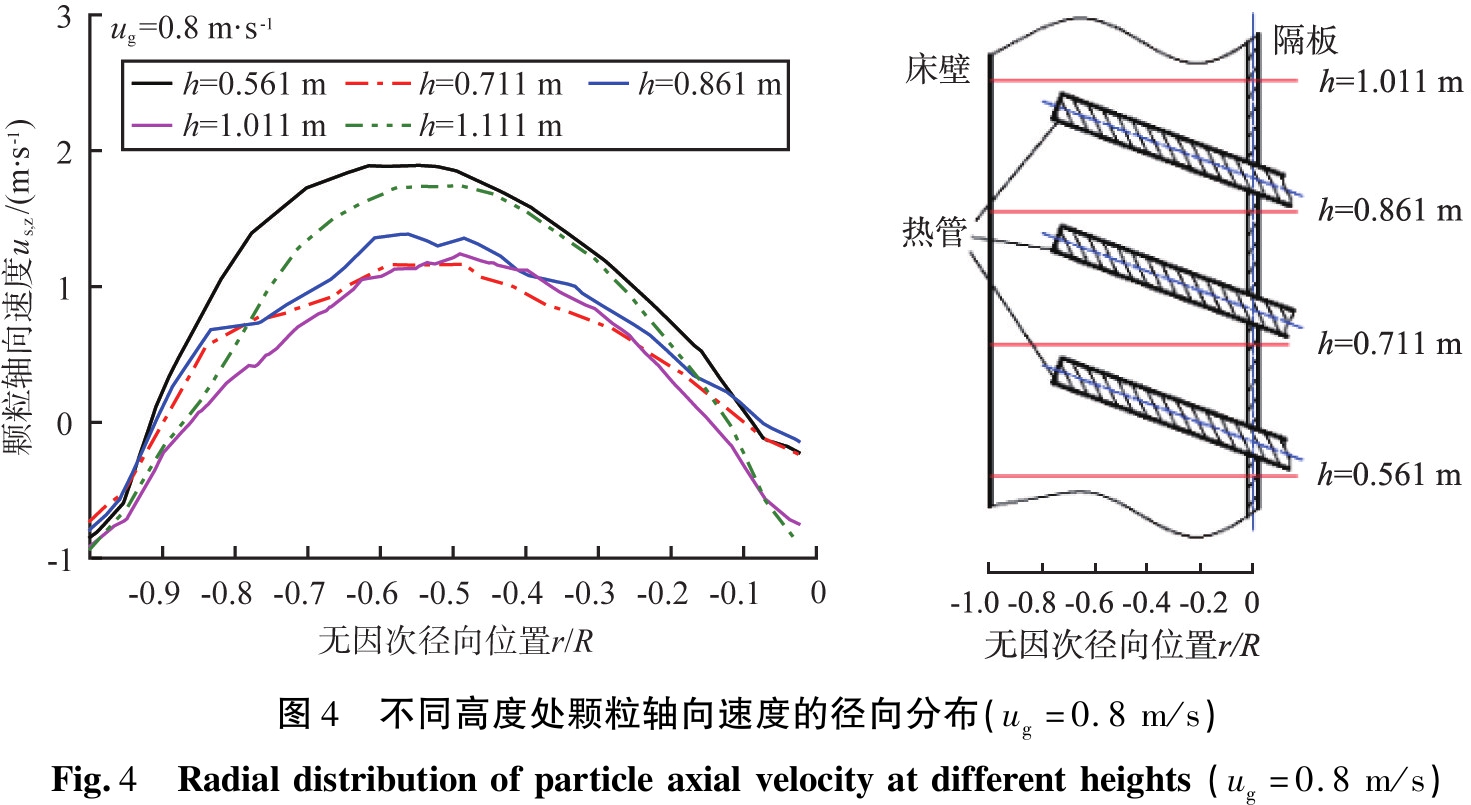
表观气速为0.8 m/s时,不同高度处颗粒轴向速度的径向分布如图4所示。由图4可知,选取的5个轴向位置紧临或远离热管,但都没有横穿热管,不同轴向位置处的轴向速度的径向分布均呈现为开口向下的抛物线型。床中心区域的颗粒呈上行流动,边壁附近的颗粒呈下行流动;湍流床内表观气速较高,床层中心区域的固含率较小,气体携带颗粒上行的阻力也较小,因此相比于壁面区域,床层中心区域的颗粒上行速度较大,而在床体边壁附近,气泡数量较少,大量回落的颗粒沿壁面下行,上行颗粒与壁面的摩擦以及与下行颗粒的碰撞消耗了部分动能,因此边壁区域的颗粒轴向时均速度较小。受两侧不同壁面条件的限制,颗粒轴向速度沿径向呈非对称分布,即靠近床壁一侧的颗粒下行速度和下行颗粒所占区域的尺寸均大于靠近隔板一侧的,且峰值点偏向床壁一侧,因此,可以认为壁面的曲率半径越小,气固两相流动受壁面的影响越大,颗粒轴向速度的变化越陡峭。在有内构件的流化床换热器内,颗粒轴向速度的径向分布的非对称性随轴向高度的增大而减小。
由图4还可知,在床壁附近颗粒下行速度基本一致,而在隔板壁附近,颗粒下行速度随轴向高度的增加先不变后增大。不同区域内颗粒轴向速度沿径向变化的梯度存在一定差异。在轴向高度h为0.561 m处,因其距离分布器影响区最近,所以中心区域颗粒轴向速度最大,颗粒轴向速度沿径向梯度较大。相邻热管间的区域(h分别为0.711、0.861 m)以及最上方热管的上部(h为1.011 m)颗粒轴向速度相对较小,沿径向变化的梯度也较小。这是由于颗粒和气泡上行运动受到了热管的阻挡,大气泡不断地被破碎,颗粒因碰撞、与管壁面摩擦等原因损失了一部分动能。在轴向高度h为1.111 m处的颗粒轴向速度最大值大于有热管存在区域(0.711 m<h<1.011 m)的,颗粒轴向速度的变化梯度又增大,该位置已经远离了热管的影响区,气相和颗粒相的上行运动受阻较小,气泡在远离热管的区域因合并而长大,颗粒轴向速度增大。当-0.75<r/R<-0.2时,热管所在区域(0.711 m<h<1.011 m)内,轴向高度h为0.861 m处的颗粒轴向速度相对较大,这是由于受到下部2根热管的影响,被破碎的小气泡数量较多,增加了颗粒的上行速度。
在h=0.861 m处(位于最上方与中间热管之间),不同表观气速下颗粒轴向速度的径向分布如图5所示。由图5可知,整体来看,不同气速下颗粒时均速度沿径向都呈现开口向下的抛物线型分布。床层中心区域颗粒的平均速度均随表观气速的增大而增大,受气速的影响较明显,而在壁面附近,颗粒轴向速度受气速的影响较小。不同的表观气速下,颗粒轴向时均速度的变化趋势稍有不同。气速较小(ug=0.6 m/s)时,颗粒轴向速度波动较小,沿径向的分布较平缓;随着气速的增加,气含率增加,气体对颗粒的拖曳作用增大,床层中心颗粒上行的速度明显增大,但是气速由0.7 m/s增加到1.0 m/s过程中,颗粒上行速度增幅减弱,表明在一定气速范围内热管对颗粒和气泡流动的作用效果接近,颗粒下行速度减小,表明气速增大强化了颗粒上行运动的速度。值得注意的是,当表观气速由0.9 m/s增加到1.0 m/s过程中,颗粒轴向速度变化略有不同,床层左侧区域颗粒下行速度增大,右侧区域颗粒下行速度明显减小,这与热管的倾斜安装密切相关。从图中可知,在左侧床壁附近(r/R<-0.75)颗粒下行速度较大,随气速的增大下行速度变化较小。右侧隔板壁附近(r/R>-0.15)颗粒下行速度较小,且随气速的增加颗粒下行速度明显减小,当气速ug为1.0 m/s时,隔板附近的颗粒由下行转变为上行运动,这是由于相较于隔板壁面,床壁结构具有对颗粒轴向速度更强的影响。
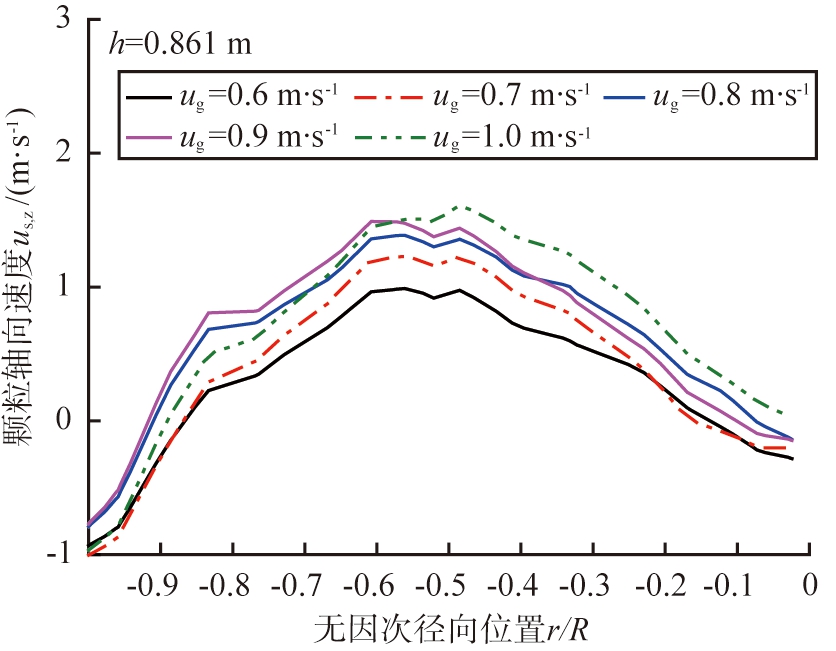
图5 不同表观气速下颗粒轴向速度的径向分布(h=0.861 m)
Fig.5 Radial distribution of particle axial velocity at different gas velocities(h=0.861 m)
综上可知,湍流床内气速较高,颗粒上行速度较大,但热管所在区域内,颗粒轴向速度降低幅度较大,颗粒上行既受热管的阻力又会获得气泡提供的动力,综合作用下使得颗粒轴向速度沿轴向呈先减小后增大再减小的复杂变化。随着气速的增加,颗粒轴向速度增加的幅度逐渐减小,气体的携带能力达到一定的极限。气速增加到较大值后,热管倾斜安装导致床层内左、右两侧速度变化不一致。因为床体边壁和隔板边壁曲率半径不同,所以其附近颗粒流动受气速的影响大不相同,曲率半径越小,颗粒运动受限越明显。热管能够影响床层内的流场分布,降低颗粒上行速度,使颗粒在径向混合更加均匀,同时抑制了大量颗粒的返混,减弱了边壁效应的影响,有利于床层与壁面间的换热。
2.2.2 热管所在高度
表观气速为0.8 m/s时,不同高度处颗粒轴向速度的径向分布如图6所示。由图6可见,颗粒轴向速度整体呈现中心向上、边壁向下的分布特征。因热管的存在,上行颗粒最大速度对应的径向位置存在偏心现象,偏向热管自由端一侧,即r/R=-0.7附近。图中所示轴向高度范围内,在热管下侧(-0.8<r/R<-0.59),径向位置越大,其与热管的轴向距离越小,在热管上侧(r/R>-0.25),径向位置越大,其与热管的轴向距离越大。在热管下侧,颗粒均呈上行运动,由于热管壁面摩擦的作用,上行速度随径向位置的增大而稍有减小,小范围内颗粒的流动比较平稳。在热管上侧,颗粒以下行运动为主,下行速度随着径向位置的增大而逐渐增大,原因主要是热管壁面对颗粒运动的限制作用逐渐减弱,上行运动的颗粒只存在于靠近热管壁面的区域,且上行速度较小。颗粒在管壁两侧截然不同的流动方式促使床层内形成内循环,增强气固沿径向的混合,使得床层密度更加均匀[15]。在热管自由端与床壁之间的区域(-1.0<r/R<-0.8),颗粒在靠近热管自由端的区域呈上行运动,在靠近床壁处呈下行运动,两种运动的临界点位于r/R=-0.9,径向位置距离临界点越远,颗粒轴向速度越大,且颗粒上行速度明显大于下行速度。颗粒轴向速度的径向分布特征与数值大小基本不随轴向高度而变化。
在h=0.788 m处,不同表观气速下颗粒轴向速度的径向分布如图7所示。由图7可见,总体来看,表观气速对床层中心区域与隔板壁面附近颗粒轴向速度的影响较明显,对床壁附近颗粒轴向速度的影响较小。不同表观气速下,热管下侧的颗粒轴向速度总是大于热管上侧的,这一速度差可以推动颗粒在径向的混合,提高床层流化质量。床壁与隔板壁的颗粒轴向速度变化趋势存在一定差异,在热管上侧区域(r/R>-0.1)的颗粒下行速度较小,受表观气速的影响较明显,床壁附近(r/R<-0.9)的颗粒下行速度较大,受表观气速的影响较小。
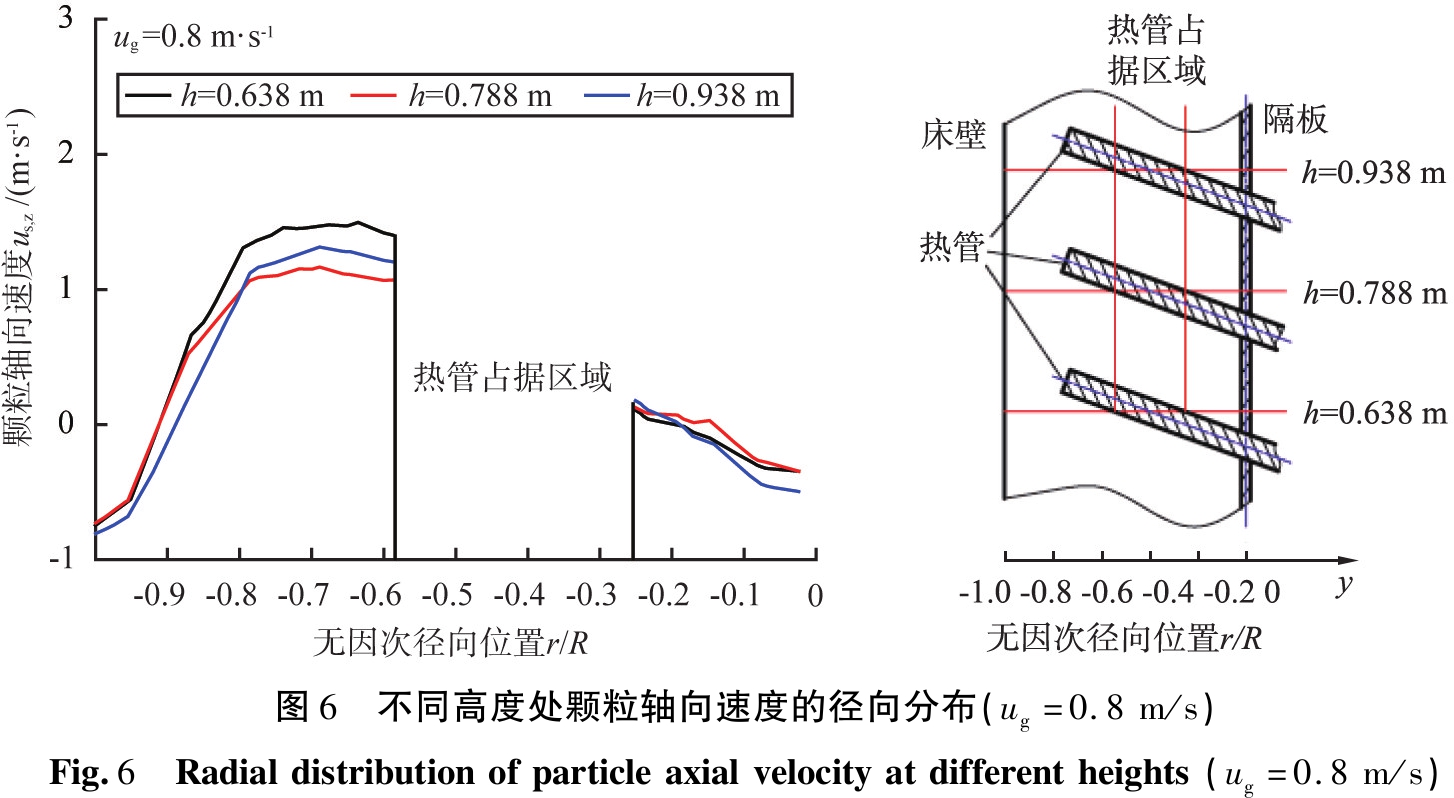
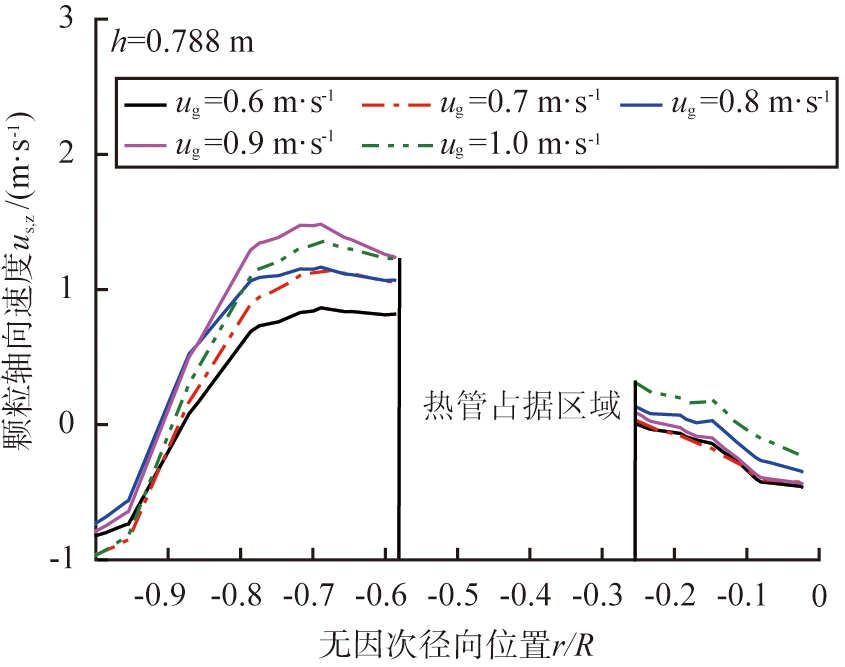
图7 不同表观气速下颗粒轴向速度的径向分布(h=0.788 m)
Fig.7 Radial distribution of particle axial velocity at different gas velocities (h=0.788 m)
2.2.3 综合分析
当ug=0.8 m/s时,不同时刻固含率云图如图8所示。通过综合分析图8中固含率云图和图4、6中颗粒轴向速度的径向分布可以发现,不同高度的颗粒轴向速度的径向分布各具特征。在热管区下部(h=0.561 m),颗粒在床层中部的上行运动速度较大;在遇到热管后(h=0.638 m),热管所在径向位置的颗粒轴向速度有所降低,且与热管间距离越小,颗粒轴向速度降低幅度越大;在流过热管后(h=0.711 m),由于气泡被热管破碎为较小气泡,因此颗粒轴向速度变小,且沿径向分布更加均匀;在流过热管区后(h=0.788 m),由于气泡稍有增大,因此颗粒轴向速度同样增大。在气固流化床内,由于颗粒在气泡的带动下运动,因此在某一轴向高度内颗粒轴向速度径向分布的最大值通常代表了大气泡的流动路径。由上述分析可知,气泡的主要运动路径为:在热管区下部,由于床壁较隔板壁有较强的壁面效应,因此气泡偏向床壁一侧运动;在遇到热管后,由于受到壁面挤压所用,因此气泡主要由热管自由端位置向上流动;在流过热管后,热管对气泡的再分配作用使得气泡主要在床中心区域流动;继续向上依次由自由端穿过热管和在床中心向上运动,因此气泡呈S形向上运动;在流过热管区后,因为热管的再分配作用且上部无热管限制,所以气泡在床中心以较高速度向上运动。
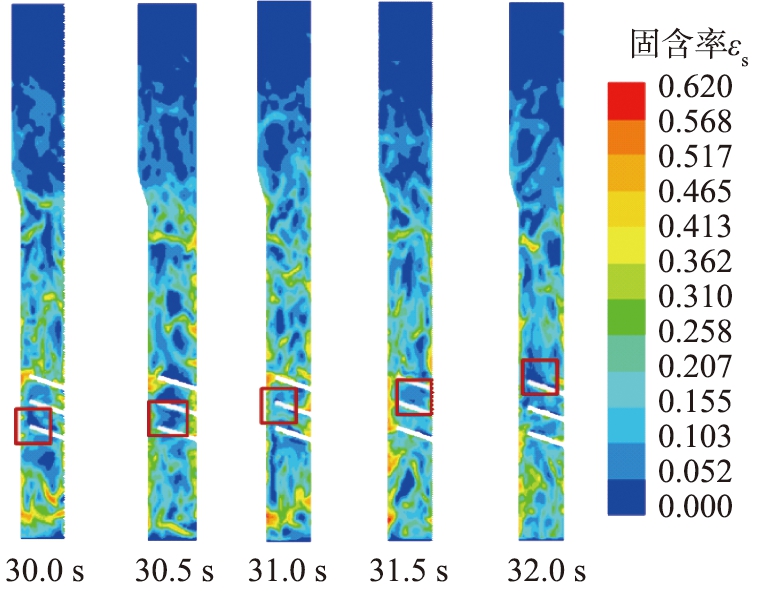
图8 不同时刻固含率云图(ug=0.8 m/s)
Fig.8 Contour of solids holdup at different times (ug=0.8 m/s)
综上可知,在流化床换热器内,虽然有热管的存在,但颗粒依然在中心区域向上运动,在边壁区域向下运动。热管的存在使最大速度对应的径向位置偏向靠近床壁一侧的热管自由端。由不同轴向高度的颗粒轴向速度分布可知,气泡在床内向上沿“S”形路线穿过热管运动,即在热管所在高度,气泡由热管自由端向上运动,在相邻热管之间区域,气泡由床中心向上运动。对于热管所在高度,表观气速对热管自由端下侧区域的颗粒轴向速度径向分布的影响最大,热管约束端上侧次之,床壁附近最小。
2.3 热管表面颗粒速度分布
通过上述分析发现,在热管的上部和下部区域存在不同的流动状态。ug=0.8 m/s时,热管表面不同周向位置的颗粒轴向速度分布如图9所示。
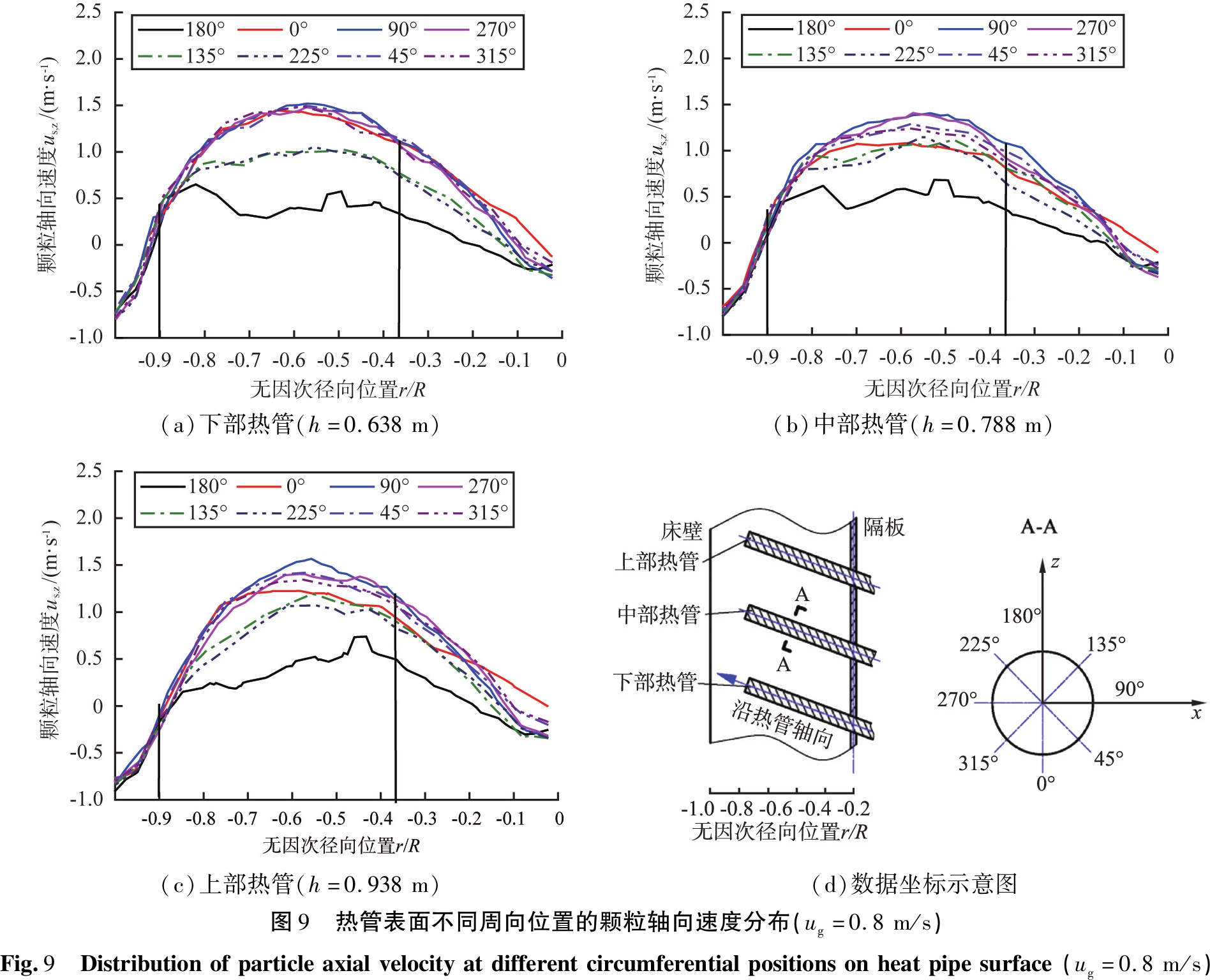
由图9(a)—(c)可见3根热管表面不同周向位置的颗粒轴向速度分布特征。总体来看,在靠近床壁的热管左侧区域,由于没有热管的存在,因此不同周向位置的颗粒轴向速度仅代表床内不同位置的颗粒轴向速度分布,又由于不同周向位置非常靠近,因此颗粒轴向速度也很接近。该位置内颗粒均在靠近床壁一侧向下运动,在靠近热管自由端一侧向上运动。在热管表面,随着径向位置远离隔板,颗粒先以较小的速度向下运动,然后沿着热管长度方向,颗粒转变为向上运动后其上行速度先增大后减小,直到与无热管区颗粒轴向速度相当。
在热管上表面周向180°位置,颗粒上行速度最小,下行速度最大,只在热管自由端位置颗粒上行速度较大,这是由于气泡趋于穿过热管自由端而向上运动(如图7所示)。热管表面周向135°和225°位置的颗粒轴向速度相当,运动趋势一致,表明沿热管表面颗粒轴向速度具有很好的对称性。该位置的颗粒轴向速度较热管上表面(周向180°)的颗粒上行速度大,较颗粒下行速度小,在远离隔板的区域(-0.80<r/R<-0.35),颗粒上行速度变化较小,在靠近隔板的径向区域(-0.35<r/R<0),颗粒轴向速度迅速减小。与热管表面固含率的轴向变化[15]进行比较发现,这是因为远离隔板的区域为气泡的主要运动路径,所以固含率较小,颗粒轴向速度较大,在靠近隔板的区域,被气泡带动而向上运动的颗粒与隔板附近下落的颗粒相遇,导致颗粒上行运动受限,因此固含率较大,颗粒轴向速度较小。热管下表面周向90°~270°范围内沿热管轴向的颗粒轴向速度均相近,仅在靠近隔板区域,热管下表面周向0°位置的颗粒轴向速度明显大于其他周向位置的。上述热管表面不同周向和轴向位置的颗粒轴向速度分布特征几乎不受热管轴向高度和相对位置的影响,但热管表面不同周向位置颗粒轴向速度的差异,随着轴向高度的增加而先减小后不变,这种差异是由热管在轴向高度的相对位置差异引起的。具体差异表现为:下部热管表面的颗粒轴向速度较大,大气泡首次被热管破碎,颗粒轴向速度减小明显;中部热管表面的气泡被下部热管减小后,继续被中部热管减小,同时受上部热管的影响,所以热管上表面(周向180°)颗粒轴向速度与下部热管上表面的颗粒轴向速度相当,但热管下表面颗粒轴向速度明显小于下部热管的;因为上部热管上表面无热管影响,所以其上表面颗粒轴向速度较大。
气固混合物在流经热管的过程中,因其与热管的相对位置不同而表现出不同的运动方向,因此需要综合分析热管表面各方向速度的分布,以明确颗粒与热管之间的相互作用。图9中结果表明,不同轴向高度热管表面具有相同的速度分布,其中下部热管表面的颗粒轴向速度周向分布的差异较明显,因此下面以下部热管表面X、Y和Z方向的速度分布为例进行分析,如图10和9(a)所示。根据图1可知,us,x为沿热管径向的颗粒速度,us,y为与热管轴向呈20°的颗粒速度,即沿床截面径向方向。图10中周向90°所在位置为X正方向。为便于分析,综合热管表面的颗粒速度和固含率分布特征,沿床层径向将热管表面进行分区:区域1位于-0.35<r/R<0.0,为热管的受约束端,称为壁面影响区;区域2位于-0.90<r/R<0.35,为热管自由端和热管外一定距离,称为主换热区;区域3位于-1.00<r/R<-0.90,称为无热管区。
当ug=0.8 m/s时,下部热管表面不同周向位置的颗粒速度分布如图10所示。综合分析图10(a)、(b)和9(a)中主换热区可以看出:在热管下表面,颗粒以向上运动为主,同时由于气泡周围不同位置气含量的不同,所以颗粒以较小的速度由热管约束端向自由端运动,即贴着热管下壁面向上运动;在热管上表面,颗粒在热管自由端,沿着热管向上向右运动,在靠近热管约束端,沿着热管向上向左运动,形成颗粒的内循环运动;在与热管同一高度的2个侧面(周向90°和270°),X方向速度相反,但数值较小,颗粒以向上运动为主;在周向45°和315°位置的颗粒在X和Z方向的速度均与周向90°和270°位置相当,Y方向速度大于周向90°和270°位置的颗粒Y方向速度,由于热管向上倾斜,所以整体表现为颗粒绕着热管表面且贴壁向上运动;在热管上表面周向135°和225°位置的颗粒速度分布与周向180°位置相近,X与Y方向速度较小,Z方向速度较大,整体呈向上运动。上述分析结果表明,在热管自由端的-0.80<r/R<-0.35范围内,热管下表面周向90°~270°周向位置,颗粒的运动较剧烈,有利于颗粒在换热表面的更新,促进热量传递。
综合比较壁面影响区内各方向速度的周向分布发现:颗粒在X和Y方向速度沿热管表面周向的分布状态与主换热区Z方向颗粒轴向速度的分布相同,数值随着靠近隔板而逐渐减小,在近璧区颗粒存在下行运动,越靠近热管上表面,下行速度越大;颗粒在近璧区以较小的速度由壁面向床中心运动,越靠近热管上表面,颗粒轴向速度越大。总体而言,颗粒在壁面影响区的下表面以向上运动为主,在上表面,颗粒上行速度降低,部分动能转变为使颗粒由隔板壁向床中心运动,即颗粒在接触到热管壁面后,以较高速度向上运动,流过热管后,由于热管向上倾斜,因此颗粒以一定速度沿着热管上表面向上运动。上述结果表明,在自由端的下表面和约束端的上表面,颗粒贴壁向上运动,因此,该位置为倾斜热管的特征换热区,该区通过热管的倾斜布置强化了颗粒在换热表面的更新速度,利于热量传递。
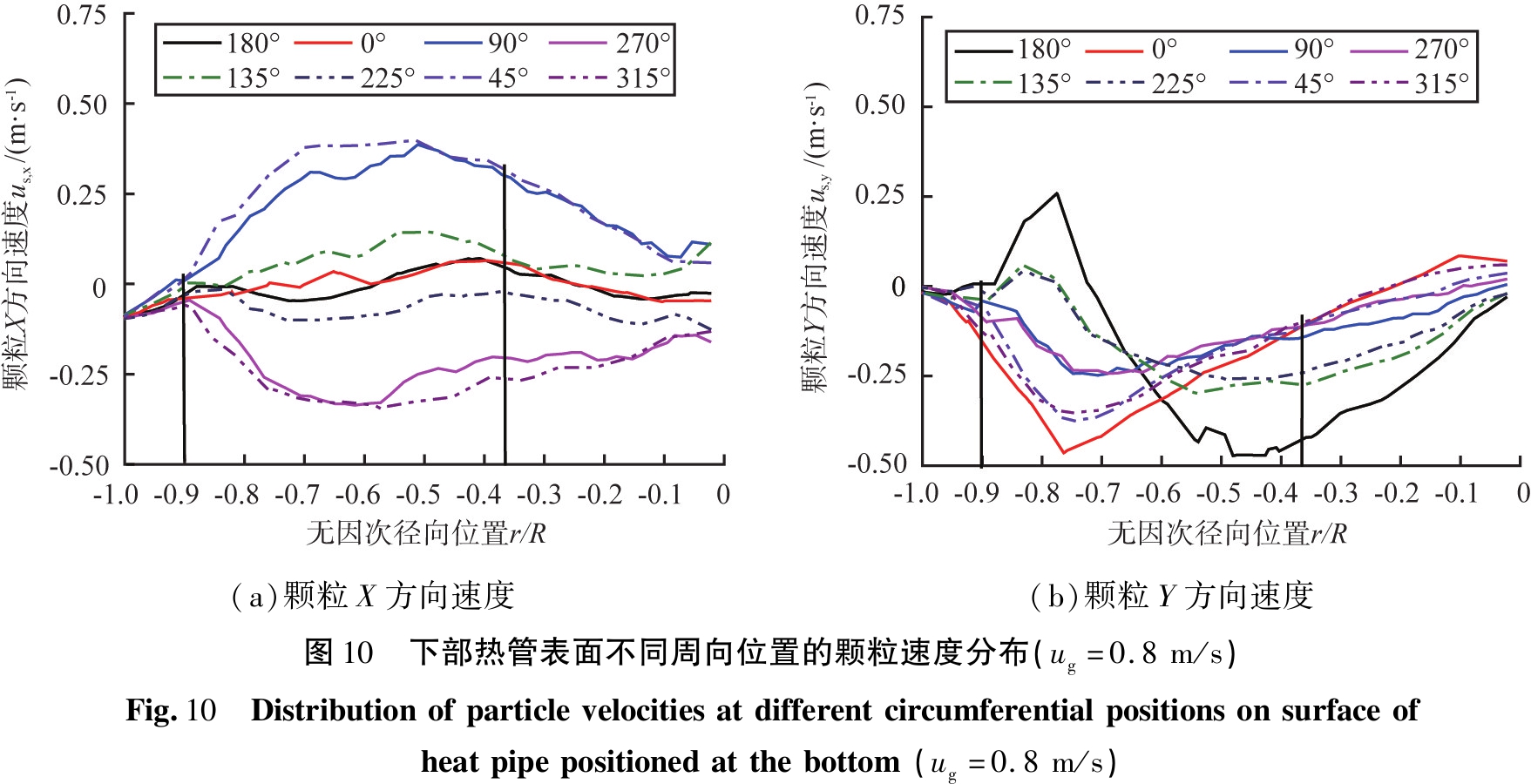
综上,在热管表面的自由端,颗粒以较大的速度向上运动;在约束端,以较小的速度向下运动。热管表面不同周向位置呈现不同的颗粒轴向速度分布:在主换热区,热管两侧和下表面的颗粒轴向速度较大,上表面次之,顶部颗粒轴向速度最小;在近璧区,热管表面颗粒轴向速度周向分布与主换热区相似,隔板壁面处,热管下表面的颗粒下落速度最小,热管上表面颗粒下落速度最大;中间位置介于二者之间。不同方向颗粒轴向速度分布表明:在热管自由端的下表面和约束端的上表面为倾斜热管的特征换热区,颗粒贴壁向上运动,热管的倾斜布置强化了颗粒在换热表面的更新速度,利于热量传递。
2.4 热管表面换热性能分析
为明确气固流化床内床层与换热表面间的传热过程,Mickley等[22]根据颗粒的流动特性提出了颗粒团更新模型,该模型包含2个重要参数,即颗粒团在换热表面的时间分率δpa和平均停留时间τpa,它们与传热系数h的关系式为
(1)
式中:kpa为颗粒团的热导率,W/(m·K);ρpa为颗粒团密度,kg/m3;cpp为颗粒的比热容,J/(kg·K);kpa、ρpa和Cpp均为物性参数。
实验测量结果[23,26]表明,颗粒团在换热表面的时间分率δpa与换热表面固含率εs正相关[22]。在一定流动距离L内,颗粒在换热表面的平均停留时间τpa与颗粒速度us成反比关系,Ostermeier等[16]认为颗粒平均停留时间与颗粒速度成反比,因此,传热系数与固含率εs和颗粒速度us均呈正比关系。同时,固含率εs与颗粒密度ρs的乘积为局部区域的床层密度ρb。局部区域的床层密度ρb与颗粒轴向速度us的乘积等于颗粒的质量流量Gs,其表达式为
Gs=ρbus=εsρsus=ρsQs。
(2)
因为ρs为定值,所以热管表面的颗粒流速Qs与传热系数正相关。
采用热管表面的颗粒流速分析颗粒与热管之间的传热过程,由于热管外伸最长径向位置为r/R=-0.8,因此只分析热管所在区域的颗粒传热性能。在ug=0.8 m/s时,热管表面不同周向位置的颗粒流速分布如图11所示。
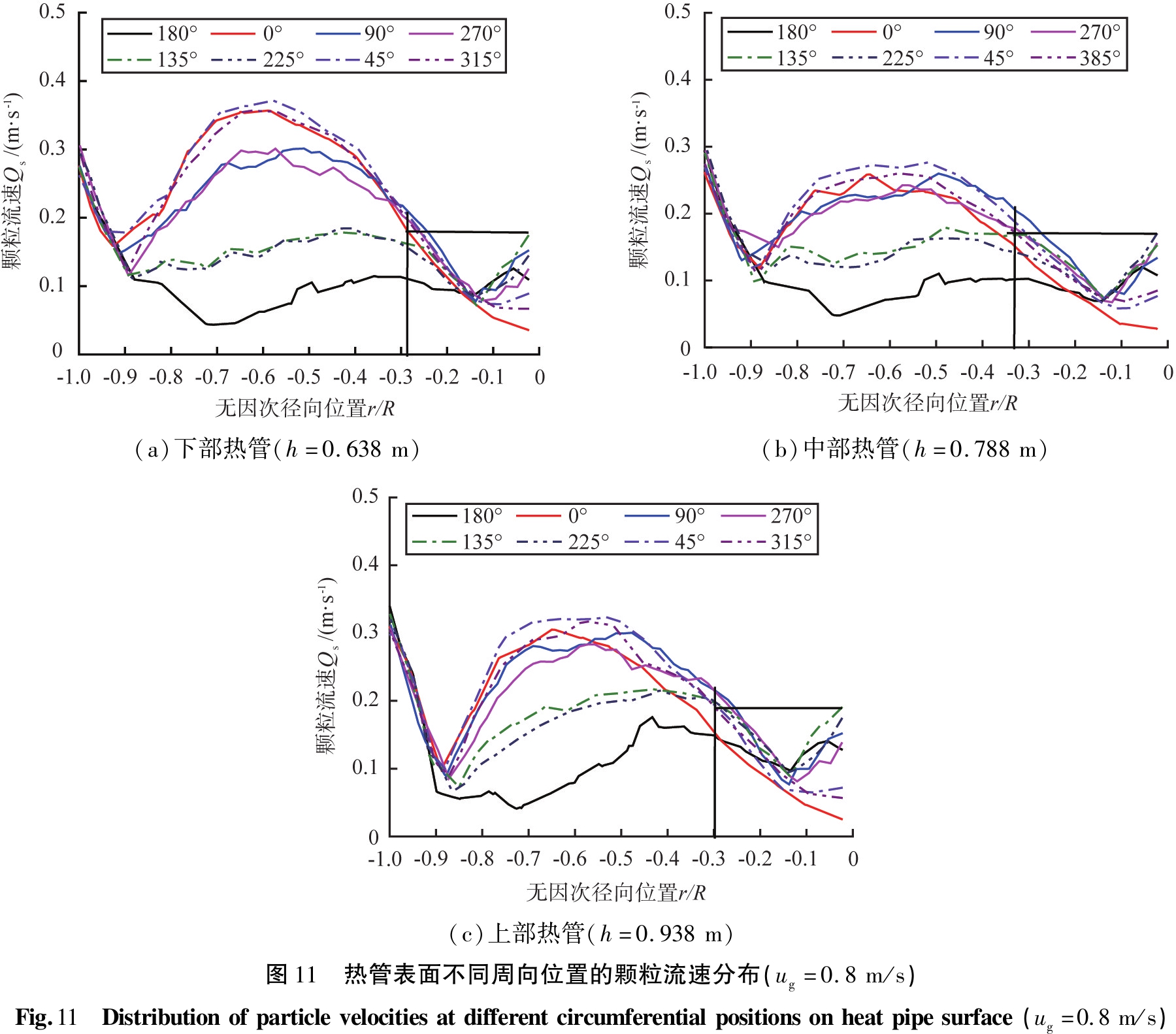
以h=0.638 m处的热管表面颗粒流速为例进行分析。由图11(a)可知,在热管自由端,下表面周向45°~315°的颗粒流速较大(其中周向45°位置的数值最大,表明换热效果最佳),热管两侧周向90°和270°位置的颗粒流速稍小于热管下表面的数值,热管上表面周向135°和225°位置处的颗粒流速明显小于下表面的数值,热管顶部周向180°位置的颗粒流速最小。Al-Busoul等[27]在较大颗粒流化床发现相近的传热系数分布。沿径向方向,由热管自由端到约束端,热管下表面周向45°~315°的颗粒流量先稍有增大后逐渐减小,在r/R=-0.6位置颗粒流速最大,换热性能最强;热管两侧面的颗粒流速先增大,再减小,后稍有增大,转折点分别位于r/R分别为-0.6和-0.15;周向135°和225°位置的颗粒流速沿径向先基本不变,然后稍有减小再增大;热管顶部的颗粒流速沿径向存在局部颗粒流速的低值,整体沿径向变化较小。通过综合分析热管表面的颗粒流速发现,热管约束端为低效换热区,其颗粒流速均小于0.18,对应的径向位置为r/R>-0.30。由图11(a)—(c)可知,不同高度热管表面的颗粒流速变化趋势相近,但数值存在差异,这一差异主要位于热管表面周向90°~270°范围。经比较发现,下部热管换热效果最好,其次为上部热管,中部热管的换热效果最差,因此,若要提高单根热管的换热效率,可在现有轴向间距基础上适当增加热管间距,这与Abid等[13]的实验结果相一致。
上述结果表明,高效换热区为-0.80<r/R<-0.30,与由固含率界定主换热区范围[15]相近。基于此,为了研究高效换热区内单根热管表面的颗粒流速随操作条件的变化,表观气速对热管表面颗粒流速的影响如图12所示。
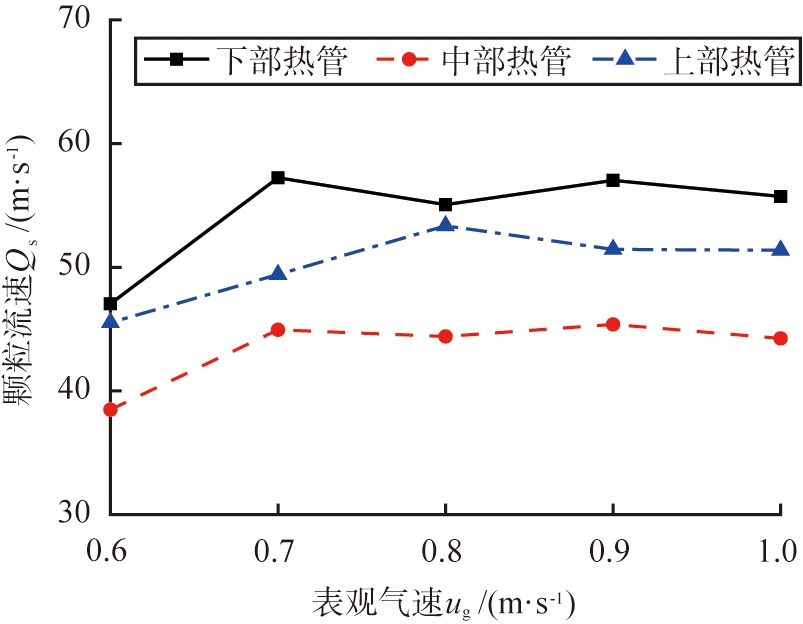
图12 表观气速对热管表面颗粒流速的影响
Fig.12 Effect of gas velocity on particle velocities on heat pipe surface
由图12可见,颗粒流速为热管表面周向和轴向数值的总和。随着表观气速的增加,不同高度热管表面的颗粒流速先稍有增大后保持不变,转折点位于ug为0.7 m/s。在不同操作条件下,随着轴向高度的增加,热管表面的颗粒流速均先减小后增大,在最下部热管表面的颗粒流速最大。
综上,基于颗粒团更新理论,提出采用局部区域的颗粒流速对热管表面不同区域的传热性能进行分析。通过比较不同高度热管表面的颗粒流速分布发现,-0.80<r/R<-0.30的径向范围为高效换热区,该区域内由热管下表面到上表面,颗粒换热性能逐渐较小。下部热管换热效果最好,其次为上部热管,中部热管的换热效果最差,若要提高单根热管的换热效率,可在现有轴向间距基础上适当增加热管轴向间距。随着表观气速的增加,每根热管的换热性能先增强后恒定,转折点位于ug为0.7 m/s;随着轴向高度的增加,热管的换热性能先减弱后增强,最下部热管的换热性能最佳。
3 结论
采用欧拉双流体模型模拟了一种能够实现2种物性相近颗粒高效换热的流化床换热器。通过比较固含率模拟值与实验值的轴径向分布,确定了所选数学模型的有效性,气固间相互作用的表达选用EMMS曳力模型,分析了颗粒轴向速度的轴、径向分布,重点考察热管表面不同周向和轴向位置的颗粒速度,并基于颗粒团更新理论,结合固含率分布特征,提出采用颗粒流速来分析传热性能。
1)热管的存在增大了热管区下侧的颗粒平均速度,热管对气泡的剪切作用减弱了颗粒的返混现象,增强了气固两相的接触。气速越大,热管对湍流床内颗粒轴向速度的影响越显著。
2)在热管所在高度,气泡由热管自由端向上运动,在热管间区域,由床中心向上运动,整体呈S形路线向上绕过热管运动。表观气速对热管自由端下侧区域颗粒轴向速度的径向分布的影响最大,热管约束端上侧次之,床壁附近最小。
3)在热管自由端的下表面和约束端的上表面为倾斜热管的特征换热区,颗粒贴壁向上运动,热管的倾斜布置强化了颗粒在换热表面的更新速度,利于热量传递。
4)提出颗粒流速来分析热管表面的传热性能,高效换热区位于-0.80<r/R<-0.30;随着表观气速的增加,每根热管的换热性能先增强后恒定,转折点位于ug为0.7 m/s处;随着轴向高度的增加,热管的换热性能先减弱后增强,最下部热管的换热性能最佳。
[1]胡敏.催化裂化烟气排放控制技术现状及面临问题的分析[J].中外能源,2012,17(5):77-83.
[2]张莉.浅析光化学烟雾的污染问题[J].四川环境,2005,24(4):74-76.
[3]胡敏.催化裂化装置可再生法烟气脱硫技术若干问题探析[J].炼油技术与工程,2021,51(11):1-6,32.
[4]郭大为,张久顺,龙军,等.脱除烟气中硫氧化物和/或氮氧化物的方法及烃油裂化方法:200610171550.5[P].2008-07-02.
[5]郭大为,张久顺,毛安国,等.一种烟气脱硫脱氮吸附剂再生过程中的换热方法:200810113392.7[P].2009-12-02.
[6]郭大为,张久顺,梁彬,等.催化裂化烟气脱硫、脱氮吸附剂的初步研究[J].石油学报(石油加工),2011,27(2):192-197.
[7]姚秀颖,卢春喜.催化裂化再生催化剂取热技术研究进展[J].石油学报(石油加工),2018,34(2):217-228.
[8]姚秀颖,李建涛,卢春喜,等.流化床间壁换热再生耦合装置:202020183168.1[P].2020-10-30.
[9]JOUHARA H,CHAUHAN A,NANNOU T,et al.Heat pipe based systems:advances and applications[J].Energy,2017,128:729-754.
[10]YAO X,ZHANG Y,LU C,et al.Systematic study on heat transfer and surface hydrodynamics of a vertical heat tube in a fluidized bed of FCC particles[J].AIChE Journal,2015,61:68-83.
[11]YANG Z,ZHANG Y,OLORUNTOBA A,et al.MP-PIC simulation of the effects of spent catalyst distribution and horizontal baffle in an industrial FCC regenerator.Part I:effects on hydrodynamics[J].Chemical Engineering Journal,2021,412:128-634.
[12]LECHER S,MERZSCH M,KRAUTZ H.Heat-transfer from horizontal tube bundles into fluidized beds with Geldart A lignite particles[J].Powder Technology,2014,253:14-21.
[13]ABID B A,ALI J M,ALZUBAIDI A A.Heat transfer in gas-solid fluidized bed with various heater inclinations[J].International Journal of Heat and Mass Transfer,2011,54:2228-2233.
[14]KIM S W,KIM S D.Heat transfer characteristics in a pressurized fluidized bed of fine particles with immersed horizontal tube bundle[J].International Journal of Heat and Mass Transfer,2013,64:269-77.
[15]姚秀颖,徐博,刘梦溪,等.倾斜热管湍流床的气固流动特性[J].中国粉体技术,2022,28(1):1-14.
[16]OSTERMEIER P,DAWO F,VANDERSICKEL A,et al.Numerical calculation of wall-to-bed heat transfer coefficients in Geldart B bubbling fluidized beds with immersed horizontal tubes[J].Powder Technology,2018,333:193-208.
[17]WAHYUDI H,CHU K,YU A.3D particle-scale modeling of gas-solids flow and heat transfer in fluidized beds with an immersed tube[J].International Journal of Heat and Mass Transfer,2016,97:521-537.
[18]SCHMIDT A,RENZ U.Numerical prediction of heat transfer between a bubbling fluidized bed and an immersed tube bundle[J].Heat and Mass Transfer,2005,41:257-270.
[19]LEE J M,LIM E W C.Heat transfer in a pulsating turbulent fluidized bed[J].Applied Thermal Engineering,2020,174:1-29.
[20]BISOGNIN P C,FUSCO J M,SOARES C.Heat transfer in fluidized beds with immersed surface:effect of geometric parameters of surface[J].Powder Technology,2016,297:401-408.
[21]WANG S,LUO K,HU C,et al.Investigation of gas-solid flow dynamics and heat transfer in fluidized beds by using DEM-LES coupling approach[C]//Proceedings of the 7th International Conference on Discrete Element Methods:2017.Singapore:Springer,2017:1023-1035.
[22]MICKLEY H S,FAIRBANKS D F.Mechanism of heat transfer to fluidized beds[J].AIChE Journal,1955(1):374-384.
[23]YAO X,ZHANG Y,LU C,et al.Systematic study on heat transfer and surface hydrodynamics of a vertical heat tube in a fluidized bed of FCC particles[J].AIChE Journal,2015,61:68-83.
[24]傅梦倩,姚秀颖,范怡平,等.双层喷嘴提升管进料区内气固流动特性的数值模拟[J].过程工程学报,2020,20(7):757-769.
[25]徐逞祥.无序环流取热器内气固两相流动和内循环特性研究[D].北京:中国石油大学(北京),2020.
[26]LI J,YAO X,LIU L,et al.Bed-to-wall heat transfer in a gas-solid fluidized bed with external solids circulation:modified packet renewal model[J].Powder Technology,2021,383:19-29.
[27]AL-BUSOUL M A,ABU-EIN S K.Local heat transfer coefficients around a horizontal heated tube immersed in a gas fluidized bed[J].Heat and Mass Transfer,2003,39(4):355-358.