石灰-粉煤灰结合料简称二灰,二灰稳定碎石是石灰、粉煤灰和碎石加水拌和形成的混合料。二灰稳定碎石在我国被广泛应用于各类道路的基层与底基层,具有无侧限抗压强度(以下简称抗压强度)高、承载能力强、刚度大、整体性强和抗裂性好等优点[1-2]。国内外研究者已经通过大量的室内实验研究了二灰与碎石质量比和龄期等因素对二灰稳定碎石抗压强度的影响[3-5]。就二灰稳定碎石抗压强度形成机理而言,其主要来源于石灰与粉煤灰的火山灰反应,而火山灰反应与温度、龄期等因素密切相关。在实际工程中,二灰稳定碎石基层温度受气候和地理分区的影响,难以保证与室内实验相同的温度条件,因此,研究一种能够较为准确地反映温度与龄期综合作用下的二灰稳定碎石抗压强度的预测方法尤为重要。
成熟度方法是一种可以将温度与龄期对抗压强度的影响有机结合起来的抗压强度预测方法。胡裕新等[6]、胡立志等[7]、代金鹏等[8]通过对实验数据进行回归,分别得到了成熟度-强度方程、粉煤灰混凝土在不同温度条件下的28 d抗压强度值以及成熟度与抗压强度的指数函数模型、双曲函数模型和对数函数模型等。与混凝土类似,二灰稳定碎石的力学性能受养护温度的影响较大,其抗压强度适合采用成熟度的方法进行预测[9-10]。
本文中,首先制备含有不同质量分数粉煤灰的4种二灰稳定碎石试件,通过室内实验测试其在不同温度条件下的抗压强度,再根据成熟度原理研究抗压强度与成熟度之间的关系,将成熟度方程进行优化和修正后,建立适用于不同条件下的二灰稳定碎石的成熟度-抗压强度预测模型,最后通过对比实测值验证其准确性,为使用成熟度方法预测二灰稳定碎石抗压强度提供一定的参考和理论依据,期望具有一定的应用前景和工程实用价值。
1 实验
1.1 原材料
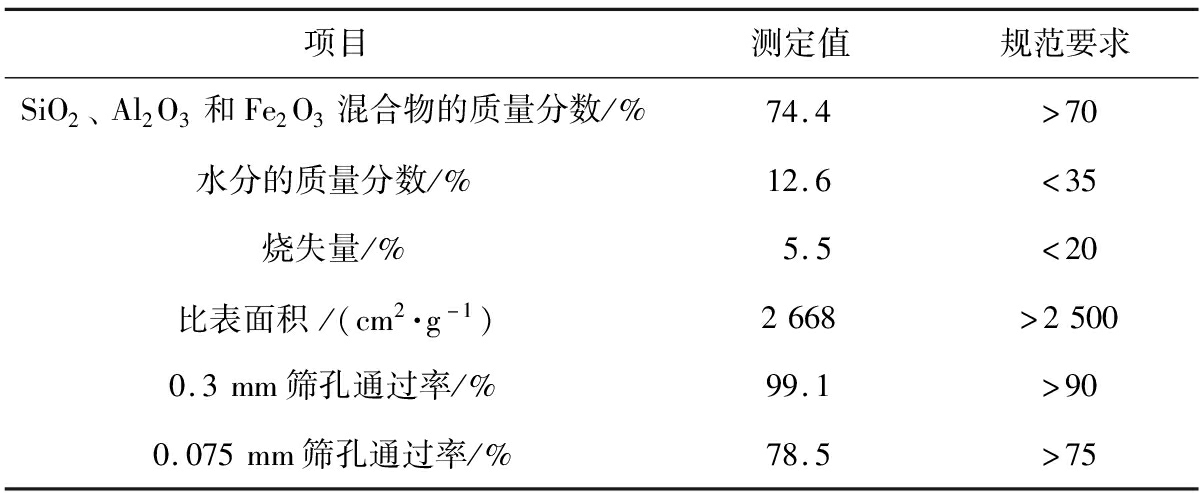
实验所使用的生石灰及其消化后的消石灰的有效氧化钙和氧化镁的质量分数分别为76.8%和63.7%,满足规范中Ⅱ级的要求。粉煤灰的化学组分与物理性质如表1所示。实验所使用碎石的主要技术指标如表2所示。
表1 粉煤灰的化学组分与物理性质
Tab.1 Chemical compositions and physical properties of fly ash
项目测定值规范要求SiO2、Al2O3和Fe2O3混合物的质量分数/%74.4>70水分的质量分数/%12.6<35烧失量/%5.5<20比表面积/(cm2·g-1)2668>25000.3mm筛孔通过率/%99.1>900.075mm筛孔通过率/%78.5>75
表2 碎石的主要技术指标
Tab.2 Main technical indicators of macadam

表观密度/(kg·m-3)松散堆积密度/(kg·m-3)紧实堆积密度/(kg·m-3)压碎值/%针片状碎石的质量分数/%所含泥的质量分数/%27101485174515.78.90.3
1.2 二灰稳定碎石试件各组分配比
结合《公路路面基层施工技术细则》(JTG/T F20—2015),在优先考虑养护环境和施工变异性的条件下,采用骨架密实结构[11]。使用边长系列为0.075、0.600、2.360、4.750、9.500、19.000、31.500 mm的方孔筛进行分级和搭配,筛分实验所确定的二灰稳定碎石级配曲线如图1所示。
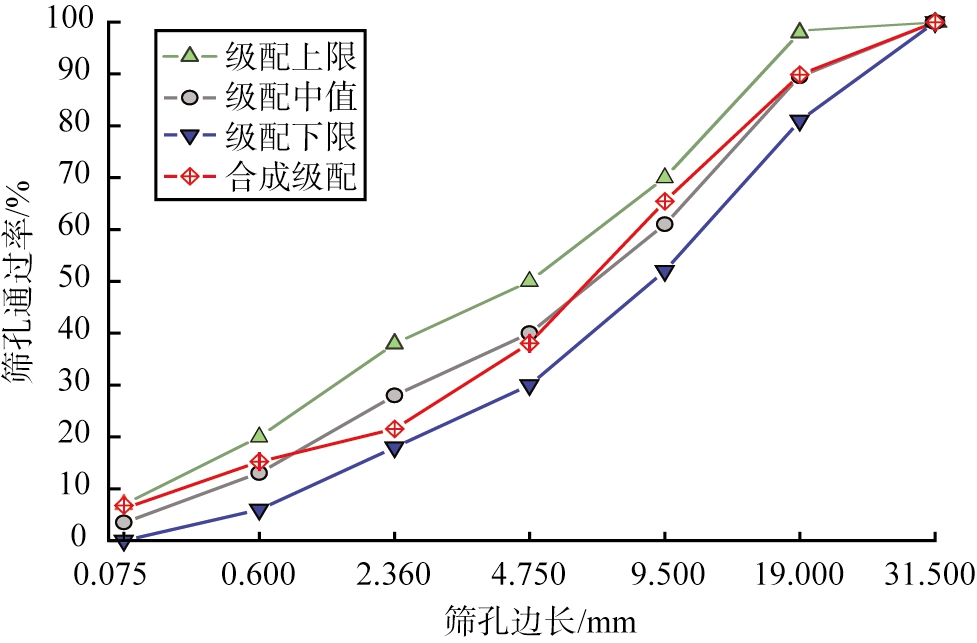
图1 筛分实验所确定的二灰稳定碎石级配曲线
Fig.1 Gradation curve of lime fly ash stabilized macadam determined by sieve test
根据设计要求,级配曲线上的每个值点都落在合成级配的上限和下限内。施工完成后,可以通过碎石间相互挤压形成致密的骨架结构。根据《公路路面基层施工技术细则》(JTG/T F20—2015)中推荐的二灰质量比(记为m石灰∶m粉煤灰),制备4种石灰、粉煤灰和碎石质量比(记为m石灰∶m粉煤灰∶m碎石)的二灰稳定碎石试件,分别记为L1、L2、L3、L4,二灰稳定碎石试件的质量比如表3所示。
表3 二灰稳定碎石试件的质量比
Tab.3 Mass proportions of lime fly ash stabilized macadam specimens

编号m石灰∶m粉煤灰m石灰∶m粉煤灰∶m碎石L11∶25∶11∶84L21∶34∶12∶84L31∶26∶13∶81L41∶35∶14∶81
1.3 振动压实实验
使用DZY-09型振动压实仪进行振动压实及试件成型实验,设置振动压实仪的振动频率为28 Hz、激振力为7 200 N,振幅为25 mm。为了确定二灰稳定碎石试件的最大干密度和最佳含水量质量分数,对4种二灰稳定碎石试件分别进行振动压实实验,振动时间为120 s。在进行抗压强度实验之前,将所有试件浸入水中24 h[12]。抗压强度公式为
Rc=P/A,
(1)
式中:Rc代表试件的抗压强度,MPa;P为最大破坏载荷,N;A为试件截面积,mm2。
抗压强度实验所使用的二灰稳定碎石圆柱形试件直径为150 mm、高为150 mm,其振动压实时间为60 s,使之达到98%的压实度[13];使用塑料袋包裹成型试件,依据分组分别放置在空气湿度在95%以上的养护室中进行养护,将养护温度设置为10、20、30、40 ℃,并保持各个养护室温度浮动不超过±2 ℃。二灰稳定碎石试件成型及抗压强度实验现场如图2所示。
2 实验结果与分析
2.1 最大干密度和最佳含水量
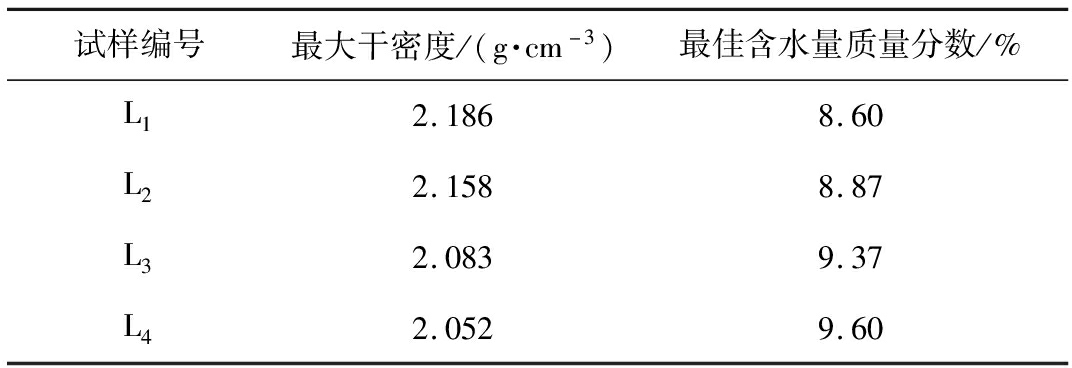
二灰稳定碎石试件的最大干密度和最佳含水量如表4所示。由表4可知,随着粉煤灰质量分数的增加,二灰稳定碎石试件的最大干密度逐步下降,最佳含水量逐步上升。这是由于二灰的比表面积远大于碎石的比表面积,在拌和过程中需要更多的水,因此使最佳含水量呈现出上升的趋势;但即使吸收了更多的水,二灰的密度依然远低于碎石的密度,这使得最大干密度随着粉煤灰质量分数的增加而减小。

(a)二灰稳定碎石试件成型(b)抗压强度测试(c)力学测试系统1—上车系统;2—下车系统;3—夯板;4—夹具;5—试模;6—电动机;7—试件;8—加载头。图2 二灰稳定碎石试件成型及抗压强度实验现场Fig.2 Experimentalsiteofformingandcompressivestrengthoflimeflyashstabilizedmacadamspecimen
表4 二灰稳定碎石试件的最大干密度和最佳含水量
Tab.4 Maximum dry density and optimum water content of lime fly ash stabilized macadam
试样编号最大干密度/(g·cm-3)最佳含水量质量分数/%L12.1868.60L22.1588.87L32.0839.37L42.0529.60
2.2 二灰稳定碎石试件抗压强度的影响因素
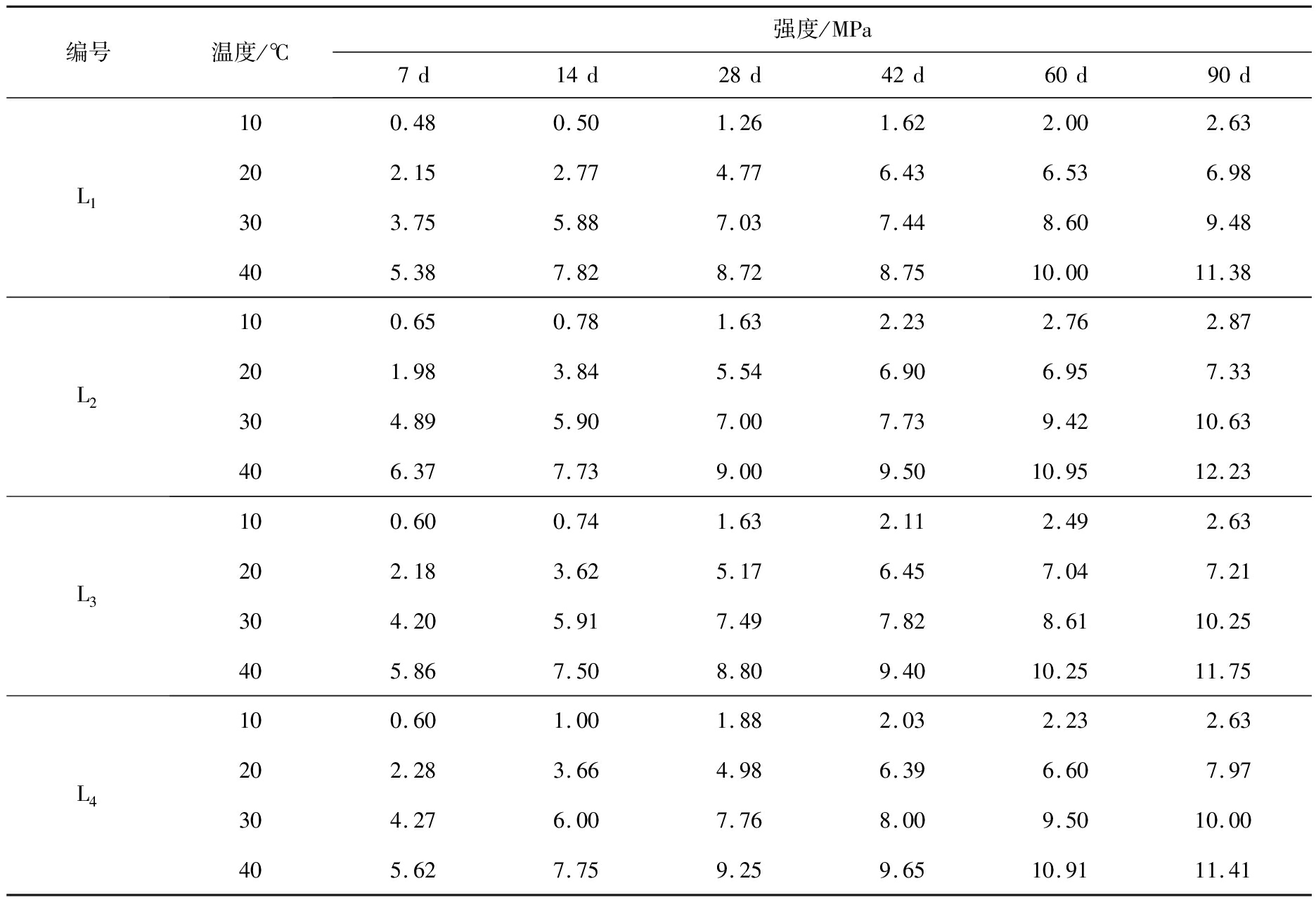
在不同养护温度和龄期条件下,4种二灰稳定碎石试件的抗压强度如表5所示。根据表5数据,不同温度条件下二灰稳定碎石试件的抗压强度随龄期的变化规律如图3所示。
由表5和图3可知,在不同养护温度条件下,4种试件的抗压强度随龄期增大而增大;在相同龄期条件下,抗压强度随着温度的增高而增大。10 ℃下养护的试件在被养护到90 d龄期时,抗压强度才能达到20 ℃下养护7 d龄期的水平;20 ℃下养护的试件在14 d前的抗压强度增大比较缓慢,14~28 d的抗压强度增大明显加快;而40 ℃下养护的7 d抗压强度普遍超过了20 ℃下养护28 d的抗压强度。随着二灰质量分数的升高,抗压强度先升高后降低,L2试件(即二灰质量分数为16%、粉煤灰质量分数为12%时)的抗压强度达到峰值12.23 MPa,但是,不同二灰质量比的二灰稳定碎石试件的90 d抗压强度相差最多不超过1.15 MPa。相比较温度与龄期的作用,二灰质量比的影响微乎其微,基本可以忽略不计。总之,二灰稳定碎石试件的抗压强度与龄期、温度均正相关,温度的影响大于龄期的,二灰稳定碎石试件抗压强度适合采用成熟度方法进行计算。
表5 不同养护温度和龄期条件下二灰稳定碎石试件的抗压强度
Tab.5 Compressive strength of lime fly ash stabilized macadam at different curing temperatures and ages
编号温度/℃强度/MPa7d14d28d42d60d90dL1100.480.501.261.622.002.63202.152.774.776.436.536.98303.755.887.037.448.609.48405.387.828.728.7510.00 11.38 L2100.650.781.632.232.762.87201.983.845.546.906.957.33304.895.907.007.739.4210.63 406.377.739.009.5010.95 12.23 L3100.600.741.632.112.492.63202.183.625.176.457.047.21304.205.917.497.828.6110.25 405.867.508.809.4010.25 11.75 L4100.601.001.882.032.232.63202.283.664.986.396.607.97304.276.007.768.009.5010.00 405.627.759.259.6510.91 11.41
当龄期为42 d时,不同养护温度下L2试件的电子扫描显微镜(scanning electron microscope, SEM)图像如图4所示。由图4可见,不同养护温度条件下相同龄期的二灰稳定碎石试件内部结构出现了较大的差异。图4(a)中粉煤灰微珠水化产生的钙矾石(aluminate ferrite trisulphate hydrate phase, AFt)和水化硅酸钙(calcium-silicate-hydrate,C-S-H)混合在一起,一个微珠上同时存在较光滑的部分和已反应部分;图4(b)中,L2试件内部火山灰反应比较均衡,C-S-H呈块状堆积,整个粉煤灰微珠的表面均发生了反应;图4(c)中,反应的产物是以针状AFt为主,并初步造成了内部结构的疏松;而图4(d)中所示养护温度40 ℃时的火山灰反应要剧烈得多,整个粉煤灰微珠完全被AFt所覆盖,块状的C-S-H上也可以观察到AFt存在,过多的针状AFt反而造成了试样的内部产生收缩裂缝。
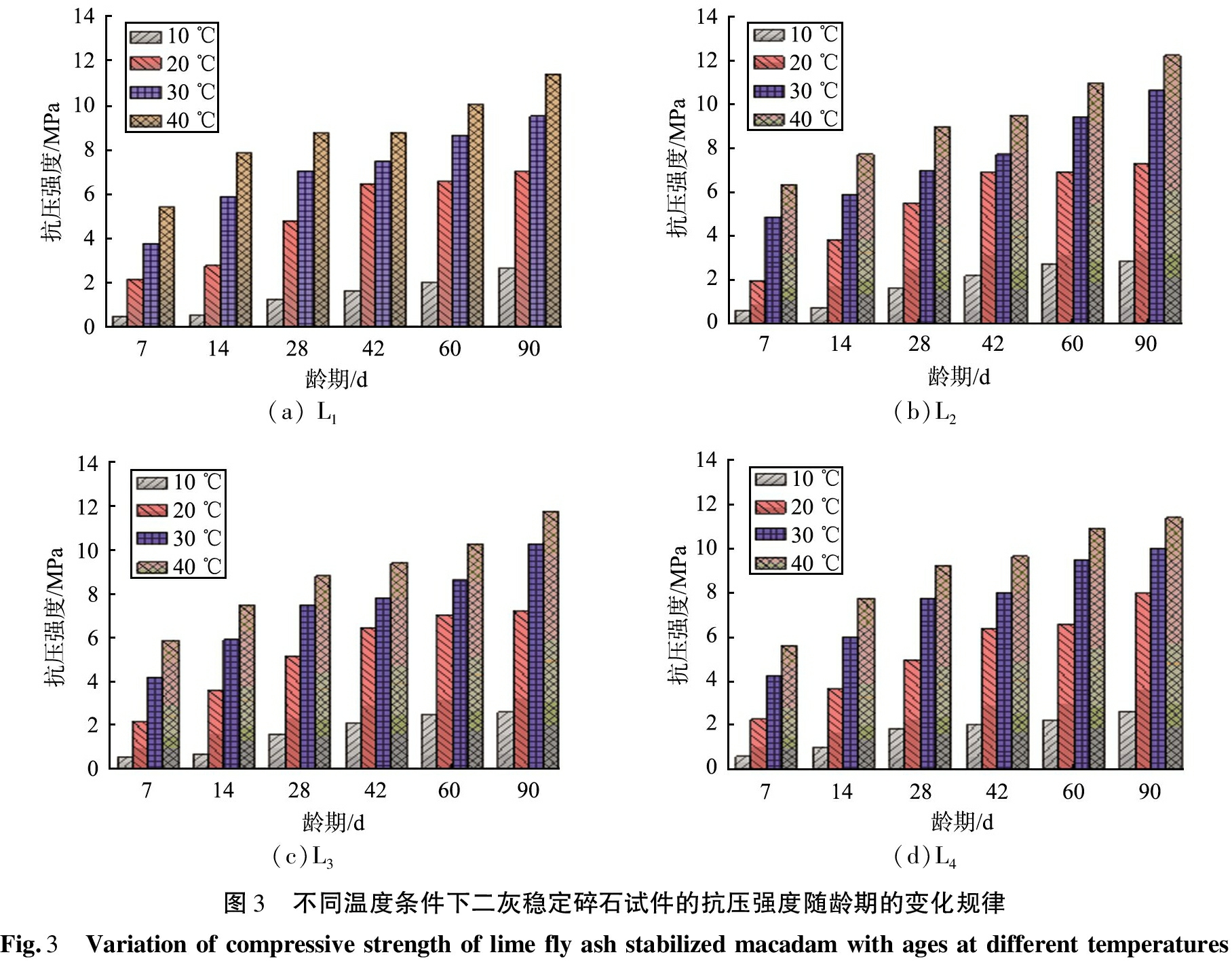
(a)L1(b)L2(c)L3(d)L4图3 不同温度条件下二灰稳定碎石试件的抗压强度随龄期的变化规律Fig.3 Variationofcompressivestrengthoflimeflyashstabilizedmacadamwithagesatdifferenttemperatures
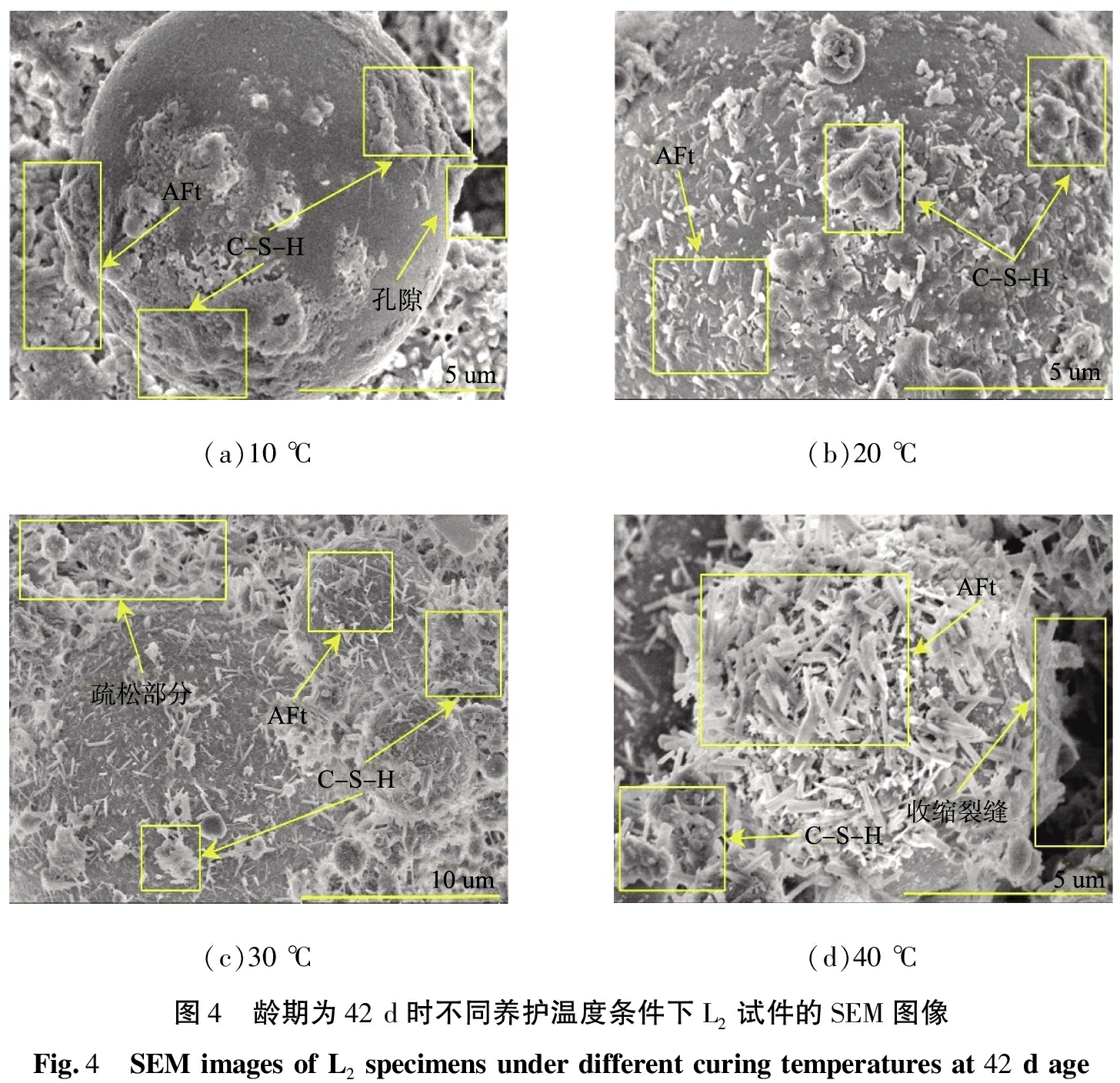
(a)10℃(b)20℃(c)30℃(d)40℃图4 龄期为42d时不同养护温度条件下L2试件的SEM图像Fig.4 SEMimagesofL2specimensunderdifferentcuringtemperaturesat42dage
3 预测模型
3.1 基于活化能成熟度方法的预测模型
活化能(activation energy, Eα)方程[14]为
(2)
式中:k是反应速率常数, d-1;A为指前因子,无量纲;Eα是活化能,kJ/mol;R是气体常数,取值为8.314 J/(mol-1·k-1);T是养护温度,K。在实际的使用中,往往对式(2)等式两边取对数,整理后的活化能方程[14]为
(3)
不同二灰稳定碎石试件的活化能如表6所示。
表6 不同二灰稳定碎石试件的活化能
Tab.6 Activation energy of different lime fly ash stabilized macadam
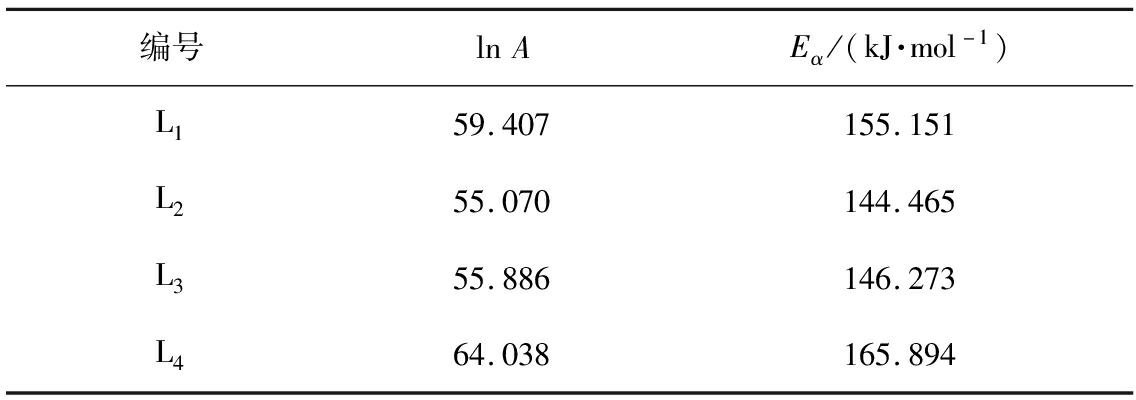
编号lnAEα/(kJ·mol-1)L159.407155.151L255.070144.465L355.886146.273L464.038165.894
根据式(3)进行计算,在不同养护温度条件下4种二灰稳定碎石试件的反应速率常数k值如表7所示。
表7 在不同养护温度条件下二灰稳定碎石试件的反应速率常数
Tab.7 Reaction rate constants of lime fly-ash stabilized macadam specimens under different curing temperatures d-1
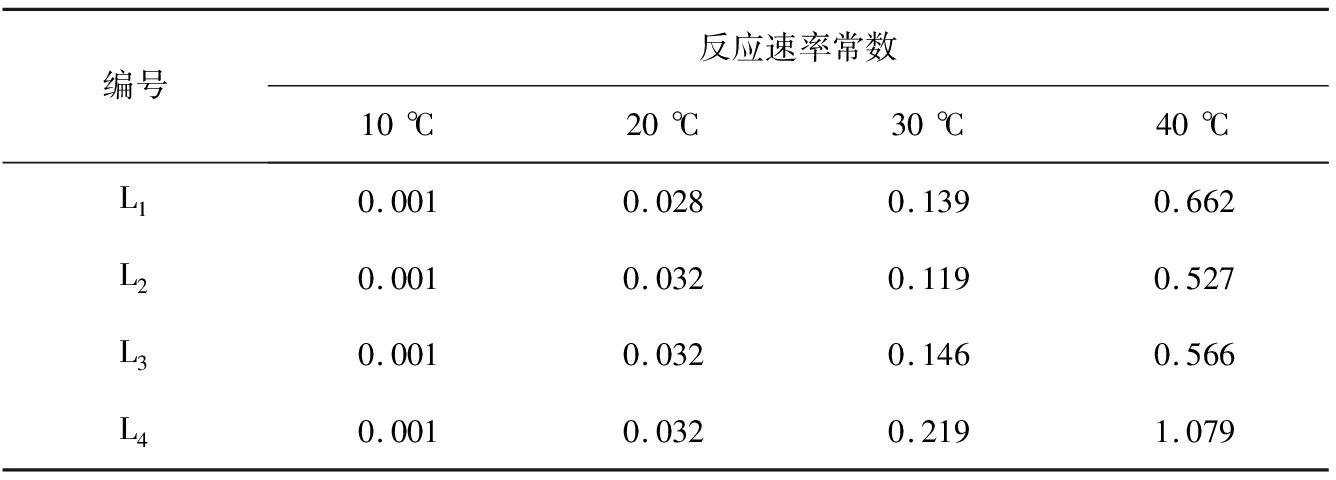
编号反应速率常数10℃20℃30℃40℃L10.0010.0280.1390.662L20.0010.0320.1190.527L30.0010.0320.1460.566L40.0010.0320.2191.079
基于活化能成熟度方法的二灰稳定碎石试件的抗压强度预测模型[15]为
(4)
式中:Rcu是二灰稳定碎石试件达到极限水化的抗压强度,MPa;t是养护龄期,d;t0是二灰稳定碎石试件强度形成时间,d。
由于二灰稳定碎石试件的抗压强度有随养护龄期的增加而增加的趋势,因此可以采用成熟度方法中的等效龄期法,将不同养护温度下的实际龄期转化为20 ℃养护温度下的等效龄期,构建活化能成熟度模型。等效龄期的计算公式为
(5)
式中:te表示等效龄期,d;Ti是养护温度,℃;Tr是二灰结合料的基准温度,℃。因而,可以在式(5)得到等效龄期的基础之上使用式(4)对二灰稳定碎石试件的抗压强度进行预测。
3.2 在恒定温度下基于度时积成熟度方法的预测模型
利用成熟度方法,可以通过度时积方程将二灰稳定碎石试件的抗压强度与养护温度和养护龄期2个参数进行有机结合,计算出不同龄期的二灰稳定碎石试件的抗压强度,在不损坏基层完整性的情况下,可以预测出较为准确的抗压强度数值。结合度时积公式和基准温度,成熟度及抗压强度预测模型为
M=(Ti-T0)Δt,
(6)
Rc=a+bln M,
(7)
式中:M为成熟度,℃·d;Δt是时间间隔,d;T0是基准温度,设定为-10 ℃;a、b是参数,无量纲。
在养护温度分别为10、20、30、40 ℃条件下,根据式(6)、(7)分别进行计算,得到4种二灰稳定碎石试件的抗压强度随成熟度变化的曲线,如图5所示。由图5可见,随着成熟度的增大,二灰稳定碎石试件的抗压强度呈增长趋势;在养护温度高于标准温度时具有较快的增长速率,在养护温度低于标准温度时增长速率较小;养护温度由低到高时,抗压强度的增长值依次减小,表现为4条拟合曲线间距的依次减小。
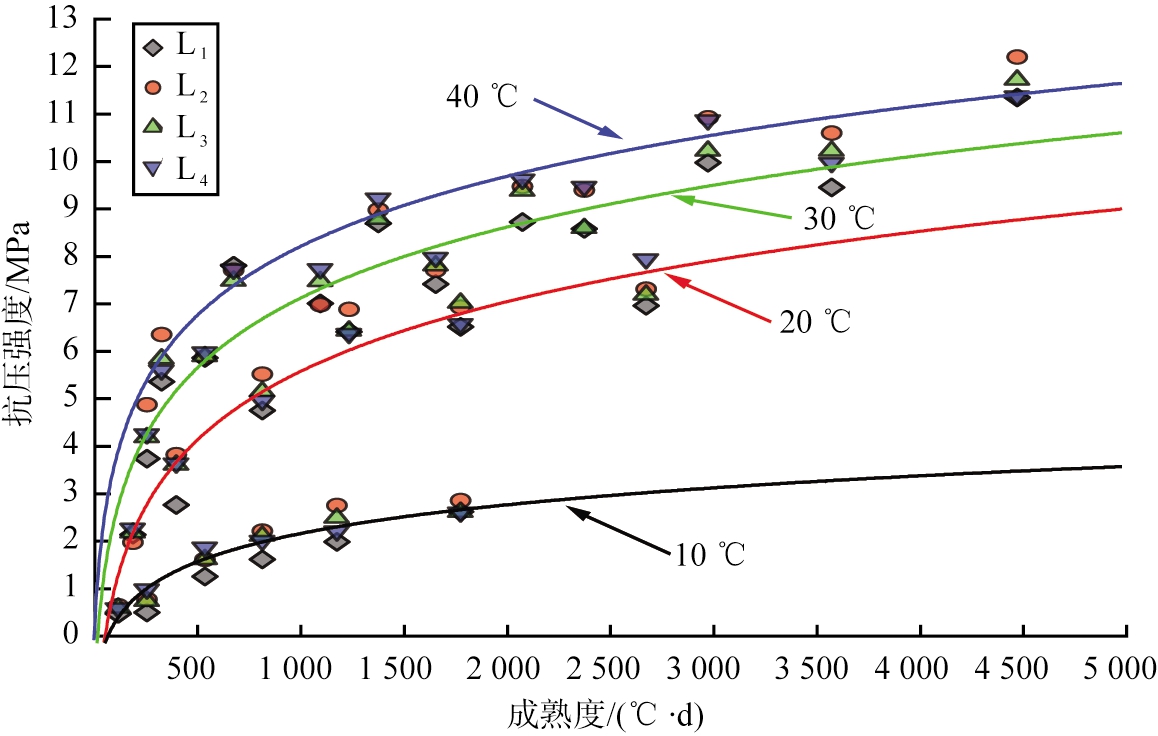
图5 不同养护温度下4种二灰稳定碎石试件的抗压强度随成熟度变化的曲线
Fig.5 Variation curve of compressive strength with maturity of 4 kinds of lime fly ash stabilized macadam specimens under different curing temperatures
不同养护温度条件下的成熟度-抗压强度拟合方程如表8所示。由表可以看出,式(7)拟合程度非常高,相关系数(R)都大于0.9,说明在不同的温度条件下,度时积成熟度方法对二灰稳定碎石试件的抗压强度增长过程有较好的预测能力。
表8 不同养护温度条件下的成熟度-抗压强度拟合方程
Tab.8 Maturity-compressive strength fitting equations at different curing temperatures

温度/℃abRc=a+blnMR210-4.000.89Rc=-4.00+0.89lnM0.91420-9.382.16Rc=-9.38+2.16lnM0.96030-8.112.20Rc=-8.11+2.20lnM0.95840-6.812.17Rc=-6.81+2.17lnM0.956注:R为相关系数。
3.3 在变温度下基于度时积成熟度方法的预测模型
3.3.1 成熟度计算公式的修正
虽然在某种特定养护温度条件下的二灰稳定碎石试件成熟度与抗压强度间具有良好的拟合关系,但是在实际的施工和养护中,恒定的养护温度是无法满足的,一天中的气温会随时间出现低—高—低的循环变化,基层温度受到气温影响也会出现温度循环,这种温度的变化往往具有较大的温差,显然,这时若采用恒定温度条件的成熟度方法预测二灰稳定碎石试件的抗压强度,准确性无法得到保证。
为了进一步探究二灰稳定碎石成熟度与抗压强度的关系,获得根据二灰稳定碎石试件成熟度预测抗压强度所需的关键数据,在仅考虑成熟度为唯一变量时,将式(6)计算的结果与抗压强度按照式(7)进行拟合,4种二灰稳定碎石试件抗压强度随成熟度变化的曲线如图6所示。
由图6可见,拟合曲线两侧依次是10%、25%、50%误差线,通过式(6)计算得到的成熟度在变温度条件下拟合程度非常低;在相近的成熟度范围内,所对应的抗压强度值不规则地分布在拟合曲线的两边,上限超过25%误差线,下限达到了50%误差线。这是由于,成熟度理论最初是用于解决水泥混凝土抗压强度估算问题的,式(6)中所给出的T0是对应水泥的反应停止时间,为-10 ℃[16]。二灰稳定碎石试件中不含水泥,其强度形成是依靠石灰与粉煤灰的火山灰反应,具有更高的温度敏感性,因此导致计算得到的二灰稳定碎石试件成熟度不仅虚高,且相关性差。拟合的结果表明,对于二灰稳定碎石试件,T0设置为-10 ℃是不合理的。由于二灰稳定碎石试件的抗压强度的增长与养护温度呈正相关的关系,因此可以仿照水泥停止反应时间的概念提出二灰的近似基准温度对式(6)进行修正。
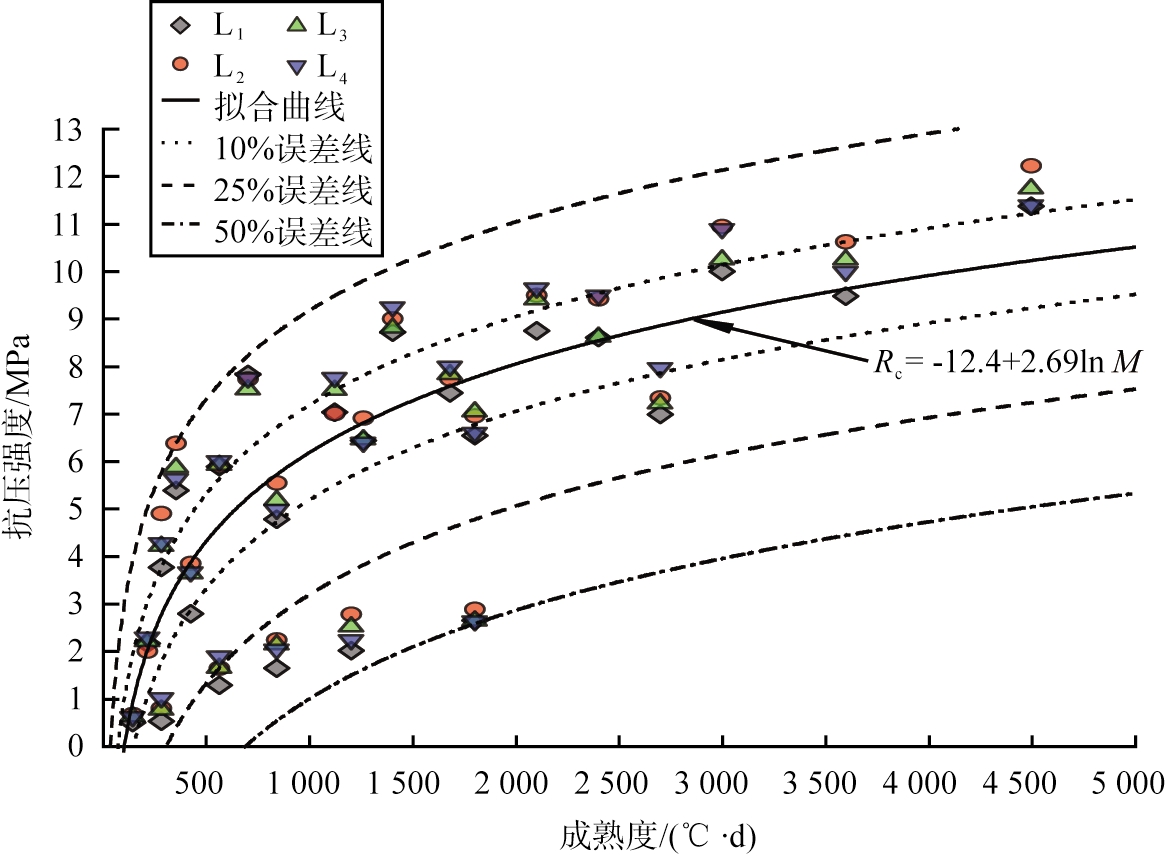
图6 4种二灰稳定碎石试件抗压强度随成熟度变化的曲线
Fig.6 Variation curve of compressive strength of 4 kinds of lime fly ash stabilized macadam specimens with maturity
在10 ℃时不同养护龄期的二灰稳定碎石试件L2的SEM图像如图7所示。由图7可见,试件L2内部的火山灰反应速率已经降低到十分低的水平,在28 d之后也很难明显观察到水化产物的生成,仅在42 d之后勉强可以辨认出少量C-S-H。

(a)14d(b)28d(c)42d图7 在10℃时不同养护龄期的二灰稳定碎石试件L2的SEM图像Fig.7 SEMimagesoflimeflyashstabilizedmacadamspecimenL2withdifferentcuringagesat10℃
结合表5与图3可知,在10 ℃的养护环境中,4种二灰稳定碎石试件的抗压强度增长均十分缓慢,养护90 d后抗压强度仅相当于20 ℃下养护7 d左右的水平,其抗压强度无法满足《公路路面基层施工技术细则》(JTG/T F20—2015)的要求。
通过对低温养护条件下试件的力学性能与微观结构分析可知,在7 ℃养护条件下,试件内部的水化反应极其微弱,可以近似认为已经停止反应,因此设置Tc为7 ℃作为二灰稳定碎石试件材料的近似基准温度,而式(5)中的Tr也可以代入为7 ℃;因此,将二灰稳定碎石试件材料的成熟度方程修正为
M=(Ti-Tc)Δt,
(8)
式中:Tc是近似基准温度,设定为7 ℃。
3.3.2 修正后抗压强度预测模型
通过式(8)重新计算得到修正后的二灰稳定碎石试件成熟度-抗压强度曲线如图8所示。
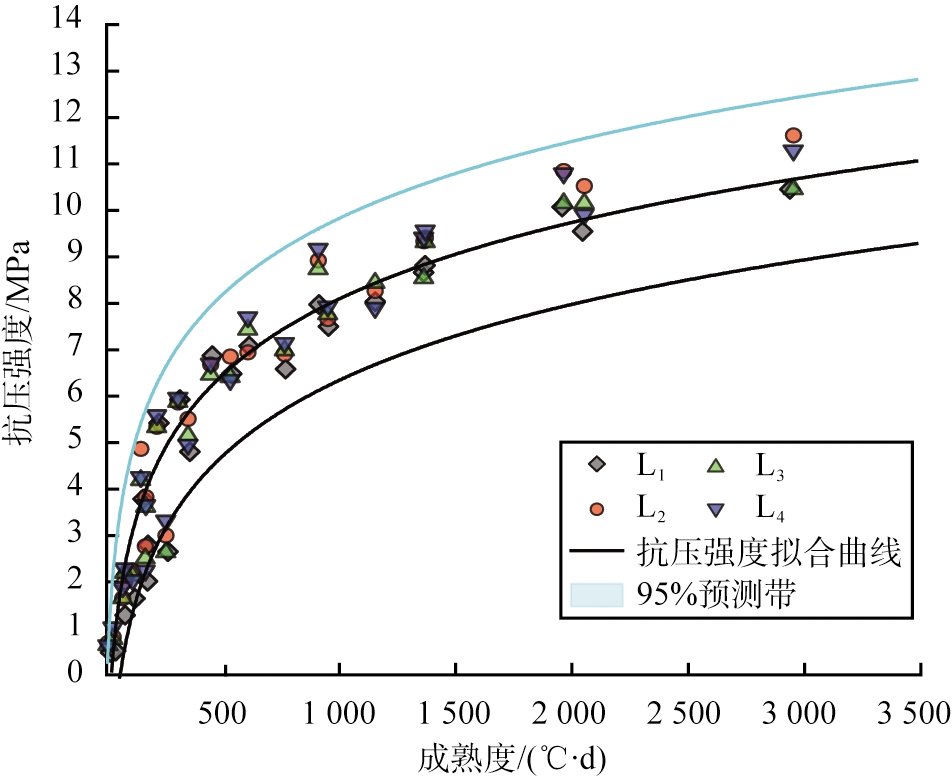
图8 修正后的二灰稳定碎石试件成熟度-抗压强度曲线
Fig.8 Modified maturity-compressive strength curve of lime fly ash stabilized macadam specimens
重新计算后的成熟度-抗压强度数据更加紧凑,数据点基本都落在拟合曲线95%预测区间内,二灰稳定碎石试件抗压强度预测模型为
Rc=-8.676+2.432ln M。
(9)
在Tc为7 ℃时,二灰稳定碎石试件的抗压强度与成熟度拟合程度较高,其相关系数为0.925。从抗压强度增长机理上来看,虽然成熟度是由温度与龄期运算而来的[17],但实际上反映的是二灰稳定碎石试件内部火山灰的反应程度,由于二灰与水泥在活性成分、反应类型上的不同,将T0上调到Tc之后,可以更加接近二灰稳定碎石试件内部火山灰反应的真实情况。在同等成熟度下,粉煤灰的质量分数与二灰稳定碎石试件的抗压强度具有负相关的关系,重新计算后的二灰稳定碎石试件成熟度数值减小,但各个值点关于式(6)的拟合程度得到了提高,说明设置二灰碎石的近似基准温度为7 ℃与真实情况比较相符,在实际工程运用中式(9)的预测结果更优。
3.4 预测结果与验证
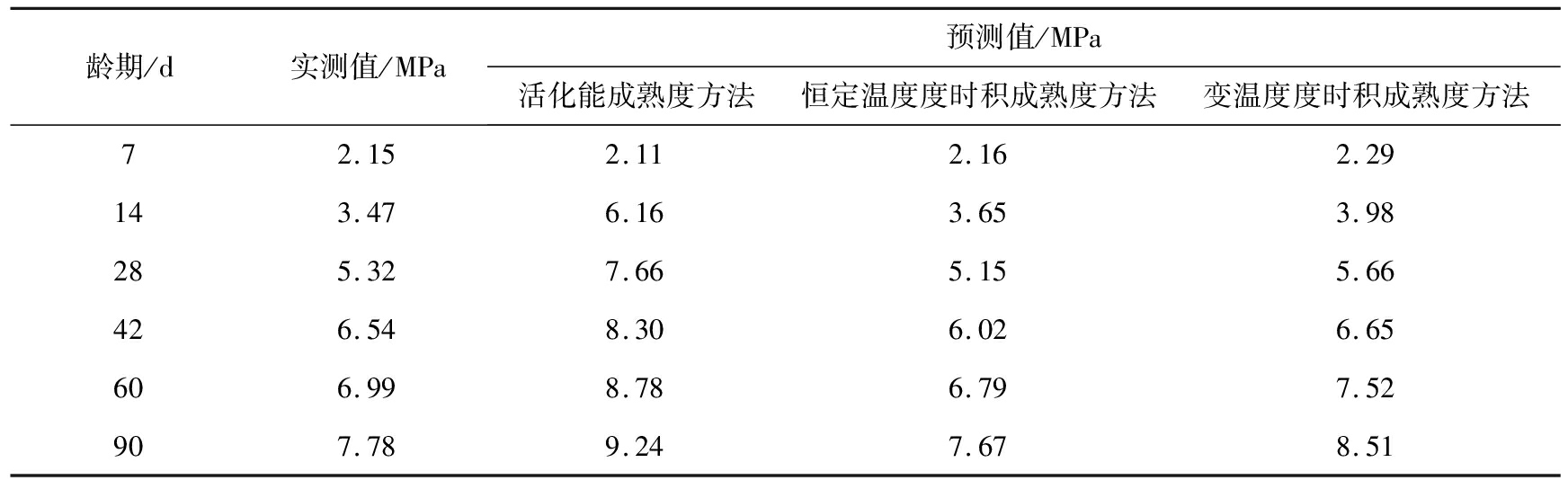
为进一步验证不同方法对二灰稳定碎石试件抗压强度预测的准确性,在养护温度为20 ℃时,以质量比m石灰∶m粉煤灰∶m碎石=5∶12∶83制备二灰稳定碎石试件L5,使用活化能成熟度方法与2种度时积成熟度方法各自预测试件L5在不同龄期的抗压强度。二灰稳定碎石试件L5的抗压强度实测值与3种方法的预测值如表9所示。
表9 二灰稳定碎石试件L5的抗压强度实测值与3种方法的预测值
Tab.9 Comparison between predicted compressive strength of lime fly ash stabilized macadam with 3 models and measured value
龄期/d实测值/MPa预测值/MPa活化能成熟度方法恒定温度度时积成熟度方法变温度度时积成熟度方法72.152.112.162.29143.476.163.653.98285.327.665.155.66426.548.306.026.65606.998.786.797.52907.789.247.678.51
由表9可知,基于活化能成熟度方程的预测结果误差较大,一方面是由于使用式(4)确定活化能Eα的过程需要至少跨过3个不同养护温度,这一过程中的误差难以避免,因而造成Eα数值偏大;另一方面,Arrehenius活化能关系并不适用于较复杂的反应,二灰稳定碎石试件的火山灰反应过程具有较高的复杂性,在高、低温度下的产物也有较大不同,因此活化能方法预测数值与实测值差距较大。基于度时积成熟度方程的2种预测方法都具有较高的准确性。恒定温度度时积成熟度方法在养护早期具有更高的准确度,在龄期超过14 d之后,恒定温度度时积成熟度方法计算得到的抗压强度值略低于实测值。变温度度时积成熟度方法计算得到的抗压强度值均高于实测值。这些结果说明,3种成熟度方法预测模型在实际使用中均有一定的准确性。
4 结论
1)二灰稳定碎石试件的抗压强度与龄期、温度均正相关,养护温度的影响大于养护龄期和二灰质量比的影响。二灰稳定碎石试件抗压强度适合采用成熟度方法进行计算。
2)由于数据处理的要求和反应复杂性的影响,采用活化能成熟度方法预测得到的二灰稳定碎石试件抗压强度预测值与实测值结果的误差较大,但该方程可以通过计算等效龄期,结合成熟度方法为二灰稳定碎石工程应用中不同环境下养护时间的确定提供有效依据,具有一定的便捷性。
3)恒定温度度时积成熟度方法在预测早期抗压强度时更接近实际值,在龄期为14 d以后预测值较实际值略小。
4)使用变温度度时积成熟度方法预测二灰稳定碎石试件抗压强度时,需要将近似基准温度Tc设置为7 ℃。计算得到的二灰稳定碎石试件抗压强度不受二灰质量比、养护温度等因素干扰,抗压强度的预测具有更高的实用性。
[1]LIU S T, LI Z Z, LI Y Y, et al.Strength properties of bayer red mud stabilized by lime fly ash using orthogonal experiments[J].Construction and Building Materials, 2018,166: 554-563.
[2]LIAO F X, XIAO F, CHEN Z D, et al.the Influence of different subbase materials on the crack of cement stabilized macadam base during construction[J].Advanced Materials Research, 2012,591/592/593: 955-959.
[3]CONSOLI N C, SALDANHA R B, MALLMANN J E C, et al.Enhancement of strength of coal fly ash-carbide lime blends through chemical and mechanical activation[J].Construction and Building Materials, 2017, 157: 65-74.
[4]XUE J S, JIANG Y J.Analysis on the fatigue properties of vertical vibration compacted lime fly ash-stabilized macadam[J].Construction and Building Materials, 2017,155: 531-541.
[5]DUAN K R, GAO Y L, YAO H, et al.Comparison of performances of early aged pre-vibrated cement-stabilized macadam formed by different compactions[J].Construction and Building Materials, 2020,239: 117682.
[6]胡裕新, 郑慧良.现浇混凝土成熟度——强度曲线方程的应用[J].建筑技术, 2014, 45(1): 23-26.
[7]胡立志, 刘士清, 宋正林, 等.粉煤灰混凝土抗压强度和成熟度之间的规律研究[J].混凝土, 2014(8): 61-63, 73.
[8]代金鹏, 王起才, 屈伸, 等.基于成熟度理论的低温养护混凝土强度预测模型[J].材料科学与工程学报, 2018, 36(2): 263-267.
[9]ANDAVAN S, PAGADALA K V.Experimental study on addition of lime and fly ash for the soil stabilization[C].Materials Today: Proceedings, 2020, 22: 1065-1069.
[10]ASSOGBA O C, TAN Y Q, ZHOU X Y, et al.Numerical investigation of the mechanical response of semi-rigid base asphalt pavement under traffic load and nonlinear temperature gradient effect[J].Construction and Building Materials, 2020(235): 117406.
[11]交通运输部公路科学研究院.JTG/T F20—2015:公路路面基层施工技术细则[S].北京:人民交通出版社,2015.
[12]交通运输部公路科学研究院.JTG E51—2009:公路工程无机结合料稳定材料试验规程[S].北京:人民交通出版社,2009.
[13]DENG C Q, JIANG Y J, LIN H W, et al.Mechanical-strength-growth law and predictive model for cement-stabilized macadam[J].Construction and Building Materials, 2019(215): 582-594.
[14]BENTZ D P.Activation energies of high-volume fly ash ternary blends: hydration and setting[J].Cement and Concrete Composites, 2014(53): 214-223.
[15]UPADHYAYA S, GOULIAS D, OBLA K.Maturity-based field strength predictions of sustainable concrete using high-volume fly ash as supplementary cementitious material[J].Journal of Materials in Civil Engineering, 2015, 27(5): 04014165.
[16]YAHIA A A.The maturity method: modifications to improve estimation of concrete strength at later ages[J].Construction and Building Materials, 2006, 20: 893-900.
[17]SUN B C, NOGUCHI T, CAI G C, et al.Effect of temperature and relative humidity on the development of the compressive strength of surface-layer cement mortar[J].Construction and Building Materials, 2021,281: 122626.