催化裂化的再生烟气中含有大量的硫氧化物和氮氧化物,如果直接排向大气,不仅带来环境污染,而且不能满足环保排放要求[1]。需要在烟气放空前采用流化床工艺在吸附剂作用下干法脱除烟气中的硫氧化物和氮氧化物[2]。为了保证吸附剂的循环使用,吸附剂在吸附后需要进行连续再生,其再生效率对温度的要求相对苛刻,若达不到足够高的温度,则再生效果很难保证,需要外部补充热量。传统的重油催化裂化的再生过程放出的热量远大于反-再系统所需的热量,所以为满足热平衡要求,通常采用外取热方式,将过剩热量取出[3]。郭大为等[4]提出利用催化裂化催化剂再生过程产生的过剩热量,通过固-固直接混合换热实现2个过程的热量互供,但这2种催化剂物性相近,混合换热后难以分离,因此迫切需要开发高效的间壁式换热设备。郭大为等[5]设计了一种含有管程和壳程的换热装置,热载体和冷却介质均以流化态操作,分别走管程和壳程,管程为单管或列管式。管程内颗粒流动和换热过程受换热管尺寸的限制,影响流化和换热效果。同时当换热管数量较少时,仅有与换热管管壁接触的颗粒能进行换热,换热量可调范围窄。
为了实现2种物性相近或相似颗粒的高效换热,姚秀颖等[6]提出了一种流化床间壁换热再生耦合装置及其网格划分,如图1所示。

图1 模拟对象及网格划分
Fig.1 Simulation objects and meshing
该换热再生器由2个流化空间组成,分别用于流化催化裂化催化剂和烟气吸附剂的再生,中间设置一隔板,隔板上倾斜布置多组热管,2个空间的流化颗粒通过热管实现高效间壁传热。热管的导热系数最高可达105 W/(m·℃),是铝、柴铜、银等金属的几百甚至上千倍[7-8],因此控制性热阻为流化颗粒与热管壁间的对流传热。在该传热过程中,传热系数随着操作气速的增大,先逐渐增大后几乎不变,转折点位于湍流点附近[9-10]。为了保证待生吸附剂的高效再生和再生催化剂的高效换热,2种催化剂分别流化于湍流和鼓泡流化状态[11]。
本文中详细考察湍流床一侧的气固流动状况,分析热管的存在与否对颗粒浓度轴径向分布的影响。对于带有水平换热管的流化床,不同周向位置的传热系数受到操作速度、颗粒直径、管径等多种条件的影响。Kim等[12]通过测量粒径为258 μm的石英砂、气速为0.055~0.161 m/s的流化床内水平换热管(热管直径为25.3 mm)不同周向位置的气固流动和传热情况,发现水平换热管两侧的传热系数最大,底部次之,顶部最小,这是因为在水平管的顶部存在固含率较高的颗粒垫,在底部存在气泡垫,而在水平管两侧的浓度中等,且颗粒的更新频率较高。由于颗粒的比热远大于气体,所以颗粒对流传热过程起主要作用[9]。
颗粒团更新理论[13-14]表明,传热系数受颗粒在换热表面的浓度和更新频率的影响。Al-Busoul和Abu-Ein[15]通过测量不同直径油页岩和沙粒的流化床内水平管的传热系数周向分布,发现较低气速下,传热系数的周向分布与Kim等[12]的结果一致,随着操作气速的增加,不同颗粒的流化床内传热系数周向分布趋势均发生变化,变为管上部区域最大,沿水平管周向向下逐渐减小,在底部区域又稍有增加。在较低气速(u<0.184 m/s)和较高气速(u>1.245 m/s)时,传热系数的周向分布均匀性较中等气速(0.184~1.245 m/s)时更加均匀。流化颗粒直径越小,传热系数越高[16]。在粒径为475 μm、气速为0.352 m/s的流化床内,对于固含率较小的稀相区,直径为57 mm的水平管顶部和底部的传热系数较大,两侧的较小,且随着轴向高度的增加,传热系数逐渐减小[17]。
由于水平换热管周向流动状况的不同,导致其换热情况有所不同,而本文中所研究的流化床换热器内热管为倾斜布置,其周向浓度分布与水平管的有明显不同,因此需要详细考察热管不同周向位置的流动状态,并明确轴向高度和表观气速对热管表面流动状况的影响。
1 模拟对象及建模
1.1 模拟对象
本文中模拟对象为基于专利技术[6]的流化床间壁式换热器实验装置,如图1所示,换热器主体为圆柱形结构,内径为0.50 m,由厚度为12 mm的隔板将其分为2个部分,左侧处于湍流床操作,右侧处于鼓泡床操作,隔板上布置3根热管,用于将湍流床内颗粒的热量传递给鼓泡床内颗粒。热管布置在距底部分布器的高度分别为0.60、0.75、0.90 m处,以减小分布器影响区的作用。为了减小颗粒带出量,将换热器变径设置,变径后内径为0.60 m,变径处位于轴向高度1.8 m处。为了节省计算资源,装置总高设为3.2 m,由顶部流出的催化剂通过用户自定义子程序返回床内,以保证物料守恒。热管外径为30 mm,长度为425 mm,与水平方向夹角为20 °,且在鼓泡床一侧倾斜向下。除热管所在区域采用非结构化网格外,其他位置均采用结构化网格(见图1)。
流化颗粒为FCC平衡催化剂,平均粒径为70 μm,颗粒密度为1 500 kg/m3,流化介质为常温常压下的空气,密度和黏度分别为1.225 kg/m3和1.782×10-5 Pa·s。湍流床操作气速为0.6~1.0 m/s。
1.2 建模方法
流化床换热器内颗粒浓度较大,考虑到模拟精度和计算量,选用双流体模型进行模拟研究,其控制方程如下。
气、固相连续性方程为
(1)
(2)
式中:ε为体积分数;ρ为密度,kg/m3;u为速度,m/s;t为时间,s;下标g代表气相,p代表颗粒相。
气、固相动量守恒方程为
(3)
(4)
式中:p为压力,Pa;τ为应力,Pa;β为相间曳力系数,kg/(m3s);g为重力加速度,m/s2;下标e代表EMMS。
气、固相的应力为
(5)
(6)
固相的压力为
pp=εpρpΘ[1+2g0εp(1+e)]。
(7)
固相的体积黏度为
(8)
固相的黏度为
(9)
颗粒的温度方程为
(10)
径向分布函数为
(11)
颗粒能量的扩散系数为
(12)
碰撞耗散能为
(13)
颗粒拟温度为
(14)
式中:μ为黏度,Pa·s;e为颗粒碰撞恢复系数。
对于湍流床的CFD模拟,气固之间的相互作用是影响模拟结果的关键因素。Wang等[18]采用基于EMMS-亚网格尺度模型的欧拉方法模拟了大尺度湍流床,发现密相悬浮上升流与快速床流动共同存在。吴诚等[19]采用修正三段曳力模型模拟获得表观气速和静床高的变化可使固含率的S型和指数型分布相互转变。Lan等[20]采用基于格子-玻尔兹曼的曳力模型,获得了颗粒尺寸分布对双组份湍流床内气固流动行为的影响。Chen等[21]采用基于结构的曳力模型对湍流床进行模拟,获得了内部的非均匀结构。Chang等[22]通过考虑颗粒团当量直径提出了一个适用于工业过程的曳力模型,模拟发现工业湍流床同时存在2个流区,即底部稠密的鼓泡区和上部稀薄的分散流区。Varghese等[23]通过模拟Geldart B类颗粒湍流床,比较了不同曳力模型对模拟结果的影响,发现Gidaspow、Syamlal&O’Brien曳力模型的模拟结果与实验值吻合较好。本文中所研究的湍流床内颗粒属于Geldart A类,流化过程中存在颗粒聚团现象,因此采用EMMS曳力模型对气固相间曳力进行计算[24],其表达式为
βe=βHd,
(15)
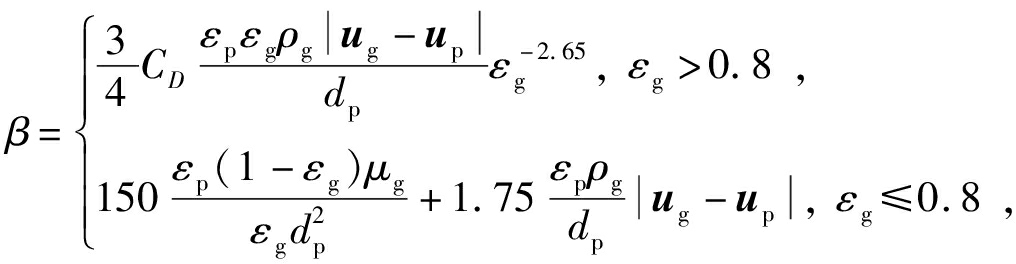
(16)
其中,曳力系数为
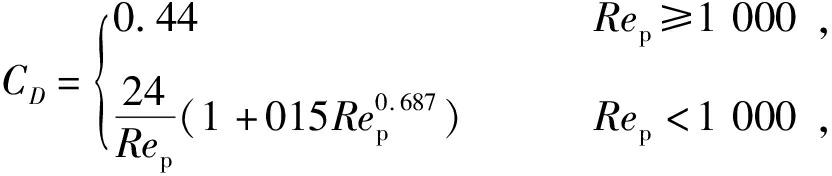
(17)
(18)
非均匀结构因子Hd拟合方程见表1所示[25]。
表1 非均匀结构因子Hd
Tab.1 Heterogeneity index Hd

εmf=0.4,Hd=a+b×εg+c×ε2g范围(εmf≤εg≤1)u=0.66~0.22m/s a=33.63238,b=-111.8059c=93.59667{εmf≤εg≤0.59 a=0.048,b=-0.19c=0.8535{0.59≤εg≤0.98 a=1,b=0c=0{0.98≤εg≤1u=0.6m/s a=17.7088,b=-67.5177c=65.0533{εmf≤εg≤0.54 a=-0.00815,b=-0.02549c=0.66844{0.54≤εg≤0.98 a=1,b=0c=0{0.98≤εg≤1u=0.7~1.0m/s a=16.7058,b=-63.1875c=60.4041{εmf≤εg≤0.55 a=0.0064,b=-0.06167c=0.65799{0.55≤εg≤0.98 a=1,b=0c=0{0.98≤εg≤1
如图1所示,在几何模型中,气固两相在底部入口均设为速度入口边界条件;上部出口均设为压力出口边界条件;对于气相,壁面采用无滑移边界条件,颗粒相采用Johnson和Jackson提出的部分滑移边界条件,表达式如表2所示,镜面系数在湍流床设为0.1[26],鼓泡床设为0.05[25]。颗粒-壁面碰撞恢复系数ep为0.9,时间步长为0.001 s。采用Fluent 6.2进行求解,初始固含率为0.6,初始速度为0.003 5 m/s。为保证2个空间的膨胀高度相近,鼓泡床初始堆积高度设为1.0 m,湍流床的初始堆积高度为0.8 m,模拟研究表明,床层在25 s后达到稳定流化状态,故取25~40 s之间的数据进行统计平均以分析不同区域的流动状态。
表2 Johnson和Jackson边界条件表达式
Tab.2 Expression of Johnson and Jackson boundary conditions

项目表达式速度/(m·s-1)up,w=-6μpεp,max3πφρpεpg0Θ,pp∂up,w∂n颗粒拟温度/(m2·s-2)Θw=-kΘγw∂Θw∂n+3πφρpεpu2p,slipg0,ppΘ3/26εp,maxγwγw=3π(1-e2w)εpρpg0,pΘ3/24εp,max
1.3 网格无关性验证
对于流化床的模拟,相比于时间步长,网格对模拟结果更为敏感,因此为了保证网格尺寸对模拟结果的独立性,本文中采用流化床换热器实验结果[27]进行网格无关性和模型验证。图2比较了采用不同网格尺寸所模拟的平均固含率与实验数据。由图可以看出,采用网格尺寸为10 mm(42.7万,网络个数,下同)和12 mm(25.3万)所模拟的床层固含率相近,且均与实验数据吻合较好,而尺寸为24 mm(2.9万)网格所模拟的截面平均固含率明显小于实验所得固含率。
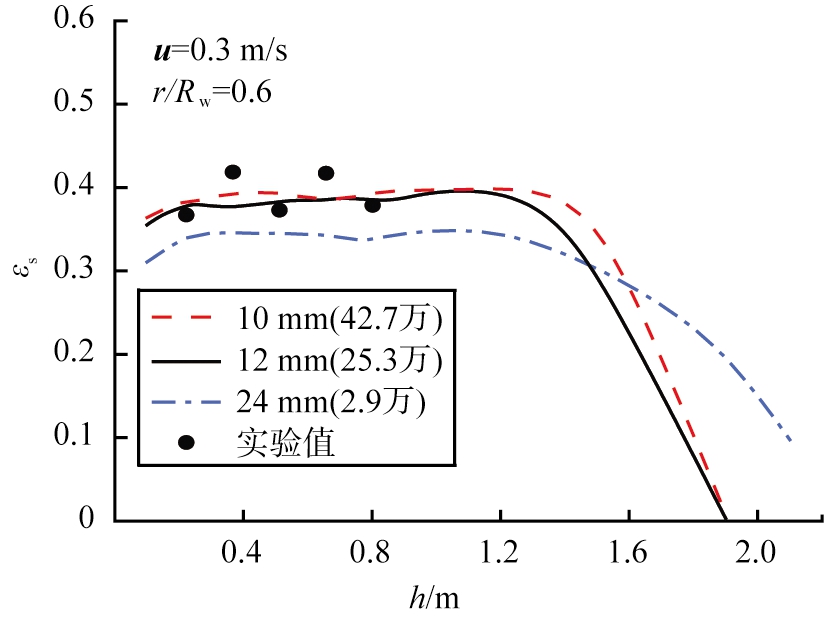
图2 网格尺寸对流化床换热器内固含率轴向分布的影响
Fig.2 Effect of mesh size on axial distribution of solids holdup in fluidized bed cooler
图3描述了不同网格所模拟固含率的空间分布特征,采用尺寸为10、12 mm的网格所得模拟结果能够很好地描述气泡的边界,且可以分辨出气泡在上升过程中尺寸逐渐变大,而采用24 mm网格的模拟结果仅在床层下部区域可分辨出气泡,且不能分辨出气泡的上升和变大。为了保证数值模拟的经济性,本文中研究选用12 mm的网格对流化床换热器进行研究。
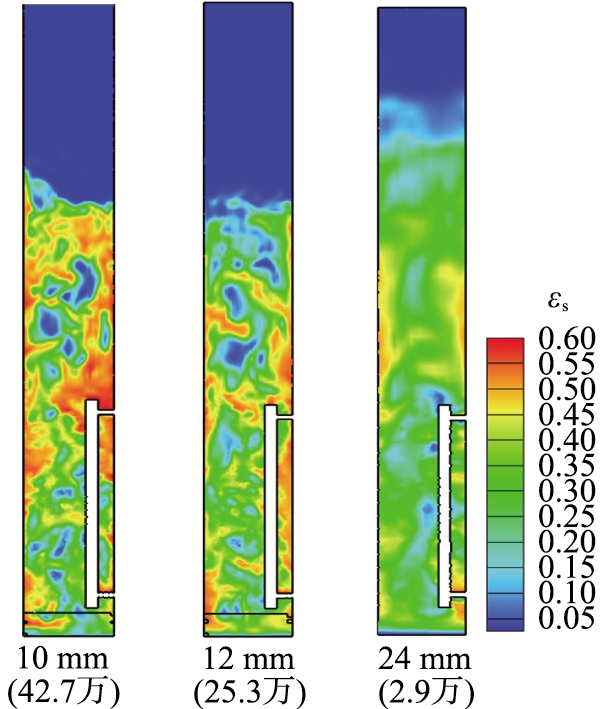
图3 不同网格尺寸下固含率的空间分布特征
Fig.3 Spatial distribution of solids holdup in fluidized bed cooler with different mesh sizes
1.4 模型验证
图4给出了表观气速为0.5 m/s,换热管位于r/Rw=0.6处,时均固含率的径向分布。其中r为内半径,Rw=R-rt,R为换热器半径,rt为换热管半径。由图可以看出,固含率呈现“中心低、边壁高”的分布特点,模拟结果能够很好地描述流化床内固含率的分布特征,且与实验数据吻合较好。这些结果表明该模型在网络尺寸为12 mm的几何模型下,可以很好地描述湍流床内气固两相的流动和分布特征。
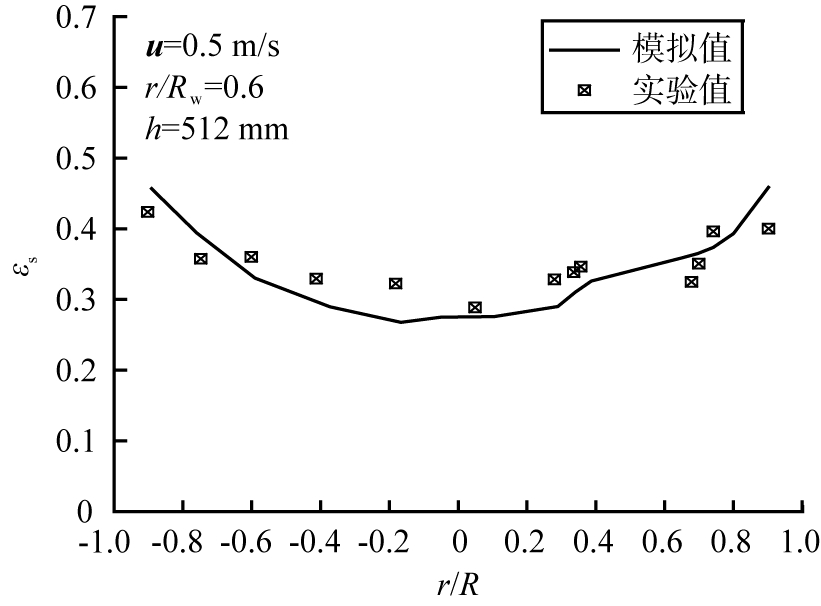
图4 时均固含率沿径向的分布
Fig.4 Radial distribution of time-averaged solids holdup
2 结果与讨论
2.1 轴向分布特征
图5比较了表观气速分别为0.6、0.8 m/s时,有热管和无热管的湍流床内固含率轴向分布。随着表观气速的增大,在床层下部区域,不同高度固含率均减小,固含率的差值随着轴向高度的增大而逐渐减小,而在床层上部区域,由于气体夹带作用,固含率的差值逐渐增大。相比于无热管流化床,表观气速对有热管流化床内固含率的影响更加明显。
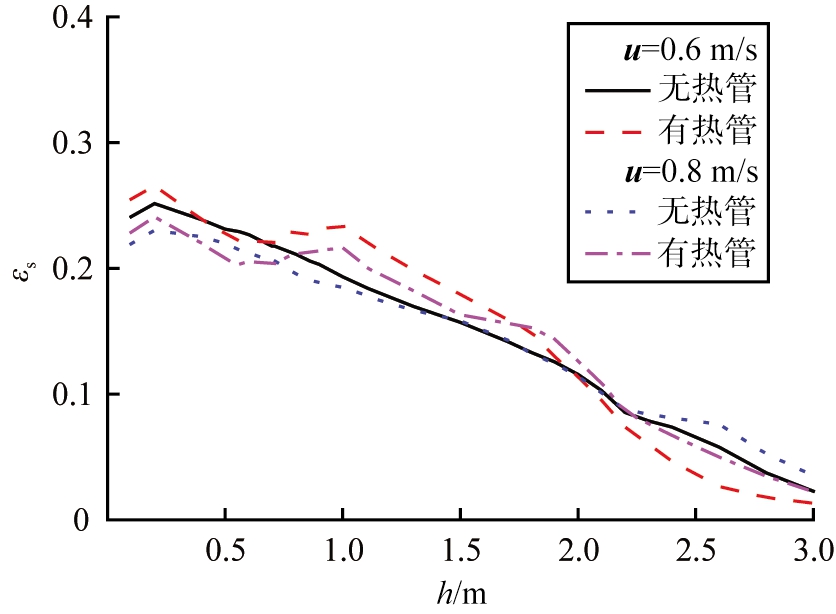
图5 热管对时均固含率轴向分布的影响
Fig.5 Effect of heat pipes on axial distribution of time-averaged solids holdup
在无热管流化床内,随着轴向高度的增大,固含率均逐渐减小。在有热管流化床内,固含率随轴向高度先逐渐减小,稍有增大后,继续减小。2种流化床取热器均无明显料面,这一分布特征符合湍流床固含率分布特征。热管的存在对固含率影响较大,当气固混合物流过热管时,固含率先稍有减小,然后稍有增大。这说明管束的存在阻隔了其下部区域气泡的上升,使气泡易聚集。而在管束所在区域,气泡因受到多根热管的剪切作用而破裂、变小,使得固含率有所增大。这一现象可由图6中瞬时固含率分布图充分印证。在热管上部区域,气泡继续长大,固含率逐渐降低。
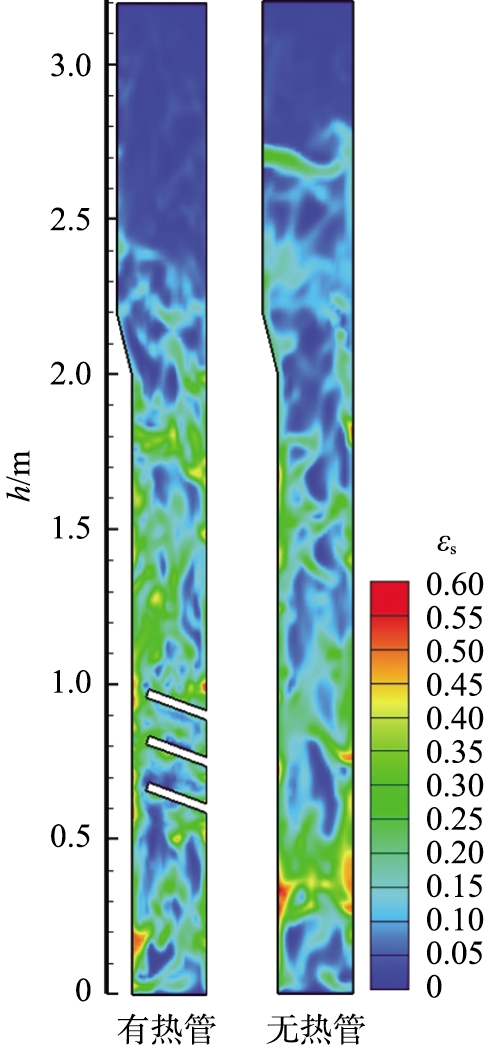
图6 热管对瞬态固含率分布的影响(u=0.8 m/s)
Fig.6 Effect of heat pipes on contours of instantaneous solids holdup(u=0.8 m/s)
图6比较了表观气速为0.8 m/s时,有、无热管的湍流床内固含率的瞬时分布特征。由图可看出,热管具有减小气泡尺寸、减小热管下部区域固含率、增大热管上部区域固含率、减小颗粒夹带量的作用。
图7给出了热管所在局部区域固含率的轴向分布随表观气速的变化。由图可以看出,不同气速下,因受热管的影响,随轴向高度的增大,固含率先减小,然后在热管所在区域几乎不变,流过热管后,固含率继续减小。这一变化趋势不受表观气速影响,说明热管对湍流床内流动状态的影响不因操作条件而改变。同时,热管所在区域,固含率受轴向高度影响较小,说明热管起到了破碎气泡的作用,使该区域的气泡变得更均匀,改善了流化质量。因此,可通过在湍流床内设置热管的方式定量调节流动状态,从而实现气固接触状态的改善[28]。同时,由于热管下部区域受到分布器的影响,固含率降低的幅度大于热管上部区域的。气体对颗粒的夹带作用也使得表观气速越大,固含率的降低幅度越小。
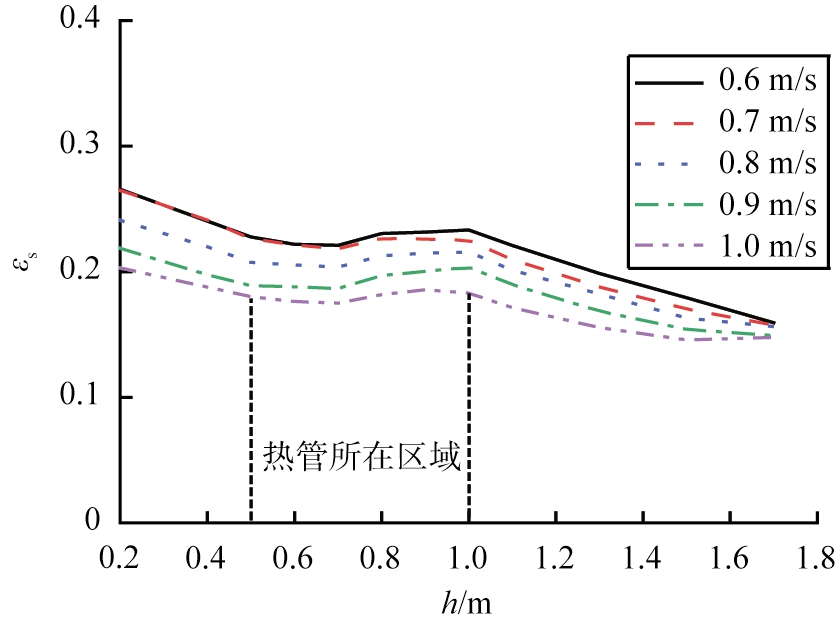
图7 表观气速对固含率轴向分布的影响
Fig.7 Effect of superficial gas velocity on axial distribution of solids holdup
2.2 径向分布特征
图8比较了有、无热管情况下,不同高度处床内固含率的径向分布。其中h=0.561 m处位于3根热管下侧,h=0.711 m处位于第1和第2根热管的中间高度,h=0.861 m处位于第2和第3根热管的中间高度,h=1.111 m处位于3根热管上侧。r/R=-1.0为靠近床壁一侧,r/R=0为靠近隔板一侧。可以看出,在各高度处,固含率均呈现中心低、边壁高的“U”型分布特征,然而这一分布并不对称,而是在靠近床壁一侧固含率较大,靠近隔板一侧固含率较小,这是由于两侧的限制壁面形状不同。这一分布特征即不受轴向高度影响,也不受热管存在与否的影响。比较2种流化床可以看出,在热管区下部和上部区域,固含率分布趋势相一致。在h为0.711、0.861 m位置,由于受第1和第2根热管的影响,热管的存在使得其所在径向位置处的固含率小于无热管流化床的固含率,并且在热管末端固含率更小。越靠近隔板壁面,两者差异越小,这是由于越靠近隔板,所在轴向高度越远离热管。
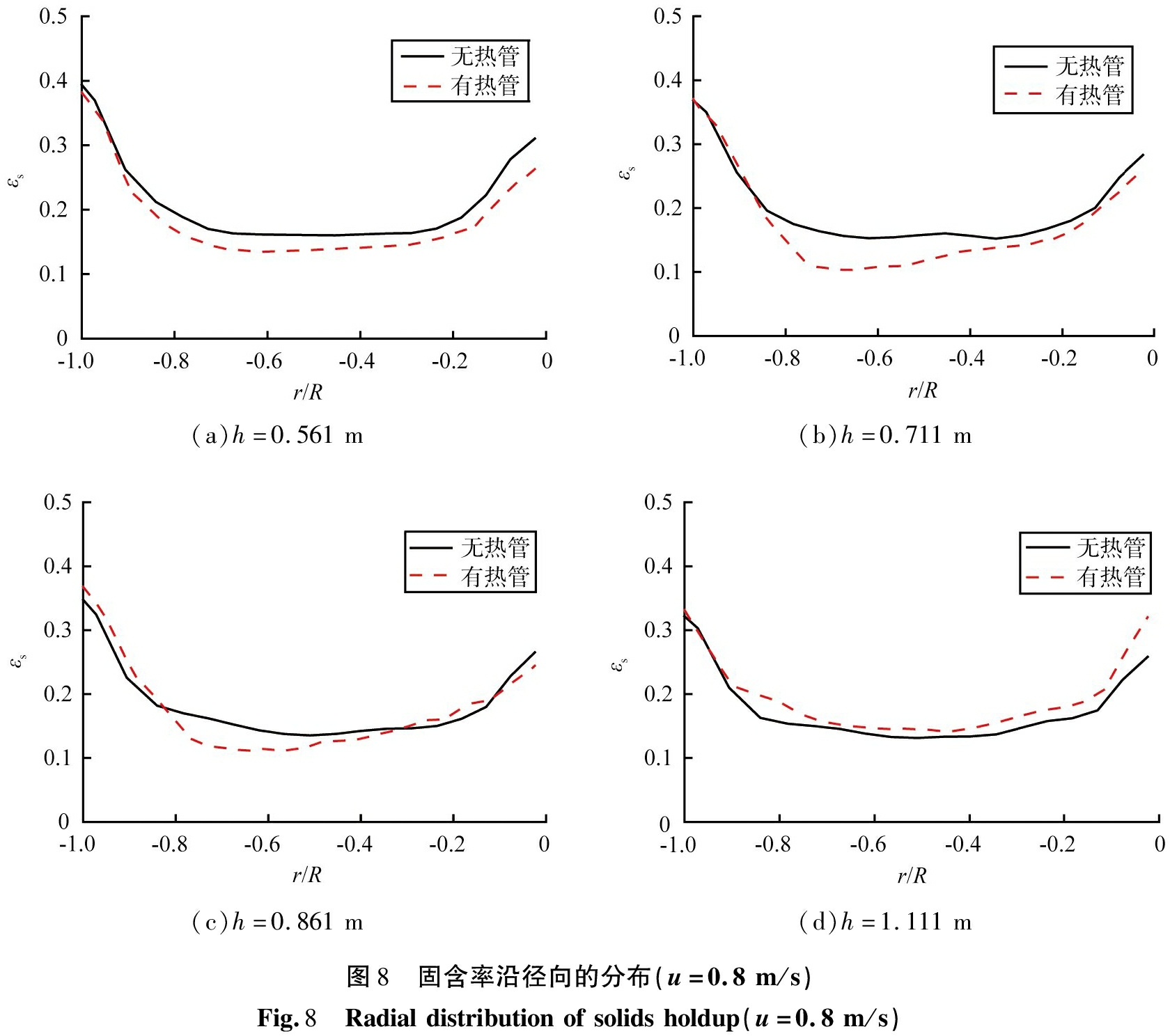
(a)h=0.561m(b)h=0.711m(c)h=0.861m(d)h=1.111m图8 固含率沿径向的分布(u=0.8m/s)Fig.8 Radialdistributionofsolidsholdup(u=0.8m/s)
图9给出了表观气速为0.8 m/s时,不同高度处的时均固含率沿径向的分布曲线。图中的5个轴向高度均紧临或远离热管,但没有横穿热管。不同高度处的固含率沿径向均呈现非对称的“U”型分布,越靠近下部区域,偏心程度越明显,即靠近隔板的固含率越小,靠近床壁的固含率越大。这是因为热管所在的区域大部分被气体占据,热管的存在阻碍了气泡上升而停留在床层下部区域(详见图6)。在相邻热管之间的轴向位置,即h为0.711、0.861 m,径向位置r/R=-0.75附近,固含率出现极小值,该位置为热管的末端所处的径向位置。由于热管的倾斜布置,该位置的轴向高度非常靠近下部的热管,径向位置越小,越远离热管。通过与其他位置的固含率分布相比较发现,气泡只有同时受下侧热管的破碎作用、上侧热管的阻滞作用,气固分布状态才会发生明显的变化,且热管对其影响程度会随着与热管的轴向距离而变化,导致不同轴向高度的固含率差异沿径向逐渐减小。在h为1.011、1.111 m、r/R>-0.5的位置,固含率偏大,这是由于气泡因受热管的破碎作用而尺寸减小,颗粒上行速度减小,存在颗粒聚集现象。
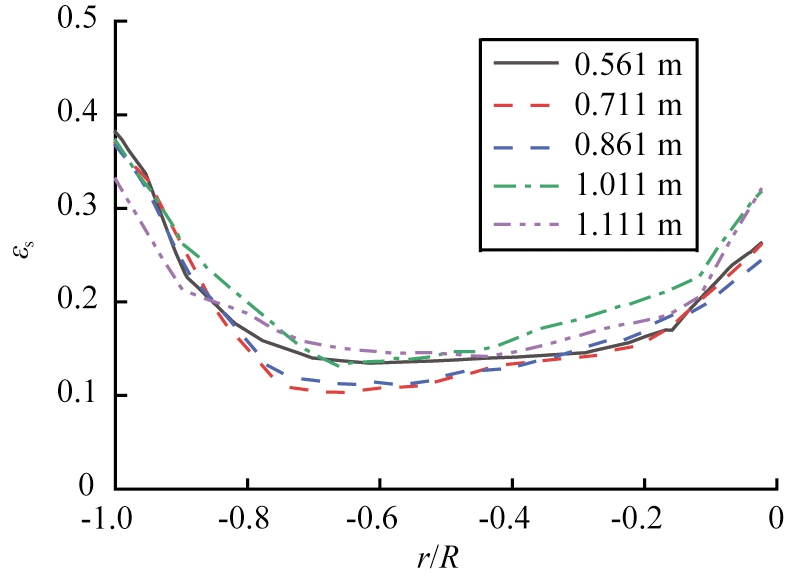
图9 不同轴向高度下固含率的径向分布
Fig.9 Radial distribution of solids holdup at different heights
图10给出了h=0.861m处,表观气速对时均固含率径向分布的影响。总体来看,固含率沿径向的非对称“U”型分布不受表观气速的影响。随着表观气速的增大,床层中间和隔板附近区域时均固含率明显减小,而床体壁面附近固含率变化较小,受气速的影响较小。表观气速增大到0.8 m/s之后,床层中间位置的颗粒含量变化较小,气体对颗粒的曳力作用,即颗粒受气体向上的夹带能力达到一定极限。
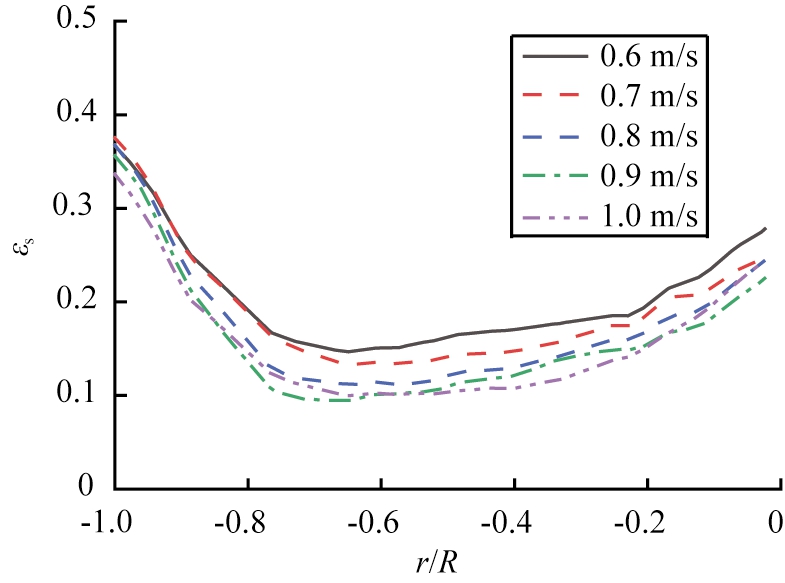
图10 不同表观气速下固含率的径向分布(h=0.861 m)
Fig.10 Radial distribution of solids holdup at different gas velocities(h=0.861 m)
综上可知,湍流床内热管壁面上、下侧区域的固含率分布各有特点,说明不同表观气速下,热管改变床内气固两相流动结构的能力不同,但产生的效果都是促进气固两相的混合均匀。
图11给出了表观气速为0.8 m/s时,时均固含率沿径向的分布曲线,图中的3个轴向高度均横穿热管。从整体来看,固含率沿径向呈非对称的“U”型分布,且两侧壁面的固含率差异较图9所示两侧壁面固含率的差异要小,固含率极小值出现在热管末端所在的径向位置。单独看热管两侧的固含率分布可以发现,热管左侧区域(即靠近床壁一侧),固含率呈非对称的“U”型分布,越靠近床壁和管壁固含率越大;在热管下侧区域,气泡因受热管的阻滞作用而出现短时停留,因此固含率虽然也越靠近管壁越大,但数值较床壁一侧的偏低;热管右侧区域(即靠近隔板壁一侧)均位于热管的上侧,其对气泡的破碎作用使固含率较热管下侧区域的值大,同时隔板壁面的摩擦作用,使得固含率越靠近壁面其值越高。相同高度处,管壁上侧附近的固含率总是高于管壁下侧的。
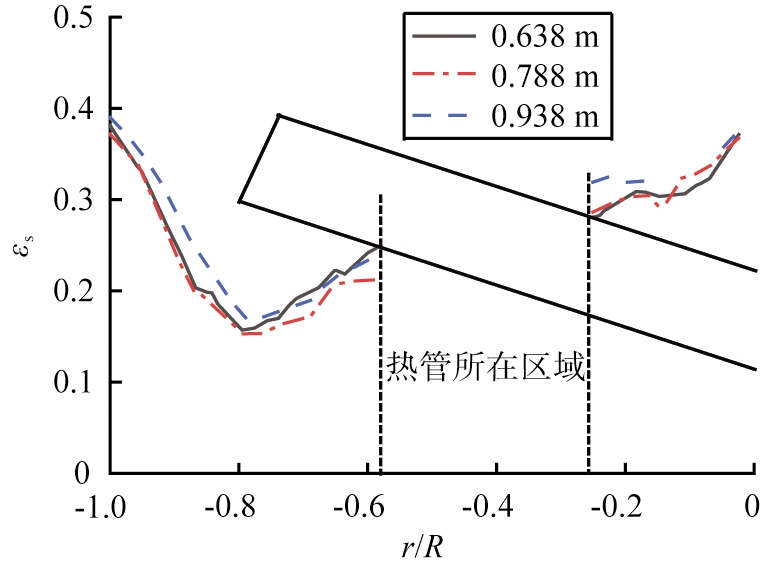
图11 不同轴向高度下固含率的径向分布
Fig.11 Radial distribution of solids holdup at different heights
在热管下部,即-0.8<r/R<-0.58,固含率随径向位置的增大而增大,h=0.788 m处的固含率低于其他两个高度的值,该位置受上下两根热管的影响。在非热管所在区域(-1.0<r/R<-0.8)和热管上部(-0.26<r/R<0.0),h=0.938 m位置的固含率最大,这表明,在多排热管的影响下,气泡尺寸减小,固含率增大。位于h=0.788 m热管壁上侧在r/R=-0.15附近固含率出现极小值,可能是因为流动空间狭小,大气泡未被破碎而占据了流道,使得该处固含率减小。
图12给出了不同表观气速下,h=0.788 m处时均固含率的径向分布。由图可知,各径向位置的固含率均随着表观气速的增大而增大,不同之处在于床体边壁附近的固含率受气速影响较小,热管下部区域的固含率受气速影响较大,这表明被破碎的小气泡在热管下侧汇聚,气泡数量较多,形成一个低密度区,其可强化颗粒轴向的返混。在热管右侧区域,随着径向位置的增加,固含率总体逐渐增大,但在r/R=-0.15附近,固含率出现一个极小值,说明一直有少量的小气泡流经此处并受到上方管壁低密度区的影响,使得该位置的固含率始终处于较低值。这种分布状态不随表观气速而变化。因右侧区域位于热管的上部,所以表观气速对固含率的影响程度大于其他径向位置,表明了热管的存在具有强化操作条件对固含率分布影响的作用。同时,相同气速下,管壁上侧附近的固含率总是高于管壁下侧的,而且表观气速越大,它们间的差异越小。
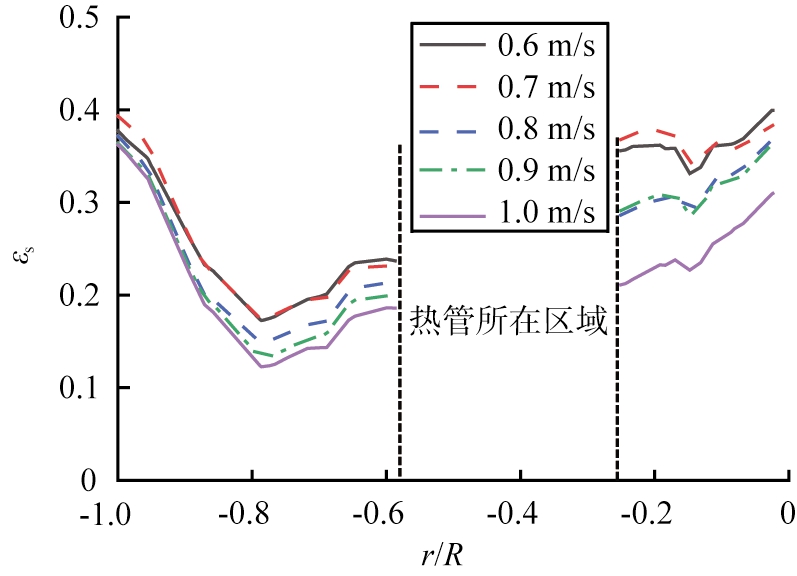
图12 不同表观气速下固含率沿径向的分布(h=0.788 m)
Fig.12 Radial distribution of solids holdup at different gas velocities(h=0.788 m)
综上可知,低密度区的存在,说明被破碎的小气泡有在管壁下侧聚集的趋势。管壁上、下侧固含率分布情况大不相同,表明气固混合物在流经热管后得到重新分配和调整。同时由于热管安装在隔板壁面,所以隔板处固含率变化受气速的影响与床体边壁附近不同。比较图9和11可知,无热管的径向位置,两侧壁面的固含率相差较大,而热管所在截面,两侧壁面的固含率数值相近。这是因为无热管流化床内两侧壁面的影响不同导致固含率差异较大,而有热管存在时,隔板侧固含率因受热管的影响而增大,使得两侧壁面的固含率相近。
比较图10和12可知,表观气速对固含率的影响不同,无热管时固含率沿径向均匀变化,且影响较小,而有热管时热管上侧的固含率受气速的影响强于其对下侧的影响,这是因为热管具有破碎气泡、增大固含率的作用,这一作用会随着与热管距离的增加而减弱,而气速具有减小固含率的作用。此导致表观气速对热管上侧固含率的影响最大,下侧次之,无热管时最小。
2.3 周向分布特征
图13给出了表观气速为0.8 m/s、位于h=0.788 m处的热管表面不同周向位置的固含率沿热管轴向方向的分布。由图可以看出,在热管表面180°位置,固含率先逐渐减小,然后逐渐增大,最低值位于r/R=-0.6处;在热管表面90°和270°处,固含率先逐渐减小后基本不变,再逐渐增大;在热管表面0°位置,固含率随着径向位置的增大,变化较小,只是稍有增大。135°和225°的固含率介于0°和90°数值的中间,45°和315°的固含率介于90°和180°数值的中间。
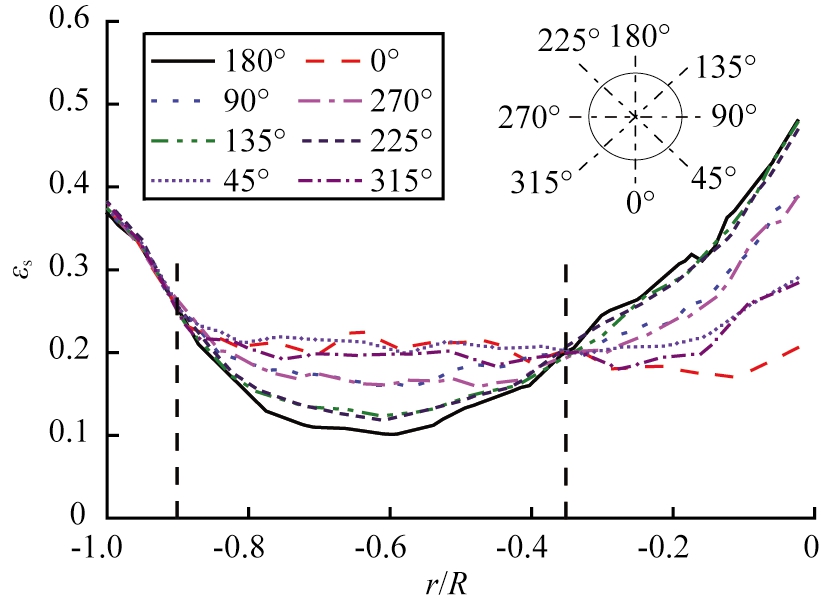
图13 热管表面固含率沿热管周向的变化(u=0.8 m/s)
Fig.13 Variation of solids holdup on heat pipe surface at different circumference of heat pipe(u=0.8 m/s)
沿热管轴向方向,不同位置的固含率周向分布差异较大。在靠近隔板的径向区域(-0.35<r/R<0),固含率由热管上部(180°)到热管下部(0°)逐渐减小,固含率较高的3个位置的数值相当,即180°、135°和225°,其他对称位置(即90°与270°、45°和315°)的固含率数值相近。热管表面固含率沿周向差异的大小随着径向位置远离隔板而逐渐减小。在r/R=-0.35处,各周向位置的固含率相当。在热管表面、远离隔板的径向位置(即-0.80<r/R<-0.35)和热管外侧一定距离(即-0.90<r/R<-0.80),热管不同周向位置的分布状态与靠近隔板区域的完全相反,即,热管上部(180°)的固含率低于下部区域(0°)的,同样是固含率较高的3个位置的数值相当,即0°、45°和315°,其他对称位置(即90°与270°、135°和225°)的固含率数值相近。热管周向的固含率差异随着径向位置的增大,先逐渐增大后逐渐减小,到热管末端而离开热管之后,由于已经远离热管,各周向位置的固含率保持一致。
综合上述分析可按照热管表面固含率的周向分布状态沿床层径向位置分为3个区域。区域1为热管表面的近壁区,即靠近隔板壁面的区域,-0.35<r/R<0.0;区域2为热管表面自由端(即热管表面远离隔板壁面的区域)和热管外一定距离,-0.90<r/R<-0.35;区域3为无热管区域,即1.00<r/R<-0.90。根据上述分布,区域1与区域2的热管表面为2种完全不同的流动状态,因此径向位置r/R=-0.35作为区分两种流动状态的关键位置。由于区域1的气固流化性能受到隔板壁面的影响,因此将区域1命名为壁面影响区,区域2为主换热区。
图14分别给出了位于3个区域的截面固含率云图。在区域1,热管的下部存在局部的固含率低值区,其他位置的固含率相当,且热管与床壁之间区域为固含率较低的气泡流道,该流道内固含率随着轴向高度的增加而逐渐增大。在区域2,在热管中部和下部存在固含率高值区,该区域的尺寸随着轴向高度的增大逐渐减小,且越靠近区域2的中间位置,该区域的尺寸越大。区域3总体固含率的差异较区域1和2更加均匀。
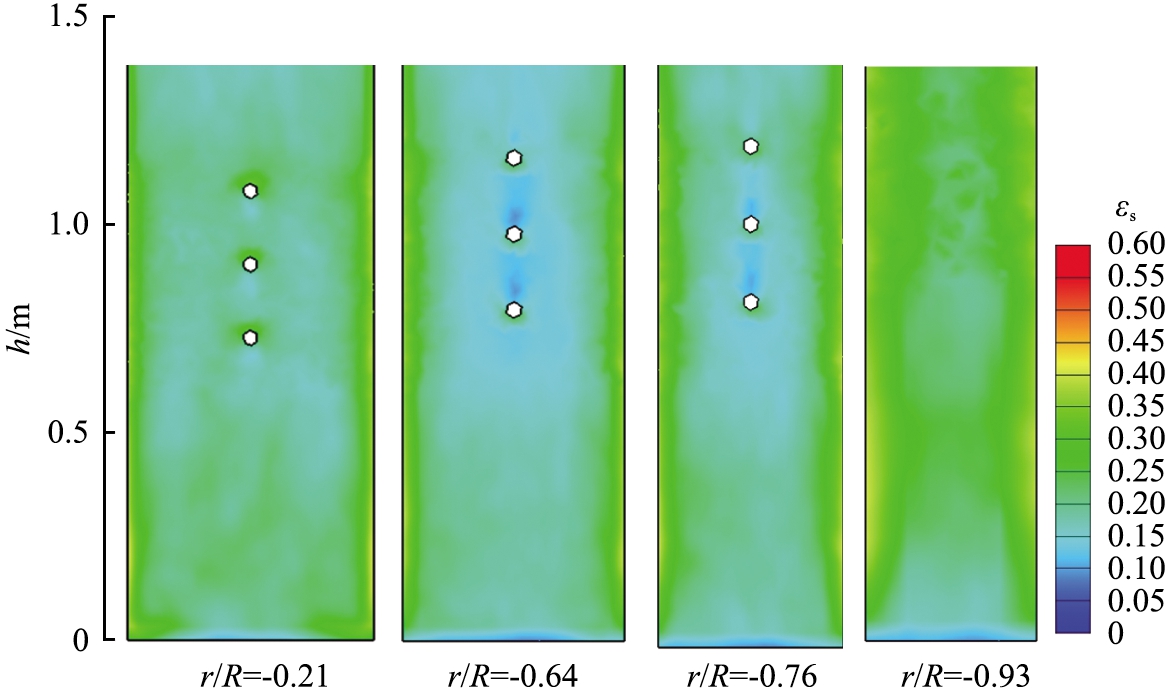
图14 热管所在周向截面的固含率分布云图(u=0.8 m/s)
Fig.14 Contour of solids holdup on circumferential section of heat pipe(u=0.8 m/s)
图15给出了固含率周向分布分界点随轴向高度和表观气速的变化。由图可以看出,随着热管位置的升高,分界点的位置逐渐远离隔板,且热管各周向位置的固含率差异逐渐减小(见图14)。这表明,随着轴向高度的增加,气泡尺寸逐渐减小,床层分布更加均匀,如图6所示,因此热管表面不同周向位置的固含率差异减小。也就是说,随着轴向高度的增加,边壁效应逐渐增大,主换热区逐渐减小。
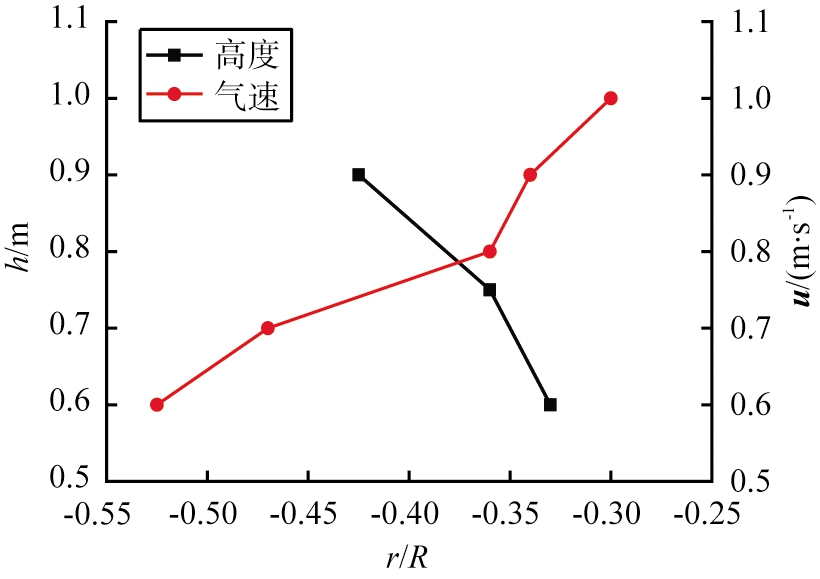
图15 热管表面固含率周向分布分界点随热管高度和表观气速的变化
Fig. 15 Variation of demarcation point of circumferential distribution of solids holdup with height of heat pipe and superficial gas velocity
图16给出了主要换热区的r/R=-0.6处,垂直于热管平面的时均固含率轴向分布随表观气速的变化。由图可以看出,热管表面各周向位置的固含率均随表观气速的增加而逐渐减小,但减小的幅度较小。除热管顶部即180°位置外,其他各周向位置固含率的减小幅度相同。热管顶部的固含率在表观气速小于0.8 m/s时,固含率减小幅度大于其他周向位置的。当表观气速为0.6 m/s时,热管顶部和中部的固含率相当,随着表观气速增加到0.8 m/s,这2个位置的固含率差异逐渐增大,当气速大于0.8 m/s时,各周向位置的固含率之间的差异相当。导致图15中,固含率分界点随着表观气速的增大而逐渐靠近隔板,即主换热区逐渐增大,边壁效应逐渐减小。
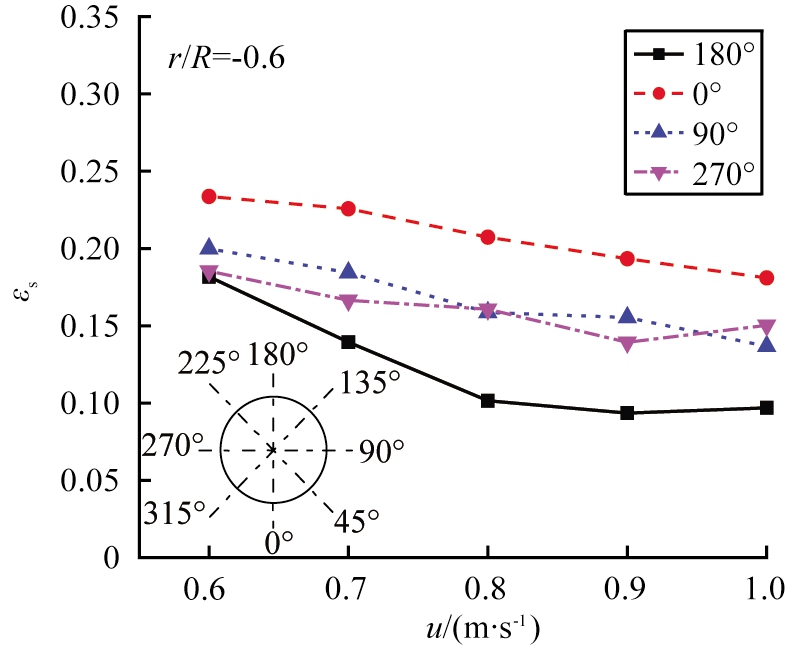
图16 管壁周向的时均固含率随表观气速的变化
Fig.16 Variation of solids holdup on the pipe surface with superficial gas velocity
3 结论
采用欧拉-欧拉双流体模型结合EMMS曳力模型,模拟了带有多根倾斜换热管的流化床换热器内气固流动状态。为了获得其内部的流场信息,首先基于已有实验数据,验证了适宜的网格尺寸为20 mm,通过比较固含率的轴径向分布确定了所用模型的有效性。
1)固含率轴向分布表明,热管具有减小气泡尺寸、减小热管下部区域固含率、增大热管上部区域固含率、减小颗粒夹带量的作用。随着轴向高度的增加,热管对固含率的影响逐渐减小。热管对流化床内流动状态的影响不因操作条件的变化而改变。
2)固含率的径向分布表明,热管对固含率径向分布影响最明显的轴向高度位于相邻两根热管之间的位置,其对固含率的影响主要位于热管末端,且随着热管与隔板间距的减小,热管对固含率的影响逐渐减小。热管所在高度的固含率在热管末端的值最小,随着径向位置靠近两侧壁面而逐渐增大。表观气速对床壁附近固含率的影响较小,对隔板附近固含率的影响较大,特别是在所在截面处。
3)沿热管轴向方向,在靠近隔板壁面处,即隔板影响区,热管上部的固含率最大,下部最小;在靠近热管自由端,即主换热区,热管下部固含率最大,上部最小。随着热管轴向高度的增加,主换热区逐渐减小,随着表观气速的增大,主换热区逐渐增大。
[1]张海莹,赵东风.催化裂化烟气脱硫脱硝优化技术研究[J].当代化工, 2019, 48(4): 851-854.
[2]刘克宁, 刘同仁, 李磊.催化裂化再生烟气净化催化剂研究进展[J].山东化工, 2017, 46(14): 51-54.
[3]姚秀颖, 卢春喜.催化裂化再生催化剂取热技术研究进展[J].石油学报(石油加工), 2018, 34(2): 217-228.
[4]郭大为, 张久顺, 张执刚, 等.一种烟气脱硫脱氮吸附剂再生过程中的换热方法: 200910162162.4[P].2011-03-23.
[5]郭大为, 张久顺, 毛安国, 等.一种烟气脱硫脱氮吸附剂再生过程中的换热方法: 200810113392.7[P].2009-12-02.
[6]姚秀颖, 李建涛, 卢春喜, 等.流化床间壁换热再生耦合装置:202020183168.1[P].2020-10-30.
[7]JOUHARA H, CHAUHAN A, NANNOU T, et al.Heat pipe based systems-Advances and applications[J].Energy, 2017, 128: 729-754.
[8]徐连青.热管技术在热能工程中的应用[J].科技传播, 2012, 5:140-141.
[9]YAO X, ZHANG Y, LU C, et al.Systematic study on heat transfer and surface hydrodynamics of a vertical heat tube in a fluidized bed of FCC particles[J].AIChE J, 2015, 61: 68-83.
[10]GERHARD H, GERHARD S, TOBIAS P.Acting on hydrodynamics to improve the local bed-to-wall heat transfer in bubbling fluidized beds[J].Chem Eng Res Des, 2018, 134: 309-318.
[11]YANG Z, ZHANG Y, OLORUNTOBA A, et al.MP-PIC simulation of the effects of spent catalyst distribution and horizontal baffle in an industrial FCC regenerator.part I: effects on hydrodynamics[J].Chem Eng J, 2021, 412: 128-634.
[12]KIM S W, KIM S D.Heat transfer characteristics in a pressurized fluidized bed of fine particles with immersed horizontal tube bundle[J].Int J Heat Mass Transf, 2013, 64: 269-77.
[13]MICKLEY H S, FAIRBANKS D F.Mechanism of heat transfer to fluidized beds[J].AIChE J, 1955, 1: 374-384.
[14]LI J, YAO X, LIU L, et al.Bed-to-wall heat transfer in a gas-solid fluidized bed with external solids circulation: Modified packet renewal model[J].Powder Technol, 2021, 383: 19-29.
[15]AL-BUSOUL M A, ABU-EIN S K.Local heat transfer coefficients around a horizontal heated tube immersed in a gas fluidized bed[J].Heat Mass Transf, 2003, 39(4): 355-358.
[16]TAWFIK M, REFAAT D M, MOHMED A H.An experimental investigation of wall-bed heat transfer and flow characteristics in a swirling fluidized bed reactor[J].Appl Therm Eng, 2019, 155: 501-507.
[17]BAO Z, HUANG Y, DUAN L, et al.Heat transfer characteristics of horizontal tubes in the dilute phase of the pressurized fluidized bed[J].Int Commun Heat Mass,2021, 126: 105-370.
[18]WANG J.Flow structures inside a large-scale turbulent fluidized bed of FCC particles: eulerian simulation with an EMMS-based sub-grid scale model[J].Particuology,2010, 8(2): 176-185.
[19]吴诚, 高希, 成有为, 等.湍动流化床过渡段固含率分布特征的实验及数值模拟[J].化工学报,2013, 64(3): 858-866.
[20]LAN X, YAN W, XU C, et al.Hydrodynamics of gas-solid turbulent fluidized bed of polydisperse binary particles[J].Powder Technol,2014, 262: 106-123.
[21]CHEN J, LI H, LV X, et al.A structure-based drag model for the simulation of Geldart A and B particles in turbulent fluidized beds[J].Powder Technol,2015, 274: 112-122.
[22]CHANG J, ZHAO J, ZHANG K, et al.Hydrodynamic modeling of an industrial turbulent fluidized bed reactor with FCC particles[J].Powder Technol,2016, 304: 134-142.
[23]VARGHESE M M, VAKAMALLA T R, MANTRAVADI B, et al.Effect of drag models on the numerical simulations of bubbling and turbulent fluidized beds[J].Chem Eng Technol,2021, 44(5): 865-874.
[24]孟振亮, 刘梦溪, 李飞, 等.新型气固环流反应器内颗粒流动的CFD模拟[J].化工学报, 2016, 67(8): 3234-3243.
[25]MENG Z, LIU M, XIE J, et al.Comparative study on the hydrodynamics and mixing characteristics of a new-type particle mixer[J].Powder Tech, 2018, 332: 90-105.
[26]傅梦倩, 姚秀颖, 范怡平, 等.双层喷嘴提升管进料区内气固流动特性的数值模拟[J].过程工程学报, 2020, 20(7): 757-769.
[27]徐逞祥.无序环流取热器内气固两相流动和内循环特性研究[D].北京: 中国石油大学(北京), 2020.
[28]ZHANG Y, LU C.Experimental study and modeling on effects of a new multilayer baffle in a turbulent fluid catalytic cracking regenerator[J].Ind Eng Chem Res, 2014, 53(5): 2062-2066.