进入21世纪以来,我国制造业得到了快速发展,随之对机械加工制造工艺和加工环境提出了更高的要求,真空手套箱作为一种重要的加工平台在越来越多的领域得以应用。真空手套箱的工作原理是,利用其中的惰性气体将箱体内的氧气、 水蒸气等排出或控制箱内气体成分和比例。真空手套箱广泛应用于锂离子电池、 半导体等领域。除此之外在生物学领域也有应用,例如厌氧菌培养、 细胞低氧培养等[1]。
在实际生产过程中,手套箱的结构会根据生产环境、可利用空间、箱体内放置设备形状等因素,做出相应的改变。目前,国内手套箱生产企业多以仿制为主,对手套箱结构变化之后的对应流场状态的改变研究很少,缺乏相应的理论支撑,导致箱体内产生理想氛围时间较长,或者不能够达到理想氛围要求。本文中主要对一种结构外形类似大写字母H,同时满足增材制造和减材制造的手套箱内流域进行流固耦合仿真分析,手套箱内增材制造过程主要运用选择性激光烧结(selective laser sintering,SLS)[2]打印工艺,该过程主要运用金属、陶瓷等高分子材料。在打印时,材料并非是丝线状,而是聚合物粉末,使得打印过程会产生“烟雾”[3]。为了优化打印区域气体氛围质量,减少烟雾量,提高产品质量,解决企业在生产过程中遇到的问题,本文中主要研究气固两相流动特性,优化箱体加工环境,降低企业人力物力消耗,为现有特种工况手套箱的设计提供参考。
1 物理建模
传统手套箱系统是由净化器、手套箱以及箱体内设备共同组成,需求不同,手套箱系统的结构往往也不尽相同[4]。本文中的箱体结构是根据客户需求设计的,该箱体左侧腔室放置一台3D打印机,右侧腔室放置一台重型压机,工件可以在箱体中部传送、检验,该H型手套箱系统三维模型结构图如图1所示;二维主视图和右视图如图2所示。
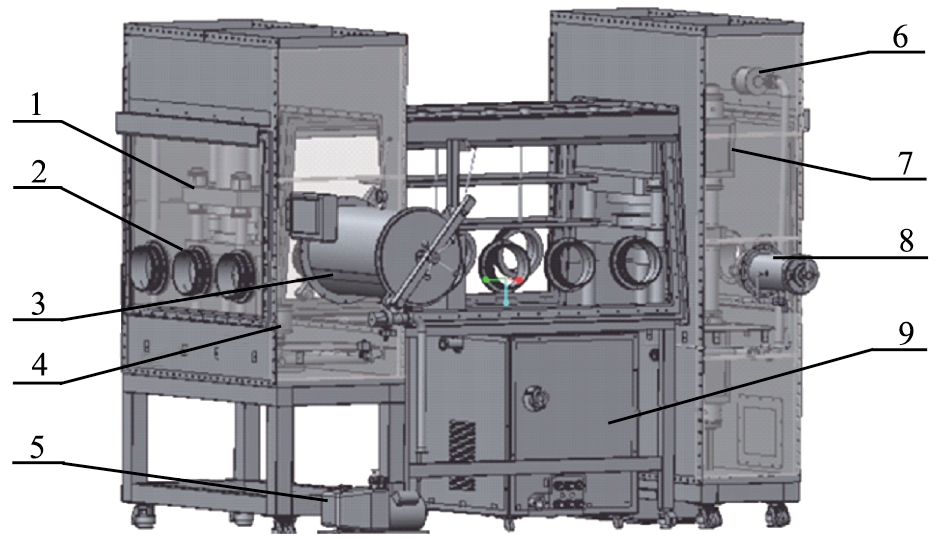
1—激光增材制造设备; 2—手套箱孔圈; 3—大过渡舱; 4—进气孔; 5—真空泵; 6—出气孔; 7—减材制造设备; 8—小过渡舱; 9—净化器。
图1 H型手套箱系统三维模型结构图
Fig.1 Standard view of 3D model of H-type glove box system
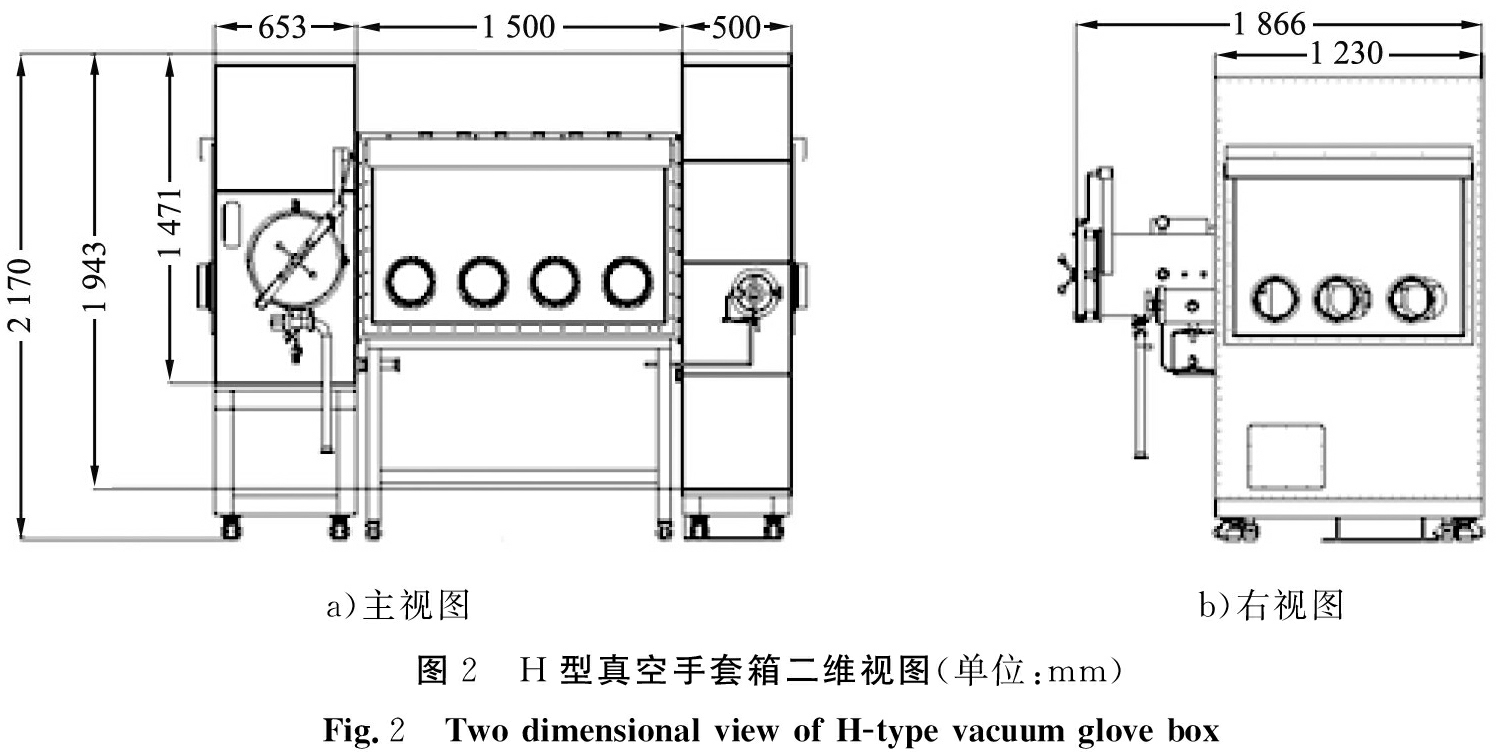
a)主视图b)右视图图2 H型真空手套箱二维视图(单位:mm)Fig.2 Two dimensional view of H-type vacuum glove box
2 网格模型
手套箱内部结构较为复杂,包括置物盘、 手套、 增材制造、 减材制造设备、 大小过渡仓等,在流体分析时,如果考虑这些因素则流道抽取比较困难,个别结构对流场分析影响比较小,可以对模型进行简化,忽略次要因素[5-6],图3为模型简化后的流场结构图。
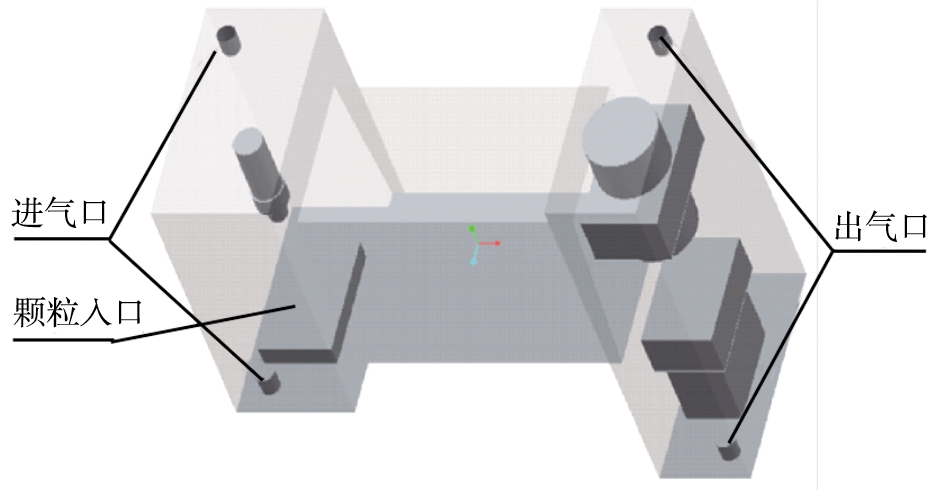
图3 模型简化后流场结构图
Fig.3 Flow field structure after model simplification
为了分析网格质量对数值模拟结果的影响,最大网格尺寸参数分别设置为100、 70、 50、 30 mm,划分好网格后,进气口速度恒定为4.777 m/s,分别求出不同网格数量对流道对称面直线ab上速度值的影响,见图4。从图中可以看出,在最大网格尺寸小于70 mm时,数值模拟结果较为吻合。为了降低计算机的运算量,将网格划分尺寸设置为70 mm,并将局部网格加密,壁面增长率为1.2[7],采用的网格数为270 766万左右,最小体积为111.154 2 cm3,最大体积为297.622 1 cm3,最差的网格质量为0.992。网格划分示意图如图5所示。
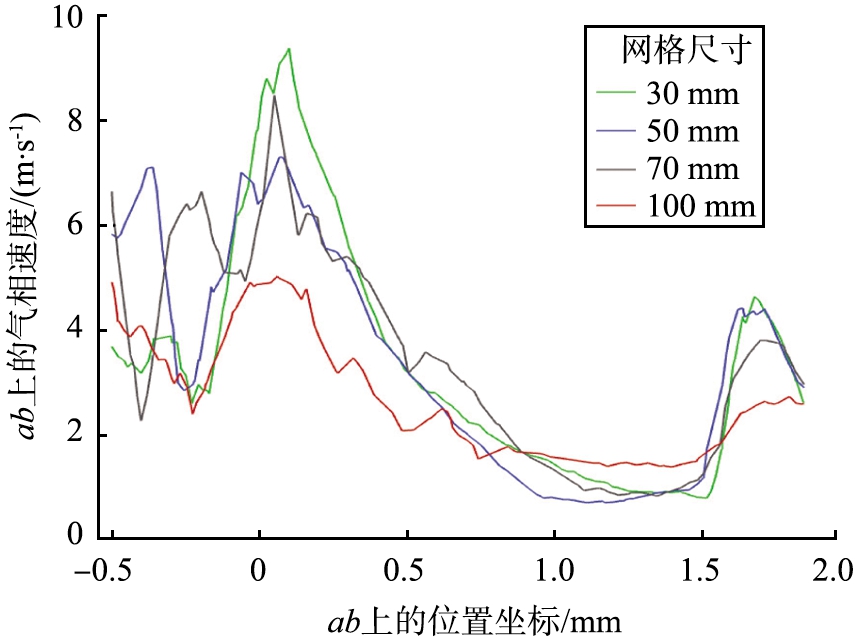
图4 不同网格数量对直线ab上速度值的影响
Fig.4 Influence of different grid number on simulation results

图5 网格划分示意图
Fig.5 Grid generation diagram
3 数学模型
3.1 控制方程的选择
3.1.1 基本假设
在建立数学模型时,忽略影响较小的因素,做如下的假设: 1)气相、固相均为连续性流体且在空间上共存; 2)箱体内两相流动均为湍流且固相体积浓度均匀分布于工作台表面; 3)固体颗粒为刚性球体且表面光滑; 4)仅考虑固体颗粒的阻力和重力并忽略其他力[8-9]。
3.1.2 基本方程
在研究过程中,忽略吸热、放热等能量交换,应用的基本方程为续性控制方程和动量控制方程[10]。
连续性方程为
(1)
式中: ρ为流体密度,kg/m3; t为时间,s;u、 v、 w分别为x、 y、 z方向的速度分量,m/s。
动量方程为
(2)
(3)
(4)
式中: fx、 fy、 fz分别为x、y、z方向的作用力,该作用力包含体积力和表面力。
5个模型:标准k-ε、重整化群(RNG) k-ε、可实现k-ε、标准k-ω和湍流模型剪切应力输运(SST)k-ω,是使用最广泛的湍流模型[11]。标准k-ε模型是Launder and Spalding提出的适用范围广、经济、合理的精度模型,它是个半经验的公式,是从实验现象中总结出来的。RNG k-ε模型来源于严格的统计技术,它和标准k-ε模型很相似,但是有以下改进: 1)RNG模型在ε方程中加了一个条件,有效地改善了精度; 2)考虑到了湍流漩涡,提高了在这方面的精度; 3)RNG理论为湍流Prandtl数提供了一个解析公式,然而,标准k-ε模型使用的是用户提供的常数; 4)标准k-ε模型是一种高雷诺数的模型,RNG理论提供了一个考虑低雷诺数流动粘性的解析公式。可实现的k-ε模型出现较晚,与标准k-ε模型相比有2个主要的不同点: 可实现的k-ε模型为湍流粘性增加了一个公式; 为耗散率增加了新的传输方程。标准k-ω模型是基于Wilcox k-ω模型,为考虑低雷诺数、可压缩性和剪切流传播而修改的。标准的k-ε模型的一个变形就是SST k-ω模型,这个模型由Menter发展,以便在广泛的领域中可以独立于k-ε模型,在近壁自由流中k-ω模型有广泛的应用范围和精度。
综合考虑本项目的特点和不同湍流模型的特点,选择标准k-ε模型公式进行求解计算[12-13]。
湍流模型为
(5)
(6)
式中: ε为湍流耗散率; Gk为因速度梯度引起的湍动能增加项; Gb为因浮力引起的湍动能k的增加项; ui为液相速度分量,m/s; μt为湍流黏性系数; ρ为流体密度g/cm3; C1ε为经验常数,一般分别取0.09、1.40、 1.92。
3.2 边界条件的设定
由于我们模拟的是固体小颗粒在手套箱内的运动,进气口速度是已知的,因此进气口处边界条件选择速度入口;出气口处边界条件选择压力出口,颗粒入口设置为wall-jet,其余的边界设置为固体壁面边界条件[14]。
4 模拟结果分析
4.1 气固两相速度分布
为了更好地观察箱体内气相和固相的速度分布,分别选取z为-150、 -580.5、 -101 1 mm; x为-500、 675.5、 1 840 mm截面为研究对象,分别得到当进气口速度为4.777 m/s时,各个截面的速度离散图和速度云图。
图6为不同z值截面的速度离散图。通过图6 a)可以看到,进气口速度为4.777m/s,气体由进气口进入流道之后,因为气体的发散性,速度值逐渐减小,并且逐渐向周边区域扩散。z=-150 mm右侧为箱体壁面,箱体壁面有一定的粗糙度,导致速度值减小,速率较大;在z=-150 mm至z=1 840 mm区域内,气相速度值变化较小,恒定为1 m/s左右;当处于流道出口时,速度再次增大,在流道末端速度值增加较快。由于增材制造设备产生固体颗粒占用一定的空间,会出现气相在出气口处速度大于进气口处速度的现象。
通过图6 b)可以看出,在增材制造加工平台,热气流上升带动周围固体小颗粒上升,随后在高速气体的带动下,使固体颗粒速度明显增大,从最初的0.6 m/s增大至2.5 m/s左右。之后在气流组织的带动下,固体颗粒伴随气流组织在箱体内流动,整体速度与气相速度正相关,在箱体出口附近,气相速度增大,则固体相颗粒速度逐渐增大,最终随着气相排出箱外。
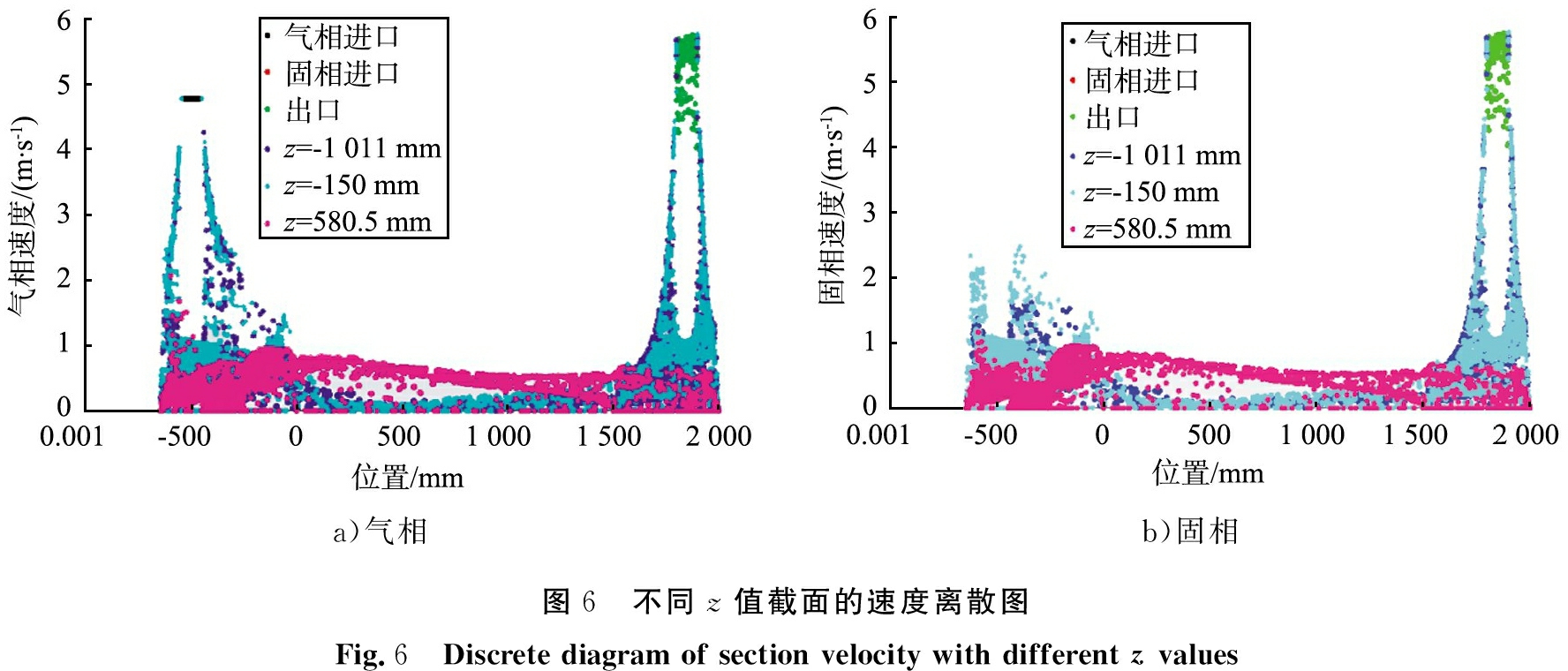
a)气相b)固相图6 不同z值截面的速度离散图Fig.6 Discrete diagram of section velocity with different z values
图7为不同z值截面的速度云图,图中z为-150和-1 011 mm截面气相在进气口速度值最大,进入流道后,流域空间增加,气体逐渐向四周扩散。在左侧箱体壁面的作用下,气体速度方向发生改变,整体分布表现为箱体壁面处速度值较大,中间区域速度较小。在出气口位置附近,速度分布较为均匀,但是在近壁面附近的壁面粗糙,导致气相速度较小,出气口速度大于入气口速度,这是因为在流场运动的过程中,不断有固体颗粒的加入,导致流域体积空间发生变化。固相在进气口附近速度值大于固相入口速度,其原因在于固相在流域内游离,在进气口附近高速气体的带动下,固相速度有所增加。在出气口附近表现出固体颗粒粒径较小,固相气相伴随性良好的特点。固相速度随着气相速度逐渐增加到最大,最后固体颗粒随着高速气体排出箱体外。在z=-580.5 mm截面,可以看到气相和固相速度变化不大,基本趋于稳定,在左侧存在内部设备,表现为气相和固相在设备表面处速度值增大。固体颗粒释放速度相对于进气口气相速度较小,所以在整个速度云图中并不能明显观察到固相速度入口附近区域的速度变化。
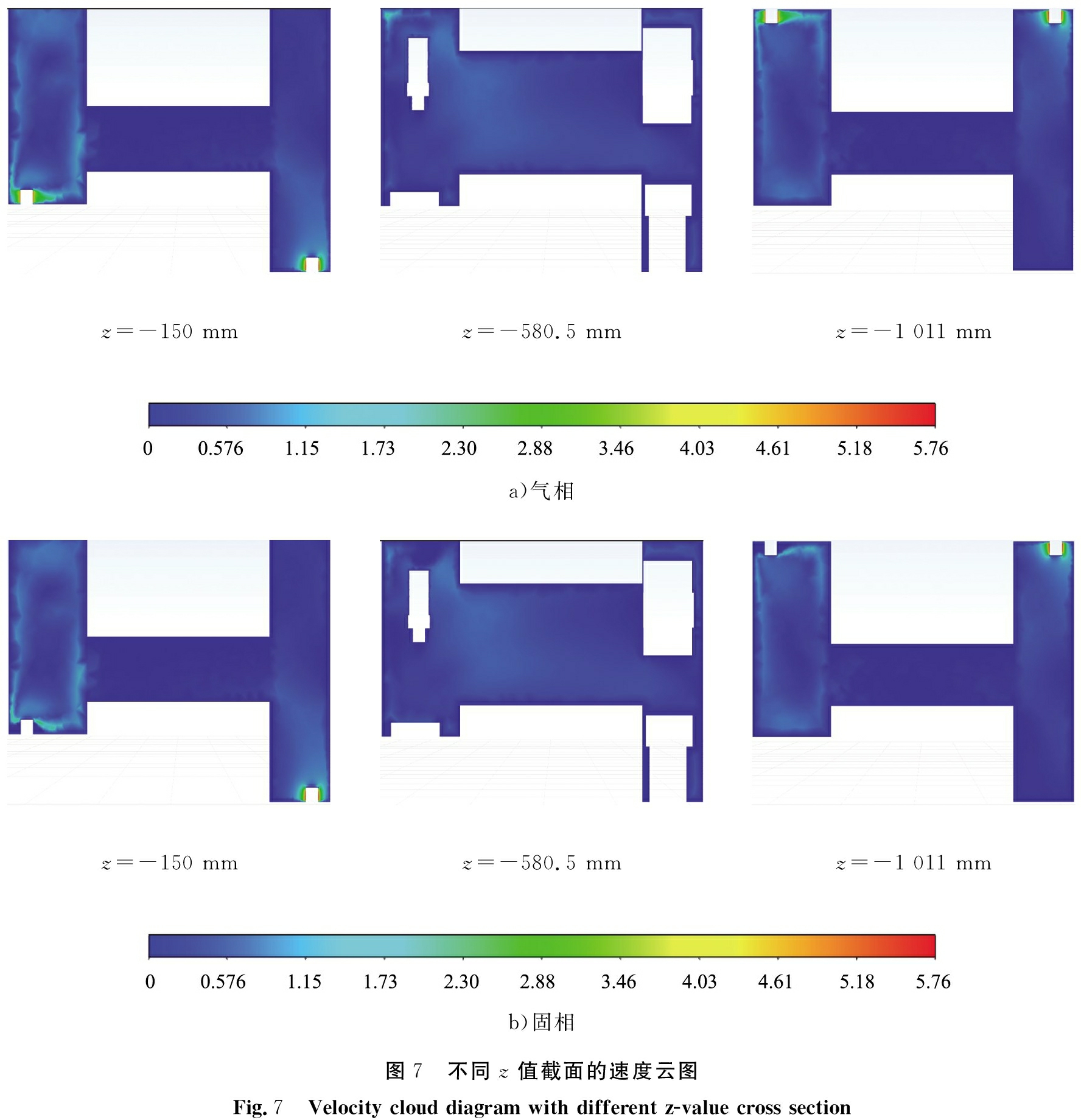
z=-150 mmz=-580.5 mmz=-1 011 mma)气相z=-150 mmz=-580.5 mmz=-1 011 mmb)固相图7 不同z值截面的速度云图Fig.7 Velocity cloud diagram with different z-value cross section
图8为不同x值截面的速度离散图,其中红色区域为进气口截面,黑色区域为出气口截面,绿色区域为箱体中间对称面。由图中红色区域可以看出,箱体在上、下端进气口速度值呈喇叭形状散开,速度减小,由于流道中设备占用空间,导致上端进气口气相速度衰减较为缓慢,下端进气口速度快速衰减至一定值;黑色区域可以看出,箱体上、下端出气口,速度分布较为均匀,表现出一定的规律性,由图8 a)明显可以看出,出气口速度值大于进气口速度值,进气口速度为4.777 m/s,出气口速度为5.7 m/s左右;从绿色区域可以看出,流道内气相在中心区域速度值较大,靠近箱体壁面处速度值较小,从壁面到中心区域速度逐渐增加,增加幅度较为平缓,中心区域固相速度值最大可以达到1 m/s。
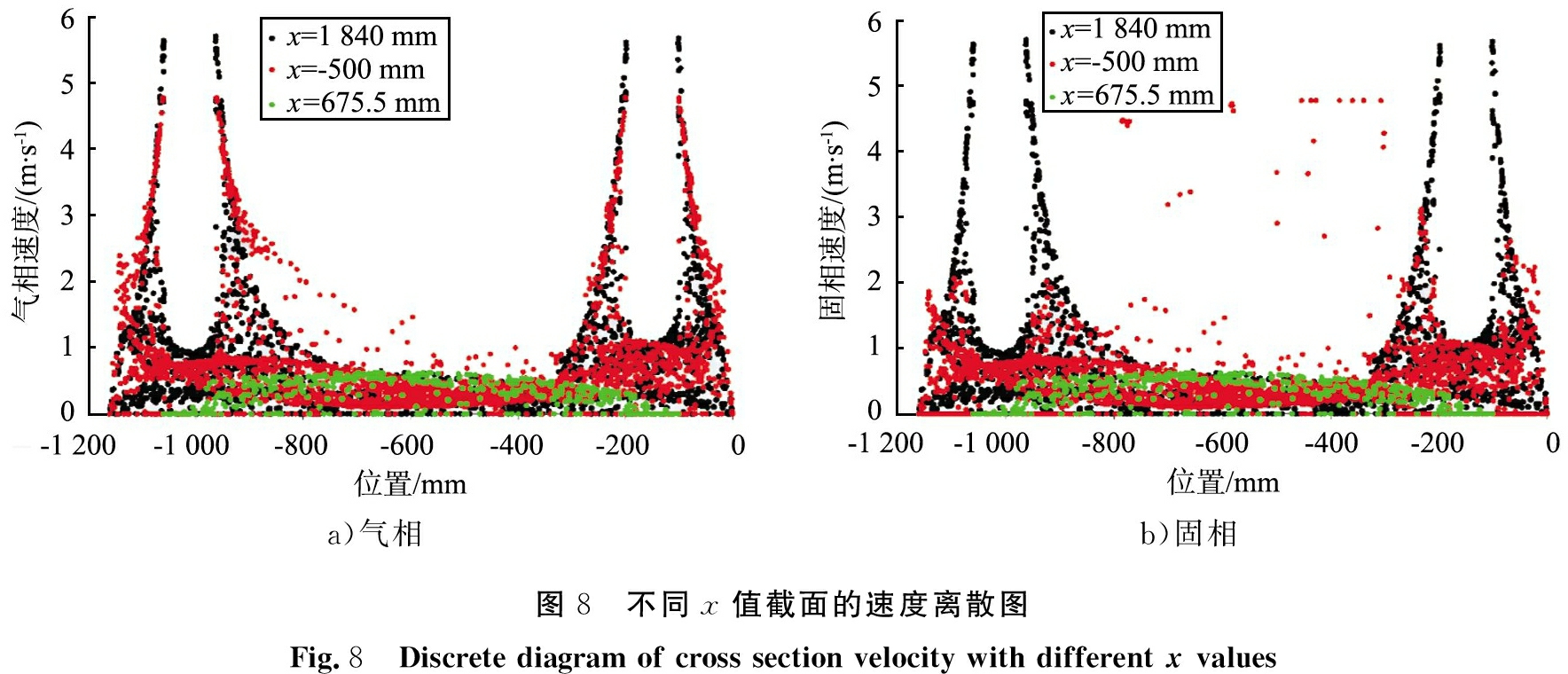
a)气相b)固相图8 不同x值截面的速度离散图Fig.8 Discrete diagram of cross section velocity with different x values
由图8 b)中红色区域可以看出,固相在上、下端进气口速度值大于增材制造加工表面固相速度,箱体中部流域由于高速气体的作用,部分固体颗粒表现出较高的速度;由黑色区域可看出,箱体上、下端出气口,固相速度分布较为均匀,表现出一定的规律性,与气相速度分布基本一致,呈现出固相随气相流动的现象;从绿色区域可以看出,流道内中心区域速度值较大,靠近箱体壁面处速度值较小,从壁面到中心区域逐渐增加,增加幅度较为平缓,中心区域固相速度值最大可以达到1 m/s。
图9为气相不同x值截面的速度云图。由图中可以看出,x=-500 mm截面处,由于内部流道的布置,气相速度主要沿箱体近壁面处分布,且速度衰减较快,流道中间流域速度较小;在进、出气口附近区域,固相小颗粒伴随气相运动,固相颗粒速度小幅度增加。x=-675.5 mm截面处,气相速度较小且变化不大,气、固两相速度在中部区域略大于壁面处。x=1 840 mm截面处,气相在靠近出气口位置速度均匀增加,到达出气口时,速度值达到最大。在此区域固相速度随气相速度增加而增加,固相颗粒随着气体从出气口排出箱体外部。
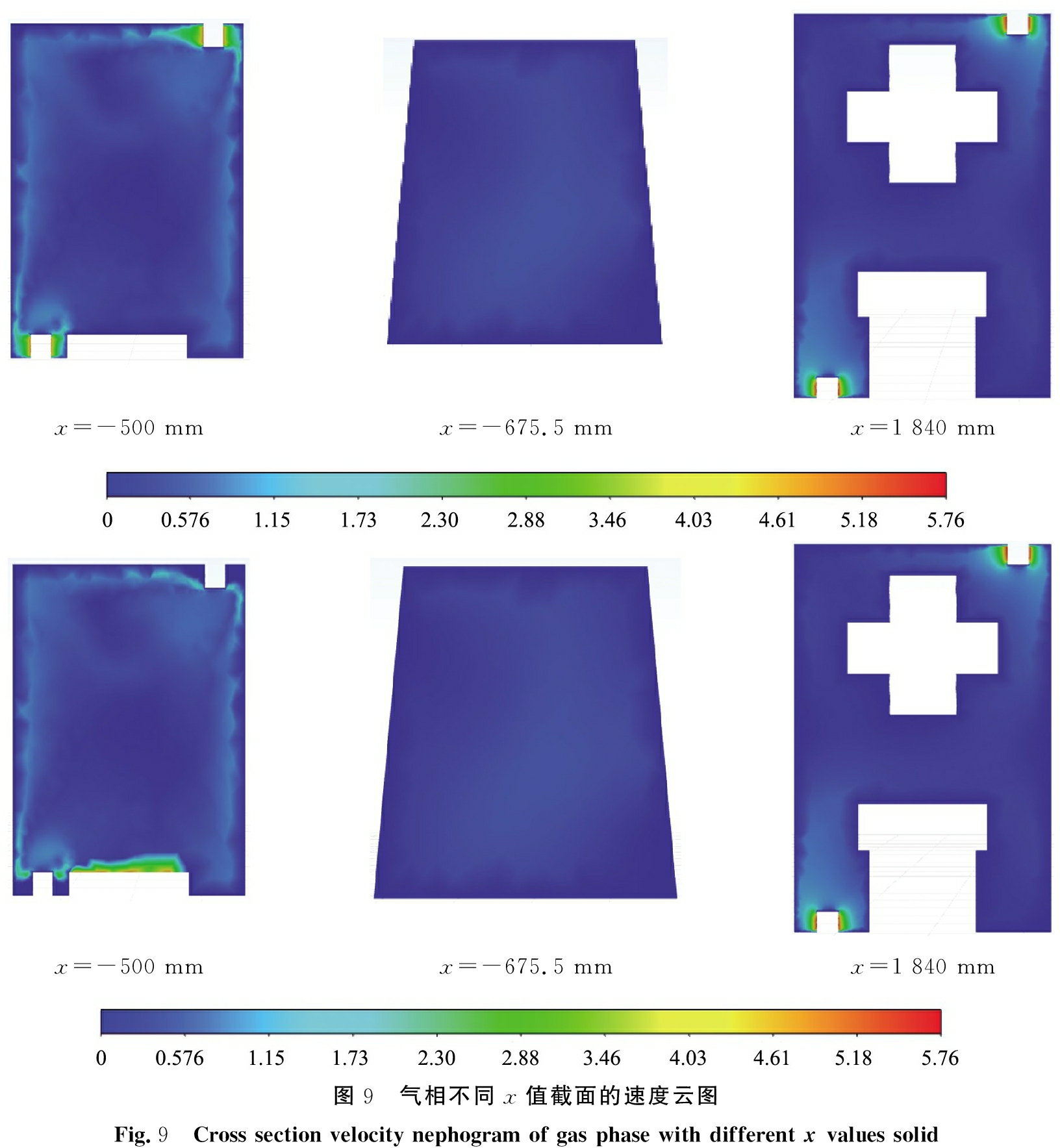
x=-500 mmx=-675.5 mmx=1 840 mmx=-500 mmx=-675.5 mmx=1 840 mm图9 气相不同x值截面的速度云图Fig.9 Cross section velocity nephogram of gas phase with different x values solid
4.2 入口气体速度对固相速度的影响
为了探究进气口气体速度与箱体内气、 固两相流动特性的关系,令进、 出气口尺寸不变,多相流参数不变,通过改变入气口气体速度,分别对气、 固两相流动进行数值模拟,最后对比分析在5种不同入口气体速度下,箱体内过点a(-500, 475.5, -580.5)、 b(1 840, 475.5, -580.5)直线上的固相速度。工况1—5的气体入口速度分别设置为1.592、 2.213、 2.654、 3.715、 4.777 m/s,气体密度均设置为1.2 kg/m3,固体颗粒直径设置为90 nm,固体颗粒密度设置为2 713 kg/m3。
图10为不同进气口速度对直线ab上固相速度的影响,由5种工况下的固相速度对比图可看出,随着进气口速度逐渐增加,固相速度在箱体内速度变化规律类似,具体表现为:x=-500至x=-400 mm区域,固相第1次加速;x=-400至x=-100 mm区域,固相颗粒上升力与空气阻力逐渐达到平衡状态,使固相速度区域平缓,并且有略微的减速现象;x=-100至x=300 mm区域,固相颗粒物第2次加速,速度分别增加至对应最大值;x=300至x=1 500 mm区域,固相颗粒进入流道中间区域,速度值减小。空气阻力与固相颗粒速度成正比,所以进气口气相速度值越大,该速度衰减速度越快;x=1 500至x=1 800 mm区域的内部设备占用流道空间,导致固相颗粒快速衰减至一个较小的值,并且这个区域存在进气口气相速度值越大,速度衰减越快的现象。
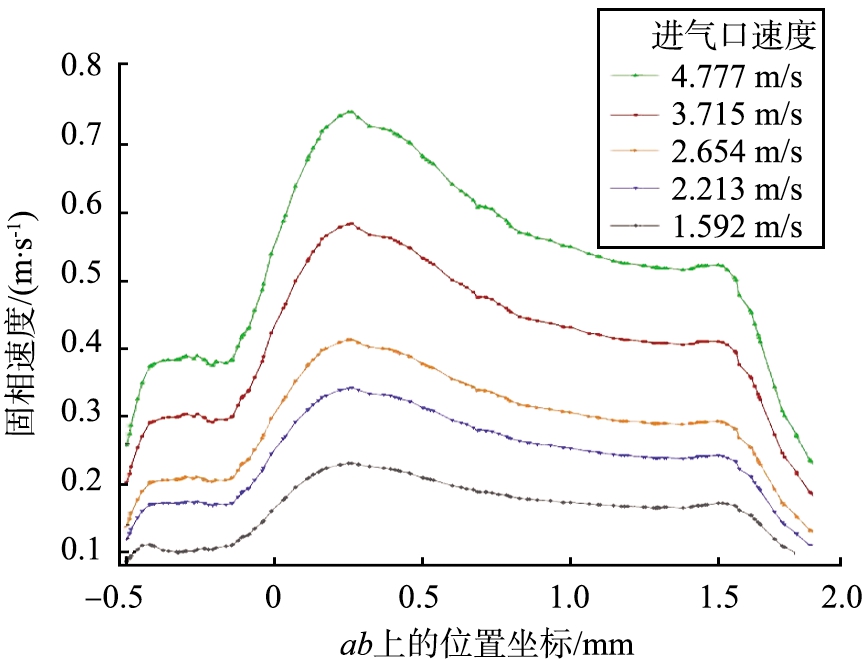
图10 不同进气口速度对直线ab上固相速度的影响
Fig.10 Effect of different inlet velocities on solid phase velocity at straight line ab
4.3 固相颗粒粒径对固相速度的影响
在箱体实际应用过程中,颗粒物会凝并,左侧3D打印区域产生的粉体粒径大小会有差异,故此,为了更加深入地研究箱体内部粉尘的运动规律,达到理想的除尘效果,在保证流场分析参数不变的情况下,改变颗粒物粒径,对箱体内流域中的固相颗粒速度进行分析,工况6—10的固体颗粒直径分别设置为0.09、 0.9、 9、 5、 10 μm,气体入口速度均设置为1.592 m/s,气体密度设置为1.2 kg/m3。
对5种工况进行模拟,得到5种工况下固体颗粒在ab线上的速度对比图,见图11。由图可以看出,当进气口速度v=1.592 m/s恒定时,固体颗粒在线ab上的速度总体上随着固体颗粒粒径的增大而减小。当颗粒直径d小于5 μm时,表现为在x=-500至x=-400 mm区域,固相速度增加; 在x=-400至x=-100 mm区域,由于固相颗粒上升力与空气阻力共同作用,固相速度出现小范围减速; 在x=-100至x=300 mm区域,固相颗粒物速度再次增加; 在x=300至x=1 500 mm区域,速度值缓慢减小; x=1 500 mm至x=1 840 mm区域,由于左侧箱壁的作用,固相速度快速减小。当颗粒直径d≥10 μm时,在x=-500至x=-300 mm区域,固相颗粒物速度值急剧减小; 在x=-300 mm至x=600 mm区域,速度随着高速气流作用增加,固相颗粒物速度快速增加; 在x=600 mm至x=1 500 mm区域,速度值缓慢减小,由于惯性较大,速度减小较为缓慢; x=1 500 mm至x=1 840 mm区域,与颗粒直径d≤5 μm的固体颗粒相同。综上所述,当3D打印时产生的烧结颗粒直径为5 μm以下时,设定的初始空气流量依然可以满足箱体内的除尘要求。
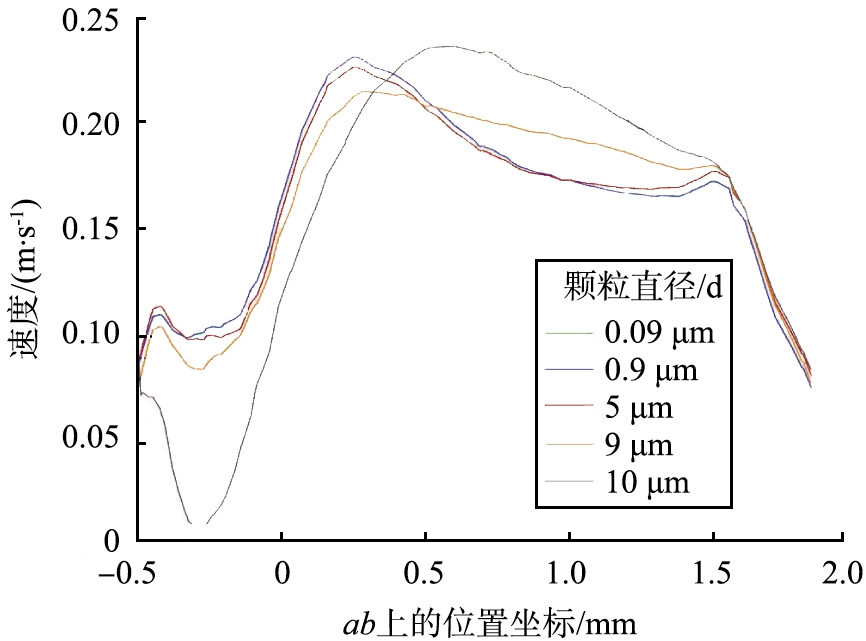
图11 5种工况下固体颗粒在ab线上的速度对比图
Fig.11 Velocity comparison of solid particles on abline under five working conditions
4.4 实验验证
依据已构建的物理模型,进行箱体强度静力学分析,干涉性校验之后,搭建实验平台,对气固两相流动仿真分析出的现象进行工程实际验证,1∶1实物实验平台如图12所示。

a)正视图b)侧视图图12 1∶1实物试验平台Fig.12 1∶1 Physical test platform
H型真空手套箱主要为产品提供低含水量、低含氧量、无尘的的加工环境,通常水、氧的体积分数均小于10-6,进而保证箱体内产品质量以及产品材料的原有属性。当固相颗粒粒径较小时,固相颗粒物对气相有较好的伴随性,所以本实验通过箱体内氧含量的变化,反映理论流体仿真分析结果的可靠性。通过实际测试,手套箱水、氧含量变化趋势图如图13所示。
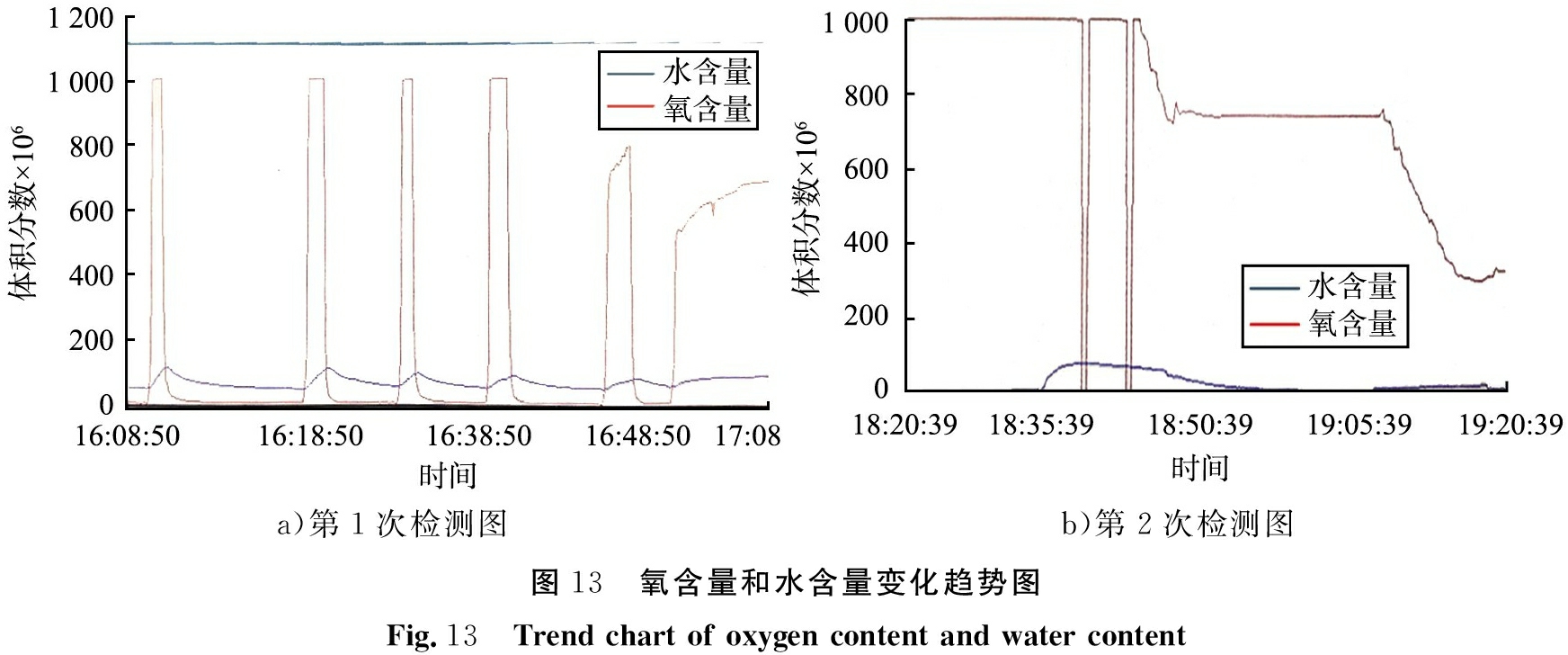
a)第1次检测图b)第2次检测图图13 氧含量和水含量变化趋势图Fig.13 Trend chart of oxygen content and water content
图13中,第1次检测氧含量在1 h内一直处于波动状态,其中前30 min氧含量变化的幅度较大;第2次检测氧含量波动频率较小,在长时间内氧含量不能达到稳定状态。通过2次箱体内部氧含量检测试验,验证箱体数值模拟结果,即当前手套箱系统内部流场流动不均匀、局部空气涡流,使水、氧含量不能在较短时间内达到生产制造的氛围要求。
5 结论
1)对H型特殊结构手套箱内部气固两相速度进行数值模拟,分析在生产过程中不能快速达到加工标准氛围原因,通过关键位置速度云图、速度离散图发现,箱体内速度分布不均匀,局部产生较严重涡流区,进而表现为局部烟雾、或者局部颗粒物沉积。
2)通过对箱体内工况进行分析,发现当固相颗粒物粒径(d=90 nm)不变时,随着进气口速度的增加,固相速度随之增大,固相对气相表现出良好的伴随性。
3)考虑到颗粒物的凝并现象,研究了当进气口速度恒定,依次增加颗粒物粒径,分析固相速度得到,当颗粒粒径小于5 μm,固相对气相表现出较好的伴随性,当颗粒粒径大于等于10 μm时,固相颗粒物对气相的伴随性较差。
4)通过分析不同参数变化对气相、固相速度的影响,阐释H型手套箱内气固两相流动特性,虽然不能直接适用于所有手套箱设备,但对于类似问题研究具有一定参考价值。
[1]马纯. 微重力科学手套箱系统的设计与实现[D]. 北京: 北京邮电大学, 2018.
[2]KUNDERA C, KOZIOR T. Evaluation of the influence of selected parameters of SelectiveLaser Sintering technology on surface topography[J]. Journal of Physics: Conference Series, 2019, 13(10): 1742-6596.
[3]贾仕奎, 李云云, 张向阳, 等. 3D打印成型工艺及PLA材料在打印中的应用最新进展[J]. 应用化工, 2020, 49(12): 3185-3190.
[4]郭婷婷, 王元仕. 全自动封帽机手套箱结构优化设计[J]. 轻工科技, 2019, 35(7): 43-48.
[5]韩力. 双循环圆液力缓速器流场仿真分析与结构优化设计[D]. 武汉: 武汉纺织大学, 2018.
[6]范雪妮, 王海东, 胡毅冰. 基于粗网格CFD模拟方法的室内空气污染物实时寻源反计算研究[J]. 流体机械, 2020, 48(7): 77-83.
[7]胡琼, 张子繁, 王衍, 等. 螺旋槽干气密封仿真计算网格高质高效划分方法[J]. 液压气动与密封, 2020, 40(5): 7-12.
[8]路保平, 徐曾和. 井眼周围可变形储层流-固耦合数学模型[J]. 石油学报, 2006(5): 131-134.
[9]林彦川, 王晓彤. 空调用绝热填料除湿器数学模型的建立与验证[J]. 建筑节能, 2011, 39(5): 24-26.
[10]周兵. 计算流体力学中常用的控制方程离散化方法概述[J]. 科技经济导刊, 2017(21): 114-146.
[11]张显雄, 张志田, 张伟峰, 等. 五种湍流涡粘模型在二维方柱绕流数值模拟中的对比研究[J]. 空气动力学学报,2018, 36(2): 339-349.
[12]MIRZAEI F, KASHI E. Turbulence model selection for heavy gases dispersion modeling in topographically complex area[J]. Journal of Applied Fluid Mechanics, 2019, 12(6): 1745-1755.
[13]GARY B,DAVID F, JEREMY L, DAVID W. Investigation of turbulence model selection on the predicted flow behaviour in an industrial crystalliser—RANS and URANS approaches[J].Chemical Engineering Research and Design, 2018, 34(5): 204-220.
[14]杜世元, 赵耀华. 矩形微槽蒸发薄液膜新边界条件的设定[J]. 工程热物理学报, 2011, 32(7): 1203-1207.