中国科学院工程热物理研究所开发了分级气化工艺[1],该工艺通过将中温循环流化床气化炉和高温下行床气化炉耦合,实现煤气化过程的分级控制,从而有效提高系统气化性能。利用循环流化床反应器的优势,可以有效降低系统对煤种及原料粒径要求; 同时,利用下行床反应器的优势,可以极大提高气化过程的碳转化率。在该工艺中,如果热半焦和热煤气在同一位置进入下行床气化炉,气固燃料未采取有效分离,热煤气将优先与氧化剂发生均相反应,导致热煤气中的可燃组分被大量消耗; 并且,热半焦与气化剂反应比例相应降低,进而影响系统冷煤气效率和碳转化率的提升。为了解决这一问题,中国科学院工程热物理所利用双排料管-下排气式旋风分离器[2],作为循环流化床反应器与下行床反应器之间的二级分离器,以实现热煤气与热半焦的有效分离。气固分离后的热煤气通过排气管直接进入下行床中,避免与气化剂直接接触,而高浓度的热半焦优先与气化剂进行充分混合,发生气化反应。由此,通过加入二级分离器,可以促进热半焦的转化,减少热煤气的燃烧反应。二级分离器对分级气化工艺的性能及整体系统布置具有重要意义。
下排气式旋风分离器是一种新型的旋风分离器,其排气管和排料管均位于旋风分离器的下部[3]。由于分离的热半焦与热煤气都要进入下行床气化炉中,就布置方式而言,下排气式旋风分离器更加适合分级气化工艺,但是,立式分离器在实际应用中,存在工业现场布置困难、建造成本增加等问题[4]。在兼顾分离效率的前提下,从系统布置方便的角度出发,中国科学院工程热物理研究所的研究人员提出了卧式单排料管-下排气式的二级旋风分离器的设计方案,设计中分离器与水平面呈倾斜向上10°,可以充分利用两级气化单元之间的水平段,实现降低成本的目标。
分离效率、压降、漏气率是考察下排气式旋风分离器性能的重要指标,针对这些参数学者进行了相关的试验研究。Gauthier等[5]对下排气式旋风分离器进行了早期试验研究,试验物料采用平均粒径为20 μm的玻璃珠,在入口气速为25 m/s,分离效率最高可达99.9%。Oh等[6]考察了下排气式旋风分离器的分离效率、压降与排气管插入深度之间的关系,结果显示,在排气管插入深度取中间值193 mm时,分离效率达到最大值99.7%;并且在入口气速为5.2~13.0 m/s时,对于不同排气管插入深度,分离器压降均在210 Pa以下。冷碧霞等[7]研究了一种新型扩散式气固分离器,考察了导流锥倾角、底径和位置以及出气管入口高度对性能的影响。整体来看,导流锥倾角越大,其分离效率越好,而压降随角度变化的差异较小。宋博等[8]开展了下排气旋风分离器分离机理的研究,主要考察了结构参数对分离性能的影响。当导排间距为0.5倍筒体直径,导流体长度为0.75倍筒体直径时,分离器综合性能最优,分离效率高于90%,压降低于800 Pa。除此之外,有很多学者采用数值模拟的方式对下排气式旋风分离器进行研究,余战英等[9]进行了分离器流场测定研究以及相应的数值模拟,认为分离器内的切向速度是由靠近导流体的准强制涡和靠近外筒壁的准自由涡组成,这与上排气式旋风分离器的特性基本一致[10]。杨仲卿等[11]通过数值模拟考察了进口形式、导流体和排气管结构参数对分离效率和压降的影响。通过将排气管进口改为渐缩型、 位置下移并采用圆台进口,可以提高分离效率至86.5%,并且,改造后的分离器对细颗粒分离效率明显增强。王磊等[12]通过数值计算,对5种导流体形状进行了研究,入口气速设定为16 m/s,颗粒入口质量浓度设定为28.9 g/m3,计算结果显示对于小于35 μm的颗粒,采用杯型和圆锥型导流体的分离器分离效率较高;对于直径在35~50 μm之间的颗粒,圆锥形导流体对应的分离效果最好,接近96%。
以上研究都是针对立式下排气式旋风分离器,对于卧式下排气分离器的相关研究鲜有报道。结构参数对分级气化工艺所关注的分离效率、 漏气率、 压力分布等指标影响的程度尚不明确。有必要对结构参数对下排气式旋风分离器的影响进行系统的试验研究,为分级气化中试装置设计提供关键数据参考。本文中主要通过设计冷态试验系统,考察关键结构参数,即排气管直径、 排气管与排料管夹角以及导流体长度对分离器性能的影响;同时,将分离器与喷嘴结构相结合,考察在分级气化工艺中,喷嘴内环气体的存在对分离器性能的影响。研究工作可为后续分级气化中试装置二级分离器的设计提供一定的数据参考。
1 试验
1.1 装置及工艺流程
冷态试验工艺流程如图1所示。试验系统主要由供风系统、 试验台本体、 给料系统、 尾部管道、 布袋除尘器和测控系统组成。供风包括分离器入口空气和喷嘴内环空气,试验台由单排料管-下排气式旋风分离器、喷嘴及气化炉构成。其中分离器本体如图2所示,由进气管、 导流体、 旋风筒、 排气管和排料管组成,主要结构参数见表1。为了便于试验时观察流动状况,分离器直筒部分采用亚力克材质;下部锥段部分采用碳钢材质。在分级气化实际应用中,排气管连接下行床气化炉的顶部,排料管通过喷嘴与气化炉炉膛相连通,喷嘴内通道介质为来自分离器的固体物料及携带的空气、 喷嘴内环空气。喷嘴直径为200 mm,炉膛直径为680 mm。
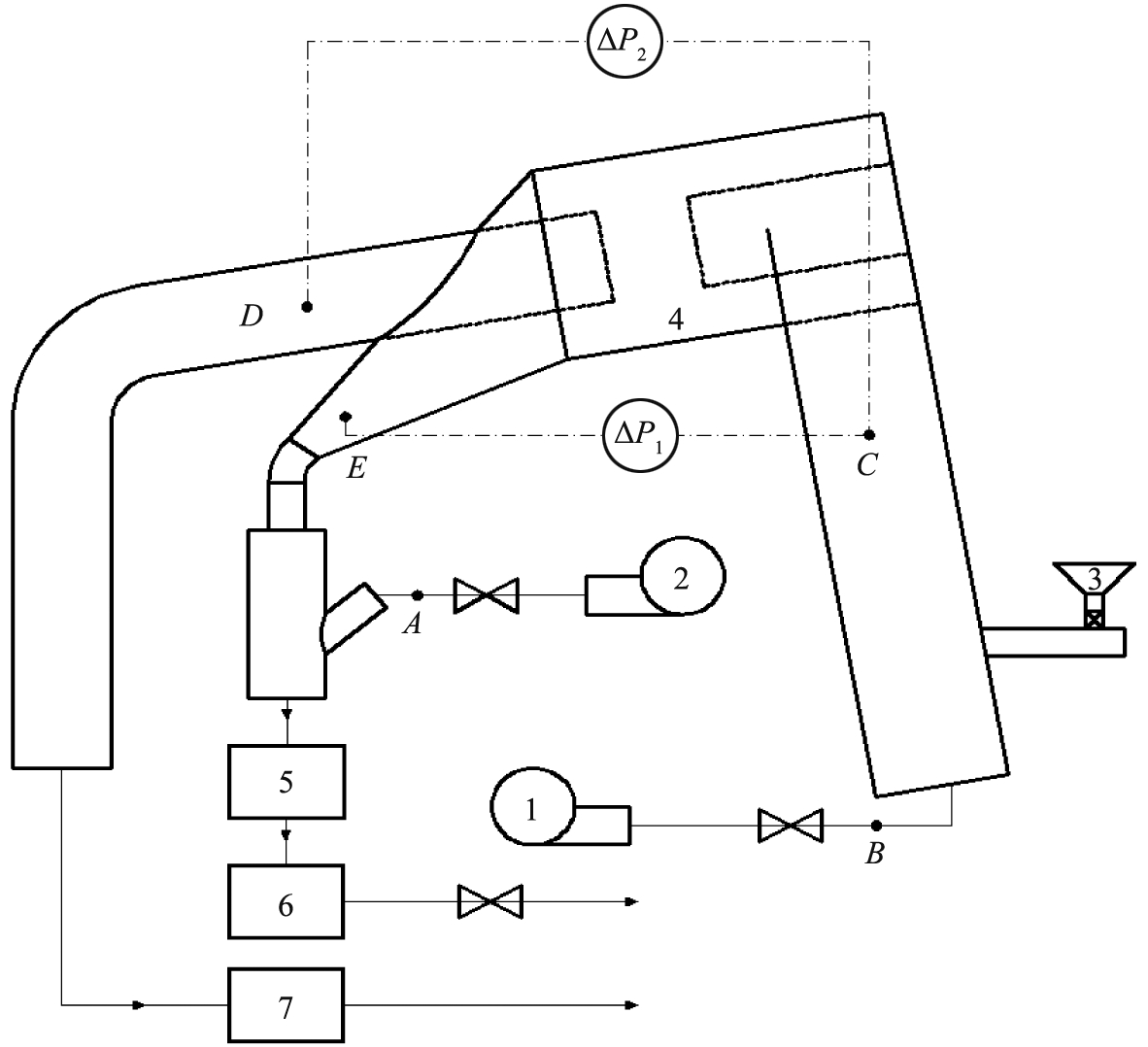
1、 2—罗茨风机; 3—给料装置; 4—卧式单排料管-下排气式旋风分离器; 5—气化炉炉膛; 6、 7—布袋除尘器;A—喷嘴入口气体压力测点;B—分离器入口气体压力测点;C—分离器切向入口气体压力测点;
D—排气管内气体压力测点;E—排料管内气体压力测点。
图1 工艺流程图
Fig.1 Process flow figure
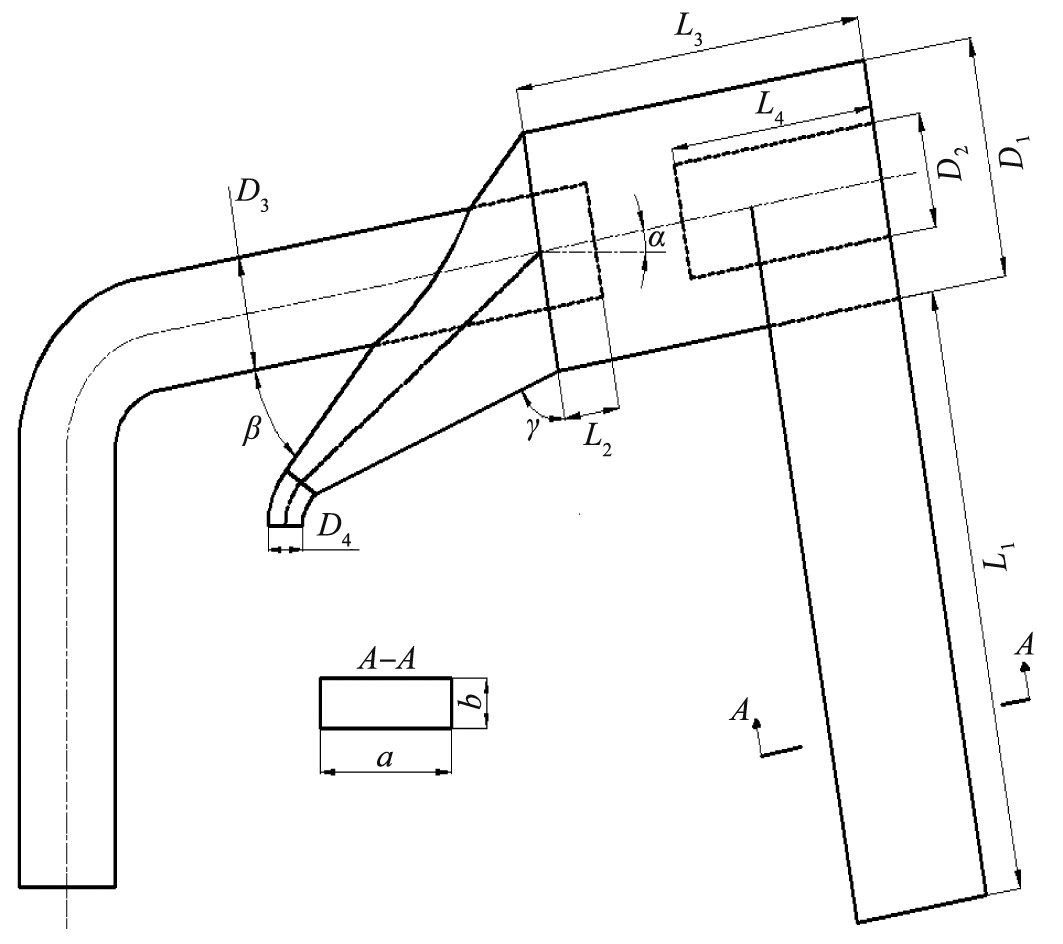
图2 单排料管-下排气式旋风分离器结构简图
Fig.2 Schematic diagram of the horizontal cyclone separator with single discharge pipe
表1 分离器的结构参数
Tab.1 Dimensions of cyclone
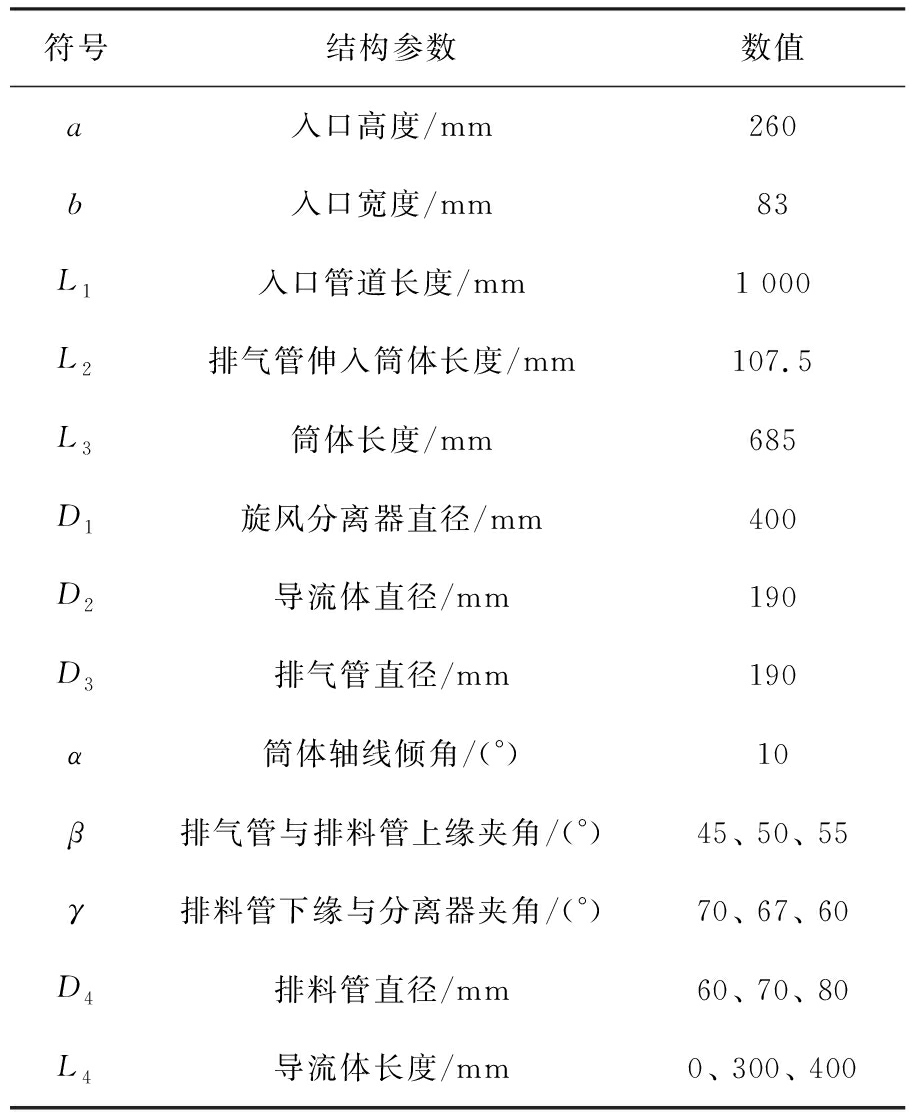
符号结构参数数值a入口高度/mm260b入口宽度/mm83L1入口管道长度/mm1 000L2排气管伸入筒体长度/mm107.5L3筒体长度/mm685D1旋风分离器直径/mm400D2导流体直径/mm190D3排气管直径/mm190α筒体轴线倾角/(°)10β排气管与排料管上缘夹角/(°)45、 50、 55γ排料管下缘与分离器夹角/(°)70、 67、 60D4排料管直径/mm60、 70、 80L4导流体长度/mm0、 300、 400
在试验过程中,分离器入口及喷嘴内环空气流量分别由1号与2号风机变频控制;物料经过螺旋给料机给入系统,并通过变频控制石英砂质量流率。石英砂与空气快速混合后被携带切向进入分离器,空气裹挟着石英砂在导流体和筒体的作用下螺旋斜向下运动。被分离的固体物料经由排料管离开分离器,而后被布袋除尘器捕集;被分离的气体经由排气管进入尾部管道排空。试验系统中共有7个压力测点、 3个流量测点。其分离效率η 和漏气率δ可通过定义式计算得到。
η=Wo/Wi×100%
(1)
δ=(Qo-QA)/Qc×100%
(2)
式中: Wo为布袋除尘器收集的物料质量,kg; Wi为给入分离器的物料质量,kg; Qo为布袋除尘器尾部气体流量,m3/h; QA为喷嘴内环气体流量,m3/h; QC为分离器进口气体流量,m3/h。
表2 运行参数
Tab.2 Operating parameters
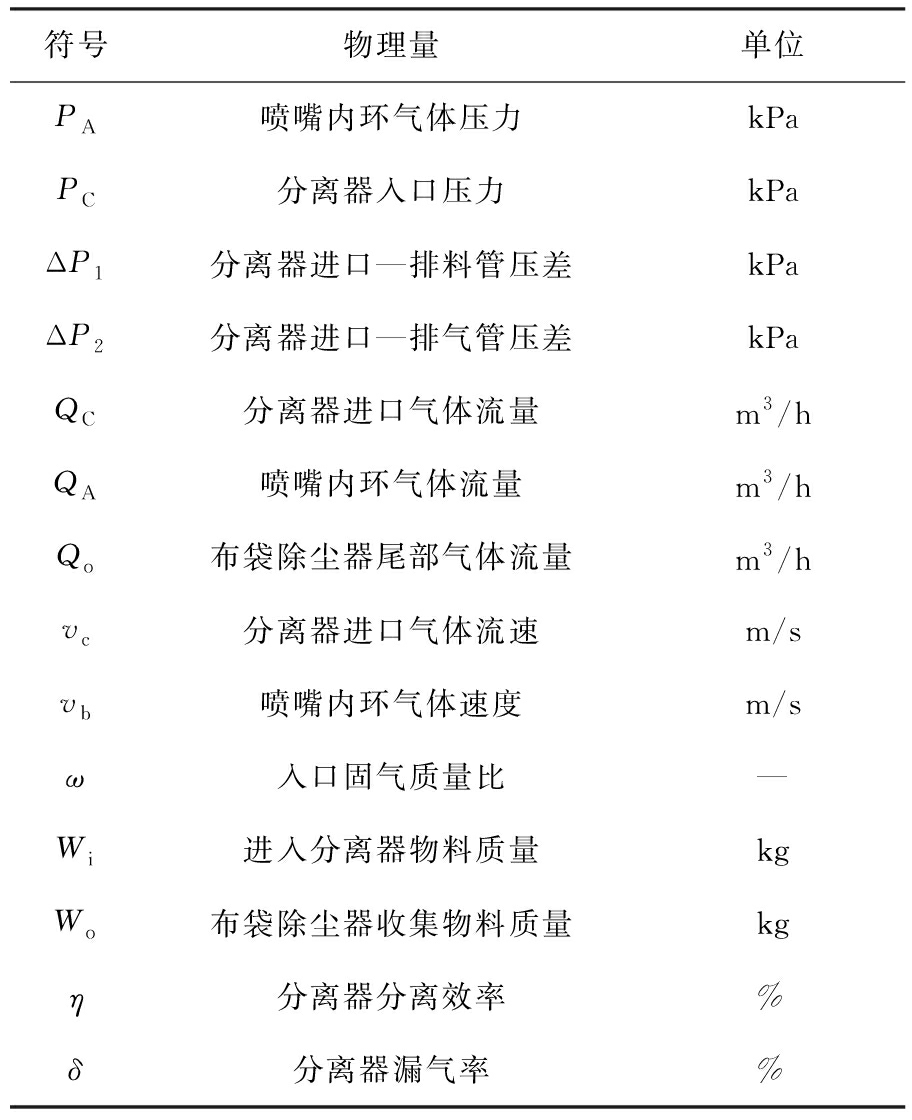
符号物理量单位PA喷嘴内环气体压力kPaPC分离器入口压力kPaΔP1分离器进口—排料管压差kPaΔP2分离器进口—排气管压差kPaQC分离器进口气体流量m3/hQA喷嘴内环气体流量m3/hQo布袋除尘器尾部气体流量m3/hvc分离器进口气体流速m/svb喷嘴内环气体速度m/sω入口固气质量比—Wi进入分离器物料质量kgWo布袋除尘器收集物料质量kgη分离器分离效率%δ分离器漏气率%
1.2 物料
试验物料采用d10、 d50、 d90分别为1.9、 45.8、 104.5 μm的石英砂颗粒。
1.3 方法
本试验中自变量有3组: 排气管直径(60、 70、 80 mm)、 排气管与排料管上缘夹角(45°、 50°、 55°)和导流体长度(400、 300、 0 mm),采用控制变量法进行试验,具体试验结构参数见表3。
表3 试验结构参数
Tab.3 Experiment structures parameters
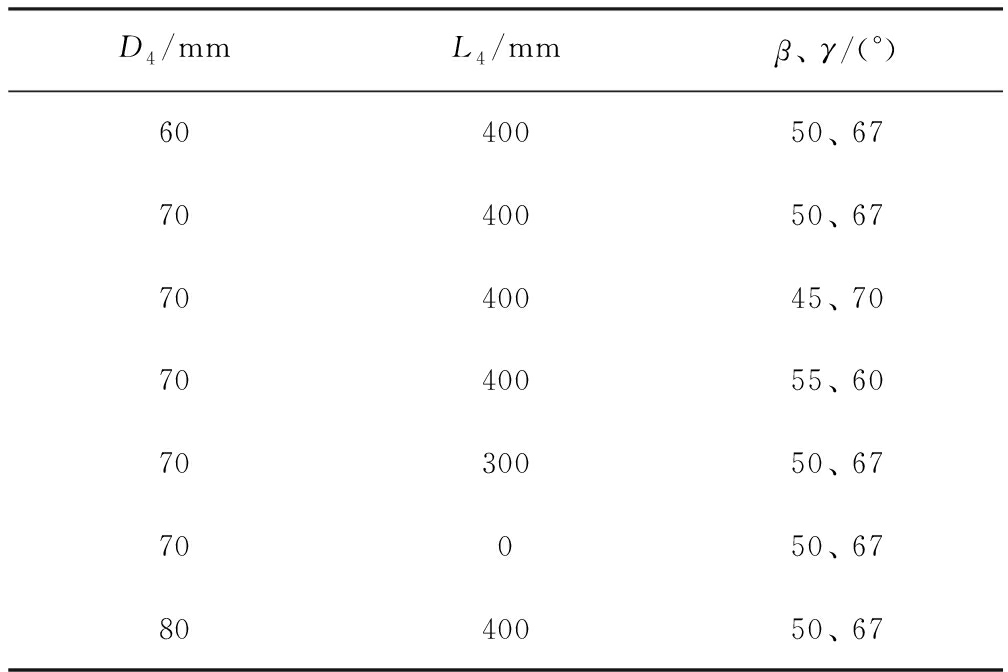
D4/mmL4/mmβ、 γ/(°)6040050、 677040050、 677040045、 707040055、 607030050、 6770050、 678040050、 67
以无内环气流工况为例,首先向料斗中加入石英砂,其质量Wi为100 kg,开启并调节风机1使得分离器入口流量QC约为1 900 m3/h,对应入口气速vc为24.5 m/s,待系统稳定运行后进行记录,作为空床工况数据;记录完毕后,开启给料机调至所需频率,待运行稳定后记录数据,作为负载工况数据;结束后,依次关闭给料机和风机,称量布袋除尘器收集物料质量Wo。对于给入内环气流工况,则需要同步开启并调节风机1及风机2,使得分离器入口流量约为1 900 m3/h,喷嘴内环气体流量QC约为500 m3/h,对应喷嘴内环气速vb为17 m/s,其他操作不变。
2 结果与分析
2.1 排料管直径对分离器性能的影响
排料管直径的变化直接改变固体颗粒和气体在排料管内的流速,并且影响到排料管内部两相流的流动形态,从而改变整个分离器内的流动特性,因此,有必要通过试验探究排料管直径对分离效率η、 漏气率δ以及压降ΔP1、 ΔP2的影响规律。
图3 a)为排料管直径D4对分离效率η的影响。从图可知,当D4在60、 70、 80 mm变动时,η变化范围在94.9%~95.6%之间,变化幅度小于1%,可见D4对η的影响不大;同时,由图3 a)可以发现,加入内环气流对η的影响很小,η的变化范围小于0.6%。
图3 b)为排料管直径D4对漏气率δ的影响。由图可知,在内环气流量近似相同的试验条件下,负载状况下漏气率较空床状况减少5%~10%。这是由于固体物料占据了一部分排料管的流动空间,使得通过排料管进入炉膛内的气体量减少。从整体来看,δ随D4增大而增大,分析认为对于相同的固体质量流率,D4越大,可供气体通过的截面积越大,相应的δ越大。
图3 c)为排料管直径D4对ΔP1的影响。由图可知,旋风分离器的空载阻力损失ΔP1大于相应的负载阻力损失,且负载工况下ΔP1约为空载的60%。这一方面是由于物料的存在,使得气流旋转速度降低,径向压力变化减小,旋流强度减弱[13],降低了分离时的压力耗散;另一方面,颗粒的加入使得湍流脉动中的高频部分减少,低频部分增加,从而使得湍流耗散减少[2],减少了阻力损失。同时,相较于空床条件,在负载条件下D4对ΔP1的影响较小,这是因为颗粒的存在加大了气流的摩擦阻力,使得摩擦导致的阻力损失占比增大,因此在物料存在的情况下ΔP1随排料管径变化幅度较小。
结合图3 b)与图3 c)可以发现,δ随D4的变化规律与ΔP1随D4的变化规律相近。这是由于排料管处压力越高,窜入排料管中的气流越少。对于有内环气流而言,喷嘴入口处压力与2号风机出口压力大体相同,导致排料管内压力较无内环气流高,所以进入排料管内的气流较少,δ较低。对于无内环气流而言,D4从60 mm增大至70 mm时,δ大幅度增加。这是由于随着D4的增大,排料管内可供气体通过的截面增大,从而导致通过排料管内的气流增大,δ增大; 而D4从70 mm增大至80 mm时,由于通过排料管的气量已达到饱和,即便截面增大,气体流量也不会有较大幅度的增大,因此δ变化幅度较小。
图3 d)为排料管直径D4对ΔP2的影响,通过观察图3 d)可以发现,无内环气流条件下的ΔP2较有内环气流时偏大,这同样是由内环气流入口压力较大导致的。在负载情况下,由于ΔP2随D4变化幅度在0.2 kPa以内,变化区间较小,可以认为在负载情况下D4对其影响较小。对于空床条件,排料管直径为70 mm时,ΔP2最大,且对于整体而言,内环气流的存在使得ΔP2增大。这是由于通过给入内环气流,使排料管内压力上升,通过排料管的气量下降,从而通过排气管的气体含量上升,排气管内气速上升,气流动能耗散[14]及动压增加,因而静压减小。
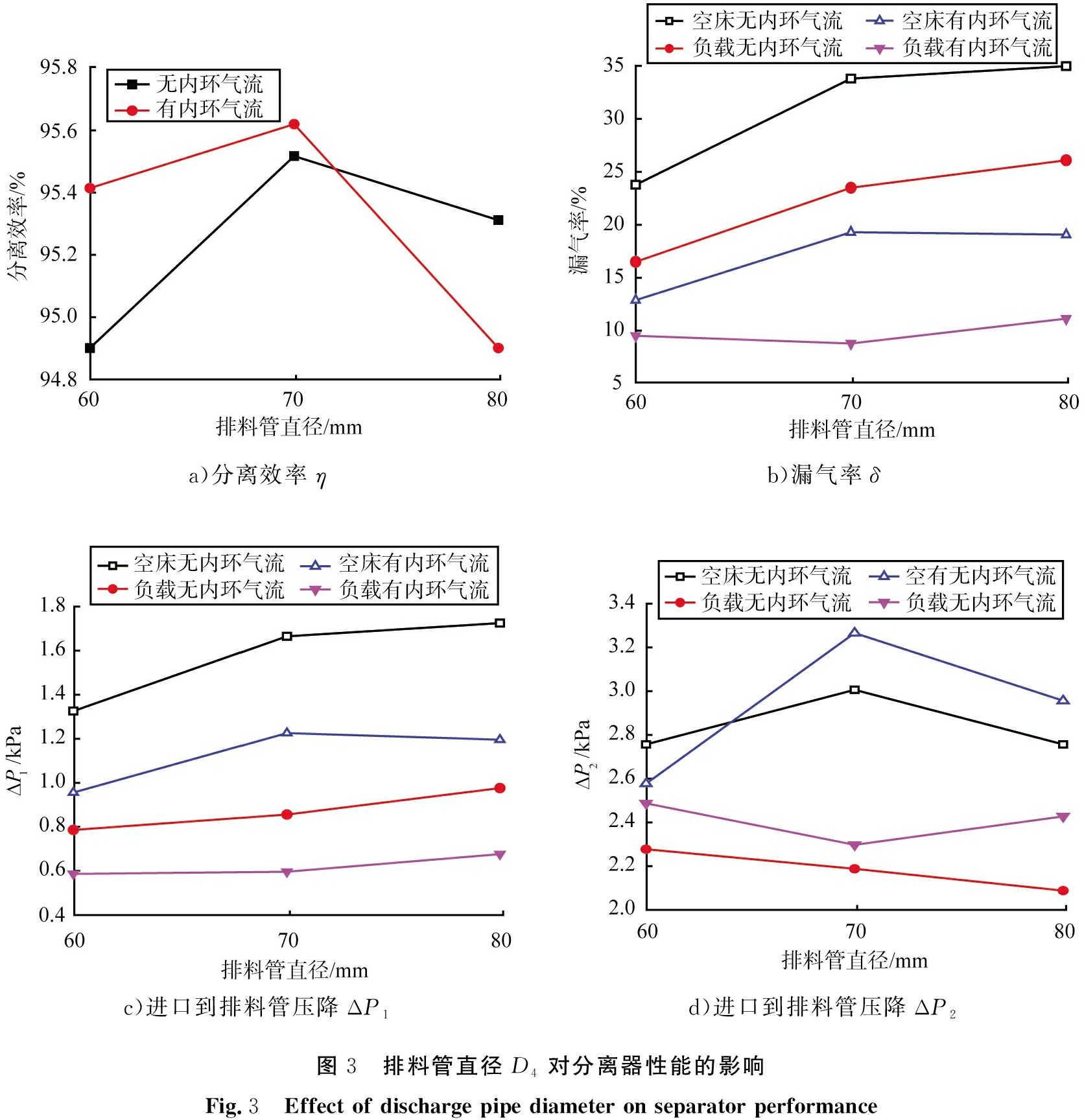
a)分离效率ηb)漏气率δc)进口到排料管压降ΔP1d)进口到排料管压降ΔP2图3 排料管直径D4对分离器性能的影响Fig.3 Effect of discharge pipe diameter on separator performance
2.2 排料管与排气管夹角对分离器性能的影响
通过分析分离器内流场可以发现,旋转气流下行至排料管锥体与上行气流相遇,获得一个向上的动量,同时又有排料管从侧面引出,并且为非对称布置,两者耦合使得涡流中心与几何中心不一致[11],从而导致分离效率η、 漏气率δ以及压降ΔP1、 ΔP2随排料管锥体偏置角度的变化而变化。
图4 a)为夹角β对分离效率η的影响。由图可以看出,在无内环气流条件下,η变化幅度小于1%,可以认为试验选取的β对η无明显影响;在有内环气流存在的条件下,η随着β的增大有较大幅度的增大 。这是因为给入内环气流与夹角变大的耦合作用,使得排料管斜体内的气固混合减弱,减少了气流对颗粒的二次夹带。
图4 b)为夹角β对漏气率δ的影响。由图可知,无内环气流的δ较有内环气流的情况大,这与图3 b)所示的结果一致。同样是由于喷嘴内环气流的给入,提高了喷嘴入口的压力,减少了通过排料管的气体流量,并且差值在空床和负载工况下一致,均在15%上下波动。在负载情况下,β为50°时,δ出现最小值,这与空床情况恰好相反。整体而言,δ随β变化幅度较小。
图4 c)为夹角β对ΔP1的影响。由图可以发现,在负载及空床无内环气流情况下,ΔP1在β为50°时达到最大值。在空床有内环气流条件下,ΔP1随β变化先是近似不变,而后减少。这与图3 c)结果相近,在空床工况下的ΔP1较负载下的偏高,说明颗粒的加入抑制了β的变化对排料管内流场的影响。对于负载有内环气流工况,ΔP1随β变化幅度较小,变化区间为0.47~0.6 kPa,幅度仅为0.13 kPa。
图4 d)为夹角β对ΔP2的影响。在空床工况及负载无内环气流条件下,ΔP2在β为50°时达到最大值3.27 kPa;在负载有内环气流条件下,ΔP2先是近似不变,而后增大。与ΔP1相类似,对于负载有内环气流工况,ΔP2随β变化幅度很小,仅为0.12 kPa。相较于空床状况,负载状况下ΔP2随β变动幅度较小,这是由于颗粒的加入使得更多的气体直接进入排气管内,减少了经由排料管折返入排气管内的气体流量,因而减弱了β的影响。

a)分离效率ηb)漏气率δc)进口到排料管压降ΔP1d)进口到排料管压降ΔP2图4 夹角β对分离器性能的影响Fig.4 Influence of angle on separator performance
2.3 导流体长度对分离器性能的影响
导流体是旋风分离器的主要组成部分之一,其作用主要体现在以下2个方面:一方面引导气流做旋转运动;另一方面与外筒体形成的环形空间影响着气流旋转速度的大小[15]。卧式分离器相对于立式分离器在流动特性上存在差别,因此,考察导流体对于卧式分离器的分离效率η、漏气率δ以及压降ΔP1、 ΔP2的影响具有重要意义。
图5 a)为导流体长度L4对分离效率η的影响。由图可以发现,对于选取的3种结构参数,在无内环气流的情况下,无导流体结构的分离效率最高,且L4为400 mm的结构分离效率最低。这是由于气流随导流体的旋转运动延伸到达分离器底部,形成底部吹起,降低了分离效率[16]。在有内环气流的情况下,分离效率随L4的增加先降低后上升,出现上升的趋势说明了内环气体的给入,使得分离器底部旋流增强,更多的物料被扬起,而导流体阻挡了部分物料随气流进入排气管内,所以η随L4的增加而增加。
图5 b)为导流体长度L4对漏气率δ的影响。大部分情况下,L4为300 mm时漏气率较低。对于负载状况,δ随L4变化较小,这是由于固体物料的存在,使得排料管内可供气体流通的空间变小,由此δ的波动幅度减小。与之前的试验规律相同,相较于无内环气流,在存在内环气流的情况下,漏气率δ有15%~20%的下降,这是因为内环气流的给入,增大了排料管处的压力,减少了通过排料管的气体流量。
图5 c)为导流体长度L4对ΔP1的影响。由图可以观察到,在负载状况下,导流体L4为300 mm时,ΔP1最小,而不是在无导流体时取最小值[12]。这是主要是因为去掉导流体后,流体在分离器内流动轨迹的扰动增加,使得湍流耗散增加;同时固体物料的存在又可以减少旋流强度,减少旋流耗散,两者综合,使得导流体L4为300 mm时ΔP1最小。由图还可以发现,在空床状况下,无导流体时的压降ΔP1达到最小值。这是由于去掉导流体后,气流旋转速度降低,离心力降低,从而压力损失下降,又因为不存在固体物料,气流内部的湍流耗散没有得到有效消除,导致空床与负载的规律不尽相同。
图5 d)为导流体长度L4对ΔP2的影响。在负载状况下,导流体长度L4为300 mm时,ΔP2最小,这与ΔP1的规律一致。由于去掉导流体后,耗散增加以及物料的存在降低了旋流强度,两者的耦合作用使得导流体长度在300 mm时,ΔP2最小。通过观察图5 c)、 5 d)可以发现,去掉导流体后,压降并不一定比存在导流体结构的压降小,这与先前的研究结果[12]相类似,说明选取合适长度的导流体,会使得压降达到最小值。
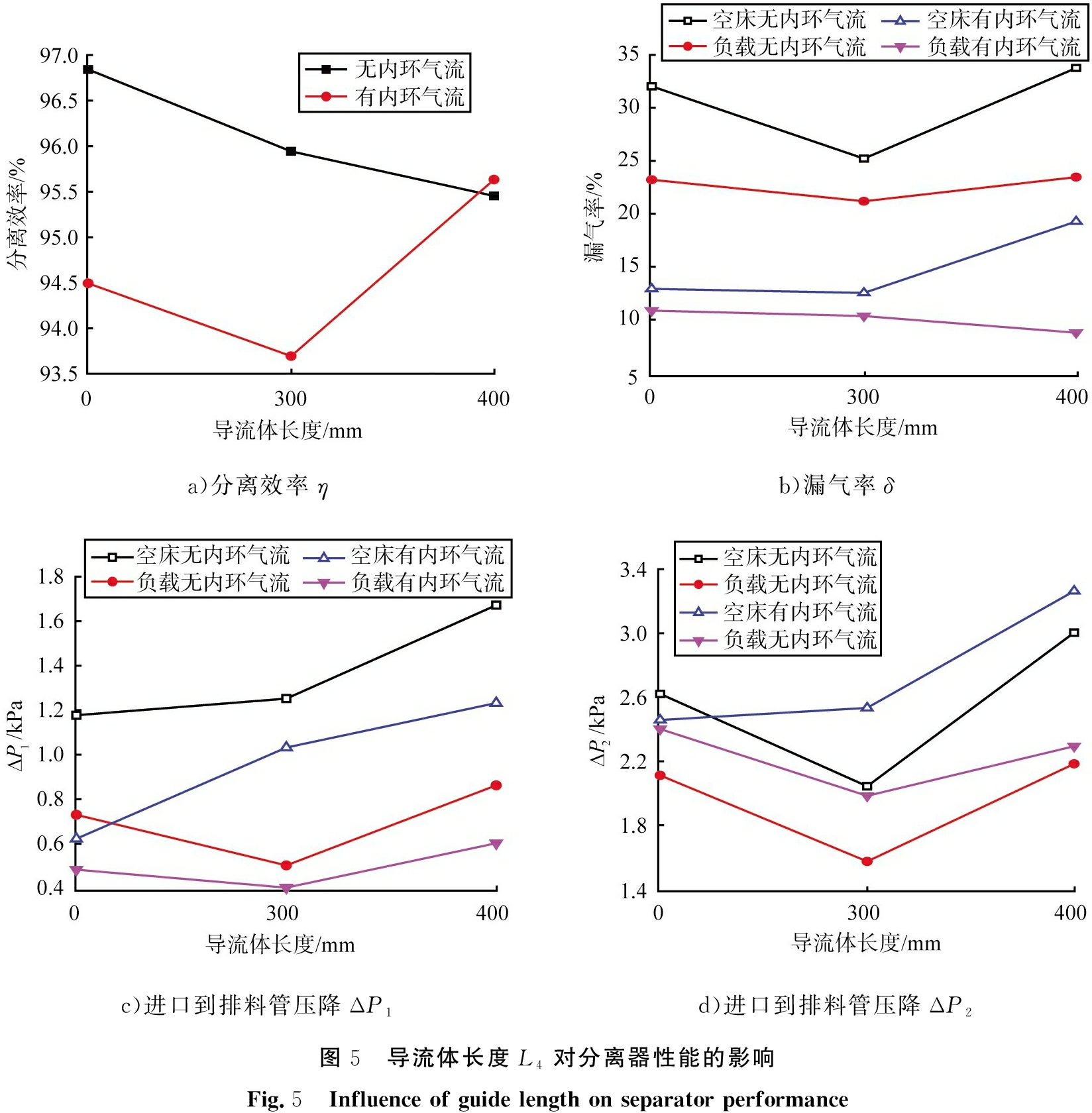
a)分离效率ηb)漏气率δc)进口到排料管压降ΔP1d)进口到排料管压降ΔP2图5 导流体长度L4对分离器性能的影响Fig.5 Influence of guide length on separator performance
3 结论
1)排料管直径D4对分离器性能影响较小。设计工况下,随着D4从60 mm增大至80 mm,η的变化范围为94.9%~95.6%,变化幅度较小;δ与ΔP1随D4增大而增大,ΔP2先下降后上升,且ΔP2的变化幅度大于ΔP1。
2)在设计工况下,β为55°时,η达到最大值; β为45°时,δ出现最小值; β为45°时,由于几何中心与旋流中心的偏置程度较小,ΔP1和ΔP2出现最小值。
3)导流体长度L4的增大会加大流体的内的耗散作用,增大阻力损失。设计工况下,当L4为300 mm时,η较小,ΔP1和ΔP2出现最小值,这是由导流体和物料对流动的耦合作用所导致的; 同时,δ随L4变化幅度在2%左右。
[1]梁晨. 循环流化床预热气化工艺试验研究[D]. 北京: 中国科学院大学, 2019.
[2]孙思敏,郭帅,王小芳,等. 运行参数对双排料管下排气式旋风分离器的性能影响[J]. 中国粉体技术, 2021, 27(2): 54-62.
[3]MUSCHELKNAUTZ U, PATTIS P, REINALTER M, et al. Design criteria of uniflow cyclones for the separation of solid particles from gases[C]//International Conference on Circulating Fluidized Beds & Fluidization Technology-cfb, 2014.
[4]张知翔,王海超,赵钦新,等. 卧式分离器出口结构数值优化分析[J]. 华北电力大学学报(自然科学版), 2010, 37(5): 68-72,97.
[5]GAUTHIER T A, BRIENS C L, BERGOUGNOU M A, et al. Uniflow cyclone efficiency study[J]. Powder Technology, 1990, 62(3): 217-225.
[6]OH J, CHOI S, KIM J, et al. Particle separation with the concept of uniflow cyclone[J]. Powder Technology, 2014, 254: 500-507.
[7]冷碧霞, 陈由旺, 吴学安. 新型扩散式下排气气固分离器实验研究[J]. 热能动力工程, 2002, 17(3): 251-253.
[8]宋博, 金晶, 姜江, 等. 低阻高效抛煤机锅炉飞灰分离装置的实验研究[J]. 洁净煤技术, 2009, 15(5): 98-100, 112.
[9]余战英, 奚金祥, 徐通模, 等. 下排气旋风分离器流场的测定及数值模拟[J]. 动力工程, 2002, 22(5): 1941-1944.
[10]柳绮年, 贾复, 张蝶丽, 等. 旋风分离器三维流场的测定[J]. 力学学报, 1978(3): 182-191.
[11]杨仲卿, 唐强, 张力. 下排气旋风分离器结构优化研究[J]. 环境工程学报, 2011,5(1): 166-170.
[12]王磊, 卢新宇, 崔明. 导流体结构对下排气旋风分离器的影响研究[J]. 山东冶金, 2011, 33(4): 33-35.
[13]郭大江, 朱治平, 刘志成, 等. 窜气对旋风分离器性能影响的实验研究和数值模拟[J]. 锅炉技术, 2010, 41(2): 38-42.
[14]陈建义, 时铭显. 旋风分离器压降计算模型[C]//中国颗粒学会. 中国颗粒学会2006年年会暨海峡两岸颗粒技术研讨会论文集: 2006年卷. 北京: 中国颗粒学会, 2006: 585-92.
[15]王文. 下排气旋风分离器气固两相流动和优化的研究[D]. 重庆: 重庆大学, 2007.
[16]刘振斌, 孙国刚, 时铭显. 顺流式旋风分离器的分离性能研究[J]. 过滤与分离, 2006, 16(2): 16-8, 41.