撞击流的概念最早是在20世纪60年代由苏联科学家Elperin提出的[1]。撞击流技术的基本原理是两股高速流体在一个封闭的空间内沿同轴相向运动产生撞击,较高的相对速度使得相互碰撞的两相之间进行大量渗透,从而为相间传质传热提供了有利的条件。随着相关研究的深入,撞击流技术被广泛应用于气体吸收[2-4]、 纳米粒子制备[5]、 燃烧[6-7]、 混合[8-9]、 干燥[10-11]等场合,具有很高的工程应用价值。
目前对于撞击流的相关研究中,有关单相撞击流的研究是较为全面深入的,有关气固两相撞击流的研究相对较少,且研究模型多为单颗粒模型。Wu等[12]采用高阶有限差分法和拉格朗日粒子追踪研究了层流状态下的同轴对称撞击流粒子的运动行为,结果发现粒子的碰撞对粒子的空间分布、速度及停留时间有重要影响。Liu等[13]研究了非对称撞击流的流体流动特性及颗粒运动特性,发现非对称撞击流的撞击区域向低速流体偏移, 相比于对称撞击流能够提高颗粒在撞击区的停留时间。 Liu等[14]用直接模拟蒙特卡罗方法研究了气固两相撞击流的流动特性和入口气体速度和颗粒旋转的影响,发现气相场中形成了两对反向旋转的涡流,冲击区颗粒浓度随气速增大而减小,颗粒的旋转推动粒子逃离冲击区。Sun等[15]采用大涡模拟与离散相相结合的方法研究了圆柱状对撞燃烧炉内的气固两相湍流行为,发现粒径减小及初始气速增加能够有助于离散涡旋的横向扩展,较大初始气速下的颗粒分布更均匀。实验分析方面,杜敏等[16-17]通过搭建气固两相流试验台,改变碰撞参数条件对气固两相撞击流颗粒撞击特性进行了研究,得出了不同条件下的颗粒运动规律;利用高速摄像机研究了撞击流颗粒旋转特性,得出了碰撞后的颗粒转速随气体速度增大而增大、小粒径颗粒具有更大的平均转速的结论。Li等[18]用两相PIV测量技术对轴对称对置喷流中的湍流修正进行了实验研究,发现颗粒的存在可以明显影响包括宏观湍流统计和介观湍流结构等气相的特征。
根据对文献的回顾,可以发现撞击流反应器的物理属性会对反应器内的气相流场、 固相颗粒的运动及分布产生不同的影响。鉴于此,本研究中探究了在不同物性颗粒气固撞击流作用下的颗粒碰撞及运动扩散规律,利用CFD-DEM方法对2种不同颗粒同轴撞击后的颗粒运动状态进行模拟,对不同气相速度及喷嘴间距下的颗粒运动状态进行分析,对颗粒碰撞的激烈程度的规律进行归纳总结。
1 模型描述
1.1 气相运动方程
气相的连续性方程和动量方程以及不含化学反应和源项的湍流模型表示如下。
质量守恒方程为
(1)
式中: ρ为气相密度, kg/m3; ui表示气相速度在笛卡尔坐标方向上的分量, m/s。
动量守恒方程为
(2)
式中: p为静压,Pa; τij为应力张量(微元表面上黏性应力的分量); ρgi和f分别为重力体积力和外力体积力(如与颗粒相作用产生的力)在该方向的分量及其他源项, N/m3。
湍流流场采用雷诺平均法进行描述,其未知的湍流黏性通过k-ε方程模型来表达。由于气固两相撞击流的流场内一般具有回流,故而使用带旋流修正的Realizable k-ε湍流模型以实现其强烈的回流旋流计算,其中湍动能k和湍动能耗散率ε的输运方程为
(3)
(4)
式中:![]() 式中:Gk为平均速度梯度引起的湍流动能; Gb为由于浮力而产生的湍流动能, YM为可压缩湍流中脉动膨胀对整体耗散率的影响; C1ε和C3ε均为常数; υ为运动黏度, m2/s; σk和σε分别为k和ε的湍流普朗特数; μt表示涡流黏度;S表示平均应变率张量模量。
式中:Gk为平均速度梯度引起的湍流动能; Gb为由于浮力而产生的湍流动能, YM为可压缩湍流中脉动膨胀对整体耗散率的影响; C1ε和C3ε均为常数; υ为运动黏度, m2/s; σk和σε分别为k和ε的湍流普朗特数; μt表示涡流黏度;S表示平均应变率张量模量。
1.2 颗粒运动方程
本文中利用离散元模型模拟质点的运动行为,颗粒相在流场中受到的力主要有颗粒本身的重力,气相对颗粒的曳力、 颗粒与颗粒的接触碰撞力,以及其余的颗粒运动阻力等。岑可法等[19]给出了压力梯度力、虚拟质量力、Staffman升力等对颗粒的影响较小的结论。同时颗粒的旋转对于其运动具有较为明显的影响[14],故本模拟中仅考虑颗粒的重力、 气相对颗粒的曳力、 颗粒间的接触碰撞力、 颗粒旋转引起的Magnus升力。
根据牛顿第二定律,质点在笛卡尔坐标系下的运动方程及转动平衡方程为
(5)
(6)
式中: up为颗粒速度; FD为气相对颗粒产生的曳力, N; FG为颗粒所受的重力, N; FM为由于颗粒旋转引起的马格努斯力, N; Fi为颗粒间的碰撞接触力,N; Ip为颗粒转动惯量,kg·m2; ωp为颗粒角速度, rad/s; cω为旋转阻力系数; Ti为颗粒在流场中的扭矩大小, N·m; Ω为流体与颗粒的相对角速度, rad/s; Ti为颗粒间的接触力产生的扭矩大小, N·m。
1.2.1 曳力方程
气相对颗粒的曳力FD采用Gidaspow模型[20],表达式为
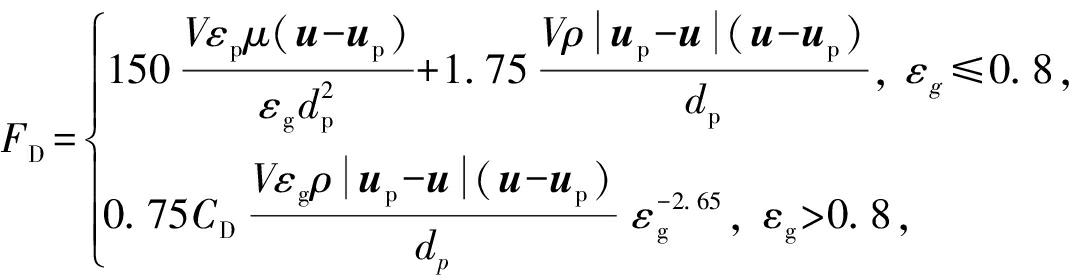
(7)
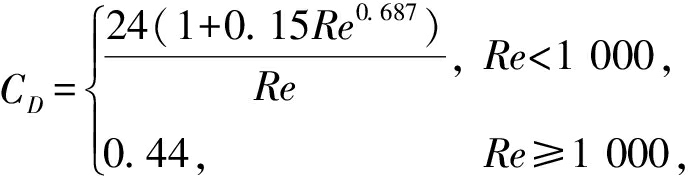
(8)
(9)
式中:V为颗粒体积, m3; u为流体的速度, m/s; 曳力系数CD主要是由相对雷诺数Re决定的; εg和εp分别为气相和颗粒相的体积分数; μ为气相的黏度, N·s/m2; dp为颗粒的直径,m。
1.2.2 Magnus力方程
Magnus力FM的表达式为
(10)
式中: dp为颗粒直径, m; V为颗粒对流体的相对速度, m/s; CRL为转动升力系数是自旋参数的函数[21],定义为
(11)
式中T为自旋参数,定义为![]()
1.2.3 颗粒碰撞力方程
颗粒在运动过程碰到其他颗粒或壁面时会产生接触碰撞力,颗粒的运动状态会因此而改变,故而需要考虑到接触力的影响。颗粒与颗粒、壁面之间的相互作用力采用Hertz-Mindlin接触理论进行描述[22-23]。
图1表示任意2个颗粒接触碰撞的受力情况,颗粒之间的受力有切向分量和法向分量,对于任意的粒子i,其与空间内j个粒子的接触力Fi应为

图1 颗粒碰撞受力示意图
Fig.1 Schematic diagram of particle collision force
![]()
(12)
其中,法向力Fnij表达式为:
(13)
式中: νi和νj为泊松比; Ei和Ej分别为相接触的两颗粒的杨氏模量, Pa; Eij为当量杨氏模量, Pa; δnij是法向重叠量, m。
其中,法向阻尼力![]() 表达式为:
表达式为:
(14)
式中: e为恢复系数; νren为相对速度的法向分量, m/s; mij为等效质量, kg; Snij为法向刚度, N/m。
其中,切向力Ftij表达式为:
Ftij=-Stijδtij,
(15)
式中: Stij为切向刚度, N/m; δtij为切向重叠量, m。
其中,切向阻尼力![]() 表达式为:
表达式为:
(16)
式中:vret为相对速度的切向分量,m/s。
在模拟计算过程中,滚动摩擦则是通过在接触表面施加一个力矩来进行考虑。
(17)
式中: μr是滚动摩擦系数; ωi是物体在接触点处单位角速度矢量,rad/s。
另外,颗粒与壁面的碰撞则是将其中一个颗粒半径等效为无穷大并进行相应的计算处理。
1.3 物理模型及模拟条件
本文中采用了以下假设:固相颗粒为均质球体,并在模拟中不产生任何变化,为计算方便,将颗粒直径统一设为0.1 mm,气相为空气,撞击流反应区域包括2个沿同一轴线对称放置的喷嘴及一个壁面隔绝、单向出口的反应容腔,模拟条件及气相性质由表1给出。
表1 撞击流反应器的几何参数及气相性质
Tab.1 Properties of gas phase and geometric parameters of impinging stream reactor

参数单位数值气体密度kg·m-31.225黏度kg·m-1·s-11.789 4×10-5喷嘴直径mm25喷嘴间距mm25,50,75,100,125,150,175,200
撞击流装置的几何尺寸如图2所示,其中喷嘴的对称面设为YZ坐标平面,喷嘴轴线设为X坐标轴,气相出口轴线为Y坐标轴,尺寸对应参数列在表1中。采用ICEM进行非结构网格划分,并对尖锐处的网格进行加密处理,得到网格节点数为389 061,网格单元数为2 194 019,网格平均质量为0.88,不同喷嘴间距条件下的物理模型网格均按照上述方法获得,得到网格质量均大于0.85。
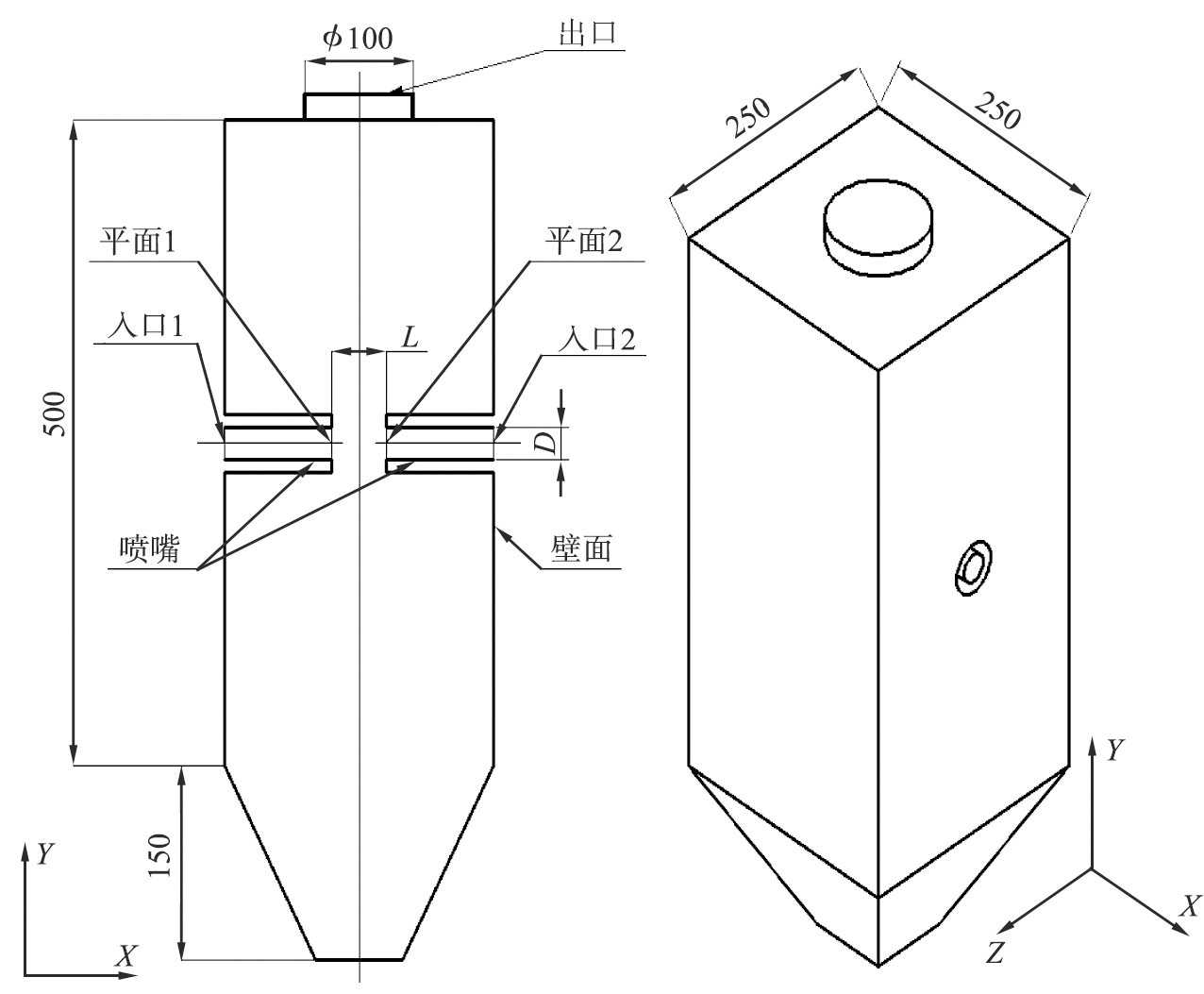
图2 撞击流反应器几何尺寸图
Fig.2 Geometric model of impinging stream reactor
颗粒相的参数通过参考相关文献资料选取能够直接得到的参数值并计算相关的参数,本模拟中所用到的相关的颗粒物性参数及颗粒间接触参数由表2和表3给出。
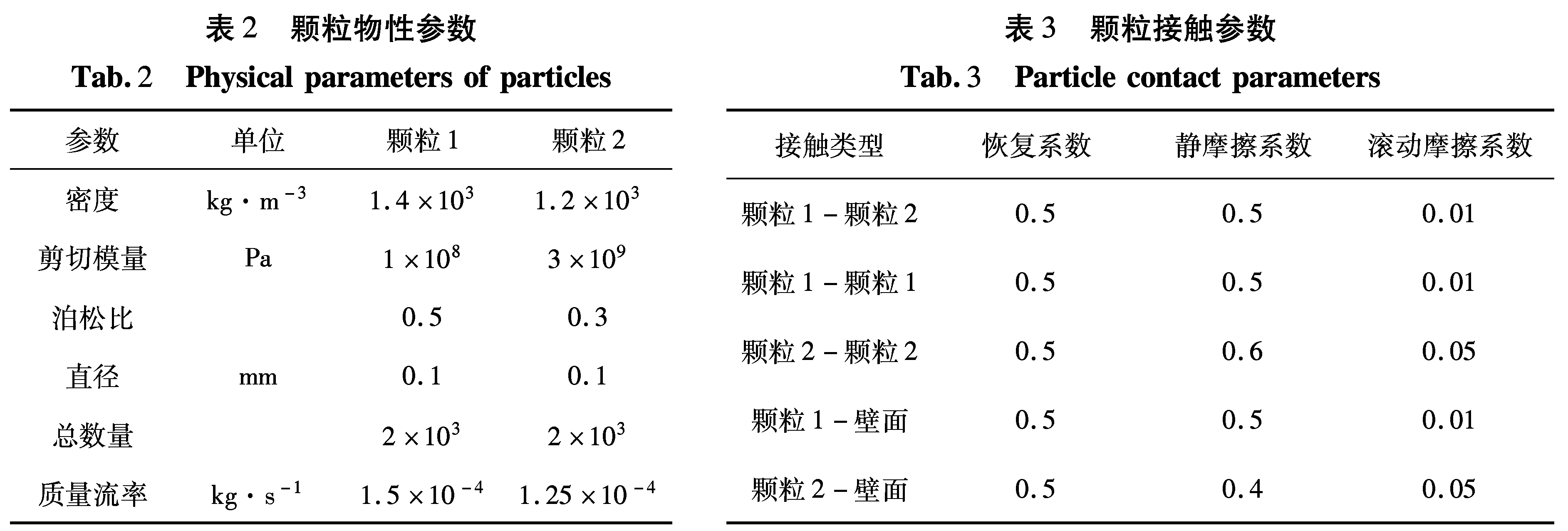
表2 颗粒物性参数Tab.2 Physical parameters of particles参数单位颗粒1颗粒2密度kg·m-31.4×1031.2×103剪切模量Pa1×1083×109泊松比0.50.3直径mm0.10.1总数量2×1032×103质量流率kg·s-11.5×10-41.25×10-4表3 颗粒接触参数Tab.3 Particle contact parameters接触类型恢复系数静摩擦系数滚动摩擦系数颗粒1-颗粒20.50.50.01颗粒1-颗粒10.50.50.01颗粒2-颗粒20.50.60.05颗粒1-壁面0.50.50.01颗粒2-壁面0.50.40.05
在DEM模拟计算中,2种不同的颗粒相分别在喷嘴出口截面处平面1和平面2位置随机生成,颗粒的初始速度按气相输入速度的0.7倍进行设置[18],颗粒相的时间步长按DEM软件计算,取整设为1×10-6 s,仿真总时间设置为0.5 s。
在CFD计算中,采用压力求解器进行瞬态模拟,气相由入口1和入口2中输入,两侧输入速度保持为一致,入口处气相采用速度入口,出口处采用自由流出,壁面设置为速度无滑移,采用有限体积法对气相进行求解,压力-速度耦合采用simple算法实现。综合考虑仿真可靠性及仿真时长,将时间步长设置为DEM时间步长的100倍[24],取为1×10-4 s。颗粒相生成时间设为气相计算开始后的0.1 s。具体的模拟工况条件如表4所示。
表4 模拟工况条件
Tab.4 Simulation conditions
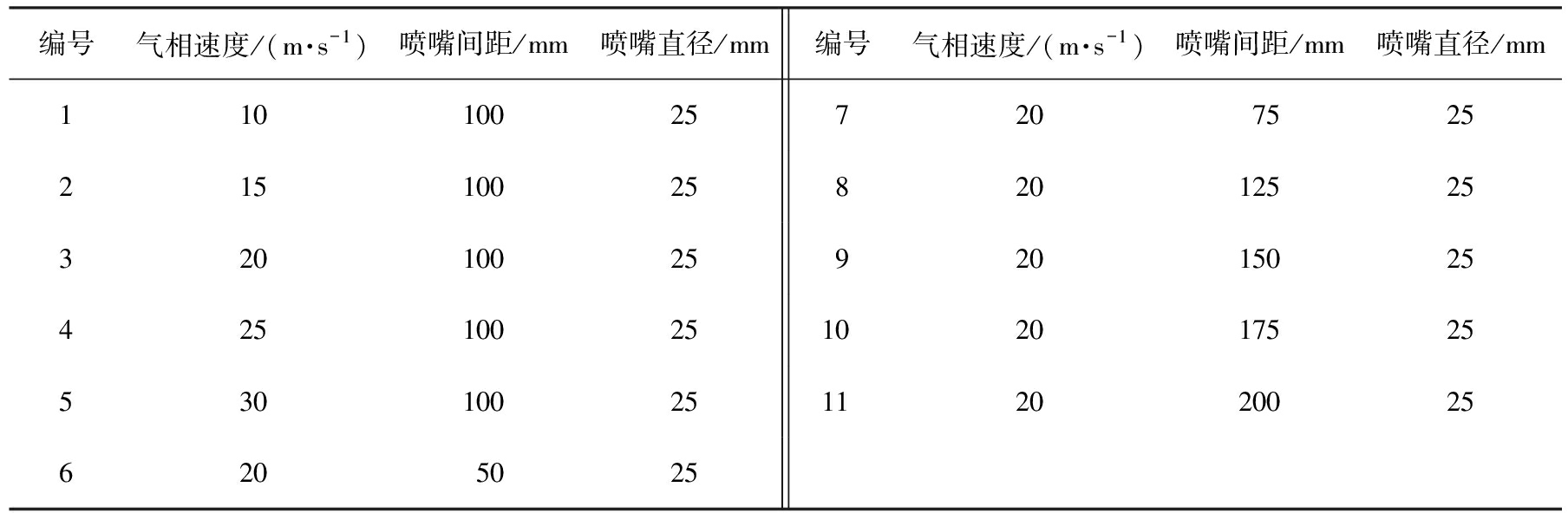
编号气相速度/(m·s-1)喷嘴间距/mm喷嘴直径/mm编号气相速度/(m·s-1)喷嘴间距/mm喷嘴直径/mm110100257207525215100258201252532010025920150254251002510 20175255301002511 20200256205025
2 结果与讨论
为了探究撞击流反应器内不同物性颗粒的运动扩散状态,本研究中首先明晰颗粒在气相流场的运动状况,得出颗粒间碰撞的规律,再对颗粒在撞击区的碰撞情况进行分析,最后通过改变不同模拟条件来探究喷嘴间距及气相速度变化对颗粒碰撞的影响特性,得出较为合适的撞击流反应条件参数。
2.1 气相流场及颗粒运动状态的分析
图3为撞击流反应器内气相速度矢量图。如图所示,两股气流在反应器的中心区域产生了撞击,中心区域的气相速度明显大于其他区域,将这一块区域称为撞击区,在此区域内由于高速气体相向运动产生了巨大的冲击,使撞击区中心沿喷嘴轴向的气速降到接近0,气体速度方向由沿喷嘴轴向变为沿喷嘴径向。如图3 c)所示,由于壁面的阻挡,气相在XZ平面内产生了沿喷嘴轴线对称分布的涡旋;图3 a)中XY平面内在喷嘴下方形成了2个涡旋,喷嘴上方气相沿壁面向出口运动,未发现有明显的涡旋现象。撞击区及出口处的气相速度较大,靠近壁面的气相速度较小,同时由撞击区向其他区域气相速度衰减较快。由图3 c)可以发现,气相速度矢量并非沿YZ平面对称分布,其原因是相互碰撞的两种颗粒物性参数不同,其动量亦不相同,使得撞击面沿颗粒密度更小的一方产生了偏移。
图4所示是气相速度为20 m/s, 喷嘴间距为100 mm时的颗粒运动过程, 总共选取了颗粒自0.1 s释放后6个时刻的撞击流反应器内部状态。 颗粒于0.11 s完全释放, 在2个喷嘴之间的撞击区(如图3所示)经过相互的渗透扩散及碰撞, 逃离撞击区并向反应器壁面运动。 如图4 e)所示, 颗粒在0.3 s左右已完全离开撞击区, 到0.5 s时颗粒已接近壁面。 在整个过程中, 2种颗粒有明显的相互渗透分布现象, 但总体上2种颗粒各分布于其释放喷嘴一侧, 这是由于撞击区颗粒碰撞以及气相涡旋带动的影响, 从而使不同颗粒在空间上产生了分散分布的效果。 颗粒经过相互碰撞后并未在撞击区产生聚集, 而是以撞击区为中心向四周发散, 这与杜敏等[16]通过实验得到的颗粒撞击后的运动规律是相符合的。

a)XY平面b)YZ平面c)XZ平面图3 撞击流反应器内气相速度矢量图Fig.3 Vector diagram of gas phase velocity in impinging stream reactor
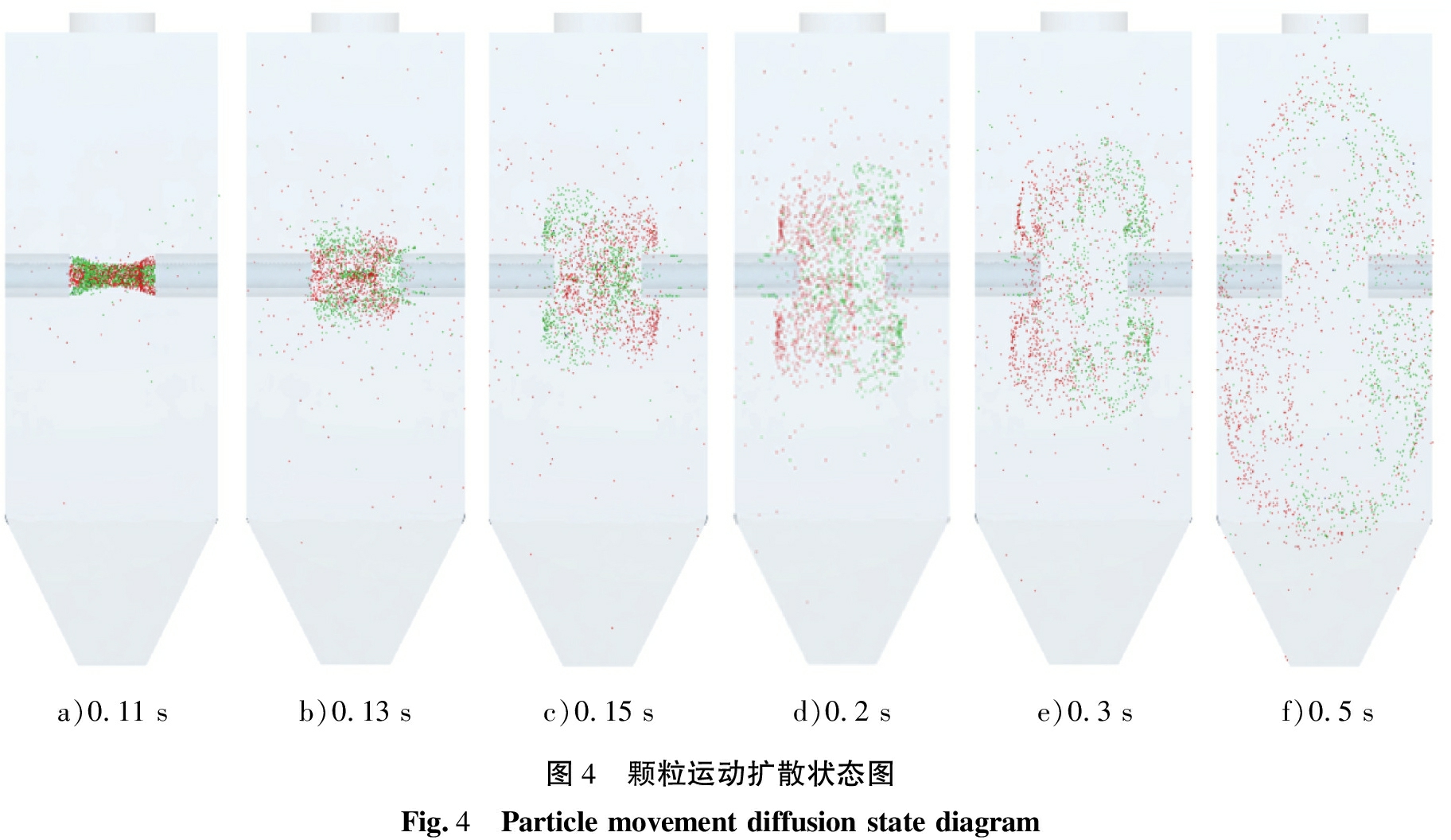
a)0.11 sb)0.13 sc)0.15 sd)0.2 se)0.3 sf)0.5 s图4 颗粒运动扩散状态图Fig.4 Particle movement diffusion state diagram
图5所示为气相速度为20 m/s、 喷嘴间距为100 mm时得到的颗粒碰撞次数随时间变化的曲线。由图可知,颗粒由0.1 s时释放,经过0.01 s颗粒释放完毕,短暂的相向运动后颗粒之间进行了相互碰撞。颗粒间的碰撞主要都集中在0.1~0.15 s的时间段内,在此时间段内颗粒发生了激烈的碰撞,包括2种颗粒之间的碰撞以及同种颗粒之间的碰撞。在0.15 s之后颗粒向壁面运动,则可以说明颗粒之间的传热与传质仅发生在2种颗粒相向运动并碰撞的过程,颗粒向壁面的扩散过程中相互之间的运动未受到颗粒碰撞的干扰。结合图4所示的颗粒运动过程,碰撞过后的颗粒随着气相运动向反应器内壁扩散,由于颗粒本身粒径较小,使得颗粒在散开的过程中不再具有激烈碰撞的现象。
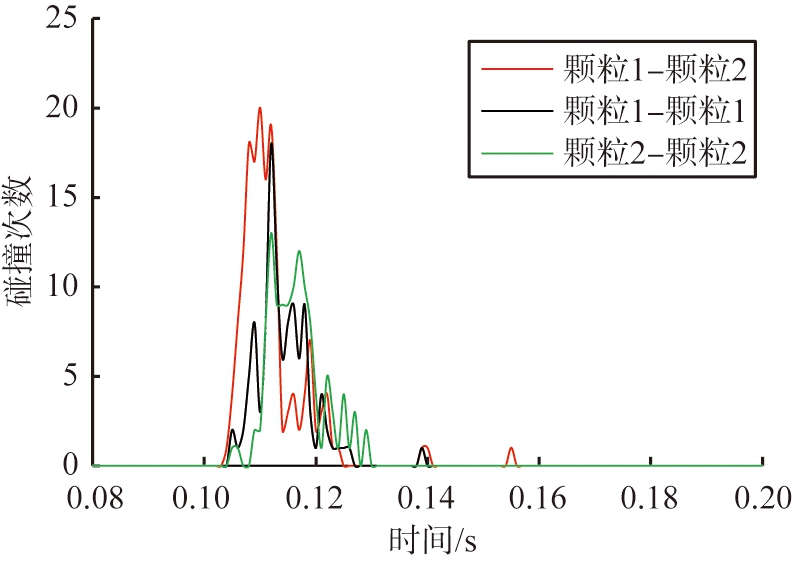
图5 颗粒碰撞次数随时间的变化曲线
Fig.5 Curve of particle collision number over time
2.2 喷嘴间距及气相速度对颗粒运动与碰撞的影响分析
图6所示为不同喷嘴间距下统计得到的2种颗粒之间的碰撞次数的变化趋势,喷嘴间距和喷嘴直径的比值由2增加到8。据图可知,喷嘴间距由50 mm增大到100 mm时,2种颗粒之间的碰撞次数逐渐增加;在喷嘴间距为100 mm时达到最大,此时喷嘴间距和喷嘴直径比为4;喷嘴间距由100 mm增大到200 mm的过程中,2种颗粒之间的碰撞次数逐渐减少。其原因是喷嘴间距较大的情况下颗粒分布比较分散,撞击区空间也更大,故碰撞的概率就比较小,在喷嘴间距较小的情况下颗粒又过于密集导致同种颗粒之间阻碍了进一步的碰撞。不同颗粒的传质传热通过颗粒之间的接触来进行,不同颗粒之间的碰撞有助于撞击混合的效果,故在模拟工况条件下,喷嘴间距与直径比设为4从理论上而言更有助于颗粒之间的混合。
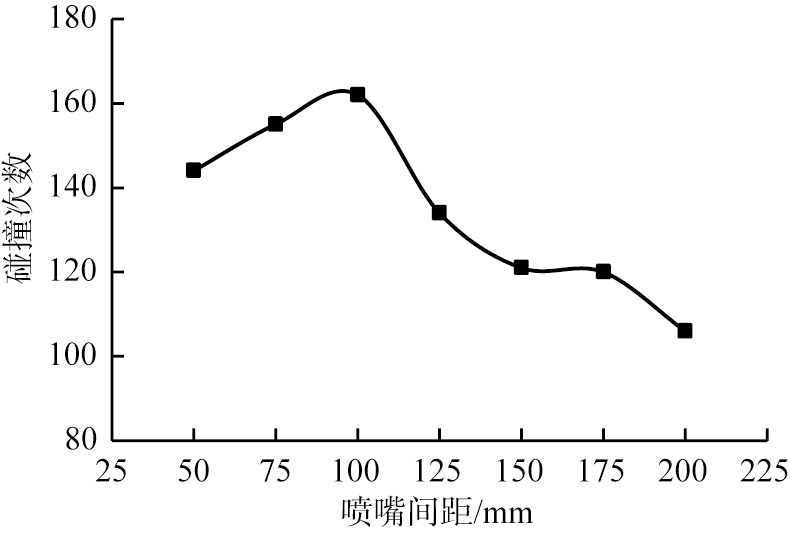
图6 撞击区颗粒碰撞次数随喷嘴间距的变化曲线
Fig.6 Variation curve of number of particle collisions with distance between nozzles
2.3 气流速度对颗粒碰撞的影响分析
图7所示是喷嘴直径为25 mm、 喷嘴间距100 mm条件下不同入口气速得到的颗粒1与颗粒2碰撞次数的变化曲线图。由图可以发现,气速由10 m/s提高到30 m/s的过程中,2种颗粒之间的碰撞次数略有起伏,但整体呈现下降的趋势。由于碰撞的随机性以及得到的各气速下的碰撞次数的差别较小,故可以认为在当前模拟条件下的颗粒碰撞次数与气速变化的关系不大。
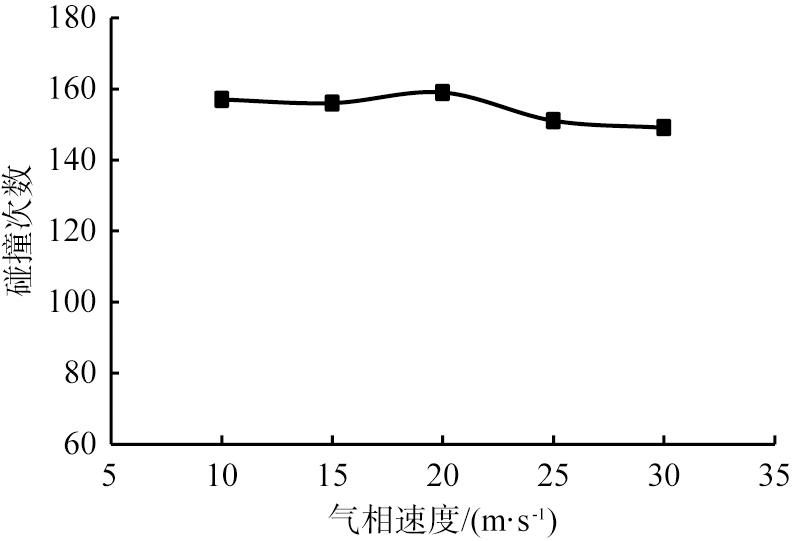
图7 撞击区颗粒碰撞次数随入口气相速度的变化曲线
Fig.7 Variation curve of number of particle
collisions with gas velocity
3 结 论
1)气固两相撞击流颗粒间的碰撞主要发生在颗粒释放后进入撞击区后的短时间段内,颗粒离开撞击区向壁面运动的过程中几乎没有相互之间的碰撞。
2)喷嘴间距逐渐增大过程中,2种颗粒间的碰撞次数先增大后减小,在喷嘴间距与喷嘴直径比值为4的时候达到最大。
3)在撞击流过程中,气相速度对2种颗粒相互碰撞次数影响不大。
[1]ELPERIN, IT. Heat and mass transfer in opposing currents[J]. Journal of Engineering Physics, 1961,6(6): 62-68.
[2]WU Y, LI Q, LI F. Desulfurization in the gas-continuous impinging stream gas-liquid reactor[J]. Chemical Engineering Science, 2007, 62(6): 1814-1824.
[3]LI Y, LI F, QI H. Numerical and experimental investigation of the effects of impinging streams to enhance Ca-based sorbent capture of SO2[J]. Chemical Engineering Journal, 2012, 204/205/206(1): 188-197.
[4]WU H, PAN D, XIONG G, et al. The abatement of fine particles from desulfurized flue gas by heterogeneous vapor condensation coupling two impinging streams[J]. Chemical Engineering & Processing, 2016, 108(1): 174-180.
[5]ZHOU C, WANG Y, DU L, et al. Preparation of highly dispersed SiO2 nanoparticles using continuous gas-based impinging streams[J]. Chemical Engineering Journal, 2017, 327(1): 734-742.
[6]NI J, LIANG Q, ZHOU Z, et al. Numerical and experimental investigations on gas-particle flow behaviors of the opposed multi-burner gasifier[J]. Energy Conversion & Management, 2009, 50(12): 3035-3044.
[7]XU J, ZHAO H, DAI Z, et al. Numerical simulation of opposed multi-burner gasifier under different coal loading ratio[J]. Fuel, 2016, 174(1): 97-106.
[8]BERTRAND M, LAMARQUE N, LEBAIGUE O, et al. Micromixingcharacterisation in rapid mixing devices by chemical methods and LES modelling[J]. Chemical Engineering Journal, 2016, 283(1): 462-475.
[9]BRITO M S C A, DIAS M M, SANTOS R J, et al. Fully resolved modelling and simulation of micromixing in confined impinging jets[J]. Chemical Engineering Science, 2020, 211(1): 115299.
[10]KHOMWACHIRAKUL P, DEVAHASTIN S, SWASDISEVI T, et al. Simulation of flow and drying characteristics of high-moisture particles in an impinging stream dryer via CFD-DEM[J]. Drying Technology, 2016, 34(4): 403-419.
[11]THUWAPANICHAYANAN R, KUMKLAM P, SOPONRONNARIT S, et al. Mathematical model and energy utilization evaluation of a coaxial impinging stream drying system for parboiled paddy[J]. Drying Technology, 2020, 1(1): 1-17.
[12]WU D, LI J, LIU Z, et al. Numerical study of particle behaviorin laminar axisymmetric opposed-jet flows[J]. Powder Technology, 2015, 270(1): 176-184.
[13]LIU X, YUE S, LU L, et al. Simulations of an asymmetric gas-solid two-phase impinging stream reactor[J]. Numerical Heat Transfer Part A Applications, 2018, 74(2): 1032-1051.
[14]LIU X, CHEN Y. Analysis of gas-particle flow characteristics in impinging streams[J]. Chemical Engineering and Processing: Process Intensification, 2014, 79(1): 14-22.
[15]SUN W, ZHONG W. LES-DPM simulation of turbulent gas-particle flow on opposed round jets[J]. Powder Technology, 2015, 270(1): 302-311.
[16]杜敏, 周宾. 气固两相撞击流内颗粒运动规律的实验研究[J]. 热能动力工程, 2013, 28(6): 611-615.
[17]杜敏, 陈威, 王助良, 等. 撞击流中颗粒旋转特性[J]. 化工学报, 2016, 67(5): 1878-1883.
[18]LI J, WANG H, XIONG Y, et al. Experimental investigation on turbulence modification in a dilute gas-particle axisymmetric opposed jets flow[J]. Chemical Engineering Journal, 2016, 286(1): 76-90.
[19]岑可法, 樊建人. 工程气固多相流动的理论及计算[M]. 杭州: 浙江大学出版社, 1990: 319-335.
[20]GIDASPOW D. Multiphase flow and fluidization: continuum and kinetic theory description[M]. Boston: Academic Press, 1994.
[21]TSUJI Y, OSHIMA T, MORIKAWA Y. Numerical simulation on pneumatic conveying in horizontal pipe[J]. KONA Powder Sci Tech Japan, 1985, 3(1): 38-51.
[22]MINDLIN R D, DERESIEWICZ H. Elastic spheres in contact under varying oblique forces[J]. J Appl Mech Asme, 1953, 20(3): 327-344.
[23]TSUJI Y, TANAKA T, ISHIDA T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J]. Powder Technology, 1992, 71(3): 239-250.
[24]胡国明. 颗粒系统的离散元素法分析仿真[M]. 武汉: 武汉理工大学出版社, 2010: 147.