管道流场中颗粒速度急剧变化带来气固两相剧烈的能量交换,引起气固两相温度变化,从而影响气体、颗粒两相压力特性[1],进而影响颗粒在管道内的分布。
Pazouki等[2]利用双拉格朗日模型研究了稀相悬浮流中管道内颗粒的径向分布,发现随着雷诺数增大,单个颗粒稳定横向位置越来越靠近管道壁面;Silva等[3]利用混合模型对管道内高浓度固液流中的颗粒分布进行研究,并对不同曳力模型下的颗粒分布情况进行比较,发现Schiller曳力模型与实验结果更加拟合;Geng等[4]利用欧拉-拉格朗日法研究了流化床提升管中柔性颗粒的分布特性,发现颗粒浓度在不同条件下呈现规律性的变化,在轴向方向上低密、 上稀,横向方向上中间稀、 近壁密;Jiang等[5]研究了液固流化床中的流体力学特性和颗粒分布特性,发现液相流量对颗粒分布的影响大于颗粒数量的影响;熊庭等[6]利用欧拉-拉格朗日模型[7]研究了粗颗粒在管道内分布特性和浓度分布特性,验证了欧拉-拉格朗日模型仿真的可靠性。Zhou等[8]发现提高固体浓度和输送速度可以使颗粒在管道内的分布更加均匀。
国内外研究人员虽然取得了一定的研究结果,但考虑温度场对管道内颗粒分布特性影响的研究较少。本文中利用欧拉-拉格朗日模型对管道内颗粒分布特性进行仿真分析,并重点研究温度场对颗粒分布的影响。
1 模型的建立
1.1 物理模型
图1为供料器管道的结构示意图。如图1所示,供料器管道包括气体入口、颗粒入口和2个出口。X轴向长度L1为1 800 mm,出口管道Z轴向长度L2为800 mm,弯管弯曲半径为600 mm,且三通管道的角度为90 °。气体从左侧入口进入,颗粒从上侧入口进入,颗粒与气体在异型供料器内实现初步混合,随后气体、颗粒从供料器的出口1和出口2处流出。
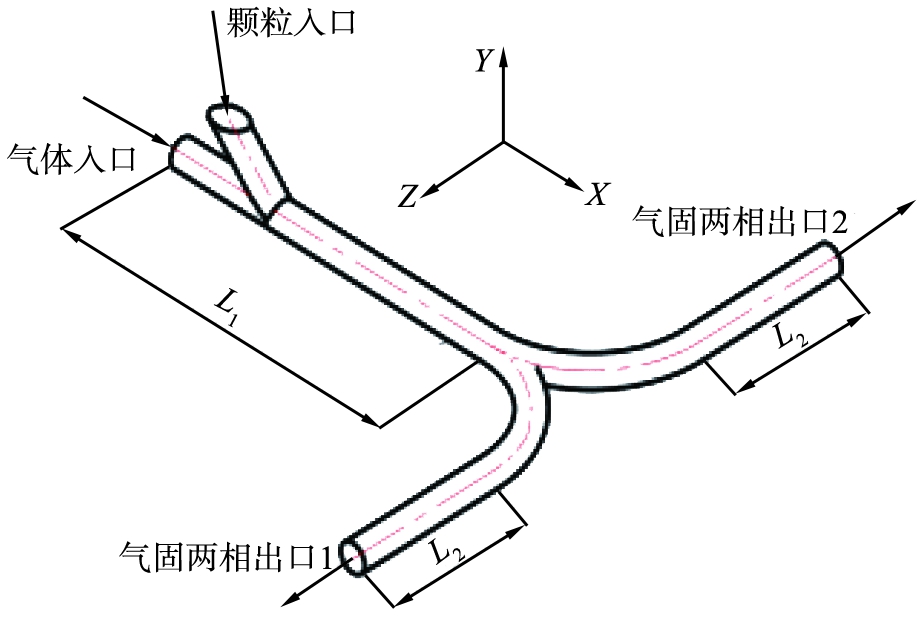
图1 供料器管道结构示意图
Fig.1 Schematic diagram of structure of feeder pipeline
颗粒为储能材料粉末颗粒,靠重力从颗粒入口下落,气固两相的主要参数设置如表1所示。
表1 气固两相主要参数
Tab.1 Main parameters of gas-solid two-phase flow

参数气相颗粒相参数气相颗粒相密度/(kg·m-3)1.184987初始质量流率/(kg·s-1)4动力黏度/(Pa·s)1.789 4×10-5颗粒直径/mm0.01初始温度/℃2622比热容/(J·( kg· K)-1)1 006.431 200初始速度/(m·s-1)300热导率/(W·(m·K)-1)0.024 22
1.2 数学模型
因为气相是连续性的,颗粒相是离散的,符合Fluent 2020 R2软件中的DPM模型的使用条件。DPM模型采用欧拉坐标系描述气相运动,采用拉格朗日坐标系描述颗粒相的运动。
1.2.1 气相控制方程
气体的欧拉连续性方程为
(1)
式中:Sm为单元体积内离散相到连续相的质量传递源项, kg/s; ρ为空气密度, kg/m3; V为气相速度, m/s。其中,Sm的计算公式为
Sm=Mnew=Mold+α(Mc-Mold),
(2)
式中: Mnew为单位体积内新变化的质量源项, kg/s; Mold为单位体积内变化之前的质量源项, kg/s; α为颗粒的下松弛因子; Mc为单位体积内的计算质量源项, kg/s。 Mc的计算公式为
(3)
式中: ΔMp为颗粒的质量变化, kg; Mp0为颗粒初始质量,![]() 为颗粒初始注入时的质量流量, kg/s。因为模拟中气固两相不存在化学反应,所以质量传递源项可视为0。
为颗粒初始注入时的质量流量, kg/s。因为模拟中气固两相不存在化学反应,所以质量传递源项可视为0。
气相的动量方程为
![]() +
+ (ρVV)=-
(ρVV)=- ρ+
ρ+ (ξ)+ρg+FW,
(ξ)+ρg+FW,
(4)
式中: ξ为气相微元体表面上的黏性应力张量; g为作用在微元体上的重力体积力, 取为9.81m/s2; FW为作用在微元体上的其他外部体积力之和, N。 FW计算公式为
(5)
式中: μ为流体分子的黏度, Pa·s; Cd为曳力系数; Rep为颗粒雷诺数; ρp为颗粒密度,kg/m3; dp为颗粒的直径, m; up为颗粒的速度, m/s; uf为气相速度,m/s; Fi为颗粒在流场中所受的其他力,包含热泳力和Magnus力;![]() 为颗粒的质量流率, kg/s;Δt表示时间步长,s。
为颗粒的质量流率, kg/s;Δt表示时间步长,s。
为了考虑温度场的影响,建立气相的能量方程为
(6)
式中: E为流体微元总能,J; keff为有效导热系数; T为气相的温度,![]() 为气相组分j的扩散通量; ∑jhjJj为由组分扩散所引起的能量传递,J;τeff V为黏性耗散所引起的能量传递, J; Sh为热源相,表示为颗粒通过流体单元时的热能变换,J。
为气相组分j的扩散通量; ∑jhjJj为由组分扩散所引起的能量传递,J;τeff V为黏性耗散所引起的能量传递, J; Sh为热源相,表示为颗粒通过流体单元时的热能变换,J。
1.2.2 固相控制方程
对固相颗粒轨迹的研究能更好地了解颗粒的行为,有助于提高计算精度。因为在拉格朗日坐标系下利用牛顿第二定律方程来描述颗粒运动,所以需要确定颗粒在管道流场中受到的力。仿真中颗粒皆为球形颗粒,颗粒在流场中受到等效重力、 空气对颗粒的曳力、 热泳力和Magnus力(与重力的数量级相差大约10%[9]),忽略压力梯度力、虚拟质量力和Basset力[10]。根据颗粒的受力平衡和惯性,得出离散相的颗粒运动方程为
(7)
式中: ρf为流体密度, kg/m3; τr表示颗粒松弛时间; (uf-up)/τr为曳力相; g(ρp-ρf)/ρp为有效重力, N; F为外力,包含Magnus力和热泳力,N。其中τr计算方程为
(8)
颗粒的转动平衡方程为
(9)
式中: T为颗粒在流场中的扭矩大小, N/m; Ip为颗粒惯性矩,kg·m2; ωp为颗粒角速度, rad/min; Cω为旋转阻力系数; Ω为流体与颗粒的相对角速度, rad/min。其中,球型颗粒惯性矩Ip为
(10)
Magnus力方程为
(11)
式中:FRL为Magnus力, N; Ap为投射颗粒表面积, m2; V′为相对气体的颗粒速度, m/s; CRL为转动升力系数,Tsuji[12]统计大量的实验数据后,认为CRL是自旋参数的函数,定义为
(12)
式中: S为自旋参数,定义为
(13)
对于球形颗粒,热泳力方程[13-14]为
(14)
式中: Cs=1.17; K为流体相和固相的热导系数比; Ct =2.18; Kn为努比森数; Cm=1.14; K的计算公式为
(15)
式中: k代表流体的导热系数; kp代表颗粒的导热系数。
对于球形颗粒,曳力系数方程[15]为
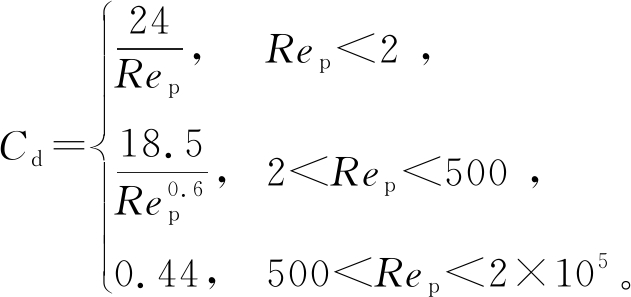
(16)
1.2.3 边界条件设置
在计算机流体设计(computer fluid design, CFD)中,选用压力型求解器。气体入口压力设为标准大气压,采用DPM离散相模型和realizable k-ε湍流模型,在颗粒入口设置DPM面射流源,材料属性设为惰性颗粒,颗粒与管道壁面的静摩擦系数设为0.5,与管道碰撞后的弹性恢复系数设为0.7。为了与离散相模型中的颗粒追踪时间步长相匹配,进行时间步长0.001 s的瞬态模拟。模拟所采用的边界条件设置如表2所示。逃逸边界条件被标记为escaped,并终止轨道计算;反射边界条件为颗粒在此处反弹而发生动量变换。
表2 边界条件设置
Tab.2 Boundary condition setting

项目气相边界类型固相边界类型气体入口速度入口逃逸边界条件颗粒入口逃逸边界条件壁面无滑移边界条件反射边界条件出口自由流出逃逸边界条件
2 结果与讨论
首先明确气固两相混合过程中引发的温度变化,然后分析温度场变化对系统压力特性的影响,接着进行流场压力实验验证CFD仿真结果,最后与不考虑温度场影响的颗粒分布情况的仿真结果进行比较,分析气固混合阶段温度场对管道内颗粒分布特性的影响。
2.1 温度场分析
管道中X轴方向上气固两相流的温度变化如图2所示。 从图2可以看出, 气固混合后, 颗粒相温度开始升高, 在1 800 mm处达到22.8 ℃; 气相温度在与颗粒相接触后开始降低, 在1 800 mm处达到24.9 ℃。 在颗粒相与气相开始接触时, 气固两相温度不同导致两相之间进行热量交换, 由于气相不断地通过管壁与外界进行热交换, 因此气相温降值比颗粒温升值要多出0.3 ℃。
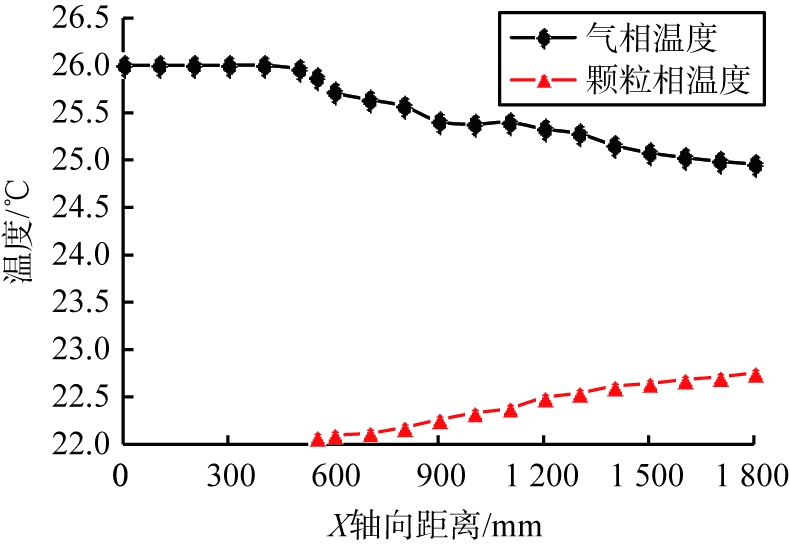
图2 管道中X轴方向上气固两相流温度变化
Fig.2 Temperature change of gas-solid two-phase flow in pipe along X-axis direction
两侧出口管道内气固两相流的温度变化图3所示。从图3可知,在距离Z轴原点600 mm时,气固两相运动从弯管转向直管,此处气相温度为24.6 ℃左右,在到达出口时,温度降为23.8 ℃左右;颗粒相在进入直管时2个位置的温度为23.1 ℃左右,在到达出口时,温度升高到23.9 ℃左右,由于气相通过管道壁面与外界进行热交换,因此气相的温度略低于固相。
2.2 温度场对压力场的影响
管道中的压力云图如图4所示。由图4可知,无论是否考虑温度场影响,管道内的绝对压力都是从气固两相混合后开始下降的,但考虑温度场影响的管道内压降更大。
温度场对管道中X轴方向上的绝对压力的影响如图5所示。从图5中可知,考虑温度场影响的绝对压降明显大于不考虑温度场影响的情况。这是由于,气相与颗粒混合之初,颗粒相与气相并未充分混合发展,两相之间的能量交换较弱,使得温度场对流场压降值的影响不大;随着气固两相的混合运动,颗粒相与气相充分混合发展,带来剧烈的能量交换,使得温度场对压降的影响变大。
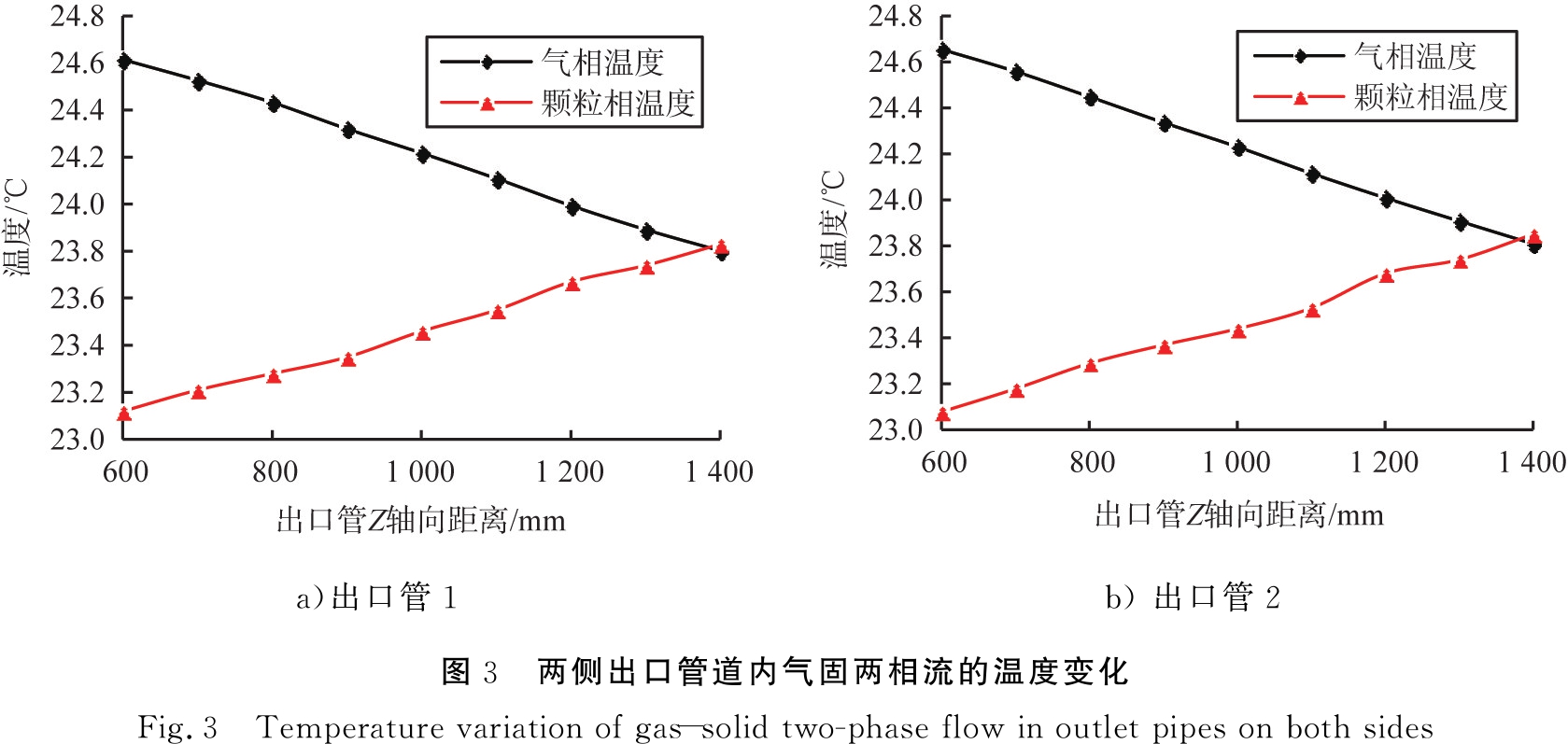
a)出口管1b) 出口管2图3 两侧出口管道内气固两相流的温度变化Fig.3 Temperature variation of gas-solid two-phase flow in outlet pipes on both sides
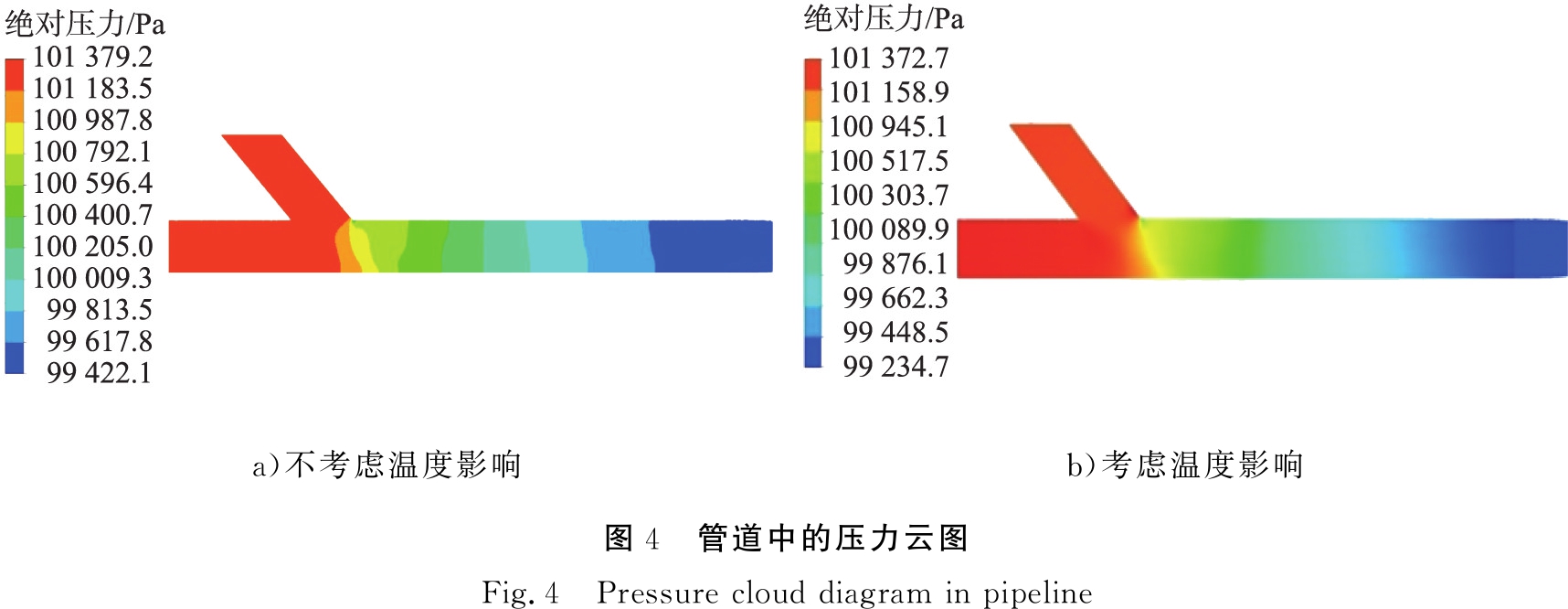
a)不考虑温度影响b)考虑温度影响图4 管道中的压力云图Fig.4 Pressure cloud diagram in pipeline
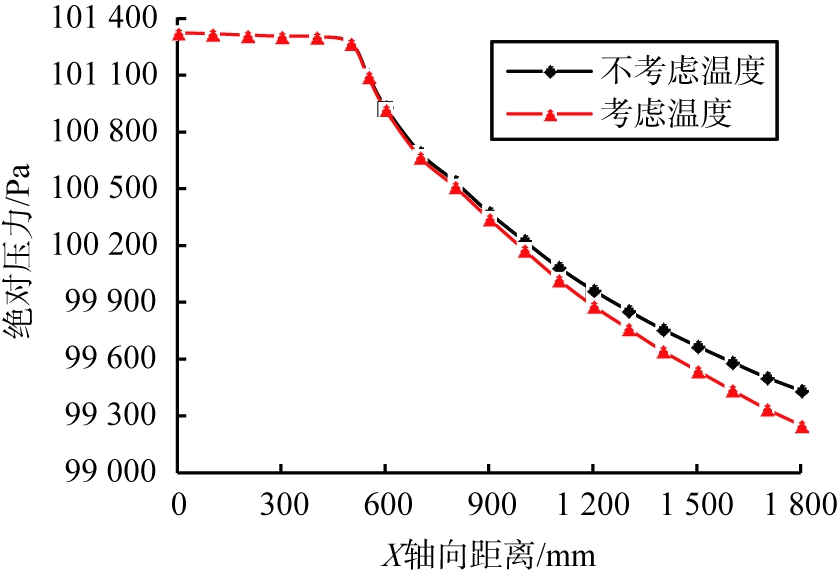
图5 温度场对管道中X轴方向上绝对压力的影响
Fig.5 Effect of temperature field on absolute pressure in pipeLINE along X axis
温度场对两侧出口管内压力流场的影响如图6所示。由图6可知,由于气固两相需要通过弯管才能进入到2个出口直管中,气固两相的速度在弯管中降低,因此弯管中动压减小,相对压力降低,使得距离Z轴原点600 mm处的初始绝对压力要大于x=1 800 mm处的绝对压力值。从图6 a)可知,在气固两相出口处,考虑温度场和不考虑温度场的压降相比于进气口处分别为2 217.9、 2 977.3 Pa,两者相差了759.4 Pa,相比于不考虑温度场,考虑温度场情况下压降增大了34.2%。从图6 b)可知,在气固两相出口处, 考虑温度场和不考虑温度场的压降相比于进气口处分别为2 203.2、 2 966.4 Pa,两者相差了763.2 Pa,相比于不考虑温度场,考虑温度场情况下压降增大了34.6%。
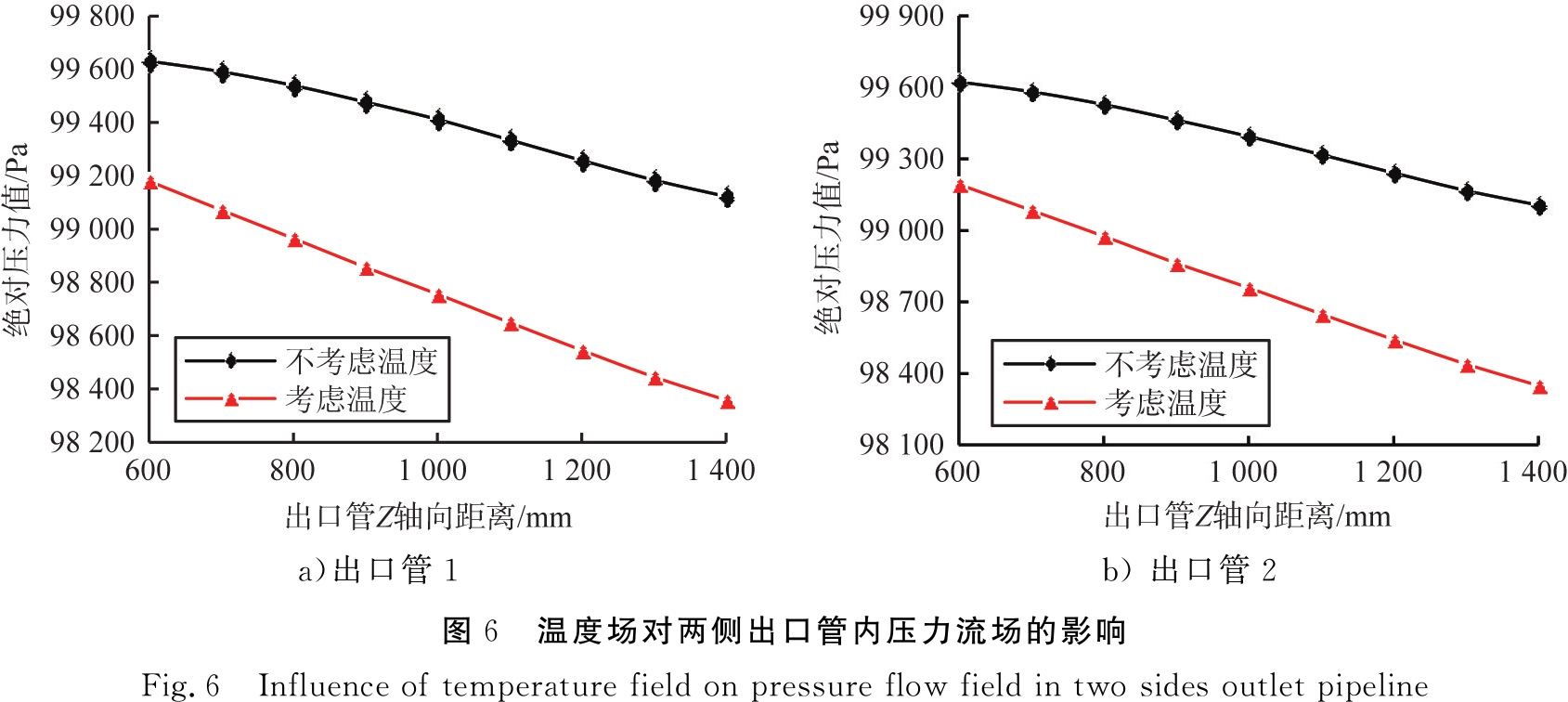
a)出口管1b) 出口管2图6 温度场对两侧出口管内压力流场的影响Fig.6 Influence of temperature field on pressure flow field in two sides outlet pipeline
2.3 压力实验验证
图7为气力式混合机实验平台。由图7可知,实验平台包含供料器、 输料管道、 气固分离器、 风机、 消声器等部件,各个输料管道之间通过气动阀进行控制,风机可提供-50 KPa的真空度。
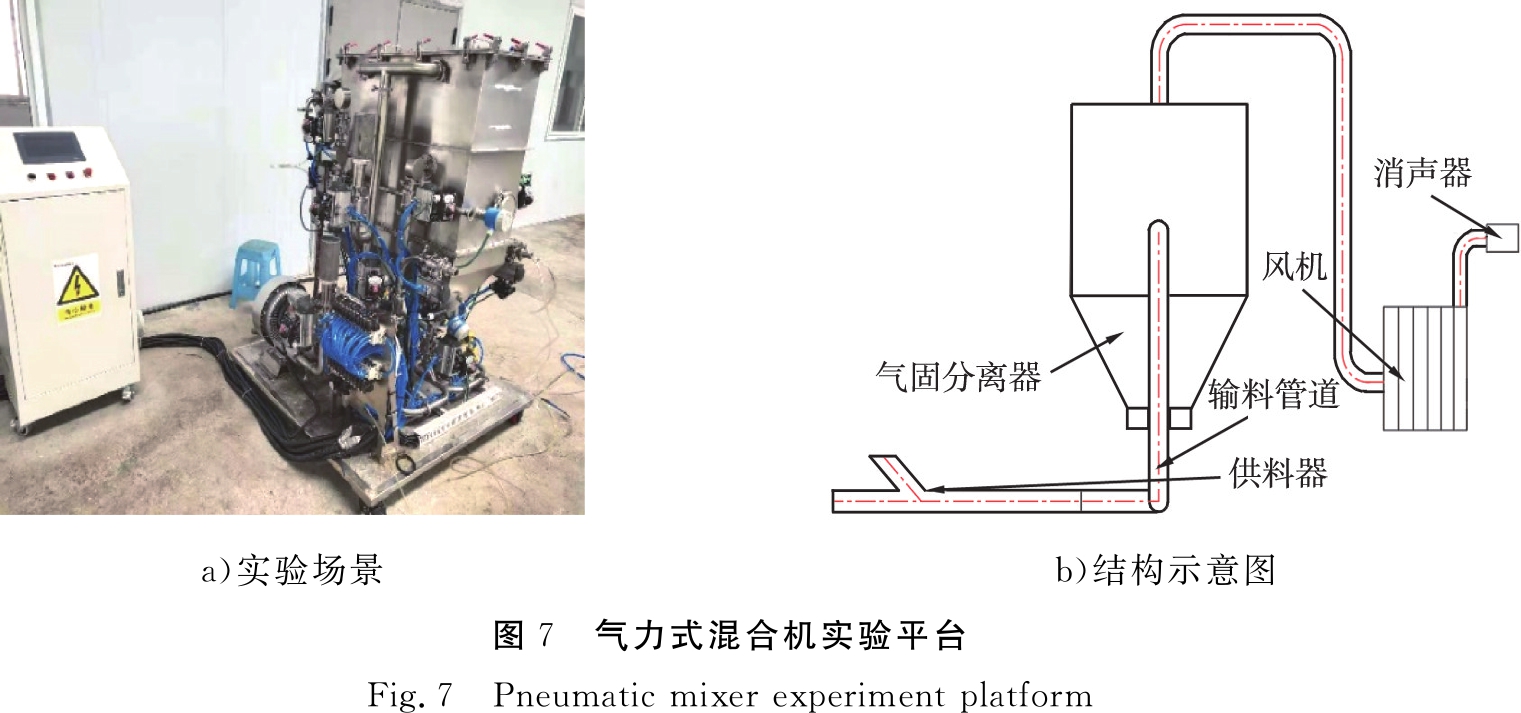
a)实验场景b)结构示意图图7 气力式混合机实验平台Fig.7 Pneumatic mixer experiment platform
供料器内压力测试点位置如图8所示。由于实验采用的是负压吸送,进气口的气压为标准大气压,管道内的压力小于进气口的压力,常用测压表测量的是相对气压,因此选择每一小格量程为100 Pa的负压量程表,通过螺纹连接安装在管道上。考虑到测压表的实际尺寸,在X轴向0、 550、 1 800 mm处和2个出口管道Z轴向600、 1 400 mm等7处安装测压表。
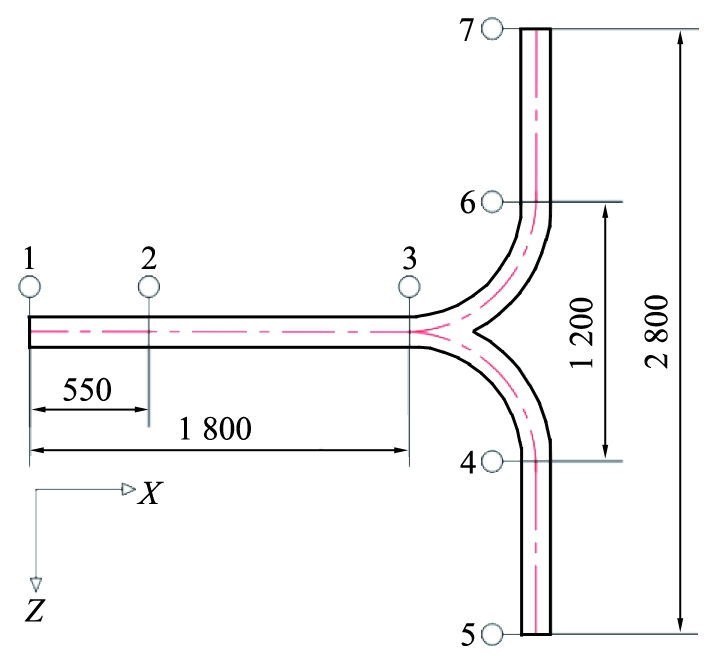
图8 供料器压力测试点位置
Fig.8 Position of feeder pressure test point
每个测试点测量3次,不同测试点的压力测量值如表3所示。
表3 不同测试点的压力测量值
Tab.3 Pressure measurements at different test points

测试点压力/Pa第1次第2次第3次平均值绝对压力/Pa1-510-480-520-503100 822 2-720-710-720-717100 608 3-2 570-2 530-2 590-2 56398 7624-2 650-2 610-2 670-2 64398 6825-3 460-3 430-3 460-3 45097 8756-2 630-2 600-2 640-2 62398 7027-3 490-3 450-3 480-3 47397 852
将实验数据与仿真数值进行比较,X轴方向上仿真和实验结果对比如图9所示。由图9可知,实验所测得的压力数据小于考虑温度场影响的仿真数据。这是因为,在x=0处,在实验中风机与供料器的进口处仍有一段距离,气流需要经过一段弯管后才能到达供料器,导致压力损失;在x=1 800 mm处,实验测得压降与考虑温度影响的仿真压降分别为2 072.7 Pa和2 563 Pa,两者相差了490.3 Pa,实验所测得的压降比考虑温度场影响的仿真结果增大了23.6%。
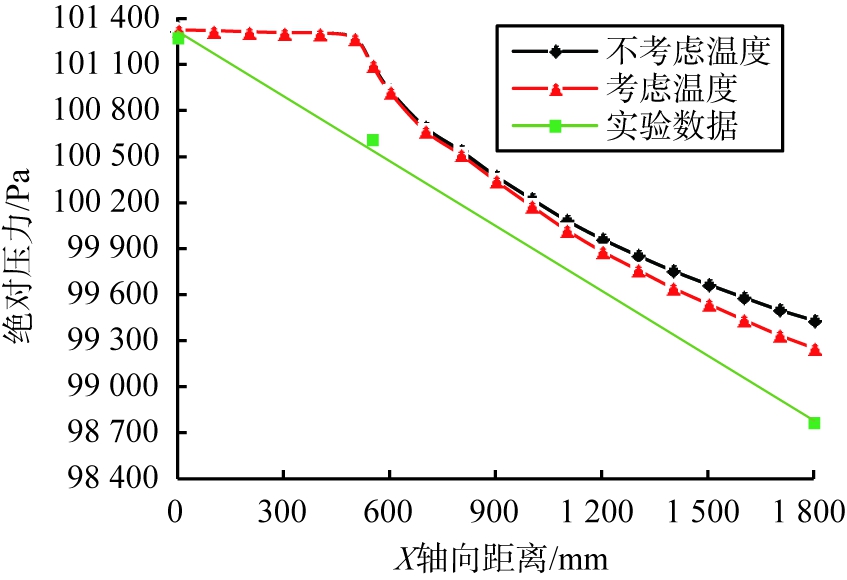
图9 X轴方向上仿真和实验结果对比
Fig.9 Comparison of simulation and experiment results in X axis direction
两侧出口管内仿真与实验对比图如图10所示。如图10所示,实验所测得的压力值皆小于仿真值。在2个出口处,实验测量压降值比考虑温度场影响的仿真值增大了16%左右,相比不考虑温度场影响的仿真值增大了38%左右,所以,考虑温度场影响的管道内仿真流场更符合实际情况。与实验数据产生偏差的原因可能是在仿真过程中未考虑颗粒之间的碰撞、整个管道气体泄漏以及管壁粗糙度不一致等。
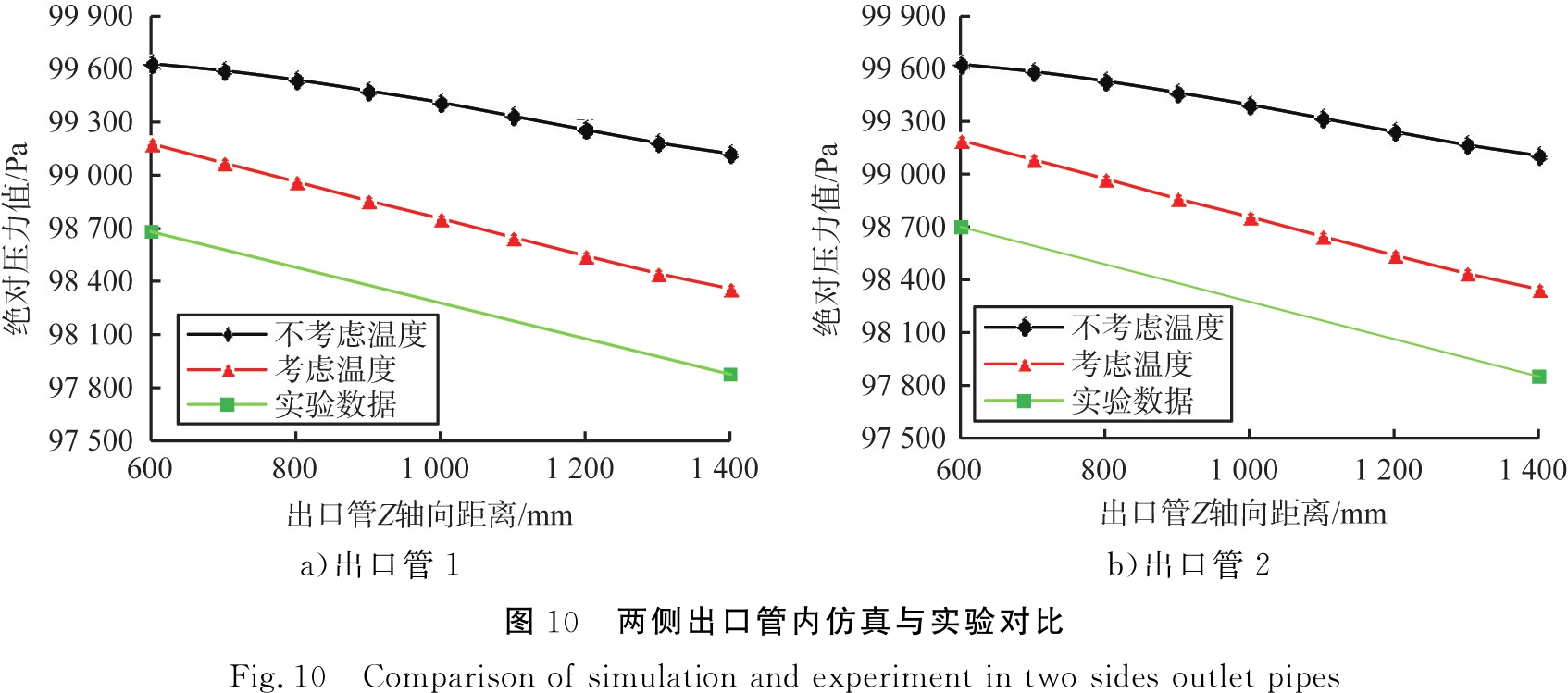
a)出口管1b)出口管2图10 两侧出口管内仿真与实验对比Fig.10 Comparison of simulation and experiment in two sides outlet pipes
2.4 颗粒质量浓度分布
为深入研究管道内气固两相流中的颗粒分布,对管道不同监测圆截面位置如图11所示。供料器管道中X轴方向上温度场对颗粒浓度的影响如图12所示。由图11、 12可知,在a圆截面处,气固两相开始接触混合,由于重力的作用颗粒逐渐向管道底部沉降,直至b圆截面处颗粒质量浓度达到峰值;考虑温度场影响时,颗粒在流场中受到热泳力的影响,转速降低,导致颗粒的Magnus力减小,下降到管道底部的速度变快,所以颗粒质量浓度较不考虑温度场影响时高;由于颗粒相与管道下壁面发生碰撞并反弹,因此c圆截面附近颗粒质量浓度再次达到峰值,又由于颗粒相在反弹中损失了一部分能量,颗粒上升速度降低,因此第二次颗粒质量浓度峰值大于第一次峰值。
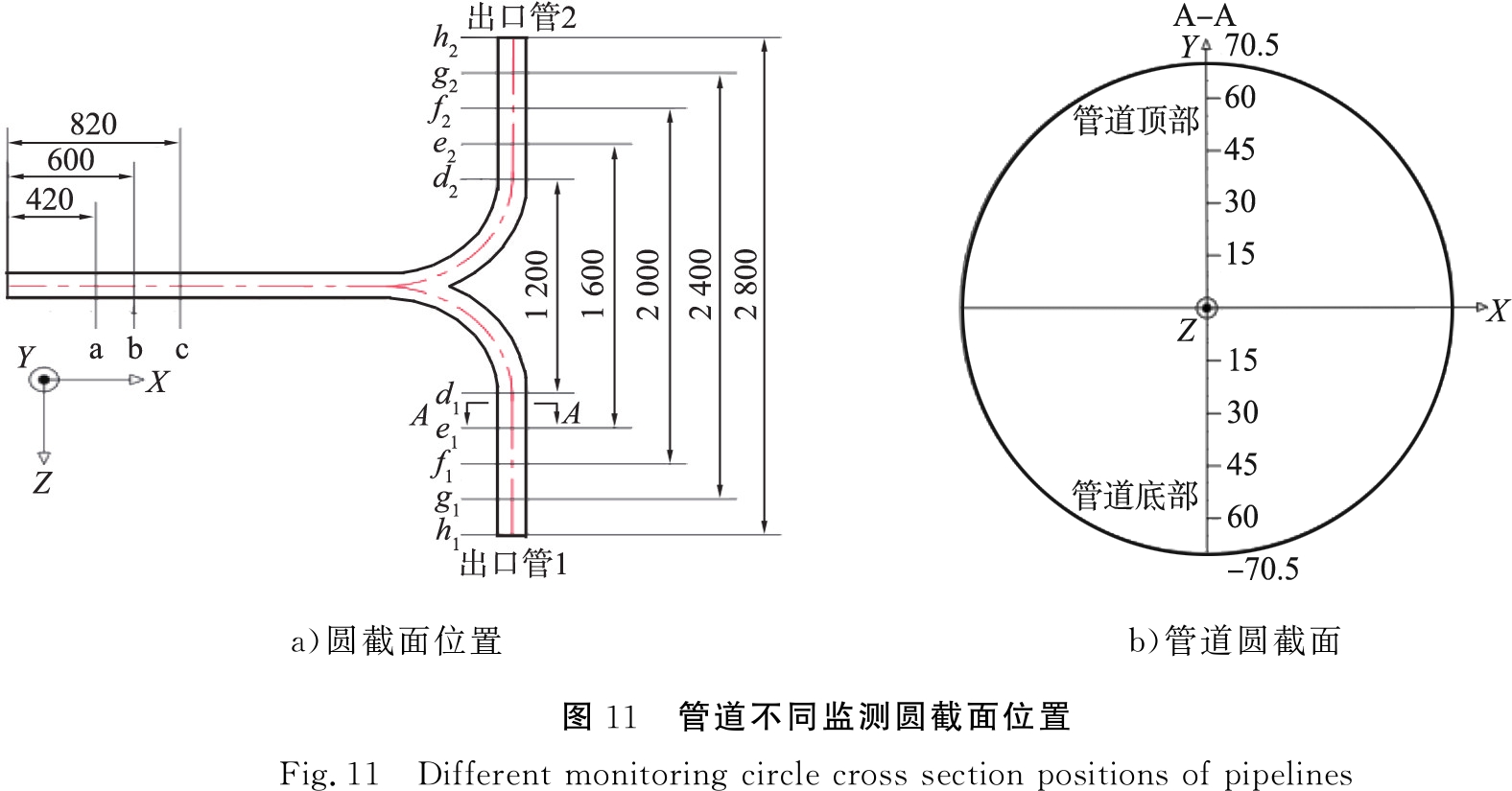
a)圆截面位置b)管道圆截面 图11 管道不同监测圆截面位置Fig.11 Different monitoring circle cross section positions of pipelines
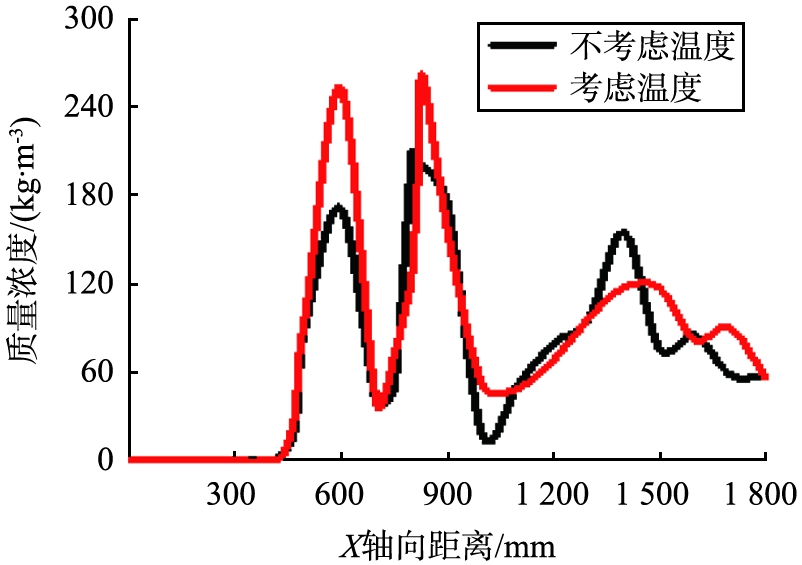
图12 X轴方向上温度场对颗粒质量浓度的影响
Fig.12 Effect of temperature field on particle mass concentration along X axis
出口管1管道圆截面上温度场对颗粒质量浓度的影响如图13所示。由图13可知,出口管1中管道圆截面底部颗粒的质量浓度高于顶部的;随着Z轴向距离的增加,颗粒质量浓度分布从管道圆截面中心处低、壁周面高逐渐变为整个管道圆截面上近似均匀分布;在h1圆截面上时,考虑温度场影响的管道圆截面的颗粒质量浓度比不考虑温度影响的降低了3%;管道圆截面内形成均匀颗粒质量浓度分布的位置,考虑温度场影响时在g1处、 不考虑温度场影响时在f1处,说明考虑温度场影响时在管道圆截面上形成稳定均匀的颗粒质量浓度分布所需要的Z轴向距离要长。
出口管2管道圆截面上温度场对颗粒质量浓度的影响如图14所示。由图14可知,出口管2中管道圆截面底部的颗粒质量浓度低于顶部的;随着Z轴向距离的增加,颗粒质量浓度分布从管道圆截面中心处低、壁周面高逐渐变为整个管道圆截面上近似均匀分布;在h2圆截面上时,考虑温度场影响的管道圆截面中心处的颗粒质量浓度比不考虑温度影响的降低了8.7%;管道圆截面内形成均匀颗粒质量浓度分布的位置,考虑温度场影响时在h2处、 不考虑温度场影响时在g2处,说明考虑温度场影响时在管道圆截面上形成稳定均匀的颗粒质量浓度分布所需要的Z轴向距离要长。
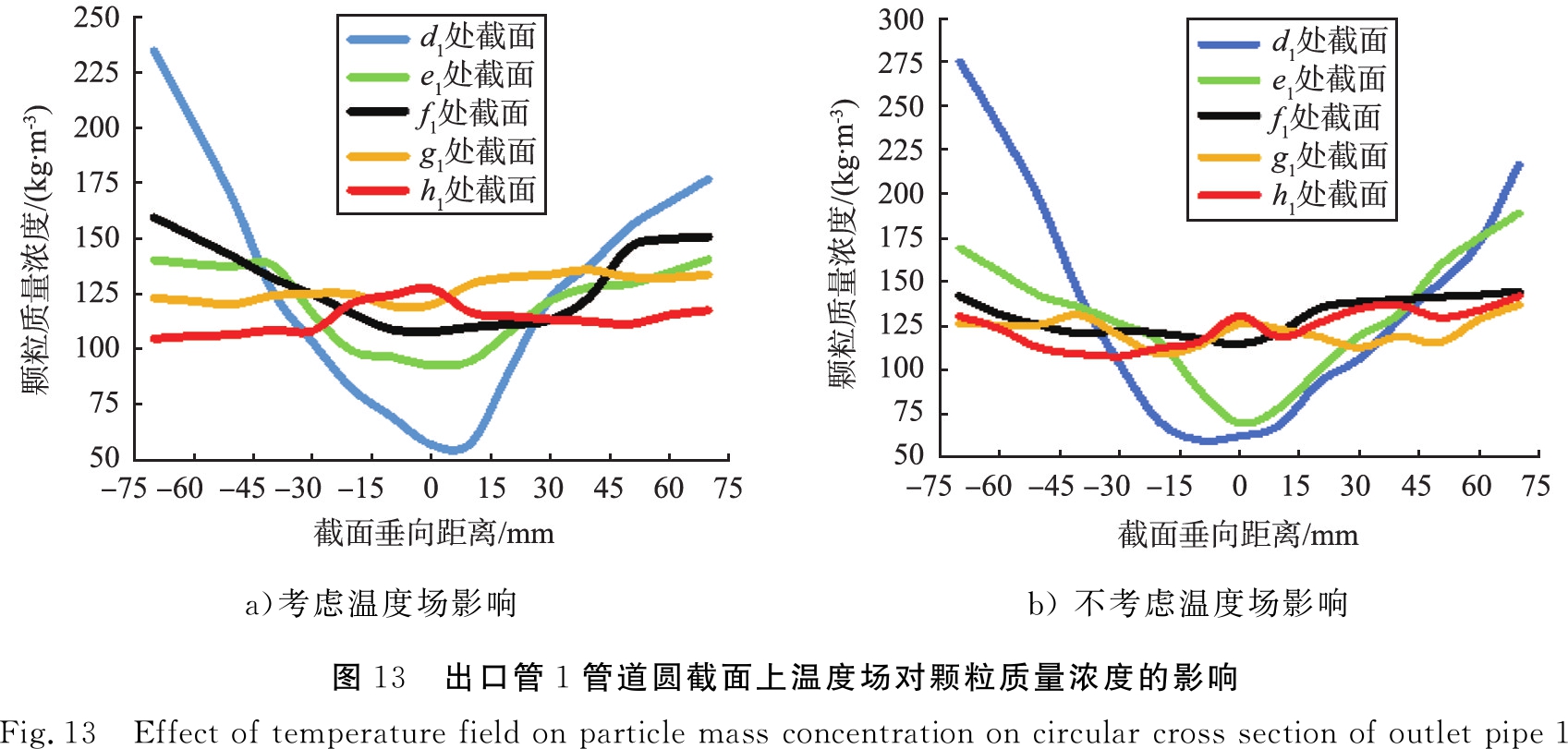
a)考虑温度场影响b) 不考虑温度场影响图13 出口管1管道圆截面上温度场对颗粒质量浓度的影响Fig.13 Effect of temperature field on particle mass concentration on circular cross section of outlet pipe 1
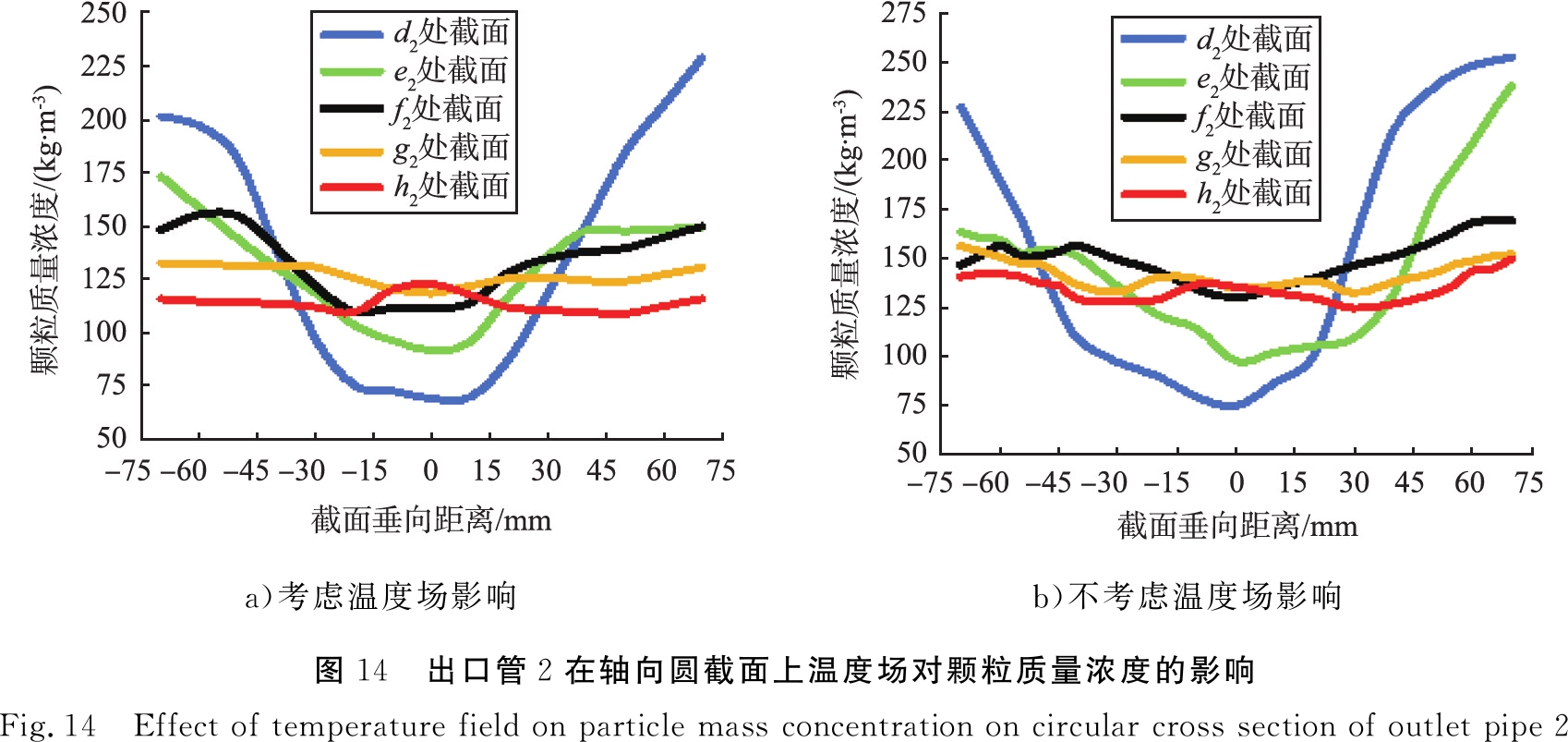
a)考虑温度场影响b)不考虑温度场影响图14 出口管2在轴向圆截面上温度场对颗粒质量浓度的影响Fig.14 Effect of temperature field on particle mass concentration on circular cross section of outlet pipe 2
3 结论
1)在颗粒相与气相开始接触时,气固两相温度不同导致两相之间进行热量交换;气固混合后,颗粒相温度升高,气相温度降低,直至气固两相温度一致。
2)考虑温度场影响的管道中的绝对压降明显大于不考虑温度场影响的情况;实验测量压降值比考虑温度场影响的仿真值增大了16%左右,比不考虑温度场影响的仿真值增大了38%左右,所以考虑温度场影响的管道内流场仿真更符合实际情况。
3)在管道入口段X轴线方向上, 考虑温度场影响时颗粒质量浓度的峰值大于不考虑温度场影响时, 而且随着X轴向距离的增加, 管道圆截面上颗粒质量浓度趋于一致; 在两侧管道出口段, 随着Z轴向距离的增加, 颗粒质量浓度分布从管道圆截面中心处低、 壁周面高逐渐变为整个管道圆截面上近似均匀分布; 考虑温度场影响时, 管道圆截面中心处的颗粒质量浓度比不考虑温度影响的降低了3.0%~8.7%, 在管道圆截面上形成稳定均匀的颗粒质量浓度分布所需要的Z轴向距离要长。
[1]柳波, 尹高冲, 孙凯, 等. 考虑温度场条件下的Y型喉管流场特性分析[J]. 河北农业大学学报, 2018, 41(2): 122-128.
[2]PAZOUKI A, NEGRUT D. A numerical study of the effect of particle properties on the radial distribution of suspensions in pipe flow[J]. Computers and Fluids, 2015, 108: 1-12.
[3]SILVA R, COTAS C, GARCIA F A P, et al. Particle distribution studies in highly concentrated solid-liquid flows in pipe using the mixture model[J]. Procedia Engineering, 2015, 102: 1016-1025.
[4]GENG F, TENG H X, GUI C G, et al. Investigation on distribution characteristics of flexible biomass particles in a fluidized bed riser[J]. Fuel, 2020, 271: 18-35.
[5]JIANG F, SHEN Y, QI G P, et al. Hydrodynamics characteristics and particle distribution in a liquid-solid circulating fluidized bed boiler[J]. Powder Technology, 2021, 377: 41-54.
[6]熊庭, 陈芊屹, 吴强, 等. 基于Eulerian-Lagrangian模型的粗颗粒管道输送数值模拟[J]. 水动力学研究与进展(A辑), 2018, 33(4): 461-469.
[7]CAPECELATRO J, DESJARDINS O. An Euler-Lagrange strategy for simulating particle-laden flows[J]. Journal of Computational Physics, 2013, 238(31): 1-31.
[8]ZHOU M M, WANG S, KUANG S B, et al. CFD-DEM modelling of hydraulic conveying of solid particles in a vertical pipe[J]. Powder Technology, 2019, 354: 893-905.
[9]LIU Y, ZHANG S F, ZHANG W. Study on particles distribution characteristics through a circulation fluidized bed with the spiral flow generator[J]. Energy Procedia, 2012, 14: 1111-1116.
[10]袁竹林, 朱立平, 耿凡, 等. 气固两相流动与数值模拟[M]. 南京: 东南大学出版社, 2013: 33-36.
[11]GOSMAN A D, LOANNIDES E. Aspects of computer simulation of liquid-fuelled combustors[J]. Energy, 1983, 7(6), 482-490.
[12]TSUJI Y, OSHIMA T, MORIKAWA Y. Numerical simulation of pneumatic conveying in a horizontal pipe[J]. KONA Powder and Particle Journal, 1985, 3: 38-51.
[13]SAGOT B. Thermophoresis for spherical particles[J]. Journal of Aerosol Science, 2013, 65: 10-20.
[14]董双岭, 曹炳阳, 过增元. 作用在粒子上的热泳升力研究[J]. 工程热物理学报, 2015, 36(5): 1063-1066.
[15]YANG N, WANG W, GE W, et al. CFD simulation of concurrent-up gas-solid flow in circulating fluidized beds with structure dependent drag coefficient[J]. Chemical Engineering Journal, 2003, 96(1): 71-80.