布朗运动是微小粒子或者颗粒在流体中做的一种无规则运动，它最早是由英国植物学家Brown[1]在1827年研究流体中悬浮的花粉颗粒时发现的。直到1905年Einstein[2]从理论上解释了这一现象，认为这是液体中的水分子碰撞花粉颗粒，使得它们在不停地做随机运动。1908年，法国物理学家Perrin[3]通过实验证实了爱因斯坦的假设，为此他赢得了1926年的诺贝尔物理学奖。对科学家而言，这种无规则的随机运动不仅仅是一个奇观，而且具有广泛的应用前景。例如，制作人工布朗马达[4]、 作为自驱动活性物质[5-6]、 用于研究黏弹性物质的微流变学[7]以及量子混沌涨落-耗散理论[8]等。此外，由于生命信息科学中出现了新的交叉学科研究，因此基于中尺度结构的布朗运动在软物质[9]和生物细胞领域[10]的应用研究显得尤其重要。
光的传播能把动量传递给物体并对物体施加一个沿光传播方向的力， 这就是所谓的辐射压力。 辐射压力的概念得到了经典电磁学理论的验证，为进一步研究光力奠定了坚实的理论基础。自从Ashkin第一次证明了激光势阱[11]的存在，并展示了利用辐射压力捕获和操控微米大小的粒子，光镊技术已成为一种强有力的工具，被广泛应用于捕获和操控原子、分子、纳米粒子、活的生物细胞和细胞器。已有研究表明：光的偏振态为微粒操控提供了重要的调控手段，基于不同偏振光的强聚焦少数颗粒的微操控在各个领域得到了快速发展[12-16]，但是，却鲜有弱聚焦情况下，偏振光对布朗运动颗粒影响的相关报道，尤其是对大量颗粒的研究几乎还是空白。鉴于此，在本文中基于差分动态显微技术[17-19]，从实验上定量研究线偏振光和圆偏振光对颗粒布朗运动扩散系数的影响。
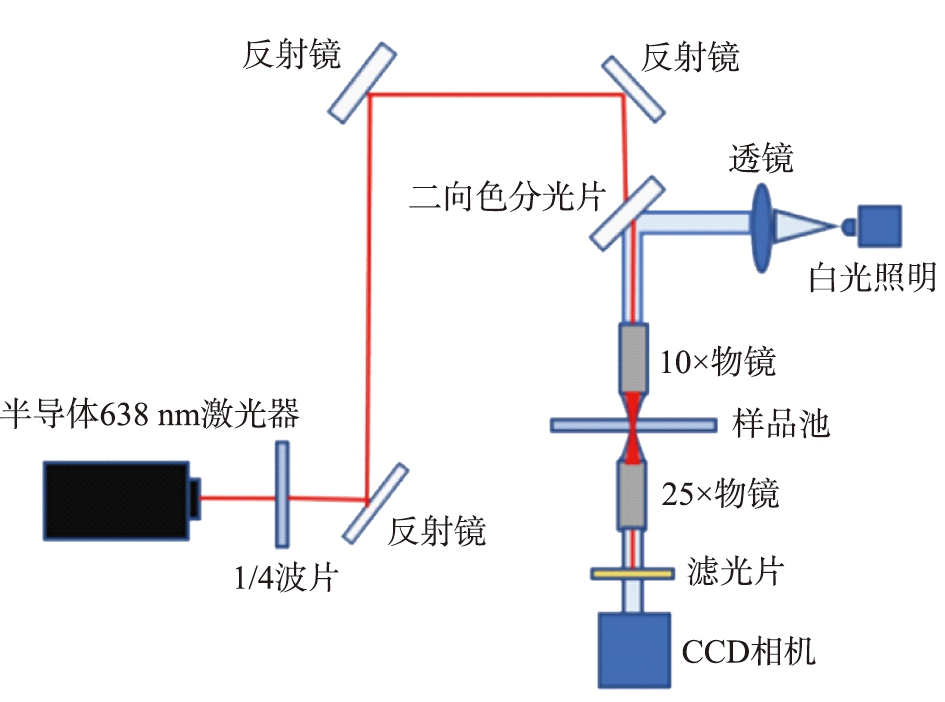
图1 实验装置示意图
Fig.1 Schematic of experimental setup
1 实验
1.1 实验光路的设计
我们设计了如图1所示的实验光路。 半导体激光器的波长为638 nm， 产生偏振度为2 000∶1的线偏振光， 经1/4波片变成圆偏振光。圆偏光先后经过反射镜的反射，到达二向色分光镜，再经过10倍(数值孔径为0.25)物镜聚焦，产生直径约为260 μm的光斑照射到长方形样品池上。样品池的长、 宽、 高分别为50、 10、 2.4 mm, 上下两壁的距离为1.2 mm。
实验前，将粒径为687 nm的聚苯乙烯微球原溶液与超纯水按照体积比1∶1 000配制成颗粒水溶液，实验时将该溶液注满样品池。小球在溶液中做布朗运动，激光被聚苯乙烯颗粒散射，然后由25倍数值孔径为0.4的物镜收集，投影到高速CCD相机(型号为FR180，分辨率为2 048×1 088,采集速率在165 帧/s以上)。同时，照明光LED(型号为GCI-060411, 波段为440～670 nm, 功率为1 W)白光源经过透镜聚焦，再被二向色镜反射与激光共轴进入样品池。为了在CCD中观察到颗粒清晰的布朗运动， 我们在CCD相机之前加了一个带通滤光片(型号为HSPH-600-D25)用来去除波长为638 nm的激光对图像的影响。
图2 0.1 s时刻687 nm聚苯乙烯颗粒的显微图像
Fig.2 Microscopic image of 687 nm polystyrene particles at 0.1 s
1.2 照明光实验测试
在对光路进行准直之后， 首先测量只有照明光时， 溶液中聚苯乙烯颗粒做布朗运动的扩散系数。 具体做法如下， 实验室温度为25.5 ℃， 实验用聚苯乙烯颗粒水溶液样品， 采用动态光散射纳米粒度仪(BT-90)测得其粒径大小为687 nm。为了避免石英样品池壁对颗粒运动的影响，将接收物镜聚焦面放置在样品池的中间位置。利用高速CCD相机以每秒160 帧的采样速度对颗粒的散射光连续拍摄15 s，共获得2 400张大小为512×512像素的颗粒运动显微图像，0.1 s时刻687 nm聚苯乙烯颗粒的显微图像如图2所示。
基于差分动态显微技术，对图像做光强差分运算。将第2张显微图像到第2 400张显微图像,分别与第1张图像进行灰度值相减，从而得到时间差为1/160 s到15 s的图像光强差值图。为了便于分析，用符号
表示t时刻和0时刻图像的光强差异性，即
(1)
其中，
(2)
表示图像中像素点
在t时刻和0时刻的光强差值。从理论分析可知，颗粒在做布朗运动，在时间间隔Δt较小时，t时刻的散射光强与0时刻的散射光强的差异性
随着Δt的增大而增大；而当时间间隔Δt较大时，这时的散射信号与初始时刻的散射信号之间的差异程度趋于饱和，不再随时间大幅度变化，即将趋于一个常数。利用傅里叶变换，将光强差异性函数等效到频谱空间,可以获得聚苯乙烯小球做布朗运动的功率谱函数:
=A(q)[1-exp(-Δt/τ(q))]+B(q)。
(3)
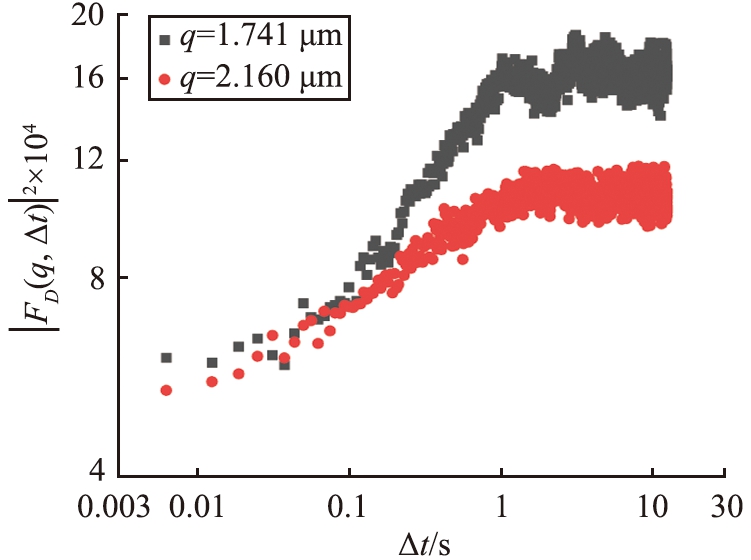
图3 不同波矢的功率谱曲线
Fig.3 Power spectrum at different wave vectors
式中， A(q)为与颗粒布朗运动有关的散射信号； B(q)为背景噪声。这里为了表述方便，用波矢q代替了空间频率，在图像中，
q=(2πp)/(L×1.33)，
(4)
式中， p为图像的像素点； L=(512×5.5)/(25×0.5)=225.28 μm，这与显微图像的大小、 CCD相机单个像素点的大小、接收物镜的倍数以及水的折射率有关。其中波矢q=1.741 μm-1和q=2.160 μm-1的功率谱曲线如图3所示。
通过对功率谱曲线的拟合，可以得到波矢q对应的特征时间τ(q)的值。波矢与特征时间的关系式为
τ(q)=1/Dmq2。
(5)
通过式(5)的拟合，得到颗粒布朗运动扩散系数的实验值Dm。理论上，作布朗运动的球形颗粒的扩散系数满足斯托克斯-爱因斯坦关系:
Dm=kBT/6πηr。
(6)
式中， kB为玻尔兹曼常数； T为绝对温度； η为水的黏滞系数， 与温度有关； r为聚苯乙烯小球的半径。 由式(6)计算得到的理论值为0.720 8 μm2/s。 重复做6次只有照明光时聚苯乙烯颗粒的扩散系数测量的实验， 对获得的扩散系数取平均值， 最后， 得到只有照明光时聚苯乙烯颗粒的扩散系数为Dm=0.722 9 μm2/s， 实验值与理论值非常符合， 两者偏差为0.3%， 表明实验系统和实验数据是可靠的。
2 结果与分析
2.1 线偏振光实验时的结果与分析
在照明光的实验条件下，首先研究激光不同入射功率时，线偏振光对颗粒布朗运动扩散系数的影响，实验结果见表1。
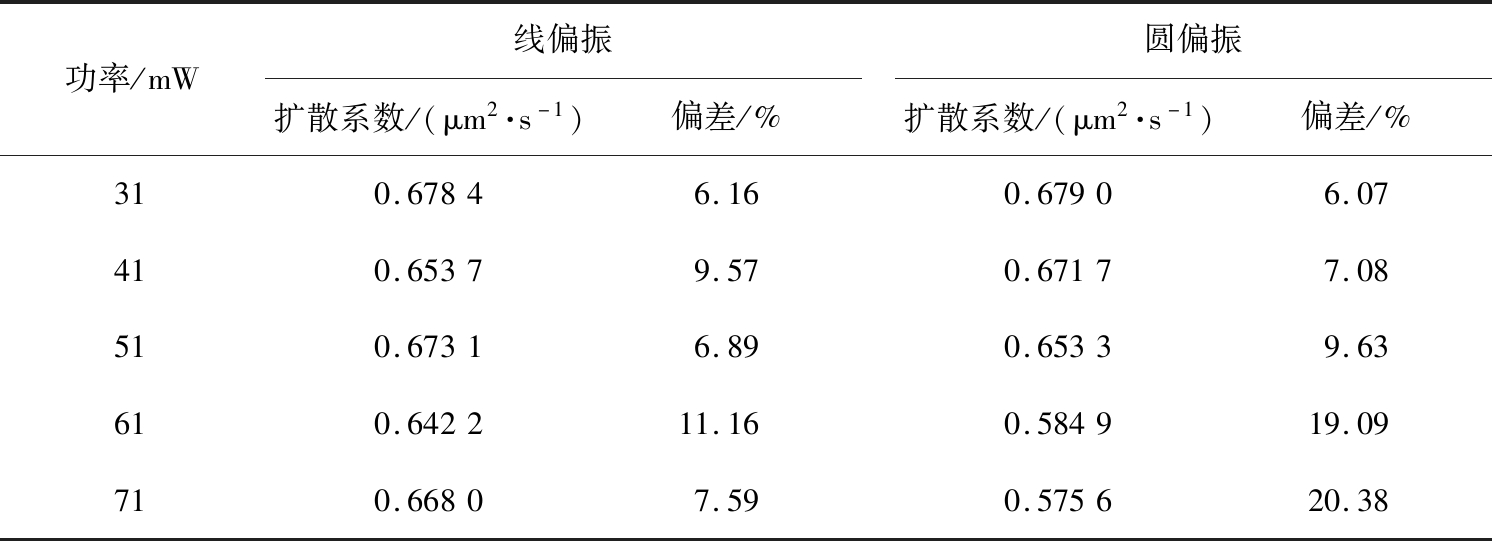
表1 光的偏振对布朗粒子扩散系数的影响
Tab.1 Polarization light influence on the diffusion coefficient of Brownian particles
功率/mW线偏振扩散系数/(μm2·s-1)偏差/%圆偏振扩散系数/(μm2·s-1)偏差/%310.67846.160.67906.07410.65379.570.67177.08510.67316.890.65339.63610.642211.16 0.584919.09 710.66807.590.575620.38
由表1可以看出， 当到达样品池的激光功率为31 mW时， 实验测得做布朗运动的聚苯乙烯小球扩散系数为0.678 4 μm2/s， 与只有照明光时的扩散系数0.722 9 μm2/s相比较，其偏差为6.16%。而当激光功率为41 mW时，偏差为9.57%，其对应的扩散系数是0.653 7 μm2/s。随着入射光功率的继续增大，颗粒布朗运动的扩散系数反而增大， 如功率为51 mW时， 扩散系数变为0.673 1 μm2/s。但是，在功率为61 mW时，聚苯乙烯小球的扩散系数反而减小到0.642 2 μm2/s，偏差达到11.16%，远小于只有照明光时的扩散系数。当调节激光功率进一步增大到71 mW，相较于61 mW时其扩散系数又变大了，变为0.668 0 μm2/s。
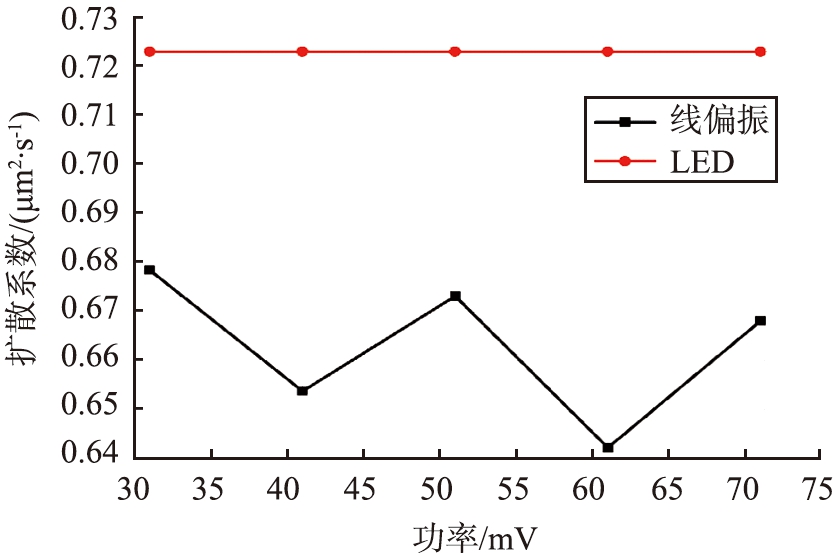
图4 线偏振光时颗粒扩散系数随功率的变化
Fig.4 Experimental diffusion coefficient at different laser powers under linearly polarized light
图4为线偏振光时颗粒扩散系数随功率的变化。如图中黑线所示，当激光为线偏振光时，随着激光功率的增大，溶液中聚苯乙烯小球的扩散系数出现了振荡。从图4可以看到，有激光照射时的扩散系数均比仅有照明光(红线)时的扩散系数要小，说明外加激光对做布朗运动的聚苯乙烯小球有力的束缚作用。在激光弱聚焦情况下，光形成一个大的弱光学势阱，对处于其中的粒子有限制作用，从而阻碍了颗粒的运动，使得其扩散系数比自由扩散时要小。随着激光功率的增加，线偏振照射下颗粒的扩散系数表现出振荡的现象，这与我们之前的研究结果[19]不同。又由于实验过程中，无法预知受到辐射压力作用的颗粒达到平衡状态所需的时间，因此，我们认为扩散系数出现波动现象，可能原因是在实验测量过程中，受到辐射压力作用的、做布朗运动的聚苯乙烯小球还处于非平衡状态，所以实验测得的扩散系数会出现波动，这一点有待于我们后续进一步加以实验验证。
2.2 圆偏振光实验的结果与分析
为了研究了圆偏振光对聚苯乙烯小球布朗运动扩散系数的影响，在图1所示的光路中加入1/4波片,将线偏振光变为圆偏振光,获得右旋圆偏振光。实验结果如表1所示，在圆偏振光照射下，随着激光功率的增大，颗粒布朗运动的扩散系数在减小。当圆偏振光入射到样品池的功率为31 mW时，聚苯乙烯小球的扩散系数为0.679 0 μm2/s，这与线偏振光时的扩散系数0.678 4 μm2/s几乎相等；而当激光功率变为41 mW时，其扩散系数为0.671 7 μm2/s，这比31 mW圆偏光照射时的扩散系数有细微的减小；当功率继续增大到51 mW时，扩散系数有了明显的减小，变为0.653 3 μm2/s，与只有照明光时的扩散系数偏差达到了9.63%。
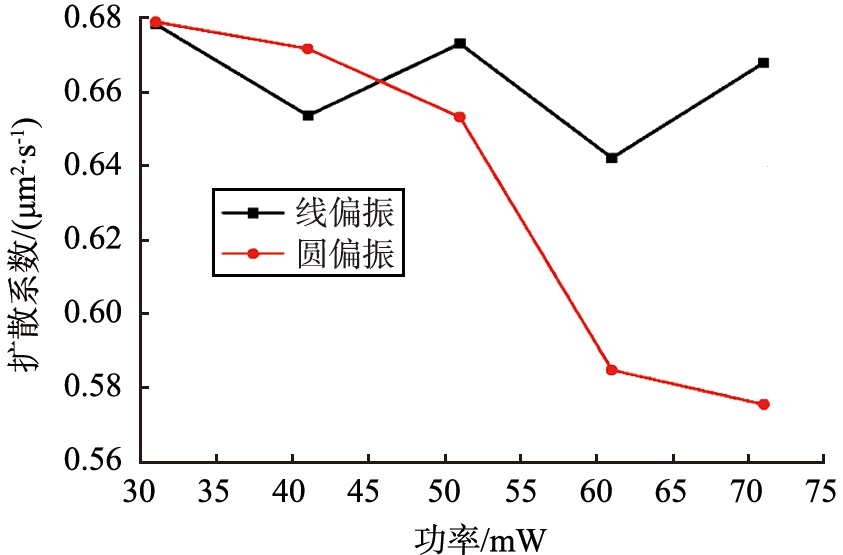
图5 线偏光和圆偏光对布朗运动扩散系数的影响对照图
Fig.5 Comparison diagram of effect of linearly and circularly polarized light on diffusion coefficient of Brownian motion
图5为线偏振光时颗粒扩散系数随功率的变化， 如图中红线所示， 当激光入射功率为61 mW时， 聚苯乙烯小球扩散系数有一个快速的下降， 变为0.584 9 μm2/s，偏差为19.09%；当我们进一步增大激光入射功率到71 mW时，实验测得颗粒的扩散系数是0.575 6 μm2/s，这比61 mW时扩散系数又有减小。从图5中可以看出，相同功率下，圆偏振光(红线)照射时的扩散系数要小于线偏振光(黑线)的；相比较线偏振光照射时，扩散系数随光功率增大表现出振荡特性，而圆偏振光照射下的扩散系数却随着功率的增大而减小。这是因为在圆偏振光照射时，除了光波线动量会给粒子一个束缚作用外，光的角动量也会给粒子施加一个自旋的运动趋势，这就使得圆偏振光的扩散系数比线偏振时的要小。
从光的传播过程中能流分布来看，线偏振光照射时，光的线动量在光传播方向上给聚苯乙烯小球一个辐射压力；而在圆偏振光照射时，除了光波线动量对粒子的影响外，在水平面上光的自旋角动量也会给粒子施加一个自旋运动趋势。在这二者的共同作用下，将使得圆偏振光对聚苯乙烯小球扩散系数的影响大于线偏振光的，这与图5中实验结果一致。在圆偏振自旋能流的作用下，粒子由原来的随机布朗运动趋向于自旋运动趋势，功率越大，这种趋势将会越明显。在实验中，由于功率不够大且颗粒是球形的，不能看到颗粒明显的自旋运动，但是从扩散系数的变化情况还是可以看出，随着功率的变化，圆偏振光对颗粒运动的影响比线偏振光要大。
3 结论
基于差分动态显微技术，实验研究了线偏振光和圆偏振光对聚苯乙烯小球布朗运动扩散系数的影响。研究结果表明： 1)弱聚焦条件下，有外加激光照射时，聚苯乙烯小球的扩散系数小于只有白光源照射时的扩散系数，反映了激光势阱对粒子有束缚作用； 2)激光相同入射功率时，圆偏振光照射的颗粒扩散系数要小于线偏振光的扩散系数，这是因为除了光的线动量外，圆偏振光具有自旋角动量，还会给粒子施加一个自旋运动趋势，使得圆偏振光对颗粒运动的束缚作用大于线偏振光； 3)随着激光功率的增大，线偏振光照射下小球的扩散系数表现出振荡现象，而圆偏振光时扩散系数随功率增大而减小。本文中的研究结论有望为大量粒子的光学微操纵提供借鉴与参考。
[1]BIAN X, KIM C, KAMIADAKIS G E. 111 years of Brownian motion[J]. Soft Matter, 2016, 12(30): 6331-6346.
[2]EINSTEIN A. On the movement of small particles suspended in stationary liquids required by the molecular-kinetic theory of heat[J]. Annalen der Physik, 1905, 322(8): 549-560.
[3]PERRIN J. Brownian movements and molecular reality[M]. New York: Courier Dover Publications, 2005: 80-90.
[4]CHRISTIAN S, STEFAN F, URS D, et al. Experimental observation of current reversal in a rocking Brownian motor[J]. Physical Review Letters, 2018, 121： 104102.
[5]MIGUEL A F R, FABIO G, LAURA A, et al. Feedback-controlled active Brownian colloids with space-dependent rotational dynamics[J]. Nature Communications, 2020, 11(3): 4223.
[6]ELGETI J, WINKLER R G, GOMPPER G. Physics of microswimmers-single particle motion and collective behavior: a review[J]. Reports on Progress in Physics, 2015, 78(5): 056601.
[7]SWAN J W, ZIA R N. Active microrheology: fixed-velocity versus fixed-force[J]. Physics Fluids, 2013, 25: 083303.
[8]CHARLIE N, DIEGO P. Quantum chaotic fluctuation-dissipation theorem: effective Brownian motion in closed quantum systems[J]. Physical Review E, 2019, 99: 052139.
[9]FREY E, KROY K. Brownian motion: a paradigm of soft matter and biological physics[J]. Annals of Physics, 2005, 14 (1/2/3): 20-50.
[10]HOFLING F, FRANOSCH T. Anomalous transport in the crowded world of biological cells[J]. Reports on Progress in Physics, 2013, 76(4): 046602.
[11]ASHKIN A. Acceleration and trapping of particles by radiation pressure[J]. Physical Review Letters, 1970, 24: 156-159.
[12]PETER G, PAL O. Orientation of flat particles in optical tweezers by linearly polarized light[J]. Optics Express, 2003, 11(5): 446-451.
[13]ZHAN Q W. Trapping metallic Rayleigh particles with radial polarization[J]. Optics Express, 2004, 12(15): 3377-3382.
[14]ANGELSKY O V, BEKSHAEV A Y, MAKSIMYAK P P, et al. Circular motion of particles suspended in a Gaussian beam with circular polarization validates the spin part of the internal energy flow[J]. Optics Express, 2012, 20 (10): 11351.
[15]CHOI J M, NOH H. Investigation of the polarization-dependent optical force in optical tweezers by using generalized Lorenz-Mie theory[J]. Journal of the Korean Physical Society, 2015, 67: 2086-2091.
[16]HA G J, ZHENG H X, YU X N, et al. Polarization effect on optical manipulation in a three-beam optical lattice[J]. Physical Review A, 2019, 100: 033817.
[17]CERBINO R, TRAPPE V. Differential dynamic microscopy: probing wave vector dependent dynamics with a microscope[J]. Physical Review Letters, 2008, 100: 188102.
[18]陈一村， 张文亮， 邱健， 等. 基于差分动态显微技术的布朗运动实验研究[J]. 中国粉体技术， 2017, 23(2): 30-34.
[19]CHEN X L, LIU D M, CAI D J, et al. Coaxial differential dynamic microscopy for measurement of Brownian motion in weak optical field[J]. Optics Express, 2018, 26(24): 32083-32090.