流化床反应器具有优良的传热传质特性和气固混合性能，在工业领域得到了广泛应用,但是常规流化床在实际应用中仍存在许多问题，一些流化现象如腾涌、 沟流和扬析等，严重影响了流化床反应器的性能[1-2]。旋流流化床是通过特殊的布风板设计，在床内形成强烈气固旋流的一类新型流化床，具有防止过大气泡生长和颗粒适用范围广等优点[3]。相关研究表明，旋流流化床解决了常规流化床中布风板和床层压降大、 横向混合差等常见问题，具有更好的气固接触与颗粒混合特性，显著改善了流化质量，还可以消除布风板上方的颗粒聚团和死区[4-6]。
除流动特性外， 流化床反应器的传热特性也是决定其性能的重要因素。 Lu等[7]研究了方形旋流流化床内传热系数与风量、 颗粒性质的关系， 结果表明，换热系数随流化速度增大而增大， 且与颗粒粒径相关。 Mohideen等[8]研究了Geldart D类颗粒在旋流床内的传热行为，测定了壁面与床层颗粒间的换热系数， 指出换热系数随床层高度增加而减小。 Sirisomboon等[9]研究了双旋流锥形流化床锅炉的传热特性，探究了不同旋流数的布风板与风速对传热特性的影响，实验表明， 传热系数随布风板一次风流量和旋流数的增大而明显增大。Tawfik等[10-11]对旋流流化床的传热特性和流动特性进行了研究，考察了颗粒尺寸和中心体结构的影响，结果表明，减小颗粒尺寸可以增大传热系数，而锥形中心体的使用可以有效提升旋流流化床的传热性能。目前，尽管有一些学者对旋流流化床的流动和传热特性进行了一些实验研究，但旋流流化床中流动和传热的相互作用机理尚未明晰，有待进一步研究。
在流化床运行过程中，反应器的磨损问题通常是一种新型反应器能否推广应用的关键，而旋流流化床因床内强烈气固旋流的存在，磨损问题更加值得进行研究。由颗粒撞击壁面引起的反应器磨损是个比较复杂的动态过程，理论分析法通过将颗粒撞击壁面的问题简化为简单的理想模型再进行分析，得到了广泛的应用。Finnie[12]对单颗粒冲击磨损的数学模型进行了推导，其表达式将入射角作为自变量，冲击磨损量作为因变量，该模型在分析材料的磨损情况时准确度较高，但在角度较大时误差较大。20世纪60年代，Bitter[13]提出了变形导致磨损的相关理论，并对模型进行了相应的简化，认为材料磨损是靶材的塑性变形和颗粒的切削作用一起造成的，材料在垂直冲击角下的磨损是由机械因素引起的，这仅与颗粒冲击靶材的变形有关，而与切削作用无关。Oka等[14]通过分析壁面磨损与颗粒撞击壁面撞击角度的关系，提出了Oka磨损计算公式。
本文中采用欧拉-拉格朗日混合方法对旋流流化床中Geldert D类颗粒的流动及传热行为进行了数值模拟研究，对床层空隙率及颗粒旋流速度进行了预测，并讨论了不同操作条件下反应器的磨损行为，在此基础上，分析了气固混合接触与传热行为之间的关系，并对床层-壁面以及气-固相间的传热特性开展了相关研究。
1 数学模型
1.1 控制方程
本文中通过一种混合欧拉-拉格朗日方法， 即稠密离散相模型(dense discrete phase model， DDPM)来描述气固两相流动及传热过程[15]。 其将流体相视为连续相， 将颗粒相视为离散相， 在拉格朗日框架下对计算颗粒的运动轨迹进行追踪。 相较于双流体方法， 能获得更为丰富的流场信息。 对于气相， 在欧拉框架下进行描述， 控制方程包括连续性方程、 动量和能量平衡方程。 气体连续性方程和动量平衡方程为
+
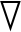·(εf ρfuf)=0，
(1)
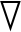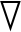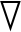+·(εf ρfufuf)=-εfpf+·τ+εf ρfg+β(up-uf)，
(2)
式中： pf和τf分别表示气相压力与应力； up和uf分别表示固相与气相速度； εf和ρf分别表示气相体积分数与密度； β表示曳力系数，在本文中通过Gidaspow曳力模型计算得到[16]。
气体能量平衡方程为
+·(εfρfufhf)=-εf
+τf ∶uf-·qf+Sen，
(3)
式中： hf为气相比焓； Sen代表相间热传递。
对于离散相，基于DDPM，并引入Parcel的概念来表示具有相同物理性质的一组颗粒，从而达到节约计算资源的目的[17]。颗粒的运动由牛顿第二定律进行描述，
(4)
式中： Fc表示颗粒之间的接触力，其通过离散元模型(discrete element model， DEM)框架下的弹簧-阻尼滑块模型进行计算，从而更加真实的描述颗粒间的相互作用。此模型下，接触力包括法向与切向分量[18]：
(5)
(6)
式中： k和η分别表示弹性系数和阻尼系数； μ表示摩擦系数。这里使用Oka模型描述壁面的磨损行为[14]，
(7)
f(γ)=(sin γ)n1(1+Hv(1-sin γ))n2。
(8)
颗粒的能量平衡方程为
(9)
式中： Tp和Ts分别表示颗粒与壁面温度； h和kp分别表示相间传热系数和比热容； Ap和Ac分别表示颗粒表面积和颗粒接触面积； dsp表示颗粒和壁面之间的距离。
1.2 实验系统及模型
在Tawfik等[10]的实验装置基础上，选择带有环形叶片式布风板的旋流流化床为研究对象，其装置如图1所示。
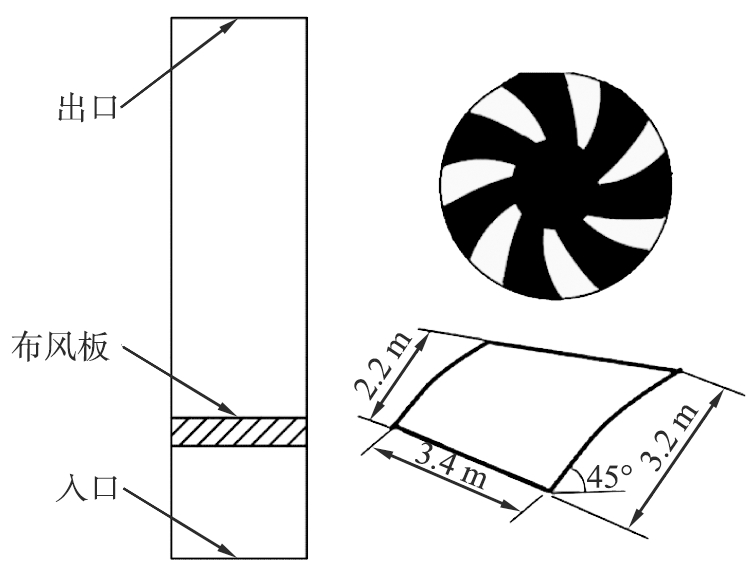
图1 旋流流化床实验装置
Fig.1 Sketch of swirling fluidized bed[10]
流化床反应器的高度为0.5 m，直径为0.1 m。流化气通过环形叶片式布风板进入流化床反应器中，布风板由7个与水平成45 °角的弯曲叶片组成。装置的详细参数见表1。
表1 流化床反应器的物性参数和操作条件
Tab.1 Geometrical structure parameters and operating conditions of numerical simulation
变量数值单位变量数值单位床高500mm叶片内径30mm直径100mm叶片外径100mm叶片数量7—进口气速1.7～2.1m·s-1叶片倾角45(°)环境温度289K
床料包括PE颗粒和砂粒2种颗粒，均属于Geldart D类颗粒。初始状态床质量为400 g，PE颗粒和砂粒的所占质量分数分别为0.75和0.25。颗粒的具体物理参数见表2。
表2 颗粒物理参数
Tab.2 Physical property parameters in simulation
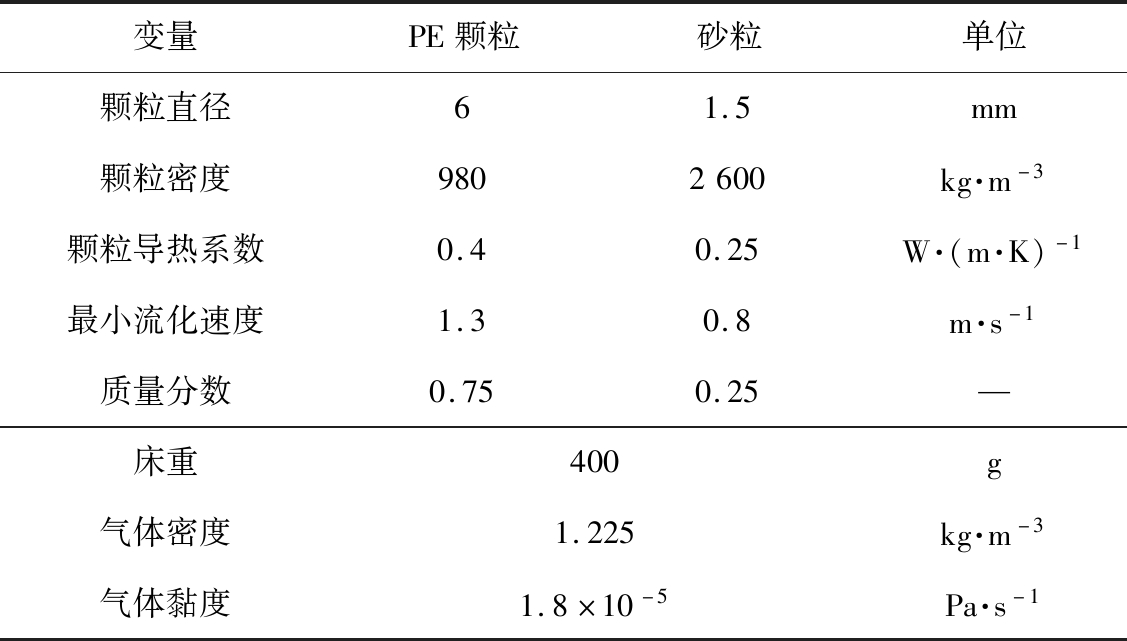
变量PE颗粒砂粒单位颗粒直径61.5mm颗粒密度9802600kg·m-3颗粒导热系数0.40.25W·(m·K)-1最小流化速度1.30.8m·s-1质量分数0.750.25—床重400g气体密度1.225kg·m-3气体黏度1.8×10-5Pa·s-1
基于Ansys Fluent 19.0，对旋流流化床进行三维数值模拟。床层颗粒被入口高温流化气体加热，压力出口位于反应器顶部，对于壁面，采用无滑移条件。床层与壁面之间的传热系数被定义为
(8)
式中： Q表示输入的热量； Ap表示流化床壁面面积； Ts表示固相温度； Tb代表床层温度,
Tb=εgTf+(1-εg)Tp。
(9)
式中： Tf表示气相温度； Tp表示固相温度； εg表示气相体积分数。
2 结果与讨论
2.1 流动特性
在进行模拟研究之前，采用3种精度不同的网格划分方式对网格无关性进行验证，均采用非结构化网格，网格参数如表3。
表3 网格具体参数
Tab.3 Meshing parameters
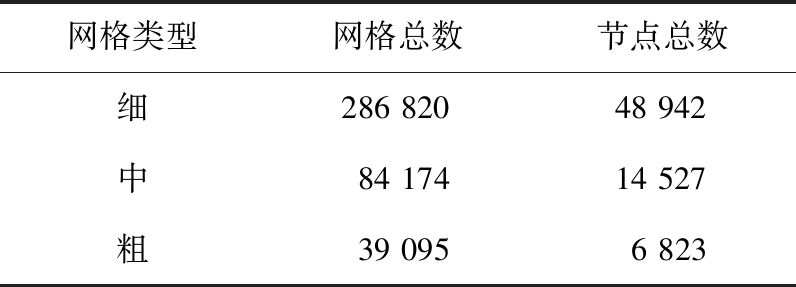
网格类型网格总数节点总数细28682048942中8417414527粗390956823
图2为不同网格精度下的床层压降计算结果对比。粗网格与另2种网格的模拟结果相比差异较大，模拟结果失真较多，不予采用。中网格与细网格的结果较为相近，故本文中采用中网格进行旋流流化床的模拟计算。
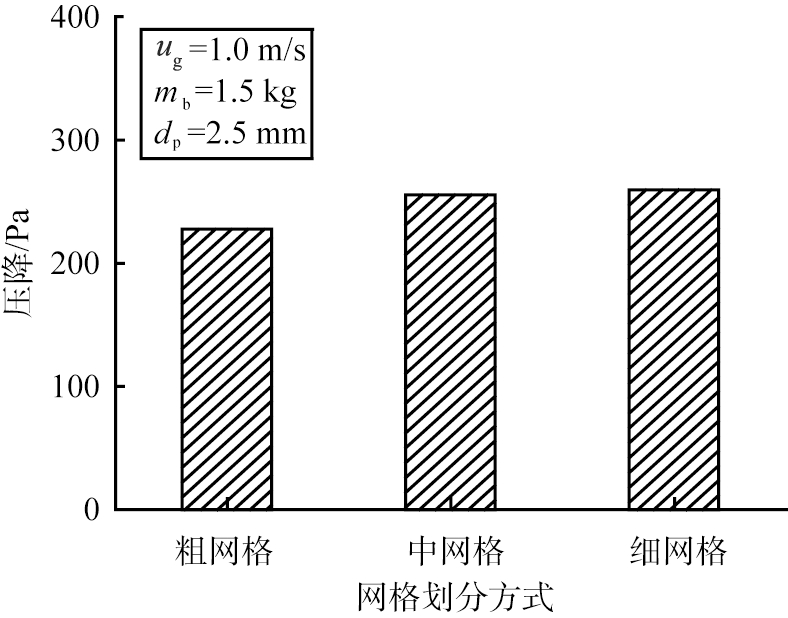
图2 网格划分精度对计算压降的影响
Fig.2 Influence of mesh accuracy on pressure drop
模型所预测的床层压降与实验结果的对比见表4。结果表明，模拟结果与实测数据吻合较好。随着操作气速增加，压降先增大而后趋于平缓，最后不断增大。与常规流化床不同的是，在旋流流化床中，床层压降在稳定流化后进一步增大，这是由于旋流运动的颗粒受到离心力的作用，与流化床壁面之间产生额外的摩擦力，带来额外的床层压降。随着颗粒的旋流运动扩散至整个床层，床层压降增大速度到达一定值，床层压降稳定增大。
表4 实验结果与模拟结果对比
Tab.4 Comparison of simulation and measured data
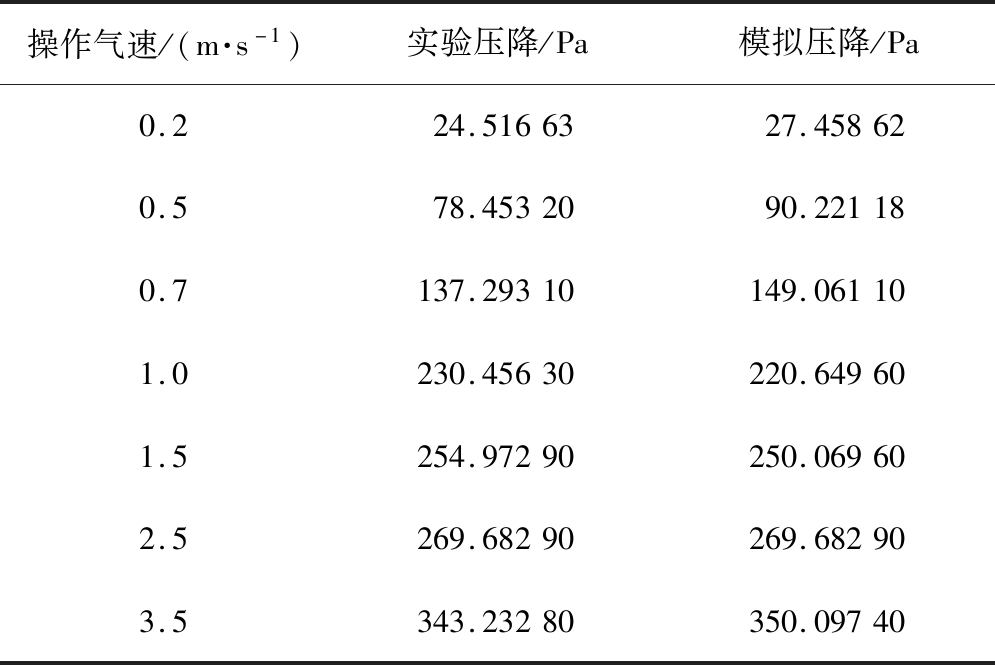
操作气速/(m·s-1)实验压降/Pa模拟压降/Pa0.224.5166327.458620.578.4532090.221180.7137.29310149.061101.0230.45630220.649601.5254.97290250.069602.5269.68290269.682903.5343.23280350.09740
图3给出了旋流流化床内距布风板不同高度处床层空隙率及颗粒速度分布，其中云图代表床层空隙率，矢量图代表界面内颗粒横向运动趋势。在分层流化形态下，底部颗粒形成连续旋流，上层颗粒呈强烈鼓泡状态，底层的空隙分布较为均匀。在稳定旋流形态下，旋流流化床内颗粒均进行连续的旋流运动，形成完整的旋流流化床，鼓泡现象消失。上层颗粒旋流运动更为强烈，颗粒有向外侧移动的趋势，中心处空隙率较大，证明旋流流化床在高速下会因离心力导致不良流化现象产生。
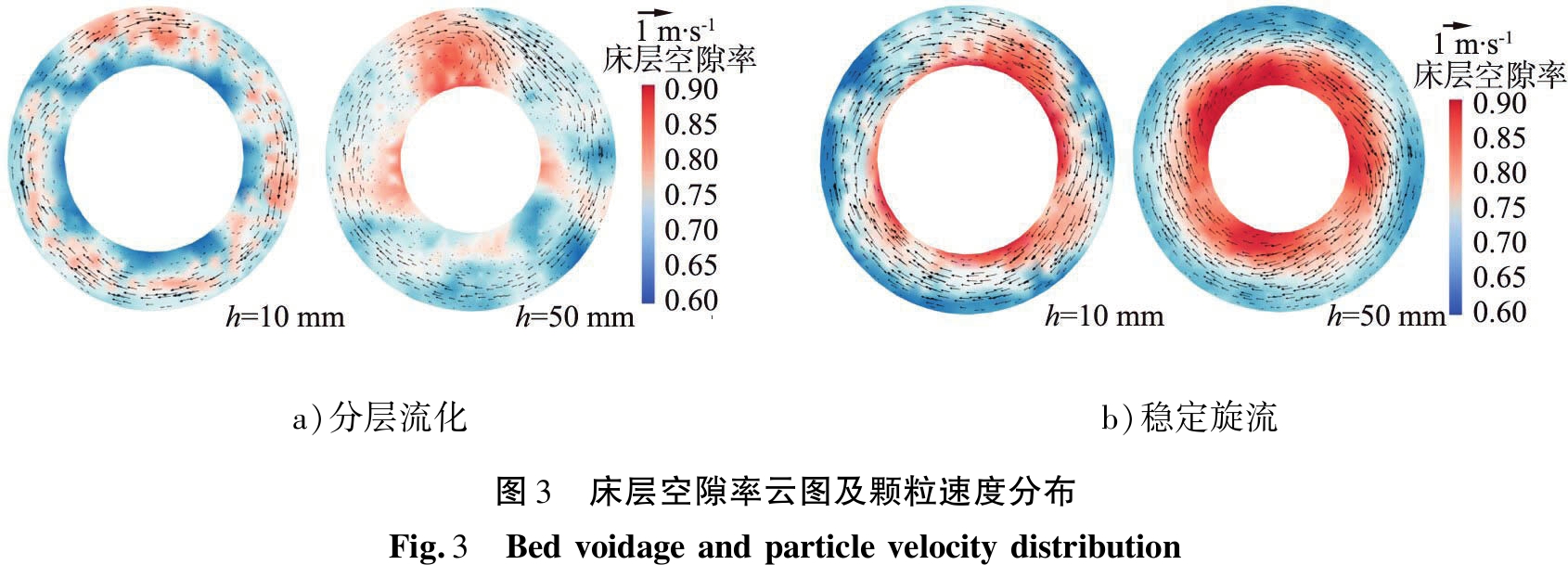
a)分层流化b)稳定旋流图3 床层空隙率云图及颗粒速度分布Fig.3 Bedvoidageandparticlevelocitydistribution
图4为不同运行状态下旋转流化床的局部床层空隙率和颗粒旋流速度的径向分布。在底层，2种运行状态在壁面附近均具有相同的空隙率分布，但是沿径向向内，两者床层空隙率的变化趋势截然相反，分层流化状态在床层中心处具有较低的床层空隙率，因此分层流化状态床层中心处颗粒旋流较弱，旋流集中于壁面附近。稳定旋流状态颗粒旋流速度较大，峰值位于床层中心处。对于上层，分层流化状态和稳定旋流状态的床层空隙率分布完全不同，颗粒分别聚集于床层中心和壁面附近。分层流化状态下床层中心处颗粒无旋流存在。
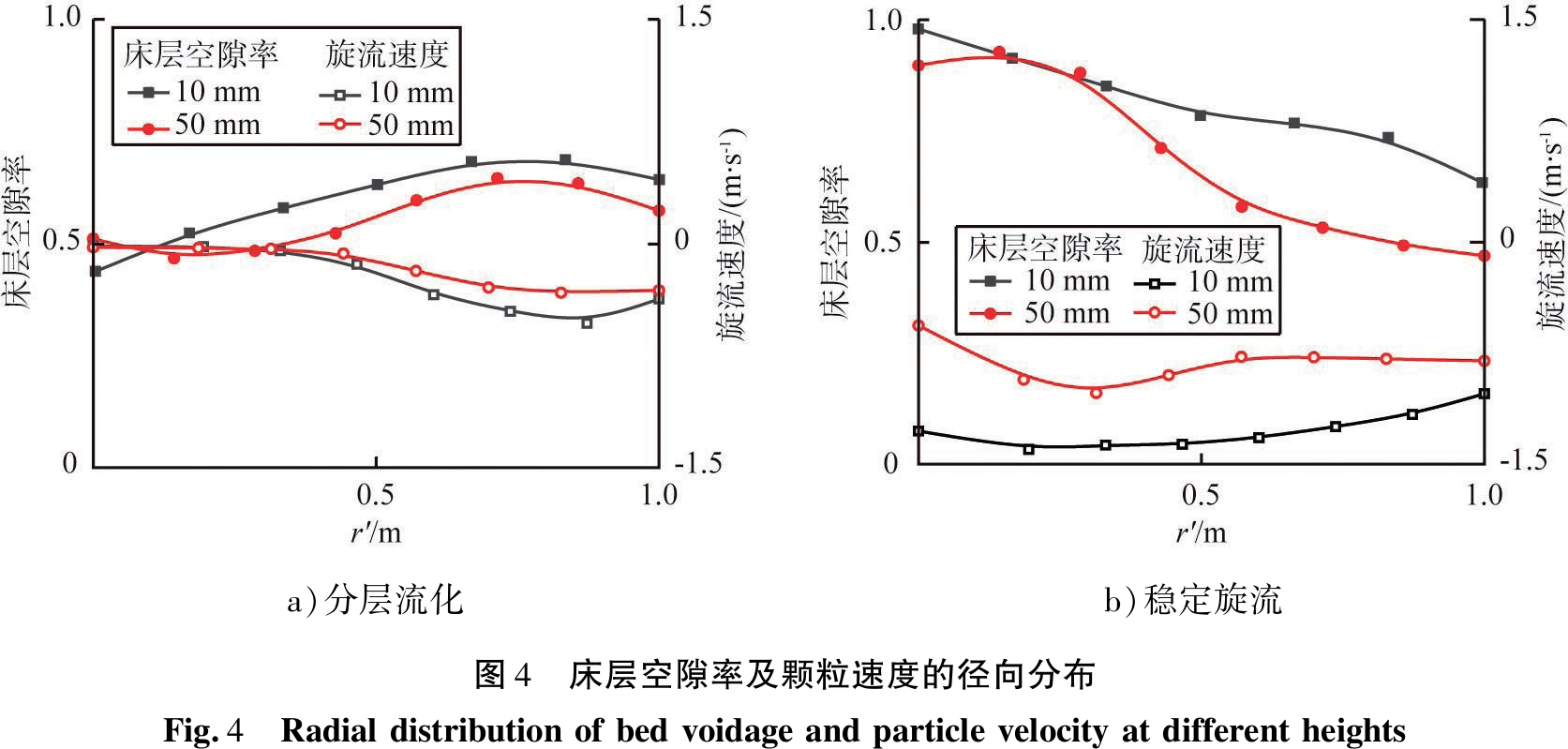
a)分层流化b)稳定旋流图4 床层空隙率及颗粒速度的径向分布Fig.4 Radialdistributionofbedvoidageandparticlevelocityatdifferentheights
2.2 壁面磨损行为
在流化床运行过程中，磨损带来的问题严重，而旋流流化床因为床内强烈气固旋流的存在，磨损将更加剧烈。基于Oka模型，选取表观气速为2.5、 3.2 m/s 2种工况分别代表分层流化与稳定旋流运行状态，对旋流流化床在不同运行状态下的磨损特性进行了研究，并对布风板和壁面分别进行了考察。图5展示了旋流流化床在不同运行状态下运行5 s时布风板和壁面的最大磨损量。从图中可以看出，在低速下，布风板与壁面的最大磨损量相差无几，壁面略大一点，而高速下两者磨损量均大幅上升，且壁面发生了更为严重的磨损。
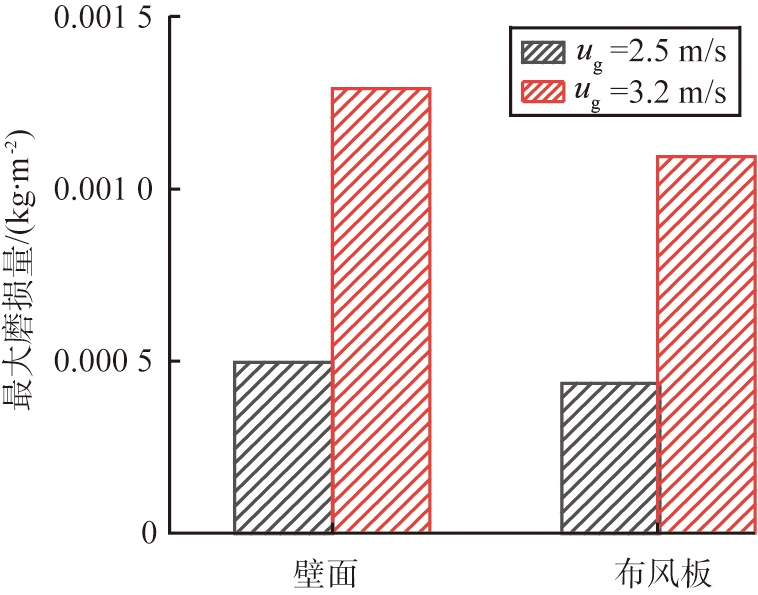
图5 不同操作条件下壁面及布风板最大磨损量
Fig.5 Maximum wear of wall and air distributor under different regimes of operation
图6给出了旋流流化床在不同运行状态下运行5 s时，壁面磨损情况的云图。为方便比较，将柱形壁面展开为平面。从图中可以看到，旋流流化床中壁面磨损发生在反应器下方，但在接近布风板的位置磨损却较轻。稳定旋流状态下壁面磨损位置未发生变化，但磨损区域中心处磨损明显增强，可见运行状态并不会对发生磨损的位置造成影响。
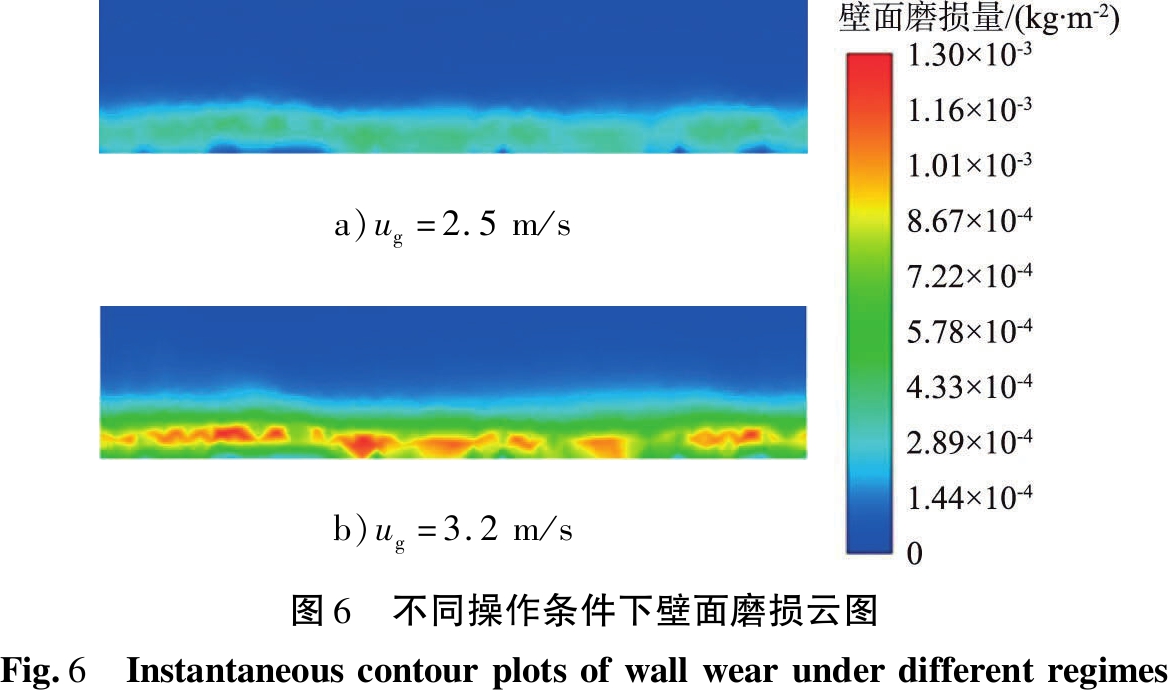
a)ug=2.5m/sb)ug=3.2m/s图6 不同操作条件下壁面磨损云图Fig.6 Instantaneouscontourplotsofwallwearunderdifferentregimes
图7给出了旋流流化床在不同运行状态下运行5 s时，壁面局部磨损量随高度的变化趋势，从图中可以看出，磨损集中发生在高度为0.1 m以下的区域，布风板附近壁面磨损最为剧烈，表观气速的增大使布风板上方磨损量剧烈增大，但峰值所处高度未发生变化，在其余区域，壁面磨损量并不会因运行状态的变化而变化。可见在旋流流化床的实际运行过程中，布风板附近的磨损更应得到重视。
2.3 床层-壁面传热行为
为验证本文中所建立模型的准确性与可行性，对旋流床床层与壁面之间的传热系数进行了统计，并与Tawfik等[10]的实验数据进行比较，结果如图8所示。由图可以看出，在不同操作速度下，模型所预测的传热系数与实验数据较为吻合，其误差来源可能为模型忽略了颗粒的尺寸分布。另外，实验中被加热的空气携带热量进入流化床之前，可能会产生一些能量损失。总体上来说，模拟结果与实验数据相对误差小于10%，在可接受的范围内，本模型可用于旋流流化床传热过程的预测。
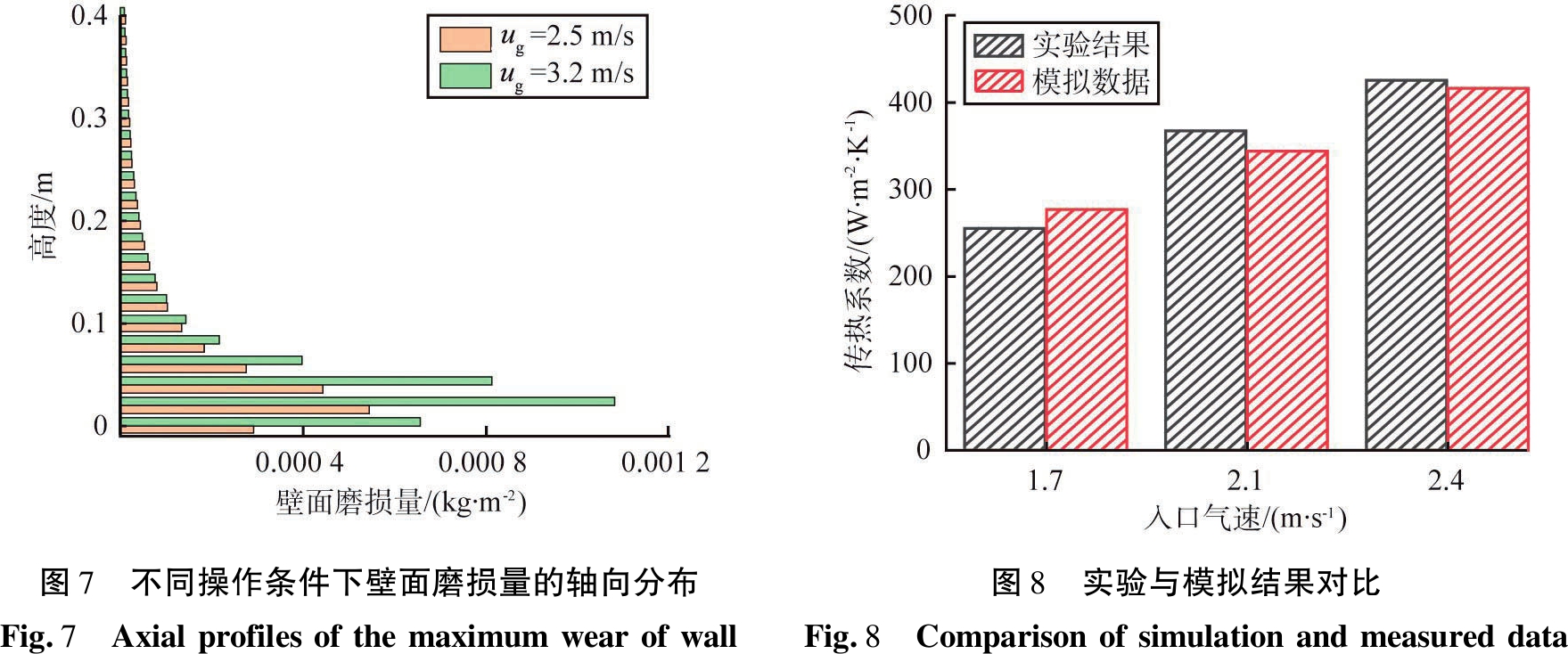
图7 不同操作条件下壁面磨损量的轴向分布Fig.7 Axialprofilesofthemaximumwearofwall图8 实验与模拟结果对比Fig.8 Comparisonofsimulationandmeasureddata
旋流流化床通过引入切向气流分量，有效增强了气固混合，同样会对传热过程产生影响。为探究操作速度对旋流流化床床层与壁面间传热行为的影响，待旋流床内床层与壁面之间的传热行为稳定后，对旋流流化床不同高度处床层及壁面温度进行统计如图9所示。从图中可以看出，旋流床壁面温度沿轴向向上逐渐减小。进口气速较小时，壁面温度变化幅度较大，这是因为床层颗粒的存在强化了床层与壁面之间的传热，使进口附近壁面温度较高，而出口附近只有气相与壁面的对流换热，所以温度较低。另外，操作速度的增大降低了壁面温度变化幅度，而床层温度基本一致，在轴向上变化并不明显。
图10给出了不同操作速度下，旋流流化床内床层与壁面之间的传热系数的轴向变化。图中传热系数沿轴向向上逐渐减小，因底部旋流运动较强，导致传热系数的明显变化。随着高度的增加，旋流运动减弱，使得温度的变化趋于稳定状态。操作速度增大后，传热系数整体上有所增大，这意味着可以通过提高旋流流化床操作速度来获得更好的传热性能。进口气速较小时，传热系数随轴向高度的变化较为明显，变化幅度较大。另外，操作速度增大传热系数在轴向上的变化幅度减小，这是由床内颗粒的运动增强，混合强度增大所致。
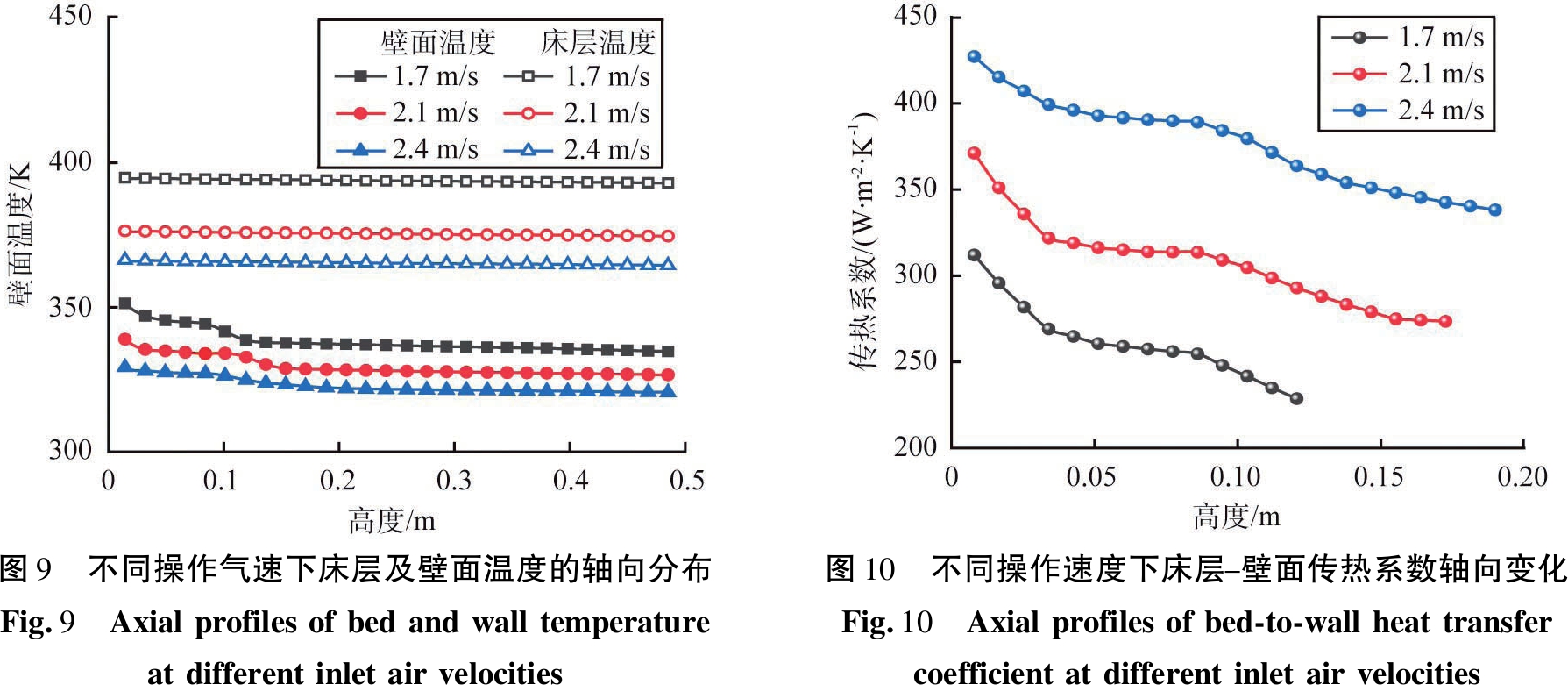
图9 不同操作气速下床层及壁面温度的轴向分布Fig.9 Axialprofilesofbedandwalltemperatureatdifferentinletairvelocities图10 不同操作速度下床层-壁面传热系数轴向变化Fig.10 Axialprofilesofbed-to-wallheattransfercoefficientatdifferentinletairvelocities
2.4 相间传热特性
床层温度由气相温度和颗粒温度构成，而气相与颗粒之间的温差导致了相间热传递过程的产生。此过程对于颗粒性质的变化较为敏感，在本研究中，颗粒相为小密度大颗粒与大密度小颗粒组成的二元混合物。图11给出了不同进口气速下砂粒相间传热系数的轴向分布。从图中可以看到，在不同的进口气速下，砂粒的对流传热系数在轴向上变化明显，且传热系数随操作速度增大而增大。另外，观察到进口附近有峰值产生。这是因为旋流床内底层颗粒的旋流运动带来良好的气固接触，有效促进了气固相间换热，而进口气速的上升使相间传热系数在轴向上的变化幅度明显减小。从颗粒的分布情况上来看，在旋流床进口附近，砂粒均有较明显的聚集现象，且有强烈的扬析。
图12给出了不同进口气速下PE颗粒相间传热系数的轴向分布。从整体上看，PE颗粒的对流传热系数要小于砂粒的，沿轴向传热系数的变化较小，且其相间传热系数不随操作速度变化而变化。由此可见，尺寸较小的颗粒对操作速度的变化更加敏感，同时有更强的相间传热性能。另外，轴向上PE颗粒的分布较为均匀，在进口处聚集的颗粒较少。
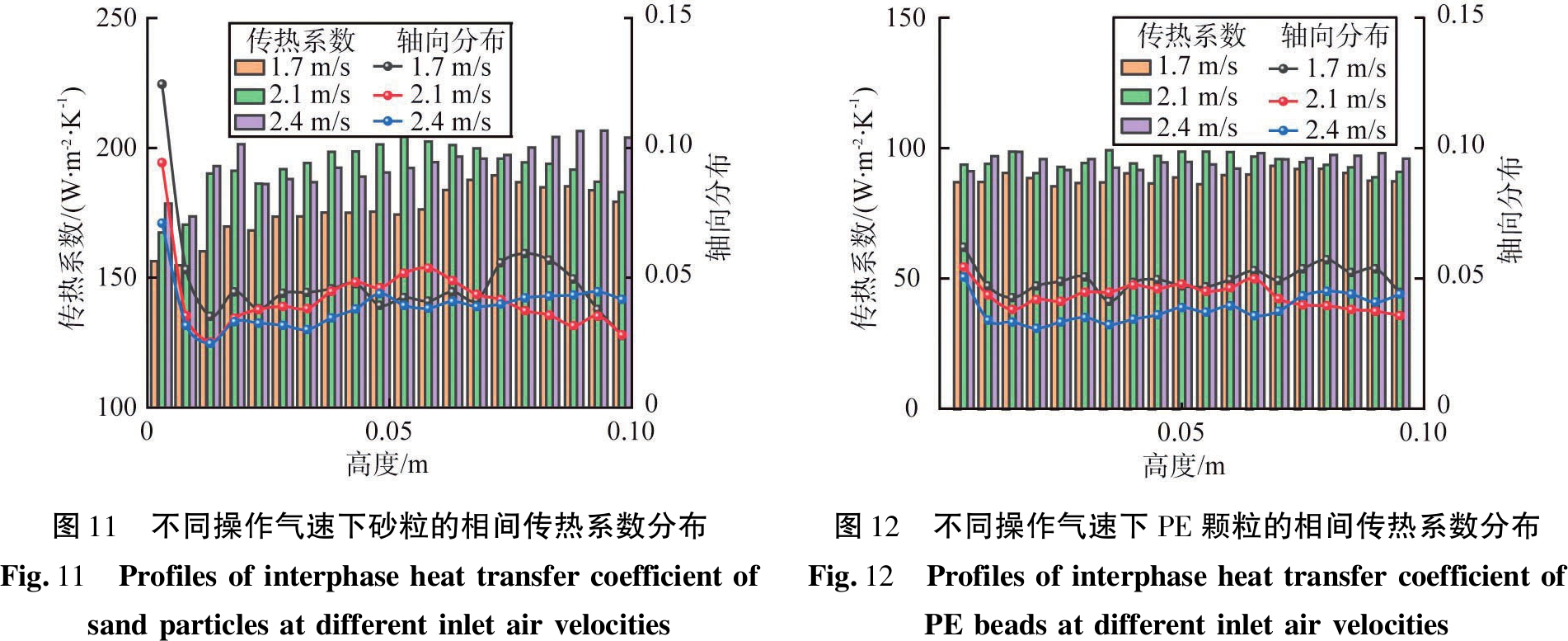
图11 不同操作气速下砂粒的相间传热系数分布 Fig.11 Profilesofinterphaseheattransfercoefficientof sandparticlesatdifferentinletairvelocities 图12 不同操作气速下PE颗粒的相间传热系数分布Fig.12 ProfilesofinterphaseheattransfercoefficientofPEbeadsatdifferentinletairvelocities
3 结论
1)所建立的流动及传热模型与实验结果吻合较好，具有较高的可行性。旋流流化床床层空隙率分布以及颗粒旋流速度大小对于操作速度的变化较为敏感。旋流流化床中壁面的磨损最为严重，操作速度的变化使磨损量大幅上升；但是不会影响磨损发生的位置，因此应重视旋流流化床反应器中布风板附近区域的磨损行为。
2)旋流流化床中，旋流运动的产生有效强化了床层-壁面传热过程。对于二元混合物，小颗粒相较于大颗粒表现出了更好的相间传热性能。
3)旋流流化床内，操作速度的增大有效增强了床层-壁面的传热过程，而小尺寸颗粒在流动及传热过程之中对于操作速度的变化更为敏感。
[1]WANG S, YIN W, LIU S, et al. Numerical studies of mass transfer performance in fluidized beds of binary mixture[J]. Applied Thermal Engineering, 2019, 158: 113465.
[2]ZHANG Y, ZHAO Y, GAO Z, et al. Experimental and Eulerian-Lagrangian-Lagrangian study of binary gas-solid flow containing particles of significantly different sizes[J]. Renewable Energy, 2019, 136: 193-201.
[3]NAKAMURA H, TOKUDA T, IWASAKI T, et al. Numerical analysis of particle mixing in a rotating fluidized bed[J]. Chemical Engineering Science, 2007, 62(11): 3043-3056.
[4]MITROFANOVA O V. Hydrodynamics and heat transfer in swirling flows in channels with swirlers (analytical review)[J]. High Temperature, 2003, 41(4): 518-559.
[5]AWORINDE S M, HOLLAND D J, DAVIDSON J F. Investigation of a swirling flow nozzle for a fluidised bed gas distributor[J]. Chemical Engineering Science, 2015, 132(18): 22-31.
[6]CHUWATTANAKUL V, EIAMSA-ARD S. Hydrodynamics investigation of pepper drying in a swirling fluidized bed dryer with multiple-group twisted tape swirl generators[J]. Case Studies in Thermal Engineering, 2019, 13: 100389.
[7]LU P, CAO Y, PAN W P, et al. Heat transfer characteristics in a horizontal swirling fluidized bed[J]. Experimental Thermal and Fluid Science, 2011, 35(6): 1127-1134.
[8]MOHIDEEN M F, SREENIVASAN, SULAIMAN S A, et al. Heat transfer in a swirling fluidized bed with Geldart type-D particles[J]. Korean Journal of Chemical Engineering, 2012, 29(7): 862-867.
[9]SIRISOMBOON K, LAOWTHONG P. Experimental investigation and prediction of heat transfer in a swirling fluidized-bed combustor[J]. Applied Thermal Engineering, 2019, 147(25): 718-727.
[10]TAWFIK M H M, REFAAT D M, MOHMED A H. Heat transfer and hydrodynamics of particles mixture in swirling fluidized bed[J]. International Journal of Thermal Sciences, 2020, 147: 106-134.
[11]TAWFIK M H M, REFAAT D M, MOHMED A H. Heat transfer and bed dynamics study on a swirling fluidized bed under various inlet configurations[J]. International Journal of Thermal Sciences, 2020, 158: 106523.
[12]FINNIE I. Erosion of surfaces by solid particles[J]. Wear, 1960, 3(2): 87-103.
[13]BITTER J G A. A study of erosion phenomena part I[J]. Wear, 1963, 6(1): 5-21.
[14]OKA Y I, OKAMURA K, YOSHIDA T. Practical estimation of erosion damage caused by solid particle impact[J]. Wear, 2005, 259(S1/2/3/4/5/6): 95-101.
[15]WANG S, XU S, LIU S, et al. Prediction of sorption-enhanced reforming process on hydrotalcite sorbent in a fluidized bed reactor[J]. Energy Conversion and Management, 2019, 180(15): 924-930.
[16]GIDASPOW D. Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. New York: Academic Press, 1994.
[17]JAIN V, KALO L, KUMAR D, et al. Experimental and numerical investigation of liquid-solid binary fluidized bed: radioactive particle tracking (RPT) technique and DDPM simulations[J]. Particuology, 2017, 33: 112-122.
[18]CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 2008, 30(3): 331-336.