旋风分离器是一种极其重要的颗粒分离设备,在火力发电、石油、化工、水泥、钢铁、冶金等工业领域应用广泛。虽然旋风分离器具有结构简单,内部无转动部件,造价低、占地小、易操作维修,适用于高温、高压,且浓度较高的工艺气体等优点;然而,由于其内部颗粒分离过程涉及一种极为复杂的三维、 气固强旋流运动, 理论与试验研究困难很大, 因此至今仍无法建立一套完整的数学模型指导其结构设计工作[1]。 如何通过优化旋风分离器结构、 匹配尺寸, 实现旋风分离器性能提升是其结构设计的难点。
压降和分离效率是优化旋风分离器结构设计、 性能评价的重要指标。自1886年旋风分离器的首次应用以来,国内外已开发了几种用于计算压降和分离效率的模型,包括基于力平衡和停留时间等的理论或半经验模型、统计模型、计算流体力学(CFD,computational fluid dynamics)模型。 理论或半经验模型[2]是由物理描述和数学方程推导出来, 需非常详细地了解旋风气流中气体流动结构和能量耗散机制。 例如, Stairmand模型通过动量平衡获得速度分布, 并结合旋风气流中静压的损失, 估算进口和出口压降损失[3]。 该模型忽略入口损失, 假设摩擦系数恒定, 且不考虑颗粒质量载荷对压降的影响。 而与Stairmand模型等其他模型相比, Muschelknautz模型既考虑了壁面粗糙度, 又考虑了质量载荷和雷诺数对旋风分离器性能的影响, 此外还考虑旋风中的气流速度变化[4]。 由于不同理论或半经验模型是基于不同的假设和简化条件提出的, 导致不同模型的预测结果, 以及预测结果和测量结果之间均存在显著差异。 此外, 统计模型在1980年就被作为计算旋风分离器压降的另一种方法。 由Casal等[5]和Dirgo等[6]基于不同结构的旋风分离器压降数据, 采用多元回归分析方法建立统计模型。虽然统计模型能够预测旋风压降, 但受限于实验数据和统计方法, 一方面很难确定最合适的相关函数对实验数据进行拟合, 另一方面模型的外推性也存在一定的缺陷。
近年来,CFD数值模拟手段作为气固两相流系统分析的有效工具,为旋风分离器结构优化提供了一种新的方法[7-11]。Elayed等[12]采用CFD数值模拟方法对比了基于Stairmand模型[3]和Muschelknautz模型[4]优化改造后的旋风分离器性能。Sgrott等[13]采用CFD数值模拟方法对旋风分离器结构进行优化。李强[14]、曹晴云[15]、Karagoz 等[16]、赵新学等[17]、高翠芝等[18]采用CFD数值模拟方法研究了排气管插入深度、排尘口直径、排气管直径等结构参数以及气速等操作条件对旋风分离器气相流场的影响规律。Gong等[19]、Gronald等[20]、Winfield等[21]、付烜等[22]采用CFD数值模拟方法研究了入口类型、入口结构、气速等对旋风分离器气固流动行为和性能的影响。上述研究大多数只考察了单因素的影响,没有考虑多因素的交互作用。熊攀等[23]虽然采用CFD数值模拟方法,结合响应曲面模型,以排尘口直径、排气口直径、入口速度作为设计变量,进行三因素的优化设计分析,但仅考察了排尘口直径、排气口直径对旋风性能的影响。
国内外学者对旋风分离器内流场特性、 结构优化、 尺寸比例进行了大量研究[24-27], 并在旋风分离器的分离机理、 性能计算模型[6,26-28]、 设计优化方法和工程运行状况检查等方面取得重大进展, 然而, 针对旋风分离器,系统地研究其结构参数及参数间交互作用对其性能的影响鲜有报道。本文中采用CFD-DPM(discrete particle model)数值模拟方法, 结合响应曲面法(RSM), 保持筒体直径不变, 以入口高度、 入口宽度、 排气管直径、 旋风分离器长度、 中心筒高度、 排气管插入深度、 排尘口直径为设计变量, 以压降和总分离效率为目标函数, 对上述7个结构参数尺寸比例进行设计优化, 研究各结构参数的影响程度, 以及各结构参数之间的交互作用, 为提高旋风分离器性能和优化设计提供理论指导。
1 模拟对象
本文中参考熊攀等[23]以及Elayed等[12]研究,采用 Stairmand型旋风分离器[3]作为模拟对象,其几何结构如图1所示,其中入口高度a为145 mm,入口宽度b为58 mm, 中心筒直径D为290 mm, 中心筒高度h为435mm, 旋风分离器长度Ht为1 160 mm, 排气管插入深度S为145 mm,排尘口直径Dc为107.3 mm,排气管直径Bx为145 mm,排气管高度Le为145 mm,进口管长度Li为290 mm。
旋风分离器中湍流行为的准确描述是CFD成功模拟的关键,因此湍流模型的选择至关重要。Hoekstra等[30]对比不同湍流模型的模拟结果发现,雷诺应力模型能较好地预测组合涡的结构,适用于气旋流场的计算。本文中所涉及的模拟工况中气流处于湍流状态,因此,在本文中湍流模型采用RSM模型。控制方程采用有限体积法离散,通过SIMPLEC算法求解压力与速度耦合。气体和固体入口均采用速度入口,气、固出口边界条件为压力出口,具体见表1,其他的模拟参数参考Khairy等[16]的研究报道。颗粒粒径的累积分布采用式(1)来描述。
(1)
式中: F为颗粒粒径的累积分布函数; d为颗粒粒径。
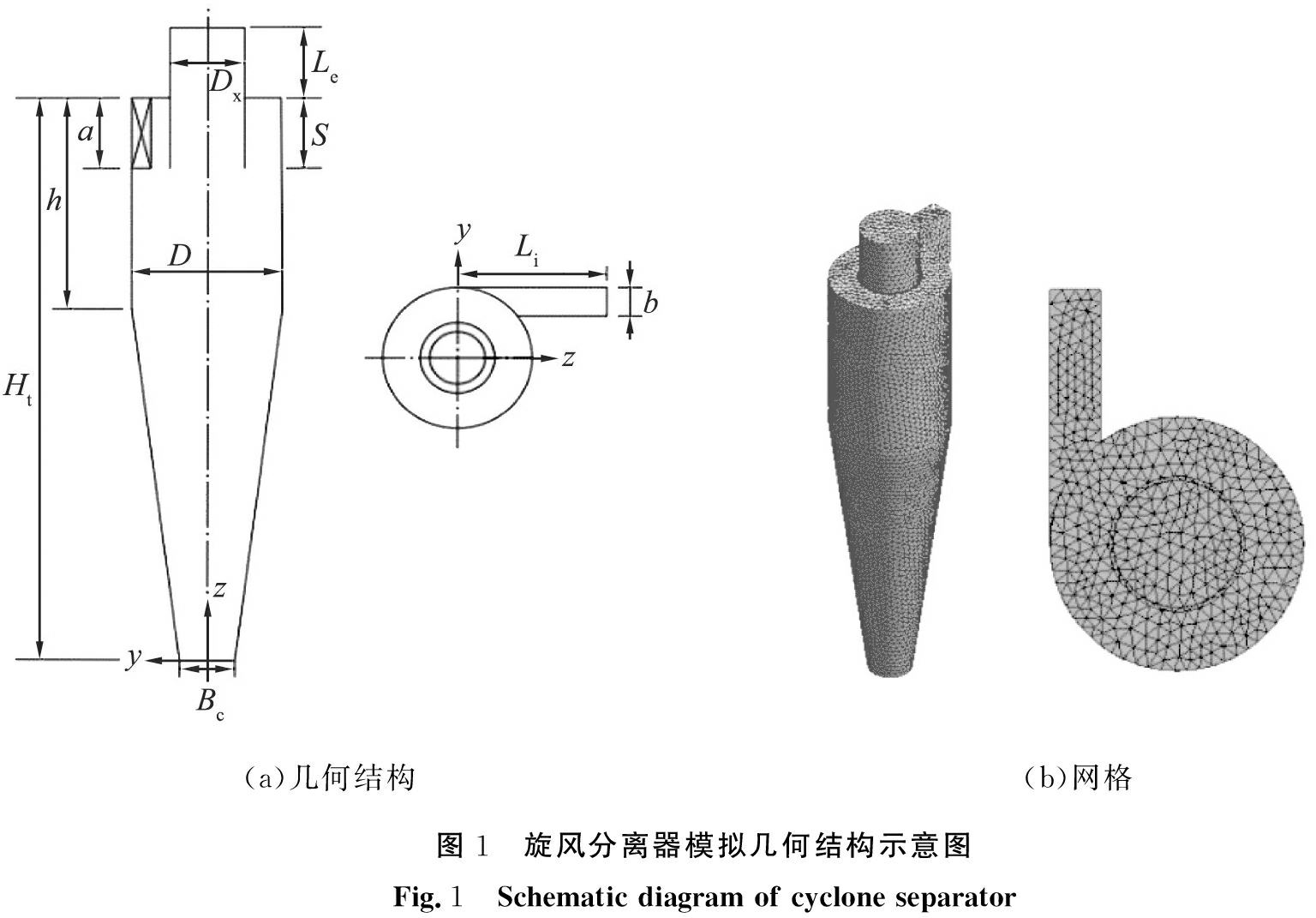
(a)几何结构(b)网格图1 旋风分离器模拟几何结构示意图Fig.1 Schematic diagram of cyclone separator
表1 模拟条件
Tab.1 Simulational conditions

参数数值参数数值颗粒粒径/μm0.5~10.0入口气速/(m·s-1)8.0、16.0颗粒密度/(kg·m-3)1 450.0气、固相温度/K293.0气体密度/(kg·m-3)1.205时间步长/s1.0×10-4气体运动黏度/(Pa·s)1.79×10-5模拟时间/s20.0出口压力/Pa101 325
2 CFD-DPM模型
本文中采用基于欧拉-拉格朗日框架下的CFD-DPM方法对旋风分离器进行数值模拟研究。 在CFD-DPM方法中, 气相被视为连续的流体, 采用Navier-Stocks方程进行描述; 离散相通过追踪颗粒运动轨迹求解, 颗粒运动方程[31]见式(2)—(5); 由于旋风分离器中颗粒浓度较低, 因此气体与颗粒间的相间作用力采用Muschelknautz等[32]提出的曳力模型来描述。
(2)
(3)
(4)
(5)
式中: Rep为颗粒的雷诺数; up和upi分别为颗粒的速度和第i个颗粒的速度, m/s; u和ui分别为气相速度和第i个颗粒的气相速度, m/s; FD为颗粒群的曳力系数, s-1;CD为单颗粒的曳力系数, s-1; μ为气体黏度, Pa·s; ρ和ρp分别为气体密度和颗粒密度, kg/m3; gpi为第i个颗粒的重力加速度, m/s2; t为时间, s; dp为颗粒的粒径。
3 基于响应曲面模型的模拟工况设计
响应曲面模型作为一种强大的统计分析技术,适应于响应受多个变量影响,且各变量间又存在交互作用的复杂多变量体系的建模,目标是优化响应。
本文中基于响应曲面模型进行模拟工况的设计,选取了a、 b、 Dx、 Ht、 h、 S、 Bc,对应的无量纲结构参数(与中心筒直径的比值):a/D、 b/D、 Dx/D、 Ht/D、 h/D、 S/D、 Bc/D的取值范围,包括最小取值、中间取值、最大取值,见表2,其中, D保持不变。采用CFD-DPM模拟计算的压降和分离效率,作为模拟工况设计的响应,利用响应曲面模型进行多元回归拟合,以压降和总分离效率为目标函数,研究上述7个结构参数对它们的影响。
由于结构参数间的交互作用对本研究很重要,因此采用拟合二阶多项式最常见的设计方法——中心复合设计(CCD)方法[33]。根据表2中7个结构参数对应的取值范围,得到63种结构组合,并对这些组结构分别采用CFD进行建模、网格划分、模拟计算,获取对应的压降和总分离效率,以便进一步预测参数间的非线性交互作用。
表2 结构参数取值范围
Tab.2 Values of geometrical parameters m
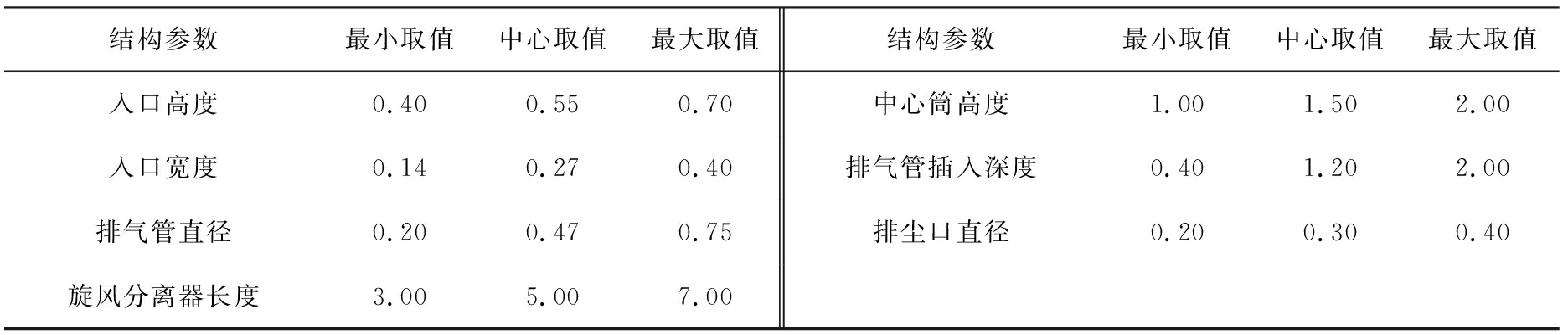
结构参数最小取值中心取值最大取值结构参数最小取值中心取值最大取值入口高度0.400.550.70中心筒高度1.001.502.00入口宽度0.140.270.40排气管插入深度0.401.202.00排气管直径0.200.470.75排尘口直径0.200.300.40旋风分离器长度3.005.007.00
基于上述CFD模拟结果,构建响应曲面模型,用于生成响应面曲线。具体步骤是:首先找出响应变量和独立变量之间的函数关系,通常用二阶多项式表示,进一步利用最小二乘拟合得到多项式模型的系数,响应变量
(6)
式中: Y为响应变量;b0、 bi、 bij、 bii分别为截距、线性系数、交互作用系数、二次项系数; xi、 xj分别为设计变量。
最后,在进行多项式回归前,按下式进行归一化,将变量归一化到区间[0,1],得到
(7)
式中: Xorig、 Xnorm分别为设计变量的初始值和归一化值。
4 结果与讨论
4.1 模型验证
在工业过程中,总分离效率通常是一个最常用的评价指标。本文中采用CFD-DPM模拟计算过程中,通过在旋风分离器入口释放一定数量的单分散颗粒,监测从出口逃逸的颗粒数量来获得。为了验证数学模型的准确可靠性,对比了入口气速为8 m/s时,分离效率随粒径变化的模拟结果和试验数据,如图2所示。由图可知,采用CFD-DPM模型的预测值与试验值吻合较好, 说明该模型可以较为准确地预测旋风分离器性能。
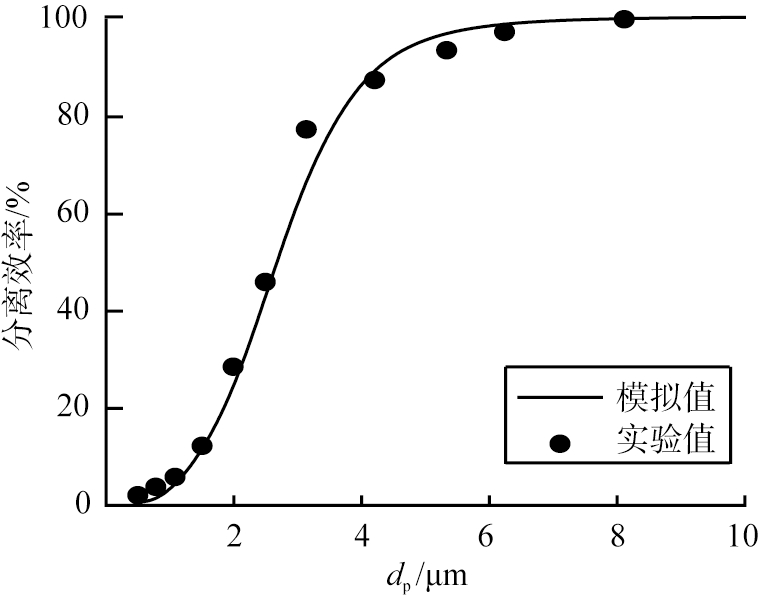
图2 对比分离效率的实验与模拟结果
Fig.2 Comparison of separation efficiency between
experimental and simulation data
4.2 方差分析
表3呈现了方差分析结果。其中,A为a/D、 B为b/D、 C为Dx/D、 D为Ht/D、 E为h/D、 F为S/D、 G为Bc/D, AB表示A、 B 2个因素的交互作用, A^2表示A因素的二次项的影响。多元决定系数R2用来衡量模型对数据的拟合近似程度。由表可知,压降和分离效率的R2分别为0.954 1和0.980 8,均接近1,表明所建立的二次多项式模型能够较准确地描述所研究的独立变量对响应的影响。
图3对比了旋风的压降和效率的CFD-DPM模拟计算结果和多项式模型预测结果。由图可看出,本文中所建立的多项式模型的预测结果和CFD-DPM的模拟结果吻合较好,进一步证明了该模型的准确性。
表3中的F值和P值可用于评价二次多项式模型中各变量的显著性。 当F值越大, P值较小(通常小于0.05)时, 模型中该变量对响应有显著影响, 当P值大于0.1时, 该变量的影响不显著。 由表3可知, 在一次项中, 对压降影响最大的结构参数是排气管直径, 然后分别是入口高度、 入口宽度及旋风分离器长度, 而中心筒高度、 排气管插入深度及排尘口直径的影响不显著(P>0.05)。 在二次项中, 排气管直径和入口高度、 排气管直径和入口宽度对压降也有显著影响(P<0.05), 其余5项的影响不显著。 入口高度与排气管直径, 及入口宽度与排气管直径的交互作用对压降的影响较为显著(P<0.000 1), 其余项的交互作用影响不显著。
此外, 由表3可知, 在一次项中, 对分离效率影响最大的结构参数也是排气管直径, 然后分别是入口高度和入口宽度、 旋风分离器长度及排气管插入深度, 而中心筒高度和排尘口直径的影响不显著(P>0.05)。 在二次项中, 入口高度、 旋风分离器长度及排气管插入深度对分离效率也有显著影响(P<0.05), 其余4项的影响不显著。旋风分离器长度与排气管插入深度,入口宽度与排气管直径,入口宽度与旋风分离器长度,及排气管直径与旋风分离器长度的交互作用对分离效率的影响较为显著(P≤0.000 1), 其余项的交互作用影响不显著。
表3 基于响应曲面方法的方差分析
Tab.3 Analysis of variance based on response surface method
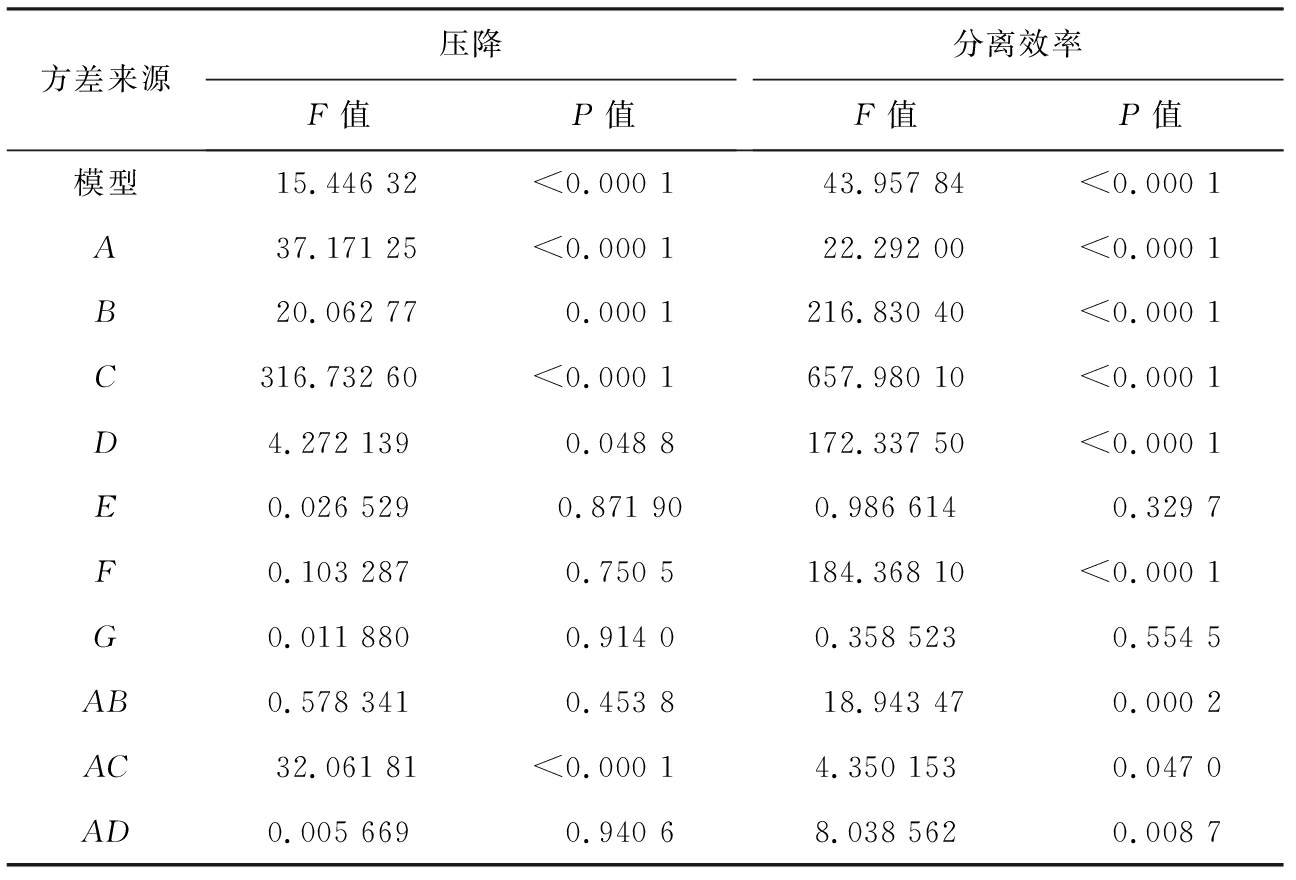
方差来源压降F值P值分离效率F值P值模型15.446 32<0.000 143.957 84<0.000 1A37.171 25<0.000 122.292 00<0.000 1B20.062 770.000 1216.830 40<0.000 1C316.732 60<0.000 1657.980 10<0.000 1D4.272 1390.048 8172.337 50<0.000 1E0.026 5290.871 900.986 6140.329 7F0.103 2870.750 5184.368 10<0.000 1G0.011 8800.914 00.358 5230.554 5AB0.578 3410.453 818.943 470.000 2AC32.061 81<0.000 14.350 1530.047 0AD0.005 6690.940 68.038 5620.008 7
续表

方差来源压降F值P值分离效率F值P值AE0.002 0780.964 00.007 3120.932 5AF0.001 0480.974 40.020 080.888 4AG0.000 0560.994 10.003 290.954 7BC24.561 88<0.000 126.512 53<0.000 1BD0.001 8770.965 822.819 11<0.000 1BE0.000 0040.998 30.007 3490.932 3BF0.000 1780.989 50.277 690.602 7BG0.000 0020.998 90.002 6370.959 4CD3.650 2050.067 119.762 730.000 1CE0.019 2640.890 70.046 860.830 3CF0.016 1990.899 712.095 640.001 8CG0.011 2440.916 40.015 4060.902 2DE0.000 6380.980 00.048 9730.826 6DF0.004 3790.947 745.165 56<0.000 1DG0.002 5840.959 90.010 8150.918 0EF0.000 0400.995 00.024 3310.877 3EG0.000 1290.991 00.018 9540.891 6FG0.000 0100.997 60.005 8550.939 6A^20.011 6470.914 90.665 370.422 1B^25.193 6710.031 193.819 17<0.000 1C^284.378 56<0.000 10.266 9290.609 8D^20.104 0080.749 737.091 03<0.000 1E^20.022 4880.882 01.186 4080.286 0F^20.089 0530.767 84.682 2660.039 8G^20.018 4390.893 00.139 8360.711 5残差8.172 581191.266 130 4R20.954 10.980 8
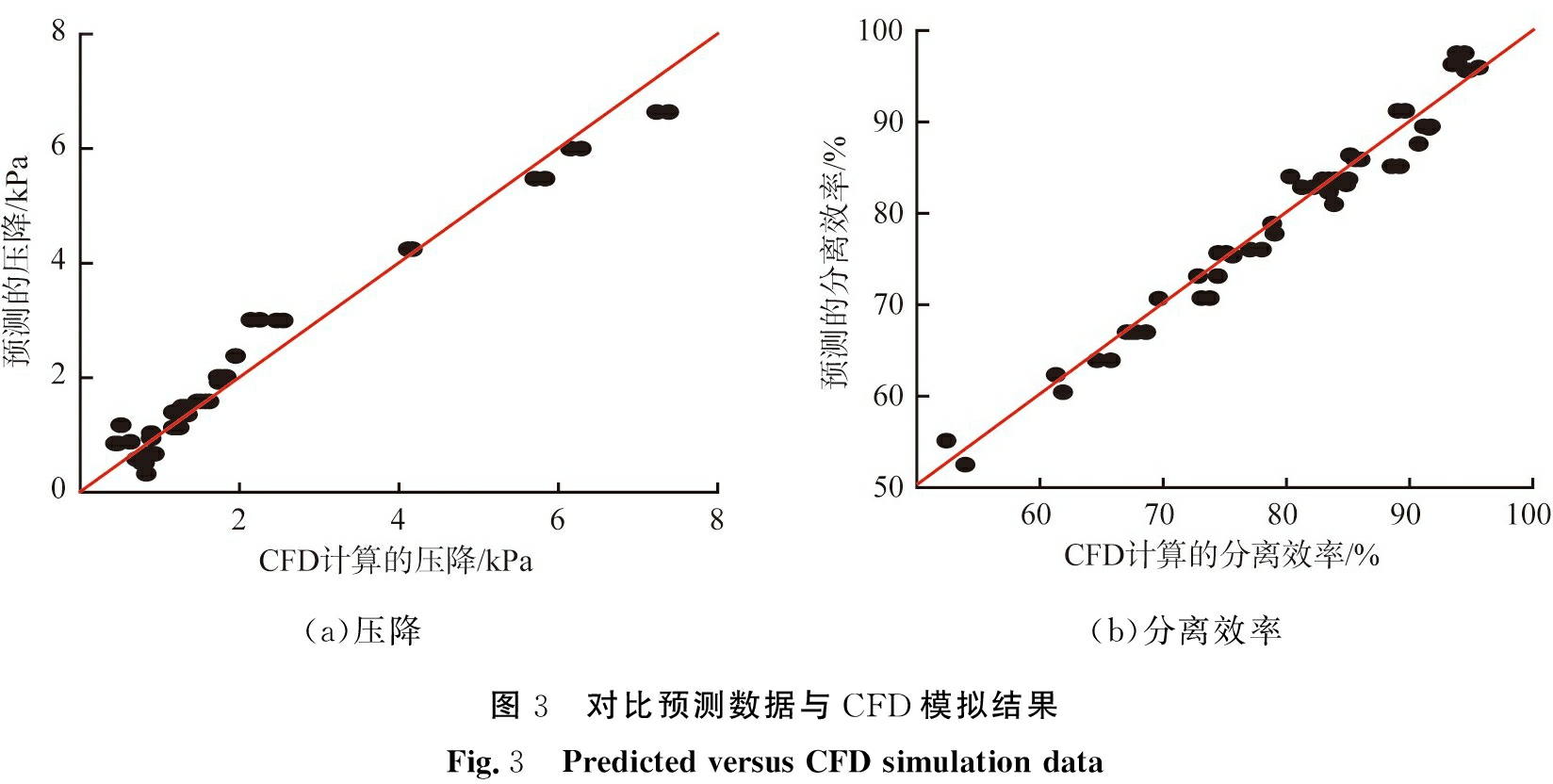
(a)压降(b)分离效率图3 对比预测数据与CFD模拟结果Fig.3 Predicted versus CFD simulation data
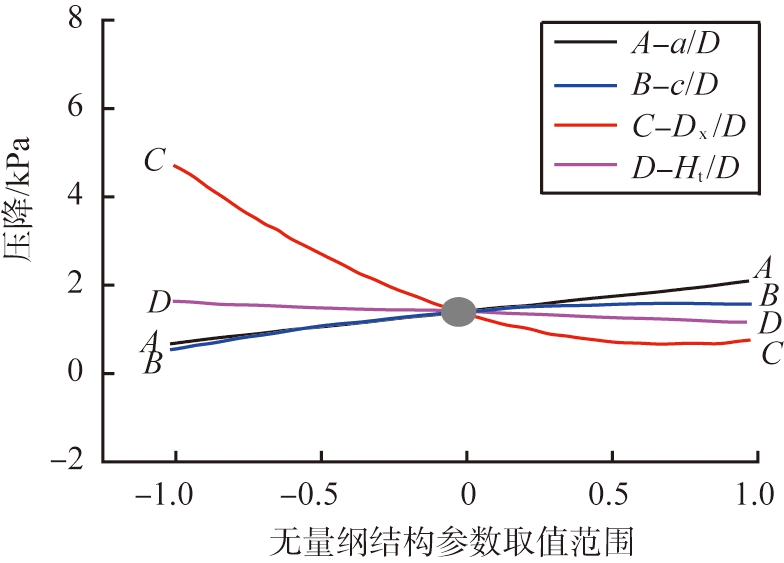
图4 不同影响因素对压降影响及其交互作用
Fig.4 Effect of different factors and their
interactions on pressure drop
4.3 结构参数对旋风分离器性能的影响
4.3.1 压降
为了能够在单个图中呈现所有设计变量对响应的影响,将上述对压降影响较大的无量纲结构参数进行归一化,并作出归一化后的结构参数对压降影响的扰动图,见图4。
非平行线和交叉线说明了这些变量之间存在不同程度的交互作用,且曲线越趋于陡坡或弯曲表明响应对该因素越敏感,而相对平坦的线则表明对该因素的变化不敏感。由图可知,对压降影响最显著的结构参数为排气管直径,随着归一化后的排气管直径由-1.0增加到1.0,压降降低了6.25倍。同时,不同结构参数间存在一定的交互作用,尤其是入口高度和排气管直径,以及入口宽度和排气管直径之间的交互作用较为显著,这也与表3的研究结果相一致。
图5和图6分别显示了其他结构参数取值为其变化范围的中间值时, 入口高度与排气管直径, 以及入口宽度与排气管直径对压降影响的交互作用。 首先, 由响应曲面图可知, 曲线的趋势均为非线性, 说明两组结构参数中的每对结构参数对压降的影响存在很强的交互作用, 与表3的统计结果相一致。 在本文中所考察的入口高度和入口宽度范围内, 压降均随排气管直径的增大而减小, 其原因主要是随着排气管直径的增大, 经排尘口分离后的上升气流的通流面积加大, 气流在排气管内剧烈的旋转时, 气流与排气管内壁之间的摩擦减小, 使得压力损失降低。
此外,由图5和图6可知,压降随入口高度或宽度的增大而增大,主其原因要是在相同的入口气速下,入口高度或者宽度增加均会使入口面积增大,单位时间内进入旋风分离器的气体量增加,引起旋转速度增加,造成流体内摩擦阻力以及流体与器壁间摩擦阻力增大,进而使得压降增大。
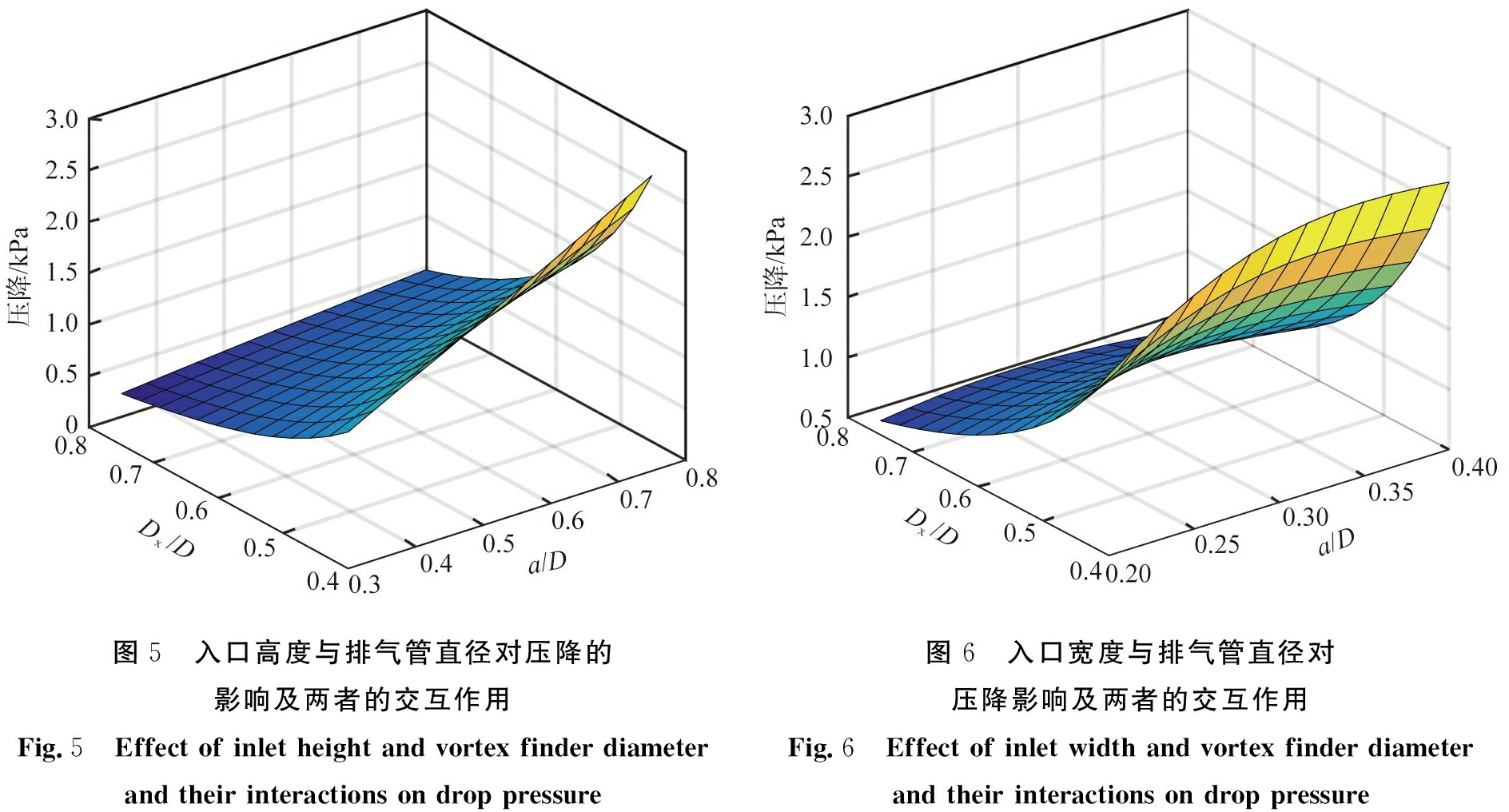
图5 入口高度与排气管直径对压降的影响及两者的交互作用Fig.5 Effect of inlet height and vortex finder diameter and their interactions on drop pressure图6 入口宽度与排气管直径对压降影响及两者的交互作用Fig.6 Effect of inlet width and vortex finder diameter and their interactions on drop pressure
4.3.2 分离效率
进一步将上述对分离效率影响较大的无量纲结构参数进行归一化,并作出归一化后的结构参数对分离效率影响的扰动图,如图7所示。由图可知,对分离效率影响最显著的结构参数也是排气管直径,随着归一化后的排气管直径由-1.0增加到1.0,分离效率降低了29.28%。此外,旋风分离器长度以及排气管插入深度对分离效率也有较强的影响,随着归一化后的Ht/D和S/D分别由-1.0增加到1.0, 对应的分离效率分别增加了20.67%,降低了16.81%,且不同结构参数间存在较强的交互作用,这也与表3的研究结果相一致。
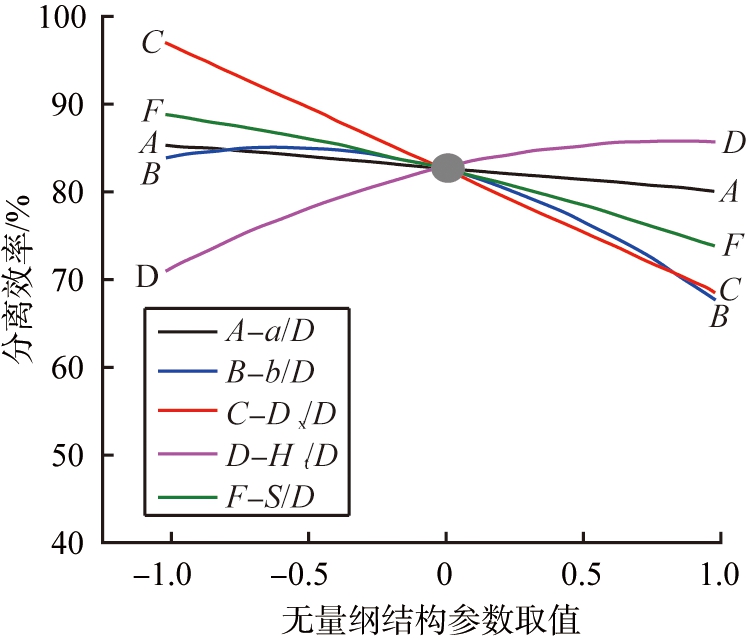
图7 不同影响因素对分离效率影响和其交互作用
Fig.7 Effect of different factors and their
interactions on separation efficiency
图8显示了其他结构参数取值为其变化范围的中间值时,排气管插入深度与旋风分离器长度对分离效率的影响及两者的交互作用。首先,由图可知,曲线的趋势为非线性,说明排气管插入深度与旋风分离器长度对压降的影响存在很强的交互作用,这也与表3的统计结果相一致。总体而言,在本文中考察的旋风分离器长度范围内,分离效率随排气管插入深度的增大而减小,尤其是在较小的旋风分离器长度下,分离效率对排气管插入深度的变化更加敏感。由于旋风除尘器内部的三维强旋流是在排气管与筒体内壁之间运动,排气管插入深度直接影响到旋风除尘器的性能。Hoffmann等[34]也指出,较好的设计原则是将排气管插入深度延伸至入口底板的位置,可同时兼顾制造和维修费用,以及应力、压力损失、短路等问题。
图9—11分别显示了入口宽度与排气管直径、入口宽度与旋风分离器长度、及排气管直径与旋风分离器长度对分离效率的影响及其两者的交互作用。由响应曲面图可知,曲线的趋势为非线性,说明所考察的2个因素对压降的影响存在很强的交互作用,这也与表3的统计结果相一致。在本文中所考察的排气管直径和旋风分离器长度范围内,入口宽度增大,分离效率均下降。这是由于在相同的入口气速下,入口宽度增加均会使入口面积增大,单位时间内进入旋风分离器的气体量增加,使得含尘气体因旋转而产生的动能及动量均增加,有利于颗粒的分离;然而,由于切向速度增大,旋风分离器边壁处的速度梯度增大,因此边壁处速度剪切层内的微涡增强,边壁处沉积颗粒容易被卷扬,不利于分离。上述两者相互作用、共同影响,使得分离效率随着入口宽度的增加而下降。
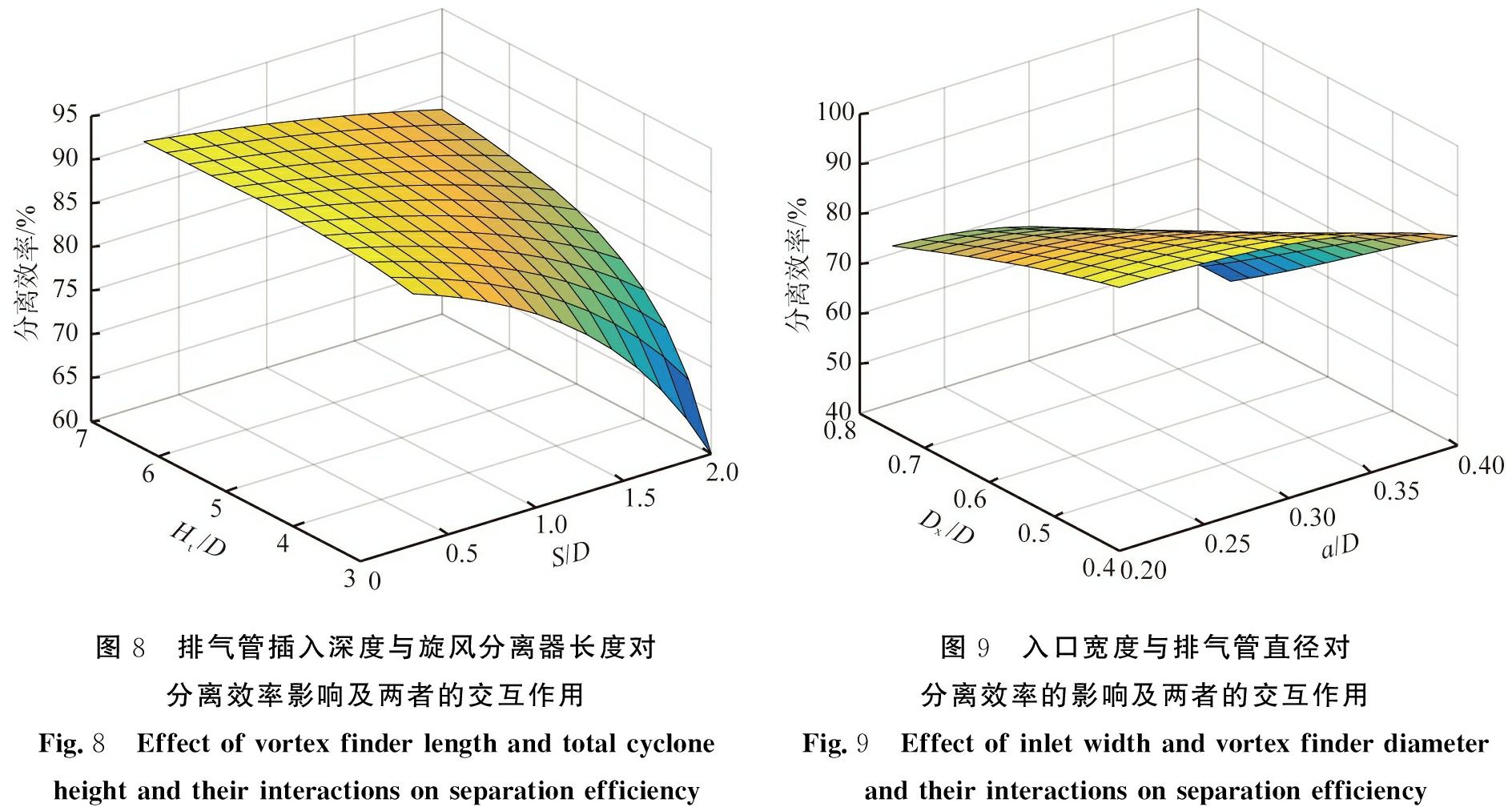
图8 排气管插入深度与旋风分离器长度对分离效率影响及两者的交互作用Fig.8 Effect of vortex finder length and total cyclone height and their interactions on separation efficiency图9 入口宽度与排气管直径对分离效率的影响及两者的交互作用Fig.9 Effect of inlet width and vortex finder diameter and their interactions on separation efficiency
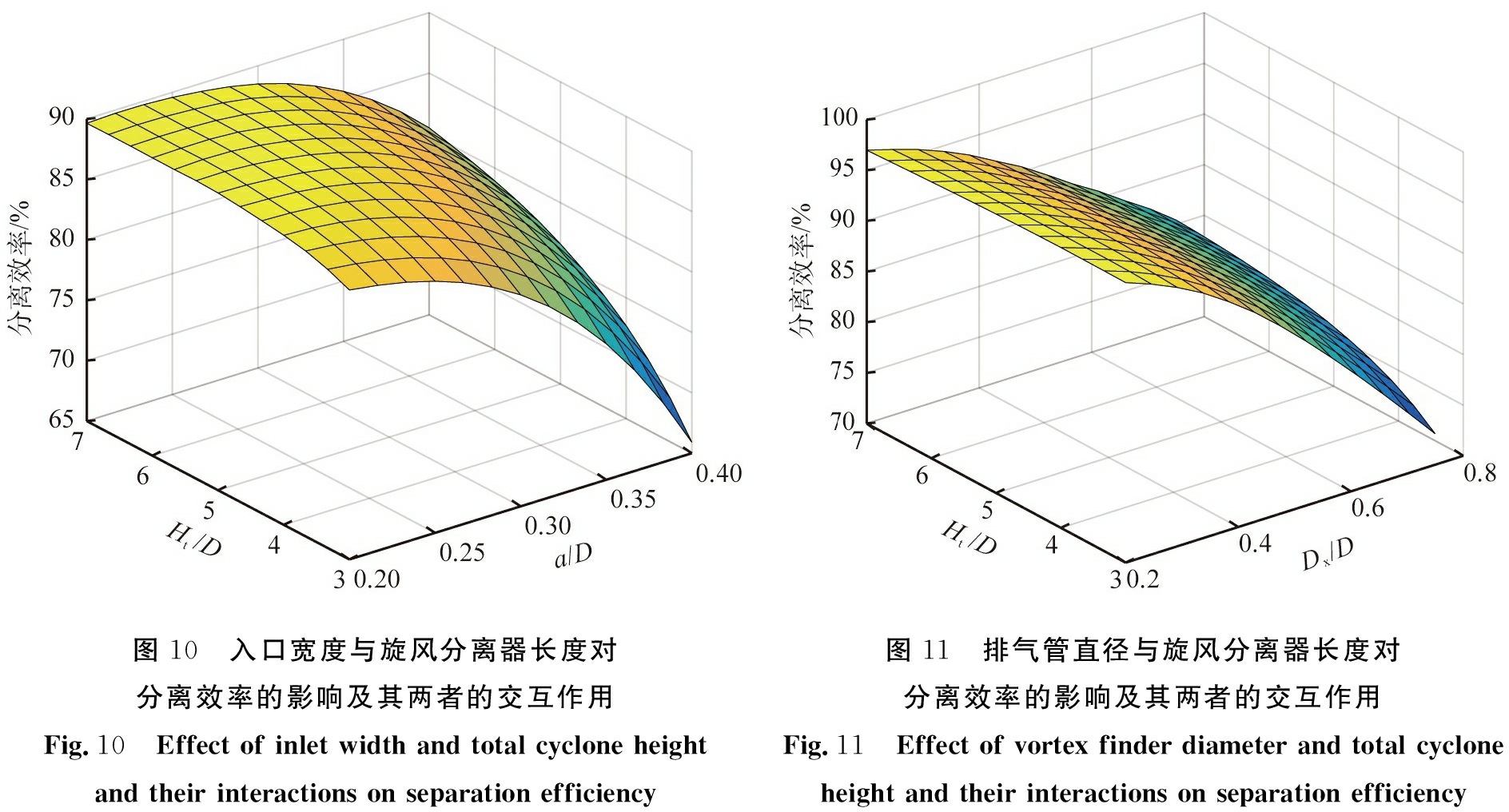
图10 入口宽度与旋风分离器长度对分离效率的影响及其两者的交互作用Fig.10 Effect of inlet width and total cyclone height and their interactions on separation efficiency图11 排气管直径与旋风分离器长度对分离效率的影响及其两者的交互作用Fig.11 Effect of vortex finder diameter and total cyclone height and their interactions on separation efficiency
由图9和图11可知,在本文中所考察的入口宽度和旋风分离器长度范围内,分离效率随排气管直径的减小而增大。这是由于排气管直径减小,分离空间断面的下降流量增加,含尘空气在旋风分离器内的停留时间增长,这些都有利于作高速旋转运动颗粒的分离,尤其是在较大的入口宽度以及较小旋风分离器长度下,分离效率对排气管直径的变化更加敏感。
此外,由图8、 10、 11可知,分离效率随旋风分离器长度的增大而增大,尤其是在较大的排气管插入深度、入口宽度以及排气管直径下,分离效率对旋风分离器长度的变化更加敏感。
4.4 结构参数优化
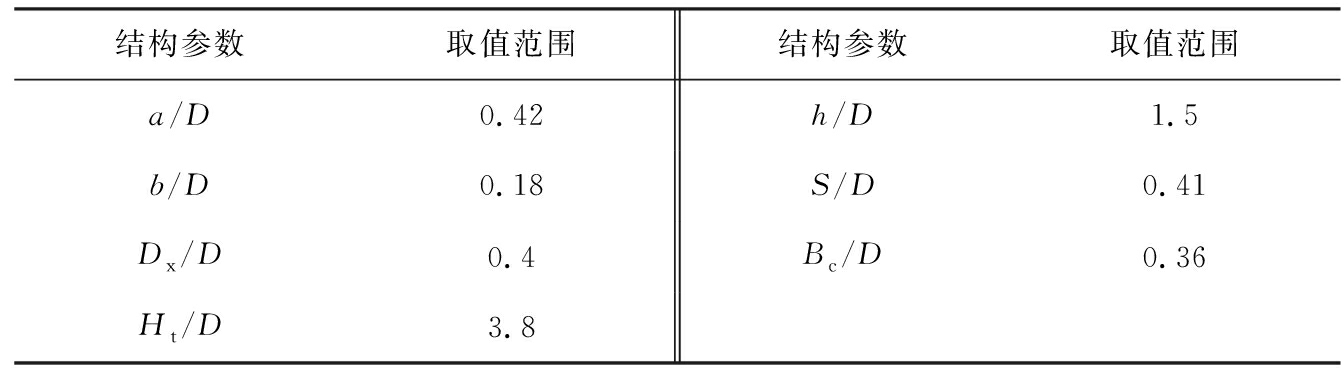
进一步对上述CFD-DPM的模拟计算结果进行数据分析,根据所考察的7个结构参数对压降和分离效率影响的显著性及其交互作用,将压降与分离效率的比例设置为相同,同时得到最低压降和最优分离效率对应的结构参数,如表4所示,对应的压降为1.67 kPa,分离效率为95.60%。
表2 结构参数取值范围
Tab.2 Geometrical parameters values based on CFD-DPM coupled with RSM
结构参数取值范围结构参数取值范围a/D0.42h/D1.5b/D0.18S/D0.41Dx/D0.4Bc/D0.36Ht/D3.8
5 结论
1)通过与实验结果的对比,本文中所建立的CFD-DPM模型能较为准确地预测旋风分离器的分离性能。在后续的结构优化过程中,采用CFD-DPM模型,结合响应曲面分析方法,构建多组工况进行模拟研究,获取不同结构参数下的旋风分离器压降和分离效率。
2)在CFD-DPM模拟结果的基础上,以压降和总分离效率为响应变量,进行多元回归拟合,并结合响应曲面法分析各结构参数及其交互作用对压降和分离效率的影响。压降和分离效率对排气管直径的变化最敏感,表明对压降和分离效率影响最显著的结构参数均为排气管直径。此外,入口高度、入口宽度、旋风分离器长度以及排气管插入深度对压降和分离效率也有显著影响。
3)从各结构参数的变化对压降和分离效率的响应曲面图来看,各结构参数之间存在不同程度的交互作用,入口宽度和入口高度与排气管直径之间的交互作用对压降的影响较为显著;旋风分离器长度与排气管插入深度、入口宽度与排气管直径、入口宽度与旋风分离器长度及排气管直径与旋风分离器长度对分离效率的影响存在较强的交互作用,其余项的影响不显著。
4)从各结构参数间的交互作用来看,在本文中所考察的结构参数范围内,压降随排气管直径的增大而急剧减小,随入口高度或宽度的增大而增大。分离效率随入口宽度、排气管直径的减小而提高,尤其是在较大的入口宽度以及较小旋风分离器长度下;分离效率随旋风分离器长度的增大而提高,尤其是在较大的排气管插入深度、入口宽度以及排气管直径下;分离效率随排气管插入深度的减小而提高,尤其是在较小的旋风分离器长度下,分离效率对排气管插入深度的变化更加敏感。
5)基于CFD-DPM模拟计算结果获得该旋风分离器在最小压降和最大效率下对应的几何结构比,即在a/D、 b/D、 Dx/D、 Ht/D、 h/D、 S/D、 Bc/D取值分别为0.42、 0.18、0.4、3.8、1.5、 0.41、0.36时,对应的压降为1.67 kPa,分离效率为95.60%。
6)上述研究结论对于无量纲入口高度、入口宽度、排气管直径、排气管插入深度、旋风分离器长度、中心筒高度、排尘口直径取值处于一定范围内的旋风分离器的结构优化均具有一定的普适性和实际应用价值。
[1]郑晨雨. 新型旋风分离器的理论分析及实验验证[D]. 武汉: 华中科技大学, 2011.
[2]LI E, WANG Y. A new collection theory of cyclone separators[J]. AICHE J, 1989, 35: 666-669.
[3]STAIRMAND C J. Pressure drops in cyclone separators[J]. Industrial & Engineering Chemistry, 1949, 16(B): 409-411.
[4]MUSCHELKNAUTZ E, TREFZ M. Design and calculation of higher and highest loaded gas cyclones[C]//Proceedings of Second World Congress on Particle Technology, Kyoto, Japan, 1990: 52-71.
[5]CASAl J, MARTINEZ-BENET J M. A better way to calculate cyclone pressure drop[J]. Chemical Engineering, 1983, 90(2): 99-100.
[6]DIRGO J. Relationship between cyclone dimensions and performance[D]. Cambridge: Harvard University, 1988.
[7]KOSAKI Y, CHONO S. Time characteristics of dust collection and particle classification performance of a cyclone[J]. Powder Technology, 2017, 305: 602-608.
[8]SAFIKHANI H, MEHRABIAN P. Numerical study of flow field in new cyclone separators[J]. Advanced Powder Technology: The Internation Journal of the Society of Powder Technology, 2016, 27: 379-387.
[9]HUANG A Y, MAEDA N, SHIBAT D, et al. Influence of a laminarizer at the inlet on the classification performance of a cyclone separator[J]. Separation and Purification Technology, 2017, 174: 408-416.
[10]BRAR L S, ELAYED K. Analysis and optimization of multi-inlet gas cyclones using large eddy simulation and artificial neural network[J]. Powder Technology, 2017, 311: 465-483.
[11]WASILEWSKI M. Analysis of the effect of counter-cone location on cyclone separator efficiency[J]. Separation & Purification Technology, 2017, 179: 236-247.
[12]ELAYED K, LACOR C. Optimization of the cyclone separator geometry for minimum pressure drop using mathematical models and CFD simulations[J]. Chemical Engineering Science, 2010, 65(22): 6048-6058.
[13]SGROTT O L, NORILER D, WIGGERS V R, et al. Cyclone optimization by COMPLEX method and CFD simulation[J]. Powder Technology, 2015, 277: 11-21.
[14]李强. 旋风除尘器优化设计及分离特性研究[D]. 长沙: 中南大学, 2008.
[15]曹晴云. CFB锅炉旋风分离器内气固两相流动的数值模拟[D]. 青岛: 中国石油大学(华东), 2008.
[16]KARAGOZ I, KAYA F. CFD investigation of the flow and heat transfer characteristics in a tangential inlet cyclone[J]. International Communications in Heat & Mass Transfer, 2007, 34(9/10): 1119-1126.
[17]赵新学, 金有海. 排尘口直径对旋风分离器壁面磨损影响的数值模拟[J]. 机械工程学报, 2012, 48(6): 142-148.
[18]高翠芝, 孙国刚, 董瑞倩. 排气管对旋风分离器轴向速度分布形态影响的数值模拟[J]. 化工学报, 2010, 61(9): 2409-2416.
[19]GONG G, YANG Z, ZHU S. Numerical investigation of the effect of helix angle and leaf margin on the flow pattern and the performance of the axial flow cyclone separator[J]. Applied Mathematical Modelling, 2012, 36(8): 3916-3930.
[20]GRONALD G, DERKSEN J J. Simulating turbulent swirling flow in a gas cyclone: a comparison of various modeling approaches[J]. Powder Technology, 2011, 205(1/2/3): 160-171.
[21]WINFIELD D, CROSS M, CROFT N, et al. Performance comparison of a single and triple tangential inlet gas separation cyclone: a CFD study[J]. Powder Technology, 2013, 235(2): 520-531.
[22]付烜, 孙国刚, 刘佳, 等. 旋风分离器进口涡旋感生速度场的减阻增效作用[J]. 化工学报, 2011, 62(7): 1927-1932.
[23]熊攀, 鄢曙光, 刘玮寅. 基于响应曲面法的旋风分离器结构优化[J]. 化工学报, 2019, 70(1): 164-170.
[24]吴小林, 熊至宜, 姬忠礼, 等. 旋风分离器旋进涡核的数值模拟[J]. 化工学报, 2007, 58(2): 383-390.
[25]高助威, 王江云, 王娟, 等. 蜗壳式旋风分离器内部流场空间的涡分析[J]. 化工学报, 2017, 68(8): 3006-3013.
[26]CHUAH T G, GIMBUN J, CHOONG T S Y. A CFD study of the effect of cone dimensions on sampling aerocyclones performance and hydrodynamics[J]. Powder Technology, 2006, 162(2): 126-132.
[27]GAO X, CHEN J, FENG J, et al. Numerical investigation of the effects of the central channel on the flow field in an oil-gas cyclone separator[J]. Computers & Fluids, 2014, 92(9): 45-55.
[28]ZHAO B. Modeling pressure drop coefficient for cyclone separators: a support vector machine approach[J]. Chemical Engineering Science, 2009, 64: 4131-4136.
[29]CASAL J, MARTINEZ-BENE J M. A better way to calculate cyclone pressure drop[J]. Chemical Engineering, 1983, 90(2): 99-100.
[30]HOEKSTRA A J, DERKSEN J J, AKKER H. An experimental and numerical study of turbulent swirling flow in gas cyclones[J]. Chemical Engineering Science, 1999, 54(S13/14): 2055-2065.
[31]ZHAO B, SU Y, ZHANG J. Simulation of gas flow pattern and separation efficiency in cyclone with conventional single and spiral double inlet configuration[J]. Chemical Engineering Research and Design, 2006, 84: 1158-1165.
[32]MUSCHELKNAUTZ E. Die berechnung von zyklonabscheidern fur gas[J]. Chemie Ingenieur Technik, 1972, 44: 63-71.
[33]王晶. 基于响应曲面法的多响应稳健性参数优化方法研究[D]. 天津: 天津大学, 2009.
[34]HOFFMANN A C, STAIN L E. Gas cyclones and swirl tubes: principles, design and operation[J]. Applied Mechanics Reviews, 2007, 56(2): B28.