木制材料以其特有的固碳、 可再生、 可自然降解、 美观和调节室内环境等天然属性, 广泛地应用于造纸、 家居、 建筑、 交通等领域[1-3]。 目前市面上常见的板材有刨花板、 胶合板、 细木工板等, 虽然它们具有较好的实用性能得到多数人的认可, 但是这类板材通常会使用酚醛树脂类的粘合剂以达到增强硬度、 防潮以及防虫的目的, 以至于此类的复合板出现燃点低、 甲醛排放量高等问题危害人体的身心健康。
为了解决上述问题, 姜鹏等[4]采用阻燃脲醛树脂制备的刨花板改变木质材料的热降解路径, 实现提高阻燃效率的目的; 黄静等[5]研究的以铜粉为添加剂的木基复合材料能阻碍裂纹地生长, 在木基复合材料中起到了弥散强化作用, 增强了相应力学性能。
以上的学者对木制板材的强度与阻燃性进行了研究,但是,对常见的木制板材的防腐、甲醛释放量等问题进行的研究相对较少。
本文中所提到的多功能木制板材解决了以上所提到的问题,通过进行正交试验、 遗传算法最优求解以及Pareto多目标遗传算法最优求解,为多功能木制板材的制备提供了详细的实验数据与理论支撑,具有重要意义。
1 试验
1.1 材料和方法
原木粉(贵州省贵阳市);氯化镁、 氧化镁(纯度(质量分数,以下同)98%,上海麦克林生化科技有限公司);无机酸、有机酸和二氧化硅(纯度>90%,宇达化工)。
1.2 正交实验
1)方法
采用四因素三水平的正交实验设计方法研究原木粉、氯化镁、氧化镁和其他添加剂对多功能木制板材整体性能的影响,每个因素各取3个水平,按正交表L9(34)进行试验[6],用以求出最佳原料配比,正交试验因素和水平如表1所示。
表1 正交试验因素和水平
Tab.1 Orthogonal test factors and levels kg

水平各因素取值原木粉A质量氯化镁B质量氧化镁C质量其他D质量11000.210521250.4251031500.65020
2)结果与分析
在最优压制成形的外部条件下,根据表1中的各种条件,制备出可以供密度(ρ)、 静曲强度(σ)、 弹性模量(E)、 内结合强度(σ⊥)测试的试件,并且根据相应的国家标准进行试验和处理试验结果数据,见表2。表3为极差分析[6]结果,其中通过对4种因素进行求极差运算,根据极差的大小来衡量某种因素对试验结果的影响,极差越大说明所对应的因素越重要,由此可以确定出主、次要因素的排列顺序。综合考虑得出各因素对试验结果影响大小顺序,依次为氧化镁添加量、其他添加剂、氯化镁添加量与原木粉添加量。
表2 试验方案及结果
Tab.2 Test scheme and results
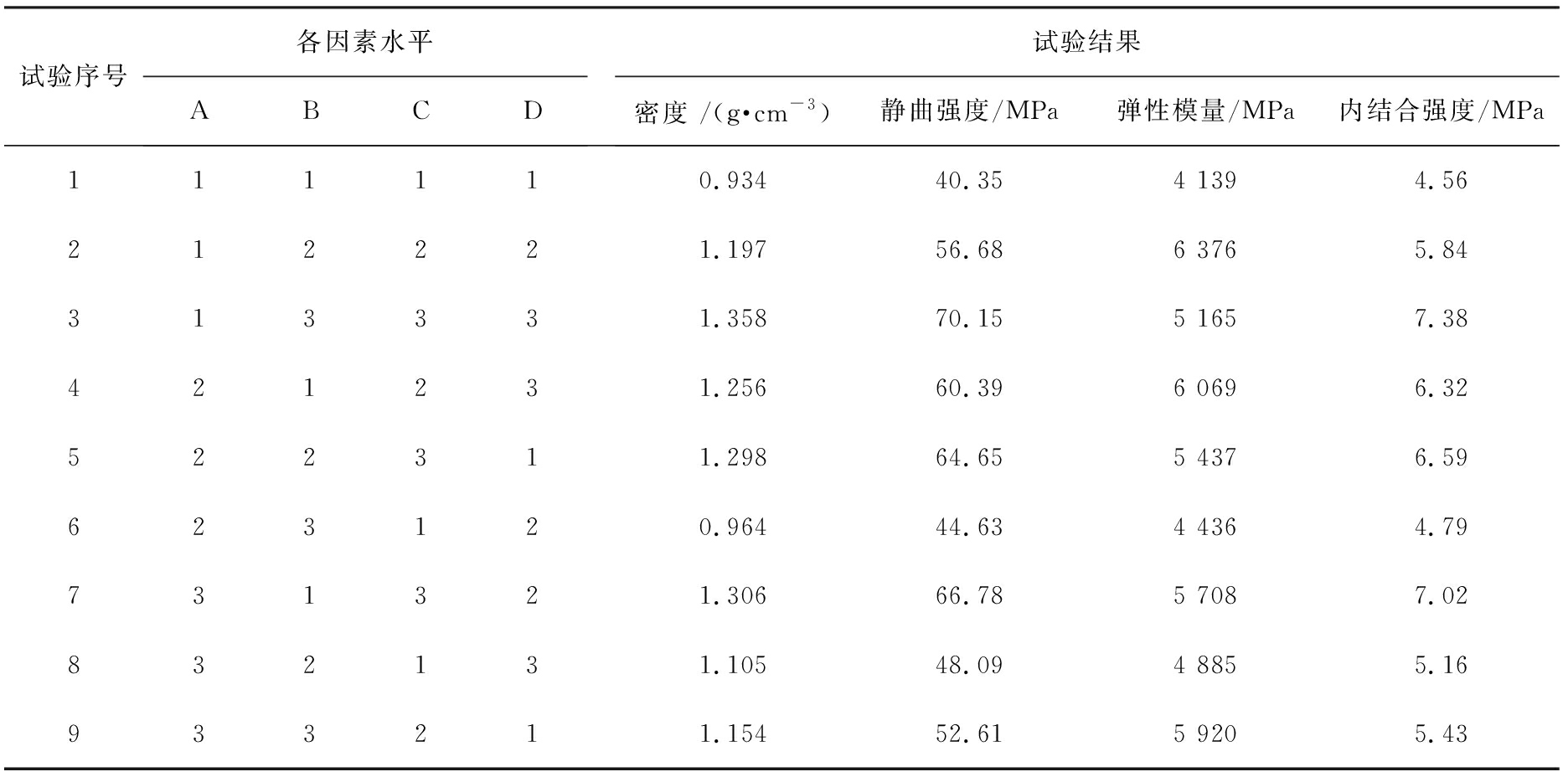
试验序号各因素水平ABCD试验结果密度 /(g·cm-3)静曲强度/MPa弹性模量/MPa内结合强度/MPa111110.93440.354 1394.56212221.19756.686 3765.84313331.35870.155 1657.38421231.25660.396 0696.32522311.29864.655 4376.59623120.96444.634 4364.79731321.30666.785 7087.02832131.10548.094 8855.16933211.15452.615 9205.43
表3 极差分析结果
Tab.3 Range analysis results
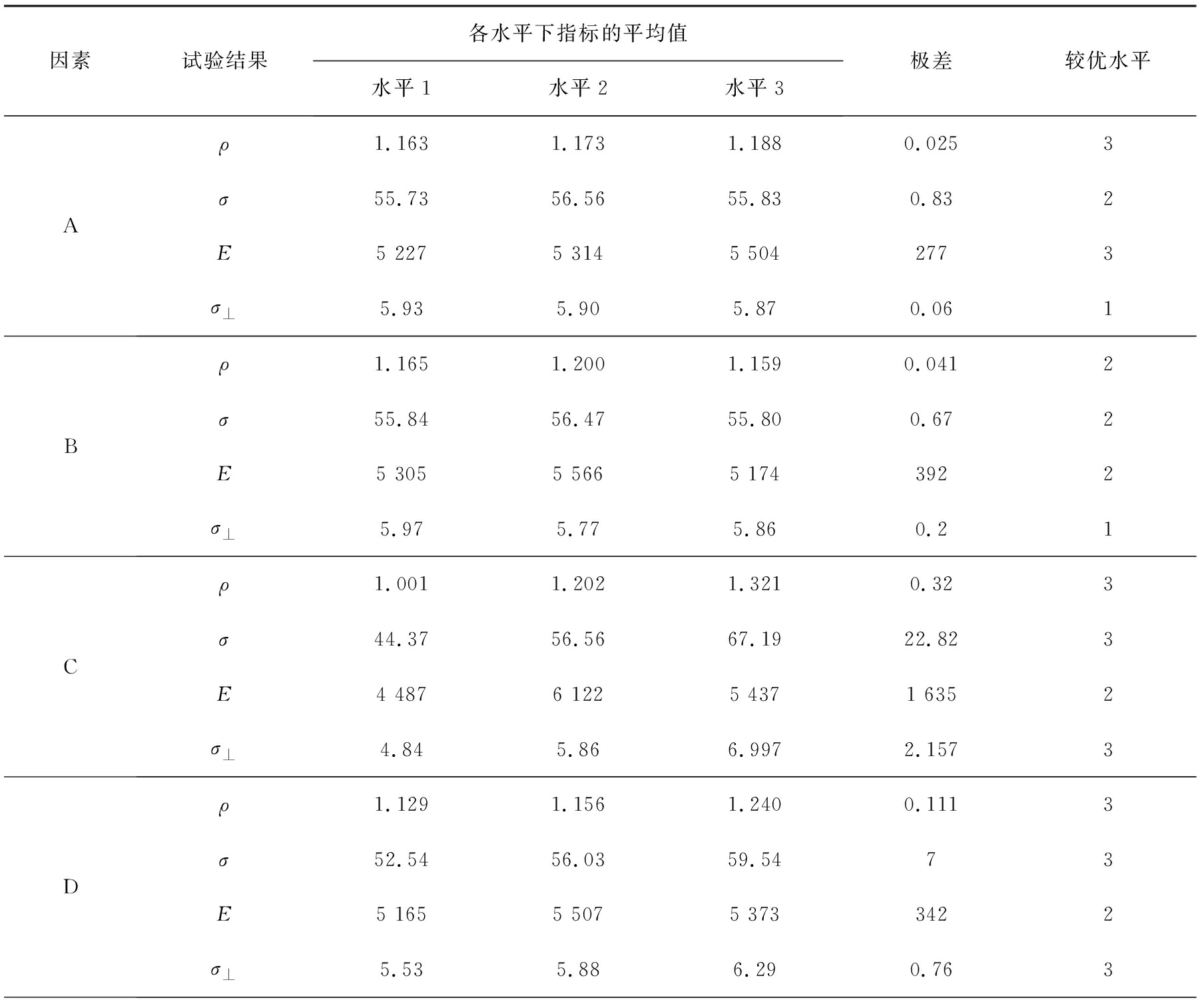
因素试验结果各水平下指标的平均值水平1水平2水平3极差较优水平Aρ1.1631.1731.1880.0253σ55.7356.5655.830.832E5 2275 3145 5042773σ⊥5.935.905.870.061Bρ1.1651.2001.1590.0412σ55.8456.4755.800.672E5 3055 5665 1743922σ⊥5.975.775.860.21Cρ1.0011.2021.3210.323σ44.3756.5667.1922.823E4 4876 1225 4371 6352σ⊥4.845.866.9972.1573Dρ1.1291.1561.2400.1113σ52.5456.0359.5473E5 1655 5075 3733422 σ⊥5.535.886.290.763
由于本文中所研究的多功能木制板材的检验标准使用一般木制板材的力学性能检测方法,故检测指标中的静曲强度、弹性模量与内结合强度的数值越大越好,取各水平指标下平均值的最大值的水平作为最优结果。由此得到原木粉添加量为150 kg、 氯化镁添加量为0.4 kg、 氧化镁添加量为50 kg、 其他添加剂为20 kg的最优配比结果。需要说明的是,最优的水平组合并不一定在由正交实验设计所指定的实验当中,所以,虽然正交试验得出结果速度快,但准确性不高,需要进一步研究。
2 基于遗传算法最优配比的数值优化
2.1 遗传算法的流程
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程自适应概率搜索算法[7-8],其流程如图1所示。
2.2 目标函数
由正交试验可知,选取密度、静曲强度、弹性模量和内结合强度作为检测标准。由于密度的大小只能反映了其本身的物理性质,对其本身的理化性能不能起到作用,故不作为评判标准考虑。静曲强度与弹性模量得到的结果类似,故取弹性模量作为评判标准。内结合强度反映了板材承受温度变化的能力,是重要的评判指标,故取弹性模量和内结合强度作为优化目标,其目标函数参数化的数学表达式[9]及约束条件分别为:
F1=max E[A, B, C, D],
(1)
F2=max σ[A, B, C, D],
(2)
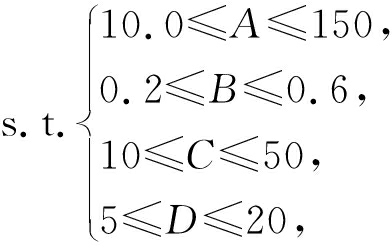
(3)
式中: F1、 F2均为目标函数参数优化的数学表达式; E表示弹性模量; σ⊥表示内结合强度; max为相应系数的最大值。
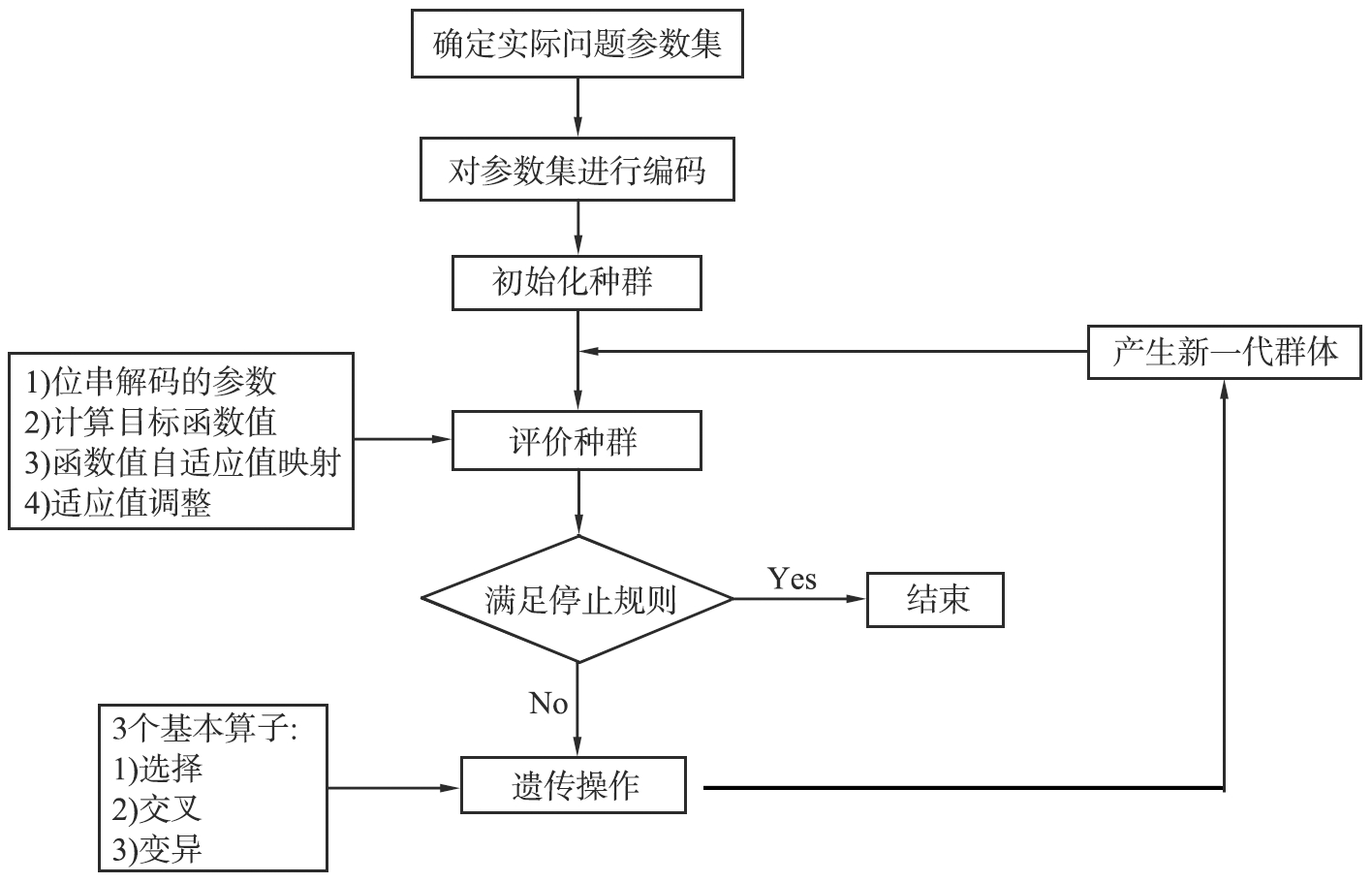
图1 遗传算法流程图
Fig.1 Flow chart of genetic algorithm
由于遗传算法最优解为最小值的特性,所以取式(4)的单目标模型作为目标函数。
Fmin=-(F1+F2),
(4)
选取初始种群大小M群=300,变量个数v=4,最大进化代数G=300,变异概率Pm=0.05,交叉概率Pc=0.95。
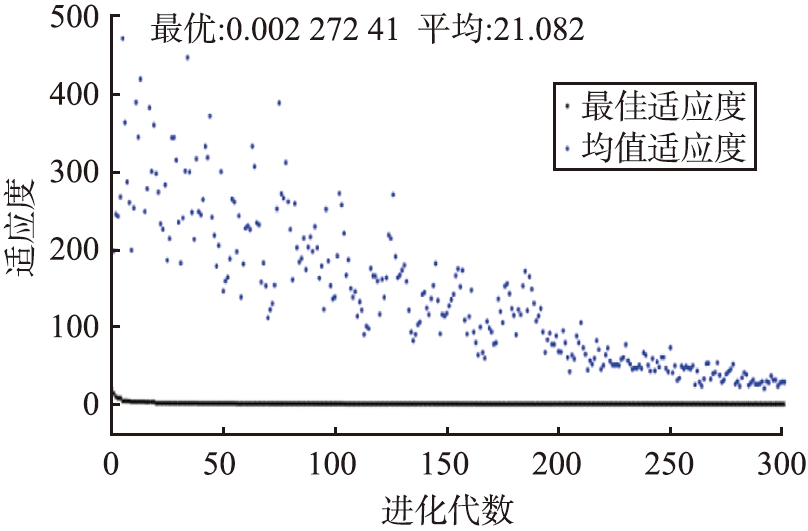
图2 目标函数值随进化代数的变化
Fig.2 Value of objective function varies
with evolutionary algebra
2.3 优化结果
经过遗传算法的优化处理与运算,得出最佳结果为:原木粉添加量为135 kg、 氯化镁添加量为0.36 kg、 氧化镁添加量为38.6 kg、 其他添加剂为16.7 kg,目标函数值随进化代数的变化如图2所示。
3 基于Pareto多目标遗传算法最优配比的数值优化
3.1 多目标优化问题
多目标优化[10-12]问题是对一个或者多个目标进行优化,目标之间通过决策变量相互联系在一起,在满足某些约束条件的情况下,使多个目标尽可能做到最优。
假设多目标优化问题由m个变量参数、 n个目标函数、 k个不等式约束条件和 l个等式约束条件组成, X为m维决策空间, Y为n维目标空间,则多目标优化问题数学描述如下:
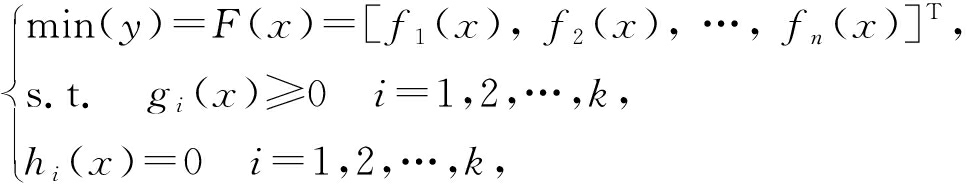
(5)
式中: x=[x1,x2,…,xm]∈X⊂Rm为决策变量; y=[y1,y2,…,yn]∈Y⊂Rn为目标向量; 目标函数F(x)表示n个映射函数, f ∶X→Y, gi(x)≥0,i=1,2,…,k和hi(x)=0, i=1,2,…,l分别为目标函数满F(x)足k个不等式的约束条件和1个等式的约束条件。
3.2 Pareto最优原理
一般情况下,针对多目标优化问题min fk(X),在约束条件下,存在设计变量可行域内的变量X,如果没有任何一个决策向量x对应的目标向量y优于决策向量x*对应的目标向量y*,使得y*=fk(X*)≤y=fk(X)成立,则x*∈X称为Pareto最优解[13-14]或非劣解。以双目标优化问题为例,将Pareto最优解或非劣解用线连接得到的曲线就为Pareto前沿,如图3所示。
根据上述情况,由Pareto多目标遗传算法得出Pareto的前沿数据见表4中的第1、2行。
3.3 Pareto遗传算法求解分析
与多数的遗传算法求解结果不同的是,运用Pareto多目标遗传算法求解得到的是一组非劣解,由于数量过多会影响最优结果的选择,所以运用下面的方法进行筛选。
由于本文中以双目标优化为研究目的,有max-min(min-max)和max-max(min-min)2种数学模型。由于所求目标函数均为求其极大值,采用max-max(min-min)模型。
1)首先,将Pareto所求出的前沿数据按照函数的大小依次编号(见图4),总共20个Pareto非劣解,其数值见表4。
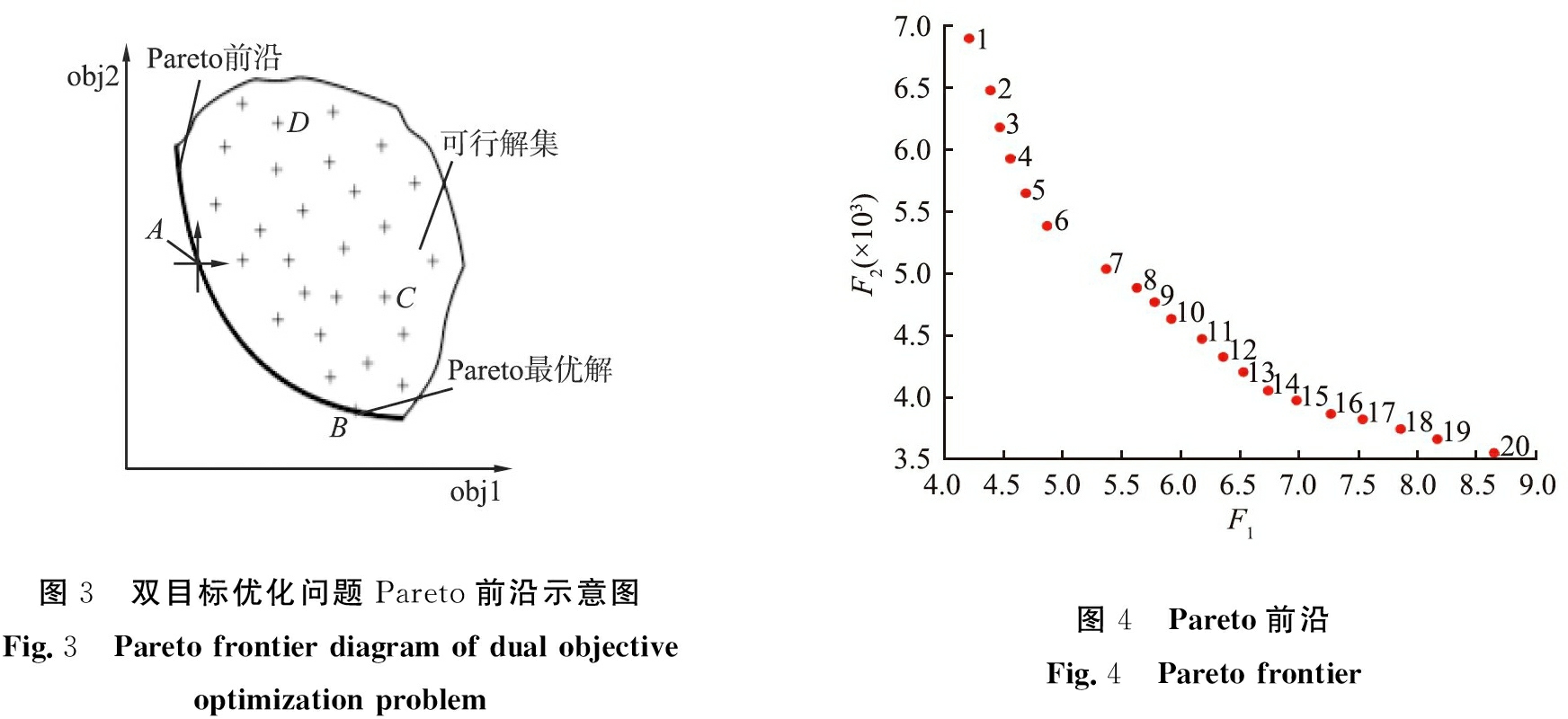
图3 双目标优化问题Pareto前沿示意图Fig.3 Pareto frontier diagram of dual objective optimization problem图4 Pareto前沿Fig.4 Pareto frontier
2)按式(6)—(8)计算平均变率,其数值见表4。
(6)
(7)
(8)
3)按式(9)和(10)计算灵敏度比[15],其数值见表4。
(9)
(10)
4)按式(11)、 (12)对灵敏比进行无量纲化[16]处理,其数值见表4。
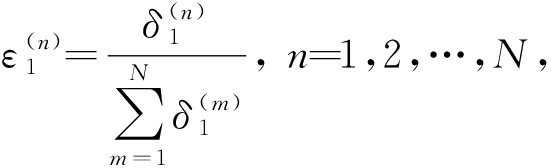
(11)
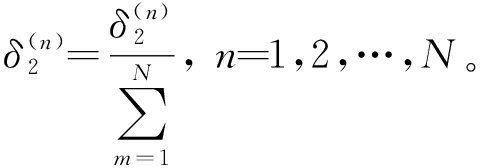
(12)
5)非劣解子集
基于灵敏比支配关系筛选非劣解子集:
(13)
根据式(13)筛选出1、 2、 5、 10、 11、 13、 16、 18、 19、 20解为支配解,皆应筛选掉。
6)在前一步的基础上,通过式(14)和(15)计算剩余的Pareto非劣子集计算出偏向度[17],见表5。
(14)
(15)
表4 Pareto非劣解相应参数
Tab.4 Pareto noninferior solution corresponding parameters
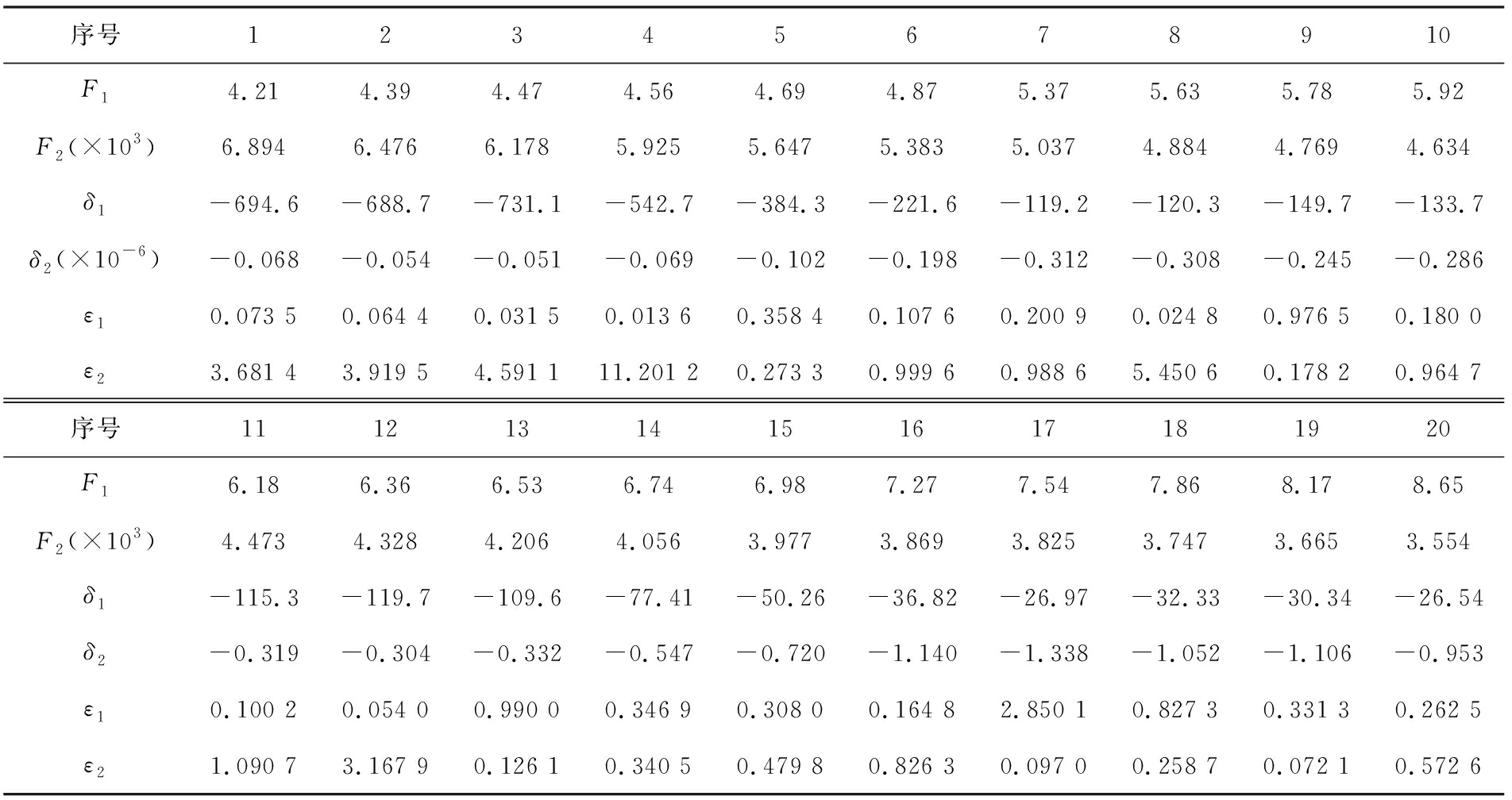
序号12345678910F14.214.394.474.564.694.875.375.635.785.92F2(×103)6.8946.4766.1785.9255.6475.3835.0374.8844.7694.634δ1-694.6-688.7-731.1-542.7-384.3-221.6-119.2-120.3-149.7-133.7δ2(×10-6)-0.068-0.054-0.051-0.069-0.102-0.198-0.312-0.308-0.245-0.286ε10.073 50.064 40.031 50.013 60.358 40.107 60.200 90.024 80.976 50.180 0ε23.681 43.919 54.591 111.201 20.273 30.999 60.988 65.450 60.178 20.964 7序号11121314151617181920F16.186.366.536.746.987.277.547.868.178.65F2(×103)4.4734.3284.2064.0563.9773.8693.8253.7473.6653.554δ1-115.3-119.7-109.6-77.41-50.26-36.82-26.97-32.33-30.34-26.54δ2-0.319-0.304-0.332-0.547-0.720-1.140-1.338-1.052-1.106-0.953ε10.100 20.054 00.990 00.346 90.308 00.164 82.850 10.827 30.331 30.262 5ε21.090 73.167 90.126 10.340 50.479 80.826 30.097 00.258 70.072 10.572 6
表5 基于灵敏比的Pareto非劣解子集及对应的偏向度
Tab.5 Pareto noninferior solution subset based on sensitivity ratio and its corresponding deviation

序号34678912141517ε10.006 80.001 20.097 20.168 90.008 20.845 70.016 80.531 90.391 00.967 1ε20.993 20.998 80.902 80.831 10.991 80.154 30.983 20.468 10.609 00.032 9
3.4 结果分析
根据表5中所求得的量化后的偏向度指标,决策者可以有更多的选择范围,如果倾向于目标F1,则可选17非劣解,此解对F1的偏向度达到了0.967 1,如果倾向于目标F2,则可选4非劣解,此解对F2的偏向度达到了0.998 8,如果都不倾向,则可选14非劣解,此解对F1和F2的偏向度分别为0.531 9与0.468 1,在所有非劣解中最为接近。
4 不同方法的对比分析
1)正交试验将试验数量范围缩小,减少运算量,可以快速得出相应结果,但是,试验样本较少,其结果在某种程度上并非最优解,有很大的偏差。
2)遗传算法将整个约束条件的范围作为实验范围,很大程度上的扩宽了实验样本,同时算法迭代筛选更优于正交试验,最优解的可靠性更为准确。
3)Pareto多目标遗传算法在遗传算法的基础上进行了更接近于目标决策的改进,在最优解集中经过筛选缩小范围,通过目标倾向性角度分析,适应不同的决策情况,为合理决策提供有效支持。
5 结论
1)正交试验运算速度快,但结果偏差较大;遗传算法试验范围广泛,结果精确,求得的最优解较为合理;Pareto多目标遗传算法所求得非劣子集结果在满足最优的基础上,同时一定程度上满足了目标倾向度的要求。
2)基于实际情况分析, 当决策者倾向于目标F1时, 此时方案为原木粉添加量为142 kg, 氯化镁添加量为0.33 kg, 氧化镁添加量为32.7 kg, 其他添加剂为14.6 kg; 当决策者倾向于目标F2时, 此时方案为原木粉添加量为128 kg, 氯化镁添加量为0.42 kg, 氧化镁添加量为45.7 kg, 其他添加剂为18.6 kg; 当决策者既不倾向于目标也不倾向于目标时, 此时方案为原木粉添加量为133 kg, 氯化镁添加量为0.39 kg, 氧化镁添加量为37.6 kg, 其他添加剂为15.8 kg。
[1]郝元恺, 肖加余. 高性能复合材料学[M]. 北京: 化学工业出版社, 2004: 1-5.
[2]化毓坤. 21世纪人造板工业发展趋势[J]. 南京林业大学学报, 2001, 25(1): 6-8.
[3]夏余平. 木质功能材料温压成形本构方程与数值模拟[D]. 长沙: 中南林业科技大学, 2017.
[4]姜鹏, 陈志林, 梁善庆, 等. 阻燃脲醛树脂制备刨花板的燃烧性能及成炭机理[J]. 木材工业, 2019, 33(5): 1-6.
[5]黄静. 新型木基复合材料制备与性能研究[D]. 长沙: 中南林业科技大学, 2012.
[6]闫其盼, 吴爱祥, 王贻明, 等. 某矿膏体充填物料配比优化研究[J]. 金属矿山, 2015(7): 39-42.
[7]朱镇, 蔡英凤, 陈龙, 等. 基于遗传算法的机液传动系统参数匹配研究[J]. 汽车工程, 2020(1): 74-80.
[8]邓晓云, 阎长罡, 来星呈. 基于遗传算法的螺杆面加工用盘铣刀廓形的计算[J]. 大连交通大学学报, 2020, 41(1): 64-68.
[9]贺福强, 姚学练, 平安, 等. 基于遗传算法的颗粒态辣椒螺旋输送机优化设计[J]. 现代制造工程, 2019(6): 120-125.
[10]邓彦舒, 方滨, 许志沛. 门式起重机结构优化设计[J]. 中国重型装备, 2020(1): 17-19, 23.
[11]单宝英, 郭萍, 张帆, 等. 基于遗传算法与方案优选的多目标优化模型求解方法[J]. 中国农业大学学报, 2019, 24(6): 157-165.
[12]巩玲君, 张纪海. 基于NSGA-Ⅱ的应急生产任务多目标优化模型及算法研究[J]. 运筹与管理, 2019, 28(12): 7-13.
[13]王凯, 王荣鹏, 刘宇, 等. 基于Pareto最优原理的钻机钻进参数多目标优化[J]. 中国机械工程, 2017, 28(13): 1580-1587.
[14]宋勇道. 基于两档双离合器自动变速器的纯电动汽车驱动与换档控制技术研究[D]. 长春: 吉林大学, 2013.
[15]BESHARATI S R, DABBAGH V, AMINI H, et al. Multi-objective selection and structural optimization of the gantry in a gantry machine tool for improving static, dynamic, and weight and cost performance[J]. Concurrent Engineering, 2016, 24(1): 83-93.
[16]MAHMODINEJAD A, FOROUTANNIA D. Generalized rational efficiency in multiobjective programming[J]. University Politehnica of Bucharest Scientific Bulletin:Series A(Applied Mathematics and Physics), 2016, 78(1): 135-146.
[17]王诺, 吴迪, 黄祺, 等. 选择Pareto非劣解最优方案的量化方法: 性价比法[J]. 系统工程理论与实践, 2018, 38(3): 725-733.