多元物理量特性分析及故障诊断等研究工作。E-mail:jiangyz186@126.com。
煤炭资源是我国能源结构的重要组成部分。到2020年,我国对湿煤的需求量为(2.1~2.9)×106 t,这样大量的湿煤开发和利用将给社会带来巨大的挑战[1],因此,湿煤采掘技术[2-4]是确保我国经济发展和煤炭开采持续健康发展的必然要求[5]。
湿煤受含水量变化的影响,湿煤载荷也会呈现不确定性。变化不规律的载荷可能会造成湿煤开采和运输机械的损坏甚至是结构失效[6]。
运用离散元法模拟煤料与煤矿机械间的相互作用,可以分析煤矿机械的受力情况及故障成因;但在模拟分析过程中,由于湿煤表面能设置规律不明确,造成建立的湿煤颗粒模型不精确且与实际物料不符合等问题,因此影响了离散元仿真模拟结果的准确性。由于对湿煤物料在离散元软件中含水率表征方法的研究鲜有报道,因此必须解决湿煤颗粒的含水率的表征方法的问题。
湿煤颗粒的含水率通常用表面能作为表征参数。为了能够简便而又准确地分析湿颗粒的运动特性,所建立的离散元接触模型准确性就显得格外重要。湿煤颗粒为典型的非连续介质[7],湿煤颗粒间的流动特性及力学特性较为复杂[8-9]。由于JKR模型引入了颗粒间表面能的概念,因此可以有效地表示湿颗粒和细小颗粒间的黏结作用[10]。
胡毅等[11]针对离散元仿真软件EDEM中的输入参数缺少含水率,导致无法对水稻种子的物理特性进行准确描述的问题,探究了表征种子含水率的参数标定方法。刑洁洁等[12]以含水率为7.8%、实际体止角为32.35 °的砖红壤为研究对象,以物理试验获取了砖红壤-砖红壤、砖红壤-触土部件间的恢复系数、静摩擦系数及滚动摩擦系数。李铁军等[13]基于10%含水率的湿煤参数标定结果,研究了表面能随粒径的变化规律、以及不同粒径混合散料内颗粒间表面能的设置规律。
本文中借助实验与仿真模拟相结合,针对湿煤料含水率与颗粒表面能参数之间的关系进行研究。由于仿真模拟中不能通过物料含水率直接获取颗粒间表面能参数,散料的流动特性却与颗粒表面能参数密切相关,因此,首先通过测量法研究含水率对煤料堆积特性及流动性的影响;然后再采用EDEM软件中的JKR接触模型进行堆积角仿真试验,获取堆积角与表面能间的回归方程;随后通过卸料实验验证回归方程的准确性;最后采用以堆积角为指标的统计分析法,确定不同含水率的煤散料内颗粒间表面能的设置规律,为离散元法中煤料含水率表征提供一种有效方法。
1 湿煤颗粒接触模型
含有一定水分的湿煤颗粒表面存在黏附作用,常用的Hertz-Mindlin接触模型仅考虑弹性变形,不考虑颗粒间的黏结作用,不能很好地模拟湿煤颗粒与煤炭开采、运输设备之间的力学行为。
然而,Hertz-Mindlin with JKR接触模型是一种凝聚力接触模型,它在Hertz理论的基础上还又考虑湿煤颗粒间的表面能(即黏结力)对湿煤颗粒运动的影响,其法向弹性接触力[14]可以很好地表征湿颗粒间的黏结力。湿煤颗粒间的法向弹性接触力FJ公式为:
(1)
(2)
式中:γ为湿煤颗粒的表面能,J/m2; E*为等效弹性模量,Pa; α为接触面半径,mm; R*为等效接触半径,mm; δ为法向重叠量,mm。其中
(3)
(4)
式中:E1、E2分别为2个接触颗粒的弹性模量,Pa; R1、R2分别为湿煤颗粒半径,mm;υ1、υ2分别为湿煤颗粒泊松比。当湿煤颗粒的表面能量γ为0时,则该模型FJ就简化为Hertz接触模型的接触力FH为:
(5)
2 堆积实验与仿真试验
2.1 含水率与堆积角关系
通过湿煤颗粒的堆积实验研究含水率与堆积角的关系。
所选取非球形煤料颗粒粒径为3~5 mm,密度为1 700 kg/m3。由于煤料颗粒较小且形状不一,采用试验筛进行筛取。
堆积角是表征颗粒流动特性的宏观参数[15]。由于研究对象为粒径为3~5 mm的湿煤料,因此采用无底圆柱筒法[16]进行堆积实验。为了分析不同含水率煤料的流动性及堆积状态,采用天平称取1 kg干煤料,对含水率为0~16%范围内间隔为2%的9组数据进行堆积角实验,煤料含水率计算公式为:
(6)
式中:w为煤料含水率,%; m1为湿煤料质量,g; m2为干煤料质量,g; mw为加入水的质量,g。
设定干煤质量m2为1 kg,通过公式(6)计算所需加入干煤料的水的质量,湿煤颗粒含水率与加水量关系如表1所示。
表1 湿煤颗粒含水率与加水量关系
Tab.1 Relationship between moisture content of wet coal particles and amount of water added

含水率w/%0246810121416加水的质量mw/g020406080100120140160
采用圆筒堆积实验测定不同含水率的煤散料堆积角。首先将与水混合均匀的煤料填装在圆筒内并待煤料处于稳定状态后,以匀速垂直上提圆筒,湿煤料从圆筒中自由落下并堆积在载料板上。湿煤料堆形成的斜面与水平载料板间的夹角即为煤料的堆积角。为了尽量减少人为因素导致的测量误差,利用MATLAB软件对采集图像进行处理,堆积角处理过程如图1所示。

a)原始湿煤料堆单侧图像

b)灰度处理

c)二值化处理
d)边缘检测
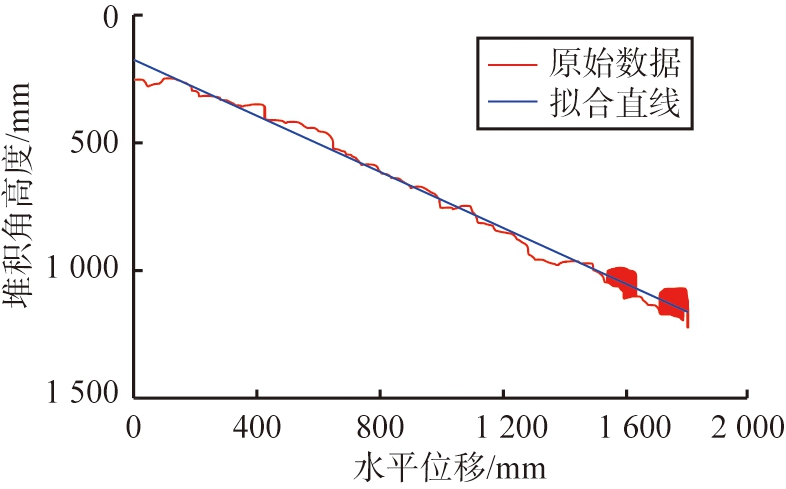
e)线性拟合
图1 堆积角处理过程
Fig.1 Stacking angle treatment process
由图1可知,首先读取原始湿煤料堆单侧图像,经灰度化处理,获得灰度图像,再通过二值边界提取获得其边界,通过边缘检测后通过最小二乘法获得线性拟合直线图。拟合直线的斜率kθ即为所需要测得的堆积角正切值。
湿煤颗粒堆的堆积角θ 的表达式为[17]:
(7)
不同含水率的湿煤颗粒的堆积角的测定结果如表2所示。
表2 不同含水率的湿煤颗粒的堆积角测定结果
Tab.2 Measurement results of stacking angle of wet coal particles with different moisture content

含水率w/%0246810121416堆积角/(°)31.6833.6934.3838.7238.6640.6037.8840.1640.92
由表2可知,随着煤料含水率的增加,湿煤料堆积角也在增加,煤料含水率为16%的堆积角与干煤料(即含水率为0 %)堆积角数值差异为22.581%,变化幅度较大;当含水率在8%内,煤料堆积角随含水率增加快速增大;在含水率大于8%之后,湿煤料堆积角随含水率的增长速度减缓。所以,在较小粒径的煤料颗粒中,含水率对煤料堆积状态和流动性的影响是不可忽略的。
2.2 表面能与堆积角关系
通过湿煤颗粒的仿真试验研究表面能与堆积角的关系。
进行仿真试验时,要首先建立湿煤颗粒仿真模型。为了提高离散元颗粒建模准确度和真实性,考虑到煤颗粒外形不规则且形状多样,因此将实际煤颗粒按相似形状分类,大致分为4种类型:扁平状、类锥状、长条状和类块状,然后在EDEM软件中针对每种类别形状建立湿煤颗粒模型。4种类型的湿煤颗粒模型如图2所示,料堆中4种类型的颗粒数量随机生成。

a)扁平状

b)类锥状

c)长条状

d)类块状
图2 4种类型的湿煤颗粒模型
Fig.2 Four types of wet coal particle models
采用无底圆筒模型进行堆积角仿真试验,除了已知的煤料颗粒大小、形状及圆筒规格外,湿煤颗粒的其他本性参数,可由测定得的不同含水率湿煤颗粒的堆积角为参照,结合文献[9]和GEMM(generic EDEM material model)颗粒通用材料数据库获取,颗粒参数如表3所示。
表3 颗粒参数
Tab.3 Particle parameters
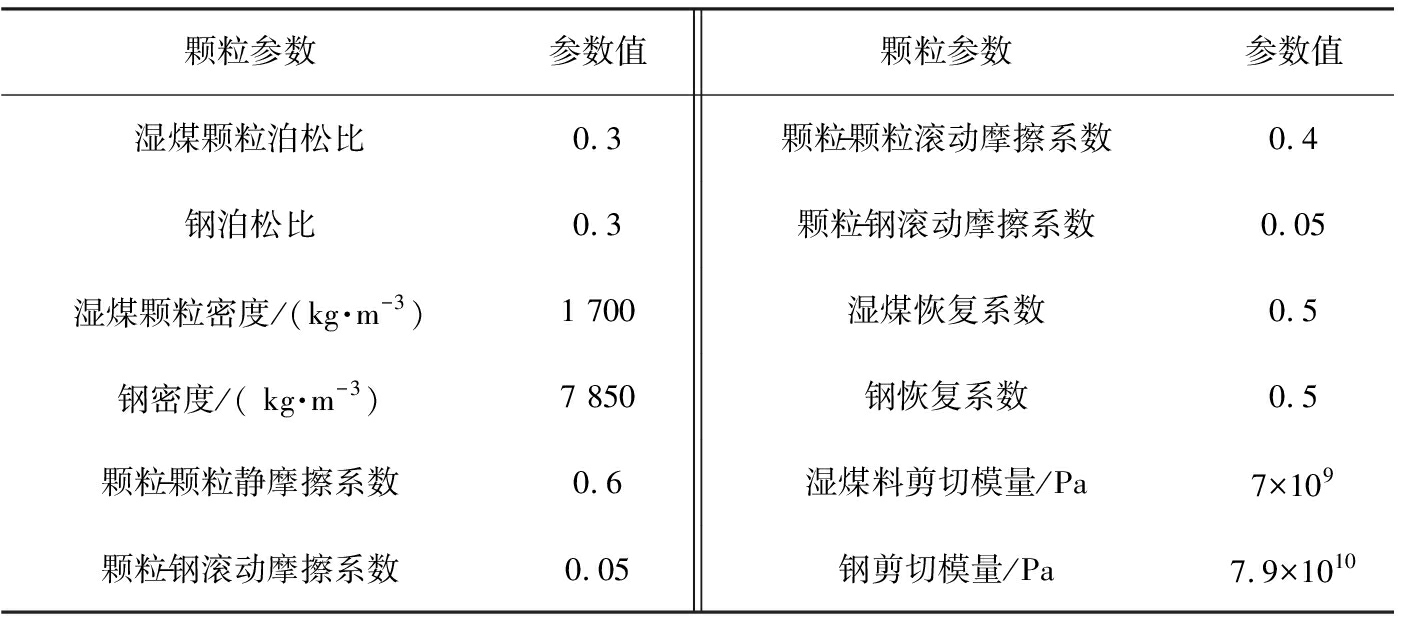
颗粒参数参数值颗粒参数参数值湿煤颗粒泊松比0.3颗粒-颗粒滚动摩擦系数0.4钢泊松比0.3颗粒-钢滚动摩擦系数0.05湿煤颗粒密度/(kg·m-3)1 700湿煤恢复系数0.5钢密度/( kg·m-3)7 850钢恢复系数0.5颗粒-颗粒静摩擦系数0.6湿煤料剪切模量/Pa7×109颗粒-钢滚动摩擦系数0.05钢剪切模量/Pa7.9×1010
在EDEM软件中,设置无底圆筒内颗粒总质量为1 kg,圆筒的提升速度为0.03 m/s,保持仿真设置与实验相同。
根据表3参数在EDEM中设置颗粒参数,分别对表面能参数为0~5 J/m2进行30次堆积角仿真试验,煤料堆积过程示意图如图3所示。

a)生成料堆

b)煤料液滴

c)湿煤料堆形成
图3 煤料堆积过程示意图
Fig.3 Schematic diagram of coal accumulation process s
为了减小测量误差,利用MATLAB图像化处理技术对煤料堆X、Y 2个方向的堆积角进行测量并取平均值,堆积试验仿真结果如表4所示。
表4 堆积试验仿真结果
Tab.4 Simulation results of stacking test
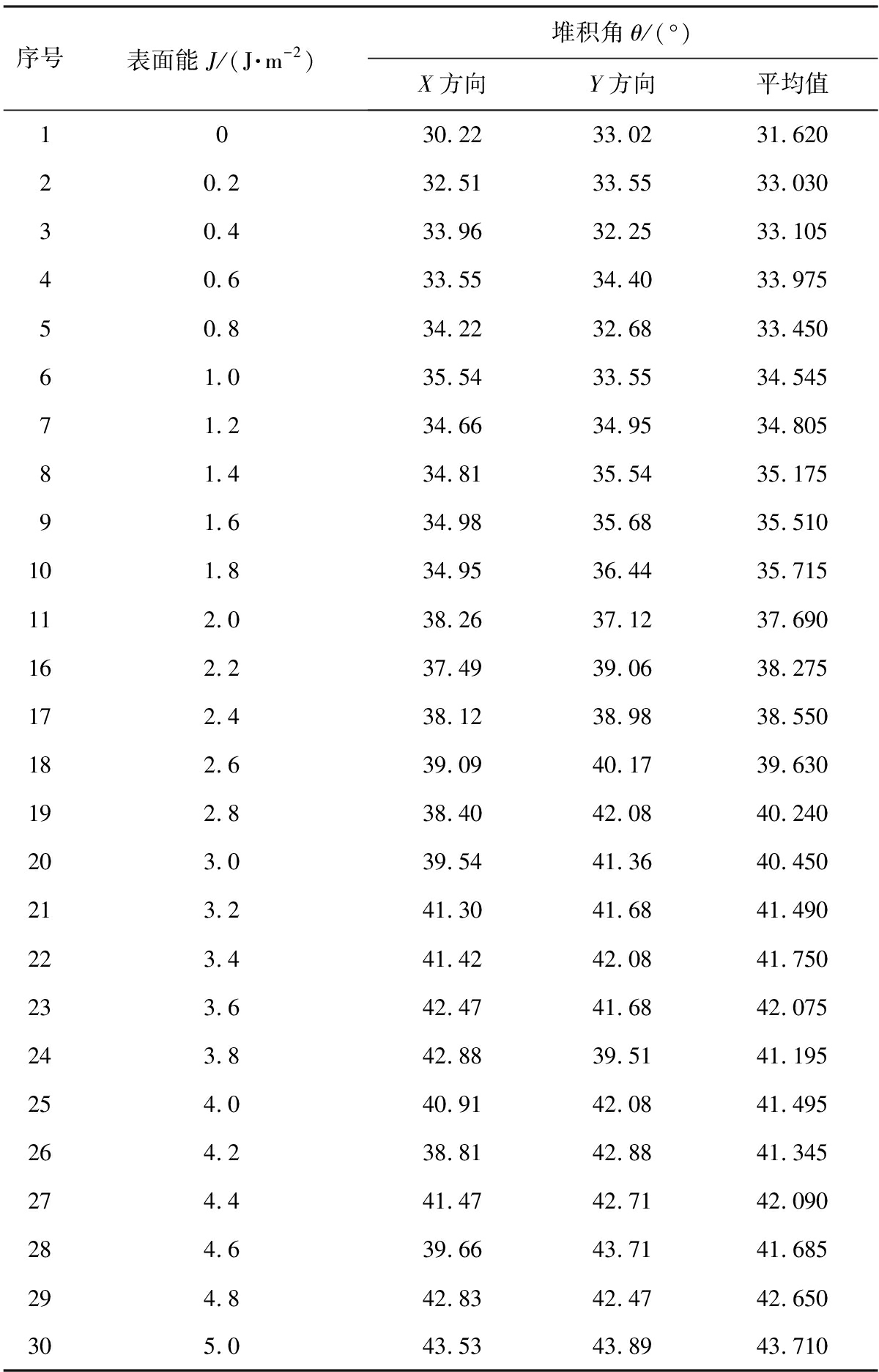
序号表面能J/(J·m-2)堆积角θ/(°)X方向Y方向平均值1030.2233.0231.62020.232.5133.5533.03030.433.9632.2533.10540.633.5534.4033.97550.834.2232.6833.45061.035.5433.5534.54571.234.6634.9534.80581.434.8135.5435.17591.634.9835.6835.510101.834.9536.4435.715112.038.2637.1237.690162.237.4939.0638.275172.438.1238.9838.550182.639.0940.1739.630192.838.4042.0840.240203.039.5441.3640.450213.241.3041.6841.490223.441.4242.0841.750233.642.4741.6842.075243.842.8839.5141.195254.040.9142.0841.495264.238.8142.8841.345274.441.4742.7142.090284.639.6643.7141.685294.842.8342.4742.650305.043.5343.8943.710
利用MATLAB对堆积试验仿真结果进行回归分析,建立表面能堆积角的回归模型,得到其回归方程式
θ=2.354 3J+32.432,R2=0.946 2。
(9)
堆积角θ随表面能J的变化见图4。由图4可知,随着表面能的增加煤料堆积角也在增加。
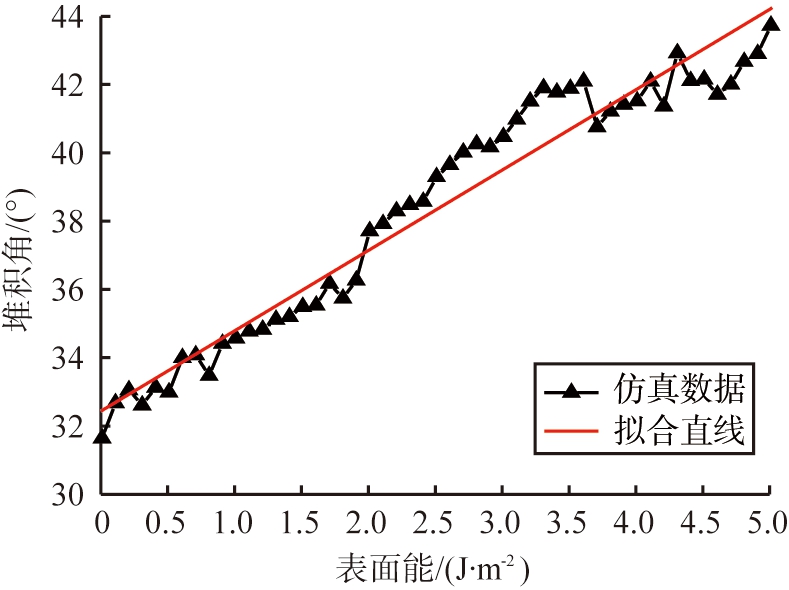
图4 堆积角随表面能的变化规律
Fig.4 Variation law of stacking angle with surface energy
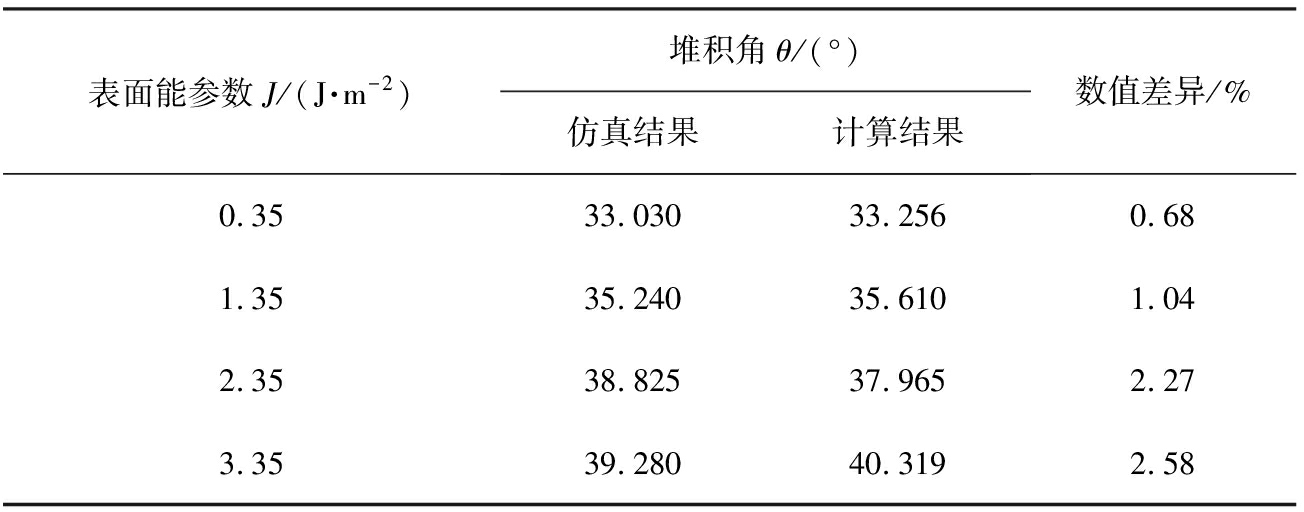
为了验证回归方程的可靠度,选取4组表面能参数为0.35、1.35、2.35、3.35 J/m2进行模拟仿真和代入方程式(8)中计算,回归方程验证结果见表5。
表5 回归方程验证结果
Tab.5 Regression equation verification results
表面能参数J/(J·m-2)堆积角θ/(°)仿真结果计算结果数值差异/%0.3533.03033.2560.681.3535.24035.6101.042.3538.82537.9652.273.3539.28040.3192.58
由表5可知,对应的表面能参数通过计算获得的堆积角和圆筒堆积实验仿真得到的堆积角数值差异率最小为0.68%,最大仅为2.58%,差异非常小,并且回归模型的相关系数R2=0.946 2,接近于1,说明该模型拟合度良好,拟合方程可靠度高。
堆积角与表面能的关系十分密切,堆积角随表面能的增加而增大,在表面能为0~2 J/m2时,堆积角随表面能的增加呈线性关系,但是其增长幅度较小;在表面能为2~3.75 J/m2时,随着表面能的增加,堆积角的增加速度变快。
3 含水率与表面能关系分析
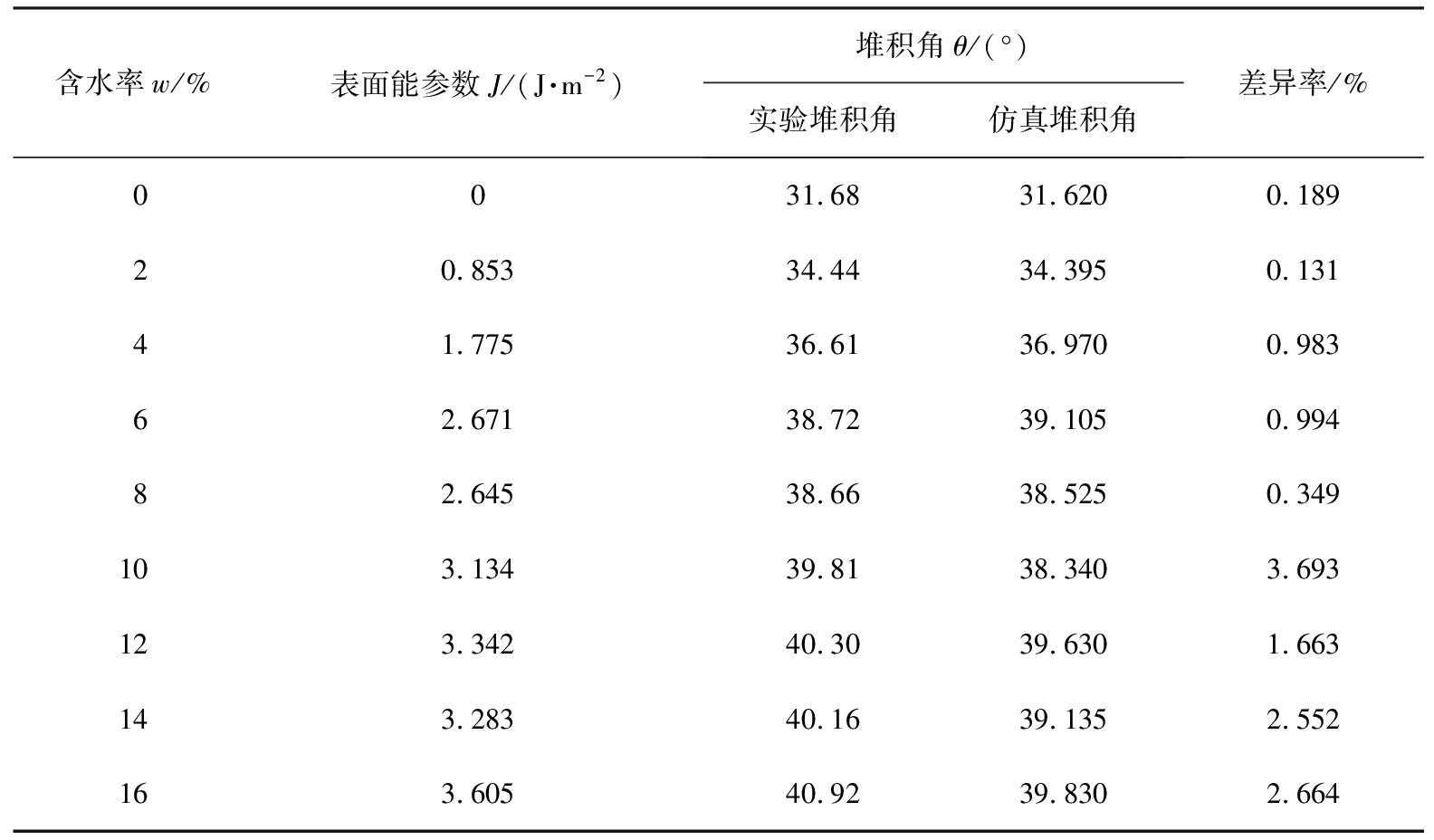
为获得湿煤散料含水率表征方法,以堆积角为指标,通过卸料实验获取不同含水率的堆积角,分别代入回归方程式(7)中获取相对应的表面能参数值,在EDEM软件中保持其他仿真参数设置不变,对计算获得的表面能参数值分别做圆筒堆积角仿真试验,堆积实验和仿真试验结果对比如表6所示。由表6可知,不同煤料含水率w计算出来的表面能参数值J仿真得到的堆积角与实验得到堆积角数值差异率最大值为3.963%,差异非常小,说明了含水率与计算所得的表面能参数值符合程度较好。
表6 堆积实验与仿真试验结果对比
Tab.6 Comparison of results between stacking experiment and simulation experiment
含水率w/%表面能参数J/(J·m-2)堆积角θ/(°)实验堆积角仿真堆积角差异率/%0031.6831.6200.18920.85334.4434.3950.13141.77536.6136.9700.98362.67138.7239.1050.99482.64538.6638.5250.349103.13439.8138.3403.693123.34240.3039.6301.663143.28340.1639.1352.552163.60540.9239.8302.664
煤料含水率与表面能的关系曲线如图5所示。湿煤散料的表面能参数随含水率的增加而增加,在煤料含水率大于8%之后,表面能参数J随含水率w的增长速度降低。
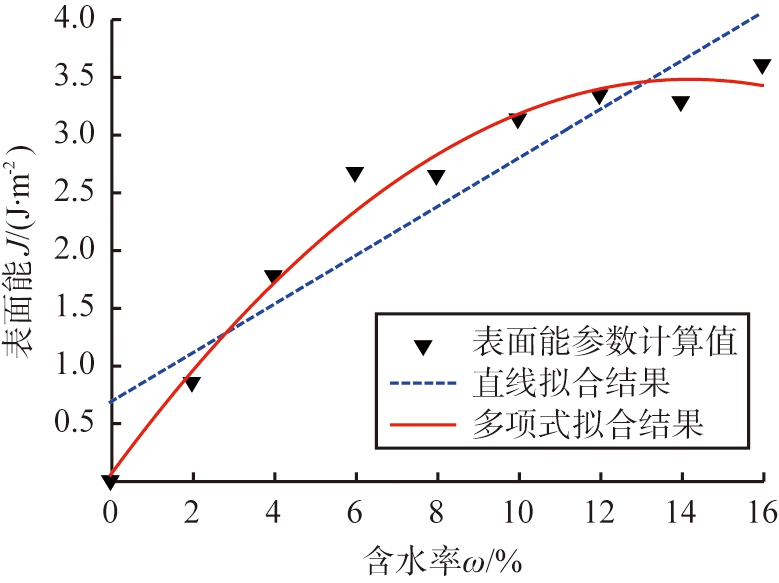
图5 煤料含水率与表面能的关系曲线
Fig.5 Relation between moisture content of coal and change of surface energy parameters
以堆积角为指标,分别用直线和二次多项式函数对含水率w与表面能参数J散点图进行拟合得到拟合方程为
J1=21.086 9w+0.680 4,R2=0.866,
(9)
J2=-169.45w2+48.2w+0.048,R2=0.980 8。
(10)
二次多项式方程 (9)拟合度更好,拟合方程的相关系数R2=0.980 8,非常接近1,更符合两者间的变化趋势,因此,可通过式(10)项,计算离散元仿真中煤散料含水率表征参数亦即表面能的值。
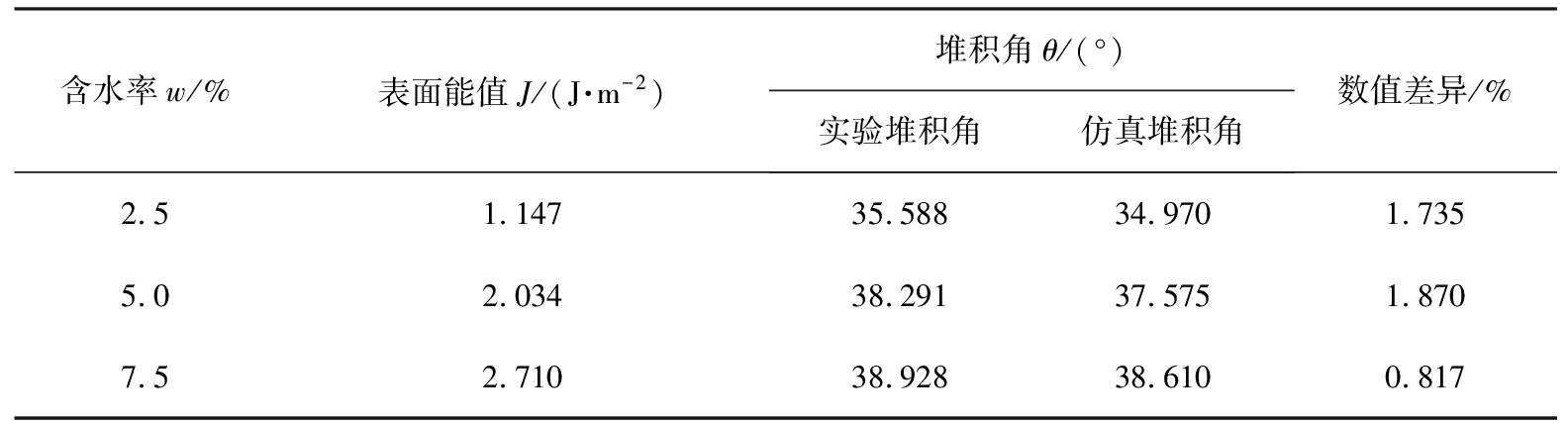
为了验证式(10)可靠度,分别将含水率为2.5%、5%、7.5%的湿煤散料做堆积角实验,并测量煤料堆的堆积角,然后再通过拟合方程式(10)计算出对应的表面能值,对其进行模拟仿真分析,含水率与表面能拟合方程验证结果见表7。
表7 含水率与表面能拟合方程验证结果
Tab.7 Verification results of fitting equation of water content and surface energy
含水率w/%表面能值J/(J·m-2)堆积角θ/(°)实验堆积角仿真堆积角数值差异/%2.51.14735.58834.9701.7355.02.03438.29137.5751.8707.52.71038.92838.6100.817
由表7可知,通过式(10)计算获得的表面能参数值进行仿真模拟,测量的堆积角与实验获得的堆积角数值差异在2%以内,差异较小。
不同含水率的湿煤料实验堆积体与仿真堆积体图像对比如图6所示。

a)2.5%

b)5%

c)7.5%
图6 不同含水率的湿煤料实验堆积体与仿真堆积体图像对比
Fig.6 Image comparison of experimental and simulated accumulations of wet coal with different moisture content
由图6可知,湿煤料仿真模拟与实验堆积体图像堆积状态符合,且含水率在10%范围内,表面能随含水率的增大幅度较大,当煤料含水率超过10%之后,表面能随含水率的变化趋势趋于平缓。结果证明通过以上方法计算湿颗粒散料在离散元软件仿真模拟中的不同含水率对应表征参数亦即表面能值是可行的。
4 结论
通过仿真模拟与实验结果的回归分析,本文中提出了一种湿煤散料含水率的表征方法,建立了表面能与含水率之间的数学模型,得出以下结论:
1)粒径为3~5 mm的湿煤料颗粒的堆积角随着含水率增加而增加。
2)当表面能为0~2 J/m2时,堆积角随表面能呈线性关系增大,但增长幅度较小; 当表面能为2~3.75 J/m2时,堆积角随表面能快速增大。
3)非球形湿煤散料颗粒含水率的数学模型与实验结果的最大误差小于2%,说明表征方法准确可靠。数学模型表明:当含水率≤10%时,表面能随含水率快速增大;当煤料含水率>10%时,表面能随含水率增大的趋势趋于平缓。
[1]罗斐.煤炭资源的现状及结构分析[J].中国煤炭,2008,34(3):91-94,96.
[2]王国法,赵国瑞,胡亚辉.5G技术在煤矿智能化中的应用展望[J].煤炭学报,2020,45(1):16-23.
[3]XU J P,GAO W,XIE H P,et al.Integrated tech-paradigm based innovative approach towards ecological coal mining[J].Energy,2018,151:297-308.
[4]ZHANG J X,ZHANG Q,SUN Q,et al.Surface subsidence control theory and application to backfill coal mining technology[J].Environmental Earth Sciences,2015,74(2):1439-1448.
[5]王双明,孙强,乔军伟,等.论煤炭绿色开采的地质保障[J].煤炭学报,2020,45(1):8-15.
[6]夏蕊,杨兆建,李博,等.煤散料含水率对16Mn钢磨损性能的影响[J].煤矿机械,2019,40(2):113-115.
[7]陈凯凯.散料离散元参数标定方法研究及应用[D].武汉:武汉理工大学,2017.
[8]王泳嘉,邢纪波.离散单元法同拉格朗日元法及其在岩土力学中的应用[J].岩土力学,1995,16(2):1-14.
[9]徐泳,孙其诚,张凌,等.颗粒离散元法研究进展[J].力学进展,2003,33(2):251-260.
[10]曹波,李文辉,王娜,等.基于JKR模型的湿式滚抛磨块离散元参数标定[J].表面技术,2019,48(3):249-256.
[11]胡毅,杜俊,杨全军,等.基于离散元法的水稻种子含水率表征方法[J].甘肃农业大学学报,2019,54(3):171-177.
[12]邢洁洁,张锐,吴鹏,等.海南热区砖红壤颗粒离散元仿真模型参数标定[J].农业工程学报,2020,36(5):158-166.
[13]李铁军.煤颗粒离散元模型宏细观参数标定及其关系[D].太原:太原理工大学,2019.
[14]JOHNSON K L,KENDALL K,ROBERTS A D.Surface energy and the contact of elastic solids[J].Proceedings of the Royal Society of London.Series A,Mathematical and Physical Sciences(1934-1990),1971,324(1558):301-313.
[15]REN J L,ZHOU J N,HAN L,et al.Analysis of the law governing the movement of bulk materials in a vertical helical conveyer[J].Reneng Dongli Gongcheng/Journal of Engineering for Thermal Energy and Power,2018,33(6):77-82,136.
[16]吴爱祥,孙业志,刘湘平.散体动力学理论及其应用[M].北京:冶金工业出版社,2002:35-40.
[17]ILLELEJI K E,ZHOU B.The angle of repose of bulk corn stover particles[J].Powder Technology,2008,187(2):110-118.