纳米颗粒具有独特的性质[1]，在过去的近十几年中吸引了越来越多来自不同学科的研究人员的注意力[2-4]。 低压冲击仪(low pressure impactor, LPI)是测量气溶胶颗粒尺度分布的重要仪器，广泛应用于气溶胶颗粒的测量。 早期的冲击仪主要是收集颗粒，并对颗粒的粒度分布进行研究。 随着计算流体动力学(computational fluid dynamics，CFD)的发展和有限差分法的应用，可以对冲击仪的流场和颗粒轨迹进行分析和研究。 通过改变低压冲击仪内部的结构，可以提高冲击仪的可靠性和精度，因此对冲击仪内部结构进行研究具有重大的意义。
低压冲击仪内部结构不断被优化，测量的颗粒范围越来越大，能够测量出尺寸更小的颗粒，并且颗粒的质量也能被实时监测收集到。 HILLAMO等[5]研究了1—6级可压缩流动的颗粒收集特性的Berner冲击仪(berner low pressure impactor, BLPI)，它是基于2个静电计的使用，一个连接到冲击器的收集板，另一个连接到备用过滤器，利用单电荷单分散邻苯二甲酸二辛酯(DOP)颗粒来测定Berner冲击仪的收集效率曲线形状。 电子低压冲击仪[6] (electronic low pressure impactor, ELPI)是一种测试颗粒物的设备，可以用于记录瞬态粒径分布。发展至今，已经被广泛应用于汽车尾气排放的测量[7-9]、药物吸入的研究[10]和大气气溶胶[11-12]等领域中，同时也有相关学者将其应用于燃烧过程微粒的测量[13-15]和颗粒团聚物的研究[16]等。GLOVER等[17]对ELPI进行了改进和优化，使其能够用于抗哮喘药物的计量吸入器(MDIs)中的气溶胶颗粒的测量。
ELPI已经能够测量越来越小尺寸的颗粒，YLIOJANPER
等[18]等设计制造了一个新的附加冲击台，该平台通过将收集到的粒度范围划分为2个不同的阶段，由此改善分辨率和提高精度，检测颗粒的范围从30 nm扩展到16.7 nm。由于冲击仪装配的尺寸是固定的，2个上级平台必须进行移动才能实现2个不同阶段的效果，因而并未被有效商业化。ARFFMAN等[19]等使用拉格朗日方法计算了粒子轨迹，并根据粒子轨迹计算出冲击器的收集效率。采用CFD求解器求解描述时间平均流场(RANS)的方程，建立了流场模型，将仿真结果与实验结果进行了对比验证，并研究了收集板间距对分辨率的影响，结果表明，当喷嘴直径与喷嘴至平板距离之比为2时，冲击仪的分辨率最高，即拦截效果最好。但是，这些文献未对实际喷嘴直径、喷嘴至冲击台距离对不同颗粒的拦截效率进行系统研究。鉴于此，本文中以ELPI结构为基础，我们采用FLUENT软件的DPM模型，对单级低压冲击仪的颗粒场进行研究，并探究冲击喷嘴直径和冲击喷嘴至收集平板的距离对颗粒拦截率的影响，以其为改进冲击仪的设计提供借鉴和参考。
1 实验模型
本研究选取多级低压冲击仪其中的一级，图1为单级低压冲击仪实物图及二维尺寸简化图。冲击仪内部结构尺寸为本次研究主要关注点。
气溶胶从入口直径d1进入冲击仪，由于采用的是压力驱动，在一定条件下，d1控制着气溶胶进入冲击仪的速度。经过入口后，气溶胶来到L1区域，L1流域较为稳定，气溶胶在此处达到层流状态。接着气溶胶进入冲击口，冲击口直径d2直接影响着冲击速度。气溶胶进入冲击流场后，改变出口与收集平板的距离L3的大小可以改变冲击流场的转向曲率半径。我们选取相对具有代表性的d2和L3来研究。所选取的参数及变化见表1。
a 实物图
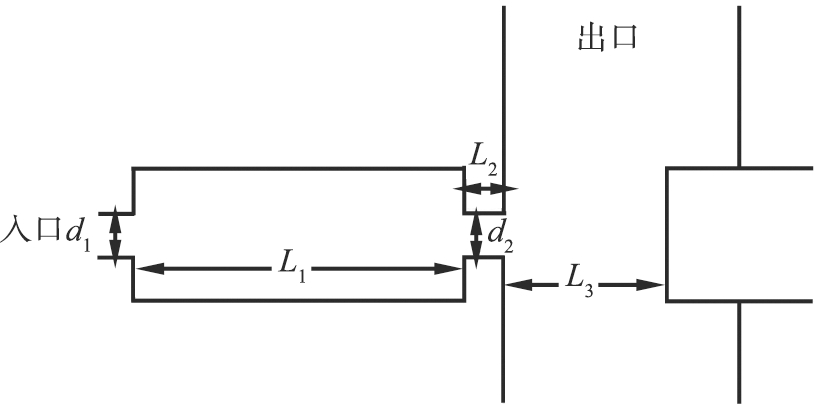
b 二维尺寸简化图
图1 单级低压冲击仪实物图及二维尺寸简化图
Fig.1 Impact meter profile and 2D size simplified diagram
表1 实验结构参数表
Tab.1 Experimental structure parameter table
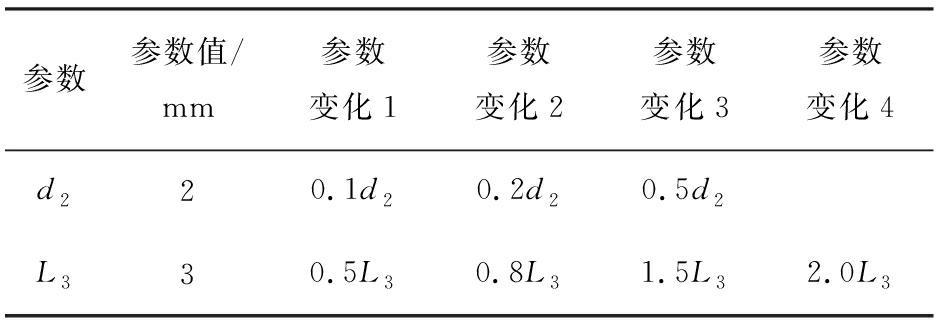
参数参数值/mm参数变化1参数变化2参数变化3参数变化4d220.1d20.2d20.5d2L330.5L30.8L31.5L32.0L3
2 收集原理及颗粒场仿真方法
2.1 收集原理
图2为多级冲击仪内部结构简图，主要由冲击喷嘴和收集平板组成。 气溶胶以一定的速度从喷嘴射出后，由于惯性，部分颗粒被收集平板所收集。 正是由于平板的存在，使得流场发生改变，形成90°拐角的流线。
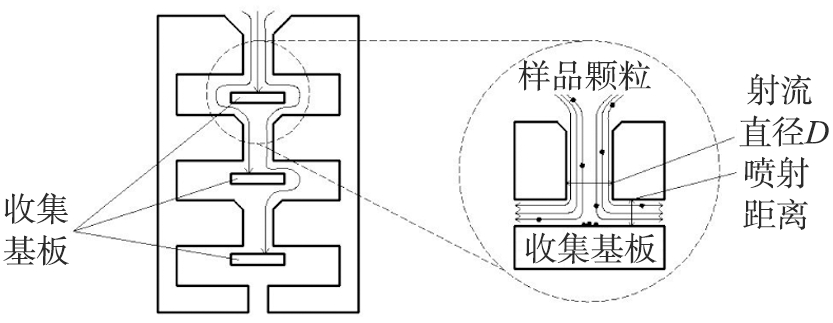
图2 多级冲击仪内部结构简图
Fig.2 Multi-level impactor internal structure diagram
在冲击仪中，利用收集效率曲线的斜率来表达冲击仪的分离性能。图3为颗粒的收集效率曲线，冲击仪理想的收集效率是一个阶梯函数，如图3中红线所示。此时，所有粒径大于特定值的颗粒都将被冲击平板所收集。同时，剩下粒径小于特定值的颗粒将跟随流场进入下一个阶段的分离流场，所以分割点的粒径称为分割尺寸、分割直径、D50。然而，在实际的分离过程中，冲击仪一般不能精准到对某一尺寸进行完全分割。某些直径大于分割直径的颗粒会因为弹跳和冲击脱落，脱离冲击平板，从而进入下一阶段的流场；同样，一些粒径较小的颗粒由于扩散作用，也有可能存在于分割点相对较大的阶段。所以，冲击仪真实的收集效率曲线应该是呈现为S状的。
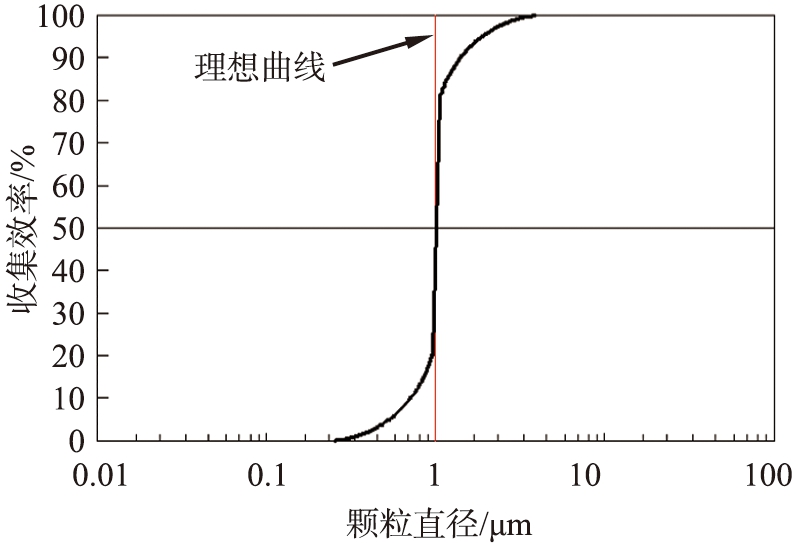
图3 收集效率曲线
Fig.3 Collection efficiency curve
本次研究中，将控制收集效率的参数称为Stokes数或者冲击参数，其表达式为
(1)
式中： u为喷嘴出口处的速度； τ为出口处速度为u的颗粒的停滞距离； Dj为射流出口直径。将原式展开后，Cc为滑移校正系数； η为动态黏度； ρp为粒子密度；dp为粒径。
一般用颗粒拦截曲线的斜率来表征冲击仪的分辨率，在本文中采用Arffman的方法来定义冲击仪的分辨率R。其表达式为
(2)
式中S0.5、 S0.8、 S0.2分别是指与收集效率50%、 80%、 20%相对应的Stokes数。
2.2 颗粒场仿真方法
现有两相流数值模拟常用的模型一般有离散相模型(discrete phase model，DPM)、 欧拉模型(Euler Model)、 混合物模型(Mixture Model)和流体体积模型(volume of fluid model，VOF)等。
其中离散相模型采用的是Lagrarian-Eulerian方法，离散相的运动是按Lagrarian方法，连续相的计算按Eulerian方法。DPM模型可以实现对单独粒子运动轨迹的追踪，但是，在此方法中不考虑颗粒对连续相的影响，所以要求颗粒对流场的影响要尽可能的小，适用于离散相体积占总体积不大于10%的流场。
模拟采用二氧化硅颗粒，颗粒的质量浓度为106 g/cm3，颗粒的直径范围为10 nm～1 μm，颗粒的体积分数小于10%,符合模型要求，所以我们选用稳态的离散相模型。选用的参数详见表2。
表2 计算模型参数设定
Tab.2 Defining the calculation model parameters
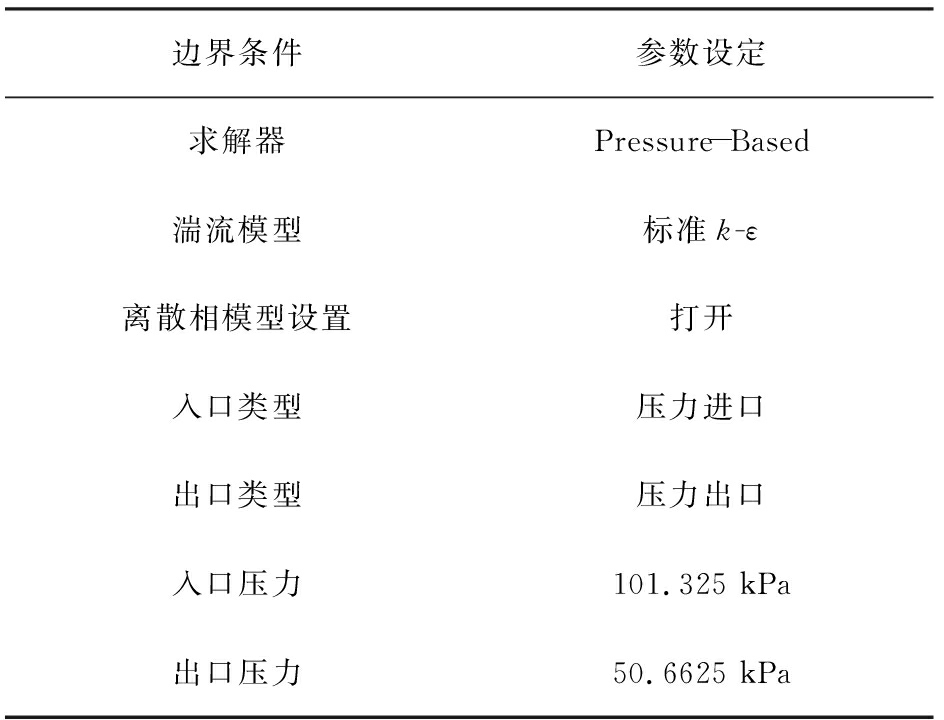
边界条件参数设定求解器Pressure-Based湍流模型标准k-ε离散相模型设置打开入口类型压力进口出口类型压力出口入口压力101.325 kPa出口压力50.6625 kPa
3 不同结构参数下仿真结果分析
3.1 冲击喷嘴直径d2的影响
流体到达冲击喷嘴区域，流场的水力直径瞬间变小，使流场的速度发生改变。图4为不同d2下中心线上的速度分布。由图可以看出，喷嘴直径d2减小时，冲击区域的速度变大。图5为不同d2下的颗粒收集效率，表3为不同d2下的拦截参数。在其他条件相同的情况下，随着d2的减小，冲击平板对某一粒径的颗粒拦截率逐渐增加；同时可以发现，冲击仪的分割直径逐渐减小。
由于冲击仪分辨率的大小由Stokes决定，而Stokes数和颗粒直径、喷嘴直径和冲击速度有关。图6为不同d2下Stokes数与收集率的关系曲线。虽然分割直径随着喷嘴直径的减小而减小，但是分辨率却下降了。当喷嘴直径为原始尺寸时，分辨率最高，但是存在2个收集峰值，所以在只有一个收集峰值的情况下，当喷嘴直径为0.5d2时，分辨率最高，可以达到1.92。
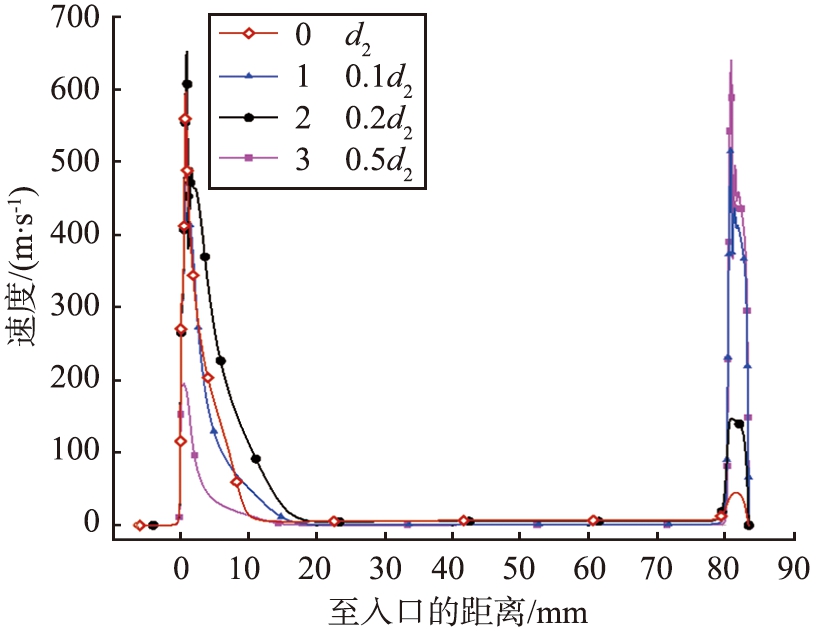
图4 不同d2下中心线上的速度分布
Fig.4 Velocity distribution on the centerline
under different d2
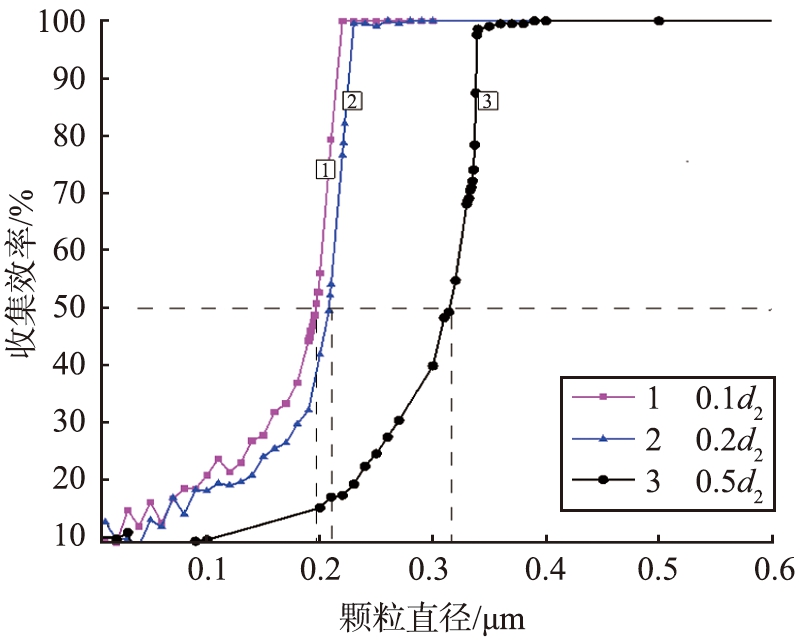
图5 不同d2下的颗粒收集效率
Fig.5 Particle collection efficiency under different d2
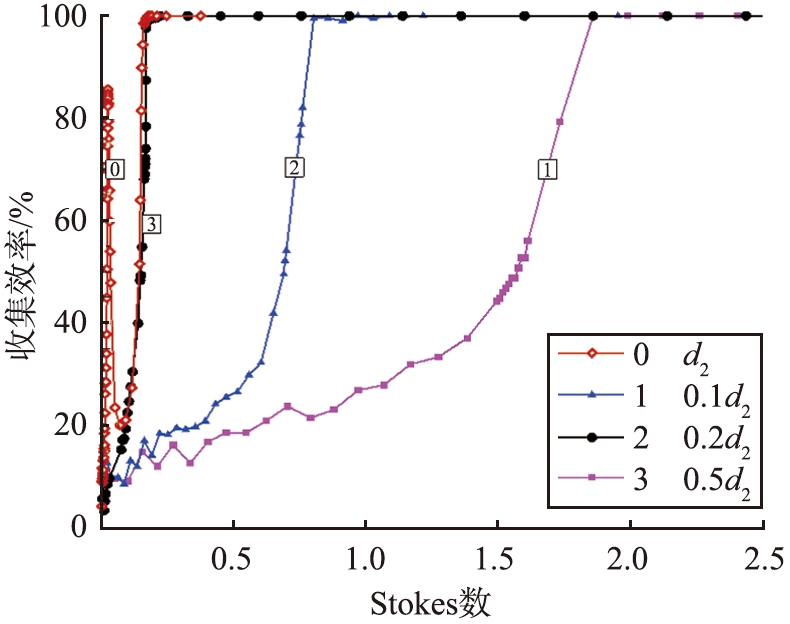
图6 不同d2下Stokes数与收集率的关系
Fig.6 Relationship between Stokes number
and collection efficiency under different d2
3.2 冲击喷嘴至收集平板的距离L3的影响
图7为不同L3下冲击区域中心线的速度分布图，图中的虚线是不同L3下冲击喷嘴的位置。对比各个案例，发现L3对冲击区中心线速度略有影响，随着L3增加，速度稍有增大。
表3 不同d2下的拦截参数
Tab.3 Intercept parameter list under different d2
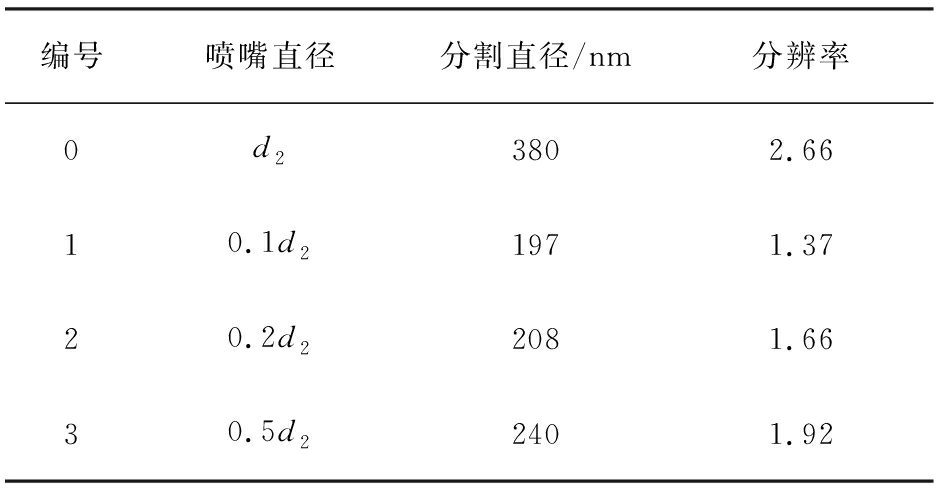
编号喷嘴直径分割直径/nm分辨率0d23802.6610.1d21971.3720.2d22081.6630.5d22401.92
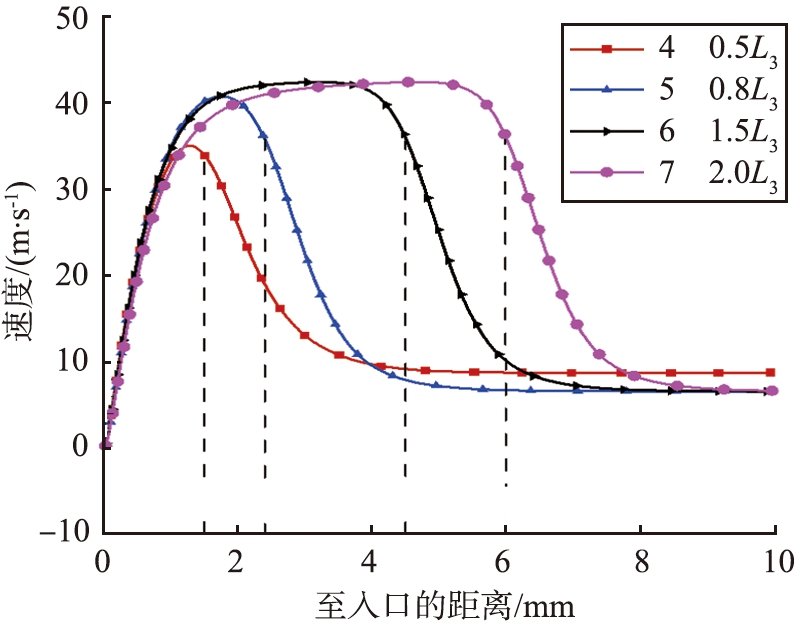
图7 不同L3下冲击区域中心线的速度分布图
Fig.7 Centerline velocity profile of
impact zone with different L3
图8为不同L3下的颗粒收集效率,从图可看出，不同L3案例中颗粒的拦截曲线十分相似，分割直径也极为接近。图9为不同L3下Stokes数与收集率的关系曲线。由于图中收集率出现局部最优的情况，所以能够计算得到3个不同的R值。表4为不同L3下的拦截参数。从表可以看出，随着L3的增加，分辨率R3随之减小，但是不能分析出L3对R1和R2产生的影响。
图10、 图11分别为d2=1 mm时的颗粒收集效率和Stokes数与收集效率的关系曲线。 由于原始结构的拦截曲线出现了非理想峰值，因此我们重新选择拦截曲线相对较好的3号算例，喷嘴直径为1 mm，进一步加入L3变量进行研究，结果如图10、 图11及表4中的算例8和9，结果并未出现多个峰值。 此时，随着冲击长度L3的减小，其分割直径由314 nm降至215 nm；同时分辨率由1.92升至6.8。在这部分案例中，当L3/d2=0.5时，得到了相对较为理想的曲线，此时冲击仪的拦截效果达到最佳。
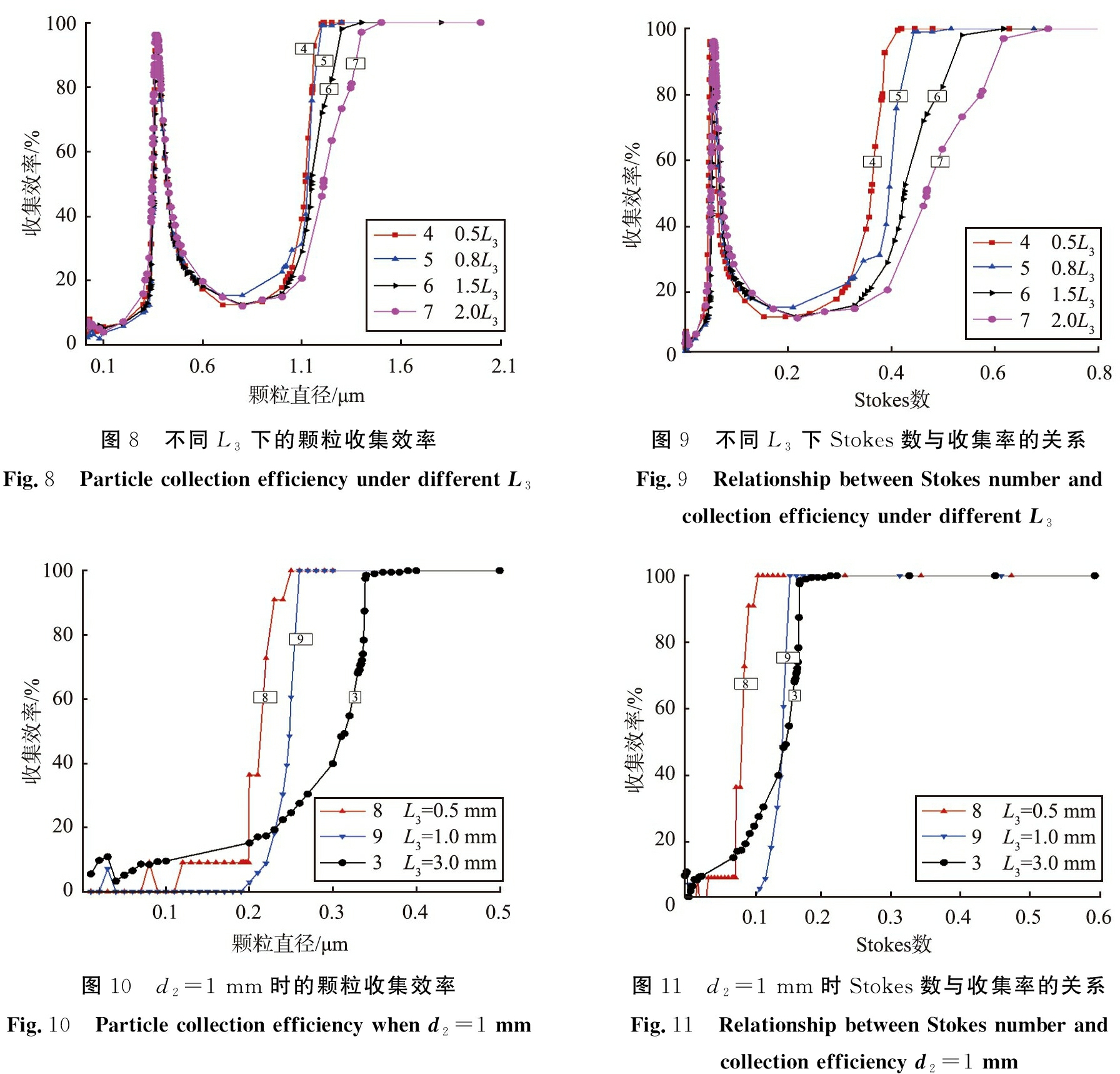
图8 不同L3下的颗粒收集效率Fig.8 Particle collection efficiency under different L3图9 不同L3下Stokes数与收集率的关系Fig.9 Relationship between Stokes number and collection efficiency under different L3图10 d2=1 mm时的颗粒收集效率Fig.10 Particle collection efficiency when d2=1 mm图11 d2=1 mm时Stokes数与收集率的关系Fig.11 Relationship between Stokes number and collection efficiency d2=1 mm
表4 不同L3下的拦截参数
Tab.4 Intercept parameter list under different L3
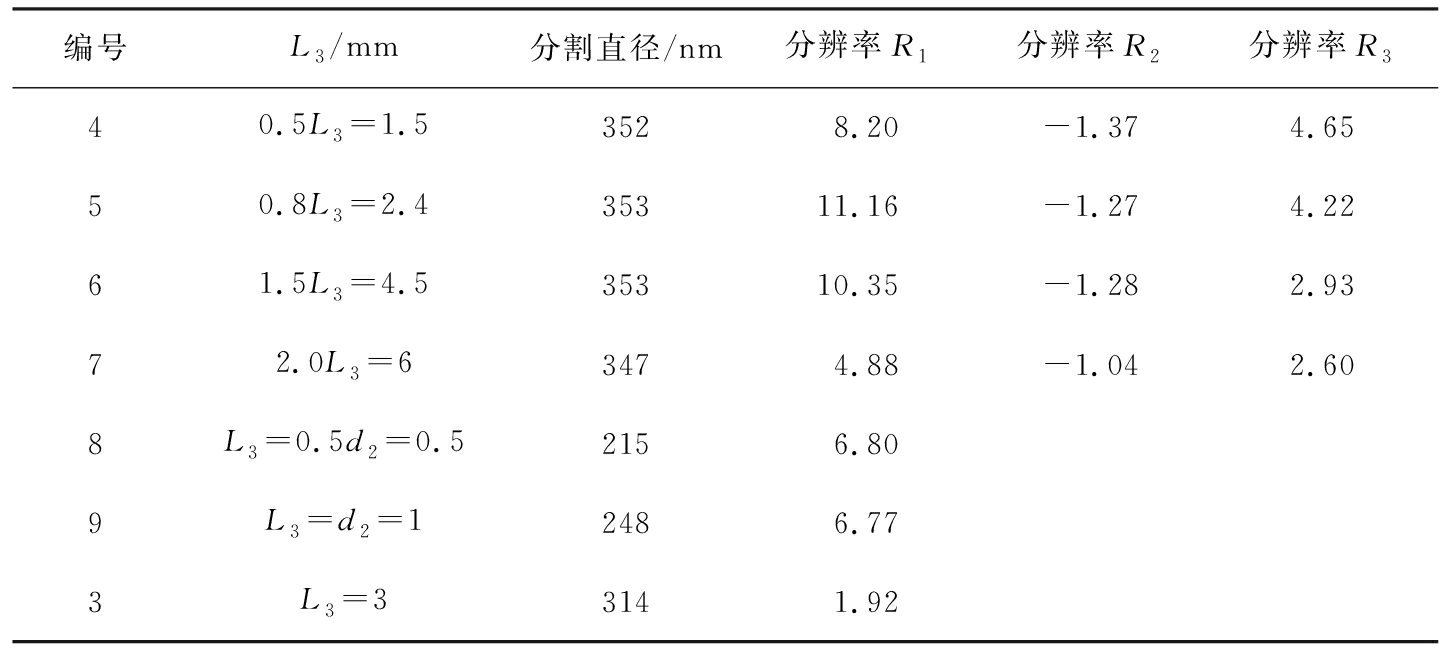
编号L3/mm分割直径/nm分辨率R1分辨率R2分辨率R340.5L3=1.53528.20-1.374.6550.8L3=2.435311.16-1.274.2261.5L3=4.535310.35-1.282.9372.0L3=63474.88-1.042.608L3=0.5d2=0.52156.809L3=d2=12486.773L3=33141.92
4 结论
以电子低压冲击仪(ELPI)的结构为基础，采用FLUENT软件对单级低压冲击仪的颗粒场进行仿真。 研究不同结构参数下颗粒的拦截情况，结论如下。
1)在其他结构参数不变的情况下，当冲击喷嘴直径d2逐渐减小时，冲击区域的速度逐渐升高，得到了理想的收集曲线，分割直径明显降低，但分辨率下降了。 当冲击喷嘴直径为原始喷嘴直径的一半时，可得到理想形状收集曲线，分辨率最高，可以达到1.92。
2)在原始结构即冲击喷嘴直径为d2的情况下，改变喷嘴至收集平板的距离L3，得到的拦截曲线形状不变，但是分割直径的大小会改变。由于原始结构的颗粒拦截曲线出现2个峰值，所以对上一结论中，能够得到理想拦截曲线的算例即冲击喷嘴直径为0.5d2时，不同的L3进行模拟研究，结果表明，当L3为0.5 mm时，收集曲线形状理想，分割直径仅为215 nm，分辨率为6.8，此时低压冲击仪的拦截效果最好, 喷嘴至收集平板的最佳距离为0.5 mm。
[1]SHEIKHOLESLAMI M, HAQ R, SHAFEE A, et al. Heat transfer behavior of nanoparticle enhanced PCM solidification through an enclosure with V shaped fins[J]. International Journal of Heat and Mass Transfer, 2019, 130: 1322-1342.
[2]PETERS R J, VAN BEMMEL G, MILANI N B, et al. Detection of nanoparticles in Dutch surface waters[J]. Science of the Total Environment, 2018, 621: 210-218.
[3]SHEIKHOLESLAMI M, ZAREEI A, JAFARYAR M, et al. Heat transfer simulation during charging of nanoparticle enhanced PCM within a channel[J]. Physica A: Statistical Mechanics and its Applications, 2019, 525: 557-565.
[4]BUIARELLI F, DIFILIPPO P, MASSIMI L, et al. Ultrafine, fine and coarse airborne particle mass concentration in workplaces[J]. Atmospheric Pollution Research, 2019, 10(5): 1685-1690.
[5]HILLAMO R E, KAUPPINEN E I. On the performance of the Berner low pressure impactor[J]. Aerosol Science and Technology, 1991, 14(1): 33-47.
[6]LEPISTÖ T, KUULUVAINEN H, JUUTI P, et al. Measurement of the human respiratory tract deposited surface area of particles with an electrical low pressure impactor[J]. Aerosol Science and Technology, 2020: 1-14.
[7]余卓君, 吴建会, 张裕芬, 等. 垃圾焚烧厂排放颗粒物组分粒径分布特征[J]. 环境科学, 2019, 40(6): 2533-2539.
[8]郭红松, 方茂东, 陆红雨, 等. MMT对轻型GDI车辆PM2.5排放的影响[J]. 内燃机学报, 2014, 32(5): 432-436.
[9]YANG B, NING L, CHEN W, et al. Parametric investigation the particle number and mass distributions characteristics in a diesel/natural gas dual-fuel engine[J]. Applied Thermal Engineering, 2017, 127: 402-408.
[10]KWOK P C L, CHAN H K. Electrostatics of pharmaceutical inhalation aerosols[J]. Journal of Pharmacy and Pharmacology, 2009, 61(12): 1587-1599.
[11]PELLERIN G, MARO D, DAMAY P, et al. Aerosol particle dry deposition velocity above natural surfaces: quantification according to the particles diameter[J]. Journal of Aerosol Science, 2017, 114: 107-117.
[12]刘锡尧. ELPI测定环境空气PM2.5的现场比对研究[J]. 环境科学与管理, 2016 (1): 83-85.
[13]张进生, 吴建会, 马咸, 等. 钢铁工业排放颗粒物中碳组分的特征[J]. 环境科学, 2017, 38(8): 3102-3109.
[14]PENG Y, SUI Z, ZHANG Y, et al. The effect of moisture on particulate matter measurements in an ultra-low emission power plant[J]. Fuel, 2019, 238: 430-439.
[15]肖正航, 唐勇, 卓建坤, 等. 煤粉燃烧初期碱金属与碳烟相互作用的研究[J]. 工程热物理学报, 2017, 38(2): 399-405.
[16]周栋. 多种颗粒源的声波团聚实验研究与模拟[D]. 杭州：浙江大学, 2016.
[17]GLOVER W, CHAN H K. Electrostatic charge characterization of pharmaceutical aerosols using electrical low-pressure impaction(ELPI)[J]. Journal of aerosol science, 2004, 35(6): 755-764.
[18]YLIOJANPER
J, KANNOSTO J, MARJAMKI M, et al. Improving the nanoparticle resolution of the ELPI[J]. Aerosol and Air Quality Research, 2010, 10(4): 360-366.
[19]ARFFMAN A, MARJAMKI M, KESKINEN J. Simulation of low pressure impactor collection efficiency curves[J]. Journal of Aerosol Science, 2011, 42(5): 329-340.