气固两相流动在颗粒输送、 流化床技术和粉末喷涂技术等各种工业过程中非常普遍。 一般根据输送状态可分为浓相输送和稀相输送2类[1]。 浓相气力输送因其功耗较低而优于稀相气力输送，已成为研究热点[2]。 由于浓相气力输送的固有复杂性，因此仅从实验中很难观察和捕捉浓相气力输送的过程和规律。 数值模拟作为一种有效的补充和必要的方法，可以为研究颗粒流动过程提供有价值的见解。
为了提高输送效率，在保证管道不堵塞的前提下，需要尽可能提高粉料流量。 由于浓相气力输送控制困难，可能会直接导致输送管道内出现流动堵塞[3]，因此，越来越多的研究者开始关注流动堵塞，并通过大量的模拟和实验研究了抑制流动堵塞的临界条件。 流动堵塞仍是一个潜在的工程问题，当浓密相流不稳定时，管道很容易发生堵塞[4]。 通常，当输送过程中出现流动堵塞时，需要在管道中增加一些加压装置，这是很多工厂的解决方案[5]。额外的增压装置将增加事故的潜在风险，降低整个输送系统的效率，因此，应采取相应的措施，加快易发生堵塞的管道段的栓塞坍塌，减少严重的管道堵塞事故。
在过去的几年里，管道旋转方法一直受到研究者的关注，它对设备中流体的流动状态有很大的影响。Imao等[6]研究了固体比例和流体黏度对旋转罐内固体运动的影响。通过研究管道旋转对水平管内两相流流型和压降的影响，Yosef等[7]得到了压降与转速的关系，进而发现流型变化很大等有趣现象。为了找到有效的加快堵塞坍塌的方法，本文中尝试管道旋转方法。在旋转输送管道中，颗粒的运动受附加离心力和相关的周向摩擦力的影响较大，使得颗粒的运动轨迹与载体流体的流线有较大的偏离。在旋转系统中颗粒-湍流相互作用的机理变得更加复杂和有趣[8]。基于上述论述，本文中从几个方面研究了管道旋转对堵塞坍塌的影响，特别是坍塌速度和质量流量。
1 模型的建立
1.1 物理模型
图1为管道中流动堵塞的物理模型图。 如图所示，在计算流体力学(CFD)软件中建立了水平管道，其长度为3 000 mm，内直径为80 mm，长度为450 mm的栓塞被放置在管道前端。使用ICEM15.0软件，对网格进行预处理加工，并且仅仅使用了正六面体网格。横截面上的网格数目为2 700，整个网格共有单元数量为1 080 000。近壁面区采用了加密网格处理，既兼顾气相的无滑移条件，同时兼顾近壁面区的边界层效应，提高了模拟精度。
图1 流动堵塞物理模型图
Fig.1 Flow blockage physical model diagram
图2为几何的边界与网格图。如图所示，给出模拟的结构、边界和未细化的网格。表1中给出输送粉料的主要参数。
1.2 气相控制方程
CFD与离散单元法(DEM)的耦合模型可对流体相进行连续描述，这种耦合方法受到研究人员的青睐。本文中采用了压力梯度模型。
图2 边界与未细化的网格的典型几何图
Fig.2 Typical geometric sketch with unrefined
mesh and boundaries
表1 聚丙烯酰胺的重要参数
Tab.1 Properties of polyacrylamide materials
内摩擦角/(°)壁面摩擦角/(°)休止角/(°)堆积密度/(kg·m-3)真实密度/(kg·m-3)比表面积/(m3·cm-2)36.7212.7139600.241 3020.015
连续性方程如下：
(1)
动量方程如下：
,
(2)
式中： ε为空隙率； p为气体压力； τ是黏性应力张量； ρf是气体密度；
是重力系数；
是气固两相的交换源项, 根据Feng等[9]和Zhu等[10]的公式计算，源项可以根据下面公式计算：
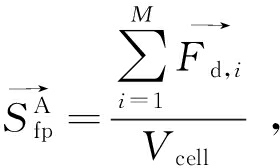
(3)
式中： M是网格中的颗粒数量； Vcell是计算网格的体积；
是网格中颗粒受到的曳力。
1.3 固相控制方程
颗粒的运动会受重力、浮力、接触力和气流共同作用。只有悬浮流通过震波或喷嘴时，压力梯度力、虚拟质量力和贝瑟特力才会产生[11]。范德华力是存在于分子间的一种吸引力，在流体流动过程中，范德华力仅出现在紧靠壁面处，但作用力极其微弱，因此，这些力在本文的模拟中都被忽略了。每一个颗粒都是用软球模型计算的，并由牛顿平动和转动运动方程描述，因此，固相控制方程为
(4)
(5)
式中：
分别为颗粒p的质量、 密度、 接触力和相互接触的颗粒的数量；
和
是作用在颗粒p上的切向与法向的力矩；
分别是作用在颗粒p上的转动惯量、角速度和流体力矩。
1.4 CFD-DEM接触模型
在每个时间步长中，为了评估每个计算单元中的孔隙率和颗粒-流体力，DEM提供了单个颗粒的位置和速度等信息。然后，CFD模型利用这些信息来确定气体流场，从而获得作用在单个颗粒上的颗粒-流体力。通过将产生的力合并到DEM中，可以确定单个粒子在下一个时间步中的运动。
1.4.1 曳力方程
在稠密的气固系统中，相互作用项的主要贡献者是曳力。在数值模拟中采用了基于颗粒曳力模型的流固耦合方法。曳力
是基于曳力平衡与欧拉-欧拉法[12]之间的流固耦合所求得，
(6)
式中： β为气固两相流动的阻力系数，取自Gidaspow模型[13]，其作为Wen & Yu模型[14]与Ergun方程[15]的组合，此模型是管道气固两相流动最合适的选择。当ε>0.8时，
(7)
并且，当ε≤0.8时，
(8)
式中： dp为颗粒的粒径； μf为气流的动力黏度； Cd为曳力系数，可表示为
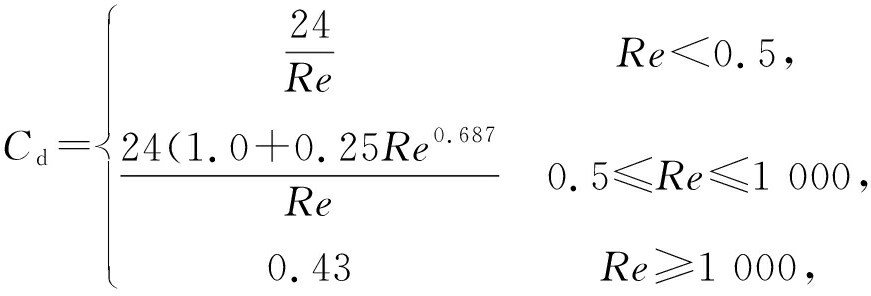
(9)
式中： Re为雷诺数，其表达式为
(10)
1.4.2 萨弗曼升力方程
在颗粒流中，压力差是由颗粒周围的速度梯度差引起的。压差引起颗粒上升的力称为萨弗曼升力，萨弗曼升力定义为
(11)
式中，
为流体横向速度梯度的绝对值。由于萨弗曼提出的lift模型受到各种条件的限制，为了克服这一问题，Mei[16]提出了2种相关方程:
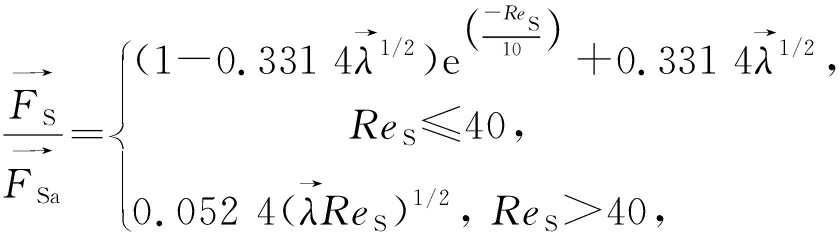
(12)
式中： ReS为滑动雷诺数； ν为流体的运动黏度；
为剪切速度，由下式给出:
(13)
1.4.3 马格努斯升力方程
流场中颗粒两侧的速度梯度对固体颗粒的作用力不均匀，导致固体颗粒在剪切转矩作用下旋转。固体颗粒的旋转将产生一个垂直于流体流动方向的力，称为马格努斯力。根据Oesterle等[17]和Lun[18]的实验结果，可以得到马格努斯升力表达式为
(14)
式中：
为流体的速度散度；
为颗粒的角速度；
为颗粒的转动雷诺数； CL为升力系数并且由下式可得:
。
(15)
1.5 边界条件
在CFD计算中，采用压力型求解器，进行时间步长为0.000 1 s的瞬态模拟。假定气相符合管壁无滑移条件，采用非平衡壁面函数进行近壁处理。将进气口设置为速度入口，速度为25 m/s，旋转管出口设置为自由流动。为了考虑旋流和湍流，采用了realizable湍流模型。利用压力与速度之间的强耦合的优点，采用相耦合的SIMPLE迭代算法进行压力-速度耦合，采用二阶迎风离散格式计算动量和湍流方程。
在DEM模拟中，在CFD-DEM并行耦合之前，为了获得一个栓塞，在管道的入口处建立了一个颗粒工厂。在CFD-DEM耦合后，将计算域设置为管道及其内部，并对DEM中的管壁设置一定的转速。监测仪被放置在管道沿线的各个位置，特别是在以0.001 s的间隔记录粒子速度的步骤上，总的运行时间为0.1 s。模拟中使用的模型和边界条件如表2所示。
表2 模拟中使用的模型和边界条件
Tab.2 Model and boundary conditions used in simulation
项单位数值流体/(空气)密度/(kg·m-3)1.225黏度/(kg·m-1·s-1)0.000 017 94进口速度入口/(m·s-1)25出口自由流出壁面剪切条件无滑移粗糙度/mm0.001粗糙度常数0.5离散化二阶迎风时间步长/s0.000 1颗粒形状球形半径/μm700密度/(kg·m-3)1 302剪切模量/MPa1 960时间步长0.000 002 5泊松比0.25机构运动线性转动颗粒-颗粒弹性恢复系数0.15滚动摩擦系数0.05静摩擦系数0.56接触模型赫兹·明德林软球模型颗粒-壁面弹性恢复系数0.5滚动摩擦系数0.01静摩擦系数0.5接触模型赫兹·明德林软球模型
2 结果与讨论
当管道转速为0时，堵塞的坍塌过程如图3所示。 从图中可以清楚地看出，由于重力和管道摩擦，整个栓塞的尾部颗粒被滞留在管道底部，形成连续层。 由于堵塞波处的颗粒体积分数比连续层小，堵塞波将提前运动。 沿着整个栓塞存在着固相浓度的变化，堵塞前端的颗粒群密度小，前缘更松散； 后部的颗粒群密度大，后端更密实。 在堵塞中颗粒运动方面，相同的运动图像被Klinzing[19]和Li等[20]所描述。 在本文的模拟中，认为该栓塞在模拟时间为0.06 s时完全坍塌，这是由于该管道上半部分出现了较大的孔隙, 因此，本文的模拟结果均在0.06 s内。
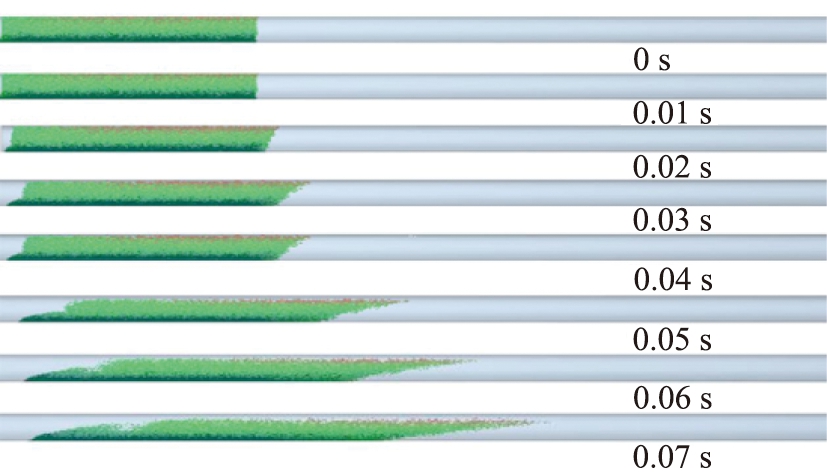
图3 栓塞坍塌过程
Fig.3 Collapse process of slug
2.1 坍塌速度
在本文中的模拟中，沿管道轴向方向的颗粒运动速度能很好地反映整个堵塞的坍塌速度，所以，用栓塞沿轴向的平均速度代表栓塞的坍塌速度。为了更好地反映管道旋转对堵塞坍塌速度的影响，本文中将关于颗粒平均速度的数据做了处理。
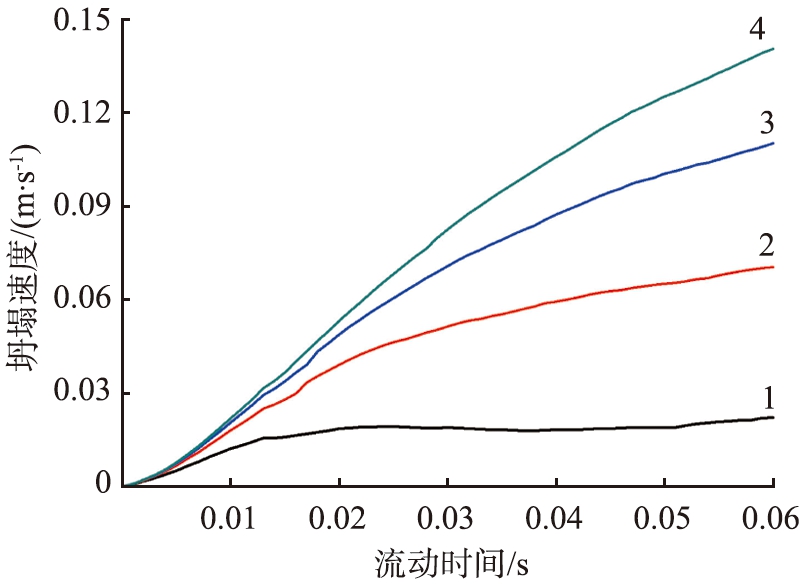
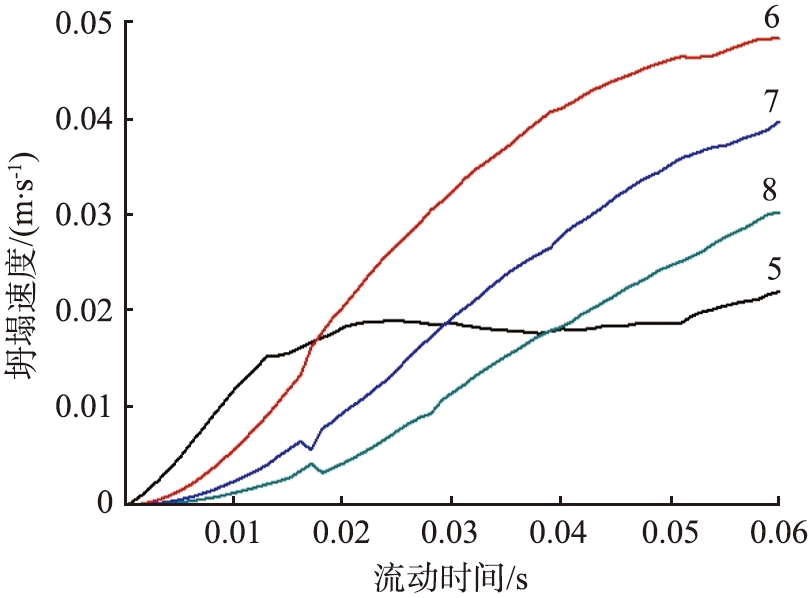
图4为相对坍塌速度图。 如图4a所示，列出了4种相对坍塌速度，并且把150 r/min相对于0，300 r/min相对于0，450 r/min相对于0，600 r/min相对于0处理，标识为情况1、 2、 3、 4。 如图4b所示，列出了4种相对坍塌速度，并且把150 r/min相对于0，300 r/min相对于150 r/min，450 r/min相对于300 r/min，600 r/min相对于450 r/min处理，标识为情况5、 6、 7、 8。
如图4a所示，相对坍塌速度情况4>情况3>情况2>情况1，直接说明管道旋转能够加快堵塞坍塌，并且旋转速度越高，坍塌速度会越大，但是，在图4b中所展现出来现象有所不同，在0.017 5 s之前，相对坍塌速度情况5>情况6>情况7>情况8，表明管道旋转速度每增加150 r/min，坍塌速度增量就会减小；然而，在0.0175 s之后，情况5会变得相对平稳，情况6>情况7>情况8，这说明堵塞坍塌效果与管道旋转速度不是正相关。本文中，管道的旋转速度由电机提供，显然，不同转速下管道的转矩可以认为相同，电机消耗功率只会与旋转速度呈正比,因此，堵塞坍塌效果与电机消耗功率非正相关，旋转速度并不是越高越好。
a 第1种变化
b 第2种变化
图4 相对平均坍塌速度
Fig.4 Relative collapse velocity
图5列出了图4b中4条曲线的斜率。 如图所示，对于4条曲线，都有相同的变化规律，即先增后降趋势，这表明图4b中的情况6、 7、 8都会在某一个时刻以后趋于平稳，并且旋转速度越高，这一时刻越往后，所以，如果综合考虑旋转后坍塌效果与能源消耗，最合适的旋转速度介于150～300 r/min之间。
2.2 颗粒质量流量
为了分析管道旋转对颗粒质量流量的影响，本文中在模拟过程中监测并记录了2个横截面处的质量流量，2个横截面分别位于距入口0.45 m(监测点1)和距入口0.1 m处(监测点2)。 距入口0.45 m处的颗粒质量流量如图6所示，距入口0.1 m处0.055 s左右颗粒质量流量达到极值。 从图7可以看出，在0.037 5 s时，最大颗粒质量流量约为5 500 kg/h，之后质量流量急剧减小，在0.042 5 s时，离入口约0.1 m处形成连续层，连续层在0.042 5 s后缓慢移动。
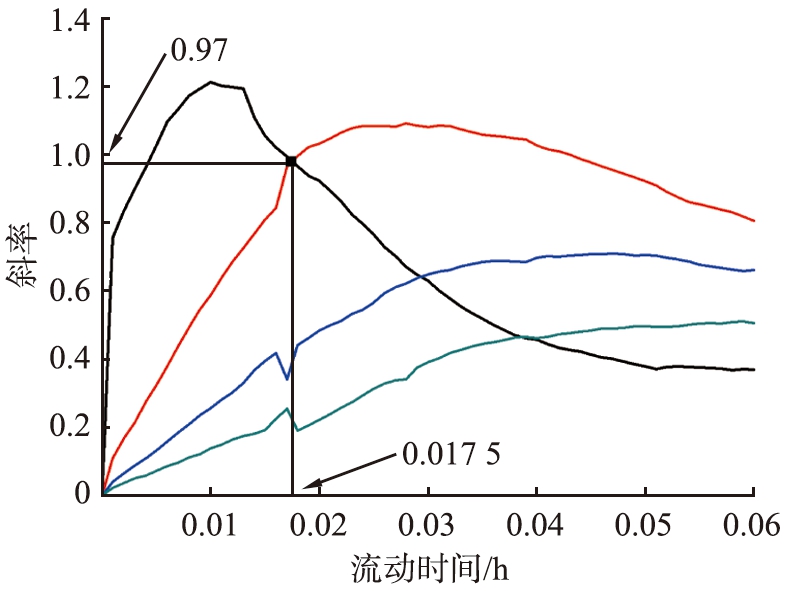
图5 图4b曲线的斜率
Fig.5 Slope of curves of figure 4b
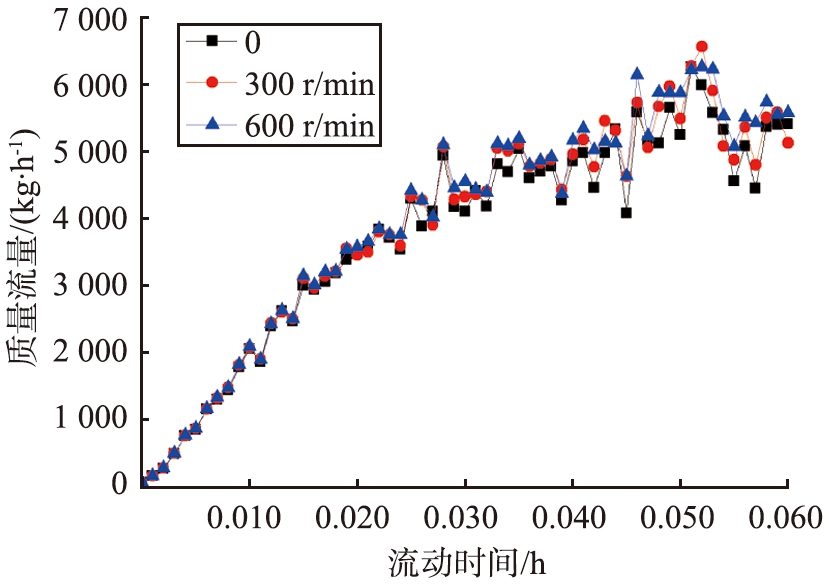
图6 距入口0.45 m处的颗粒质量流量
Fig.6 Mass flow rate at 0.45 m from entrance
的质量流量如图7所示。 在图6中，管道旋转对模拟时间0.017 5 s之前的质量流量影响不大，说明在此期间气动力占主导地位，但在0.017 5 s之后，不同转速下的质量流量变化较大，管道拥有一定的旋转速度后，会产生离心力与圆周方向的摩擦力，2种力会影响颗粒质量流量的变化。 并且从图6可以看出，栓塞从模拟时间0.017 5 s开始，颗粒质量流量不断加大，说明坍塌速度不断加快，并且在图7标注了匀加速阶段、变加速阶段和连续层阶段3个时间段。第1个转换点可以标记为加速点，第2个转化点可以标记为崩溃点。同时，可以发现第2阶段至第3阶段不是瞬间形成的，它需要较短的时间。这个时间一部分往前划归到第2阶段，一部分往后划归到第3阶段。结合图6分析可知，在0.06 s之前，横截面1处还没有形成连续层，但不可否认随着堵塞流动及坍塌，在横截面1处会出现连续层阶段。所以，无论横截面位置如何，这3个阶段都存在，但堵塞的崩溃点不同，加速点也不同。
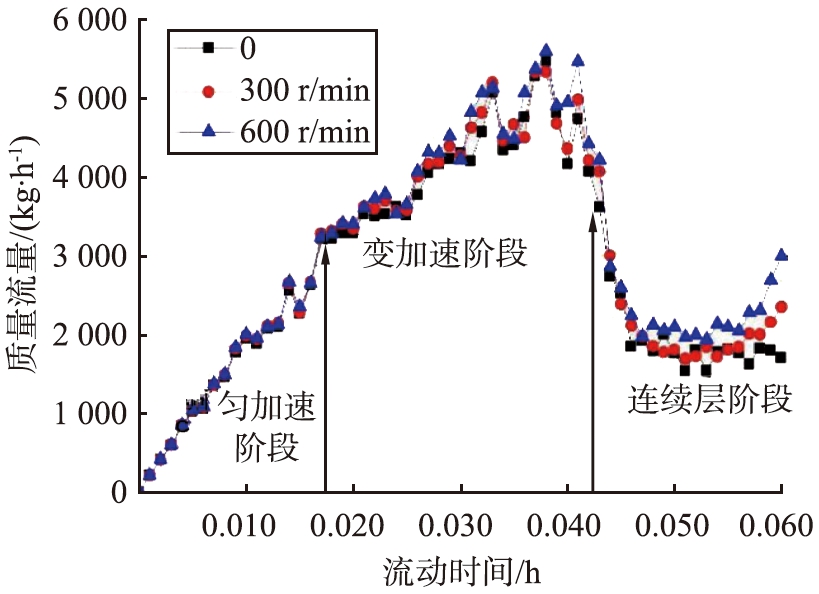
图7 距入口0.1 m处的颗粒质量流量
Fig.7 Mass flow rate at 0.1 m from entrance
从图4可以看出，在0.017 5 s之前，颗粒的平均速度较低，不同转速下的颗粒速度基本相同，连续层还没有明显形成，所以在此阶段颗粒的质量流量相对一致。颗粒质量流量在坍塌点处急剧减小，之后形成稳定的连续层。最大的颗粒质量流量出现在变加速度阶段，在变加速阶段,管道旋转对流动堵塞有很大影响，由于离心力的作用，颗粒与管壁之间的压力会增大，同时由于圆周方向的摩擦力增大，这将加强颗粒的圆周运动，因此颗粒的扰动性增强，气固动量交换加剧。
2.3 湍动能与气速分布
在模拟时间为0.055 2 s时，流态已经发展了一段时间，但没有完全发展，如图8所示。 因此我们分析了0.055 2 s时的湍动能和气速分布。
图8 模拟时间为0.055 2 s时的栓塞流流态
Fig.8 Slug flow pattern at 0.055 2 s
在Fluent中建立了一个低于中心面0.02 m的新平面，其轴向上0.055 2 s处的湍动能分布云图和气速分布云图如图9、 10所示。无转速时，湍动能的分布沿轴线对称；而有转速时，湍动能的分布是集中的。从图9中的圆圈可以看出，由于管道的旋转，湍流动能的分布发生了极化，因此管道左侧的湍动能较高，而右侧的湍动能较低，这是由管道的旋转方向造成的。从图10可以看出，在没有转速的情况下，第1个圈中的轴向气速较小，第2圈中的轴向气速较大，说明第1个圈中的固相密度大，已经形成了连续层。当管道有转速时，气速在轴向上的分布出现极化现象，且随着管道转速的增加，气速区域更宽。此外，在不同转速下，轴向的最大气流速度分别出现在最小的圆内，有利于颗粒在管道右侧更快的运动，从而加速一侧栓塞的坍塌。
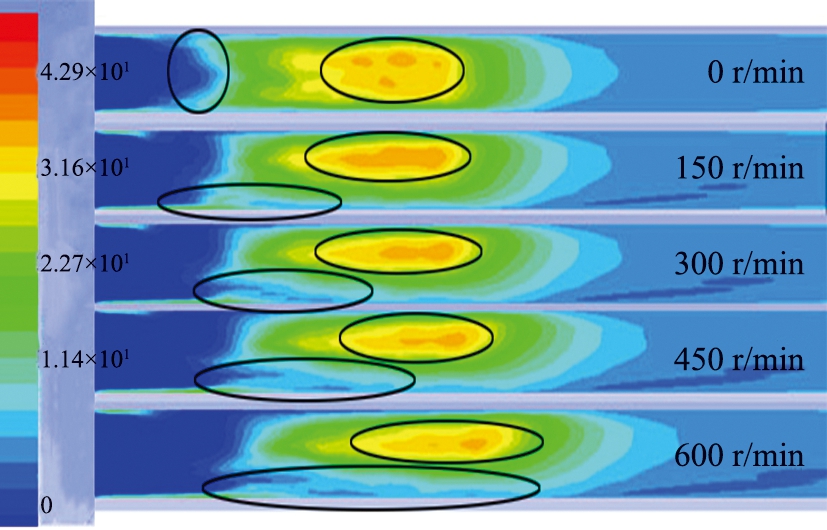
图9 模拟时间为0.055 2 s时不同转速下的湍动能分布
Fig.9 Distribution of turbulent kinetic energy at
different rotating speeds at 0.055 2 s
图10 模拟时间为0.055 2 s时不同转速下的气体速度分布
Fig.10 Distribution of gas velocity at different
rotating speeds at 0.055 2 s
图11给出了栓塞中间横截面上气速的矢量图。当管道不旋转时，管道底部的大面积气速方向垂直向下，颗粒与管壁之间存在较大的摩擦力，使得整个栓塞运动缓慢。当转速为600 r/min时，底部大面积的气速方向是水平向前的，虽然该区域的气速较低，但颗粒与管壁之间的轴向摩擦力会小。由于管道旋转产生的离心力，颗粒和壁面之间的压力增加，因此加大了圆周方向的摩擦力，在圆周方向的摩擦作用力下整个底部颗粒倾向于向右移动。由于管道的旋转方向，整个截面左侧气体速度的方向会有向上或向下弯曲的趋势，因此加剧了颗粒的扰动性，整个截面右侧的气流速度的方向表示在管道上半部分的颗粒将被席卷到右侧管道中。虽然颗粒运动变得复杂，但颗粒的扰动加速了堵塞的坍塌。
a 转速为0
b 转速为600 r/min
图11 栓塞中间横截面上气速的矢量分布
Fig.11 Vector distribution of gas velocity on
middle cross section
3 结论
1)管道旋转对堵塞坍塌起到了促进作用，但是，并不是旋转速度越高，坍塌效果越好。若综合考虑能耗与效果，最佳旋转速度为150～300 r/min。
2)在堵塞坍塌过程中，都会出现匀加速、变加速和连续层3个阶段。管道旋转对堵塞坍塌在变加速阶段和连续层阶段作用明显。
3)管道旋转会使颗粒域与气体域产生极化，先加速一侧堵塞坍塌，并且，管道旋转使颗粒扰动性增强，使颗粒运动变得更加剧烈。
[1]KONRAD K. Dense-phase pneumatic conveying: a review[J]. Powder Technol, 1986,49(1): 1-35.
[2]BEHERA N, AGARWAL V K, JONES M G, et al. Transient parameter analysis of fluidized dense phase conveying[J]. Powder Technol, 2012, 217(1): 261-268.
[3]RINOSHIKA A, SUZUKI M. An experimental study of energy-saving pneumatic conveying system in a horizontal pipeline with dune model[J]. Powder Technol, 2010, 198(1): 49-55.
[4]邵羽辛. 密相栓流气力输送的数值模拟[D]. 长春: 吉林大学, 2016.
[5]LIANG C, CHEN X, WENHAO P, et al. Flow characteristics and Shannon entropy analysis of dense-phase pneumatic conveying of pulverized coal with variable moisture content at high pressure[J]. Chemical Engineering & Technology, 2007, 30(7): 926-931.
[6]SHIGEKI I, MOTOYUKI I, TAKEYOSH H. Impact of solids fraction and fluid viscosity on solids flow in rotating cans[J]. Food Research International, 2008, 41(6): 658-666.
[7]YOSEF B, EBRAHIM H, SEYED M, et al. Effect of pipe rotation on flow pattern and pressure drop of horizontal two-phase flow[J]. International Journal of Multiphase Flow, 2018, 111(C): 101-111.
[8]YINGKANG P, TOSHITSUGU T, YUTAKA T. Turbulence modulation by dispersed solid particles in rotating channel flows[J]. International Journal of Multiphase Flow, 2002, 28(4): 527-552.
[9]FENG Y Q, YU A B. Assessment of model formulations in the discrete particle simulation of gas-solid flow[J]. Industrial & Engineering Chemistry Research, 2004, 43(26): 8378-8390.
[10]ZHU H P, ZHOU Z Y, YANG R Y, et al. Discrete particle simulation of particulate systems: theoretical developments[J]. Chemical Engineering Science, 2007, 62(13): 3378-3396.
[11]袁竹林，朱立平，耿凡. 气固两相流动与数值模拟[M]. 南京: 东南大学出版社，2013： 33-36.
[12]HOOMANS B P B, KUIPERS J A M, VANSWAAIJ W P M. Granular dynamics simulation of segregation phenomena in bubbling gas-fluidized beds[J]. Powder Technol, 2000, 109(1): 41-48.
[13]GIDASPOW D. Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. Boston: Academic Press, 1994.
[14]WEN C Y, YU Y H. Mechanics of fluidization[J]. Chem Eng Progress, 1966, 62: 100-111.
[15]ERGUN S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48: 89-94.
[16]MEI R. An approximate expression for the shear lift force on a spherical particle at finite Reynolds number[J]. Int J Multiphas Flow, 1992, 18(1): 145-147.
[17]OESTERLE B, DINH T B. Experiments on the lift of a spinning sphere in a range of intermediate Reynolds numbers[J]. Exp Fluids, 1998, 25(1): 16-22.
[18]LUN C. Numerical simulation of dilute turbulent gas-solid flows[J]. Int J Multiphase Flow, 2000, 26(10): 10-19.
[19]KLINZING G E. Dense phase (plug) conveying: observations and projections[J]. Handbook of Powder Technology, 2001, 10(1): 329-341.
[20]LI J, WEBB C, PANDIELLA S S, et al. Solids deposition in low-velocity slug flow pneumatic conveying[J]. Chemical Engineering and Processing, 2005, 44(2): 167-173.