液固两相流动广泛存在于自然界和工业过程中,在沉降分离、流态化领域有大量应用[1-3]。对颗粒运动特性分析是液固两相流进一步研究的基础,而对于液固两相流系统,其流场结构包括各相的含量、速度、压力、温度等场分布信息,且各属性依赖于不同时间与空间尺度,产生了液固两相流动的复杂性。目前,对颗粒群的研究一般是在单颗粒运动基础上进行的,颗粒沉降作为最基本液固两相流动,对其研究显得尤为重要。曳力系数是单颗粒沉降主要参数,部分学者通过理论分析与推导研究得出其常用关联式[4-5]。随着研究的深入,更多科研人员借助于数值模拟和实验测量方法对颗粒沉降进行研究分析。数值模拟方面,直接模拟法较多用于颗粒运动轨迹分析,其中直接模拟又分为两类:一类将颗粒当做质点,通过求解牛顿运动方程得到颗粒运动轨迹,求解过程中添加各种曳力模型,可实现双向耦合计算[6-9];另一类为颗粒全分辨直接模拟法,考虑流场中颗粒占有体积,通过将颗粒周围计算网格缩小到颗粒尺寸以下,求解颗粒运动[10-12],能精准预测液固两相流动,是目前液固两相流研究的热点。在实验测量方面,大多考虑无干扰式测量技术[13-15]。陈光国等[16]采用高速摄像技术对颗粒沉降进行实验研究,得到了颗粒沉降速度的影响因素;吴野等[17]利用高速相机记录钙质砂颗粒沉降过程,结合图像处理技术,得到了颗粒沉降平衡速度,从而拟合出拖曳力系数半经验模型;Liu等[18]采用粒子图像测速技术(particle image velocimetry,PIV)对喷嘴喷砂过程进行研究,得到了固体颗粒在液体中的沉降速度、运动轨迹;Corrine等[19]采用PIV方法对颗粒沉降进行研究,得到了不同湍流强度下,颗粒运动轨迹。
综上所述,目前对于颗粒自由沉降领域研究主要是对现象的描述,如沉降速度与运动轨迹,而对于产生这一规律的机理以及沉降过程中流场变化研究仍不够深入。 故此,本文中通过搭建竖管内单颗粒自由沉降实验平台,采用高速摄像测量技术与颗粒全分辨直接数值模拟相结合的方式,对颗粒沉降过程进行研究。 通过对比2种方法下颗粒的运动轨迹,从流场变化情况来解释颗粒的运动特征,验证模拟计算方法的合理性以及所得结论的准确性,为进一步研究液固两相流体系提供切实可行的方法。
1 实验系统及方法
1.1 实验装置及条件
竖管颗粒沉降实验平台如图1所示。 图1a为整体装置示意图,实验段为管内径d=32 mm、 壁厚δ=4 mm、 管长L=1 000 mm的有机玻璃管,玻璃管轴向方向(z轴)固定有分度值1 mm的标尺;图1b为实验拍摄过程所用电荷耦合器件(charge coupled device,CCD)相机。实验过程中,在竖管顶部人工释放经加工处理后粒径d=2 mm、密度ρ=2 147 kg/m3、球形度达到0.9的瓷球颗粒。为了保证所释放颗粒初始位置在管中心处,避免使其带有一定旋转角速度,对后续颗粒沉降运动轨迹产生影响,采用较短长度导引管的锥形漏斗对颗粒进行导引。

a 整体装置示意图

b CCD相机
图1 颗粒沉降实验平台
Fig.1 Particle sedimentation experiment platform
1.2 实验方法
实验过程中,首先对装置进行灌水,使水液位在锥形漏斗的导引管之上,水温为23.7 ℃;因向外漏液将使管内水存在一沿重力方向速度场,影响实验结果的精准性,故需对装置的密封性进行严格检查;同时调节CCD相机的高度、视角、焦距。由于拍摄距离与视角成正比,与清晰度成反比,综合考虑,选用竖管上部管段(0~540 mm)进行摄像处理。
2 数值模拟
2.1 颗粒运动控制方程
采用全分辨直接模拟法时,颗粒受力不是通过相间作用模型计算的,而是通过对颗粒表面黏性力和压力积分获得[12],其颗粒运动控制方程为[14]
(1)
(2)
![]() =vp
=vp
。
(3)
式中: mp、 dvp/dt、 ω、 ρ、 τ、 n分别为颗粒质量、 颗粒加速度、 颗粒角速度、 密度、 流体剪切压力矢量、 指向流体-颗粒界面∂Λp外侧的单位法向矢量,下标f、 p分别代表流体、 颗粒。
2.2 数学模型及设置
竖管内颗粒沉降实验数值计算模型尺寸如图2所示。管长L=1 000 mm,管内径d=32 mm,颗粒直径d=2 mm,球形度为1。初始时刻,颗粒位置(颗粒中心)距管顶端20 mm,且定义为坐标原点,流体定义为23.7 ℃的水,只受到重力作用(沿-z轴方向),颗粒自由沉降,使用直接数值模拟方法中的网格重构技术(动态网格技术)即6DOF模型方法对颗粒的沉降过程进行数值模拟。顶部出流口定义为pressure outlet,其余定义为wall。颗粒边线定义为moving wall。采用RNG k-ε湍流模型,PISO算法进行瞬态计算。

图2 竖管单颗粒沉降模型
Fig.2 Model of particle sedimentation in the vertical pipe
3 结果与讨论
3.1 实验结果及分析
图3为d=2 mm的瓷球颗粒在竖管内自由沉降过程中的瞬时图像,显示了固体颗粒在下降过程中残影长度的变化。

a 5 mm(0.01 s)b 5 mm(0.35 s)c 6 mm(0.70 s)d 6.5 mm(0.86 s)e 7 mm(0.97 s)f 7.5 mm(1.02 s)g 9 mm(1.19 s)h 10 mm(1.26 s)i 10 mm(1.68 s)j 10 mm(1.76 s)图3 颗粒沉降瞬时残影长度图Fig.3 FIG particle settling transient blur length
由图3可知,初始时刻颗粒自管中心位置下落,从下落过程颗粒残影位置及偏移中心可以看出,颗粒没有沿重力方向垂直下落,而是在径向发生了偏移,这说明颗粒受到径向方向的作用力,有径向方向的速度;颗粒残影长度经历了从短(5 mm左右)到长(10 mm左右)再到基本不变的过程,表明颗粒运动经历了加速到逐渐稳定的过程。
图4为经MATLAB图像处理后所得瓷球颗粒沉降的运动轨迹。 首先对原始图像进行灰度转换及增强处理,后续在此基础上对原始图像进行阈值处理,最后对处理所得含单个颗粒图像进行叠加。 由图4可以看出,在沉降过程中,颗粒的运动轨迹在径向方向上具有周期性特征。 同时,上半段时颗粒沿管中心反复穿插,下半段时颗粒位置则偏向一侧,限于CCD相机位置及视角,沉降管底部的图像并未采集,根据实验观察,颗粒在沉降管底部运动形式与沉降管顶部相同,均沿管中心反复穿插,区别在于颗粒由顶部向底部沉降过程中,轴向方向波距逐渐增大,说明颗粒的这种波动效应与沉降过程中的运动距离成正比。

图4 管内颗粒沉降运动轨迹
Fig.4 Trajectory of particles in the pipe
为获得颗粒沉降过程的详细位置坐标图,利用MATLAB软件,将原始颗粒数字图像像素坐标转化为清晰表达的物理坐标,转化的关键是对数字图像进行标定,即标定出单位像素对应的物理空间大小。实验中通过选取定长度的物体来对所拍摄的数字图像像素进行标定,即
(4)
式中:L代表物体长度大小,下标ph、 pi分别代表实际物体和数字图像。
经过处理得到如图5所示的颗粒位置分布图。图中坐标原点是选用数值模拟时颗粒的初始位置,且为实验中轴向方向(z轴)刻度40 mm处的管中心位置,故颗粒z轴坐标绝对值为各自的刻度值减去40 mm。由图5可以看出,颗粒沉降过程由初始沿管中心稳定径向摆动,到后期摆动幅度逐渐增大,且出现无规则摆动趋势,摆动的平衡位置也开始偏离管中心,可见瓷球颗粒沉降的径向运动是一个非线性放大过程,而对本实验D/d=16(管径/粒径)的颗粒沉降,管壁对颗粒运动的约束作用较小。颗粒粗糙度以及球形度使颗粒产生了绕球心的扭矩,同时,颗粒沉降对流体的影响反作用于颗粒。流体的影响使颗粒受力不均匀而产生了旋转,正是由于这种旋转,使颗粒在沉降的同时沿径向受到Magnus力的作用,在Magnus力和惯性力的共同作用下颗粒产生径向的偏移。
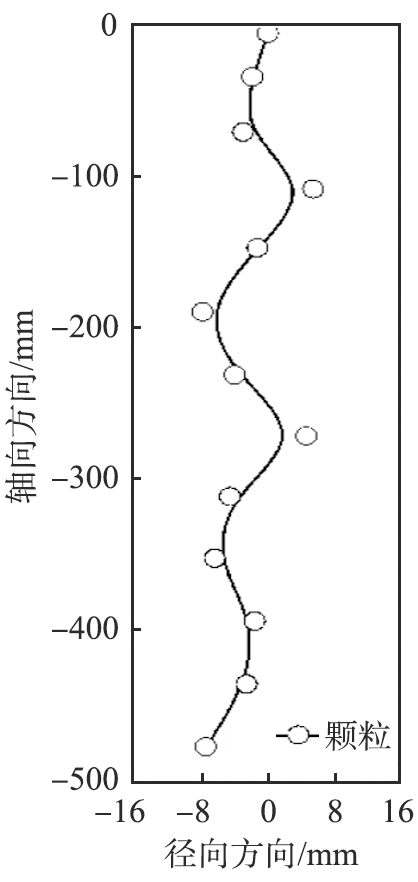
图5 颗粒位置分布
Fig.5 Particle position distribution
3.2 数值模拟结果及对比
3.2.1 速度云图
图6为颗粒沉降过程中不同时刻的速度云图及流线图。从速度标尺可以看出,颗粒经历了加速到逐渐稳定的过程,这与前面实验结果相吻合。图6a为颗粒沉降过程的初始阶段,此时管内流场与流线基本为对称分布,由于颗粒在自由沉降时处于不断排开流体的过程,故流场速度表现为从下到上的闭合曲线(开始于颗粒底部,闭合于颗粒顶部),同时在颗粒底部与顶部区域速度最大。图6b、6c中的速度逐渐变大,此时颗粒在加速运动,管内流场分布逐渐变为不对称,同时在颗粒后部开始产生涡状结构。图6d中,颗粒沉降速度基本达到稳定,由于颗粒径向运动的影响,其值略小于理论计算值,两者误差为3.26%,在可接受范围内。根据数值模拟产生的动画显示,涡状结构分布不均匀,同时,涡状结构的分离伴随着颗粒产生较大的径向运动,这说明在自由沉降过程中,涡状结构对颗粒的径向运动产生了影响。
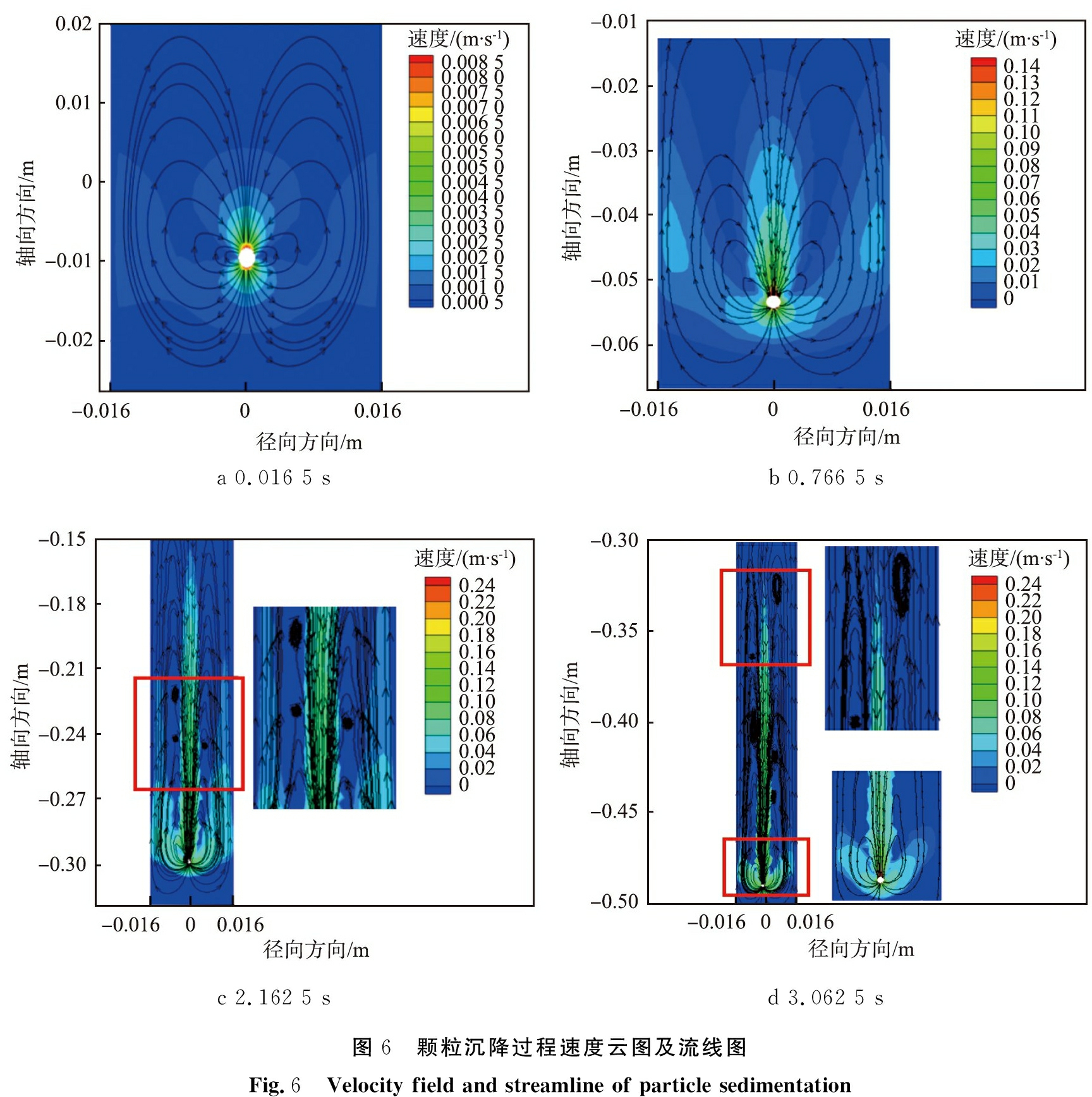
a 0.016 5 sb 0.766 5 sc 2.162 5 sd 3.062 5 s图6 颗粒沉降过程速度云图及流线图Fig.6 Velocity field and streamline of particle sedimentation
3.2.2 颗粒位置分布与对比
为进一步验证颗粒全分辨直接数值模拟法与实验的可行性与可靠性,从模拟结果中提取颗粒沉降过程的位置信息,并与实验所得颗粒位置分布进行对比研究。
实验与模拟颗粒位置对比如图7所示。 由图可以看出,数值模拟结果图线与实验所得图像能够较好地匹配,尤其是在顶部段0~-100 mm及底部段-300~-500 mm,二者所连曲线能够很好地穿插叠加在一起。而在-100~-300 mm段,实验所得颗粒位置变化曲线沿径向出现2个波峰,而模拟结果只存在一个峰值点。这是因为实验颗粒为三维运动状态,颗粒在竖管内的沉降过程呈摆动状态,因此所得颗粒位置曲线映射到二维平面应具有空间性,而数值模拟结果为二维状态下获得,这与实验所得曲线存在一定的差异,但二者径向运动的最大值仍在同一量级,波动幅度也基本一致。故此,从颗粒位置结果的对比以及管内流场的分析可知,所使用全分辨直接数值模拟方法对颗粒运动行为研究具有可行性。

图7 实验与模拟颗粒位置对比
Fig.7 Comparison of experimental and
simulated particle positions
4 结论
为探究管内颗粒沉降规律以及模拟计算的可靠性,运用高速摄像仪试验与直接模拟法对颗粒运动特征进行分析,主要结论如下:
1)由实验结果与速度云图可知,颗粒经历了由加速到逐渐稳定的沉降过程,颗粒尾部两侧流场会逐渐出现涡状结构,并且呈不对称分布,其促使颗粒产生径向运动。
2)颗粒沉降过程中,存在径向运动,其运动轨迹呈螺旋式下降,径向位置的分布具有周期性;摆动平衡位置逐渐偏离管中心,径向摆动幅度逐渐增大,并呈非线性放大过程。
3)数值模拟所得颗粒位置图线能够与实验所得颗粒位置分布实现较好的匹配。通过数值模拟与实验结果的对比,证明了颗粒全分辨直接模拟法对颗粒运动行为的研究具有可行性,实验测量与直接数值模拟法相结合的方式可为液固两相流研究提供借鉴。
[1]王勇, 杨启容, 吴荣华, 等. 污水换热器流态化在线防、除垢实验[J]. 化工进展, 2015, 34(12): 4398-4402.
[2]MADDAHI M H, HATAMIPOUR M S, JAMIALAHMADI M. Modification of heat transfer correlations in a liquid-solid fluidized bed heat exchanger with cylindrical particles in aggregative fluidization[J]. Heat & Mass Transfer, 2016, 52(11): 2391-2400.
[3]TAN M, KARABACAK R, ACAR M. Experimental assessment the liquid/solid fluidized bed heat exchanger of thermal performance: an application[J]. Geothermics, 2016, 62: 70-78.
[4]FARDIN S, AMIR H A. Particle cloud dynamics in stagnant water[J]. International Journal of Multiphase Flow, 2020, 125: 103197.
[5]BROWN P P, LAWLER D F. Sphere drag and settling velocity revisited[J]. Journal of Environmental Engin-eering, 2003, 129(3): 222-231.
[6]WEI L, SHI W D, JIANG X P, et al. Analysis on internal solid-liquid two-phase flow in the impellers of sewage pump[J]. Procedia Engineering, 2011, 2(1): 170-175
[7]CHENG W J, GU B Q, SHAO C L, et al. Hydraulic characteristics of molten salt pump transporting solid-liquid two-phase medium[J]. Nuclear Engineering & Design, 2017, 324: 220-230.
[8]WANG S, WANG X X, WANG X, et al. Numerical simulation of flow behavior of particles in an inverse liquid-solid fluidized bed with a jet using CFD-DEM[J]. Journal of the Taiwan Institute of Chemical Engineers, 2018, 82: 214-225.
[9]HWANG B, PARK H S, JUNG W H, et al. Numerical validation and investigation for the sedimentation of solid particles in liquid pool using the CFD-DEM coupling algorithm[J]. Nuclear Engineering and Design, 2019, 355: 110364.
[10]熊红兵. 基于光滑粒子流体动力学方法的多相流直接数值模拟[C]//中国力学学会流体力学专业委员会. 第七届全国流体力学学术会议论文摘要集, 2012: 52.
[11]UHLMANN M. An immersed boundary method with direct forcing for the simulation of particulate flows[J]. Journal of Computational Physics, 2005, 209(2): 448-476.
[12]王兵. 大涡模拟与直接模拟研究稀疏气固两相湍流规律综述[J]. 工程力学, 2009, 26(11): 213-221.
[13]李轶. 多相流测量技术在海洋油气开采中的应用与前景[J]. 清华大学学报(自然科学版), 2014, 54(1): 88-96.
[14]王丽燕, 孙志强, 周天, 等. 基于PIV图像处理法的管内低浓度液固两相流颗粒运动特性研究[J]. 工程热物理学报, 2018, 39(9): 1970-1978.
[15]JAIN V, KALO L, KUMAR D, et al. Experimental and numerical investigation of liquid-solid binary fluidized beds: radioactive particle tracking technique and dense discrete phase model simulations[J]. Particuology, 2017, 33(4): 112-122.
[16]陈光国, 阳宁, 唐达生, 等. 垂直管道颗粒及颗粒群沉降运动规律研究[J]. 泥沙研究, 2010(4):16-21.
[17]吴野, 王胤, 杨庆. 考虑钙质砂细观颗粒形状影响的液体拖曳力系数试验[J]. 岩土力学, 2018, 39(9): 3203-3212.
[18]LIU P, LAM K M. Two-phase velocity measurement in a particle-laden jet[J]. Journal of Hydro-environment Research, 2013, 7(1): 18-29.
[19]JACOBS C N, MERCHANT W, JENDRASSAK M, et al. Flow scales of influence on the settling velocities of particles with varying characteristics[J]. Plos One, 2016, 11(8): e0159645.