自上世纪以来,伴随物理粉碎及化学合成等粉体制备技术的发展,超细粉体因其具有区别于原固体材料的优异特性走入国民经济各大市场[1]。服务于超细粉体生产的超细粉包装机成为近年来的研究热点[2-4]。超细粉充填计量机械系统是自动化超细粉包装机的关键部件,目前市场可见超细粉充填方式有气吹式、泵送式和螺杆式等[5]。螺杆式作为常用于颗粒体及普通粉料的充填方式也常见于超细粉体的充填计量装置。在超细粉阀口袋的清洁化包装中,水平输送螺杆更是超细粉充填计量机械系统中的关键零件。
超细粉体的粒径小,含气量大,是介于固体与流体之间的第4种物质状态,故超细粉在水平螺杆输送的过程中兼具有颗粒体与流体的特性,即微观上的离散特性和宏观上的连续特性。
本文中针对超细粉体阀口袋包装形式,设计其螺杆式供送充填计量机械基本结构,主要讨论充填计量机构中的关键零件水平输送螺杆相关几何参数对充填效率的影响,为相关水平输送螺杆及包装机械设计提供参考。
1 充填计量系统设计
1.1 充填计量机械结构
图1为超细粉充填计量机械结构示意简图,主要由电机驱动系统、进料仓、搅拌扇叶、水平输送螺杆、套筒、固袋装置、吹气卸料装置和振动称量装置组成。

1—电机驱动系统;2—进料仓;3—搅拌扇叶;4—搅拌扇叶电机;5—负压排气口;6—水平输送螺杆;7—套筒;8—固袋装置;9—吹气卸料装置;10—超细粉包装袋;11—振动称量装置。
图1 超细粉充填计量机械结构示意简图
Fig.1 Filling and metering system of ultrafine powder
超细粉体通过进料仓进料,搅拌扇叶充分搅拌超细粉体,使其拥有较好的分散性;水平输送螺杆在电机驱动系统的驱动下开始旋转,实现超细粉体的水平输送。套筒在排气段上开设有负压排气口,连接负压系统排除超细粉体中的部分气体;在密实段,水平输送螺杆有一段变螺距设计,通过改变螺距的大小,从而改变每一圈螺旋容积;当超细粉体从大容积螺旋输送到小容积螺旋,超细粉体中的部分气体将被排出,2次排气处理保证了在卸料段超细粉体以较低的含气量充填进入由固袋装置吸附固定于套筒上的阀口袋中。吹气卸料装置在充填结束后吹气1次,将积滞在水平螺旋出口的超细粉吹落进阀口袋中。
1.2 水平输送螺杆关键参数
水平输送螺杆是超细粉阀口袋充填计量机械结构中的关键零件,其性能的好坏对整个机械系统都有着非常大的影响,水平输送螺杆的质量直接决定了超细粉阀口袋充填计量系统的最终性能[6-9]。输送量和充填效率是衡量螺杆质量的2个重要指标。输送量一般由实际生产需求所决定,但与螺杆的几何参数相关,充填效率也与螺杆的几何参数相关[10]。其中,输送量Q可粗略计算为
Q=ρAv,
(1)
式中:Q为水平螺杆输送量,t/h;ρ为超细粉的密度,t/m3;A为水平输送螺旋套筒的横截面积,m2;v为超细粉在螺杆输送过程中的轴向速度,m/h。
充填效率可定义为:
(2)
式中:VS为出口实际体积流量,m3/s;VL为出口理论体积流量,m3/s;
式中:S为水平输送螺杆螺距;n为水平输送螺杆转速。
单头水平输送螺杆螺旋套筒横截面积[11]可计算为
(3)
式中:D为水平螺杆外径,m;d为水平螺杆内径,m;e为水平螺杆螺旋叶片厚度,m;H为水平螺杆螺旋槽深,![]() m;α为水平螺杆螺旋升角,α=arctan
m;α为水平螺杆螺旋升角,α=arctan![]() ,rad,其中S为螺距。
,rad,其中S为螺距。
综上,由式(1)—(3)可知,水平输送螺杆的外径、内径、螺距、螺旋叶片厚度,螺旋槽深和螺旋升角等几何参数会影响水平输送螺杆的性能,因此进一步确定内外径及螺距等水平输送螺杆的相关几何参数,是水平输送螺杆的设计及优化关键。
对于常见的工业超细粉末如钛白粉、铝粉及钴粉等,25 kg阀口袋装为常用中袋包装,基本尺寸如图2所示。
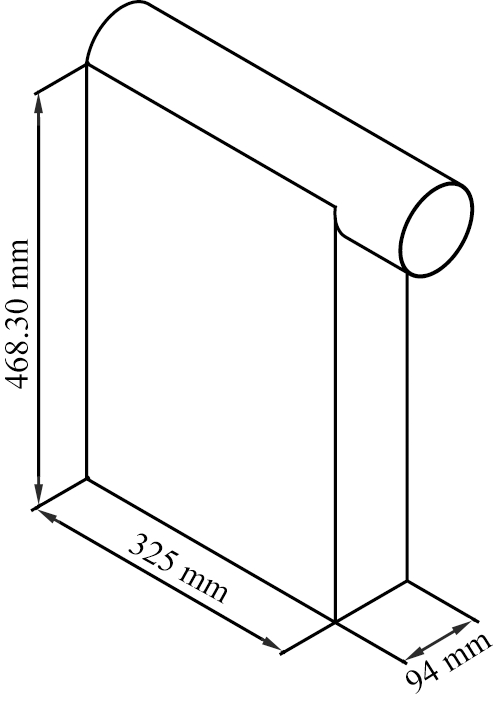
图2 25 kg超细粉阀口袋基本尺寸
Fig.2 Basic size of 25 kg ultrafine powder valve pocket
由图可知,25 kg超细粉阀口袋其阀口直径在94 mm左右,考虑固袋装置、套筒等结构需求空间以及获得更大输送量等因素,可确定25 kg阀口袋装的水平输送螺杆外径为D=80 mm较为合适。当外径D确定之后,水平螺杆内径与螺旋槽深为反比关系,螺旋升角及螺距为正比关系,2对关系中皆是确定其中一个参数,就可对应固定另一参数,因此需要进一步确定的水平输送螺杆的关键参数是螺旋升角、螺旋槽深和螺旋叶片厚度。
2 正交试验设计
由于正交试验设计具有优良的均衡分散性和整齐可比性,设计的试验点具有代表性,因此在工艺改革等多因素试验设计问题中,往往能以较少的试验次数,分析出各因素的主次顺序以及对试验指标的影响规律,筛选出较满意的试验结果。正交试验法应用广泛,具有较高的经济效益,是多因素试验设计问题中的常用手段[12-13]。
基于上述水平输送螺杆关键参数的确定,对螺旋升角、螺旋槽深和螺旋叶片厚度3个影响因素进行正交试验设计,由于Q又可写成Q=3 600VS,因此以实际体积流量VS和充填效率η作为试验结果参考指标。
因素A螺旋升角:在工业生产常见的水平螺杆中,为便于加工制造,常取S=D,即螺旋升角α≈17 °,因此在正交试验设计中,取螺旋升角的3个水平为12 °、17 °和22 °。
因素B螺旋槽深:水平输送螺杆的轴径一般可计算为d=(0.2-0.35)D[4],则有螺旋槽深H=(0.325-0.4)D,取螺旋槽深的3个水平为0.35D、0.375D、0.4D。
因素C螺旋叶片厚度:2 mm为常见螺旋叶片厚度,取螺旋叶片厚度3个水平为2、4、6 mm。
综上可得因素水平,见表1。
表1 试验因素水平
Tab.1 Test factor level

因素螺旋升角A/(°)螺旋槽深B/mm螺旋叶片厚C/mm水平112282水平217304水平322326
正交表L9(34)最多可以安排4个3水平因素,3因素3水平可用该表格安排,所列试验条件见表2。
表2 试验条件
Tab.2 Test conditions
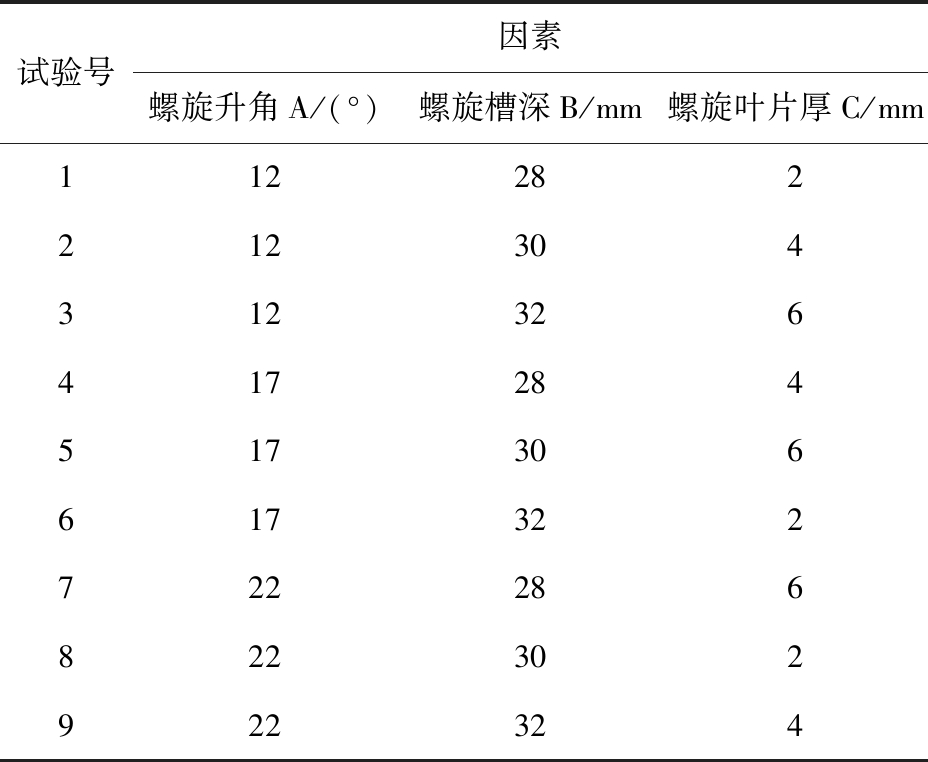
试验号因素螺旋升角A/(°)螺旋槽深B/mm螺旋叶片厚C/mm112282212304312326417284517306617322722286822302922324
3 数值模拟试验
计算机流体力学(computational fluid dynamics,CFD)是目前国际上热门研究领域,是进行传热、传质、动量传递及燃烧、多相流和化学反应研究的核心和重要技术,广泛应用于管柱设计、流体机械设计、航天设计、汽车设计以及生物医学、化工处理等诸多工程领域。CFD的计算方法具有成本低和能模拟较复杂或较理想的过程等优点,Ansys Fluent软件是通用的CFD软件包,可用来模拟从不可压缩到高度可压缩范围内的复杂流动[14-16]。
超细粉体因其粒径小、含气量大的物性在水平螺杆输送的过程中具有流体的特性,因此可采用Ansys Fluent对其水平螺杆充填的过程进行数值模拟[17]。
3.1 模型建立
取超细粉充填计量机械结构中料仓、水平输送螺杆和套筒3个充填相关零件并结合对应试验号中螺杆相关参数,分别在Solidworks软件中建立水平螺杆充填模型,并使用布尔运算获得水平输送螺杆充填流体域模型[18],如图3所示。
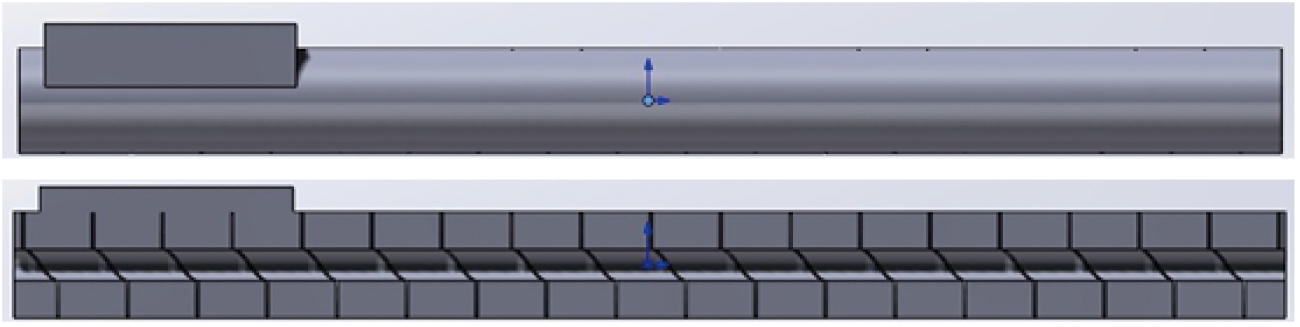
图3 水平输送螺杆流体域模型
Fig.3 Fluid model of horizontal conveying screw
在Ansys Workbench工作界面添加流体分析项目,并将水平输送螺杆的流体域模型导入项目树中的Geometry,设置模型状态为流体,并对模型的入口、出口、旋转壁面及静止壁面等边界进行命名。
3.2 网格划分及质量检查
对流动问题进行数值计算的第1步是生成网格,即要对空间上连续的计算区域进行剖分,把它划分成许多个子区域,并确定每个区域的节点[19-20]。实际上,流动问题数值计算结果的最终精度及计算过程的效率取决于所生成的网格与所采用的算法。
由于网格质量直接影响计算精度,因此网格生成之后需检查网格质量。网格质量一般由扭曲率(skewness)及正交质量(orthogonal quality)来进行判断。一般来说,网格扭曲率最大值应小于0.95,平均值应小于0.33,正交质量平均值应大于0.5。
针对螺杆旋转的3D流动[21],采用非结构化网格对整个流体域进行网格划分(见图4),并采用对壁面设置膨胀层、面加密和线加密等局部加密的方式提高网格质量(见图5)。
图4 网格划分
Fig.4 Meshing

图5 网格质量检查
Fig.5 Quality check
3.3 边界条件及算法设置
根据模型3D旋转流动的特点,选择Ansys Fluent中的压力基耦合求解器(coupled)进行求解计算。并选择两相流模型及在旋转流动中能体现更大优势的SST k-ω的湍流模型[22]。设置螺杆旋转流动介质边界条件为移动坐标参考系(moving reference frame),并设定旋转方向为X轴正方向,旋转速度为200 r/min。设置入口边界条件为压力入口,出口边界条件为压力出口,相应壁面边界条件为对应移动及静止壁面。
设置完成之后,对入口及出口体积流量进行监视设置,数据初始化后开始计算。
4 结果
通过Solidworks的对应参数建模和Ansys Fluent数值模拟计算之后,得到9个试验的结果,如表3所示。
表3 数值计算结果
Tab.3 Results simulation of numerical
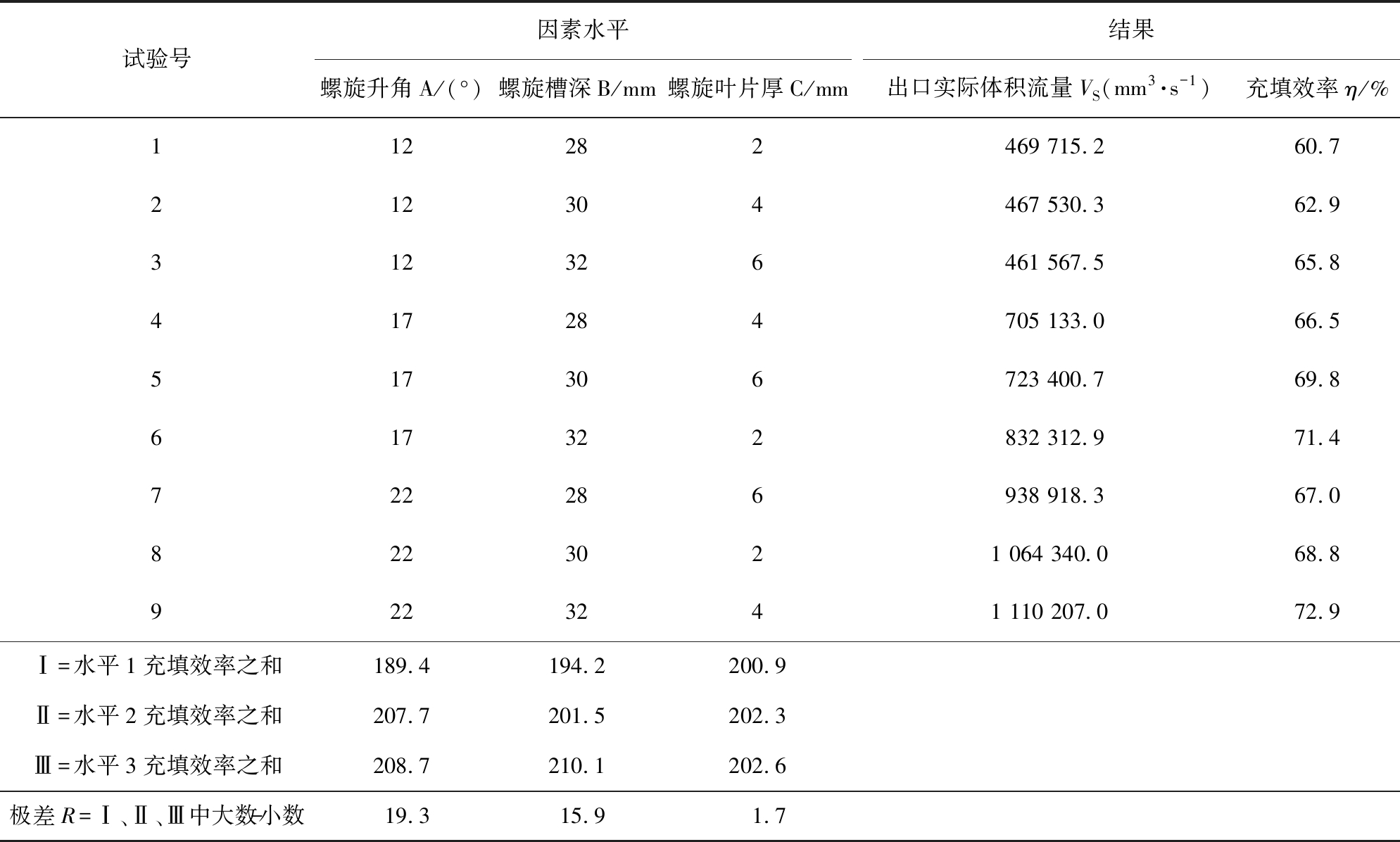
试验号因素水平螺旋升角A/(°)螺旋槽深B/mm螺旋叶片厚C/mm结果出口实际体积流量VS(mm3·s-1)充填效率η/%112282469 715.260.7212304467 530.362.9312326461 567.565.8417284705 133.066.5517306723 400.769.8617322832 312.971.4722286938 918.367.08223021 064 340.068.89223241 110 207.072.9Ⅰ=水平1充填效率之和189.4194.2200.9Ⅱ=水平2充填效率之和207.7201.5202.3Ⅲ=水平3充填效率之和208.7210.1202.6极差R=Ⅰ、Ⅱ、Ⅲ中大数-小数19.315.91.7
直观分析:直接比较9个试验的充填效率可以看出,第9号试验的充填效率为72.9%,为最高,第6号试验的充填效率为71.4%,次之,且第6号试验和第9号试验充填效率差别不大。另一指标出口实际体积流量,第9号试验结果为1 110 207.0 mm3/s,明显大于第6号试验的832 312.9 mm3/s。
极差分析:比较因素A、B和C的3个水平的充填效率之和可以看出螺旋升角22 °,螺旋槽深32 mm,螺旋叶片厚度6 mm的水平输送螺杆有较高的充填效率。比较3个因素的极差可发现,螺旋升角和螺旋槽深对水平输送螺杆的充填效率有较为明显的影响,螺旋叶片厚度对水平输送螺杆的充填效率影响较小。
图6为因素水平趋势图。水平趋势分析:由图6中3个因素的水平趋势图可以看出,螺旋槽深越大能获得更大充填效率,结合表3,亦有螺旋槽深与出口实际体积流量成正比关系,因此在H=(0.325-0.4)D的范围内,水平3即H=0.4 D=32 mm为最佳值,固定螺旋槽深水平3;螺旋叶片厚度越大也能获得更大的充填效率,但其增长较小,结合表3,螺旋叶片厚度对出口实际体积流量的影响是反向关系,即螺旋叶片厚度越大,出口体积流量越小,计算3个水平的出口实际体积流量之和:VS1=2 366 368.1 mm3/s,VS2=2 255 271.0 mm3/s,VS1=2 123 886.5 mm3/s降比为10.2%,远大于螺旋叶片厚度增加所带来的充填效率1.7%的升幅,因此,为了实现更大的输送量,将螺旋叶片厚度固定在水平1即2 mm;螺旋升角由12 °增大到17 °时,螺杆的充填效率有大幅度的提升,由17 °增大到22 °时,螺旋升角的充填效率增幅较小,结合表3可以看出,螺旋升角的增大对出口实际体积流量的影响也是正向的,因此可预测获得最佳充填效率的螺旋升角大于22 °或在17 °~22 °之间,要获得最佳螺旋升角,需做进一步单因素试验。
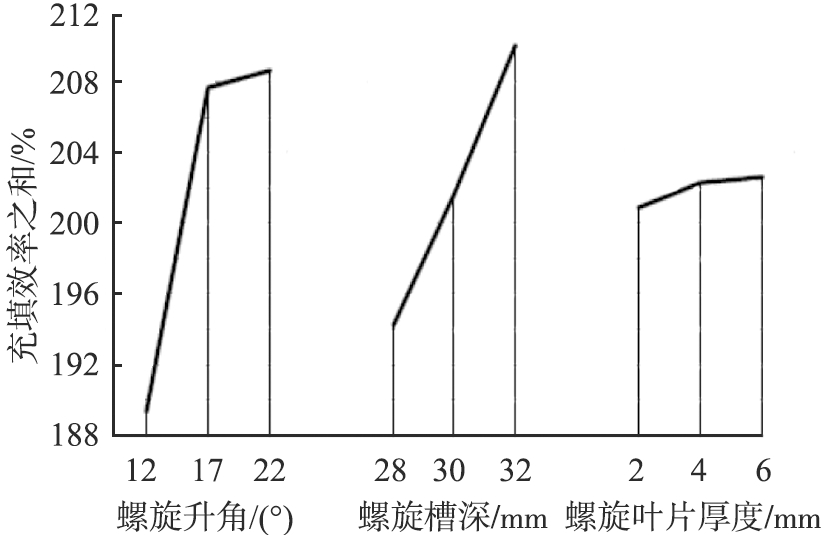
图6 因素水平趋势图
Fig.6 Trend chart of factors
5 最佳螺旋升角
基于正交试验结果,已确定的水平输送螺杆参数:D=80 mm,d=16 mm,e=2 mm,H=32 mm。为确定最佳螺旋升角,固定其他因素,做螺旋升角单因素试验,通过分析因素水平趋势图,确定在α=17 °~25 °区间增加取样密度,在α<17 °和α>25 °区间保持原取样密度。确定各试验条件后,重复数值模拟试验,最终得到如表4所示结果。
表4 螺旋升角与充填效率的关系
Tab.4 Relationship between helix angle and filling efficiency
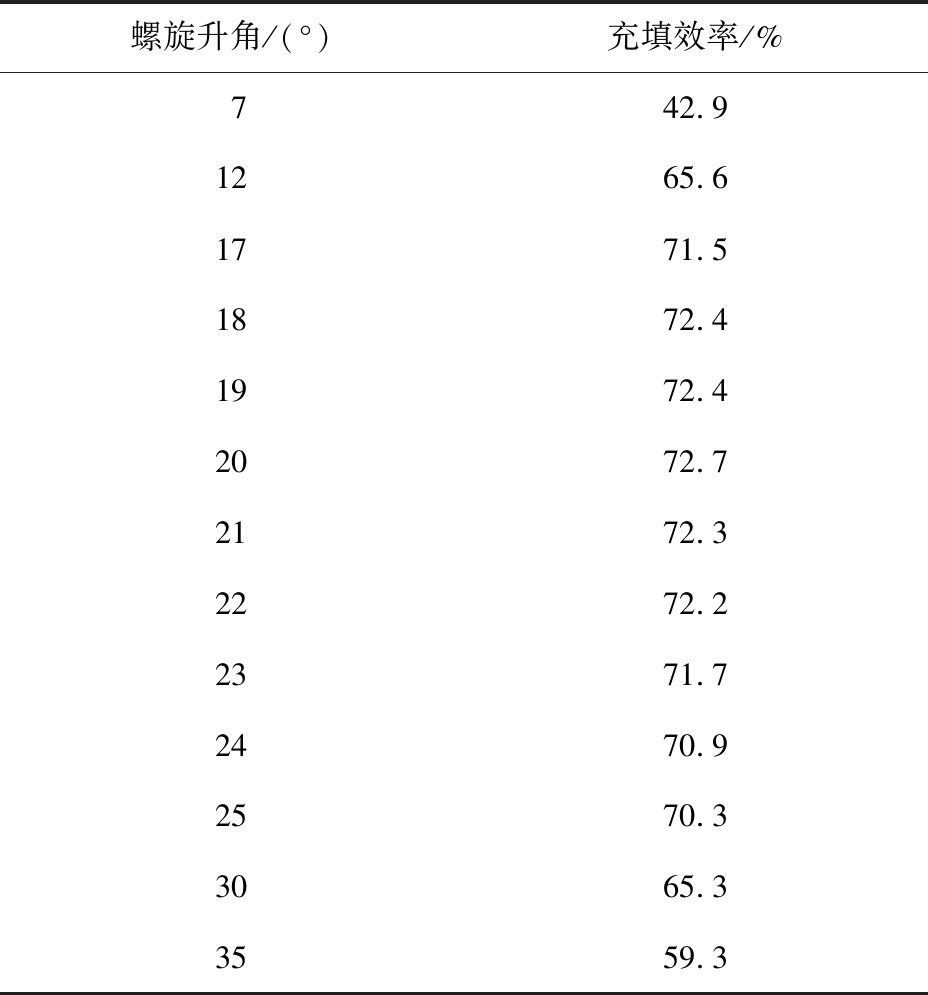
螺旋升角/(°)充填效率/%742.91265.61771.51872.41972.42072.72172.32272.22371.72470.92570.33065.33559.3
由表可以看出,螺旋升角在20 °时,水平输送螺杆有最大的充填效率,为加工制造方便,取螺旋升角17 °~25 °之间都能使水平输送螺杆获得较大的充填效率。若需求更大输送量,可取螺旋升角大值。
6 结论和讨论
1)基于超细粉在水平输送螺杆充填过程中的类流体特性,根据计算机流体力学理论,为超细粉充填螺杆设计提供一种新方法。
2)结合CFD通用软件包Ansys Fluent与正交试验设计对不同几何参数下的水平输送螺杆充填进行模拟,以充填效率为主要指标,输送量为次要指标,确定了影响水平输送螺杆质量的螺杆参数及主次顺序为螺旋升角、螺旋槽深和螺旋叶片厚度。
3)对25 kg阀口袋装超细粉水平输送螺杆相关几何参数进行了设计确定,当D=80 mm,d=16 mm,e=2 mm,H=32 mm,α=20 °时,水平输送螺杆可取得较大充填效率。
4)相关设计计算方法和参数可为其他粉体及流体充填螺杆设计提供参考。
[1]铁生年,李星.超细粉体表面改性研究进展[J].青海大学学报(自然科学版),2010,28(2):16-21.
[2]夏梦,陆佳平,李国华,等.一种新型粽子真空软塑包装工艺[J].包装与食品机械,2015,33(4):45-47.
[3]毋伟,陈建峰,卢寿慈.超细粉体表面修饰[M].北京:化学工业出版社材料科学与工程出版中心,2004:10-30.
[4]铁生年,李星,李昀珺.超细粉体材料的制备技术及应用[J].中国粉体技术,2009,15(3):68-72.
[5]周丹,王利强,卢立新,等.超细粉的充填计量技术综述[J].包装工程,2019,40(17):159-167.
[6]徐余伟.螺旋输送机设计参数的选择和确定[J].面粉通讯,2008(5):29-33.
[7]郝友莉,唐正宁,季婷婷.粉体包装机密实输送螺杆的设计[J].轻工机械,2017(5):19-22.
[8]陈静,王志山,徐雪萌,等.基于模糊控制的失重秤粉体包装精度研究[J].包装工程,2019,40(17):153-158.
[9]杨晓,董娜,王国柱.基于模糊短反馈PID控制的粉末包装计量控制系统[J].包装工程,2019,40(9):148-153.
[10]高鹏,周一届.螺杆式粉料计量包装机粉料流动分析与数值仿真[J].包装工程,2010(7):87-90.
[11]朱复华.螺杆设计及其理论基础[M].北京:中国轻工业出版社,1984:20-40.
[12]郑少华.试验设计与数据处理[M].北京:中国建材工业出版社,2004:85-100.
[13]唐益群,袁斌,李军鹏.基于正交试验的黄土泥流运动分析[J].水利学报,2015,46(2):183-189.
[14]朱约钧.FLUENT 15.0流场分析实战指南[M].北京:人民邮电出版社,2015:22-43.
[15]王超,孙炳孝.基于FLUENT的高压高速螺旋转子泵内部流场分析[J].包装工程,2017,38(23):187-191.
[16]段中喆.ANSYS FLUENT流体分析与工程实例[M].北京:电子工业出版社,2015:1-4.
[17]夏得峰,林光荣,王明贤,等.基于计算流体力学的旋风除尘器优化[J].中国粉体技术,2015,21(1):100-102.
[18]王勇,王利强,刘晓伟.电线卷热收缩包装线拍平装置仿真分析[J].包装与食品机械,2018(4):25-30,57.
[19]周俊杰,徐国权,张华俊.FLUENT工程技术与实例分析[M].北京:中国水利水电出版社,2013:39-44.
[20]冯彬彬,唐正宁.粉体在袋装充填过程中的扬尘规律[J].包装工程,2017,38(7):105-109.
[21]鄢曙光,祝振杰.基于FLUENT的孔板消减气流脉动的数值模拟[J].液压与气动,2016(7):77-82.
[22]孟坤鹏,李永祥,徐雪萌,等.粉体除静电离子风风场对粉体包装充填影响的模拟研究[J].包装工程,2019,40(15):170-174.