滚筒装备内颗粒混合与粉磨研究进展

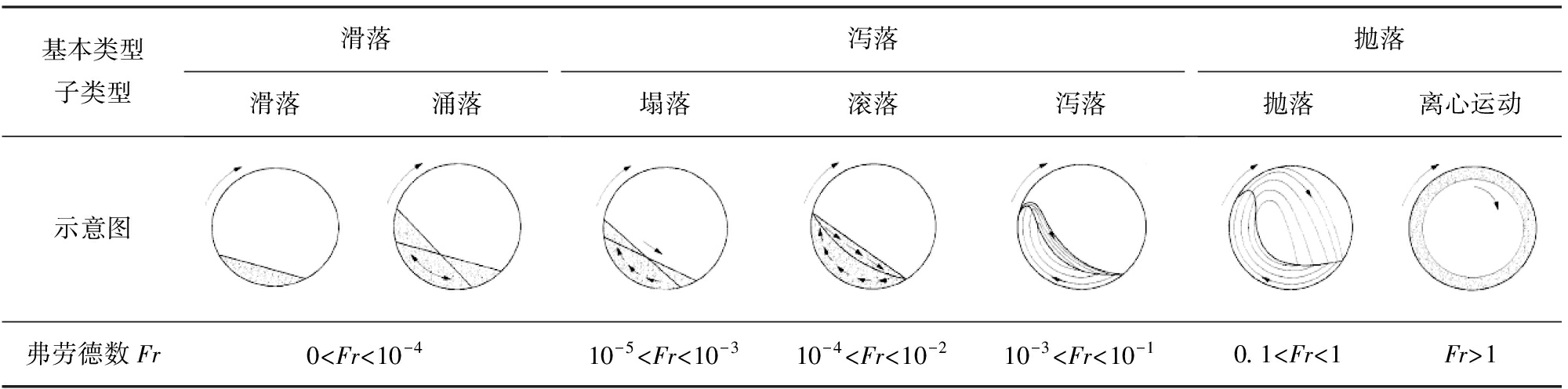
颗粒物料是指粒径大于1 μm的大量离散固体颗粒相互作用而组成的宏观复杂体系，广泛存在于工业生产过程中。滚筒是一种常用的颗粒物料处理装备，可用于颗粒物料的混合、粉磨、涂层和干燥等，在工业领域占据着重要地位，在国民经济发展中发挥着重要作用。颗粒物料对外界作用的敏感性、非线性响应和自组织行为等，使得其动力学行为十分复杂[1-3]。受操作条件的影响，滚筒装备内颗粒物料呈现出丰富的运动状态。这些运动状态大致可分为3种基本类型，即滑落、泻落和抛落；根据弗劳德数Fr可以进一步划分为7个子类型，即滑落、涌落、塌落、滚落、泻落、抛落以及离心运动，见表1[4]。其中，颗粒的滚落和泻落与颗粒混合过程密切相关，而颗粒混合对于获得高质量均质的产品非常重要；颗粒的拋落使得颗粒之间的冲击力增大，造成颗粒的破碎效果增强，因而这种运动状态常见于滚筒球磨机中，以实现颗粒的粉磨。

鉴于滚筒装备内颗粒物料行为研究具有重要的实际应用价值和理论意义，国内外学者针对滚筒装备内颗粒物料的运动特性，及其对滚筒装备性能的影响进行了大量研究；然而，由于颗粒在滚筒装备内的运动是十分复杂的随机过程，因此已有相关研究仍存在诸多不足之处。本文中对国内外滚筒装备内颗粒混合和粉磨研究进行总结和评述，在此基础上指出已有研究存在的问题，进而提出今后的研究思路，以期为滚筒装备内颗粒物料混合和粉磨的进一步研究提供借鉴，并为滚筒装备的性能改进和优化设计研究提供方向。

1 滚筒装备内的颗粒混合

1.1 颗粒混合的实验

实验研究不仅可为滚筒装备运行过程中参数调整提供参考，还可为理论模型的验证提供数据支持，是获取滚筒内颗粒混合性能的重要手段。

1999年，Puyvelde等[5]利用接触数表示颗粒混合程度，通过图像分析法实验测定颗粒物料在滚筒内的径向混合过程，研究发现，随着时间的延长，混合程度呈现增强-不变-增强的阶梯形变化趋势，且在2次增强阶段中混合速率相等。 2005年，Li等[6]采用图像分析法实验研究了滚筒内二元湿颗粒的径向混合，获得了颗粒混合-分离相图，相图中混合和分离区域的边界由二元颗粒的密度比、粒径比、润湿角余弦值之比确定。 2009年，Liao等[7]对滚筒内浸没在液体中的单一粒径颗粒的径向混合开展实验研究，利用混合指数表征混合程度，结果表明，液体黏度对最终混合程度没有影响，但是液体黏度增加引起混合速率增大。 2011年，张立栋等[8-9]实验研究了滚筒内不同粒径二元颗粒的混合，一方面基于图像分析法得到的Lacey指数评价颗粒的径向混合[8]，另一方面基于取样称重法得到的变异系数评价颗粒的径向和轴向混合[9]，获得了最优混合程度对应的填充率、滚筒倾角与转速。 2012年，Grajales等[10]采用染色示踪法，对大米颗粒在滚筒内的径向混合行为进行实验研究，发现颗粒达到均匀混合所需要的滚筒旋转周期数取决于颗粒量，而与转速无关。 2013年，李少华等[11]分析了3种常用混合程度评价指标——Lacey指数、变异系数及接触数的应用范围，得出Lacey指数适合评价径向混合，并基于滚筒内三元颗粒径向混合实验，探讨了取样方式对Lacey指数算法的影响，得出了最佳取样方式。

表2给出了上述滚筒内颗粒混合实验研究中所采用的参数条件和方法。可见，已有研究主要针对实验室规模的滚筒和毫米尺度颗粒，利用摄像机拍摄颗粒运动过程照片，通过图像分析，获得颗粒分布信息，进而得到颗粒混合程度。图像分析法有着成熟的商业化仪器，较为直观，但仅适用二维颗粒流与颗粒流表面的径向混合情况分析。

1.2 颗粒混合的数值模拟

随着计算机技术的发展，数值模拟方法成为研究颗粒混合机理和性能的有效手段。通过数值模拟，可以获得实验测试难以得到的颗粒运动微观和宏观信息。在数值模拟方法中，离散元方法(discrete element method，DEM)在颗粒混合研究中发挥着日益重要的作用。DEM的基本思想是：将颗粒物料看作由一系列离散的独立运动的单元(颗粒)组成，每个单元的运动受经典运动方程控制，颗粒行为的演变由各单元的运动和相互位置确定，因此，DEM能够从颗粒尺度考察颗粒混合过程，从而很好地反映颗粒的混合机理和性能。

2010年，Gui等[12]采用DEM模拟二维滚筒内颗粒的径向混合，结果表明，颗粒混合界面呈分形结构，在混合达到稳定前，分形维数趋于增加，较低的转速更有利于颗粒的混合；混合过程为Shannon信息熵增加过程。2013年，Liu等[13]利用DEM研究滚筒内湿颗粒的流动和混合，利用颗粒循环周期数表征径向混合特性，结果表明，液桥力的存在总体上降低了颗粒的径向混合，但也观察到其增强混合的现象；菲克扩散定律可以很好地描述颗粒的轴向混合，且扩散系数随液体表面张力的增加而增大。2015年，胡陈枢等[14]采用DEM模拟了滚筒内粒径不同的二元颗粒的运动过程，提出表观混合指数和动态混合指数的概念，并用之衡量颗粒的径向混合程度，结果表明，随着转速的增加，2种混合指数均先增加后减小。

2016年，张立栋等[15]利用接触数表示混合程度，基于DEM研究了滚筒转速、颗粒数量比对圆柱形生物质颗粒和钢球颗粒径向混合程度的影响。同年，Geng等[16]采用DEM对滚筒内颗粒的混合过程进行数值模拟，探讨了颗粒粒径、密度、不均匀度和滚筒转速对颗粒径向混合特性参数(颗粒接触数与单位面积颗粒量)的影响。针对颗粒填充率体积分数大于50%时，滚筒内颗粒混合时中心区域出现“死区”的现象(见图1[17])，2016年，Soni等[17]采用DEM模拟和实验研究相结合的方法，研究了“死区”的形成机理和影响因素，结果表明，“死区”的形成是由于能量从壁面向中心传递时，到达中心前能量被耗尽的缘故；颗粒堆积结构、颗粒尺寸对“死区”形成有重要影响，滚筒转速和几何参数的影响相对较小；在滚筒内设置适宜的挡板，可以避免“死区”的形成，从而增强颗粒的混合。

2017年，Gui等[18]建立了求解非球形颗粒碰撞的软球嵌入伪硬颗粒模型(soft-sphere imbedded pseudo-hard-particle model, SIPHPM)，该模型假设非球形颗粒边界覆盖着一系列球体，颗粒碰撞过程分为2个阶段：在预测阶段，采用传统的DEM模拟颗粒边界上球体的相互作用，球体由于受力和力矩作用偏离平衡位置；在修正阶段，边界上所有球体受到的力和力矩总和决定颗粒的运动，将颗粒按伪刚性颗粒进行处理，根据发生运动后颗粒的位置和朝向确定边界上球体新的平衡位置，进而研究了二维滚筒中三角形、四边形直至十边形颗粒的混合过程、混合程度(Lacey指数和Shannon信息熵增混合指数)、颗粒速度场、颗粒动能等。

2018年，Gui等[19]基于SIPHPM对不同转速与填充率下滚筒混合器内正四面体颗粒的径向混合开展研究，利用Lacey指数和Shannon信息熵增混合指数表示混合程度，并将其与球形颗粒进行对比，发现颗粒形状对混合性能有显著影响。

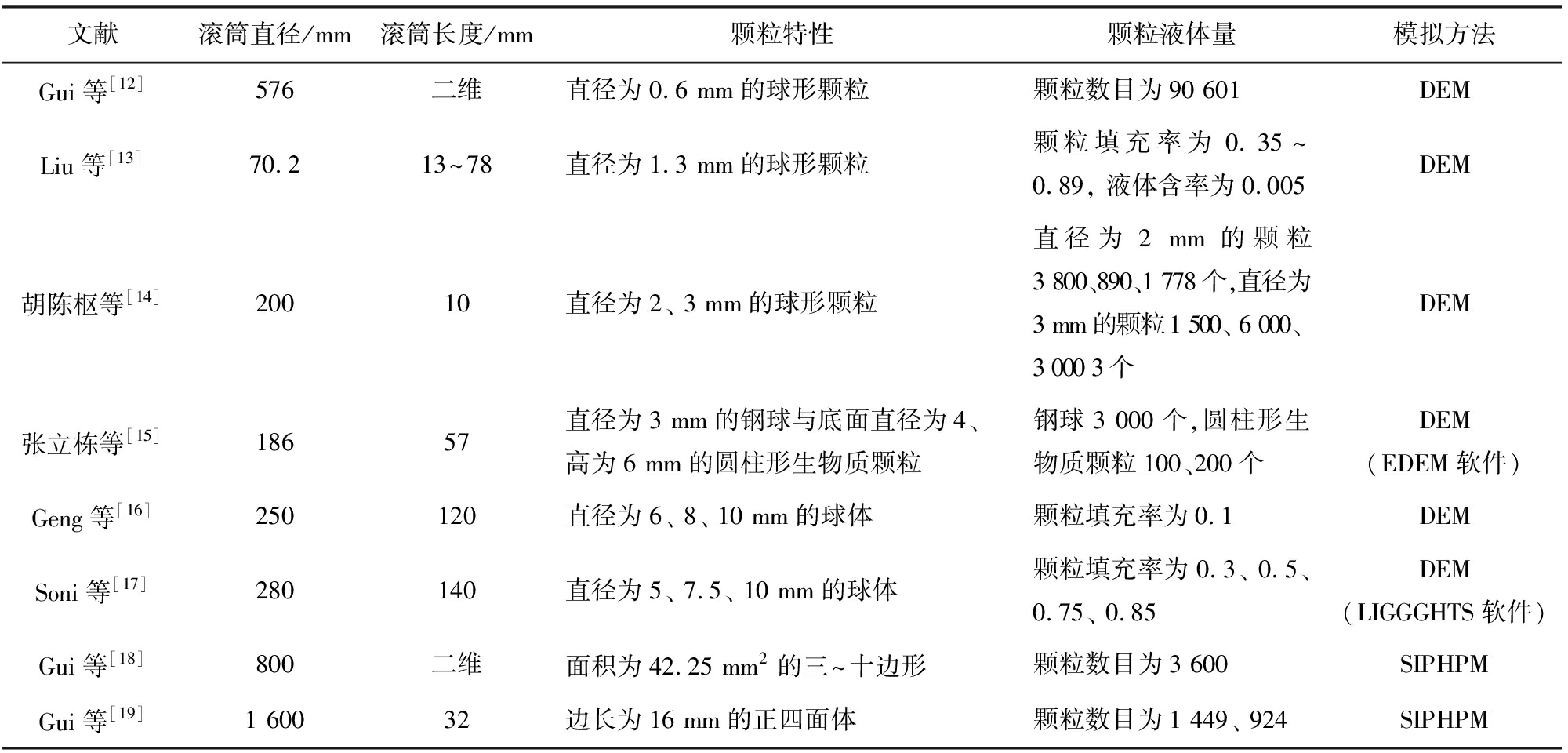
表3给出了上述滚筒内颗粒混合数值模拟研究中采用的参数和方法。由表3可以看出，数值模拟研究虽然多采用三维滚筒，但受模拟计算量的制约，滚筒长度有限，使得研究多关注颗粒的径向混合。此外，所采用的方法均涉及DEM，除了对简单形状颗粒通过自行编制程序或借助开源软件(LIGGGHTS)和商业软件(EDEM)开展DEM模拟外，对于形状更为复杂的颗粒，提出了基于DEM的SIPHPM模型。

2 滚筒装备内的颗粒粉磨

颗粒物料的粉磨是水泥、药物、食品等工业生产中的重要环节，滚筒球磨机是物料粉磨的关键装备。已有滚筒装备中颗粒粉磨的研究，多出于为降低作业过程中能耗、提高滚筒球磨机寿命的目的，关注滚筒球磨机的功耗和磨损问题。

2.1 基于DEM的功耗和磨损

早期的研究集中在对滚筒内颗粒动力学开展DEM模拟研究，并基于DEM模拟结果对滚筒功耗和衬板磨损进行预测。

2001年，Cleary[20]利用二维DEM模型系统研究了滚筒球磨机几何参数和颗粒物性参数对颗粒动力学行为和功耗的影响。2007年，Banisi等[21]借助商业力学软件实时调整滚筒球磨机工作过程中的三维衬板外形，建立了能够准确预测衬板磨损速率的模型。2008年，Kalala等[22]采用DEM研究了衬板磨损对滚筒球磨机负荷特性的影响，基于DEM获得的撞击能耗和摩擦能耗与现场实验结果一致；Cleary等[23]利用DEM研究了滚筒球磨机内颗粒流和能量流特性。2009年，Cleary[24]利用DEM研究了滚筒球磨机内颗粒物料的运动情况，并据此对滚筒球磨机功耗进行了分析。2010年，Rezaeizadeh等[25]提出预测衬板磨损速率的模型，模型预测结果与工业实际运行数据吻合良好，同时模型预测的衬板承受的压力随衬板高度、面向角的变化关系也与基于DEM模拟得到的结果一致。

以上研究分别关注滚筒球磨机衬板磨损、能量特性，实际上滚筒球磨机工作过程伴随着颗粒破碎，颗粒破碎会对颗粒流动产生影响，进而影响到衬板磨损、功耗以及粉磨效果。鉴于此，2011年，Powell等[26]提供了一种基于DEM模拟获得滚筒球磨机内球的碰撞能量谱和碰撞率并预测颗粒破碎和衬板磨损的模型，为在球磨机设计阶段兼顾性能和寿命提供了可能，但该模型中引入了磨损常数，该常数与衬板倾角有关，相应的关系式仍需进一步研究。2013年，Delaney等[27]在DEM方法的框架下，将破碎概率引入每一次颗粒碰撞，进而借助破碎函数确定破碎后新颗粒的生成，使DEM模型更接近实际滚筒球磨机内颗粒物料粉磨的物理过程。

最近，基于DEM的滚筒球磨机内颗粒粉磨相关研究再次兴起，研究内容涉及操作参数、衬板结构、颗粒特性对颗粒动力学行为、球磨机功耗和衬板磨损等的影响。2017年，Bian等[28]采用DEM研究了滚筒球磨机转速、衬板高度、衬板数目对颗粒动力学行为和球磨机功耗的影响，并将部分数值模拟结果和实验相结合，验证了DEM模拟的准确性。

2018年，Yin等[29]利用DEM研究了衬板形状对滚筒球磨机内颗粒动力学行为和功耗的影响，结果表明，梯形、波纹形和长方形衬板条件下，功耗都随着转速增加而先增加后减小；3种衬板中，采用梯形衬板时功耗最大。Xu等[30]将基于DEM的滚筒球磨机内球形颗粒动力学行为与颗粒尺度的磨损模型——剪切冲击能量模型相结合，研究衬板磨损速率，得到了和实验吻合良好的结果，在此基础上，研究了滚筒转速和衬板形状对衬板磨损速率和磨损分布的影响，并认为衬板磨损的主要原因是在颗粒加速过程中与衬板的剧烈碰撞。Govender等[31]借助基于GPU的BlazeDEM软件，采用DEM对实验室规模滚筒球磨机内球形、立方体形颗粒的行为开展研究，并结合实验结果验证模型，在此基础上，模拟研究了4种不同形状多面体(截形四面体、双凸形、拉长六角形棱柱和混合多面体)颗粒的棱角性和长宽比对球磨机功耗的影响，并展示了颗粒物料的廓线和力链结构。Pedrayes等[32]对转速、物料颗粒类型和填充率不同时试验规模滚筒球磨机内颗粒行为开展了一系列DEM模拟和实验研究，发现基于DEM模拟数据获得的功率谱分布能够用于评估磨机中颗粒填充率。

2019年，Pulgar等[33]借助商业软件RockyDEM，发展了一种获得各衬板表面以及衬板之间表面受力的方法，并利用该方法研究了试验规模滚筒球磨机中各表面受到的撞击力，获得了相应的力矩和功耗，并将模拟结果和实验测试结果进行了对比。Cleary等[34]利用DEM模拟获得了半自动滚筒球磨机内的能量谱，并探讨了转速、衬板高度、颗粒物料填充率、颗粒物料-磨球比对能量利用率的影响。Xu等[35]将DEM模拟与剪切冲击能量模型相结合的球形颗粒粉磨过程中衬板磨损预测模型推广到类正方体颗粒粉磨研究中，发现类正方体颗粒比球形颗粒对衬板造成的磨损更大，并认为其原因是非球形颗粒运动过程中的滑移效应更显著。

2.2 引入FEM的受力和磨损

一些学者致力于将有限元方法(finite element method，FEM)引入滚筒球磨机内衬板受力建模，以提高对衬板力学性能与磨损特性模拟预测的准确性。

2011年，Jonsén等[36]对试验滚筒球磨机衬板提升条的偏转进行实验测试，同时利用DEM对颗粒物料进行建模，利用FEM对衬板进行建模，通过DEM-FEM耦合对提升条偏转曲线进行预测，得到与实验合理吻合的结果，基于DEM-FEM耦合可以获得力、机械波、结构响应及其对颗粒物料运动的影响，为滚筒球磨机内接触力的预测提供了一种物理上更为正确的途径。

2012年，Jonsén等[37]利用光滑粒子动力学(smoothed particle hydrodynamics，SPH)对颗粒物料之间以及物料与磨机结构之间的相互作用进行建模，利用FEM对柔性橡胶衬板进行建模，通过SPH-FEM耦合模拟对衬板提升条偏转的预测结果与实验合理吻合，使得对结构响应及颗粒物料运动进行更为细致的模拟成为可能。

2.3 功耗和磨损实验

近几年，一些学者采用实验方法探讨了滚筒球磨机功耗和衬板磨损。2016年，Bbosa等[38]提出基于DEM与正电子发射颗粒跟踪(positron emission particle tracking，PEPT)实验技术得到的颗粒动力学参数，利用累积杠杆臂计算滚筒球磨机功耗的新方法，并利用实验室规模滚筒球磨机功耗实验验证了该计算方法的准确性。同年，Akhondizadeh等[39]分别对不同操作参数下滚筒球磨机衬板的撞击磨损和研磨磨损进行实验测试，进而结合理论分析提出能够定性预测衬板磨损的关系式，但该关系式在定量上和实验测试结果有一定的差异。

2017年，Yin等[40]利用实验室规模滚筒球磨机研究操作参数对球轨迹、衬板受到的撞击与球磨机功耗的影响，并将其与Bond半经验功耗模型以及基于DEM的功耗预测结果相对比，发现Bond半经验功耗模型的预测效果较差，而基于DEM的颗粒动力学数据获得的功耗与实验结果吻合较好。

2.4 湿式粉磨的流固耦合模拟

除上述针对干式粉磨工艺开展的研究外，近几年一些学者开展了对滚筒装备内颗粒物料湿式粉磨的探讨。湿式粉磨过程中流体的影响不能忽略，因此在数值模拟研究中，需要对流体进行建模并考虑流体与颗粒之间的相互作用，开展流固耦合模拟研究。

2014年，Jonsén等[41]利用SPH描述浆液流体流动，利用FEM描述提升条和衬板，利用DEM描述磨球运动，通过SPH-DEM-FEM耦合，模拟滚筒球磨机内浆液流体与物料以及磨机结构的相互作用，数值预测了浆液流体的压力分布，以及浆液流体黏度和密度对其阻尼效应的影响，并利用实验室规模滚筒球磨机内物料力矩实验结果验证了数值模拟的准确性。然而，这种SPH-DEM-FEM耦合模拟方法遇到的问题是当计算区域很大时，由于跟踪大量的颗粒，带来的计算量将是惊人的。

2015年，Mayank等[42]采用CFD描述连续浆液相，采用DEM求解离散颗粒相，通过CFD-DEM单向耦合对滚筒球磨机内浆液和颗粒物料的运动行为开展数值模拟，并将模拟得到的颗粒相轮廓和自由表面轮廓与基于PEPT实验测试结果进行对比，二者吻合良好。然而，该CFD-DEM模拟采用单向耦合，即只考虑颗粒对浆液的影响，而不考虑浆液对颗粒的作用，模拟结果的准确性受到了影响，模型的推广需要进一步考虑。

2018年，Cleary等[43]采用SPH-DEM耦合模型预测了滚筒球磨机内浆液和粗颗粒的运动，模型中考虑了粗颗粒破碎的影响，破碎产生的细颗粒纳入浆液中，通过调整局部浆液黏度以体现细颗粒的份额，破碎后的粗颗粒由DEM模型求解，该模型得到了试验规模滚筒球磨机实验的验证。

2019年，Jonsén等[44]采用颗粒有限元方法(particle finite element method，PFEM)对浆液流体建模，采用DEM对颗粒物料建模，采用FEM对磨机结构建模，通过PFEM-DEM-FEM耦合模拟研究颗粒物料运动受滚筒球磨机结构的影响，以及浆液的流速和压力分布，并结合小规模滚筒球磨机实验得到的转矩和颗粒物料运动特性验证了模拟的准确性。

3 主要问题及解决方案

3.1 主要问题

1)颗粒混合存在的问题

第一，已有研究主要针对实验室规模滚筒，缺少对工业规模滚筒混合器内颗粒混合过程的研究。

第二，已有研究多关注颗粒的径向混合，缺少对颗粒轴向混合的研究。

第三，工业过程中非球形颗粒物料更为常见，虽然已有实验研究中涉及油页岩颗粒、大米颗粒等非球形实际颗粒，在非球形颗粒理论模型方面提出了基于DEM的模拟规则形状多边形、多面体颗粒行为的SIPHPM模型，但是仍缺少针对不规则形状颗粒混合过程的DEM建模及数值模拟研究。

第四，已有研究主要针对毫米尺度的干颗粒，鲜见以微米尺度干颗粒或者以湿颗粒为对象的研究。

2)颗粒粉磨存在的问题

虽然借助DEM模拟研究颗粒动力学行为，进而获得衬板磨损和滚筒功耗一直是研究重点，然而相关研究仍不够完善，存在的问题如下。

第一，已有研究针对的是实验室-试验-小规模滚筒球磨机，所得的颗粒破碎、衬板磨损和滚筒球磨机功耗规律是否适用于工业规模滚筒球磨机并不为人所知。

第二，尽管研究者建立了更符合实际的粉磨过程数学模型，摆脱了预测衬板磨损和功耗时需要引入实验或理论关联式的限制，然而这些模型计算量庞大，难以在工业规模滚筒球磨机性能研究中应用。

第三，研究集中在球形毫米尺度颗粒的干式粉磨，而对非球形颗粒、微米尺度颗粒、湿颗粒的粉磨性能研究则较少。

3.2 解决方案

由于工业规模滚筒装备尺度庞大，加之颗粒物料动力学行为十分复杂，因此依靠现有的测量技术难以全面掌握颗粒动力学行为的微观和宏观信息。DEM模拟能够跟踪到每一个颗粒的运动轨迹，具有探讨颗粒尺度行为和规律的独特优势，但是DEM用于研究工业规模滚筒装备内颗粒物料行为时计算量是惊人的。虽然目前并行计算机集群和GPU计算在大规模颗粒系统数值模拟中得到应用，但是处理工业规模滚筒装备内颗粒动力学行为，特别是颗粒物料粒径在微米尺度时，仍然面临计算量大、计算成本高的挑战，因此，为获得工业规模滚筒混合器和滚筒球磨机内颗粒动力学行为，从而为工业规模滚筒装备的性能优化提供支撑，需要提出新的研究思路和方法。

3.2.1 应用相似原理

Jiang等[45]根据相似原理，提出重力加速度、滚筒直径、滚筒转速缩放比例的相互关系，并利用单颗粒和多颗粒动力学DEM模拟结果证实了所提出的比例关系的合理性。基于相似原理，利用缩小模型，在更少颗粒量下开展滚筒装备内颗粒动力学行为研究，再将所得规律外推到工业规模滚筒装备上，是工业规模滚筒装备内颗粒动力学行为研究的重要途径。然而，Jiang等[45]提出的相似准则中未考虑颗粒之间的接触力，由于滚筒装备内颗粒呈密堆积状态，颗粒间相互作用在颗粒动力学中发挥重要作用，相似原理能否成功应用于工业规模滚筒装备内颗粒动力学研究取决于能否在颗粒间相互作用相似准则上取得突破。

3.2.2 应用粗粒模型

Sakai等[46-48]提出了粗粒模型，并将该模型应用到气力输送和流化床研究中。粗粒模型在保持颗粒系统质量、动量和能量守恒的前提下，将数个实际颗粒用一个粒径更大的粗颗粒代替。由于粗粒模型跟踪的颗粒数目急剧减小，因此计算成本大大降低。粗粒模型为工业规模滚筒装备内颗粒动力学行为的研究提供了一种途径。

3.2.3 发展流固耦合模型

对于毫米尺度干颗粒，由于惯性较大，气相的黏性作用以及颗粒之间的范德华力可以忽略，在滚筒内颗粒混合和粉磨模拟研究中可以不考虑气相的影响，从而采用DEM方法进行建模和模拟，并且也无需考虑范德华力作用，给数值模拟带来了很大的方便。然而，对于微米尺度颗粒，气相的作用和范德华力作用将影响到滚筒内颗粒的行为，需采用流固耦合模拟，并在对颗粒运动建模时考虑范德华力作用。

对于湿颗粒，颗粒之间的液桥力将发挥作用，若颗粒浸没在液体中，则需要考虑滚筒转动过程中引起的液相的流动以及流场与固体颗粒的相互作用，即需要开展流固耦合模拟。

非球形颗粒几何参数的描述和受力分析都更为复杂，考虑到非球形颗粒在自然界和工业过程中的普遍性，应加强非球形颗粒与流体间相互作用的研究，以发展出能够体现颗粒形状影响的流固耦合模型。

4 结论和展望

滚筒装备内颗粒物料的混合和粉磨在工业生产领域有着广泛应用，理解和掌握滚筒装备内颗粒物料的行为规律具有重要的理论意义和应用价值。国内外研究者针对滚筒装备内颗粒物料的混合与粉磨开展过诸多实验和数值模拟，但是这些研究工作中缺少对小规模滚筒内颗粒轴向混合以及工业规模滚筒装备内颗粒混合和粉磨过程的研究，并且对不规则形状颗粒、微米尺度颗粒、湿颗粒的混合和粉磨过程的研究存在明显不足。基于已有研究中存在的问题和数值模拟研究的优势，本文提出在未来的工作中，应注重滚筒内颗粒轴向或整体混合研究，并注重相似原理与粗粒模型在工业规模滚筒装备内颗粒动力学行为数值模拟研究中的应用。在此基础上，综合考虑颗粒与流体间相互作用以及颗粒形状的影响，发展流固耦合模型，从而为工业规模滚筒装备的性能提升提供理论基础和数据支撑。

[1]刘举, 白鹏博, 凡凤仙, 等. 竖直振动下颗粒物质的行为模式研究进展[J]. 化工进展, 2016, 35(7): 1956-1962.

[2]凡凤仙, 王志强, 刘举, 等. 竖直振动管中颗粒毛细效应的离散元模拟[J]. 力学学报, 2019, 51(2): 415-424.

[3]郭宇, 凡凤仙, 白鹏博, 等. 颗粒物质在竖直振动U形管中迁移的离散元方法模拟[J]. 上海理工大学学报, 2019, 41(5): 409-416.

[4]MELLMANN J. The transverse motion of solids in rotating cylinders-forms of motion and transition behavior[J]. Powder Technology, 2001, 118(3): 251-270.

[5]PUYVELDE D R V, YOUNG B R, WILSON MA, et al. Experimental determination of transverse mixing kinetics in a rolling drum by image analysis[J]. Powder Technology, 1999, 106(3): 183-191.

[6]LI H M, MCCARTHY J J. Phase diagrams for cohesive particle mixing and segregation[J]. Physical Review E, 2005, 71(2): 021305.

[7]LIAO C C, HSIAU S S. The granular mixing in a slurry rotating drum[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2009, 7522:75221C-8.

[8]张立栋, 朱明亮, 李少华, 等. 回转干馏炉内二组元颗粒混合机理及混合度分析[J]. 化工进展, 2011, 30(11): 2382-2387.

[9]张立栋, 李少华, 余侃胜, 等. 油页岩与固体热载体在回转干馏炉内混合特性的冷态实验[J]. 化工进展, 2011, 30(3): 492-497.

[10]GRAJALES L M, XAVIER N M, HENRIQUE J P, et al. Mixing and motion of rice particles in a rotating drum[J]. Powder Technology, 2012, 222: 167-175.

[11]李少华, 朱明亮, 张立栋, 等. 回转装置内三组元颗粒径向混合评价方法分析[J]. 化工进展, 2013, 32(6): 25-30.

[12]GUI N, FAN J R, CEN K F. A macroscopic and microscopic study of particle mixing in a rotating tumbler[J]. Chemical Engineering Science, 2010, 65(10): 3034-3041.

[13]LIU P Y, YANG R Y, YU A B. Particle scale investigation of flow and mixing of wet particles in rotating drums[C]//AIP Conference Proceedings. New York, USA: American Institute of Physics, 2013: 963-966.

[14]胡陈枢, 罗坤, 樊建人, 等. 滚筒内二组元颗粒混合与分离的数值模拟[J]. 工程热物理学报, 2015, 36(9): 1947-1951.

[15]张立栋, 韦庆文, 秦宏, 等. 柱状生物质颗粒与钢球颗粒在滚筒中的混合特性[J]. 化工进展, 2016, 35(10): 3057-3064.

[16]GENG F, GANG L, WANG Y C, et al. Numerical investigation on particle mixing in a ball mill[J]. Powder Technology, 2016, 292: 64-73.

[17]SONI R K, MOHANTY R, MOHANTY S, et al. Numerical analysis of mixing of particles in drum mixers using DEM[J]. Advanced Powder Technology, 2016, 27(2): 531-540.

[18]GUI N, YANG X T, TU J Y, et al. Numerical simulation and analysis of mixing of polygonal particles in 2D rotating drums by SIPHPM method[J]. Powder Technology, 2017,318: 248-262.

[19]GUI N, YANG X T, TU J Y, et al. Numerical simulation of tetrahedral particle mixing and motion in rotating drums[J]. Particuology, 2018, 39: 1-11.

[20]CLEARY P W. Charge behaviour and power consumption in ball mills: sensitivity to mill operating conditions, liner geometry and charge composition[J]. International Journal of Mineral Processing, 2001, 63(2): 79-114.

[21]BANISI S, HADIZADEH M. 3-D liner wear profile measurement and analysis in industrial SAG mills[J]. Minerals Engineering, 2007, 20(2): 132-139.

[22]KALALA J T, BREETZKE M, MOYS M H. Study of the influence of liner wear on the load behaviour of an industrial dry tumbling mill using the discrete element method (DEM)[J]. International Journal of Mineral Processing, 2008, 86(1): 33-39.

[23]CLEARY P W, SINNOTT M D, MORRISON R D. DEM prediction of particle flows in grinding processes[J]. International Journal for Numerical Methods in Fluids, 2008, 58(3): 319-353.

[24]CLEARY P W. Ball motion, axial segregation and power consumption in a full scale two chamber cement mill[J]. Minerals Engineering, 2009, 22(9): 809-820.

[25]REZAEIZADEH M, FOOLADI M, POWELL M S, et al. A new predictive model of lifter bar wear in mills[J]. Minerals Engineering, 2010, 23(15): 1174-1181.

[26]POWELL M S, WEERASEKARA N S, COLE S, et al. DEM modelling of liner evolution and its influence on grinding rate in ball mills[J]. Minerals Engineering, 2011, 24(3): 341-351.

[27]DELANEY G W, CLEARY P W, MORRISON R D, et al. Predicting breakage and the evolution of rock size and shape distributions in AG and SAG mills using DEM[J]. Minerals Engineering, 2013, 50/51: 132-139.

[28]BIAN X L, WANG G Q, WANG H D, et al. Effect of lifters and mill speed on particle behaviour, torque, and power consumption of a tumbling ball mill: experimental study and DEM simulation[J]. Minerals Engineering, 2017, 105: 22-35.

[29]YIN Z X, LI T Q, PENG Y X, et al. Effect of lifter shapes on the mill power in a ball mill[C]//IOP Conference Series: Materials Science and Engineering. Bristol, UK: IOP Publishing, 2018: 042201/1-042201/5.

[30]XU L, LUO K, ZHAO Y Z. Numerical prediction of wear in SAG mills based on DEM simulations[J]. Powder Technology, 2018, 329: 353-363.

[31]GOVENDER N, RAJAMANI R, WILKE D N, et al. Effect of particle shape in grinding mills using a GPU based DEM code[J]. Minerals Engineering, 2018, 129: 71-84.

[32]PEDRAYES F, NORNIELLA J G, MELERO M G, et al. Frequency domain characterization of torque in tumbling ball mills using DEM modelling: Application to filling level monitoring[J]. Powder Technology, 2018, 323: 433-444.

[33]PULGAR J V, ANIBAL V M, MOLINA V C. Correlation between power and lifters forces in grinding mills[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 4417-4427.

[34]CLEARY P W, OWEN P. Effect of operating condition changes on the collisional environment in a SAG mill[J]. Minerals Engineering, 2019, 132: 297-315.

[35]XU L, LUO K, ZHAO Y Z, et al. Influence of particle shape on liner wear in tumbling mills: a DEM study[J]. Powder Technology, 2019, 350: 26-35.

[36]JONSEN P, PALSSON B I, TANO K, et al. Prediction of mill structure behaviour in a tumbling mill[J]. Minerals Engineering, 2011, 24(3): 236-244.

[37]JONSEN P, PALSSON B I, HAGGBLAD H A, et al. A novel method for full-body modelling of grinding charges in tumbling mills[J]. Minerals Engineering, 2012, 33(6): 2-12.

[38]BBOSA L S, GOVENDER I, MAINZA A. Development of a novel methodology to determine mill power draw[J]. International Journal of Mineral Processing, 2016, 149: 94-103.

[39]AKHONDIZADEH M, MAHANI M F, REZAEIZADEH M, et al. Prediction of tumbling mill liner wear: abrasion and impact effects[J]. Proceedings of the Institution of Mechanical Engineers Part J-Journal of Engineering Tribology, 2016, 230(10): 1310-1320.

[40]YIN Z X, PENG Y X, ZHU Z C, et al. Impact load behavior between different charge and lifter in a laboratory-scale mill[J]. Materials, 2017, 10(8): 1-17.

[41]JONSEN P, PALSSON B I, STENER J F, et al. A novel method for modelling of interactions between pulp, charge and mill structure in tumbling mills[J]. Minerals Engineering, 2014, 63: 65-72.

[42]MAYANK K, MALAHE M, GOVENDER I, et al. Coupled DEM-CFD model to predict the tumbling mill dynamics[J]. Procedia IUTAM, 2015, 15: 139-149.

[43]CLEARY P W, DELANEY G W, SINNOTT M D, et al. Inclusion of incremental damage breakage of particles and slurry rheology into a particle scale multiphase model of a SAG mill[J]. Minerals Engineering, 2018, 128: 92-105.

[44]JONSEN P, HAMMARBERG S, PALSSON B I, et al. Preliminary validation of a new way to model physical interactions between pulp, charge and mill structure in tumbling mills[J]. Minerals Engineering, 2019, 130: 76-84.

[45]JIANG S Q, YE Y X, TAN Y Q, et al. Discrete element simulation of particle motion in ball mills based on similarity[J]. Powder Technology, 2018, 335: 91-102.

[46]SAKAI M, KOSHIZUKA S. Large-scale discrete element modeling in pneumatic conveying[J]. Chemical Engineering Science, 2009, 64(3): 533-539.

[47]SAKAI M, SHIBATA K, KAWASAKI V M, et al. Numerical simulation of a bubbling fluidized bed by the coarse grain modeling of DEM[J]. Journal of the Society of Powder Technology, 2010, 47(1): 14-22.

[48]SAKAI M, ABE M, SHIGETO Y, et al. Verification and validation of a coarse grain model of the DEM in a bubbling fluidized bed[J]. Chemical Engineering Journal, 2014, 244: 33-43.