基于散射(衍射)原理[1]的激光粒度分布测量方法，也称弹性光散射方法[2]，在液滴、 土壤、 制药、 环保等领域均有广泛应用[3-7]。我国从20世纪80年代末开始研究激光粒度测量方法，目前激光粒度仪已经广泛应用于许多领域，但在数据算法方面仍存在许多待研究的关键问题，其主要原因在于这种方法测试的量程大，一般可达0.000 2～2 mm，而在此量程范围内，为了获得不同粒度相对测量精度一致，光电探测器的尺寸分布是非线性排列的，在解方程组过程中带来了很大问题。激光粒度分布测量算法是通过光强度分布反演粒度分布，即通过Mie散射理论或Fraunhofer衍射理论建立光学矩阵方程进行求解，从而得到粒度分布。通过模拟计算，通常在加入噪声的情况下也能得到较好的结果，但在实际测试中，反演结果往往严重偏离实际值[8]，原因是测量粒度的范围区间分布大，而测量分辨率是按相对值设定的，从而在实际测量条件下，探测器阵列、放大器、数据采集的噪声不一致，难以被消除[9]。目前的算法一般都是基于非负最小二乘法(NNLS)，国外较早采用的有Twomey算法、 Chahine算法等[10-11]。 Twomey算法虽然具有良好的抗噪声能力，但因使用了平滑因子而使结果的真实性较差； Chahine算法迭代速度快，但对噪声比较敏感； 国内有许多算法研究，如Projection算法和其改进算法等，但其收敛速度较大，且参数调整因子的引入缺少理论依据[12]。 采用改进Chahine算法[13]、 修正牛顿算法[14]和改进共轭梯度算法[15]也取得了一定效果。
本文中对激光粒度仪中的光能矩阵与粒度分布的对应关系进行了分析，在最小二乘法基础上，将这种对应关系分别采用方程组和矩阵方程2种方法进行分析，并以矩阵方程构造优化问题，采用变尺度算法进行求解，从而得到粒度分布，实现了单峰分布和多峰分布的粒度测量。
1 原理及算法
1.1 激光粒度测量原理
激光粒度仪根据颗粒对光的散射原理实现测量。当颗粒度分布远大于入射光波长时，可近似采用衍射原理，在前向小衍射角度范围内探测信号。一般地，衍射理论适用于粒度在几微米以上的颗粒度测量；如果粒度较小，应采用Mie散射理论进行测量。图1是基于Fraunhofer衍射的小角前向激光粒度测量原理。
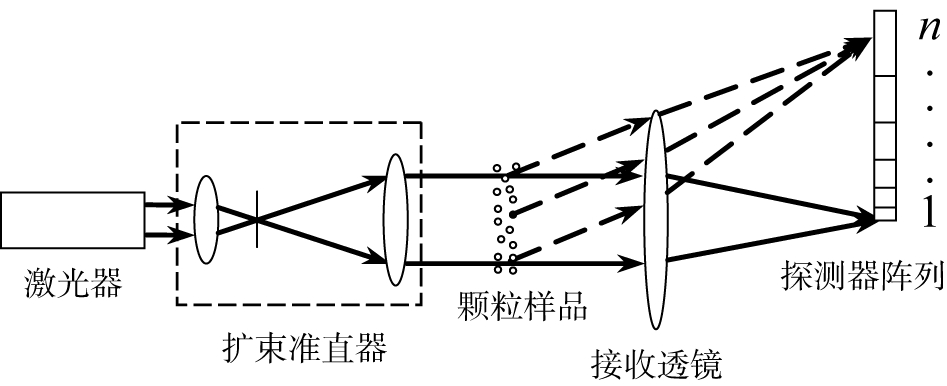
图1 激光粒度仪原理图
Fig.1 Principle of Laser particle sizer
在图1中，由激光器发出空间细光束，经2个正透镜实现扩束准直，并经位于这2个正透镜公共焦点上的针孔进行空间滤波后，形成平行光，照射到测量区中的样品颗粒上，颗粒对入射光产生衍射，衍射光强度分布与被照射颗粒的直径和数量有关。用接收透镜将所有相同方向的衍射光聚焦在焦平面上，并用光电探测器阵列接收衍射光能分布E。由于粒度分布对应于一定的光能分布，只需测量E，就可以根据对应关系求得粒度分布W，这种对应关系以矩阵方程表示为
MW=E，
(1)
式中：W=(w1,w2,…,wn)T, E=(e1,e2,…,en)T，M为衍射光能分布系数矩阵。 通过求解式(1)可以得到粒度分布W。M中的元素mij可以通过夫琅和费公式得到：
mij=
，
(2)
其中，
Xij=πdjSi/λf，
(3)
式中：dj为颗粒直径；Si为探测器环的半径；λ为波长； f为透镜焦距；J0和J1为Bessel函数。
通过求解式(1)可以得到粒度分布W。当粒径较小时，上述M也可用Mie散射理论计算得到。
1.2 反演算法分析
实际测量中，探测到的衍射光能分布E包括噪声ε=(ε1 ,ε2,…, εn)T。由上述分析可知，光电探测器阵列的接收面积是不同的，因此噪声对每个探测器的影响程度不同，方程式(1)具有病态性。根据Fraunhofer衍射原理，E接收透镜焦平面上的功率谱，对于圆形颗粒或等效圆形颗粒，E的图样分布是圆形对称的，即每种粒度总可以经接收透镜后，在焦平面上形成明暗相间的环形条纹，因此，探测器一般也需要是环形或环形的一部分。通过对功率谱分布方程求极值，可得每种粒径对应的最敏感探测环半径之间的关系为：
X=πdjSi/λf=1.357，
(4)
式中X是一个常数。 由式(4)可知，探测器外环对小颗粒衍射信号敏感； 而内环对大颗粒衍射信号敏感。 式(1)和式(2)是根据颗粒的单位体积分布得到的，设粒度比为1 ∶10的2个球形颗粒，其体积比为1∶1 000，因此，单位体积的小颗粒的衍射强度比大颗粒的衍射强度弱得多； 同时，为了使测量不同粒度时具有相似的相对精度，探测器阵列一般是外环比内环大得多，其面积比甚至达到1∶103～1∶106。基于上述原因，当实际测量中有噪声信号时，外环的εi与ei之比远大于内环的εj与ej之比，这种状况造成矩阵方程式(1)具有严重的病态，是反演算法的最大困难。
激光粒度测量的反演算法都是基于最小二乘法的最优化迭代算法，需要对迭代终止条件设置判断标准；此外，激光粒度分布测量中，小的噪声信号会引起粒度分布的强烈波动，导致结果与实际偏差很大,需要引入调整因子[16]。
为了进一步分析反演算法的适用性，本文中将其分为2类，一种是基于矩阵的算法，即对式(1)作为一个矩阵整体迭代；另一种是基于方程组的算法，即把式(1)转换成方程组，并用每个方程依次迭代。基于矩阵的算法中，矩阵方程为
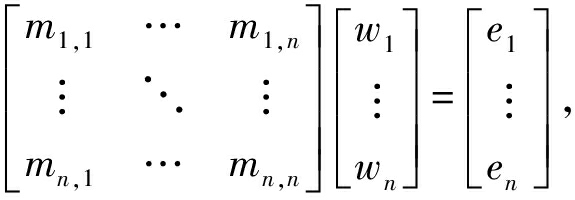
(5)
构造目标函数
f(w1,w2,…,wn)=(MW-E)T(MW-E)，
(6)
优化问题为：
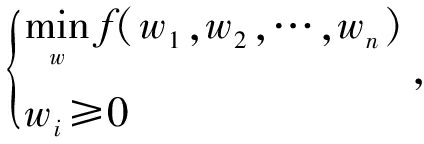
(7)
当满足如下条件时停止迭代，
(8)
其中ε根据噪声情况需要分别选取。
基于方程组的算法是将式(1)转化为
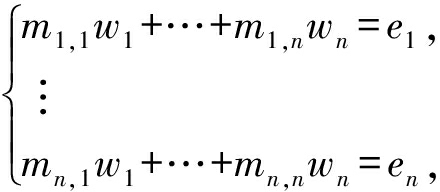
(9)
并构造目标函数为
(10)
优化问题为
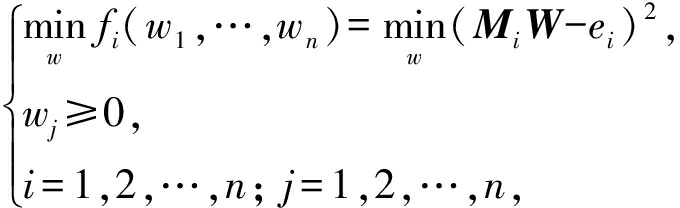
(11)
式(11)是将优化问题作为一个方程组，依次对每个方程进行迭代实现的。
基于式(7)的矩阵迭代算法，其实现过程和调整因子的处理比较复杂，迭代过程较慢，但形式容易理解；基于式(11)的方程迭代算法处理过程形式复杂，但由于是针对单一的方程处理，因此调整因子处理简单，迭代速度较快，但每个方程之间的关系处理比较复杂。
目前激光粒度反演算法中，Twomey算法、修正牛顿算法等采用了基于矩阵方程的方法，而Chahine算法、 Projection算法和改进共轭梯度算法采用了基于方程组的方法。 为了进一步分析算法的适用性，本文中采用变尺度算法并进行改进，实现了粒度反演。
1.3 基于变尺度法的粒度分布反演算法
本文中根据式(7)，采用对矩阵迭代的形式，用变尺度算法实现了粒度分布测量。
变尺度算法(Davidon-Fletcher-Powell algorithm，DFP)由Davidon提出，并由Fletcher和Powell进行演化[17]。在粒度分布测量中，构造迭代过程如下。其中
f(W(k))为f(W(k))的梯度，即
f(W(k))=2M(W(k)-W(k-1))，
(12)
设正定矩阵被定义为H(0)=I，迭代方向为：
P(k)=H(k)f(W(k))，
(13)
第k步的迭代结果为：
W(k+1)=W(k)-α(k)P(k)，
(14)
其中，
，
(15)
ΔW(k)=W(k+1)-W(k)，
(16)
(17)
(18)
由上述分析可知，噪声对矩阵方程的每个行向量影响程度不同，传统的变尺度算法不能用于粒度分布反演。在共轭梯度算法中，通过分析可知，需要针对方程组中每个方程提出的调整系数，该系数是一个数值[7]，与之相比较，在变尺度算法中，提出在式(14)中引入调整矩阵α(k)为：
(19)
其中
是衍射光能分布系数矩阵M的二范数。将α(k)代入DFP算法后，调整了算法在每个行向量上的尺寸算子，使对于噪声影响大的外环尺度(梯度)变大，而噪声影响小的内环尺度(梯度)变小，因此，对小颗粒的迭代效果增强，加速收敛；而对大颗粒的迭代效果相对减弱，减速收敛。当迭代误差小于设定的ε而终止迭代时，最终结果中小颗粒方向具有平滑性，同时大粒径方向不致因过快收敛而偏离实际值。
2 实验和结果
为了验证改进算法的有效性，采用激光粒度仪样机对微粒标准物质样品进行实验，粒度仪探测器有32环的光电探测器阵列，接收透镜的焦距为300 mm，可测量粒度范围为5.4～592 μm。
分别取适量微粒标准物质样品GBW(E)120026和样品GBW(E)120028，放在去离子水中进行测量和数据反演，结果如表1所示。
表1 单个样品结果
Tab.1 China powder science and technology
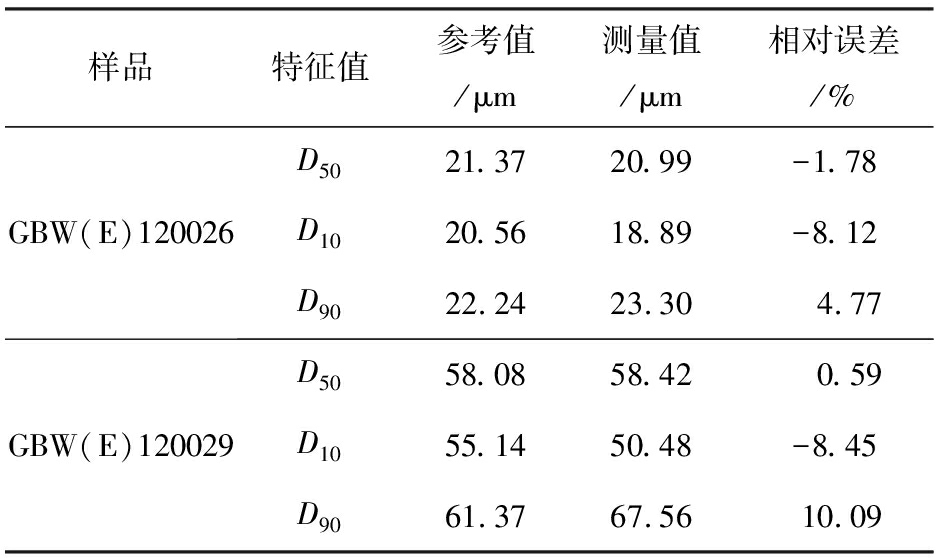
样品特征值参考值/μm测量值/μm相对误差/%GBW(E)120026D5021.3720.99-1.78D1020.5618.89-8.12D9022.2423.304.77GBW(E)120029D5058.0858.420.59D1055.1450.48-8.45D9061.3767.5610.09
在表1中，D50、 D10和D90分别表示体积中位径和下、 上限粒径，即体积的50%、 10%、 90%分别小于这些直径。由表可知，采用变尺度算法反演单峰宽分布的标准颗粒样品，D50相对误差均小于2%，而GBW(E)120026的结果误差略大，这与噪声对小颗粒的影响大、从而造成测量结果偏差大的分析是一致的。
对D10、 D90测量结果的相对误差都比D50的大，这与激光粒度仪衍射功率谱分布有关。在自然和人工形成的颗粒系中，颗粒分布总是位于中位径附近的颗粒远大于上下限附近的颗粒，而功率谱分布与颗粒分布有关，颗粒越多，对应的功率谱所占比例越大，噪声比例相对小，因此噪声对中位径附近的影响相对较小，反演精度更高。
D10的相对误差都为负，D90的相对误差都为正，表示测量结果比实际粒度分布变宽，这与算法迭代也是直接相关的，由于在式(12)中，初始迭代总是设为粒度分布最宽，并开始逐渐收缩，达到误差容限时总会因不能完全收敛使分布变宽。
对上述2种颗粒样品任取适量混合在去离子水介质中进行测量，结果如图2所示。 由图可以看到明显的2个峰，且分布不相连。 这2个峰值分别位于2种样品的中位径所在区间，与实际粒度分布相吻合，结果表明该算法能够识别多峰分布的粒径样品。
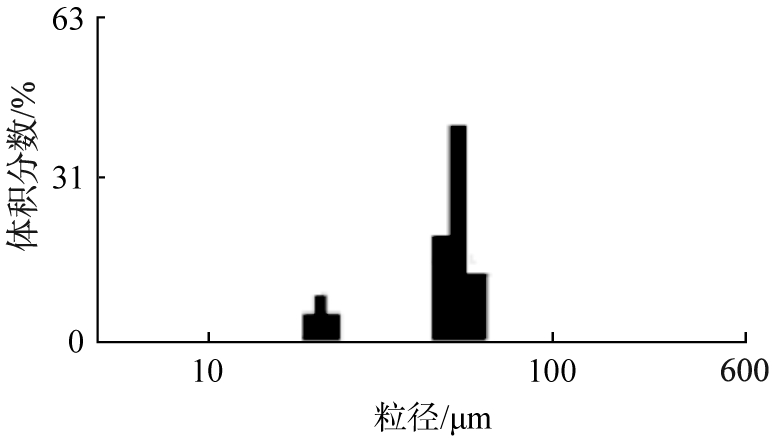
图2 DFP算法测量结果
Fig.2 Measurement results of DFP algorithm
3 结论
1)基于颗粒的激光衍射分布理论，对颗粒衍射功率谱的光能分布矩阵进行了分析，将数据反演算法按照矩阵迭代方式、方程组方式构造优化问题。
2)采用矩阵迭代方式构造了优化问题，提出采用变尺度算法，并引入迭代因子进行处理。
3)采用该算法对样机检测标准物质颗粒的数据进行反演，能够测量单一样品颗粒和混合样品颗粒，满足激光粒度测试要求。
[1]BI Y M, WANG L F, LI Y X, et al. The generalized Lorenz-Mie scattering theory and algorithm of Gaussian beam[C]// Society of Photo-optical Instrumentation Engineers (SPIE) Conference Series, 2011.
[2]SMITH Z J, CHU K, WACHSMANN-HOGIU S. Nanometer-scale sizing accuracy of particle suspensions on an unmodified cell phone using elastic light scattering[J]. PLOS ONE, 2012, 7(10): e46030.
[3]TAMBURINI A, CIPOLLINA A, MICALE G, et al. Particle distribution in dilute solid liquid unbaffled tanks via a novel laser sheet and image analysis based technique[J]. Chemical Engineering Science, 2013, 87: 341-358.
[4]PENG H T, HORTON R, LEI T W, et al. A modified method for estimating fine and coarse fractal dimensions of soil particle size distributions based on laser diffraction analysis[J]. J Soils Sediments, 2015, 15(4): 937-948.
[5]LEVOGUER C. Enhancing particle-size measurement using dry-laser diffraction particle-size analysis [J]. Pharmaceutical Technology, 2013, 37(5): 60-63.
[6]MILANA I, IGOR B, MILICA V V, et al. Size and shape particle analysis by applying image analysis and laser diffraction-inhalable dust in a dental laboratory[J]. Measurement, 2015, 66: 109-117.
[7]RICHARD F, WANG C J, OLGA M, et al. Elastic back-scattering patterns via particle surface roughness and orientation from single trapped airborne aerosol particles[J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2017, 187: 224-231.
[8]XU R L. Particle characterization: light scattering methods[M]. Dordrecht: Springer Netherlands, 2002.
[9]WEI Y J, GE B Z, WEI Y L. Noise effect in an improved conjugate gradient algorithm to invert particle size distribution and the algorithm amendment[J]. Applied Optics, 2009, 48(10): 1779-1783.
[10]徐峰，蔡小舒，苏明旭，等. 独立模式算法求解颗粒粒径分布的研究[J]. 中国激光, 2004, 31(2): 223-228.
[11]曹丽霞，赵军，孔明，等. 基于改进的Chahine迭代算法的粒径分布反演[J]. 红外与激光工程, 2015, 44(9): 2837-2843.
[12]WANG J P, XIE S Z, ZHANG Y M, et al. Improved projection algorithm to invert forward scattered light for particle sizing[J]. Appl Opt, 2001, 40(23): 3937-3945.
[13]王晨，张彪，曹丽霞，等. 颗粒粒径分布测量反演算法的改进[J]. 光学学报, 2019, 39(2): 214-221.
[14]GE B Z, LUAN Z C, LU Q N. Solution of the particle size distribution with improved Newton algorithm[J]. Optical Engineering, 2005, 44(5): 058003.
[15]WEI Y J, ZHANG S X. Inversion of particle size from light-scattering data by differentiating the distribution width and convergence threshold[J]. Optical Engineering, 2011, 50(5): 053608.
[16]WORLITSCHEK J, HOCKER T, MAZZOTTI M. Restoration of PSD from chord length distribution data using the method of projections onto convex sets[J]. Particle & Particle Systems Characterization, 2005, 22(2): 81-98.
[17]LIU Q, SANG R Y, ZHANG Q J. FPGA-based acceleration of Davidon-Fletcher-Powell quasi-Newton optimization method[J]. Transactions of Tianjin University, 2016, 22(5): 381-387.