强力混合机是一种将多种物料混合均匀的设备,广泛应用于烧结、球团、采矿、采煤等领域。进入强力混合机的物料由皮带运输,皮带与强力混合机之间的转运点存在一定的高度差,物料在下落过程中由于诱导气流和碰撞剪切气流的综合作用,会造成一定量的粉尘从进料口逸散。
国内外众多学者对于不同类型的落料产尘和诱导气流进行了研究。Cooper等[1]发现了料流在下落过程中料流核心区与料流边界层随高度的变化规律。 Wypych等[2]研究发现物料核心区的颗粒对周围气流的诱导作用比颗粒单独下落时的诱导作用弱。Ansart等[3-4]探究了粒径小于100 μm的小颗粒在自由下落过程中的产尘机理。Uchiyama等[5]采用数值模拟的方法对自由下落的颗粒流进行计算,得到了更加直观的诱导气流空间分布状态。
刘启觉[6]、严兴忠[7]推导出胶带运输机转运点诱导气流的计算公式。李小剑[8]利用高速摄像机验证了CFD模型,得出温度、质量流量对卷吸气流的影响。李小川等[9-10]自主设计了实验装置,研究了质量流量、粒径和下落高度等因素与转载点诱导气流的之间的非线性关系。陈雅等[11]采用密相DPM模型进行数值模拟,得到高溜井卸矿冲击气流与卸矿流量成幂指数关系的结论。张兴华、王式耀等[12-13]均采用与现场相应的实验装置得出诱导风量的计算公式,均对于相应现场粉尘的治理提供有效的指导。任晓芬[14]采用高速摄像机对自由下落颗粒在垂直下落阶段和与地面撞击后产尘机理进行了分析。
在CFD-DEM应用于粉尘逸散研究方面,Yu、Cheng等[15-16]利用CFD-DEM模型从气固两相运动的角度对综采工作面下粉尘扩散进行了分析,并探究了颗粒粒径对粉尘扩散的影响。
上述研究或基于特定的实体模型,或从理论角度分析而简化了颗粒间的接触力,对于定量描述强力混合机进料口的产尘与诱导气流并不适用。
本文中采取CFD-DEM耦合模型对强力混合机进料口的物料下落过程中的产尘和诱导气流了进行研究,为解决强力混合机进料口粉尘逸散问题提供研究基础。
1 数学模型
1.1 气流控制方程
计算域内为空气,连续性方程和N-S方程[17]为
![]() +
+ ·(εgρgug)=0,
·(εgρgug)=0,
(1)
- p+
p+ ·(μgεg
·(μgεg ug)-εg ρgg-S,
ug)-εg ρgg-S,
(2)
式中: ρg为气体密度,kg/m3;t为时间,s;ug为气体速度,m/s;εg为气体体积分数,p为气体压力,Pa;μg为气体动力黏度,N·s/m2;g为气体重力加速度,m/s2;S为动量交换源相。
1.2 颗粒控制方程
颗粒在气流场中受力较多,虚拟质量力、巴塞特力、萨夫曼升力、压力梯度力、热泳力以及布朗力等相对于重力和曳力在数量级上相差较大,可以不考虑,主要考虑重力、曳力、接触力的作用[18-19]。采用Hertz-Mindlin (no-slip) 接触模型,由牛顿第二定律可知
(3)
(4)
式中: mp为颗粒p的质量,kg;fcon为颗粒间作用力,N;Ip为颗粒转动惯量,kg·m2;wp为颗粒角速度,rad/s;nc表示与颗粒发生接触的颗粒数;Tpq表示扭矩,N·m。
2 仿真模型
2.1 CFD设置
2.1.1 几何模型
混合桶直径为150 mm,深度为25 mm;进料口直径为40 mm,高度为20 mm。混合桶的几何模型如图1所示。二维图如图1a所示,计算域的组成如图1b所示。其中,内流域由进料口和混合桶组成。
对计算域划分了3种网格,网格数量分别为7×104、2.7×105、5×105个。 使用3种网格对膨润土颗粒的自由下落进行了耦合计算,得到的颗粒平均速度随时间变化曲线如图2所示。 由图可知,在0.10~0.26 s之间,3种网格的颗粒平均速度随时间的变化趋势基本一致;在0.27~0.30 s之间,速度波动趋势稍有不同,在2.7×105个网格时,其速度处于中间值。综合考虑计算资源和计算精度的平衡,最终确定数量为2.7×105个网格的划分法来进行后续计算。
2.1.2 边界条件设置
流体域四周的边界面设置为对称边界条件,桶体壁设置为无滑移壁面,湍流模型采用RNG k-ε模型,流体介质为空气,并进行如下基本假设:流场稳定,无温差,气相和固相均视为不可压缩的介质。
2.2 DEM设置
2.2.1 参数标定
采用丹东市百特仪器有限公司生产的BT-1000粉体综合仪来测定3种物料的堆积角,并通过EDEM参数标定以确定颗粒接触参数。
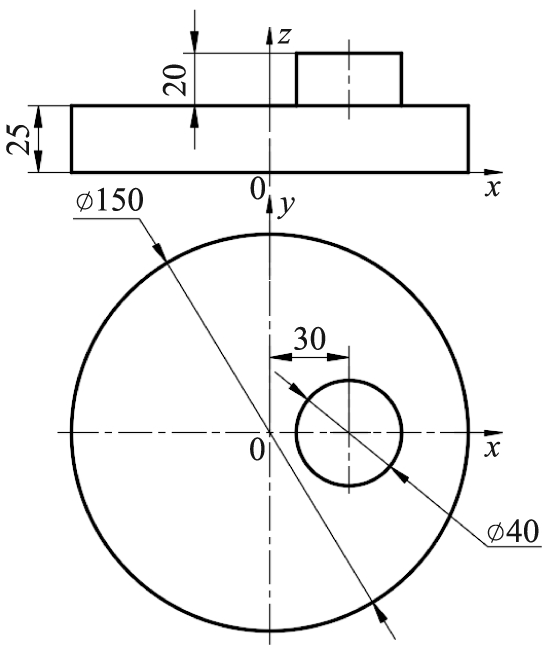
a 二维图
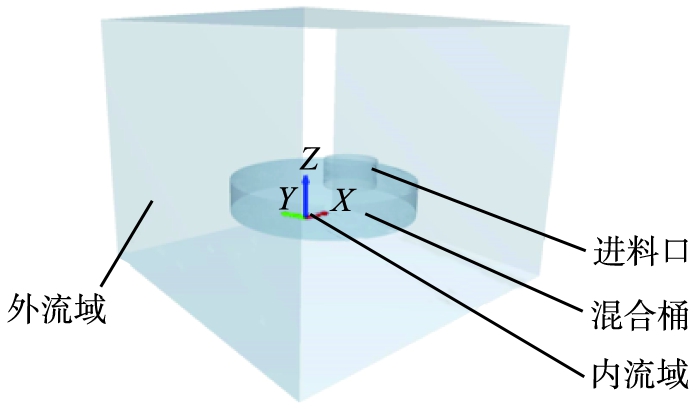
b 计算域
图1 混合桶的几何模型
Fig.1 Geometric model of mixing barrel
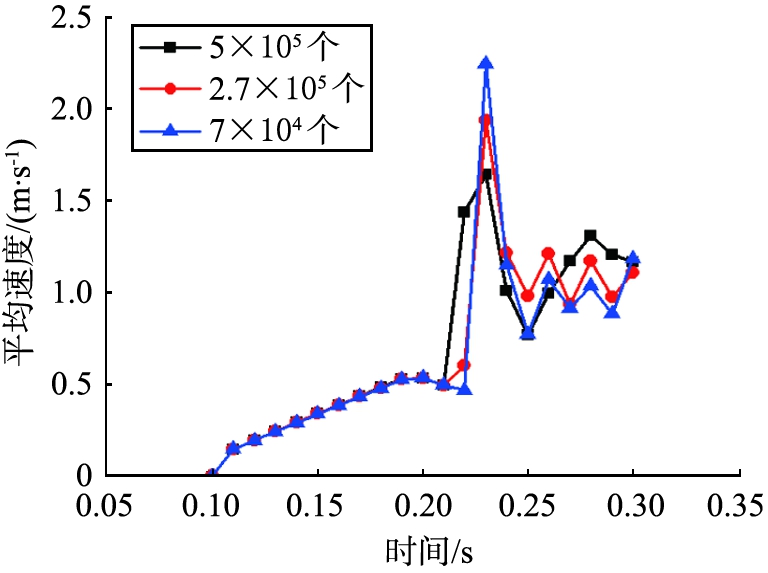
图2 颗粒平均速度随时间的变化
Fig.2 Mean velocities of particles varying with time
3种物料分别为膨润土(平均粒径为0.074 mm)、铁精粉(平均粒径为0.100 mm)及质量比为1 ∶1的二者混合物。3种物料均需要烘干,由于人工测量存在一定误差,需要测量料堆4个方位堆积角,并对每种物料多次测量后取平均值来减小误差。不同物料堆积角的测量如图3所示,最终得到膨润土、铁精粉、混合物的平均堆积角分别为39 °、38 °、42 °。

a 膨润土(平均粒径为0.074 mm)

b 铁精粉(平均粒径为0.100 mm)

c 混合物(膨润土和铁精粉的质量比为1 ∶1)
图3 不同物料的堆积角测量
Fig.3 Measurement of stacking angle of different materials
物料的材料属性如表1所示,接触属性如表2所示。 根据表1、2所示参数模拟3种物料的堆积角。 用EDEM角度测量工具测量料堆的模拟堆积角,采用与实验相同的方式减少误差。 膨润土、铁精粉、混合物的平均模拟堆积角分别为39.13 °、38.30 °、41.97 °。 与实验数值的误差小于1%,从而验证了表2所示的颗粒接触参数可以表征颗粒的真实接触状态。
表1 物料的材料属性
Tab.1 Material properties of materials
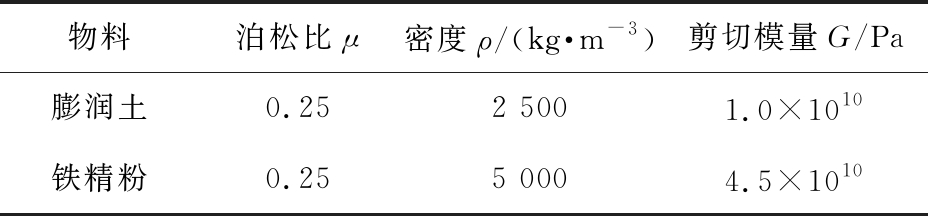
物料泊松比μ密度ρ/(kg·m-3)剪切模量G/Pa膨润土0.252 5001.0×1010铁精粉0.255 0004.5×1010
表2 物料的接触属性
Tab.2 Contact properties of materials
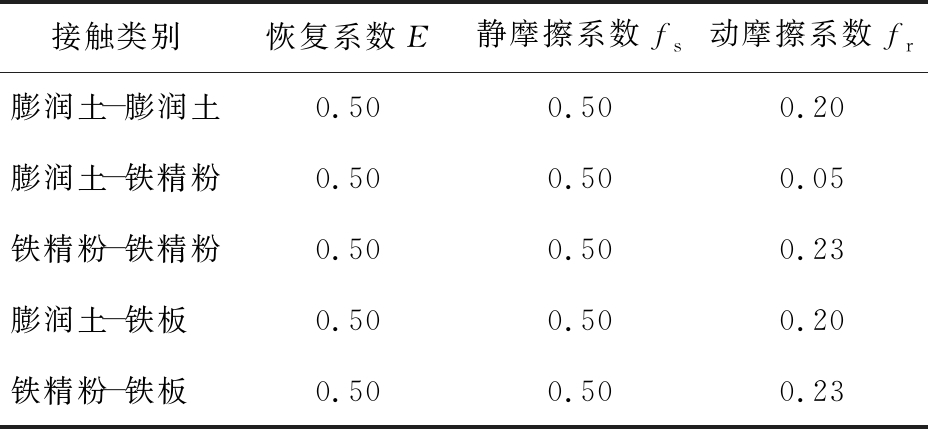
接触类别恢复系数E静摩擦系数fs动摩擦系数fr膨润土-膨润土0.500.500.20膨润土-铁精粉0.500.500.05铁精粉-铁精粉0.500.500.23膨润土-铁板 0.500.500.20铁精粉-铁板 0.500.500.23
2.2.2 颗粒参数设置
膨润土单个颗粒粒径为0.074 mm,密度为2.5 g/cm3,单个颗粒质量为4.4×10-6 g,颗粒生成速率为2×106 s-1,生成总数为4×105个。根据颗粒质量及颗粒生成速率可得料流的质量流量为8.80 g/s,颗粒从0.10 s后开始生成,颗粒下落高度为40 mm。
2.3 CFD-DEM耦合参数设置
本文中计算颗粒相的体积分数大于10%,由于气相对固相的作用力是研究的关键点,耦合模块采用欧拉-欧拉耦合算法;曳力模型采用Ergun and Wen&Yu(Gidaspow)模型[20];不考虑升力模型、传热模型;样本点取10;动量亚松驰因子、体积亚松驰因子和热源亚松驰因子均设为0.7。膨润土颗粒粒径较小,导致颗粒的瑞利时间步长(Rayleigh time step)数量级为10-7,取FLUENT的时间步长为EDEM的104倍。时间步长的设置如表3所示。
表3 时间步长的设置
Tab.3 Time step settings
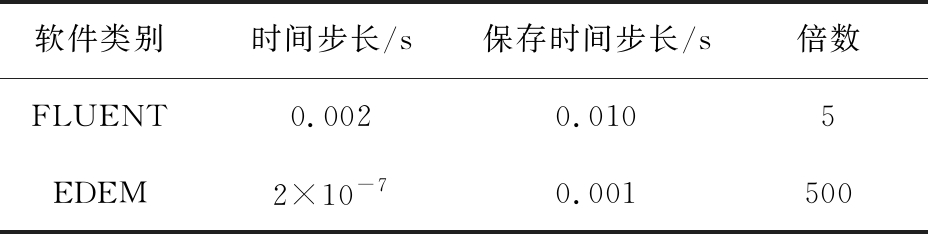
软件类别时间步长/s保存时间步长/s倍数FLUENT0.0020.0105EDEM2×10-70.001500
2.4 模型验证
2.4.1 仿真试验
以粒径为0.074 mm膨润土物料为例,不同时刻物料下落时,仿真得到的颗粒运动轨迹如图4所示。
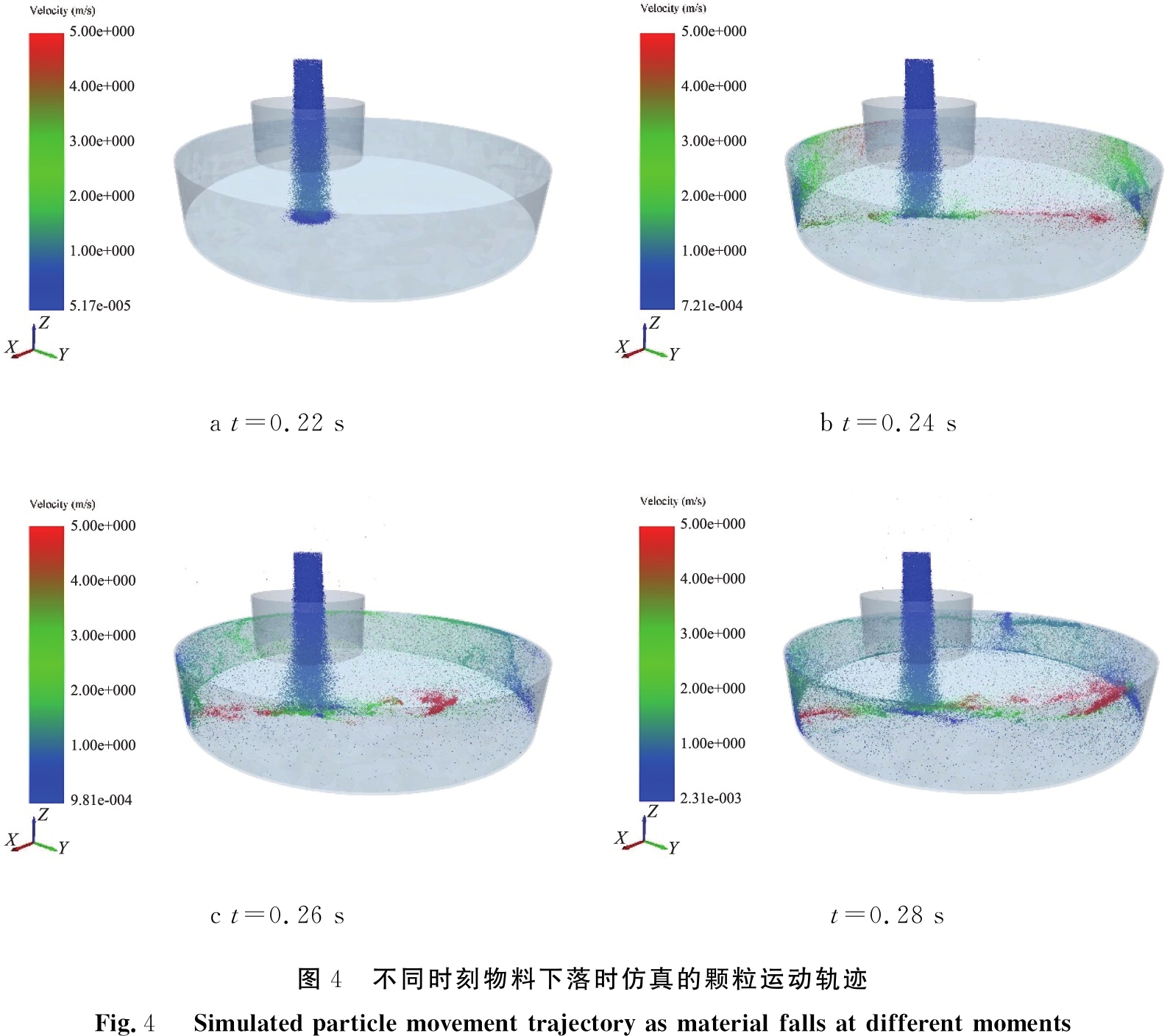
a t=0.22 sb t=0.24 sc t=0.26 st=0.28 s图4 不同时刻物料下落时仿真的颗粒运动轨迹Fig.4 Simulated particle movement trajectory as material falls at different moments
从图4可以看出,在物料下落过程中,明显可分为料流核心区和料流边界层。随着料流向下运动,料流横截面的直径增大,边界层的厚度和游离于边界层的颗粒数均会增加,并且边界层颗粒间的间距增大。料流与底面接触时,颗粒与颗粒以及颗粒与底面的接触碰撞,导致首先接触底面的料流没有形成堆积料流,而是向两侧扩散。向两侧扩散的颗粒在偏离落料点后,在近桶壁面区内沿圆周方向运动,部分颗粒从进料斗溢出并向四周逸散。
2.4.2 实验验证
为了验证数值模拟的结果,按照仿真与实验的模型尺寸比为1 ∶1进行实验,利用高速摄像机拍摄下物料落料过程并通过PIV软件处理颗粒轨迹图,得到桶体(不包括进料口)的XZ平面不同时刻颗粒速度云图。不同时刻物料下落时实际的颗粒速度云图如图5所示。
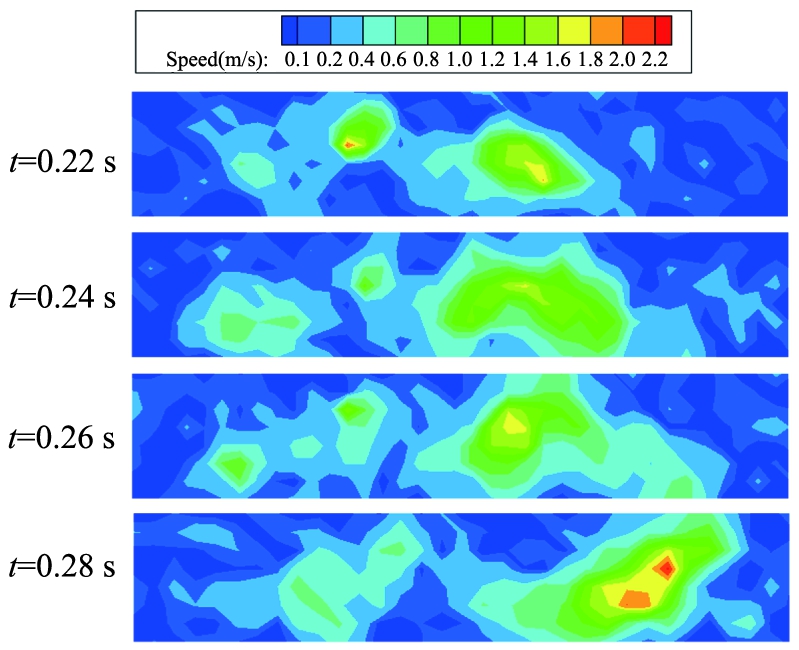
图5 不同时刻物料下落时实际的颗粒速度云图
Fig.5 Cloud image of actual particle velocity as material falls at different times
从图4、5可看出,仿真与实验的颗粒速度大小存在差异,仿真颗粒速度分布为2.00~3.00 m/s,实验所得的速度分布为1.00~1.40 m/s,但是颗粒运动形态和趋势大致相同。速度分布存在差异的原因是两侧靠近壁面的颗粒吸附在桶壁时PIV软件无法识别,并且PIV只能识别出成团的颗粒移动速度,对于单个颗粒的运动捕获效果较弱,所以速度云图上有些区域的速度值较小,几乎为零。通过对比可知,CFD-DEM模型能够用于描述强力混合机进料口和桶体内颗粒运动状态,且能更加直观地展现出每个颗粒的运动状态。
3 结果与分析
3.1 诱导气流与产尘机理
由颗粒拖曳、挤压综合作用产生的气流称为诱导气流。 为了研究诱导气流对进料口产尘的影响机理,以平均粒径为0.074 mm膨润土物料为例,选取料流气流旋涡中心位置监测点,即XZ平面中坐标为(15, 35)点处。观测不同X坐标处的诱导气流速度值,得到诱导气流速度随时间的变化如图6所示。
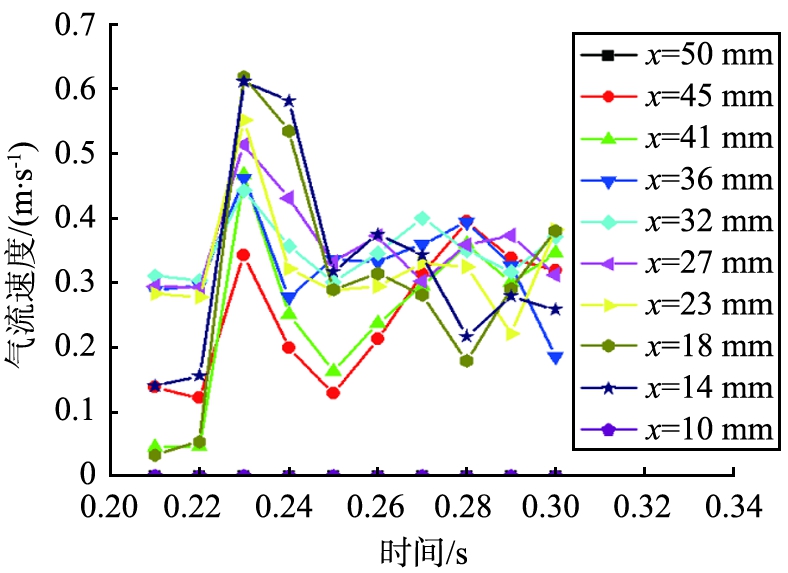
图6 诱导气流速度随时间的变化
Fig.6 Induced flow velocities varying with time
从图6可以看出,不同X坐标值的诱导气流速度均随时间先增大后减小,且速度峰值出现在同一时刻t=0.23 s。 在0.10~0.22 s时间段,诱导气体速度缓慢上升,气流速度为0~0.50 m/s;在0.22~0.24 s时间段,气体速度迅速增大到最大值然后急剧减小;在t=0.24 s以后,诱导气体速度在0.20~0.50 m/s内波动。 因此,可以将进料口物料下落过中的气固耦合过程分为3个阶段,即速度缓慢增加的垂直下落阶段、速度迅速变化的挤压碰撞阶段、速度逐渐稳定的扩散阶段。
XZ平面内的诱导气流速度矢量图如图7所示。由图7可看出,颗粒下落之前,计算域内空气处于静止状态。 开始下落后,料流上方的空气受到料流的拖曳作用而运动,并逐渐带动周围的空气运动,形成了小的气流漩涡。 料流核心区边缘的颗粒在气流旋涡的影响下而脱离,逐渐脱离核心区的颗粒形成了料流边界层。 随着运动距离的增加,边界层颗粒间的间隙越来越大。 料流核心区颗粒对气体的拖曳作用强于边界层。 如图7a所示,0.22 s时核心区的最大速率为0.50 m/s,边界层速率为0.10~0.20 m/s。
在垂直下落阶段,颗粒对气体拖曳作用产生的卷吸气流充满颗粒的间隙中,随着料流一起下落。在料流接触底面后,颗粒间的间隙会被挤压,挤压出来的空气向四周逸散,进料口处的气流方向转变为桶内向桶外溢出,气流在溢出时带动料流边界层的颗粒脱离边界层溢出进料口形成污染粉尘。
在扩散阶段,剪切运动挤压出来的气流在桶内运动,在料流两侧形成2个较大的漩涡,旋涡气流带动颗粒运动的同时也会使部分颗粒溢出进料口。
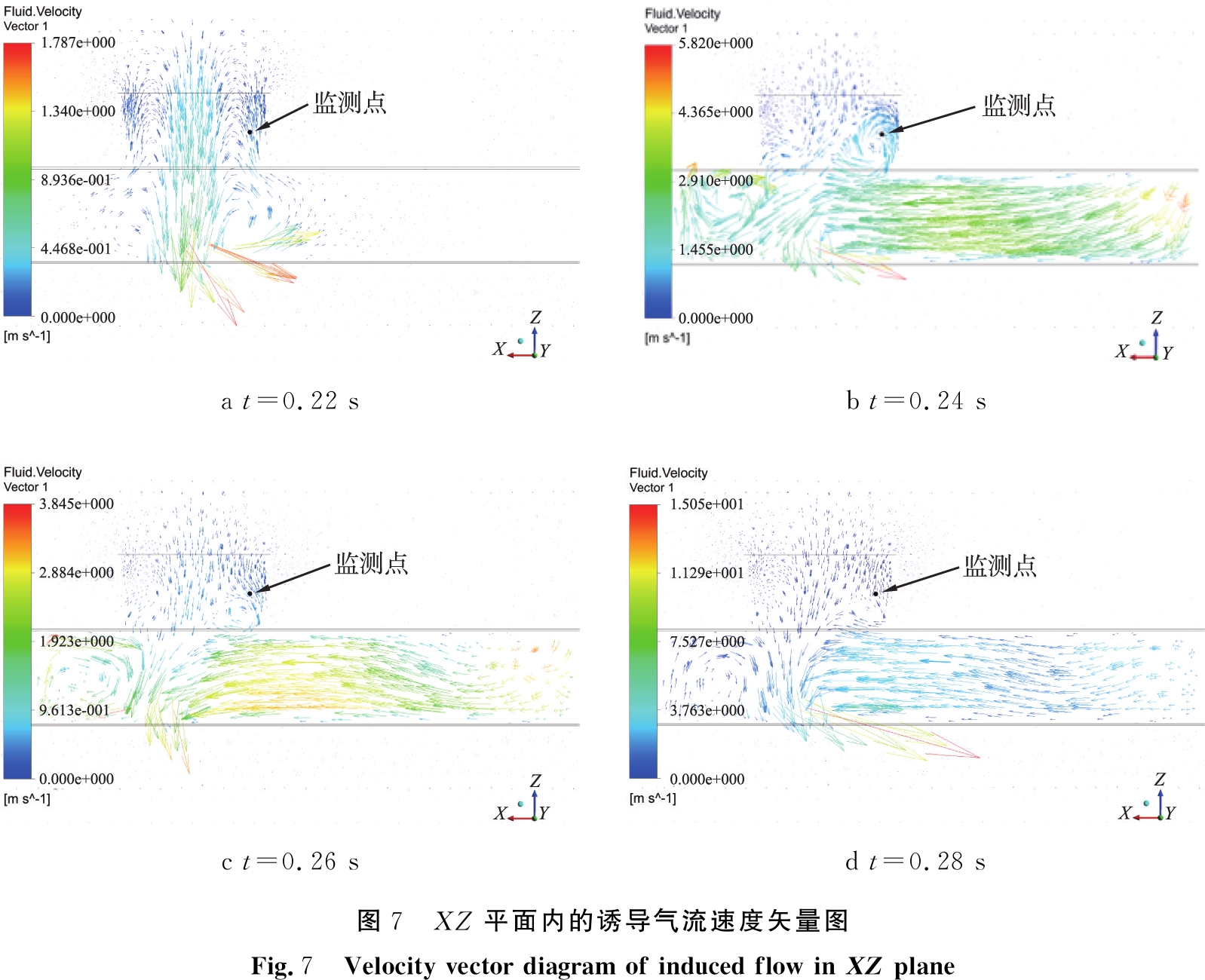
a t=0.22 sb t=0.24 sc t=0.26 sd t=0.28 s图7 XZ平面内的诱导气流速度矢量图Fig.7 Velocity vector diagram of induced flow in XZ plane
3.2 诱导气流的影响因素
以平均粒径为0.074 mm膨润土物料为例,研究质量流量和下落高度对诱导气流的影响。选取40、60、80 mm 3种下落高度,改变颗粒生成的速率依次为2×105、5×105、1×106、1.5×106、2×106 s-1,对应的质量流量依次为0.88、2.20、4.40、6.60、8.80 g/s,统计监测点诱导气流速度最大值,得到诱导气流速度随质量流量的变化关系如图8所示。
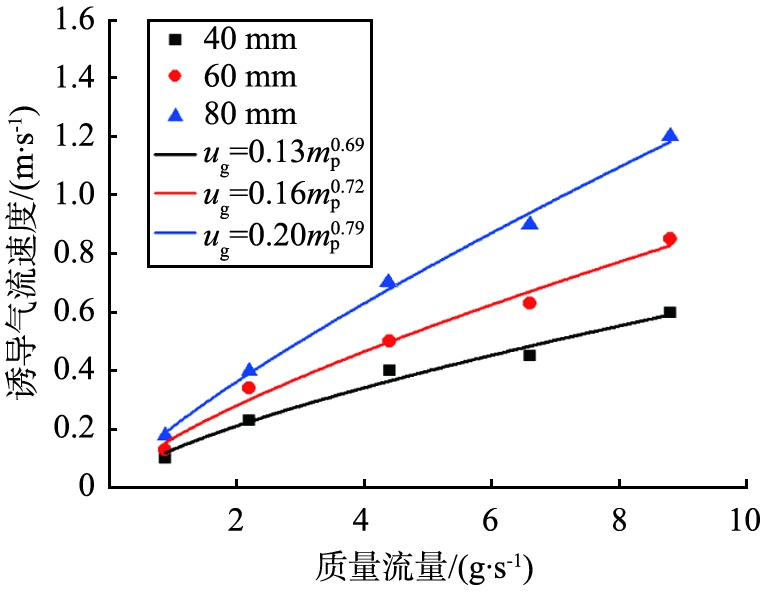
图8 诱导气流速度随质量流量的变化
Fig.8 Induced flow velocity varying with mass flow rate
从图8可看出,落料高度的诱导气流速度均随着质量流量的增大而增大。 诱导气流速度与物料质量流量成幂函数关系。 落料高度为40、60、80 mm时,诱导气流与质量流量的幂函数分别为
(5)
(6)
(7)
幂指数范围为0.69~0.79,可见,落料高度越高,幂指数越大。 其主要原因在于,质量流量越大,料流横截面颗粒数越多,质量流量从0.88 g/s增加到8.80 g/s时,进料口处料流截面颗粒数量从418个增加到2 484个,与空气接触的颗粒数越多,对空气的作用力越大;下落高度越高,料流边界层发展越充分,厚度越大,料流边界层能卷吸更多的气流,因此,落料高度越高,质量流量对诱导气流的影响越大。
3.3 不同物料的产尘特性
改变进料口的物料类型,探究不同物料下落时的产尘特性。 3种物料分别为膨润土(平均粒径为0.074 mm)、铁精粉(平均粒径为0.100 mm)及质量比为1 ∶1的二者混合物。 3种物料以8.80 g/s的质量流量下落时,单纯的膨润土、铁精粉的颗粒生成速率分别为2×106、4×105 s-1,而混合物料中的膨润土和铁精粉的颗粒生成速率分别为1×106、2×104 s-1。
t=0.3 s时,不同物料溢出进料口的颗粒数如图9所示。从图9可看出,膨润土、混合物、铁精粉溢出的颗粒数量分别为55、8、0,而混合物溢出的颗粒全部为膨润土。比较进料口处诱导气流速度最大值可知,膨润土为0.60 m/s,混合物为0.88 m/s,铁精粉为0.40 m/s。混合物物料在进料口处的诱导气流速度最大,但是溢出颗粒数却没有膨润土物料产生的多。由于混合物料是2种不同粒径颗粒的混合,在下落过程中,颗粒与颗粒之间的间隙更大,夹杂的气流量也更大,故混合物料产生的诱导气流速度更大。但是,膨润土的密度和粒径均比铁精粉小,因此膨润土物料的产尘量更大。
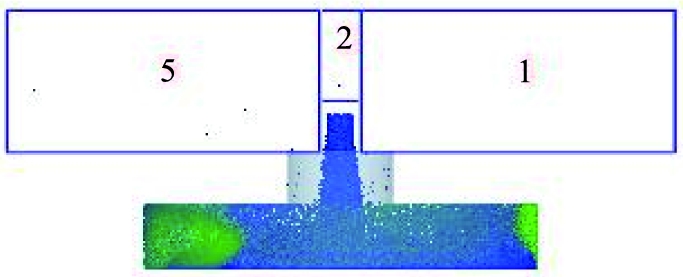
a 混合物
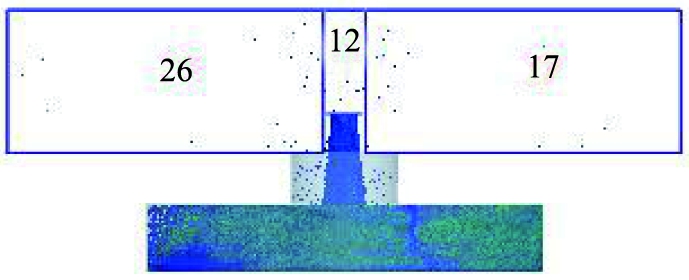
b 膨润土
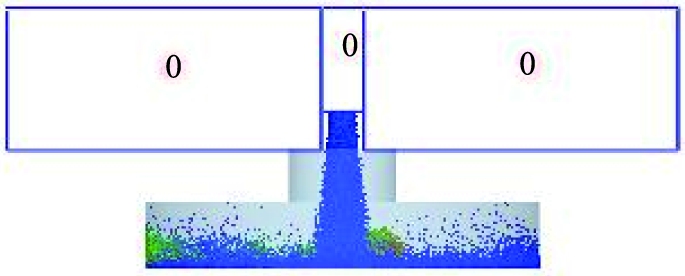
c 铁精粉
图9 t=0.3 s时不同物料溢出进料口的颗粒数
Fig.9 Number of particles spilled from different materials into inlet when t=0.3 s
4 结论
通过对比膨润土颗粒自由下落颗粒运动状态,实验验证了CFD-DEM耦合模型,为研究诱导气流和产尘特性提供了便捷、可靠的方法。结论如下:
1)通过研究进料口诱导气流的变化规律,发现诱导气流是产尘的决定性因素,进料口物料下落过中的气固耦合过程分为垂直下落、挤压碰撞、扩散3个阶段,揭示了进料口的产尘机理。
2)诱导气流速度与物料质量流量成幂函数关系,诱导气流速度均随着质量流量的增大而增大;幂指数范围为0.69~0.79,落料高度越高,幂指数越大。
3)膨润土(平均粒径为0.074 mm)、铁精粉(平均粒径为0.100 mm)及质量比为1 ∶1的二者混合物这3种物料种中,膨润土的产尘量最大。
[1]COOPER P, ARNOLD P. Air entrainment and dust generation from a falling stream of bulk material[J]. KONA Powder and Particle Journal, 1995, 13: 125-134.
[2]WYPYCH P, COOK D, COOPER P. Controlling dust emissions and explosion hazards in powder handling plants[J]. Chemical Engineering and Processing: Process Intensification, 2005, 44(2): 323-326.
[3]ANSART R, RYCK A D, DODDS J A. Dust emission in powder handling: free falling particle plume characterisation[J]. Chemical Engineering Journal, 2009, 152(2/3): 415-420.
[4]ANSART R, RYCK A D, DODDS J A, et al. Dust emission by powder handling: comparison between numerical analysis and experimental results[J]. Powder Technology, 2009, 190(1/2): 274-281.
[5]UCHIYAMA T. Numerical analysis of particulate jet generated by free falling particles[J]. Powder Technology, 2004, 145(2): 123-130.
[6]刘启觉. 理想落料诱导空气量的计算[J]. 通风除尘,1987(3):33-36.
[7]严兴忠. 落料诱导空气量的理论计算法[J]. 工业安全与防尘,1993(8):12-18.
[8]李小剑. 自由下落微粒羽流的数值模拟与实验研究[D]. 天津:天津商业大学,2007.
[9]李小川. 气流场中粉尘颗粒流动行为与湿法净化[D]. 徐州:中国矿业大学,2013.
[10]李小川,李强,张栋,等. 转运点落料诱导气流非线性变化影响因素[J]. 粉末冶金材料科学与工程,2014,19(4):508-513.
[11]陈雅,王明,蒋仲安,等. 高溜井卸矿冲击气流产生规律及其影响因素的数值模拟[J]. 煤炭学报,2017,42(S1):178-185.
[12]张兴华,葛少成,陈曦,等. 基于量纲分析的转载点诱导气流影响因素分析与应用[J]. 环境工程学报,2018,12(2):604-610.
[13]王式耀,葛少成,陈曦,等. 选煤厂转载点诱导气流影响因素的实验研究[J]. 中国安全生产科学技术,2017,13(9):53-57.
[14]任晓芬. 自由下落颗粒流扩散及产尘特性研究[D]. 西安:西安建筑科技大学,2017.
[15]YU H, CHENG W, WU L, et al. Mechanisms of dust diffuse pollution under forced-exhaust ventilation in fully-mechanized excavation faces by CFD-DEM[J]. Powder Technology, 2017, 317: 31-47.
[16]CHENG W, YU H, ZHOU G, et al. The diffusion and pollution mechanisms of airborne dusts in fully-mechanized excavation face at mesoscopic scale based on CFD-DEM[J]. Process Safety and Environmental Protection, 2016, 104:240-253.
[17]ZHOU Z Y, KUANG S B, CHU K W, et al. Discrete particle simulation of particle-fluid flow: model formulations and their applicability[J]. Journal of Fluid Mechanics, 2010, 661:482-510.
[18]施学贵,徐旭常,冯俊凯. 颗粒在湍流气流中运动的受力分析[J]. 工程热物理学报, 1989(3):320-325.
[19]岑可法,樊建人. 煤粉颗粒在气流中的受力分析及其运动轨迹的研究[J]. 浙江大学学报(自然科学版),1987(6):6-16.
[20]TSUO Y P, GIDASPOW D. Computation of flow patterns in circulating fluidized beds[J]. AICHE Journal, 1990, 36(6): 885-896.