甲醇制烯烃(methanol to olefins，MTO)技术是指以煤、天然气、生物质为原料，经甲醇、二甲醚制备低碳烯烃的核心技术。中国科学院大连化学物理研究所于2006年完成了甲醇制烯烃万吨级工业性试验，随后实现了10余套装置的工业应用[1]。该工艺被业界通称为DMTO工艺，即在流化床反应器-再生器系统中，经高温气化后的原料甲醇在SAPO-34催化剂作用下转化为以低碳烯烃为主的烃类产物，同时，在催化剂表面形成积碳使催化剂失活[2]。失活的催化剂经输送管送至再生器中进行积碳燃烧再生，失活的催化剂积碳的质量分数由6%～8%经过再生降至1%～2%，再输送至反应器进行反应，如此循环往复以维持甲醇的高效转化。由此可见，对再生器积碳燃烧反应的合理控制对于再生器的开发和平稳运行有着重要的指导意义。
流化床催化剂再生器内复杂的反应、传质、传热及相互之间强烈的耦合，给再生器的放大、设计和优化运行都带来了困难。同时，热态条件下流化床的测量仍然是一个极具挑战的问题，实验很难得到床层内部两相流动的规律以及反应数据。
计算流体力学(CFD)的数值模拟具有高灵活性、低成本的特点，因此成为研究和理解流化床内气-固流动和反应的重要方法。基于Euler-Lagrange体系的离散单元模型(DEM)是处理流化床内气-固两相流的常见数值模拟方法之一。DEM方法最早由Cundall等[3]在解决岩土力学问题时提出，基于单颗粒处理可以得到丰富的颗粒运动信息，可以用于理解流态化过程中各种微观尺度乃至介观尺度结构对流动和反应的影响。然而，DEM模拟方法对颗粒搜索需要耗费大量计算时间，无法进行大规模颗粒体系的计算。虽然CFD-DEM模拟方法已经成为研究流态化的一种标准方法，但是采用CFD-DEM模型进行工业催化过程的再生器研究并不多见[4-5]。
由于DMTO工艺过程采用不完全再生的方法，因此在连续循环再生条件下，催化剂的积碳分布对于DMTO反应器中低碳烯烃的选择性具有重要的影响。本文中采用CFD-DEM模型，利用美国国家能源实验室开发的开源软件MFIX进行分析，耦合甲醇制烯烃催化剂再生反应动力学，研究进气气速和氧含量对颗粒流动状态、颗粒温度变化、烟气组分浓度分布等的影响，进而研究这些因素对再生器内催化剂积碳分布的影响，建立DMTO流化床再生器的CFD-DEM数值模拟方法，为下一步建立连续的DMTO反应-再生系统模型，研究介观尺度结构对循环体系的催化剂积碳分布的影响打下基础。
1 模型的建立
1.1 CFD-DEM模型
在基于Euler-Lagrange体系的CFD-DEM模型中，气体运动采用Navier-Stokes方程进行描述，气相连续方程和动量守恒方程为
+
(εgρgVg)=0，
(1)
(2)
式中： g代表重力加速度；ρg为气相热力学密度；εg为气相体积分数；Vg为气相平均体积速度；Igm(m表示颗粒相)为气-固两相的动量传递相；
代表气相应力张量，其具体计算方法参见文献[6]。
颗粒作为离散相在两相流动中会产生颗粒间碰撞，造成能量耗散，运动规律遵循牛顿运动定律。本文中颗粒间碰撞采用软球模型进行描述，2个颗粒的相互作用力用弹簧-阻尼模型来表示，颗粒的位置X、线速度V、合力矩M的计算公式为
(3)
(4)
(5)
式中：F 代表颗粒相所受作用力之和；FD是流体作用在固体相的所有阻力之和(包含压力与黏性力)；FC是颗粒间的碰撞接触力之和；M是颗粒转动的合力矩，I是颗粒的转动惯量。
在DEM模型中，颗粒除受到碰撞力、压力和黏性阻力之外，还受到气固间的曳力。目前，常见的曳力模型主要有Gidaspow模型[7]、Syamlal-Obrien模型[8]和Koch-Hill模型[9]。本文中选用Gidaspow模型来描述气固间曳力，颗粒的能量守恒方程为
(6)
式中：Ti和Ci分别为颗粒的温度和比热容，Qij、Qig和Qrad是颗粒间的导热、对流传热和辐射传热，Qrea代表了化学反应的热量变化。
1.2 化学反应模型
SAPO-34分子筛作为DMTO反应的催化剂，拥有较好低碳烯烃选择性和水热稳定性，但是分子筛在甲醇制烯烃反应中极易积碳失活[10]。早期研究[11]指出，SAPO-34上的积碳物种主要由C9+-C13+的烷烃、萘、菲、芘等大分子芳烃构成，且反应过程中积碳物种会发生变化。不同的反应时间时，积碳物种可能不尽相同，对应的动力学方程也不相同。为了简化模型，采用基于工业发展的化学反应动力学数据[12]，简化为一个非均相的积碳燃烧反应，其反应方程式为
(7)
反应动力学方程为
(8)
式中：P为氧气分压，MPa；C为催化剂积碳质量分数；T为反应温度，K；R为摩尔气体常数，J/(mol·K)。
1.3 催化剂再生器的几何模型
催化剂再生器的几何模型结构示意图如图1所示。模拟的对象为方形的拟二维和三维流化床再生器，流化床高度为15 mm，宽度为5 mm，厚度1 mm(拟二维厚度0.2 mm)，床层高度为5 mm，设置SAPO-34催化剂颗粒粒径为100 μm。 为了计算方便，假设颗粒主要由2种组分构成：一种是惰性组分；另一种是覆盖在催化剂表面的积碳，初始积碳质量分数设为6%。由于积碳量较颗粒质量非常少，因此假设颗粒半径在反应中不发生变化，颗粒的密度随反应进行而逐渐减少。
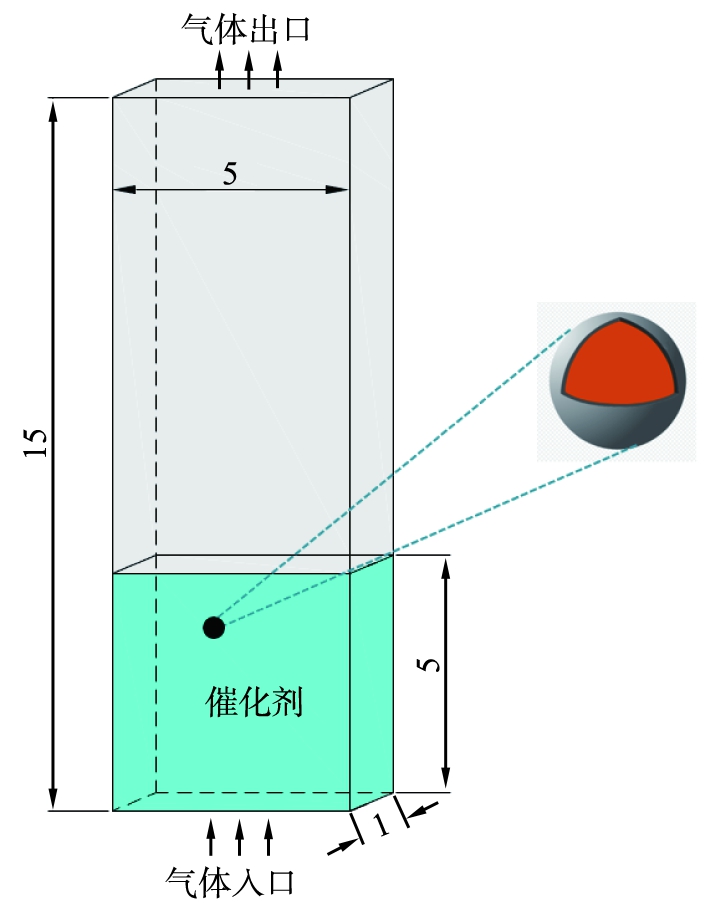
图1 催化剂再生器的几何模型结构示意图
Fig.1 Diagram of geometry model of catalyst regenerator
1.4 试验条件和参数设定
在DMTO工艺流程中，催化剂再生过程主要在鼓泡流态化区域进行。再生器的出口边界条件设置为压力出口，反应器壁面温度设为950 K，再生器入口温度为反应温度，进气组分含量根据操作条件不同而不同，气体黏度根据温度变化而变化。在初始状态下，再生器中充满空气，反应器内气体温度和催化剂颗粒温度均设置为反应温度。将再生化学反应动力学方程耦合到三维模型中，再生催化剂颗粒数设为16 928。
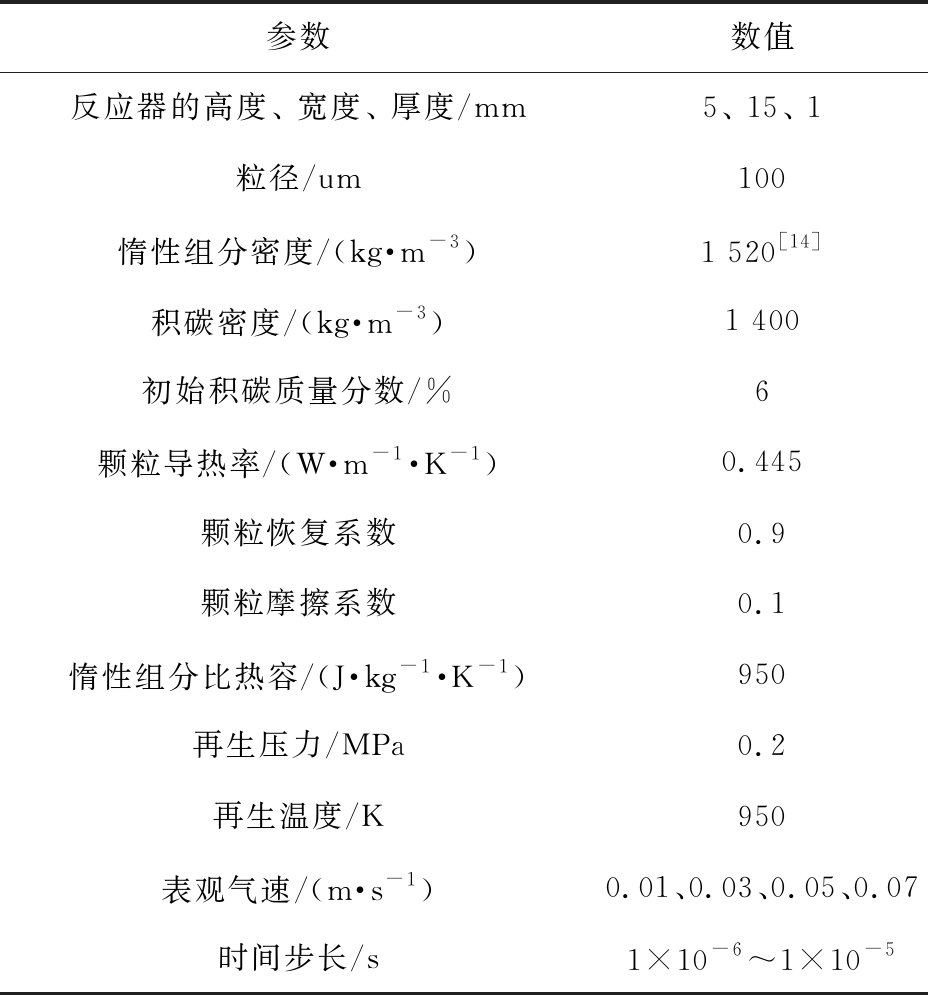
模拟的进料空气简化为2种组分，氧气的质量分数为22%，氮气的质量分数为78%，反应压力设为0.2 MPa。积碳比热容采用热化学数据库计算[13]，气体密度采用理想气体定律计算。表1为催化剂再生过程中的试验条件和模拟参数。
表1 试验条件和模拟参数
Tab.1 Experimental conditions and simulation parameters
参数数值反应器的高度、 宽度、 厚度/mm5、 15、 1粒径/um100惰性组分密度/(kg·m-3)1 520[14]积碳密度/(kg·m-3)1 400初始积碳质量分数/%6颗粒导热率/(W·m-1·K-1)0.445颗粒恢复系数0.9颗粒摩擦系数0.1惰性组分比热容/(J·kg-1·K-1)950再生压力/MPa0.2再生温度/K950表观气速/(m·s-1)0.01、0.03、0.05、0.07时间步长/s1×10-6～1×10-5
2 结果与讨论
在催化剂再生器中，催化剂颗粒的流化状态对于再生反应的结果的影响是显而易见的。气体进气速度直接影响再生器内的颗粒流化状态和再生器内的氧含量。其中，流化状态通过气-固相间接触的差异影响传热和传质，而氧含量直接影响再生反应的进行。
进气气速分别设置为0.01、0.03、0.05、0.07 m/s，研究进气气速对颗粒流型、再生催化剂积碳量和颗粒温度、气体组分浓度和催化剂积碳分布的影响，从而归纳出DMTO催化剂再生反应过程的变化规律。
2.1 再生催化剂颗粒流型
催化剂再生反应时间t=10 s时，不同进气气速时的再生催化剂颗粒流型图如图2所示。 由图2a可看出，进气气速为0.01 m/s时，三维流化床床层已经呈现一定的膨胀，颗粒在床层中已有明显的流化现象，床层中间颗粒在气体推动下向上运动，到达一定床层高度后向两侧分散，下落后形成床层内颗粒进行循环。 由图2b可看出，进气气速增加到0.03 m/s时出现鼓泡现象，流化状态更加剧烈，床层高度也有所提升。 由图2c可看出，当进气气速超过0.05 m/s时，催化剂颗粒出现了更为剧烈的鼓泡床特征，产生的气泡更大，床层中催化剂颗粒的上扬高度增加。 由图2d可看出，当进气气速达到0.07 m/s时，气体在反应器中的含量增加，反应器内出现了湍动床的流化特征，颗粒的流化速度更快。 可见，随着进气气速的增加，再生催化剂的颗粒的流化速度加快。
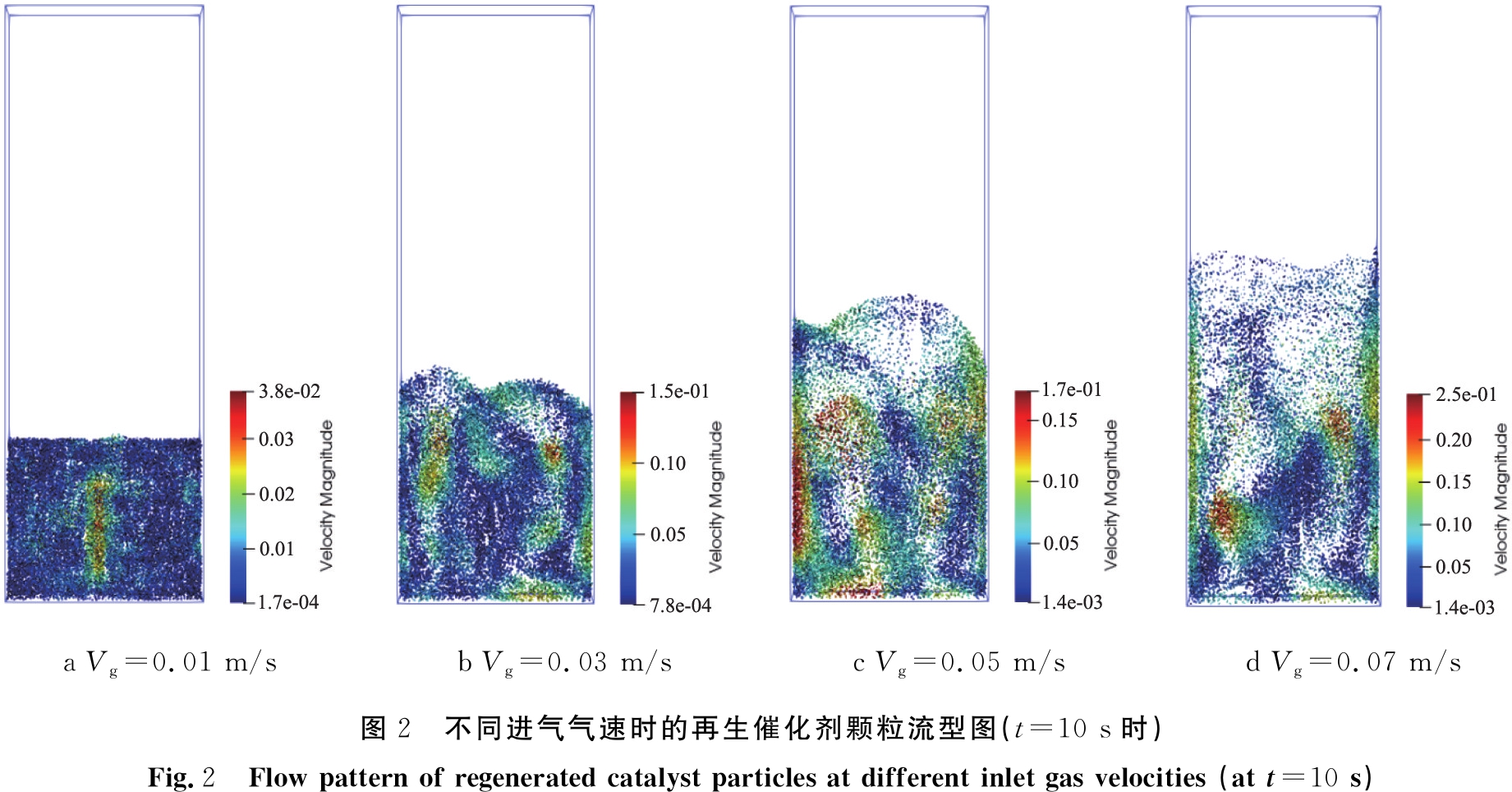
a Vg=0.01 m/sb Vg=0.03 m/sc Vg=0.05 m/sd Vg=0.07 m/s图2 不同进气气速时的再生催化剂颗粒流型图(t=10 s时)Fig.2 Flow pattern of regenerated catalyst particles at different inlet gas velocities (at t=10 s)
2.2 再生催化剂的颗粒属性
再生催化剂的积碳量和密度随时间的变化规律如图3所示。 由图3a可以看出，随着反应时间的增加，再生催化剂的积碳量由最初的6%逐渐减小。 再生反应时间为12 s时，进气气速为0.07 m/s时，催化剂积碳量减小最快，下降到了4.5%；进气气速分别为0.05、0.03 m/s时，催化剂积碳量分别减小到了4.72%、5.07%；进气气速为0.01 m/s时，积
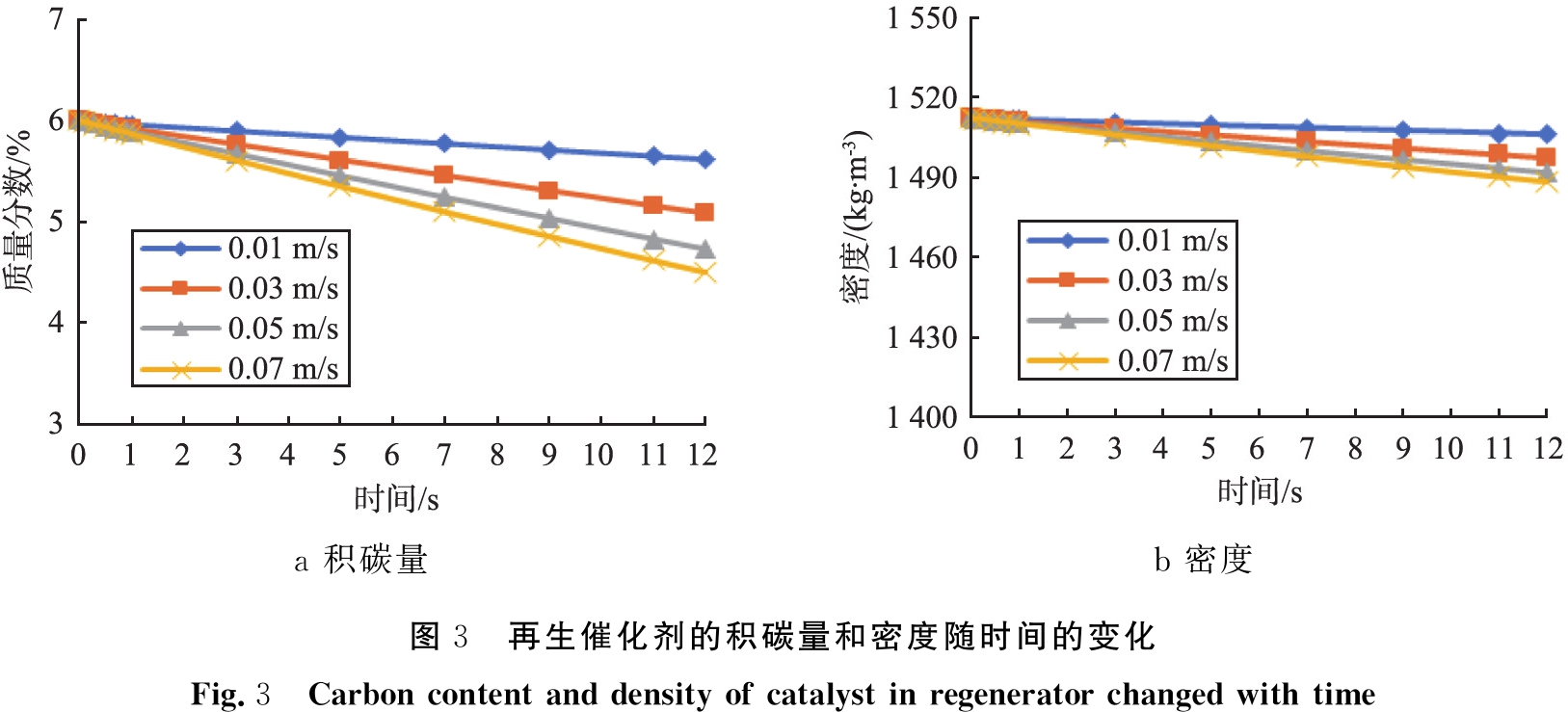
a 积碳量b 密度图3 再生催化剂的积碳量和密度随时间的变化Fig.3 Carbon content and density of catalyst in regenerator changed with time
碳燃烧速率最慢，积碳量只下降到5.62%。同时可以看到，当进气气速由0.01 m/s增大到0.03 m/s时，催化剂的积碳量变化最大，主要原因在于： 进气气速为0.01 m/s时，再生器中氧含量不足，氧气是影响反应速率的主要因素，当进气气速增大到0.03 m/s时，氧含量基本能够满足再生反应的要求；随着进气气速的继续增加，催化剂的残碳量并没有呈现线性减少，说明氧气含量已经逐步达到饱和，氧含量不再是限制再生反应的首要因素。 由图3b可以看出，催化剂密度随反应时间的增加而略有下降。 由于催化剂中活性组分中的积碳量只有6%，因此对于催化剂的密度影响不大，基本维持在1 500 kg/m3左右。 总之，再生催化剂的积碳量随着时间增加而减小，随进气气速的增大而减小速率加快，催化剂密度随反应时间的增加而略有下降。
三维流化床再生器中催化剂颗粒的平均温度随时间的变化如图4所示。 随着再生反应的进行，不同进气气速下催化剂的颗粒温度于初始温度950 K相比均有不同程度的提高，但提高幅度不大。并且可以看到，4组进气气速条件下，在初始0.7 s的反应阶段均迅速升温，而后保持该温度，基本无大幅度变化，这说明在反应初期，反应器中氧含量较多，积碳燃烧反应的速率较快，而后反应趋于稳定，整体催化剂的颗粒温度不再大幅度改变。
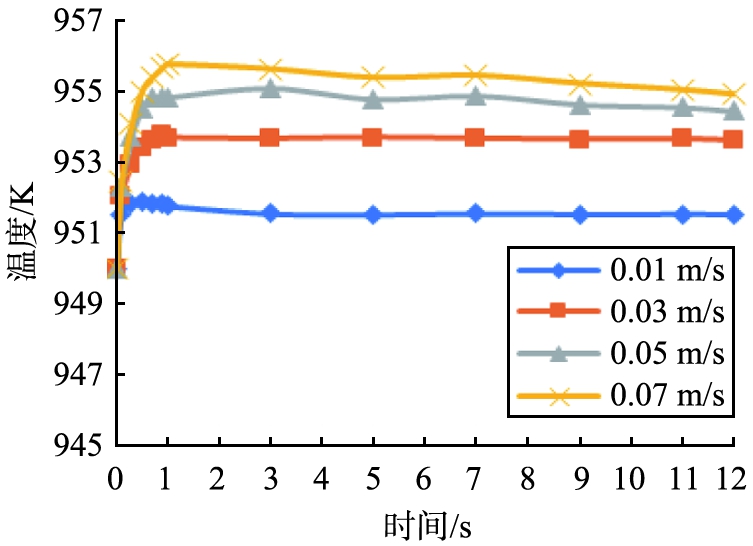
图4 再生催化剂颗粒的平均温度随时间的变化
Fig.4 Average temperature of catalyst particles in regenerator changed with time
2.3 气体组分分析
DMTO催化剂再生反应过程中，不同进气气速条件下气体组分随时间的变化如图5所示。随着催化剂再生反应的进行，CO和CO2的含量在逐渐增加，而O2的含量在减少。
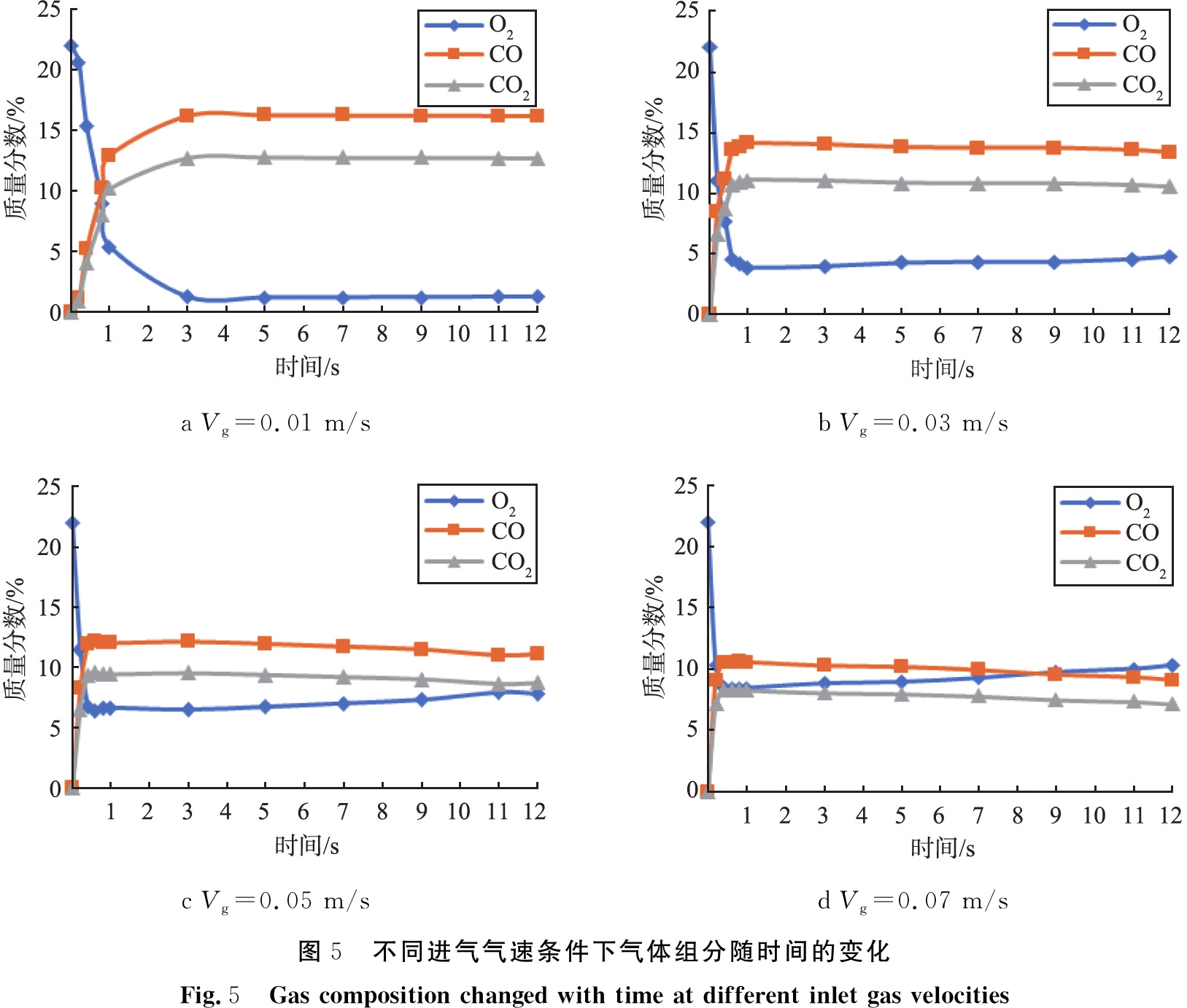
a Vg=0.01 m/sb Vg=0.03 m/sc Vg=0.05 m/sd Vg=0.07 m/s图5 不同进气气速条件下气体组分随时间的变化Fig.5 Gas composition changed with time at different inlet gas velocities
由图5a可知，进气气速为0.01 m/s时，反应时间约至3 s时，气体组分达到平衡与稳定。 由图5b、5c、5d可知，随着进气气速的增加，达到平衡状态所需的时间也在缩短，当进气气速为0.07 m/s时，气体组分瞬间达到平衡状态，这是由于进气气速提高时，气体组分中O2增加而CO和CO2减少。 尤其当进气气速大于0.05 m/s时，气体组分达到平衡后O2含量反而在逐步增加，其原因在于，对该积碳燃烧反应模型而言，进气气速为0.05 m/s时已经属于富氧燃烧，O2浓度处于饱和状态。 进气气速达到0.07 m/s时，可以更加直观地看到O2含量增大。同时，气体组分中积碳燃烧的产物CO和CO2的生成始终保持平衡状态，n(CO) ∶n(CO2)维持在2 ∶1左右，与理论数据相吻合。
2.4 再生催化剂颗粒的积碳分布
不同进气气速条件下的催化剂颗粒的积碳分布如图6所示。 由图6可以看出，随着进气气速的增大，在催化剂再生器的积碳燃烧反应中，再生催化剂颗粒积碳量的分布由宽变窄，说明气速的增大使得再生催化剂颗粒在再生器中的反应趋于均匀，颗粒流动的不均匀性在减弱。 随着进气气速的增大，气泡的扰动作用使各个床层的催化剂颗粒反应均衡，也说明了颗粒整体的流化状态均匀。
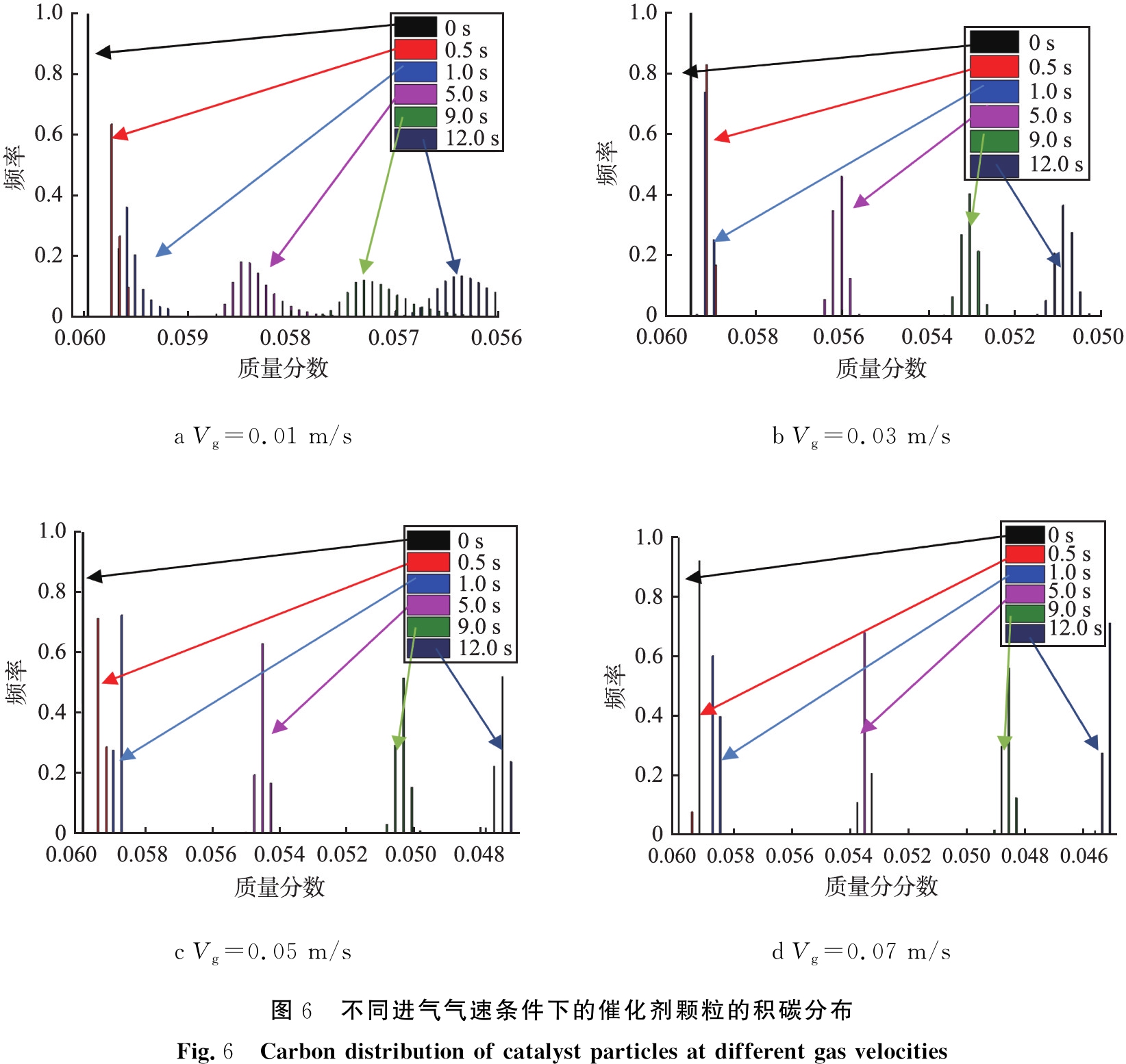
a Vg=0.01 m/sb Vg=0.03 m/sc Vg=0.05 m/sd Vg=0.07 m/s图6 不同进气气速条件下的催化剂颗粒的积碳分布Fig.6 Carbon distribution of catalyst particles at different gas velocities
为了进一步观察再生器中催化剂颗粒的积碳分布情况，进气气速为0.03 m/s时的前1 s的再生反应情况的数据进行细化扩展，再生催化剂的积碳分布如图7所示。
由图7可以看出，再生催化剂颗粒的积碳分布随时间变化而越来越宽化，说明从单颗粒角度来看，催化剂颗粒的积碳量在再生器中各处的反应并不均衡，原因在于颗粒的流动在一定程度存在不均匀性，或者颗粒所处的位置环境不同造成的。
结合图6来看，这种局部的不均匀性对于反应器中的催化剂颗粒整体而言影响非常小。
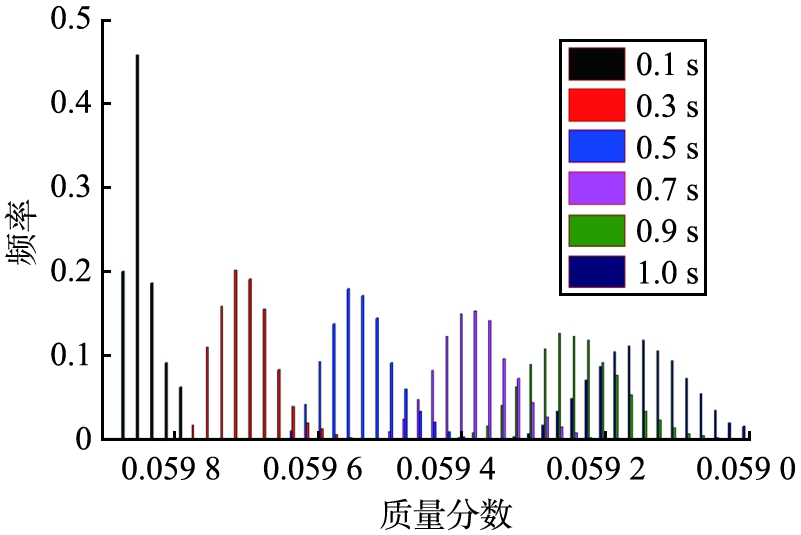
图7 进气气速为0.03 m/s时 前1 s再生催化剂的积碳分布
Fig.7 Carbon deposition distribution of regeneration catalyst in the first 1 when inlet gas velocity is 0.03 m/s
3 结论
将催化剂再生反应动力学耦合到了DEM模型，采用CFD-DEM模型对DMTO流化床再生过程进行了数值模拟，考虑了气-固相中颗粒流动、传热传质以及催化剂非均相反应的影响，构建了催化剂再生反应的数值模拟方法，研究了不同进气气速对DMTO催化剂再生反应过程的影响。结论如下：
1)随着进气气速的增大，再生催化剂颗粒的流化速度加快。
2)再生催化剂的积碳量随着时间增加而减小，随进气气速的增大而减小速率加快；催化剂密度随反应时间的增加而略有下降。
3)随着进气气速的增大，再生反应达到平衡状态所需的时间会大幅缩短；当进气气速大于0.05 m/s时，氧气可以很快达到饱和。
4)随着进气气速的增大，再生催化剂颗粒积碳分布由宽变窄，颗粒整体的流化状态趋于均匀。
可以预期，在实际的DMTO工业系统中，由于进气气速、反应器尺寸以及催化剂循环等的影响，再生器和反应器内的积碳分布将会受介观尺度气-固两相不均匀结构(如气泡、颗粒聚团等)的影响。本文中的研究成果将为研究介观尺度结构对催化剂的积碳分布的影响提供了参考。
[1]ZHAO Y, LI H, YE M, et al. 3D numerical simulation of a large scale MTO fluidized bed reactor[J]. Industrial and Engineering Chemistry Research, 2013, 52(33): 11354-11364.
[2]HAW J F, SONG W G, MARCUS D M, et al. The mechanism of methanol to hydrocarbon catalysis[J]. Accounts of Chemical Research, 2003, 36(5): 317-26.
[3]CUNDALL P A, STRACK O D L. Discussion: a discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47-65.
[4]GENG Y M, CHE D F. An extended DEM-CFD model for char combustion in a bubbling fluidized bed combustor of inert sand[J]. Chemical Engineering Science, 2011, 66(2): 207-219.
[5]ZHOU H, FLAMANT G, GAUTHIER D. DEM-LES simulation of coal combustion in a bubbling fluidized bed: part II: coal combustion at the particle level[J]. Chemical Engineering Science, 2004, 59(20): 4205-4215.
[6]SYAMLAL M, ROGERS W, OBRIEN T J. MFIX documentation theory guide[M]. Morgantown: National Technical Information Service, 1993.
[7]TSUOY Y P, GIDASPOW D. Computation of flow patterns in circulating fluidized beds[J]. AICHE Journal, 1990, 36(6): 885-896.
[8]SYAMLAL M, O’BRIEN T J. Computer simulation of bubbles in a fluidized bed[J]. AlHE Symposium Series, 1989, 85: 22-31.
[9]LU H L, GIDASPOW D, BOUILLARD J, et al. Hydrodynamic simulation of gas-solid flow in a riser using kinetic theory of granular flow[J]. Chemical Engineering Journal, 2003, 95(1/2/3): 1-13.
[10]DAHL I M, MOSTAD H, AKPORIAYE D, et al. Structural and chemical influences on the MTO reaction: a comparison of chabazite and SAPO-34 as MTO catalysts[J]. Microporous and Mesoporous Materials, 1999, 29(1): 185-190.
[11]AGUAYO A T, S
NCHEZ D C A E, GAYUBO A G, et al. Deactivation by coke of a catalyst based on a SAPO-34 in the transformation of methanol into olefins[J]. Journal of Chemical Technology and Biotechnology, 1999, 74(4): 315-321.
[12]宁英辉, 孙维金, 张飞飞, 等. 甲醇制烯烃催化剂再生动力学研究[J]. 能源化工, 2016, 37(4): 49-53.
[13]BURCAT A, RUSCIC B. Third millenium ideal gas and condensed phase thermochemical database for combustion with updates from active thermochemical tables[J]. Journal of Chemical Information and Modeling, 2005, 45(3): 572-580.
[14]刘楷. MTO反应催化剂再生动力学模型的研究[D]. 上海: 华东理工大学, 2014.