近些年来，由于鼓泡流化床具备良好的混合及传热、 传质特性，在化学工业中得到了广泛应用。其突出的传递特性主要来自于流化床内气体与固体的相互作用，通过气泡不断地破碎和聚并，极大地扰动了颗粒床层，达到强化传递的作用[1]。而气体进入流化床主要通过设置流体分布板。流体分布板是流化床装置的基本部件之一[2]，作用主要有4个：1)气流分布均匀， 避免出现滞留区[3]； 2)加强空气通过分布板后的扰动，强化气体与颗粒的掺混[4]； 3)阻力适合[5-6]； 4)能支撑床料[7]。分布器设计是否合理，直接关系到流态化操作的成败。
根据分布板的不同结构，流化床的进风方式也有所不同，但是总的原则是保证气体均匀进入床层，避免局部出现死区，影响气体与颗粒间的传质、传热过程[8]。以往研究者主要集中在分布板对流态化的特性研究[9]以及相关的数值模拟[10-15]。田昊一等[9]考察了4种分布板的性能，并与固定床的热模实验结果进行了比较。结果表明：随着气速的增加，直孔分布板的压降以二次函数的形式增大，斜孔分布板则呈现一次函数关系。 另外， 圆面斜孔分布板的流化质量最好， 而圆面斜孔分布板下的还原率较高。 王霄等[16]通过流化床反应器冷态实验， 比较了3种孔径(1、 2、 3 mm)分布板对流态化特性的影响。 结果显示： 孔径越小， 压降越大， 临界流化气速越低， 床层膨胀越显著， 且床层颗粒混合得更好。 Dong等[17]在直径为0.14 m、 高度为1.6 m的流化床内考察3种不同开孔率分布板的流化特性， 结果发现， 气泡尺寸随开孔率减小而增大， 而且颗粒的返混更剧烈。王文仲[18]进行了分布板阻力特性冷态实验和水模实验。 结果表明， 分布板阻力与风帽阻力较一致， 而在风帽结构相同的情况下， 随着风帽数量的增加， 阻力系数减小。 另外， 风帽的布置方式对阻力系数也有一定影响。 Luo等[19]研究分布板结构参数对密相流化床的影响。 结果显示， 分布板压降越大， 流化床压力波动越小， 流化质量越高。
由于气-固流动和混合的复杂性， 实验方法很难对分布板附近的多相流动进行详细分析， 而借助日益成熟的数值模拟技术可以获得较为准确的流场信息。 魏新利等[20]利用FLUENT软件， 模拟了不同气孔尺寸和布置方式下气体的局部流动和轴向压降， 发现气孔呈现三角形布置能有效改善气流的稳定性。 Yogendrasasidhar等[10]基于ASPEN PLUS软件考察了气孔大小、气孔数量及开孔率对流化床干燥特性的影响。Lu等[21]采用双流体模型，对比了不同分布板下射流速度以及气孔间隙对焚烧炉颗粒流化特性的影响。上述相关研究大部分都集中在水平分布板，对斜分布板特性的研究工作较少[22]。
鉴于此， 本文中采用烧结丝网作为分布板并倾斜放置， 研究在该结构下气体通过分布板进入床层的流动状况以及颗粒流化特性。 同时， 采用欧拉-欧拉双流体模型进行模拟分析， 保持表观气速一定， 考察该烧结丝网的不同压降对流化质量的影响。
1 实验系统及数值模拟方法
1.1 实验系统
鼓泡流化床实验系统示意图如图1所示， 主要由空压机、 缓冲罐、 压力表、 质量流量计和流化床组成。
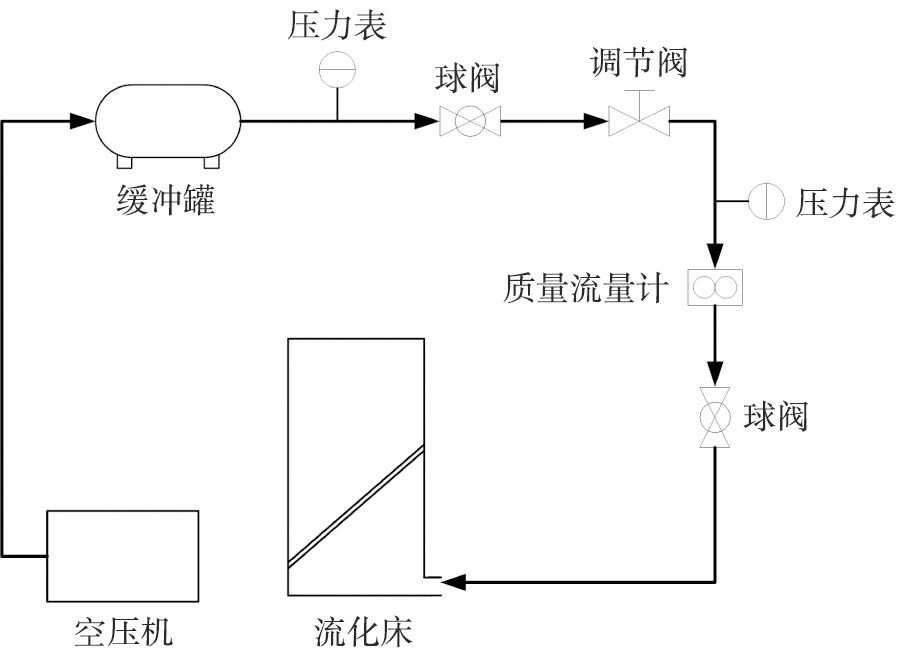
图1 流化床实验系统示意图
Fig.1 Schematic diagram of fluidized bed system
流化床的结构示意图如图2所示， 流化床高度为550 mm， 长度为300 mm， 宽度为70 mm, 其中斜分布板与水平面呈45 °。 采用空气作为流化气体， 颗粒介质选用玻璃微珠。 气体从底部一侧进入腔体， 通过斜分布板流化床层颗粒， 图中红色圆点位置标记为坐标原点(0,0)。 操作条件和物料特性如表1所示。
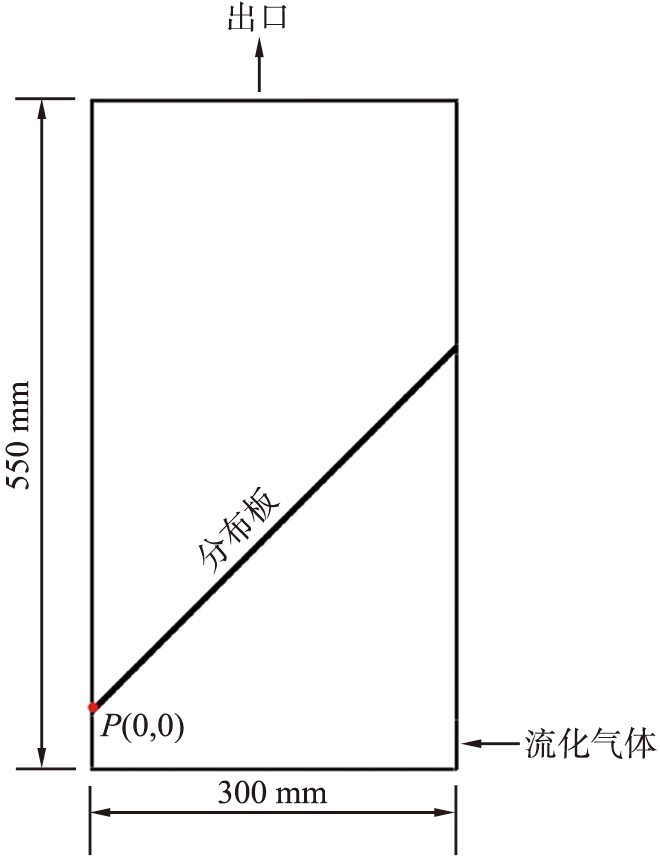
图2 流化床结构示意图
Fig.2 Schematic diagram of fluidized bed
表1 实验操作条件和物料特性
Tab.1 Operating conditions and materials property
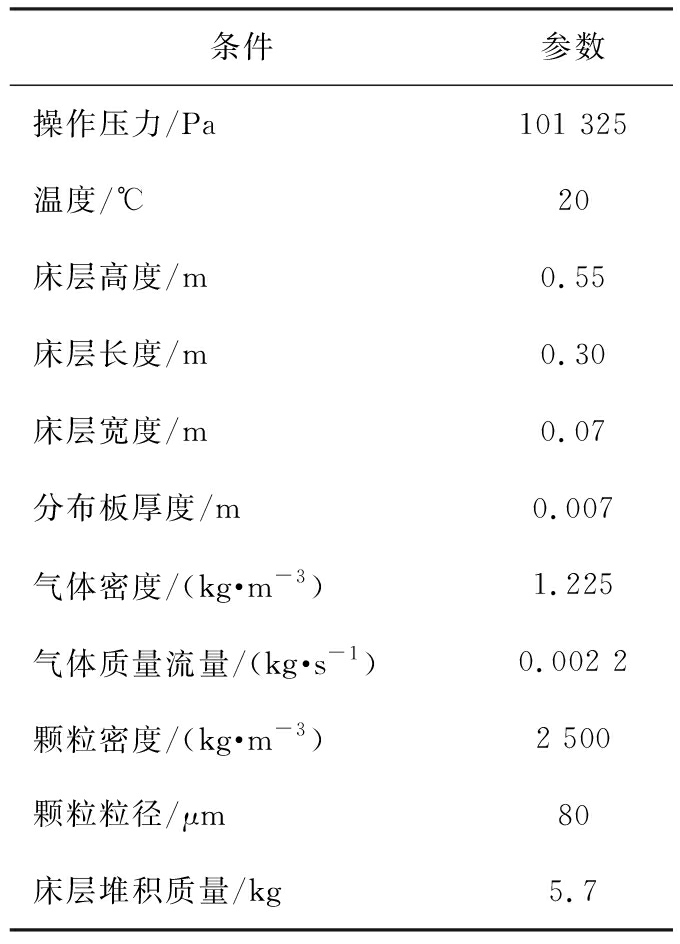
条件参数操作压力/Pa101 325温度/℃20床层高度/m0.55床层长度/m0.30床层宽度/m0.07分布板厚度/m0.007气体密度/(kg·m-3)1.225气体质量流量/(kg·s-1)0.002 2颗粒密度/(kg·m-3)2 500颗粒粒径/μm80床层堆积质量/kg5.7
1.2 数值模拟方法
应用欧拉-欧拉双流体模型模拟该流化床工况， 气体采用层流模型且不可压， 气-固曳力模型选用Gidaspow模型[23]， 固相颗粒的本构关系可以用颗粒动理论封闭[24-25]， 具体控制方程和本构关系可参考文献[26]。 另外， 鼓泡床中颗粒间的接触作用力较为显著， 需要引入摩擦应力的影响[27-28]， 本工作采用Johnson等的摩擦黏度模型和基于颗粒动理论得到的摩擦应力模型。 由于采用烧结丝网作为斜分布板， 其材料特性使得流体在分布板内部以黏性流动为主， 流动规律可以采用达西定律描述[27]。
(1)
式中：Δp为压降；e为分布板厚度；Q为气体体积流量； μg为气体动力黏度；A为分布板横截面积；Ψ为黏性渗透系数。为了工程使用方便，实际测量中只提供相对透气系数，根据公式(1)变换得到
(2)
相对渗透系数
(3)
根据厂家提供的数据和标定，实验中Kg为2 300 m3/(h·kPa·m2)。
由于烧结丝网结构复杂，网格构体难度较大，根据Depypere等[15]和Li等[28]的工作，多孔介质模型可以合理描述分布板的作用，因此，可以采用多孔介质模型代替[29]。
(4)
式中：
表示流体与多孔介质作用的动量源项，由右边第1项的黏性阻力项和第2项的惯性阻力项组成，其中1/α为黏性阻力系数，C为惯性阻力系数。由于烧结丝网内尺寸较小，以黏性阻力为主，所以可以忽略惯性阻力，即
(5)
对比公式(1)可以得到
(6)
在分布板工艺参数下，根据式(6)得到多孔介质模型在竖直方向上的黏性阻力系数为1.20×1010 m-2，假设其他方向的阻力系数为0。
2 结果与讨论
2.1 模拟结果与实验工况对比
根据表1的工艺参数进行实验，首先在床内填上大概5.0 kg的玻璃微珠，保证颗粒能够覆盖斜分布板，接着通入设定量的流化气，采用高速摄像机拍摄，获得如图3a所示的流化床内颗粒运动状态。由图可以发现，床内大多数颗粒没有流化起来，只有初始床层较低的一侧有气泡翻滚，迫使部分颗粒脱离床层流化起来。从图3b局部放大图来看，临近分布板区域存在气穴(红色虚线方框)，但是气体并没有垂直向上，而是选择从右侧床层最矮，阻力较小的路径流出。
为了确定合理的网格数，对比了网格数分别为8 575、 33 000、 128 800这3种情况下的模拟结果。沿分布板上方中心线位置的时均颗粒体积分数如图4所示。由图可以看出，在小于0.2 m区域，床层基本处于固定床状态，颗粒体积分数保持不变， 而大于0.2 m后， 开始出现流化现象， 颗粒体积分数降低， 3种网格设置得到的临界点位置基本一致。而网格越密，预测的颗粒体积分数相对越低，中间网格数给出的结果与细网格结果相对比较接近，为了兼顾计算效率和精度，选择中间网格数作为后面计算的网格设置。
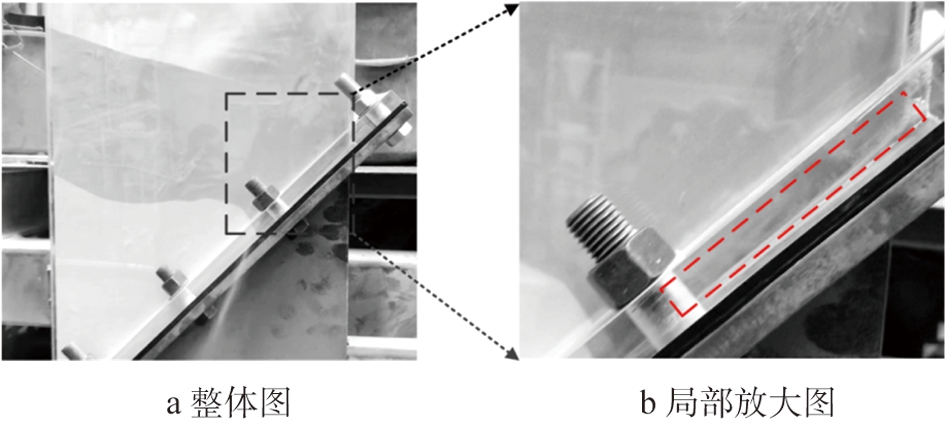
图3 流化床内颗粒的运动状态
Fig.3 Transient particle flow in fluidized bed
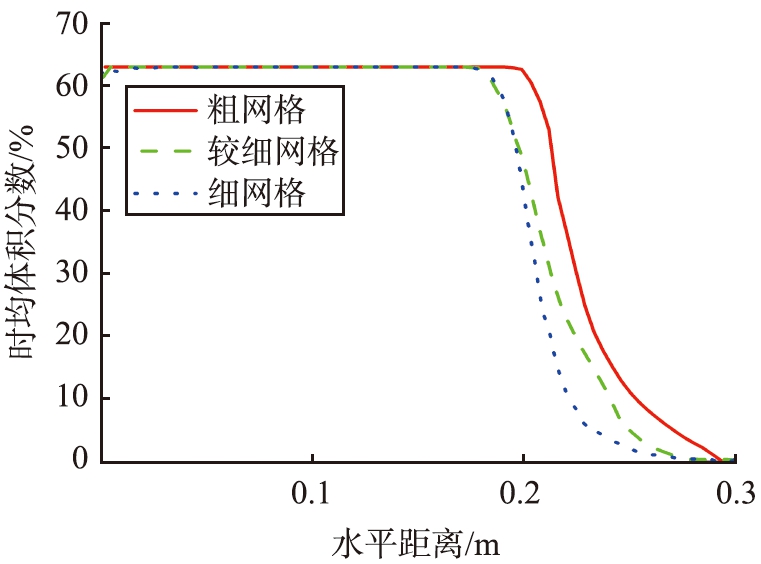
图4 不同网格密度下分布板周围颗粒的时均体积分数分布
Fig.4 Predicted averaged solids hold-up along distributor with different mesh grids
图5为模拟得到的瞬态颗粒体积分数分布云图。从定性上来看，双流体模型能给出合理的流化现象，即床层整体没有流化起来，只有床层阻力最小的右侧局部位置出现气泡和流化现象。究其原因，有可能是斜分布板的设置造成分布板上方的床层高度不一致，进而使得气体流经局部位置流化床层的压降有较大差别， 床层较高的左边所需压降比右边高约4 kPa， 而分布板的平均压降仅为0.12 kPa， 所以该分布板基本不具备整流作用，出现了“短路”现象。从图6给出的局部气体速度矢量图可以明显看出，气体选择压降较低的路径流动。
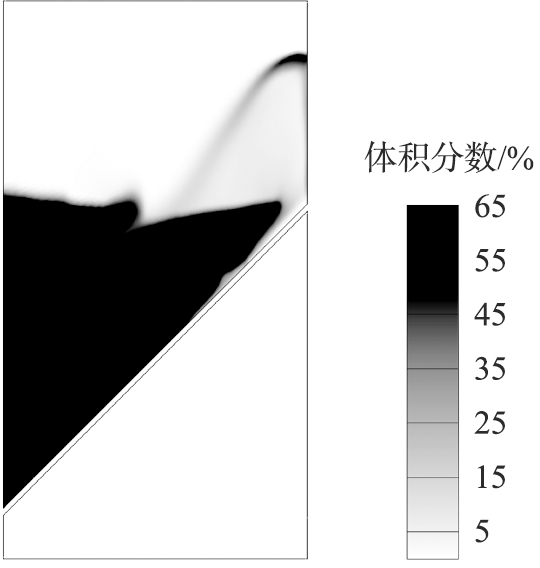
图5 模拟得到的颗粒体积分数瞬态云图
Fig.5 Predicted transient solids concentration
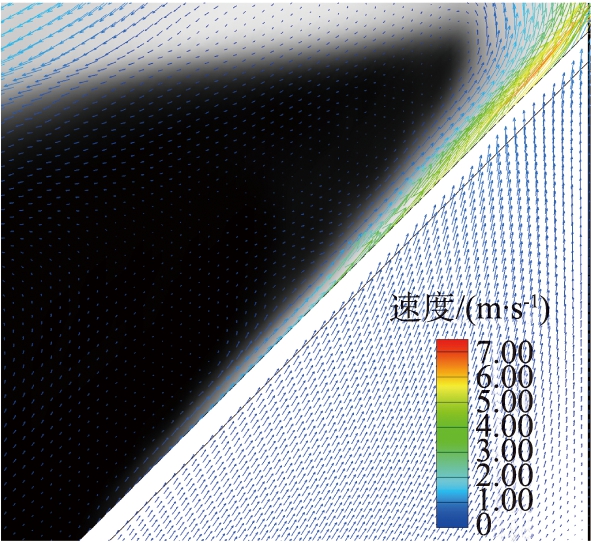
图6 模拟得到的分布板局部气体速度矢量
Fig.6 Predicted gas velocity vector near distributor
2.2 分布板压降的影响
通过模拟和实验对比，可以确定模拟结果的合理性。为了考察分布板特性对床层颗粒流化的影响，选择分布板的压降作为研究变量。相应地，可通过修改多孔介质模型参数改变分布板压降。将黏性阻力系数分别设置为4.80×1010、 1.92×1011 m-2，对应的压降为0.48、 1.92 kPa。
图7给出了不同分布板压降下颗粒体积分数的时均云图。由图可以发现，随着压降从0.12 kPa增大到0.48 kPa，分布板附近的气穴变大，而随着压降继续增大至1.92 kPa，气穴的起始点向左端靠近，并且整体床层膨胀更加明显，说明增大分布板的压降有助于斜分布板床层颗粒的均匀流化。
通过定量比较不同分布板压降下床层的轴向颗粒体积分数分布， 可以间接对比不同分布板下的膨胀程度， 图8给出了不同分布板压降下床层横截面颗粒时均体积分数随床层高度的变化趋势。 从图中可以看出， 当分布板压降比较小时， 颗粒体积分数的分布呈现“S”型分布， h=0.35 m处的颗粒体积分数约为3%。 而当分布板压降增大时， 上部稀相区域颗粒体积分数整体增大， 说明床层有少许膨胀。 当压降增大至1.92 kPa时， 轴向颗粒体积分数分布从“S”型向“C”分布转变， 且在h=0.48 m处的颗粒体积分数约为4%， 说明床层膨胀程度加剧。 而起始流化位置的变化能从侧面反映出流化质量。
为了清晰比较， 将邻近分布板上表面的颗粒体积分数数据读取出来， 得到不同分布板压降下沿分布板不同水平距离的颗粒局部体积分数变化趋势， 见图9。 当压降较小时， 起始流化位置为水平位置x=0.20 m， 该位置左边基本没有流化， 超过该位置， 颗粒体积分数逐渐减小， 说明形成了气穴。 当压降增大， 起始流化位置向左偏移， 在x=0.16 m处开始流化。 进一步增大分布板压降， 起始流化位置变为x=0.10 m，使得流化区域增大。 说明增大分布板压降有助于流化斜分布板流化床， 弱化了不同床层高度带来的短路不利因素。
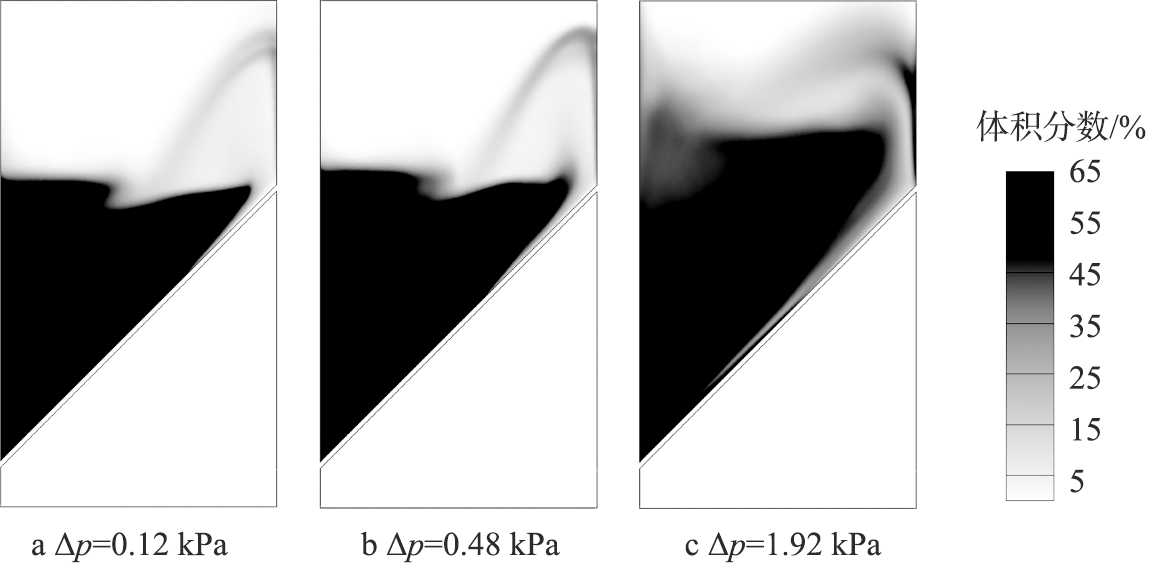
图7 不同分布板压降下颗粒的时均体积分数云图
Fig.7 Time-averaged solids hold-up under different pressure drop through distributor
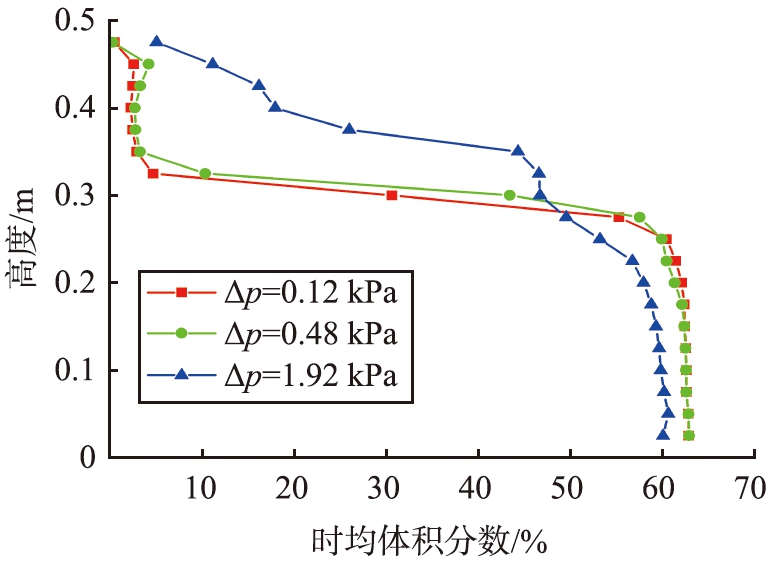
图8 不同分布板压降下轴向颗粒的体积分数分布
Fig.8 Axial solids hold-up under different pressure drop through distributor
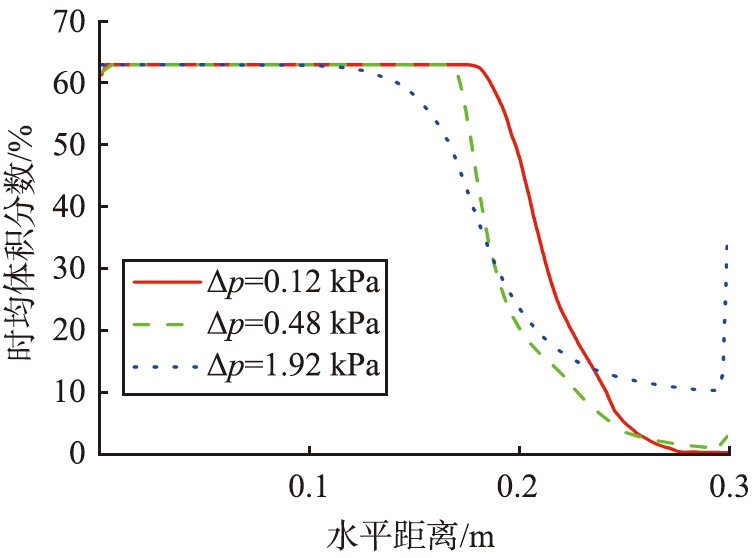
图9 不同分布板压降下周围颗粒的体积分数分布
Fig.9 Solids hold-up along distributor under different pressure drop through distributor
2.3 曳力模型的影响
流化床中曳力模型对流化床的预测有较大影响[30-31]，但鲜有文献考察在斜分布板下不同曳力模型对鼓泡床气固流动状态的影响。模拟工况条件不变，通过修改双流体模型中的气-固曳力模型，可以得到不同曳力模型下的颗粒体积分数预测结果。
在不同曳力模型下， 床层的颗粒时均体积分数分布云图如图10所示。 在本研究中选择了4种曳力模型进行对比分析， 包括Wen & Yu模型[32]、 Gidaspow模型[23]、 Syamlal & O’Brien模型[33]和Huilin & Gidaspow模型[34]。直观上，Gidaspow模型、Wen & Yu模型和Huilin & Gidaspow模型预测的床层高度比Syamlal & O’Brien模型预测的要高。为了定量对比曳力模型的影响，在不同曳力模型下预测得到分布板附近颗粒体积分数随水平距离的变化趋势以及轴向颗粒体积分数分布规律。
图11为不同曳力模型下邻近分布板上方的颗粒体积分数随水平距离的变化。从图中可知，4种模型对起始流化位置的预测基本一致，在x≈0.2 m处位置开始流化，随后Gidaspow曳力模型预测的颗粒体积分数相对另3种模型偏大。
不同曳力模型下床层轴向不同高度的颗粒体积分数分布如图12所示。在高度小于0.2 m范围内，4种模型给出的预测基本一致；当高度大于0.2 m，相对Syamlal & O’Brien模型，其他3个模型预测的颗粒体积分数偏大，说明床层的膨胀程度偏大。
图10 不同曳力模型下颗粒的体积分数时均云图
Fig.10 Time-averaged solids concentration under different drag models
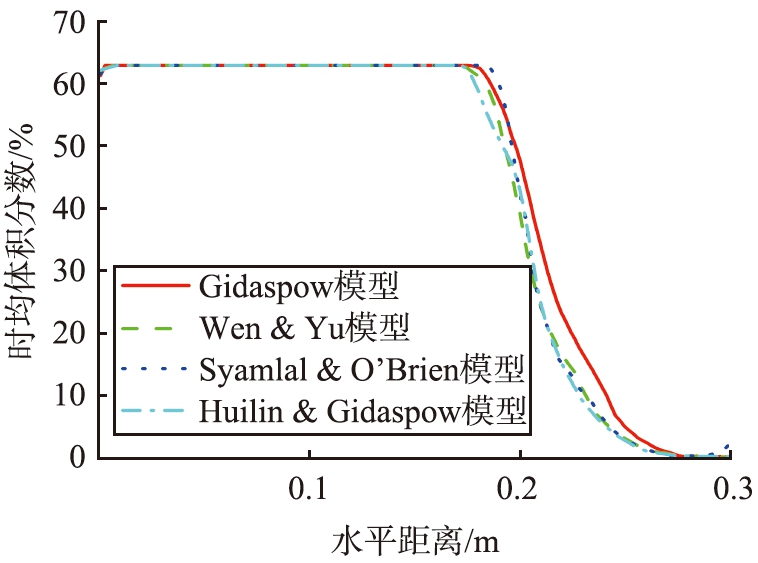
图11 不同曳力模型下分布板附近颗粒的体积分数分布
Fig.11 Solids hold-up near distributor under different drag models
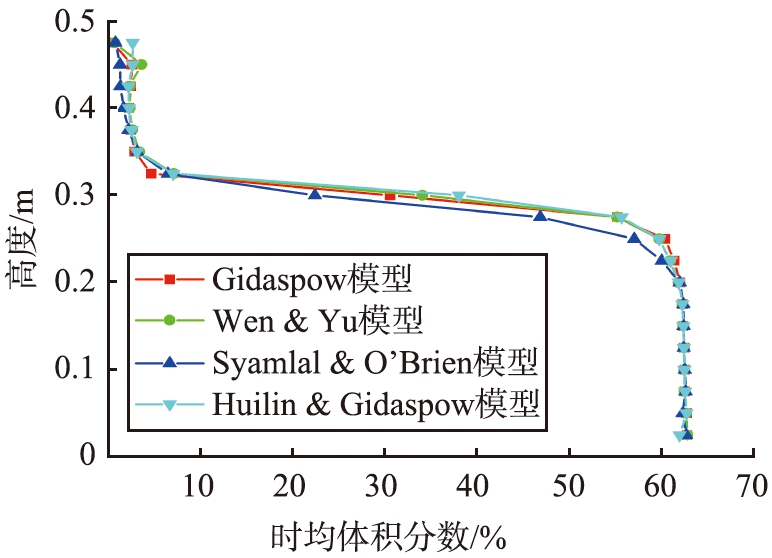
图12 不同曳力模型下轴向颗粒的体积分数分布
Fig.12 Axial solids hold-up under different drag models
3 结论与讨论
本文中分别从实验和数值模拟研究了斜分布板对鼓泡床流态化特性的影响。斜分布板的存在使得床层高度呈现出不一致，导致局部气体流化的阻力有较大差别，而流化气体通过分布板的压降占流化整个床层所需压降的比例仅约5%，基本不具备整流作用，因此出现了“短路”现象。而采用双流体模型描述气固流动， 同时将分布板简化成多孔介质，通过数值模拟可以很好地捕捉到斜分布板下的“短路”现象。
改变多孔介质阻力系数，提高分布板的压降，能使斜分布板上的起始流化位置向较高床层的水平位置偏移，弱化了短路现象带来的局部流化不利影响，使得床层较为均匀的膨胀。另外，对比分析了不同曳力模型下的流化特性，4个模型给出的起始流化位置基本一致，但Syamlal & O’Brien模型给出的床层膨胀程度相对偏小。
[1]KUNII D, LEVENSPIEL O. Phase interchange coefficients in bubbling fluidized beds[J]. J Chem Eng JPN, 1991, 24(1): 138-141.
[2]SHUKRIE A, ANUAR S, OUMER A. Air distributor designs for fluidized bed combustors: a review[J]. Engineering, Technology & Applied Science Research, 2016, 6(3): 1029-1034.
[3]S
NCHEZ-PRIETO J, SORIA-VERDUGO A, BRIONGOS J, et al. Stagnant regions estimation in fluidized beds from bed surface observation[J]. Chemical Engineering Journal, 2015, 281:109-118.
[4]SNCHEZ-DELGADO S, MARUGN-CRUZ C, SERRANO D, et al. Distributor performance in a bubbling fluidized bed: effects of multiple gas inlet jet and bubble generation[J]. Chemical Eng-ineering Science, 2019, 195:367-380.
[5]SATHIYAMOORTHY D, RAO C S. The choice of distributor to bed pressure drop ratio in gas fluidised beds[J]. Powder Technology, 1981, 30(2): 139-143.
[6]SNCHEZ-PRIETO J, SORIA-VERDUGO A, BRIONGOS J, et al. The effect of temperature on the distributor design in bubbling fluidized beds[J]. Powder Technology, 2014, 261: 176-184.
[7]范金龙. 大型循环流化床风帽阻力特性和布风板布风均匀性研究[D]. 北京：中国科学院研究生院(工程热物理研究所), 2015.
[8]郭慕孙, 李洪钟. 流态化手册[M]. 北京：化学工业出版社, 2008: 584-604.
[9]田昊一, 康明雄, 吴元欣, 等. 布风板对磷矿混合颗粒流化特性与还原反应的影响[J]. 化学工程, 2012, 40(12): 48-52.
[10]YOGENDRASASIDHAR D, SRINIVAS G, SETTY Y P. Effect of distributor on performance of a continuous fluidized bed dryer[J]. Heat and Mass Transfer, 2018, 54(3): 641-649.
[11]WARD J, GARWOOD R, BOWEN R, et al. Design and development of an improved air distributor for a large coal-fired fluidised bed combustor[C]//American Society of Mechanical Engineers. International Mechanical Engineering Congress and Exposition：2008. New York: American Society of Mechanical Engineers Digital Collection, 2008: 545-552.
[12]DEPYPERE F, PIETERS J G, DEWETTINCK K. CFD analysis of air distribution in fluidised bed equipment[J]. Powder Technology, 2004, 145(3): 176-189.
[13]AKBARI V, BORHANI T, GODINI H, et al. Model-based analysis of the impact of the distributor on the hydrodynamic performance of industrial polydisperse gas phase fluidized bed polymerization reactors[J]. Powder Technology, 2014, 267: 398-411.
[14]OSTERMEIER P, VANDERSICKEL A, GLEIS S, et al. Three dimensional multi fluid modeling of Geldart B bubbling fluidized bed with complex inlet geometries[J]. Powder Technology, 2017, 312:89-102.
[15]AKBARI V, NEJAD G, ARAMESH R, et al. Evaluation of hydrodynamic behavior of the perforated gas distributor of industrial gas phase polymerization reactor using CFD-PBM coupled model[J]. Computers & Chemical Engineering, 2015, 82: 344-361.
[16]王霄, 司慧, 郭晓慧, 等. 布风板孔径对流化特性影响的数值模拟及试验[J]. 科技导报, 2015, 33(3): 43-48.
[17]DONG S, CAO C, SI C, et al. Effect of perforated ratios of distributor on the fluidization characteristics in a gas-solid fluidized bed[J]. Industrial & Engineering Chemistry Research, 2009, 48(1): 517-527.
[18]王文仲. 循环流化床锅炉风帽及布风板的实验与数值模拟研究[D]. 北京：中国科学院研究生院(工程热物理研究所), 2009.
[19]LUO Z, ZHAO Y, CHEN Q, et al. Effect of gas distributor on performance of dense phase high density fluidized bed for separation[J]. International Journal of Mineral Processing, 2004, 74: 337-341.
[20]魏新利, 马新辉. 应用Fluent软件研究流化床中布风板结构[J]. 能源工程, 2006(2): 15-19.
[21]LU H L, ZHAO Y H, DING J M, et al. Numerical modeling of gas tubular distributors in bubbling fluidized-bed incinerators[J]. Industrial & Engineering Chemistry Research, 2006, 45(20): 6818-6827.
[22]张宏丹, 李巍, 何玉荣, 等. 倾斜布风板对流化床内颗粒流化特性影响的研究[J]. 节能技术, 2005, 23(2): 116-117.
[23]GIDASPOW D. Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. New York: Academic Press, 1994: 35-37.
[24]DREW D A. Mathematical modeling of two-phase flow[J]. Annual Review of Fluid Mechanics, 1983, 15(1): 261-291.
[25]ANDERSON T B, JACKSON R. Fluid mechanical description of fluidized beds. equations of motion[J]. Ind Eng Chem Fund, 1967, 6(4): 527-539.
[26]VAN WACHEM B G M, SCHOUTEN J C, VAN DEN BLEEK C M, et al. Comparative analysis of CFD models of dense gas-solid systems[J]. Aiche Journal, 2001, 47(5): 1035-1051.
[27]奚正平, 汤慧萍, 张健, 等. 烧结金属多孔材料[M]. 北京：冶金工业出版社, 2009:114-121.
[28]LI B, LIU W, KONG X W, et al. A novel simplified distributor model of fluidized bed based on the porous media theory[J]. Applied Mechanics & Materials, 2014, 496:715-718.
[29]FLUENT A. Ansys fluent user’s guide[M]. Pittsburgh：ANSYS Inc, 2013: 223-226.
[30]WANG J, LIU Y. EMMS-based eulerian simulation on the hydrodynamics of a bubbling fluidized bed with FCC particles[J]. Powder Technology, 2010, 197(3): 241-246.
[31]SHI Z, WANG W, LI J. A bubble-based EMMS model for gas-solid bubbling fluidization[J]. Chemical Engineering Science, 2011, 66(22): 5541-5555.
[32]WEN C Y, YU Y H. Mechanics of fluidization[J]. Chemical Eng-ineering Progress Symposium, 1966, 62: 100-113.
[33]SYAMLAL M, ROGERS W, O’BRIEN T J. MFIX documentation: theory guide[M]. Morgantown：National Energy Technology Laboratory, 1993: 9-11.
[34]HUILIN L, GIDASPOW D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures[J]. Chemical Engineering Science, 2003, 58(16): 3777-3792.