石英砂在地球岩石圈中分布广泛,质量分数约为85%,是主要的造岩矿物之一,属于重要的非金属矿,应用范围非常之广,主要应用领域有玻璃、陶瓷、耐火材料、水泥等。普通的石英砂中SiO2质量分数约为96%~99%,其性质稳定且纯度较高,只需通过对原矿进行粉碎、磨矿、分级或者采用简单的选矿工艺就能达到要求[1]。
物料在球磨机中的粉碎作用主要包括粉碎和研磨2个部分,在此过程中主要考察粉碎速率、 粉碎分布函数相关参数等,粉碎速率Si主要指i粒级物料经过粉碎进入下一粒级的速率,粉碎分布函数Bij和相关参数可以通过球磨机分批次磨矿实验计算得到[2-5]。 在磨机的粉碎过程中,影响因素主要有磨矿介质、 介质配比、 介质充填率、 磨矿量、 磨机类型、 磨矿方式等[6-8],其中磨矿介质是最易控制的因素之一。
钱海燕等[9]研究行星磨中研磨体大小对水泥熟料粉磨动力学的影响,结果显示,不同大小的介质对物料的粉磨均遵循一阶粉磨动力学方程;粉碎速率与介质大小呈正比例,介质大小在一定程度上影响粉碎参数。张柏林等[10]通过设定不同的介质配比,研究单一粒级的水泥熟料粉碎效率,研究结果表明,不同介质配比下物料的粉碎速率遵循一阶动力学模型;Si与大尺寸介质的个数呈正比例分布,同时介质配比会影响粉碎参数。Cuhadaroglu等[11]采用不同形状介质对3组单一粒级的物料进行磨矿试验,研究粉碎速率、粉碎分布函数参数的分布规律,结果表明,圆柱形介质的粉碎速率最大,短时间内圆柱形介质对粗颗粒的粉碎效果要优于钢球介质。在综上研究的基础上,探究介质形状对2种单一粒级石英砂给料在球磨机过程中粉碎速率、粉碎分布函数相关参数的影响,为石英砂的粉碎提供相关的实践指导。
1 试验
1.1 原料与设备
本试验选用石英砂产于宜兴市,二氧化硅质量分数99.4%,密度为2.65×103 kg/m3,含水率为0.4%(质量分数),粒度为2~4 mm,莫氏硬度为7,白色或少量黄色颗粒。试验设备见表1,介质参数见表2。
表1 试验设备
Tab.1 Test equipment
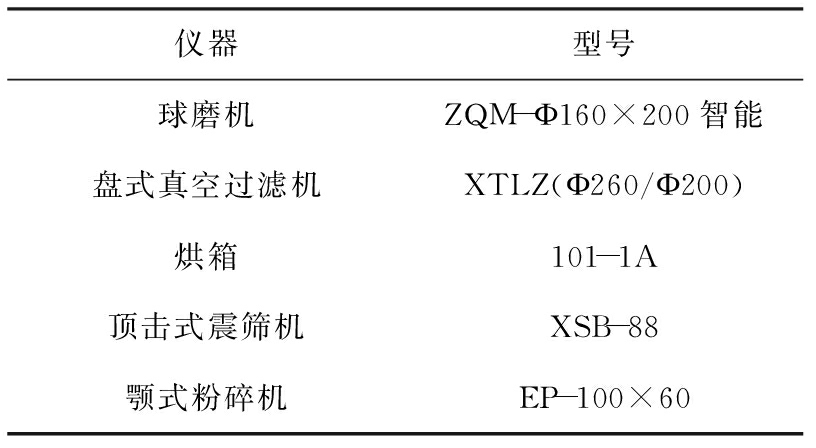
仪器型号球磨机ZQM-Ф160×200智能盘式真空过滤机XTLZ(Ф260/Ф200)烘箱101-1A顶击式震筛机XSB-88颚式粉碎机EP-100×60
表2 介质参数
Tab.2 Media parameter
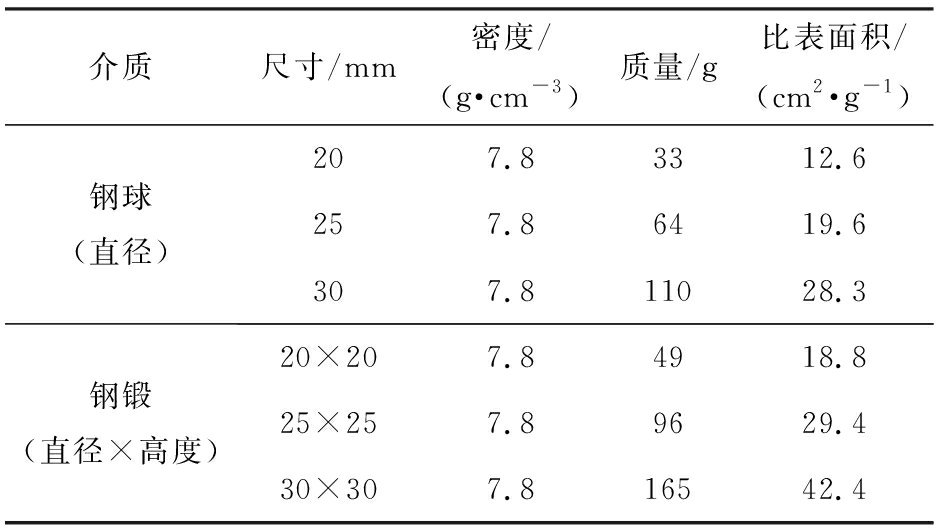
介质尺寸/mm密度/(g·cm-3)质量/g比表面积/(cm2·g-1)钢球(直径)207.83312.6257.86419.6307.811028.3钢锻(直径×高度)20×207.84918.825×257.89629.430×307.816542.4
1.2 试验方法
采用颚式粉碎机对原料进行粉碎分级,得到粒径为>2~2.36、 0.83~2 mm的物料,粉碎过程在球磨机中完成,磨机参数和试验条件见表3,磨矿时间为0.5、 1、 2、 4、 8 min,磨矿介质配比采用等表面积法[4]。
表3 试验条件
Tab.3 Test conditions
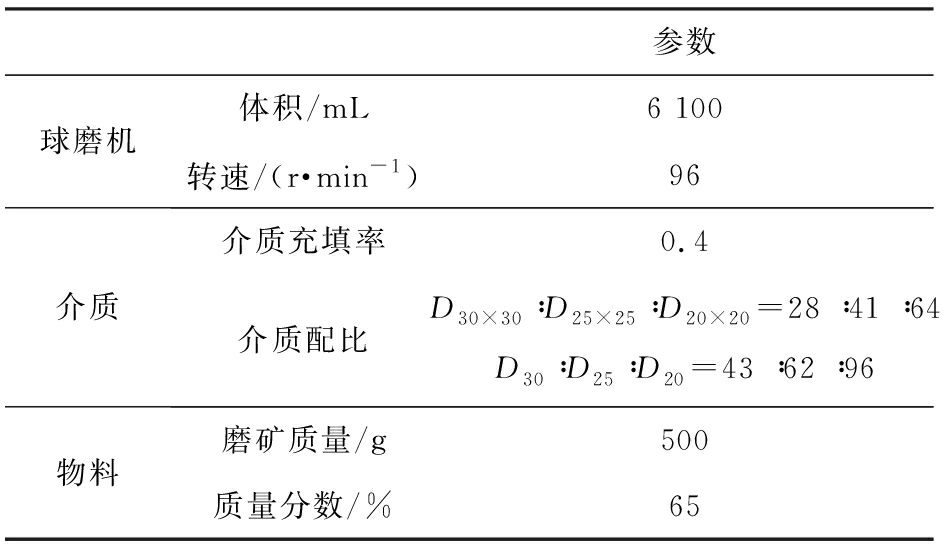
参数球磨机体积/mL6 100转速/(r·min-1)96介质介质充填率0.4介质配比D30×30 ∶D25×25 ∶D20×20=28 ∶41 ∶64D30 ∶D25 ∶D20=43 ∶62 ∶96物料磨矿质量/g500质量分数/%65
2 结果与分析
2.1 磨矿介质形状对粉碎速率的影响
单一粒级给料下,物料的粉碎速率通常遵循一阶动力学模型[12-13],因此,物料的粉碎速率方程可以表示为
wi(t)=wi(0)e-Sit
(1)
式中: wi(0)、 wi(t)表示粉碎前和粉碎t时间后i粒级物料的质量分数;Si表示该粒级物料的粉碎速率;t表示粉碎时间。
对式(1)进行推导得到:
ln(wi(t)/wi(0))=-Sit
(2)
根据公式(2)计算2组单一粒级石英砂的粉碎速率与时间的关系如图1、2所示,经过拟合计算得到不同介质形状下2种粒级石英砂的Si值见表4。
表4 不同介质形状下2种粒级石英砂的Si值
Tab.4 Values of Si two grade quartz sands under different medium shapes
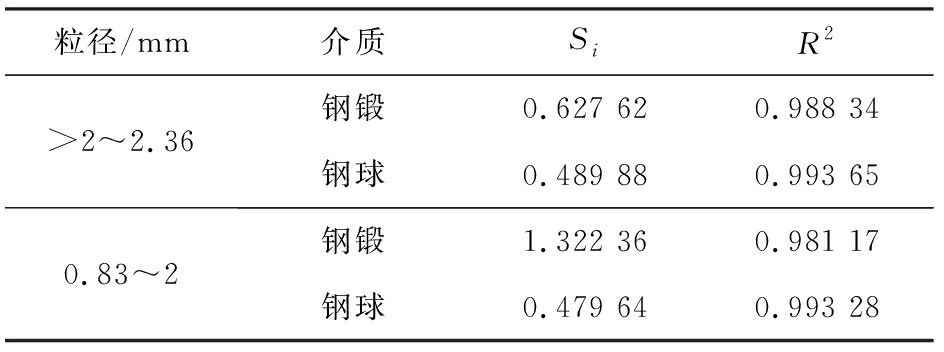
粒径/mm介质SiR2>2~2.36钢锻0.627 620.988 34钢球0.489 880.993 650.83~2钢锻1.322 360.981 17钢球0.479 640.993 28
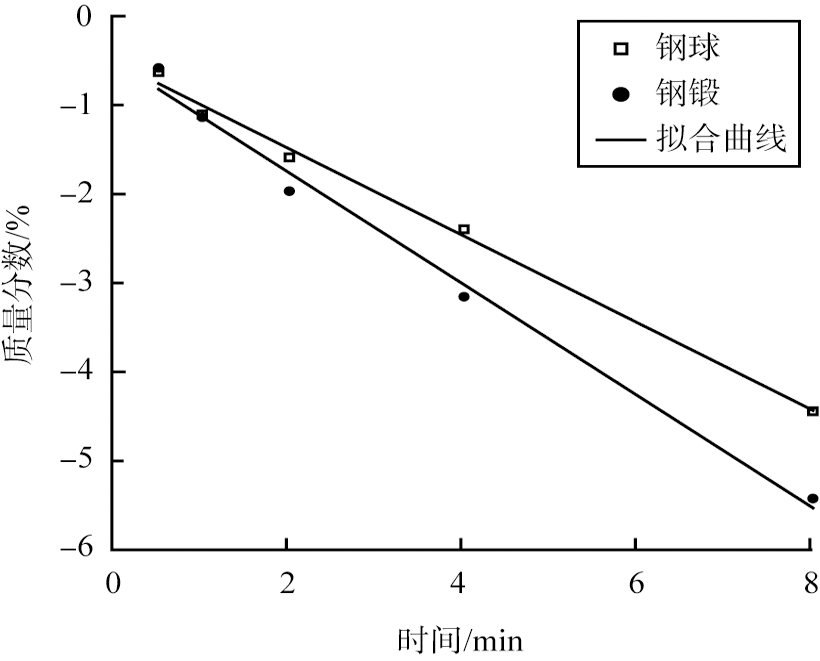
a >2~2.36 mm
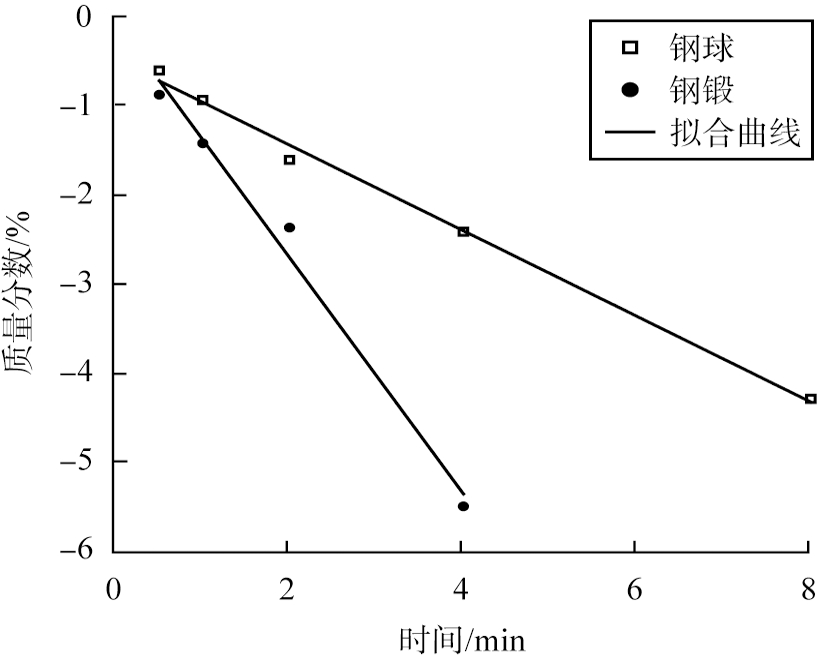
b 0.83~2 mm
图1 不同研磨介质条件下
物料的一级粉碎动力学模型图
Fig.1 First-order plots with different media for feed
从图1和表4可以得出,在不同介质下2组石英砂的粉碎速率均遵循一阶动力学模型,相关系数R2为0.981 17~0.993 65。图中钢锻介质拟合曲线斜率明显要大于钢球介质,表明钢锻介质对石英砂的粉碎速度较钢球介质快。根据碎矿与磨矿理论可知,物料的粉碎主要是介质运动过程中产生的冲击力所致。根据表2可知,尺寸相同的钢锻和钢球,前者质量要大于后者,产生的冲击力要更大;钢锻是介于球形与棒形之间的一种过渡介质,具有两者共同的优点,在碎磨初期,钢锻介质的线接触研磨方式更容易与粗颗粒物料充分接触、挤压和碎磨,因此其对物料的粉碎速率更大。
2.2 磨矿介质形状对初始粉碎分布函数相关参数的影响
Austin等[2]给出了初始粉碎分布函数的经验公式:
n≥i≥j, β≥γ≥0, 0≤φ≤1
(3)
式中,Bij为初始粉碎产品的质量分数;xi为物料中的各粒级;在Bij和粒径的对数坐标中,相关参数的几何意义:γ为曲线下半段的斜率,β为上半段的斜率,φ为下半段的截距,粉碎参数如图2所示[14-15]。
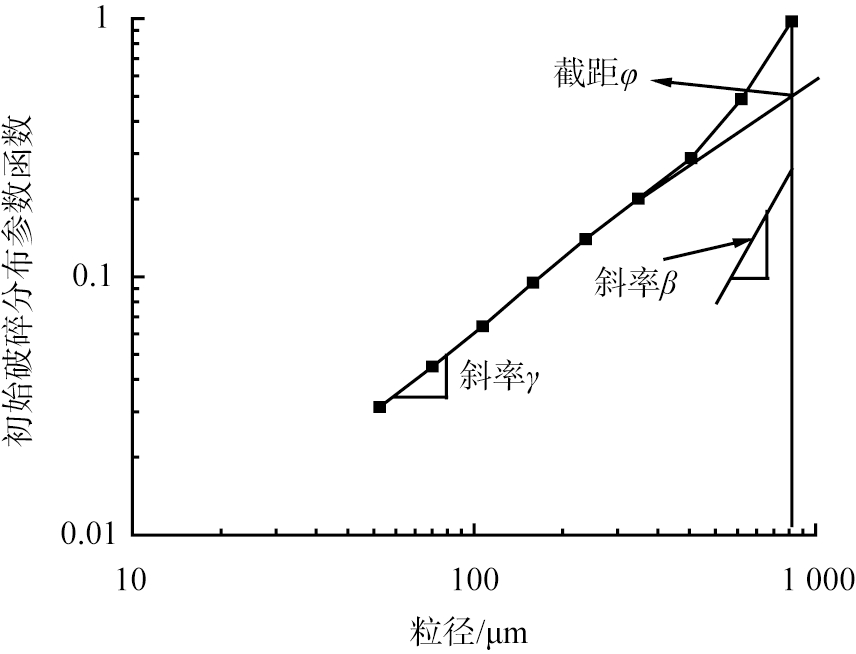
图2 磨机中单一给料物料的初始粉碎分布函数参数
Fig.2 Primary breakage distribution function
parameters of mono-size feed
由于石英砂成分单一,性质相对稳定,实验室锥形球磨机入料要求最佳粒度为≤2mm,因此选取了0.83~2 mm粒级,采用G-H的Bij值算法[16-19],粉磨时间应取较短时间,因此本试验中取粉磨时间为1 min,研究介质形状对初始粉碎分布函数与相对粒度的关系及其相关参数的影响,采用非线性回归的方法,计算得到相关参数见表5,初始粉碎分布函数与相对粒度的关系见图3。
参数γ表征i粒级物料粉碎到j粒级的比率,它的大小直接关系到粉碎效率,γ与Si呈反比例关系,γ越小物料越容易被粉碎,φ和β值则表示进料粒级的物料减少到较小粒级的速度。由表5可知,在相同时间内,钢锻介质的γ要小于钢球介质,φ、 β值要大于钢球介质,表明钢锻介质下石英砂粉碎到细粒级的速度较快。图3中钢锻介质的累积粉碎分布函数线在钢球介质的上方,表明在短时间内,钢锻介质对石英砂的粉碎效果要优于钢球介质。
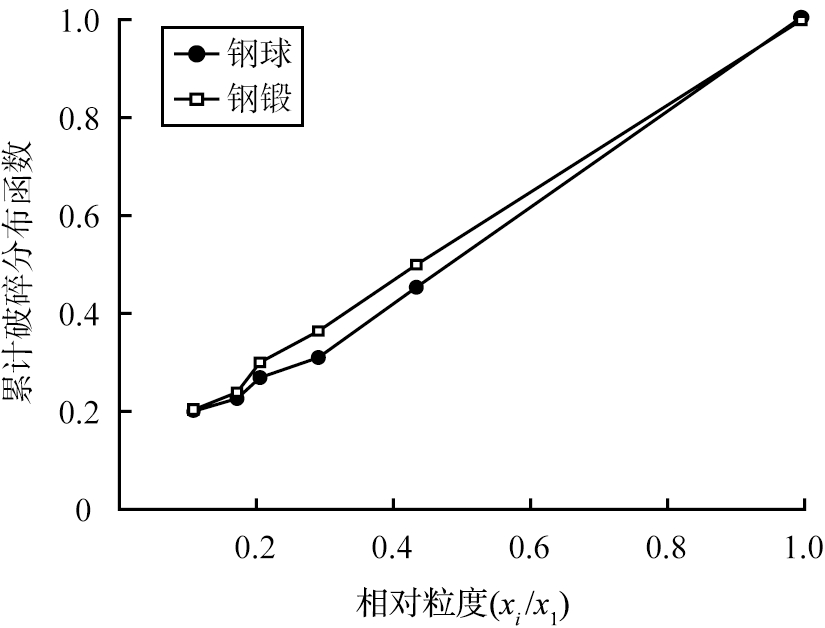
注:xi为破碎后各粒级;x1为原料粒级。
图3 不同研磨介质条件下0.83~2 mm粒级物料的
初始粉碎分布函数
Fig.3 Primary breakage distribution function plots
with different media from 0.83~2 mm feed
表5 不同研磨介质下0.83~2 mm粒级粉碎1 min得到的相关参数
Tab.5 The parameters obtained from 0.83~2 mm feed with different media in 1 min
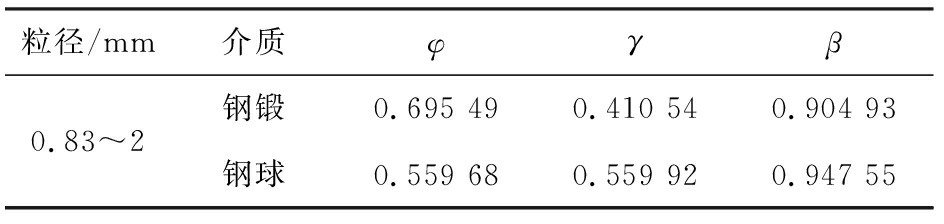
粒径/mm介质φγβ0.83~2钢锻0.695 490.410 540.904 93钢球0.559 680.559 920.947 55
3 结论
1)不同研磨介质下,石英砂的粉碎速率均遵循一阶动力学模型,在磨矿初期,钢锻介质的粉碎速率要大于钢球介质,这与碎矿与磨矿理论相符,充分发挥了钢锻介质同时具有点、线接触的优点。
2)不同的研磨介质形状在一定程度上影响粉碎参数γ、β、φ,γ值大小反应了物料粉碎的难易程度,值越小物料越容易被粉碎,φ和β值则表示进料粒级的物料减少到较小粒级的速度。钢锻介质在短时间内的γ值要小于钢球介质,φ和β值要大于钢球介质,说明在短时间内钢锻介质对物料的粉碎速率较钢球介质快。
3)石英砂的粉碎是石英砂利用过程中最重要的一步,研究表明,对于2 mm左右粒度的石英砂可以采用短圆柱形钢锻介质对其进行快速研磨,同时避免过磨造成不必要的浪费。
[1]范培强, 谢贤, 宋强,等. 国内高纯石英砂选矿与深加工研究现状[J]. 矿冶, 2018, 27(3): 22-26.
[2]AUSTIN L G, LUCKIE P T. Methods for determination of breakage distribution parameters[J]. Powder Technology, 1972, 5(4):215-222.
[3]段希祥. 碎矿与磨矿[M]. 2版,北京:冶金工业出版社, 2006: 179-180, 202-206.
[4]马少健, 陈建新. 球磨机适宜磨矿介质配比的研究[J]. 金属矿山, 2000(11):27-31.
[5]吴桂义, 安站东, 薛钢琴. 钢球级配对铁矿石的磨矿动力学研究[J]. 有色金属工程, 2018, 8(3):64-69.
[6]李同清, 彭玉兴. 研磨介质形状对铁矿石磨矿动力学研究[J]. 有色金属:选矿部分, 2018(1):84-89.
[7]SUN X, XIE W, HE Y,et al. Analyses of the energy-size reduction of mixtures of narrowly sized coals in a ball-and-race mill[J]. Advanced Powder Technology, 2018, 29(6):118-131.
[8]DIAZ E, VOISIN L, KRACHT W, et al. Using advanced mineral characterisation techniques to estimate grinding media consumption at laboratory scale[J]. Minerals Engineering, 2018, 121:180-188.
[9]钱海燕, 张柏林. 研磨体大小对水泥熟料粉磨动力学的影响[J]. 硅酸盐通报, 2010, 29(6):1308-1312.
[10]张柏林, 钱海燕, 敖林. 行星磨中研磨体级配对水泥熟料粉碎效率的影响[J]. 硅酸盐通报, 2011, 30(4):930-933.
[11]CUHADAROGLU D, SAMANLI S, KIZGUT S. The effect of grinding media shape on the specific rate of breakage[J]. Particle & Particle Systems Characterization, 2010, 25(5/6):465-473.
[12]DENIZ V, ONUR T. Investigation of the breakage kinetics of pumice samples as dependent on powder filling in a ball mill[J]. International Journal of Mineral Processing, 2002, 67(1):71-78.
[13]YEKELER M, OZKAN A, AUSTIN L G. Kinetics of fine wet grinding in a laboratory ball mill[J]. Powder Technology, 2001, 114(1):224-228.
[14]LAMECK N S, MONYS M H. Effects of media shape on milling kinetics[J]. Minerals Engineering, 2006, 19(13):1377-1379.
[15]JEAN-MARIE KONRAD Y S. Particle breakage in granular materials: a conceptual framework[J]. Canadian Geotechnical Journal, 2018, 55(5): 17-24.
[16]DRAHMAN S H, KUEH A B H, ABIDIN A R Z, et al. Efficient cumulative breakage distribution and breakage rate computation with minimal experiment intervention incorporating optimal time determination for fine grinding simulation[J]. Powder Technology, 2018, 329:313-322.
[17]GUPTA V K. Effect of size distribution of the particulate material on the specific breakage rate of particles in dry ball milling[J]. Powder Technology, 2017, 305: 714-722.
[18]SAEIDI F, YAHYAEI M, POWELL M, et al. Investigating the effect of applied strain rate in a single breakage event[J]. Minerals Engineering, 2017, 100:211-222.
[19]HASAN M, PALANIANDY S, HILDEN M,et al. Calculating breakage parameters of a batch vertical stirred mill[J]. Minerals Engineering, 2017, 111:229-237.