近年来,世界各国环保产业快速发展,各国的环保政策力度不断加大,一些发达国家已经把环保产业列为支柱产业。作为环保产业重要组成部分的环保滤料产业也迎来前所未有的快速发展机遇期。在过滤材料的研发与生产过程中,材料孔径的分析测量是指导材料研发与进行产品质量控制的关键步骤,其准确性直接关系到过滤材料性能的优劣。
目前,市场上过滤材料种类繁多,主要包括挠性介质(如滤膜、滤纸)、刚性介质(如金属烧结材料、多孔陶瓷)及松散性过滤介质(如砂、硅藻土)等。不同材料中孔的结构相差甚远(见图1),但从过滤的原理来看,材料通孔的最窄处,即孔喉直径(limiting diameter),是影响过滤性能的直接因素(见图2)。现有的材料孔径分析方法主要包括显微成像图像分析法[1-2]、标准颗粒过滤法、压汞法[3-5]、气体吸附法[6]、核磁共振法、泡点法等。其中,由于泡点法能准确测量过滤材料的孔喉直径,因此是目前最适合进行滤材孔径分析的方法之一。

a 放射状b 多重放射状c 海绵孔状d 编织状图1 滤膜材料的不同孔隙结构Fig.1 Different pore structures of membrane
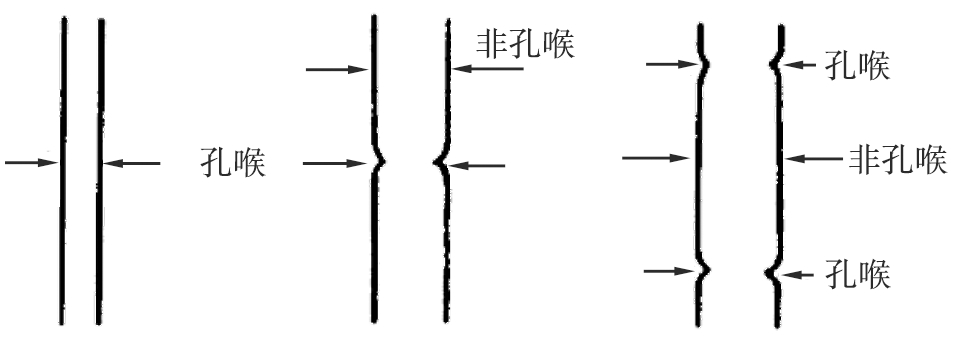
图2 材料的孔喉直径
Fig.2 Scheme of limiting diameter
现阶段,泡点孔径分析方法应用广泛,但相关的量值溯源问题尚未得到解决,缺乏计量标准及标准物质对商用仪器进行校准,导致不同仪器测量结果的一致性与准确性存在较为严重的问题,进而影响到过滤材料的研发、生产与使用。为此,本研究中提出采用标准装置—标准物质—工作级仪器的路线解决溯源性问题,通过研制泡点孔径分析方法标准装置,并以此为基础研制标准物质,实现将孔径测量结果逐级溯源至压力与流量,建立泡点孔径分析方法的溯源体系,从而保证测量结果的一致性与准确性。
1 泡点孔径分析方法的量值溯源
1.1 泡点孔径分析方法
泡点法孔径分析根据跨膜压差与通过膜材料的气体通量计算材料的最大孔径、平均流量孔径[7-9]。采用表面张力小、蒸汽压低、化学惰性的浸润液将样品完全浸润,在膜的一侧逐渐加大气体压力,令材料中被浸润的孔按孔径从大到小的顺序依次打开,同时测量跨膜压差与气体流量,即可按公式(1)计算孔径。
(1)
式中:D为膜孔喉直径,m; Δp为跨膜压差,Pa;γ为浸润液的表面张力, N/m;θ为浸润液与多孔材料的接触角。
材料的最大孔径与平均流孔径可通过干湿曲线法得到。对于材料中的孔,由浸润液封闭至完全打开的过程中得到的压力-流量曲线为湿式曲线; 在完全打开的状态下得到的压力-流量曲线为干式曲线; 将干式曲线的流量值折半,得到半干曲线(见图3)。
半干曲线与湿式曲线的交点对应的孔径为平均流量孔径。湿式曲线中,流量不为0的最小压力点称为泡点压力,对应的孔径为泡点孔径。泡点孔径即为材料最大孔径,平均流量孔径由湿式曲线与半干曲线共同决定,常用于表征材料孔径大小。
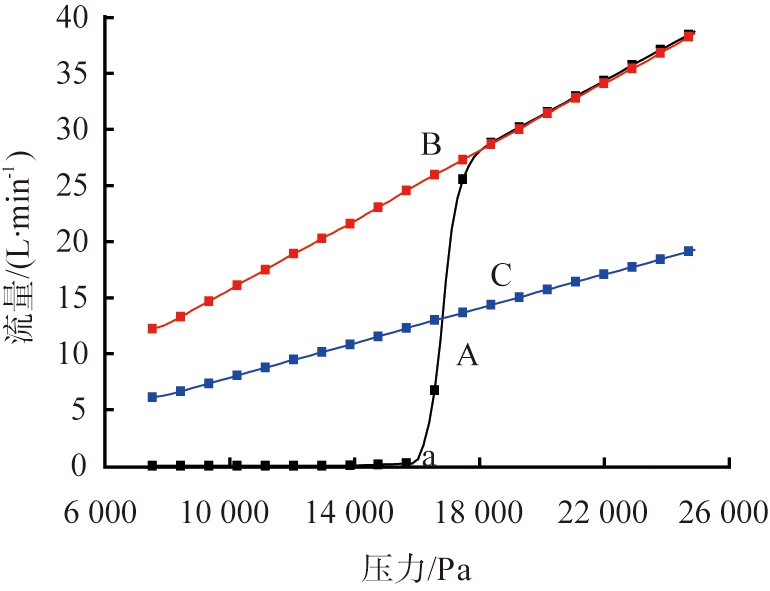
A—湿式曲线;B—干式曲线;C—半干曲线;a—泡点压力。
图3 泡点法干湿曲线图
Fig.3 Curves of dry flow and wet flow from bubble point method
1.2 量值溯源方法
根据泡点孔径分析方法的原理可知,孔径的量值溯源可通过对于表面张力、压力和流量的溯源而实现。商用孔径分析仪均未提供其内部压力计与流量计的校准接口,也难以拆卸后单独校准,目前无法对商用泡点孔径分析仪进行直接校准,因此,本研究中通过研制泡点法孔径分析标准装置和标准物质来实现工作级孔径分析仪的量值溯源(见图4)。
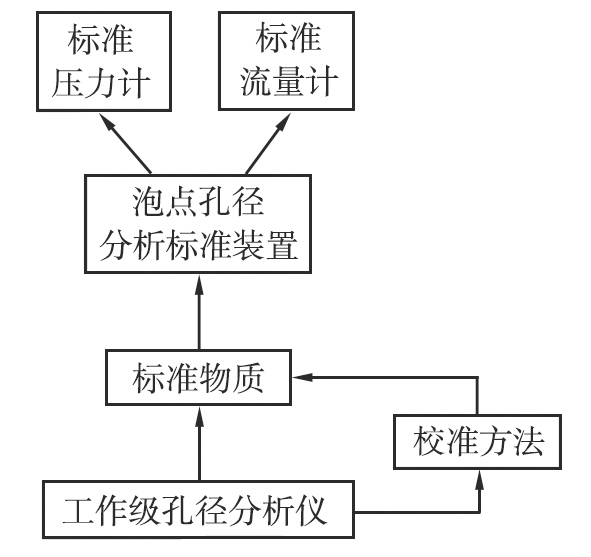
图4 孔径分析量值溯源图
Fig.4 Traceability of pore size measurement
研制一台带有校准接口的泡点法孔径分析仪作为标准装置,其压力与流量的量值分别溯源至上一级标准器。采用该标准装置对孔径标准物质进行定值,并研究相应的校准方法,以实现工作级泡点孔径分析仪的量值溯源。
2 泡点孔径分析标准装置的研制
泡点孔径分析标准装置原理如图5所示,包括干、湿式曲线测量功能与泡点测量功能,以及压力计与流量计的校准接口。
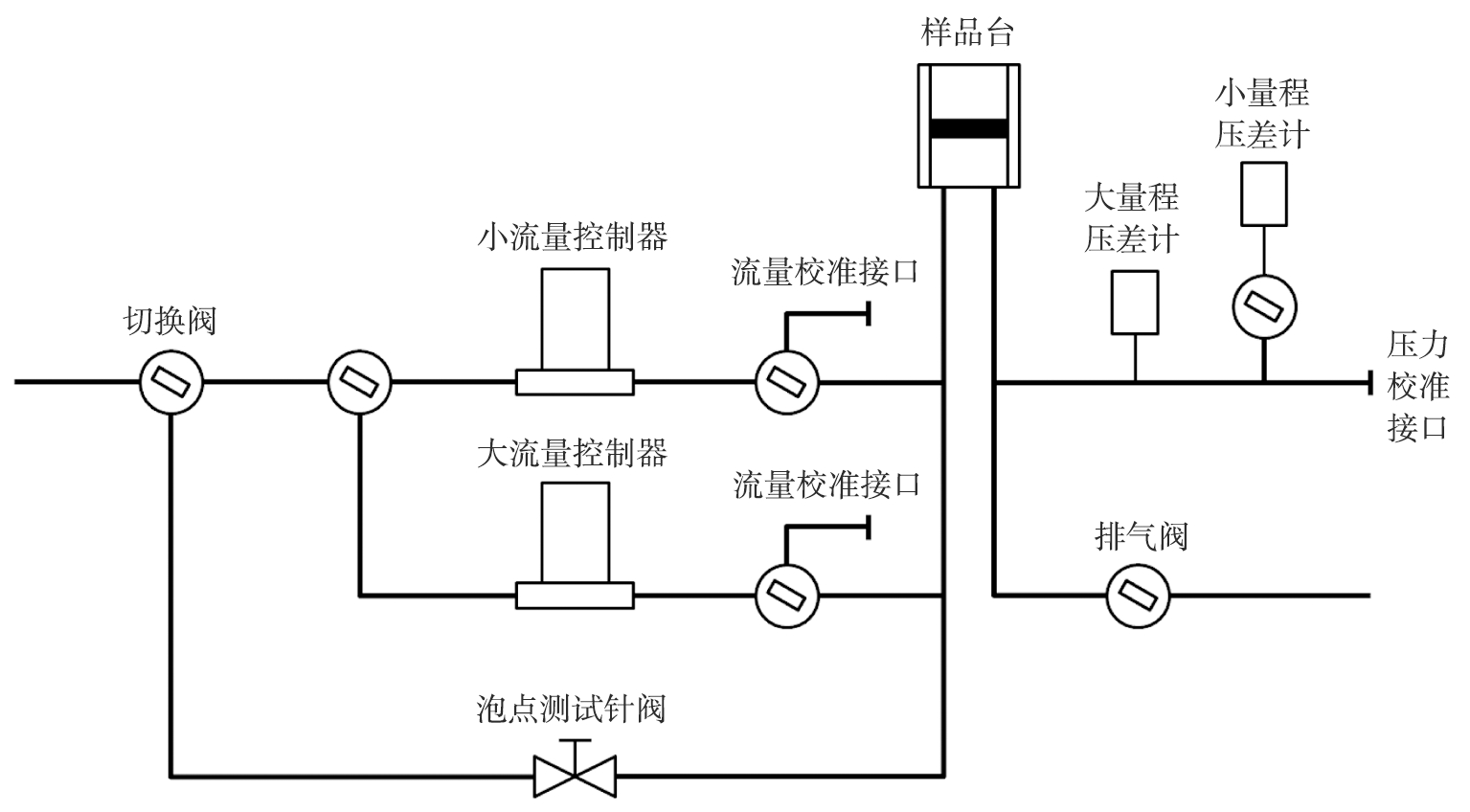
图5 泡点法孔径分析标准装置原理图
Fig.5 Schematic diagram of bubble point porometry standard device
为了保证流量与压力测量结果的准确性,尤其是小流量与小压差的准确性,在气路中增加了小量程的质量流量控制器与压差传感器,根据气体的流量与压力进行自动切换。为了解决标准装置的量值溯源问题,设有流量与压力的计量校准接口,可外接标准流量计与标准压力计进行校准。该装置中使用的流量、压力量值均溯源至国家计量基准。
该标准装置可测量滤膜的干、湿式曲线、平均流量孔径和泡点孔径。测量干、湿式曲线及平均流量孔径时,首先令气体通过小流量控制器,并开启小量程压差计测量压力。当流量或压力接近测量范围上限时自动切换至大流量控制器或压差计。对于泡点孔径,由于其对应的气体流量极小,因此通过针阀对气路进行单独控制,并监测压力的突降或人工观察气泡的出现以进行测量。
在此基础上,该标准装置还可专门测量滤膜在特定压力-流量下的压差-流量关系,从而为工作级孔径分析仪的量值溯源提供了额外的途径。对于未经浸润液浸润的干滤膜,其在不同压力-流量下的压差-流量具有固定的关系。该标准装置可通过指定压差测量流量或指定流量测量压差的方式对压差-流量关系进行准确测量,从而将压差-流量关系作为滤膜孔径标准物质的特性量值,用于判断工作级孔径分析仪压差和流量的测量准确性。
3 泡点孔径标准物质的研制
3.1 标准物质的选择与制备
标准物质候选物从滤膜、滤纸、金属烧结材料3种标准物质候选物中进行选择。实验表明,滤膜、滤纸孔径参数受环境温度、湿度影响较大,且材质易损,不适于多次反复测量,因此,选择金属烧结材料作为标准物质候选物。
分别采用粒径为5、15 μm的不锈钢粉末为原料,经高温高压压制并烧结制得直径为25 mm、厚度为1 mm的圆形金属膜片,作为标准物质候选物。其标称值分别为5、15 μm。
对于不同型号的孔径分析仪,当膜片置于样品台后,其暴露在气路中的尺寸(即膜片表面的采样面积)可有所不同,从而可导致标准物质的量值发生变化。为了消除这一影响,采用高分子材料将标准物质候选物中心以外的表面全部密封,仅保留膜片两面以中心为圆心、直径为15 mm的区域令气体或液体介质通过,以提高标准物质的适用性。
将标准物质密封置于塑封袋中,在阴凉干燥的条件下储存,减少环境温度、湿度对该物质的孔径等参数的影响。
3.2 标准物质的特性量值与定值方法
目前的商用泡点孔径分析仪均可测量干、湿式曲线、平均流量孔径和泡点孔径,因此选择压差-流量关系、平均流量孔径和泡点孔径作为标准物质的特性量值。其中,压差-流量关系采用标准装置定值。根据式(1),平均流量孔径和泡点孔径除需压差和流量量值外,还与浸润液的接触角和表面张力相关。浸润液的表面张力采用平板法定值,测量次数为20。对于接触角,根据文献,由于泡点孔径分析法所使用的浸润液表面张力小,浸润效果良好,因此普遍将接触角视为0 °。
根据图3,平均流量孔径的测量需计算半干曲线与湿式曲线的交点。该交点无法直接测量,需通过拟合计算得到。经实验测量,发现对于标准物质候选物,其半干曲线与湿式曲线在交点附近可近似为直线,因此采用直线拟合对平均流量孔径进行定值与不确定度评定。对于半干曲线与湿式曲线,分别取距交点最近的5组压差-流量测量结果进行直线拟合,并计算直线的交点得到交点处的压差,并代入公式(1)计算得到平均流量孔径。
此外,实验测量发现标准物质候选物的片间均匀性较差,故采用单片定值的方法进行定值。定值过程中,为了评价放置位置的变化对测量结果的影响,采取改变膜片旋转角度和朝向(正面向上或向下)的方法进行测量,即选定膜片的某一方向为0,依次测量膜片旋转0、90、180、270 °时的量值,每个角度测量2次,膜片正反面各测量1组,共测16次。
3.3 标准物质稳定性检验
根据式(1),平均流量孔径的测量模型中包含了压差、流量、表面张力和接触角等全部物理量,因此选择平均流量孔径量值进行稳定性检验。按照JJF 1343—2012《标准物质定值的通用原则及统计学原理》[10]的要求,采用t检验法对标准物质进行稳定性检验。稳定性检验的起止时间为2017年9月—2019年2月,每个时间点按照定值方法进行3次测量。
表1 标称值5 μm标准物质稳定性检验数据
Tab.1 Stability test data of reference materials with nominal value of 5 μm
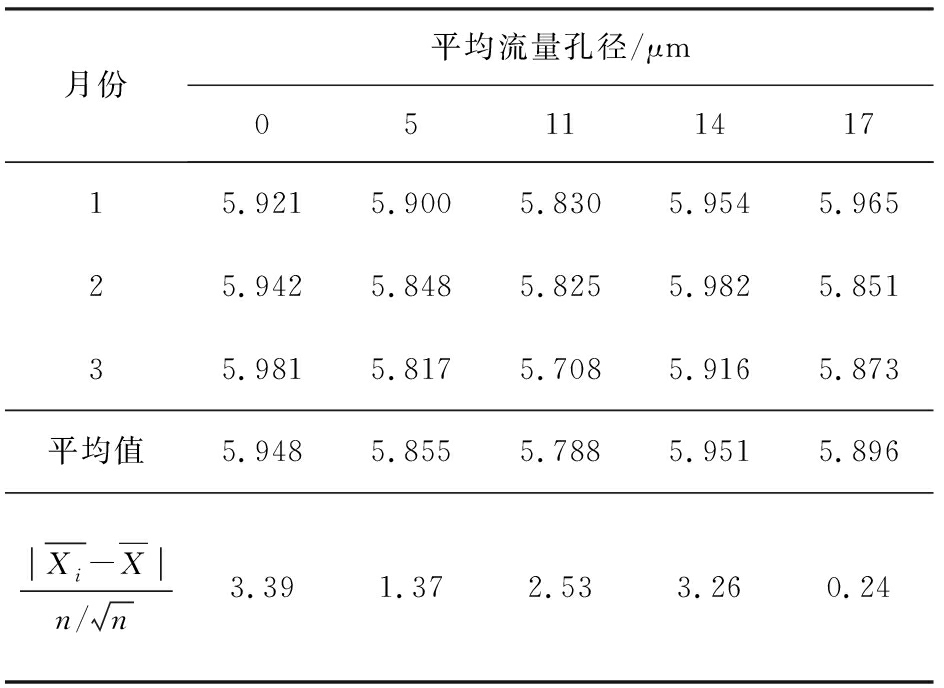
月份平均流量孔径/μm0511141715.9215.9005.8305.9545.96525.9425.8485.8255.9825.85135.9815.8175.7085.9165.873平均值5.9485.8555.7885.9515.896Xi-Xn/n3.391.372.533.260.24
表2 标称值15 μm标准物质稳定性检验数据
Tab.2 Stability test data of reference materials with nominal value of 15 μm
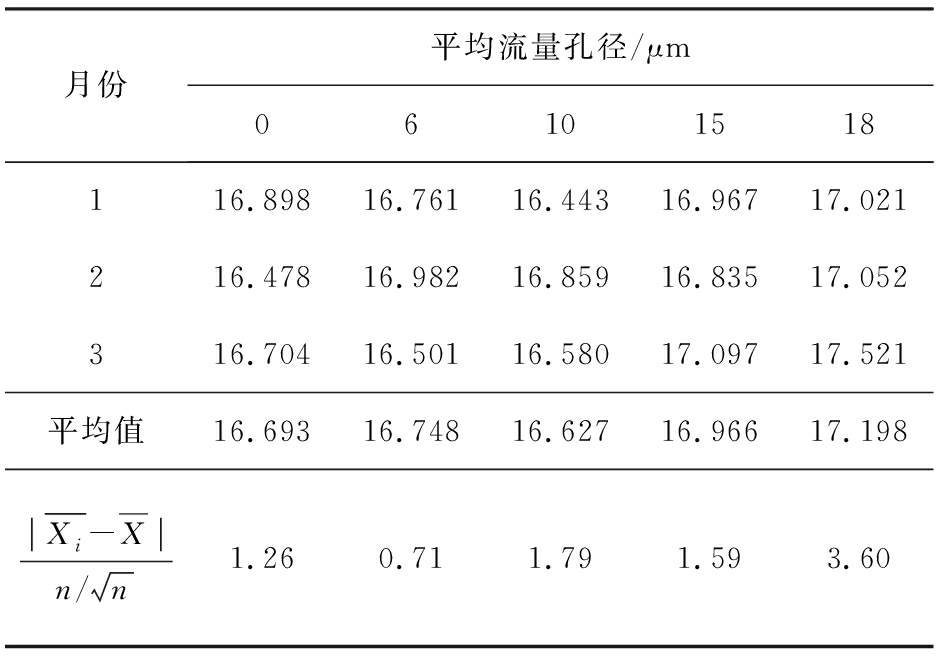
月份平均流量孔径/μm06101518116.89816.76116.44316.96717.021216.47816.98216.85916.83517.052316.70416.50116.58017.09717.521平均值16.69316.74816.62716.96617.198Xi-Xn/n1.260.711.791.593.60
从表1、2检验结果可知,标称值分别是5.0、15.0 μm标准物质稳定性统计量![]() 均小于t0.95(3-1)=4.303,可以认为该标准物质的特性量值没有发生显著性变化。
均小于t0.95(3-1)=4.303,可以认为该标准物质的特性量值没有发生显著性变化。
3.4 标准物质放置位置的影响
由于标准物质的定值采用单片定值,且单个膜片在测量过程中为整片使用,因此无需进行均匀性检验。测量时膜片放置的角度和朝向变化可对测量结果产生影响,因此在定值方法中通过改变膜片放置角度与朝向的方法考察膜片放置位置对测量结果的影响。2种标准物质的测量结果分别如表3和表4所示。
表3 标称值5 μm标准物质不同放置位置测量结果
Tab.3 Results of reference materials with nominal value of 5 μm at different positions
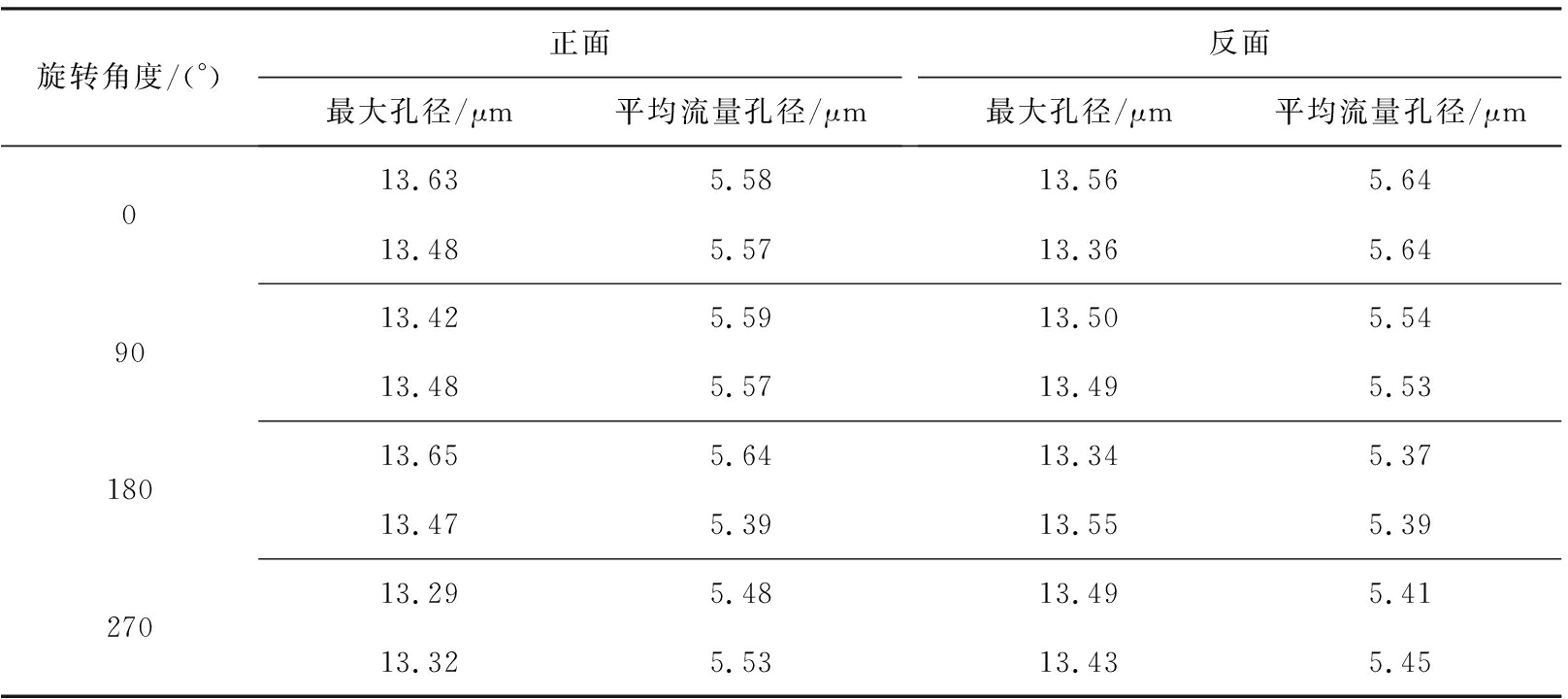
旋转角度/(°)正面最大孔径/μm平均流量孔径/μm反面最大孔径/μm平均流量孔径/μm09018027013.635.5813.565.6413.485.5713.365.6413.425.5913.505.5413.485.5713.495.5313.655.6413.345.3713.475.3913.555.3913.295.4813.495.4113.325.5313.435.45
表4 标称值15 μm标准物质不同放置位置测量结果
Tab.4 Results of reference materials with nominal value of 15 μm at different positions
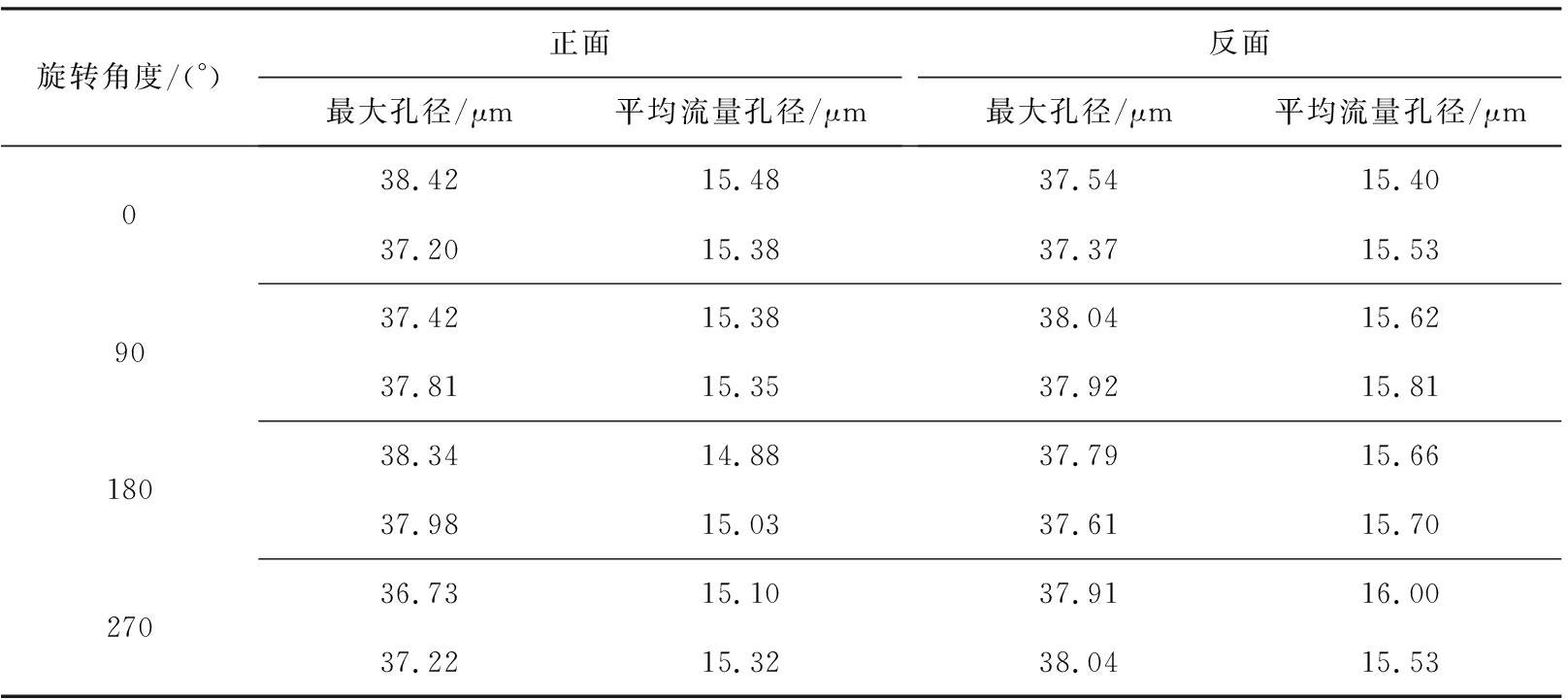
旋转角度/(°)正面最大孔径/μm平均流量孔径/μm反面最大孔径/μm平均流量孔径/μm09018027038.4215.4837.5415.4037.2015.3837.3715.5337.4215.3838.0415.6237.8115.3537.9215.8138.3414.8837.7915.6637.9815.0337.6115.7036.7315.1037.9116.0037.2215.3238.0415.53
3.5 标准物质的定值不确定度评定
标准物质的不确定度主要来源于定值方法、标准物质稳定性及标准物质均匀性。由于本标准物质为单片定值、整片使用,因此均匀性引入的不确定度由放置位置引入的不确定度代替。根据测量模型,定值方法引入的不确定度包含压差测量引入的不确定度与表面张力测量引入的不确定度。其中,对于平均流量孔径,压差由直线拟合得到,其进一步包含直线拟合引入的不确定度(见图6)。
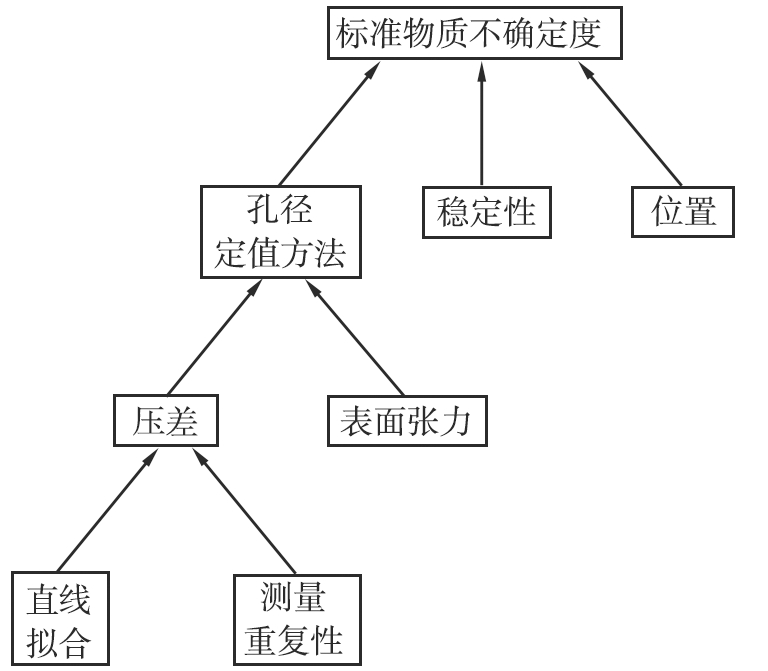
图6 标准物质不确定来源
Fig.6 Sources of uncertainty of reference materials
经统计检验,不同放置位置的最大孔径与平均流量孔径测量结果符合正态分布,因此放置位置引入的不确定度采用贝塞尔公式计算。稳定性引入的不确定度按照JJF 1343—2012《标准物质定值的通用原则及统计学原理》的要求,采用趋势分析的方法评定,即将储存时间与特性量值进行直线拟合,计算稳定性引入的不确定度。
对于定值方法引入的不确定度,根据泡点法孔径测量模型式(1),其不确定度可按式(2)计算得到。其中,表面张力引入的不确定度分量按不确定度的A类评定方法进行评定。压差引入的不确定度分量的评定方法对于最大孔径和平均流量孔径有所不同。
(2)
式中:uv为平均流量孔径测量不确定度,m; u(γ) 为浸润液表面张力不确定度,N/m; u(Δp)为压差测量值不确定度,Pa。
对于最大孔径,压差可直接测量得到,因此采用A类评定[11]的方法对其引入的不确定度进行评定。对于平均流量孔径,由于其采用半干曲线和湿式曲线分别拟合得到2条直线的交点处压差进行计算,因此其不确定度包含了2条拟合直线的斜率与截距的不确定度,如式(3)所示。由于压差和流量测量的不确定度量级接近,因此按照JJF 1507—2015 《标准物质的选择与应用》[12],直线拟合的不确定度需包含二者的不确定度,即采用双变量线性回归法计算得到拟合直线斜率与截距的不确定度。
(3)
式中: k1为湿式拟合曲线斜率,u(k1)为湿式拟合曲线斜率不确定度; b1为湿式拟合曲线截距,u(b1)为湿式拟合曲线截距不确定度; k2为半干拟合曲线斜率; u(k2)为半干拟合曲线斜率不确定度; b2为半干拟合曲线截距,u(b2)为半干拟合曲线截距不确定度。
定值过程中,定值方法各个不确定度分量及其引入的不确定度大小见表5。
表5 标准物质定值方法不确定度分量
Tab.5 Uncertainty components of reference materials

标称值/μmu(γ)/(mN·m-1)u(Δp)/Pauv/μm50.101 503.070.07150.10436.250.13
定值方法、稳定性和放置位置引入的不确定度分量最终按式(4)计算合成不确定度uc:
(4)
标准物质定值不确定度分量及计算结果见表6。标准物质定值及不确定度评定结果见表7。
表6 标准物质定值不确定度分量及计算结果
Tab.6 Uncertainty components and calculated values of reference materials
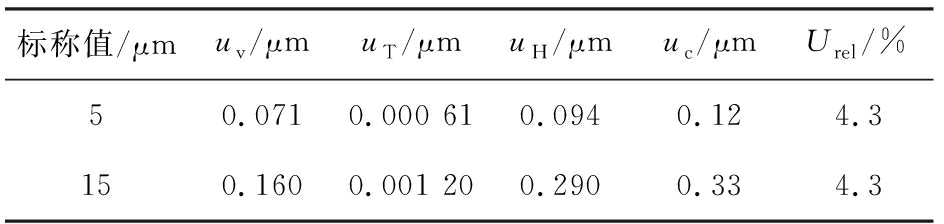
标称值/μmuv/μmuT/μmuH/μmuc/μmUrel/%50.0710.000 610.0940.124.3150.1600.001 200.2900.334.3
表7 标准物质定值及不确定评定结果
Tab.7 Certified values and uncertainty of reference materials
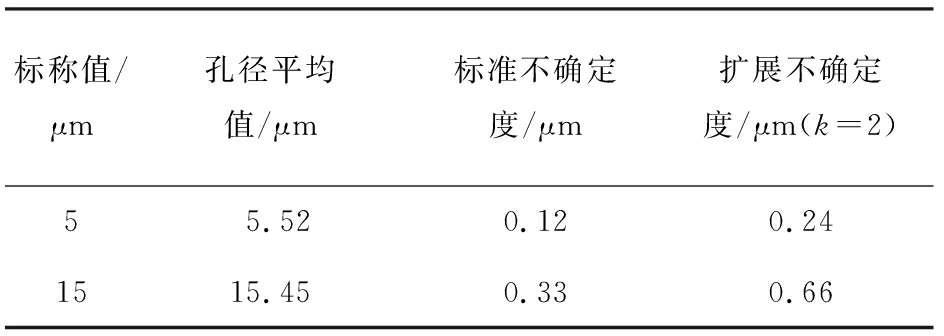
标称值/μm孔径平均值/μm标准不确定度/μm扩展不确定度/μm(k=2)55.520.120.241515.450.330.66
4 结论
1)严格按照ASTM F 316-03与ISO 4003—1977标准,选择高精度传感器,自主设计搭建了一台泡点孔径分析标准装置。该标准装置是国内首台自主研发、集校准与定值一体的标准装置,是目前国内泡点法孔径分析方法计量的最高标准。
2)制定并完善泡点孔径分析定值方法,对材料最大孔径与平均流量孔径进行定值,将定值结果溯源至基本单位压力与流量,溯源链的完整性保证实验结果的可靠性。
3)研制得到孔径标称值为5、15 μm的标准物质,定值结果分别为5.52、15.45 μm,相对扩展不确定度均为4.3%,k=2。其量值及不确定度水平可满足目前市场上商用泡点孔径分析仪的检定、校准需求,可为我国环保滤料产业的产品研发与质量控制提供准确可靠的技术支持。
[1]AGARWAL C, PANDEY A K, PATTYN D, et al. Neck-size distributions of through-pores in polymer membranes[J]. Journal of Membrane Science, 2012, 415/416(10): 608-615.
[2]HAYAMA M, KOHORI F, SAKAI K. AFM observation of small surface pores of hollow-fiber dialysis membrane using highly sharpened probe[J]. Journal of Membrane Science, 2002, 197(1/2): 243-249.
[3]王红梅. 压汞法测定多孔材料孔结构的误差[J]. 广州化工, 2009, 37(1): 109-111.
[4]CALVO J I H. Pore size distributions in microporous membranes II. bulk characterization of track-etched filters by air porometry and mercury porosimetry[J]. Journal of Colloid & Interface Science, 1995, 176(2): 467-478.
[5]谢晓永, 唐洪明, 王春华, 等. 氮气吸附法和压汞法在测试泥页岩孔径分布中的对比[J]. 天然气工业, 2006, 26(12): 100-102.
[6]VENKATARAMAN K, CHOATE W T, TORRE E R, et al. Characterization studies of ceramic membranes: a novel technique using a coulter porometer[J]. Journal of Membrane Science, 1988, 39(3): 259-271.
[7]ASTM International. Standard test methods for pore size characteristics of membrane filters by bubble point and mean flow pore test: ASTM F 316-03[S]. West Conshohocken, PA: ASTM International, 2011.
[8]International Organization for Standardization. Permeable sintered metal materials-determination of bubble test pore size: ISO 4003:1977[S]. Switzerland: ISO, 1977.
[9]LI D, FREY M W, YONG L J. Characterization of nanofibrous membranes with capillary flow porometry[J]. Journal of Membrane Science, 2006, 286(1/2): 104-114.
[10]全国标准物质计量技术委员会. 标准物质定值原则和统计学原理: JJF 1343—2012[S]. 北京:中国质检出版社, 2012.
[11]全国法制计量管理计量技术委员会. 测量不确定度评定与表示: JJF 1059.1—2012[S]. 北京:中国质检出版社,2012.
[12]全国标准物质计量技术委员会. 标准物质的选择与应用: JJF1507—2015[S]. 北京:中国质检出版社,2015.