纳米颗粒在胶体溶液中的稳定性是颗粒制备的重要参数[1-2],通过测量胶体溶液中纳米颗粒的Zeta电位,可以研究颗粒表面电荷分布情况和表面电位的高低,预测与控制胶体溶液的稳定性[3]。在乳业、酿造[4]、DNA电荷反转[5]、超滤膜污染[6]和原油采收[7]等领域中,纳米颗粒溶液 Zeta电位已成为重要的判断依据。
目前,在测量纳米颗粒溶液Zeta电位的方法中,电泳光散射法(electrophoretic light scattering,ELS)以其具有检测速度快、统计精度高、非接触和重现性好的优点成为主流方法[8-9]。该方法需要对悬浮在溶液中的表面带电纳米颗粒施加电场,使其产生沿电场方向的定向电泳运动,引起散射光出现多普勒效应,因此,电场的稳定性影响颗粒的运动速度,从而影响测量结果的准确性。
为了提高测量区域电场的稳定性,现有的技术解决方案都通过改进探测点附近的电场均匀线性分布加以实现。如:奥地利安东帕(Anton-Paar)公司生产的倒置Ω管型样品池、英国的马尔文(Malvern)公司生产的折叠式可抛弃型毛细管样品池结构以及麦克默瑞提克(Micromeritics)公司生产的扁平样品池结构。以上方法均需要改造样品池结构,工艺较为复杂,而且样品池底部清洁难度大。当探测点选取在U型样品池的底部时,电力线会因U型样品池底部的弯折,而造成不均匀分布,从而导致纳米颗粒运动的速度产生分布[10]。
为了提高纳米颗粒溶液Zeta电位测量结果的准确性,本文中探究了电场稳定性对纳米颗粒溶液Zeta电位测量的影响,从理论上分析电泳光散射技术的测量原理,讨论电场变化对于多普勒频移信号的影响。对主流的U型样品池进行了电场仿真实验,发现U型样品池底部的电场强度分布存在不均匀的问题。再根据仿真结果,选取了U型样品池两侧竖直臂的中点位置作为新的探测点,并采用粒径为800 nm的聚苯乙烯带电颗粒悬浮液设计了基于电泳光散射法的对比实验。该研究有助于实验测量中简单而有效地选取探测点,对于纳米颗粒溶液Zeta电位测量具有重要意义。
1 实验
1.1 电泳光散射原理
电泳光散射法测量Zeta电位是在激光多普勒电泳法(laser Doppler electrophoresis)技术基础上,利用光子相关光谱技术提取多普勒频移量,再由Henry关系计算出Zeta电位。图1所示为纳米颗粒运动测量原理示意图。
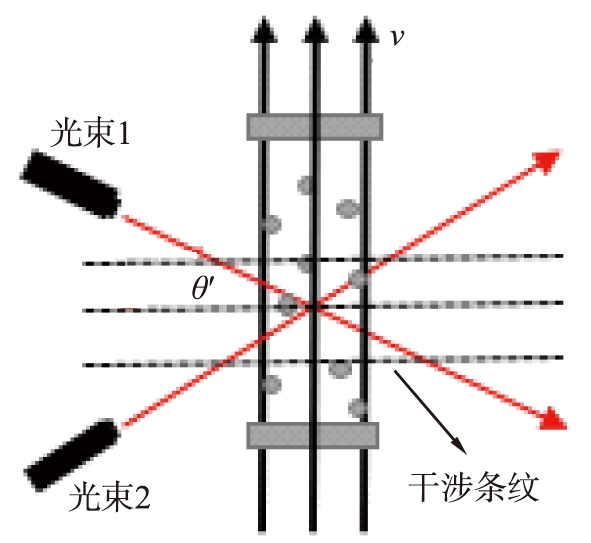
图1 纳米颗粒运动测量原理示意图
Fig.1 A schematic diagram of principle of particle motion measurement
当2束相干光在样品池中相交时形成干涉区域,产生明暗相间的条纹[11]。颗粒沿电场方向做垂直于干涉条纹的定向运动,由于多普勒效应,散射光强将随着干涉条纹的明暗变化,产生周期性的涨落信息,并通过PMT进行检测。
电泳光散射光强自相关函数图像是一个在周期的余弦信号上叠加一个衰减的指数函数,表达式[9-12]为
(1)
式中:E0为观测点散射光电场振幅;N为散射体包含的颗粒数目;Γ为衰减线宽;τ为延迟时间。光强自相关函数公式包含了指数函数与余弦周期信号的乘积项。对该曲线进行傅立叶频谱分析可以提取出周期信号的频移量f,并计算出粒子的电泳速度,
(2)
式中:λ0为激光波长;n为折射率;θ′为光路中的散射角。
得到电泳迁移率为
(3)
式中:υ为电泳速度;E为电场幅值;T为温度。
再根据Henry公式[13-14]就可得到颗粒的Zeta电位ξ,
(4)
式中:η为溶液的黏质系数;T是温度;n是折射率;ε是溶液的介电常数;θ′是光路中的散射角;E是电场强度;r为球形颗粒的半径;对于水性悬浮液的大粒子来说,![]() 通过上面的分析可知,通过测量多普勒频移即可得到颗粒的Zeta电位信息等。
通过上面的分析可知,通过测量多普勒频移即可得到颗粒的Zeta电位信息等。
1.2 样品池结构与电场仿真
在电泳光散射实验中,目前不少的仪器厂家都采用类似U型的样品池进行测量。本文中所用的样品池是基于实验室原有的插入式U型样品池的改善而来,规格为12 mm×12 mm×50 mm,结构如图2a所示(图2b为电场仿真图)。电极直插式结构增加了电极与样品液的接触面积,导电性良好而稳定[15]。图3为不同测量区域的电场强度对比图。
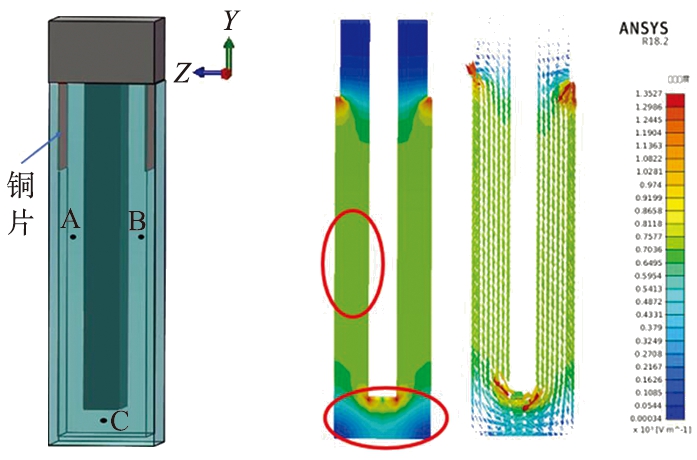
a 样品池结构 b 电场仿真图
图2 样品池结构及电场仿真图
Fig.2 Structure and simulation diagram of sample pool

a 竖直臂与底部测量区域
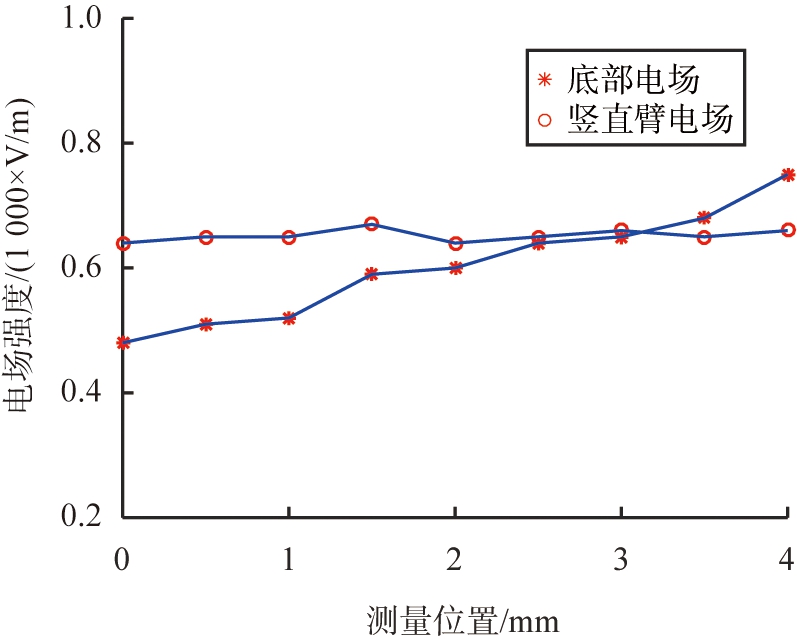
b 电场强度的对比
图3 不同测量区域的电场强度
Fig.3 Electric field intensity at different points
本文中采用有限元分析软件ANSYS对样品池进行电场模拟仿真。该软件利用有限分析的方法进行求解计算,即将求解域看成是由许多有限元的互连子域组成,对每一个单元假定一个合适的近似解,然后推导求解这个区域的满足条件,从而得到问题的解[16]。模拟电压加在U型液体柱上表面外侧顶点,数值为50 V,由电场强度分布仿真结果(图2b)知,不同的颜色代表同一样品溶液下的不同电场强度; 分别取两侧竖直臂和底部线段EG共4 mm为探测区域,中点2 mm处为理论测量点,记作F点(图3a)。以0.5 mm为取样间距,对测量区域不同取样点进行电场模拟并采集仿真数值绘制电场强度对比图(图3b)。在两侧竖直臂,电场强度稳定在0.65 V/mm;在底部,溶液颜色从下往上由蓝色变为黄色,电场强度由0.48 V/mm增加到0.75 V/mm,变化量达到0.27 V/mm,变化率达到56.3%。
仿真结果表明:样品池两侧竖直臂的电场分布比底部更均匀。
1.3 电泳电场对Zeta电位测量的影响分析
根据电泳光散射法原理和式(4)可知,当散射角和温度等外界条件一定时,颗粒产生的多普勒频移与电场强度成严格的正比例关系,但是由图3的电场仿真结果来看,在传统测量中,样品池底部的电场分布并不均匀。这将严重影响了纳米颗粒测量的准确性和重复性,降低实验的可靠度。
下面以Thermo Fisher Scientific公司的3000系列NanosphereTM聚苯乙烯乳胶微球标准颗粒为例。其标称Zeta电位为(35±3.5)mV[1],在分散介质为蒸馏水,实验温度为25 °,固体激光器的波长为532 nm的条件下,颗粒的电泳迁移率为2.741 7×10-8 m2·V-1·s-1,多普勒频移f为44.3 Hz。结合式(2)—(4),在测量散射角θ′为15 °,折射率为1.332 8的条件下,电场强度E每产生0.27 V/mm的波动,多普勒频移f改变0.72 Hz,电泳迁移率改变0.49×10-8 m2·V-1·s-1,导致Zeta电位变化0.63 mV,理论上产生了2%的测量误差,而在实际测量中可能会导致更大的测量结果误差和波动。因此,电泳电场的不均匀性将影响自相关函数周期的形成,继而影响到频率值的提取,最终影响纳米颗粒溶液Zeta电位的测量结果。
为了进一步探究电泳电场均匀性对散射光光强自相关函数的影响,本文分别在单一电场和电场存在分布的情况下,对散射光光强自相关函数进行仿真实验。该仿真实验条件均与NanosphereTM聚苯乙烯乳胶微球标准颗粒测试实验相同。首先,在单一电场的条件下,颗粒运动只产生单一频率,其频率值为140 Hz,电泳光散射光强自相关函数严格遵循表达式
(5)
其自相关函数曲线的频谱图仿真结果如图4a。假设电场分布不均匀后,标准颗粒的电泳运动速度存在分布,产生多个频率,散射光光强将遵循多个频率按照不同的比例的叠加结果,其数学表达式为
(6)
设置频率分别为50、140、160 Hz,对应比例为20%、60%和20%,其自相关函数曲线的频谱图仿真结果如图4b。

a 单一电场分布

b 多个电场分布
图4 仿真实验频谱图
Fig.4 Simulation experiment diagram
仿真实验图的X轴表示自相关函数的频率值,Y轴表示相应频率的幅值。图4说明了当存在多个电场分布时,不同位置的颗粒的电泳速度存在宽分布,产生了多个的频移量,频谱图的半高宽变宽,幅度变小,导致自相关曲线中周期性被破坏,直接降低信号的信噪比。
1.4 装置
根据ISO标准,本文基于ELS技术设计了2种不同的实验光路并选取U型样品池底部和两侧竖直臂的中点位置作为新的探测点进行探究。
图5为光路及其探测点示意图。
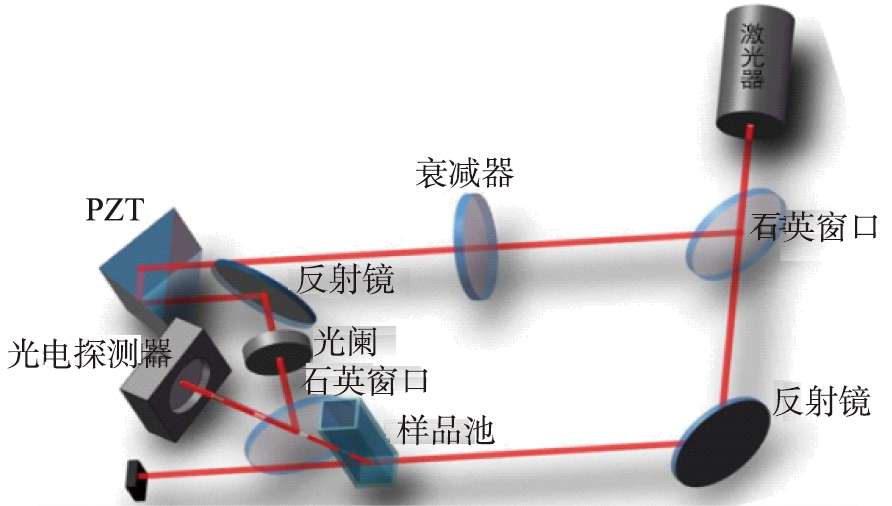
a 光路实验图
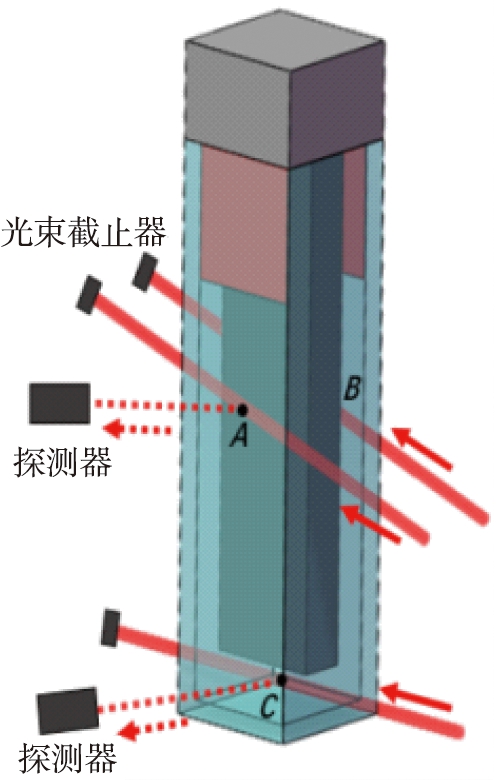
b 探测点示意图
图5 光路及探测点示意图
Fig.5 Optical path and detection point diagram
衰减器的作用是调节参考光光强,控制散射光与反射光的比例[17],以获得信噪比最佳的周期信号曲线。针孔光阑的作用是限制光斑的大小,减少杂散光进入探测器[18]。散射光信号由单模光纤接收。参考光路的光学频移装置采用压电陶瓷(简记为PZT)控制参考光与散射光的光程差,调节光学固定频移量的大小,降低系统的低频频谱分量对实验结果的影响,提高实验的信噪比。
以A点作为散射点进行说明:光源输出光经过反射镜的反射作用,以水平面Z-Y的夹角入射到样品池竖直臂,经过样品颗粒的散射作用后,只有与光轴Z平行的散射光进入探测器,并与参考光发生干涉,得到幅度强弱周期变化的信号,见图5b。
2 结果分析
2.1 光学固定频移量的测量
为了降低系统的低频频谱分量的干扰,在实验搭建过程中,增加光学频移装置,抬高多普勒频移,可以更准确地测量出微弱的电泳迁移率。本文选用的激光器为高稳定性红光激光器(波长为671 nm,功率为200 mW),单次测量时间为10 s,散射角为15 °,水溶液的黏滞系数为0.887 8×10-8,折射率为1.332 8,在室温条件下,选取粒径为800 nm的聚苯乙烯颗粒为实验样品,关闭电泳电压,开启PZT装置,设置其电泳电压为50 V,频率为2 Hz。首先对底部C探测点进行测量,实验中被测的两路光信号经探测器采集,经过硬件相关器处理。然后分别对A和B探测点测量。实验条件与上面均相同。实验所得到的是光学固定频移量,结果如表1所示。
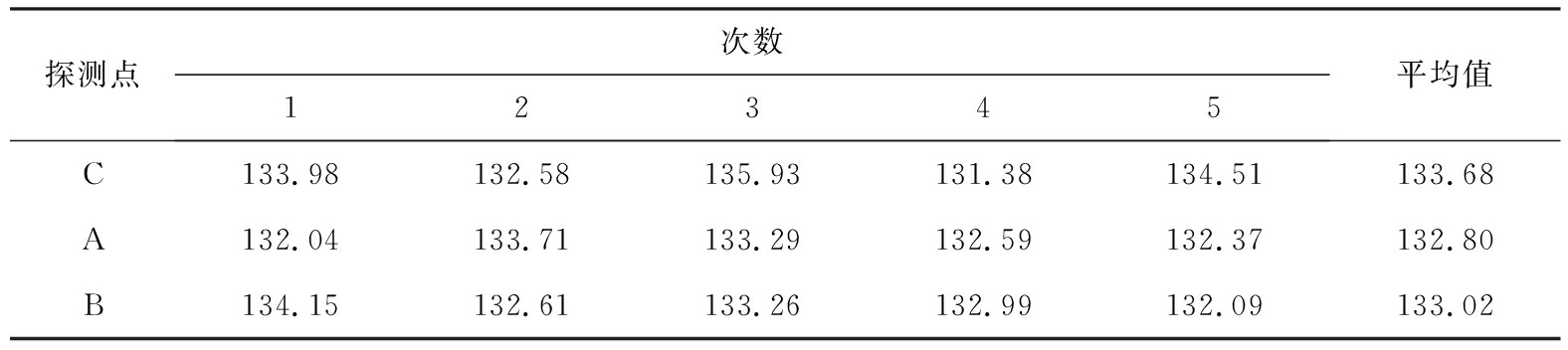
表1 C、A和B探测点的光学固定频移量测量
Tab.1 Optical fixed frequency shift measurement of detection points Hz
探测点次数12345平均值C133.98132.58135.93131.38134.51133.68A132.04133.71133.29132.59132.37132.80B134.15132.61133.26132.99132.09133.02
从表中可以看出,C、A和B探测点的光学固定频移量平均值均在133 Hz左右。在一定程度上,表明所搭建的实验光路的测量稳定性很高,满足后面频移量对比实验的要求。
2.2 同一电泳电压下稳定性对比
为了进一步探究电场稳定性对纳米颗粒溶液Zeta电位测量的影响,在与上文相同的实验条件下,对C、B和A探测点进行了2组对比实验。对比实验1:关闭PZT装置,对样品池平行板电极施加30 V的直流电泳电压,记录频谱分析的峰值作为测试结果,如表2所示。其中,C+30表示探测点在C点,施加正向电泳电压;C-30表示探测点在C点,施加反向电泳电压;以此类推。当施加正向电泳电压时,频率信号是光学固定频移量与多普勒频移之和,施加反向电泳电压时,频率信号是光学固定频移量与多普勒频移之差,籍此算出频移量值及标准差。
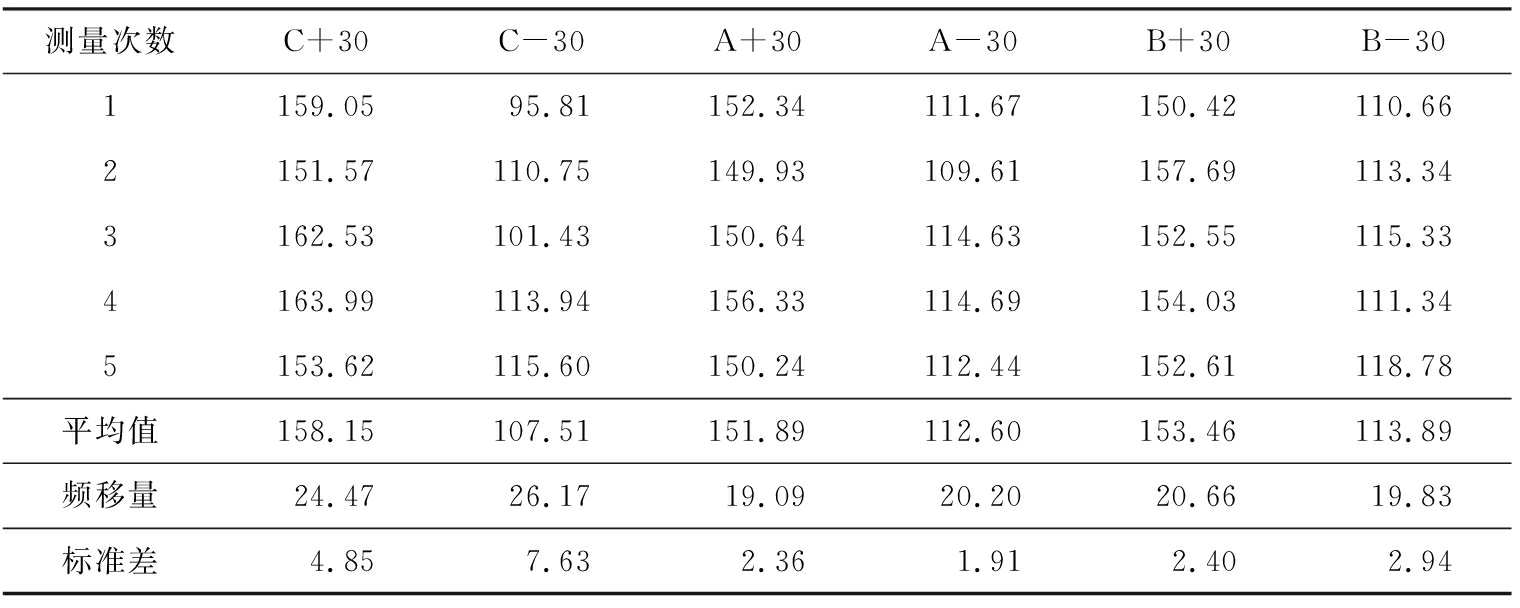
表2 不同散射点频移量的对比
Tab.2 Shift comparison basic on different scattering points Hz
测量次数C+30C-30A+30A-30B+30B-301159.0595.81152.34111.67150.42110.662151.57110.75149.93109.61157.69113.343162.53101.43150.64114.63152.55115.334163.99113.94156.33114.69154.03111.345153.62115.60150.24112.44152.61118.78平均值158.15107.51151.89112.60153.46113.89频移量24.4726.1719.0920.2020.6619.83标准差4.857.632.361.912.402.94
由表可知,在正反等值电泳电压下,C探测点的多普勒频移量相差1.7,A探测点相差1.11,而B探测点相差0.83。在误差的范围内,3个探测点的多普勒频移是相同的,但是在A、B探测点中,最大标准差为2.94,而在C点中,最小标准差为4.85,表明样品池底部的电场分布不均匀性会导致颗粒切割干涉条纹的速度不一样,继而使颗粒的多普勒频移量和电泳迁移率不稳定,因此,利用电场分布更均匀的两侧竖直臂作为探测区域,电泳运动速度更单一,多普勒频移量更稳定。
2.3 不同电泳电压下多普勒频移的测量
为了验证在不同电泳电压下的测量情况,本文中进行了对比实验2:开启PZT装置,并设置其参数为50 V、2 Hz,对样品池平行板电极分别施加20~60 V的电泳电压,实验条件与上文相同,每组实验进行5次,取其平均值。加同一电泳电压时,不更换样品;改变电泳电压时,则更换样品。实验频谱图如图6所示。
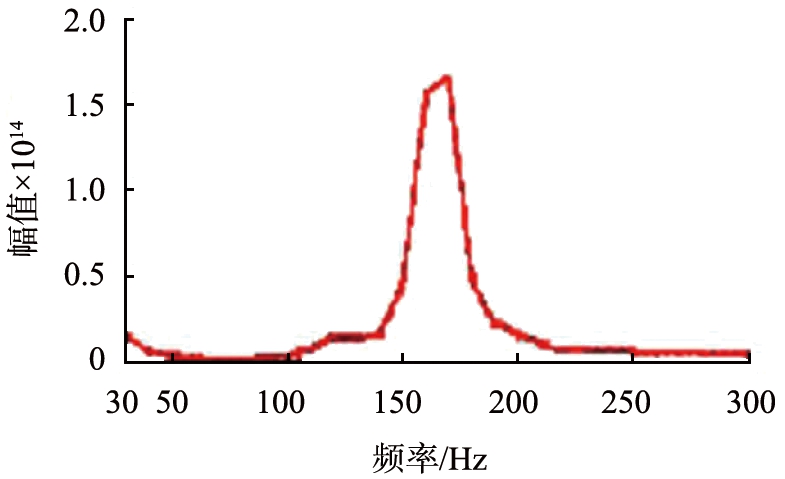
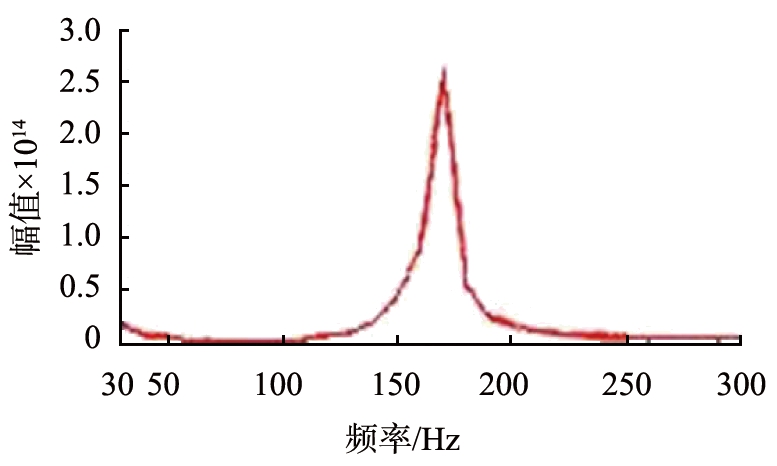
图7为电泳电压与多普勒频移关系的线性拟合图。图7中,A探测点和B探测点的频谱图半高宽分别为15、12.5 Hz,均小于C探测点的半高宽25 Hz。A、B探测点频谱图与C探测点相比,曲线中峰值位置更陡峭而明显,与噪声的对比度更明显,信噪比更高,与仿真图相符。说明当探测点选取在样品池底部时,电场的不均匀产生多个电泳运动速度,导致多普勒频移具有宽分布,影响了自相关曲线图周期信号的形成,降低了实验的信噪比。表3—5分别为C、A和B探测点的多普勒频移量和Zeta电位参数。
a C点

b A点
c B点
图6 实验频谱图
Fig.6 Experimental spectrum diagram
表3 C点颗粒Zeta电位
Tab.3 Zeta potential basic at C
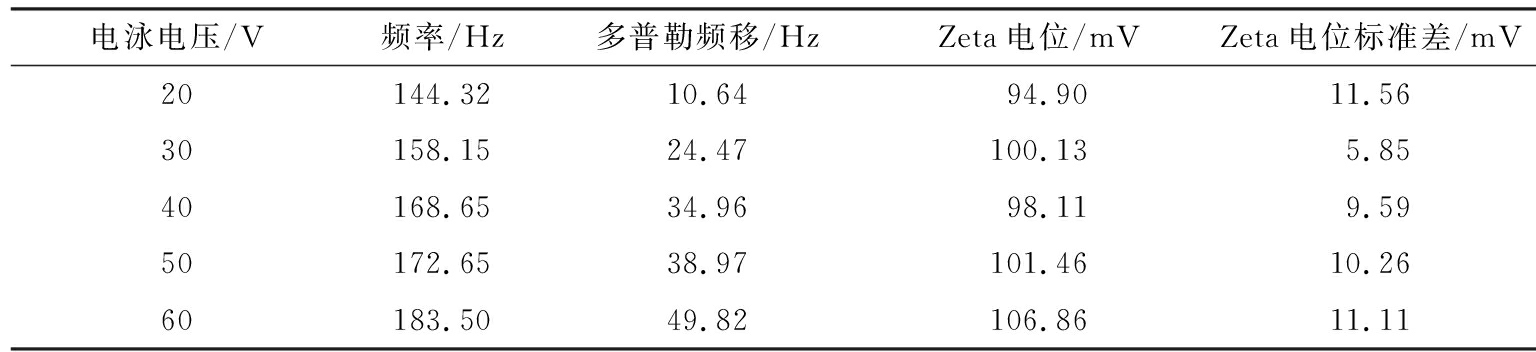
电泳电压/V频率/Hz多普勒频移/HzZeta电位/mVZeta电位标准差/mV20144.3210.6494.9011.5630158.1524.47100.135.8540168.6534.9698.119.5950172.6538.97101.4610.2660183.5049.82106.8611.11
表4 A点颗粒Zeta电位
Tab.4 Zeta potential basic at A

电泳电压/V频率/Hz多普勒频移/HzZeta电位/mV标准差/mV20144.0311.23101.892.4130151.8919.09103.082.3640162.5129.71100.262.2050174.2541.45102.901.8360186.5453.74101.752.94
表5 B点颗粒Zeta电位
Tab.5 Zeta potential basic at B
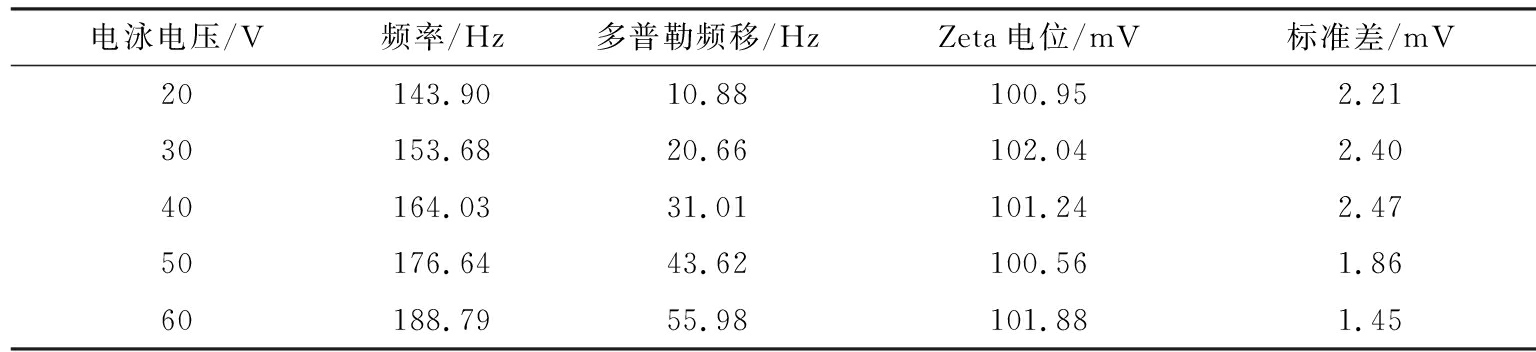
电泳电压/V频率/Hz多普勒频移/HzZeta电位/mV标准差/mV20143.9010.88100.952.2130153.6820.66102.042.4040164.0331.01101.242.4750176.6443.62100.561.8660188.7955.98101.881.45
对表3的电泳电压与多普勒频移做一次线性拟合,拟合结果如图7和表6所示。
在表3中,每增加10 V的电泳电压,多普勒频移增加约10 Hz,即纳米颗粒的多普勒频移与施加的电泳电压遵循正相关的关系。此外,在20~60 V的不同电泳电压条件下,A和B探测点的Zeta电位最大标准差为2.94 mV,是底部C探测点最低标准差的1/2。说明实验探测点选取在电场更均匀的U型样品池两侧竖直臂,纳米颗粒运动速度单一,只产生单一的多普勒频移,提高了测量结果的稳定性。
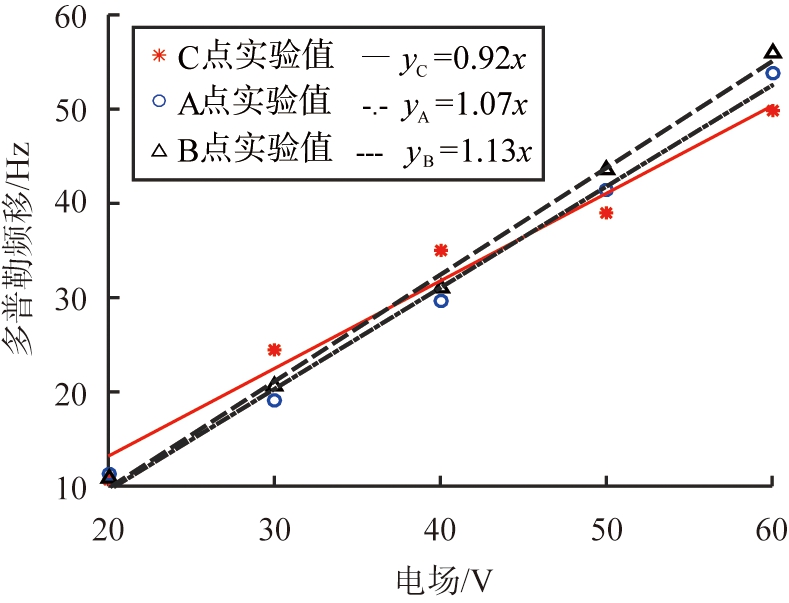
图7 电泳电压与多普勒频移关系的线性拟合图
Fig.7 Linear fitting chart of relation between voltage and doppler frequency shift
表6 电泳电压与多普勒频移的拟合曲线参数
Tab.6 Fitting curve parameters of electrophoretic voltage and doppler frequency shift

探测点拟合曲线关系式拟合度Cy=0.92x0.971 5Ay=1.07x0.993 4By=1.13x0.996 7
在表6中,A和B探测点的一次线性拟合度R2超过0.99,C探测点的一次线性拟合度R2仅为0.97。说明电场的不均匀性影响了颗粒运动的速度,使电泳速度产生宽分布,导致产生多个频移量,降低了纳米颗粒溶液Zeta电位测量的准确性和重复性。
3 结论
1)基于U型样品池改善了直插式的电极结构,通过对样品池进行电场仿真实验,发现样品池两侧竖直臂的电场强度稳定在在0.65 V/mm;而在底部,电场强度由0.48 V/mm增大到0.75 V/mm,变化率达到56.3%。
2)采用800 nm聚苯乙烯带电颗粒悬浮液设计基于电泳光散射法的对比实验,当探测点选取在电场更均匀的样品池两侧竖直臂中点时,频谱图的半高宽比底部探测点的半高宽减少40%以上;多普勒频移与电泳电压的线性拟合优度R2超过0.99,其Zeta电位值最大标准差仅为2.94 mV,是底部探测点最低标准差的一半。
3)U型样品池两侧竖直臂的电场稳定性高于底部,探测点选取在两侧竖直臂时,电泳运动速度单一,产生单一的多普勒频移,大大提高了纳米颗粒溶液Zeta电位测量的准确性和稳定性。
[1]刘伟,张珊珊,THOMAS J C,等. 基于频谱细化算法的电泳光散射Zeta电位测量方法[J]. 光学学报,2017,37(2):292-298.
[2]HUNTER R J, OTTEWILL R H, ROWELL R L. Zeta potential in colloid science[J]. Academic Press, 2013(3): 23-25.
[3]史亚荣,翁羽翔. 硅纳米颗粒大小对表面电荷特性的影响[C]//第十五届全国化学动力学会议论文集.南京:2017:137.
[4]朱龙辉. 电荷零点的测定与胶体凝聚Hofmeister效应的激光散射研究[D]. 重庆: 西南大学,2015.
[5]林瑜,杨光参,王艳伟. DNA平衡离子凝聚的动态光散射分析[J]. 物理学报,2013,62(11):554-559.
[6]王旭亮,赵静红,李宗雨,等. 基于Zeta电位法研究腐殖酸对超滤膜的污染[J]. 中国给水排水,2018,34(17):48-51.
[7]叶仲斌,徐金腾,印风军,等. 注入水成分对油藏中液固界面Zeta电位的影响[J]. 精细化工,2018,35(10):1765-1771.
[8]ANTHONYJ H, GIOVAGNOLI S. Particle size measurement[M]. Cham: Springer International Publishing, 2018: 43-53.
[9]XU R L. Books particle characterization: light scattering methods[J]. China Particuology, 2003(6): 271.
[10]聂德明. 毛细管电泳通道中的弯道效应及其消除[D]. 杭州:浙江大学,2004:69.
[11]荆兆东,白凤民. 光波干涉法在检定中的应用[J]. 品牌与标准化,2010(8):16.
[12]骆开庆,黄华娟,郑晓芬. 纳米颗粒电泳光散射法中自相关函数推导及仿真与实验结果[C]//第十七届中国科协年会——分3面向智能制造的先进测控技术学术会议论文集.2015.
[13]秦福元,刘伟,王文静,等. Zeta电位计算过程中Henry函数的优化表达式[J]. 光学学报,2017,37(10):328-335.
[14]HENRY D C. The cataphoresis of suspended particles. part I. the equation of cataphoresis[J]. Proceedings of the Royal Society. a: Mathematical, Physical and Engineering Sciences, 1931(133): 106-129.
[15]陈婷. 二氧化铅的微纳化及其电化学性能研究[D]. 济南:山东大学, 2014.
[16]李文宣,谷峰颉,蔺红,等. 基于ANSYS软件的尖-板电场分布仿真分析[J]. 中国电力教育,2014(12):249-250.
[17]李誉昌,吴晓斌,朱苏皖,等. 双分散纳米颗粒系不同光强贡献比例下的动态光散射特性研究[J]. 华南师范大学学报(自然科学版),2015,47(3):24-28.
[18]郝瑞锋,邱健,彭力,等. 基于电泳光散射的纳米颗粒Zeta电位分析仪的研制[J]. 自动化与信息工程,2018,39(2):1-7.