近年来,矿山、冶金、煤炭等行业对于矿石粉碎的需求呈现高速增长的趋势。据统计,我国每年经过粉碎工艺处理的矿石量高达150亿t,研究岩石的破碎能耗和过程具有重要意义[1]。
岩石是经过长期地质作用形成的具有各向异性的混合物。离散元法(distinct element method, DEM)能够比较直观地分析描述岩石颗粒的离散特性和力学特性,可用来建立符合真实岩石特性的岩石物理模型,是研究岩石破碎过程、岩石内部机理、预测岩石的碎后粒度的一种非常有效的方法[2-5]。
Potyondy等[6]提出了岩石颗粒粘结模型;Brown等[7]创建了水泥颗粒间粘结键模型; 母福生等[8]利用DEM进行了单轴压缩试验, 分析了颗粒的破碎能耗和概率; 孙其诚等[9]研究了岩石颗粒间的接触和粘结结构; 吴成宝等[10]构建了黏土颗粒表面的分维数学模型; 陶贺等[11]通过对椭圆形颗粒动力学效应的比较, 得出了颗粒的椭圆形颗粒模型; Wang等[12]建立了类似圆盘形状的颗粒群模型; Cheng等[13]构建了动态填充颗粒的方法, 但该方法计算量太大,计算效率较低。 尽管学者们对不同类别的矿石进行了大量研究, 建立了相对应的岩石颗粒模型, 但根据真实岩石内部细观特征构建岩石颗粒模型, 进而分析岩石的破碎特性的文献较为少见。
本文中根据岩石的异形特征和岩石递级破碎的概念,建立符合真实岩石内部特性的异形多级颗粒模型,并在振动慢剪破碎机上进行数值模拟试验;通过与破碎实验对比验证模型的正确性,为研究岩石破碎机理、预测岩石碎后粒度提供理论依据。
1 多级颗粒几何模型
自然界存在的岩石都是外形和内部极其复杂的混合物,岩石颗粒的几何形状呈现多尺度特性[14]。实验采用3类具有代表性的异形岩石模型:类圆岩石模型、类三角岩石模型、类正岩石模型。异形岩石的岩样如图1所示。

图1 异形岩石岩样
Fig.1 Rock samples of different shapes
采用关节臂测量机与Scanworks V5激光扫描相结合,获得岩石外形3D云点数据,用Geomagic Studio软件处理后导入Solidworks中,获得相应的异形岩石三维几何模型,如图2所示。

图2 异形岩石几何模型
Fig.2 Geometric models of irregular rocks
岩石是由长期的地质作用形成的聚合物,为了能更加清晰地观察岩石的内部岩相结构,利用高倍显微镜观察黑钨矿岩石的表面,岩石样本及其岩相如图3所示。

图3 岩石样本及其岩相
Fig.3 Rock samples and their petrographic facies
由图3可知,岩石是由许多亮白色的小颗粒通过某种暗黑色物质粘结在一起形成的聚合物。为了表现这一特性,需要进一步优化岩石模型。岩石是在外力作用下经由多级破碎后才由大岩石颗粒而破碎成细小岩石颗粒的,因此,定义粒径为40~50 mm的原岩石为一级岩石颗粒,对一级岩石颗粒进行填充后形成的颗粒为二级颗粒,对二级颗粒中粒径较大的颗粒进行填充后形成的颗粒称之为三级颗粒。
利用EDEM对3种形状的岩石进行颗粒填充, 形成不同形状的岩石颗粒簇, 颗粒模型的构建过程如图4所示。 由图4可以看出, 一级颗粒(即岩石模型)是由许多二级颗粒组合在一起形成的颗粒簇, 二级颗粒中的较大颗粒又是由三级颗粒组合在一起形成的颗粒簇。
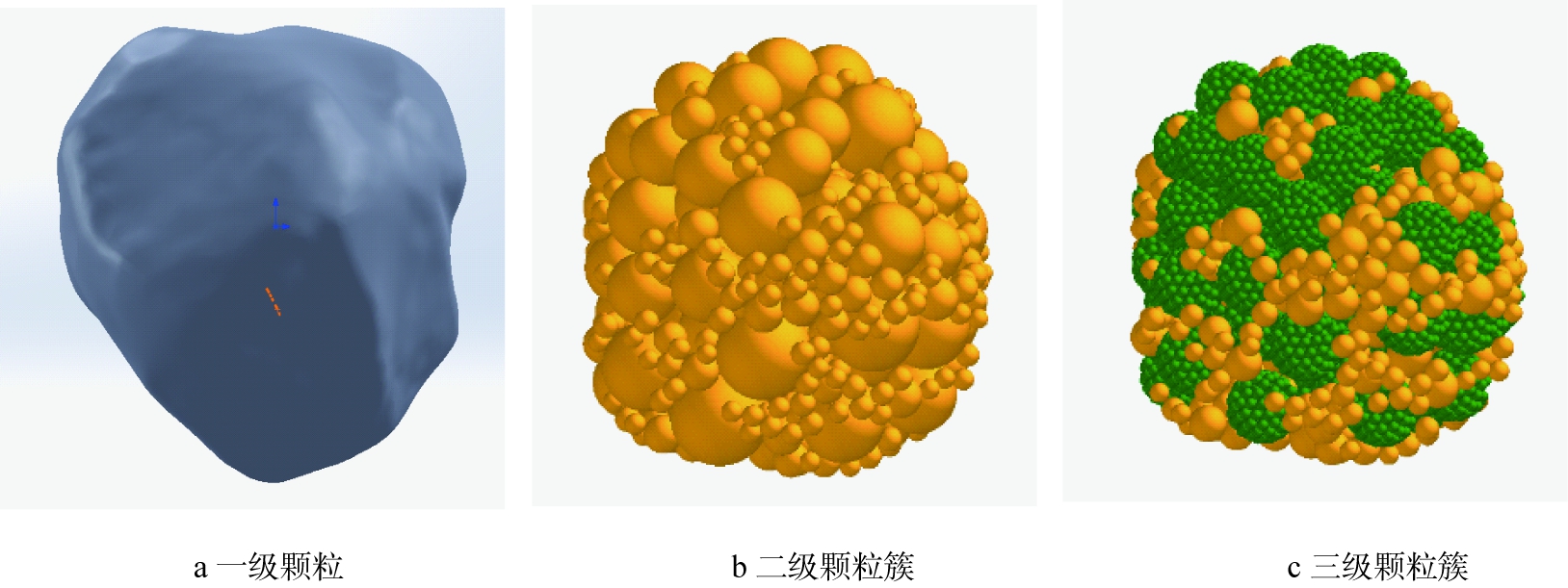
图4 颗粒模型的构建过程
Fig.4 Process of constructing particle models
当岩石受到外力作用时,二级岩石颗粒簇中的部分颗粒逐渐脱离出来,这一过程对应破碎实验中大粒径岩石破碎成中等岩石颗粒;再继续施加外力时,脱离出来的二级颗粒进一步破碎成三级岩石颗粒,对应破碎实验过程中等岩石破碎成小粒径岩石,因此,异形多级颗粒模型能很好地模拟真实岩石由大粒径岩石逐级破碎成小粒径岩石这一破碎过程。
2 多级颗粒力学模型
异形多级颗粒模型只描述了岩石颗粒的几何特征,岩石内部的力学特性还需要进行定义,即需要对图3b中的暗黑色和亮白色物质进行定义。
通过观察岩石的岩相特征发现: 二级亮白色岩石颗粒之间、 三级亮白色岩石颗粒之间、 二级与三级亮白色岩石颗粒之间都是由相同的暗黑色物质粘结在一起, 区别在于粘结的强度不一样。 结合离散元的BPM理论, 岩石的粘结模型用粘结键的强度来表示各级岩石颗粒之间的粘结强度。 当小颗粒岩石在外力的作用下脱离后, 碎后颗粒与原岩石颗粒间将不再是粘结键, 从而形成岩石颗粒间的接触。
2.1 粘结模型
根据单元BPM理论和力-位移线弹性本构模型,假设岩石颗粒与颗粒之间存在圆柱形的重叠区域(即粘结键),该区域的力学关系满足线弹性理论,即
F=KU,
(1)
式中:F为颗粒单元间粘结键所受的力,N;K为粘结键刚度矩阵;U为粘结键位移,m;其计算公式为
(2)
(3)
(4)
(5)
式中:![]() 为粘结键的法向力、切向力,
为粘结键的法向力、切向力,![]() 为法向力矩、切向力矩,
为法向力矩、切向力矩,![]() 为法向刚度和切向刚度;δn、 δt为法向和切向位移,m;θn、 θt为法向和切向角位移,rad;rb为粘结键半径,m。
为法向刚度和切向刚度;δn、 δt为法向和切向位移,m;θn、 θt为法向和切向角位移,rad;rb为粘结键半径,m。
二级岩石颗粒间的粘结键刚度与三级岩石间的粘结键刚度关系[16]为
(6)
当岩石受到外部载荷的持续作用时,岩石内部颗粒间的粘结键所受的力满足σ>σmax和τ>τmax时颗粒之间的粘结键会发生断裂,其中法向应力σ和切向应力τ满足
(7)
(8)
根据不同形状的岩石颗粒模型就可得到各模型下的各级岩石颗粒间粘结键的法向强度σ和切向强度τ。
2.2 接触模型
岩石内部颗粒的接触关系是比较复杂的,具有各向异性和非规则等特点,定义颗粒间的接触模型时选用接触刚度随位移和接触力非线性变化的Hertz-Mindlin接触模型,如图5所示为接触模型示意图。
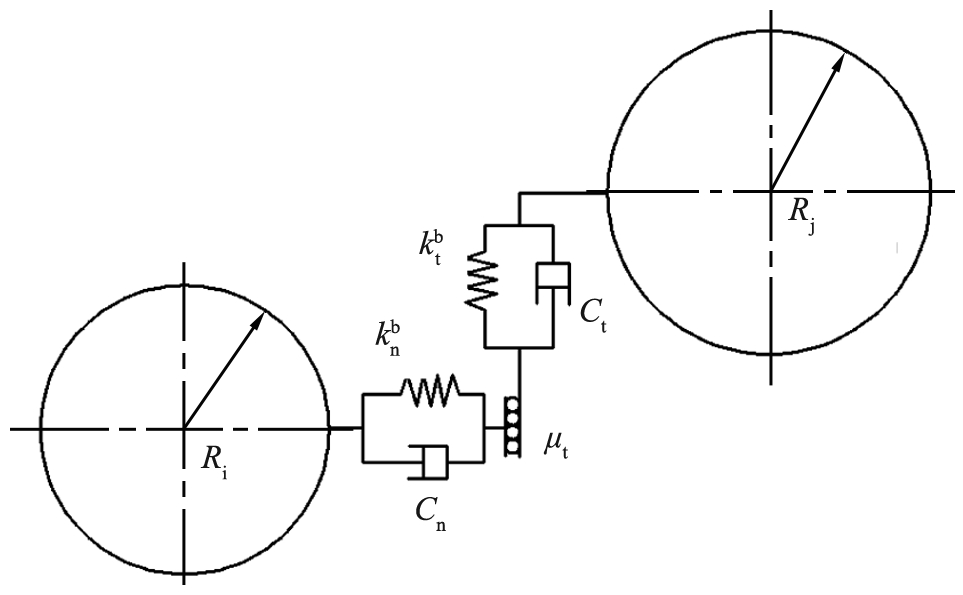
图5 Hertz-Mindlin接触模型示意图
Fig.5 Hertz-Mindlin contact model diagram
2个颗粒单元之间的力学关系满足以下关系式:
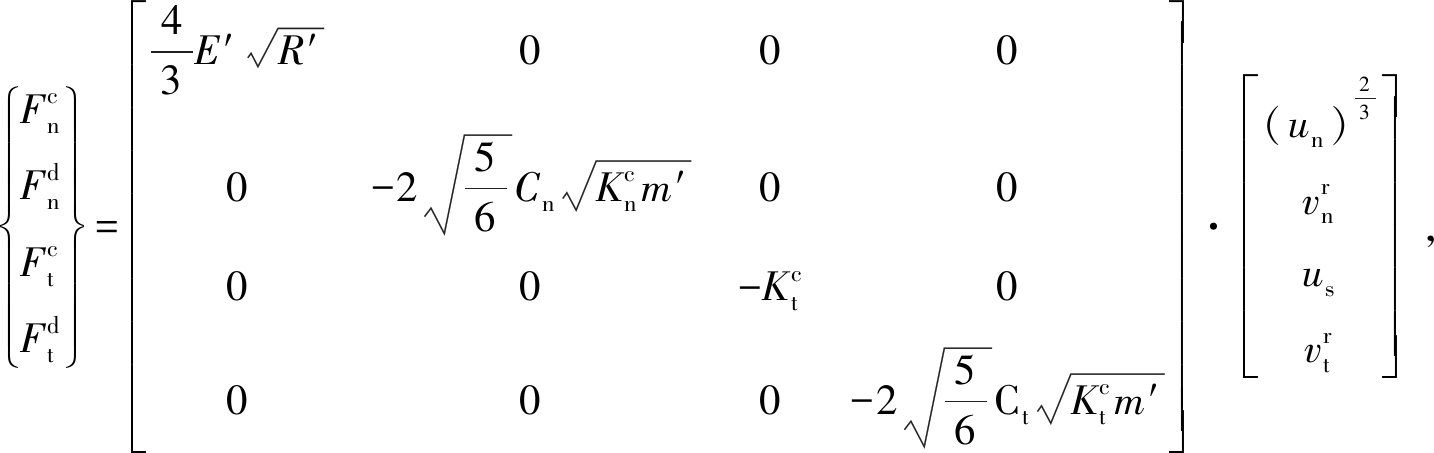
(9)
式中:E′为当量杨氏模量,GPa;R′为当量半径,mm;M′为当量质量,kg;Un、 Us为颗粒间的切向和法向位移,![]() 为颗粒间的阻尼系数;
为颗粒间的阻尼系数;![]() 为颗粒间的法向和切向刚度系数,N/m3。
为颗粒间的法向和切向刚度系数,N/m3。
当二级岩石颗粒间的粘结键断裂后形成接触,便可利用式(9)来进行颗粒间的力传递计算,从而保证岩石外部载荷的作用力能实时地作用在具有粘结键的岩石颗粒簇上。
3 模拟试验及破碎实验
3.1 破碎实验机的三维模拟模型
为了探究内聚异形颗粒模型的破碎特性,将实验室现有的振动慢剪破碎机进行简化,并利用EDEM进行数值模拟试验,破碎实验机的三维模型如图6所示。 破碎实验机主要由机架、 内锥、 外锥、 底座、 传动轴和减速器等部分组成。 外锥作圆周运动, 内锥在振动电机的作用下作正弦运动。 岩石颗粒在重力作用下落到内锥与外锥的间隙, 在外锥带动下受到挤压, 被破碎后逐步向下运动, 直至完全破碎。
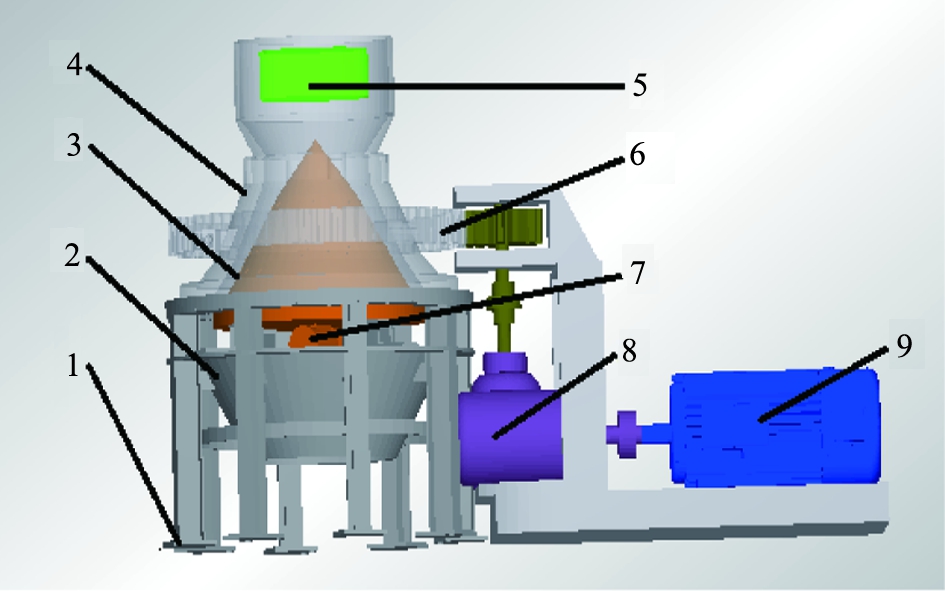
1—机架;2—底座;3-内锥;4—外锥;5—入料口;
6—传动齿轮;7—振动电机;8—减速器;9—主电机。
图6 破碎实验机的三维模型
Fig.6 Three-dimensional model of the
experimental crushing machine
振动慢剪破碎实验机的主电机功率为37 kW, 振动电机功率为2.2 kW。破碎试验机的工作参数设为:内锥振动电机频率分别为20、 30、 40、 50 Hz,外锥转速分别为15、 30、 45、 60 r/min,内、外锥排料间隙为5 mm,入料速度为50 kg/s,岩石粒径范围为40~50 mm。
3.2 岩石颗粒的材料力学特性
采用钨矿石进行破碎实验。钨矿石的本征参数如表1所示,钨矿石接触参数如表2所示。设定二级颗粒与三级颗粒的粒径比为5,根据BPM理论计算得到的颗粒簇之间的粘结参数如表3所示。
表1 钨矿石的本征参数
Tab.1 Intrinsic parameters of tungsten ore

密度/(kg·m-3) 泊松比剪切模量/GPa2 8300.3525
表2 钨矿石的接触参数
Tab.3 Contact parameters of tungsten ore
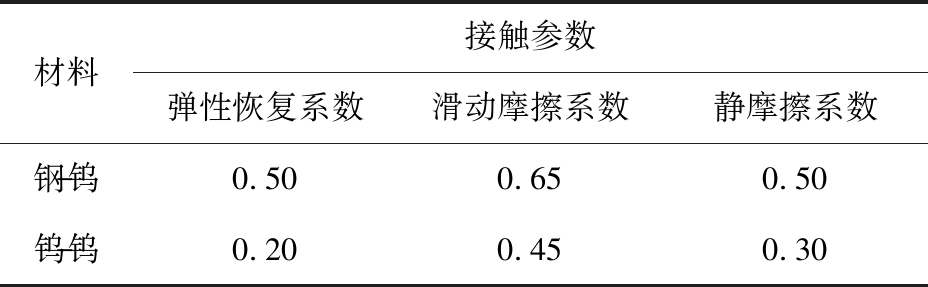
材料接触参数弹性恢复系数滑动摩擦系数静摩擦系数钢-钨0.500.650.50钨-钨0.200.450.30
表3 颗粒簇之间的粘结参数
Tab.4 Binding parameters between ore particle clusters

颗粒簇粘结刚度/(N·m-3)法向切向粘结强度/Pa法向切向二级-二级7.55E+123.26E+123.50E+092.32E+08三级-三级1.51E+126.51E+117.01E+084.65E+07
3.3 试验结果分析
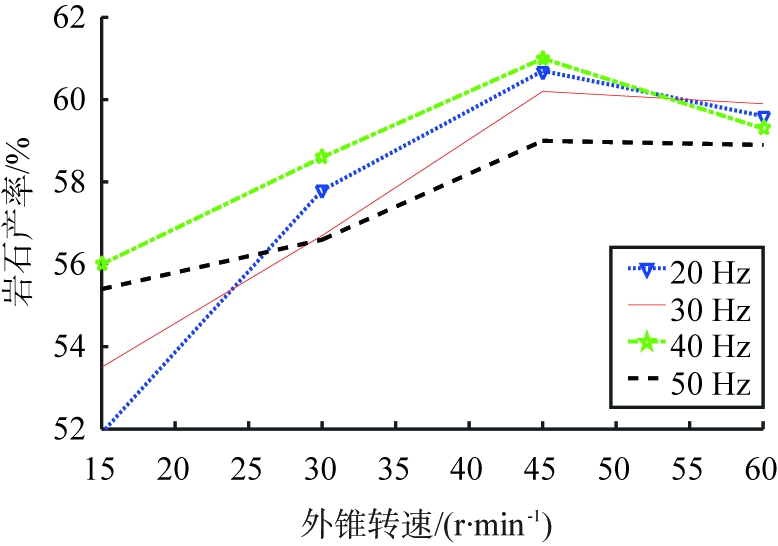
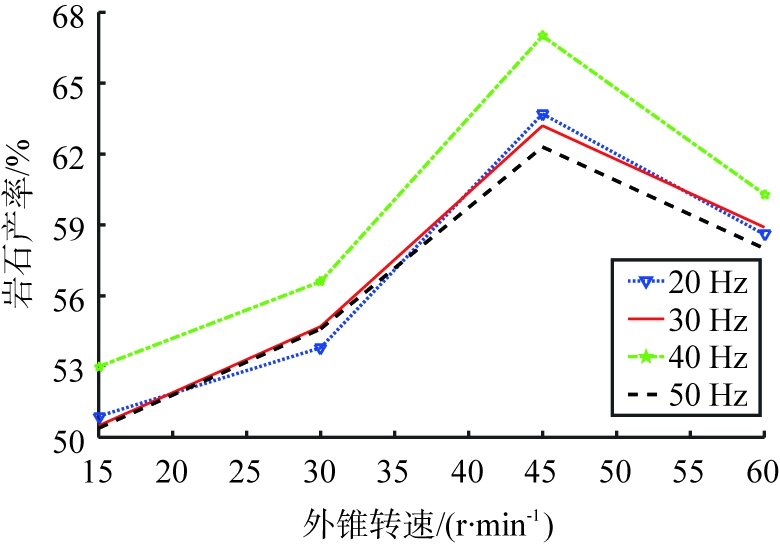
根据上述条件进行破碎实验和数值模拟试验, 分别绘制出破碎后岩石粒度<4、 <8、 ≥8 mm时外锥转速与岩石产率之间的关系曲线如图7、 8、 9所示。
a 破碎实验
b 数值模拟试验
图7 破碎后岩石粒度<4 mm时
岩石产率与外锥转速的关系
Fig.7 Relationship between rock yield and
external cone speed when particle size of crushed
rock is less than 4 mm
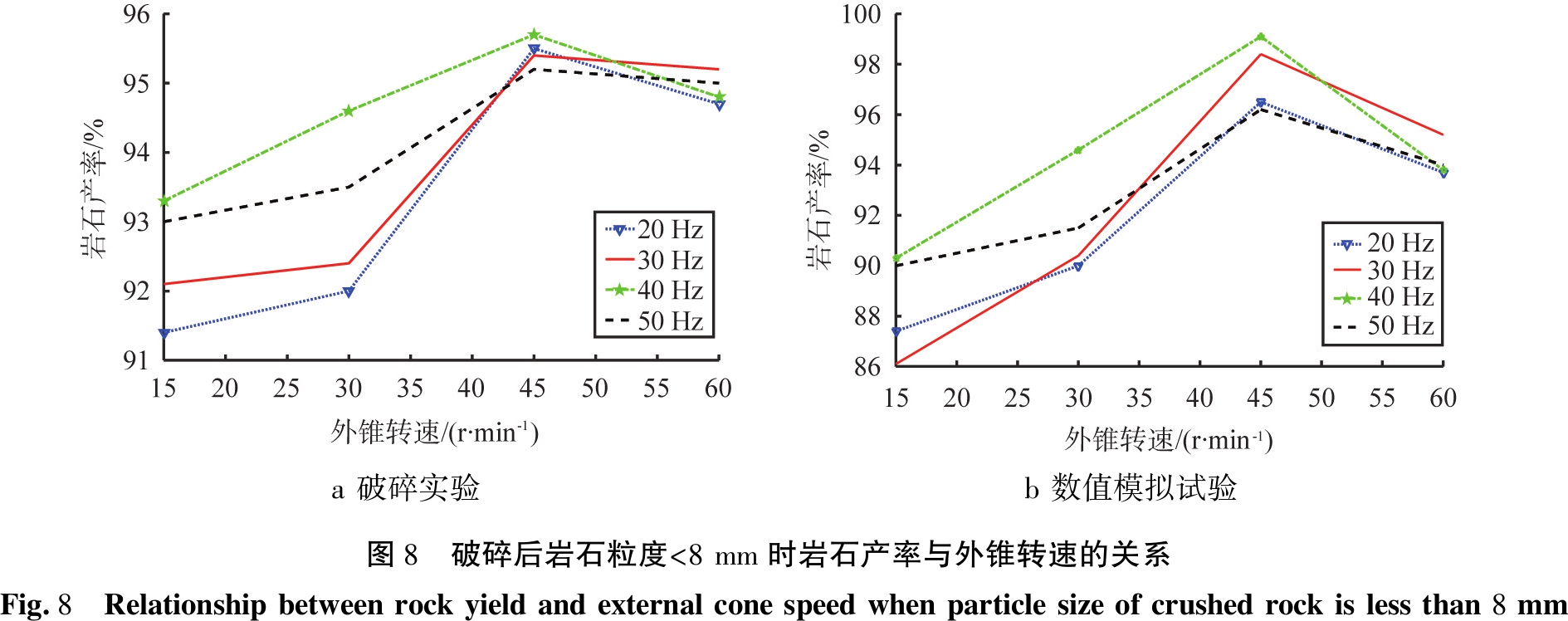
a 破碎实验b 数值模拟试验图8 破碎后岩石粒度<8 mm时岩石产率与外锥转速的关系Fig.8 Relationship between rock yield and external cone speed when particle size of crushed rock is less than 8 mm

a 破碎实验b 数值模拟试验图9 破碎后岩石粒度≥8 mm时岩石产率与外锥转速的关系Fig.9 Relationship between rock yield and external cone speed when particle size of crushed rock is greater than or equal to 8 mm
结合图7、8、9的分析结果可以发现,破碎实验与数值模拟试验的结果基本一致,即当破碎机的外锥转速为45 r/min、内锥振动频率为40 Hz时,振动慢剪破碎机的岩石产率最高,破碎效果最好,这说明建立的多级颗粒模型能模拟岩石的破碎实况。
为了分析数值模拟实验与破碎实验结果的相关性,相关系数可由下式计算得出:
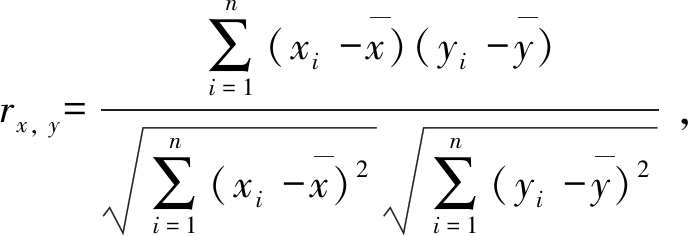
(10)
式中:n为数据的长度;xi、yi为数值模拟实验与破碎实验的曲线数据值。
在MATLAB下进行数值模拟试验与破碎实验相关度的分析计算,可知岩石粒度<4 mm时2条曲线的相关系数为0.95,<8、≥8 mm时曲线的相关系数均为0.97。表明数值模拟试验与破碎实验的结果相似度较高,故建立的异形多级颗粒模型能够预测岩石破碎实验结果。
4 结论
结合岩石的几何外形特征与内部力学特性构建了多级岩石颗粒模型,并在振动慢剪破碎三维模型试验机下进行数值模拟岩石颗粒破碎过程,与破碎实验结果进行对比分析,得到以下结论:
1)不同破碎机内锥频率下,对比岩石产率与破碎机外锥转速的关系曲线,发现数值模拟试验与破碎实验结果曲线趋势大致相同。
2)破碎机内锥频率40 Hz、外锥转速为45 r/min时,岩石产率最高,破碎效果最好。
3)最优内锥频率下的岩石产率曲线相关度表明,建立的异形多级颗粒模型能较好的模拟岩石破碎机理,为岩石破碎实验提供了有效的数值模拟三维模型。
[1]米占宽, 李国英, 陈生水. 基于破碎能耗的粗颗粒料本构模型[J]. 岩土工程学报, 2012, 34(10): 1801-1811.
[2]METZGER M J, GLASSER B J. Simulation of the breakage of bonded agglomerates in a ball mill[J]. Powder Technology, 2013, 237: 286-302.
[3]应振根, 冯凯萍, 倪成员. 基于PFC3D的研磨片研磨过程离散元仿真[J]. 机电工程, 2015, 32(6): 757-761.
[4]CUNDALL P A. Computer simulations of dense sphere assemblies[J]. Studies in Applied Mechanics, 1988, 20: 113-123.
[5]FORTIN J, MILLET O, SAXCE G. Numerical simulation of granular materials by an improved discrete element method[J]. International Journal for Numerical Methods in Engineering, 2005, 62(5): 639-663.
[6]POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(8): 1329-1364.
[7]BROWN N J, CHEN J F, OOI J Y. A bond model for DEM simulation of cementitious materials and deformable structures[J]. Granular Matter, 2014, 16(3): 299-311.
[8]母福生, 栗慧, 熊宏志. 离散单元法在单颗粒物料单向压缩下的能耗研究[J]. 有色金属(选矿部分), 2013(1): 48-51.
[9]孙其诚, 金峰, 王光谦. 密集颗粒物质的多尺度结构[J]. 力学与实践, 2010, 32(1):10-15.
[10]吴成宝, 胡小芳, 胡大为. 黏土颗粒表面分维模型的构建及其应用[J]. 土壤, 2007, 39(3): 439-442.
[11]TAO H, ZHONG W Q,JIN B S. Comparison of construction method for DEM simulation of ellipsoidal particles[J]. Chinese Journal of Chemical Engineering, 2013, 21(7):800-807.
[12]WANG L, PARK J Y, FU Y. Representation of real particles for DEM simulation using X-ray tomography[J]. Construction and Building Materials, 2007, 21(2): 338-346.
[13]BRUGADA J, CHENG Y P, SOGA K, et al. Discrete element modelling of geomechanical behaviour of methane hydrate soils with pore-filling hydrate distribution[J]. Granular Matter, 2010, 12(5): 517-525.
[14]郭进山, 蔡改贫, 卢小江, 等. 一种多尺度内聚颗粒模型的构建方法及数值模拟研究[J]. 科学技术与工程, 2016, 16(8): 72-78.
[15]蔡改贫, 肖洪力, 郭进山, 等. 基于多尺度内聚颗粒模型的挤压分级破碎研究[J]. 岩石力学与工程学报, 2018(S1):3557-3567.
[16]夏刘洋. 基于多尺度内聚颗粒模型的振动挤压破碎过程研究[D]. 赣州:江西理工大学,2016.