辊筒棒磨机是一种新型的细磨机械设备，以其结构紧凑、传动简单、磨矿效率高等特点，广泛应用于磨矿、选矿行业[1]。磨矿过程中，棒磨机的主要技术参数和工况直接影响其磨矿性能，进而影响选矿厂的经济指标，因此，无论是对于使用者还是设计制造以及研究者，高产能、高品质、节能环保的棒磨机是大家一致追求的。
多年来，人们围绕磨矿过程的优化问题进行了大量研究工作。汤素燕基于线性叠加原理设计优化实验，对棒磨机的工艺参数进行优化[2]，其优化方法实为单目标优化问题。而在实际磨矿生产过程中，磨矿目标往往不只一项，单目标规划模型很难有效表达，并且在很多情况下，磨矿目标之间相互冲突，单目标规划模型就显得无能为力[3]。对此，多目标模型的优越性在磨矿领域得以显现。盖国胜等建立了磨矿过程多目标优化模型，并将多目标优化问题转化为单目标问题进行求解[4]，但这种方法在权重的选取上存在争议，在求解过程中，很难找到让决策者满意的Pareto最优解。Mitra[5]介绍了一种应用在磨矿过程中的优化算法，但所用模型为BS模型，优化研究过程中矩阵元素难以准确测定，影响研究结果的可信度。
鉴于此，本文中以多辊筒棒磨机为研究对象，综合分析了影响棒磨机磨矿性能的因素，选取的5个主要因素作为设计变量，建立以磨机生产转化率、产物均匀度为目标函数，能源利用效率为约束条件的多目标优化模型。利用改进的遗传算法，结合实验记录数据，求解得出模型的最优解集，并用优劣解距离法(technique for order preference by similarity to an ideal solution, TOPSIS)搜寻出多目标优化的最优解。结果表明，建立的模型能较好地描述辊筒棒磨机的磨矿性能；利用改进的遗传算法，较好地解决了模型的求解问题；最终经过优化的棒磨机，磨矿性能得到了明显的提升。
1 辊筒棒磨机的工作原理
多辊筒棒磨机结构示意图如图1所示，其主要由机架、研磨筒、动力系统、拖动辊部分、传动系统和电器控制系统等组成。
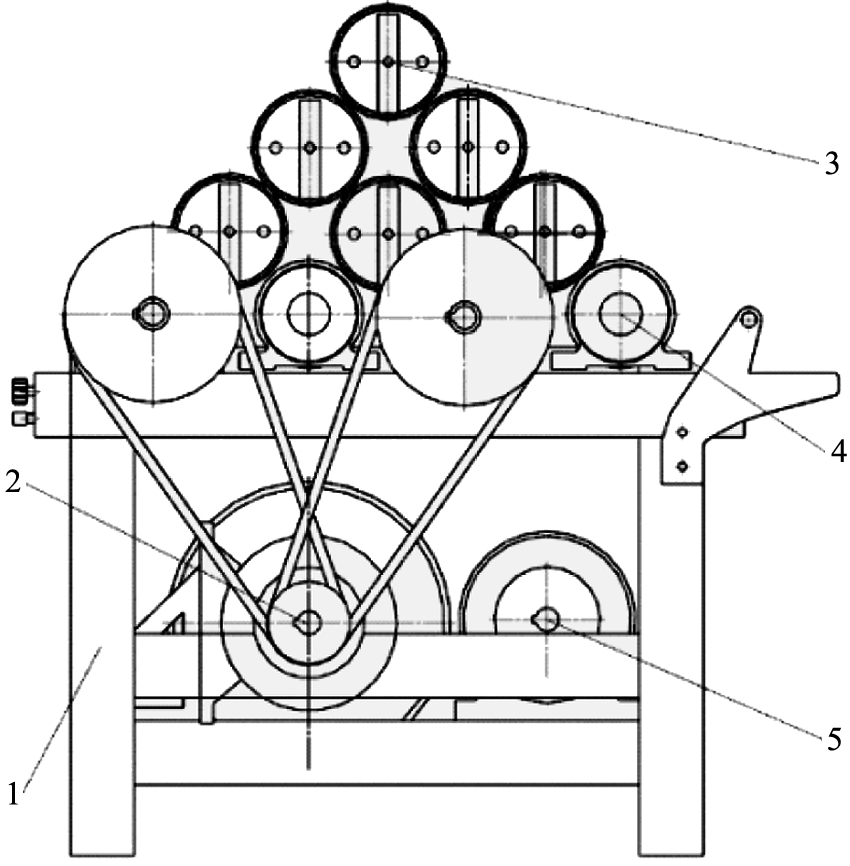
1—机架；2—减速器；3—研磨筒；4—拖动辊；5—电机。图1 辊筒棒磨机结构示意图
Fig.1 Roller rod mill structure diagram
拖动辊通过支撑轴承与机架相连，底层的研磨筒架设在相邻的2根拖动辊之间，上一层的研磨筒架设在相邻的2根研磨筒之间，研磨筒的数目可根据待磨的矿物多少来确定。矿料及磨矿介质装进研磨筒中待磨。
辊筒棒磨机运用摩擦传动方式，拖动辊在电机的带动下使研磨筒旋转,研磨筒内的钢棒撞击矿石物料,钢棒之间的粗颗粒首先破碎,而细颗粒则受到一定程度的保护；当钢棒沿筒体内壁向上提升时,夹在钢棒之间的细颗粒从缝隙中漏出,从而使粗颗粒集中受到钢棒落下时的冲击破碎。同时物料之间、物料与滚筒壁也产生碰撞、摩擦等运动,使物料研磨成粉状,达到制粉效果。其结构紧凑、传动简单，且磨矿过程具有选择性粉碎作用，不易产生过粉碎现象，从而磨矿产物粒度较均匀,磨矿效果好[6]。
2 磨矿性能评价模型
2.1 磨矿性能影响因素分析
根据多辊筒棒磨机的工作原理与结构特点分析，将影响磨矿性能的因素可归纳为3个方面：物料的性质(包括给料粒度、易磨度、产品细度)，磨机的结构和转速，操作条件(包括装棒制度、磨矿浓度和给矿速率等)[7-9]。综合考虑以上因素，在较多变量中选出稳定、具有代表性，且在现有条件下可测可控的相对参变量。以长度L、质量M、时间T为基本量纲，参变量的符号、国际单位以及量纲如表1所示。
表1 参变量的单位及量纲
Tab.1 The unit and dimension of the parameter
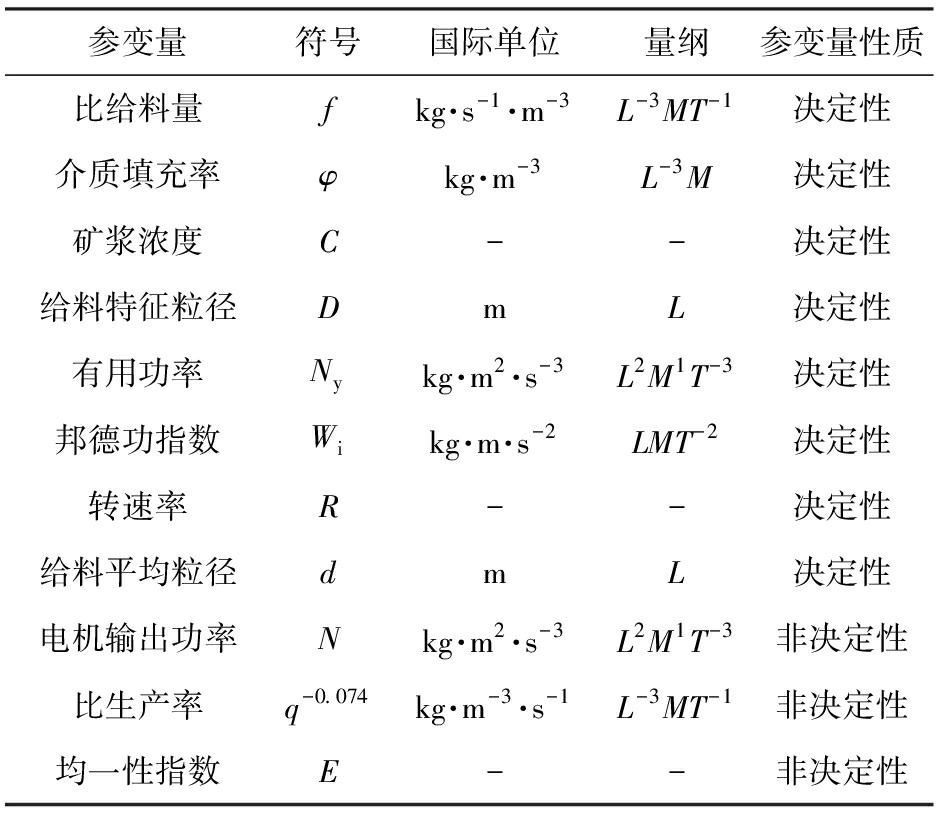
参变量符号国际单位量纲参变量性质比给料量fkg·s-1·m-3L-3MT-1决定性介质填充率φkg·m-3L-3M决定性矿浆浓度C--决定性给料特征粒径DmL决定性有用功率Nykg·m2·s-3L2M1T-3决定性邦德功指数Wikg·m·s-2LMT-2决定性转速率R--决定性给料平均粒径dmL决定性电机输出功率Nkg·m2·s-3L2M1T-3非决定性比生产率q-0.074kg·m-3·s-1L-3MT-1非决定性均一性指数E--非决定性
由上述参变量构成的磨矿过程的方程为
F(E,Wi,φ,C,R, f,q-0.074,d,D,Ny,N)=0 。
(1)
根据量纲分析的π定理[10]，得到棒磨机磨矿系统的量纲矩阵为
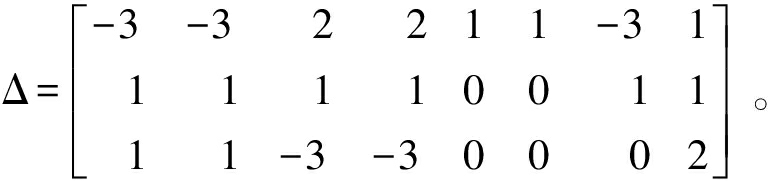
(2)
选取f、d、N为基本变量，推导得出得棒磨机磨矿过程的相似准数为
π1=q-0.074/f ，π2=D/d，
原无因次量可直接作为相似准数：
π5=R，π6=E ，π7=C。
为了使各项相似准数都具有明确的物理意义，又能便于使用，根据相似准数间算数运算的结果仍为相似准数这一特点，对所得到的相似准数进行适当演化。
π1=q-0.074/f定义为生产转化率，记为Q；π2=D/d定义为给料粒度特性系数，其描述了给料粒度特性，记为Fa；π3=Ny/N定义为能源利用率，记为
定义为介质填充特性系数，式中邦德功指数表征了矿料的可磨性，所以该无因次量综合反映了介质的填充率和给料特性，记为Fg；原无因次量R为转速率。E定义为产物的均一度指数，它反映的是产物粒度分布规律，其值越大，颗粒越均匀，产物品质越好。矿浆浓度C表示排出料浆中固体物料所占质量分数，它描述了磨机内料浆的流动特性，也是决定粉磨状态的重要变量。Q、η、E为棒磨机磨矿系统的非决定性相似准数；Fa,Fg、R、C为其决定性相似准数。
2.2 性能指标评价模型
根据相似原理第三定理，单值条件相似时，现象相似的充要条件是单值条件组成的相似准则相等，因此决定性无因次量群单独确定一组相似现象，说明每个非决定性无因次量都是决定性无因次量的单值函数。在自变量的一定范围内，都可采用指数函数形式来表达各种现象准则关系式[11]。由此得到多辊筒棒磨机的生产转化率模型方程为
(3)
能源利用率模型方程为
(4)
产品品质模型方程为
(5)
式中： e为自然对数的底； ea0、eb0、ec0为常数项； ai、bi、ci为待定参数。
2.3 模型参数的确定
为了确定上述模型中的待定参数，利用回归分析法结合实验数据对所得模型进行回归分析[12]，确定待定参数的可行范围。
选取比较常见的方铅矿为实验原料，它是提炼铅的重要矿石矿物，分布极广。常规碎矿设备的排矿粒度一般都可达到2～12 mm，实验选用的方铅矿单矿物粒度小于6 mm，密度为7.4～7.6 g/cm3。利用多辊筒棒磨机进行磨矿实验，磨矿钢棒级配为mØ12 ∶mØ14 ∶mØ16 ∶mØ18=1 ∶1 ∶1 ∶2，磨矿时间为7 min，产物D90粒度达到74 μm以下，且粒度分布均匀，衡量粒度分布宽窄的指标为均匀度，以均一性指数n表示，n值越大粒度分布越窄，颗粒越均匀，我国颁布标准规定均一性指数n大于0.7即为合格[4]。
实验前，根据磨矿过程的优化指标的要求，结合磨矿工艺，对直接影响磨矿产物的5个最主要因素：比给料量、给矿粒度、矿浆浓度、介质填充率及转速率进行参数化定义，来确定各因素的水平范围，设计五因素五水平正交试验。然后对实验值进行分析处理，根据处理结果建立多目标优化数学模型。五因素五水平正交试验表(L25(55))，如表2所示。
表2 正交实验设计表
Tab.2 Orthogonal experimental design
Table
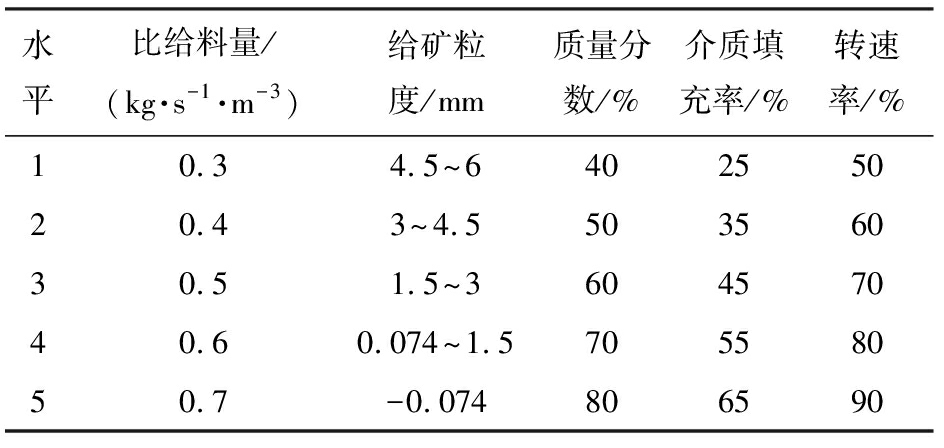
水平比给料量/(kg·s-1·m-3)给矿粒度/mm质量分数/%介质填充率/%转速率/%10.34.5～640255020.43～4.550356030.51.5～360457040.60.074～1.570558050.7-0.074806590
对上述模型两端取对数并令y1=ln Q，y2=ln η，y3=ln E； 令x1=ln Fa，x2=ln R，x3=ln C，x4=ln Fg，则得到模型的线性回归方程为
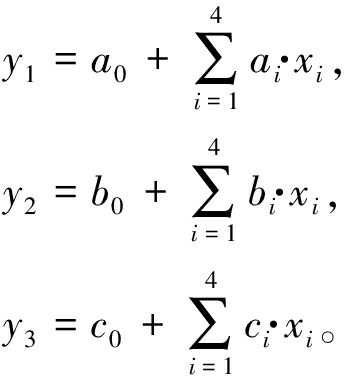
(6)
应用MATLAB提供的回归函数，结合正交实验数据，即可求得所要辨识的参数，最后得到的回归分析模型为
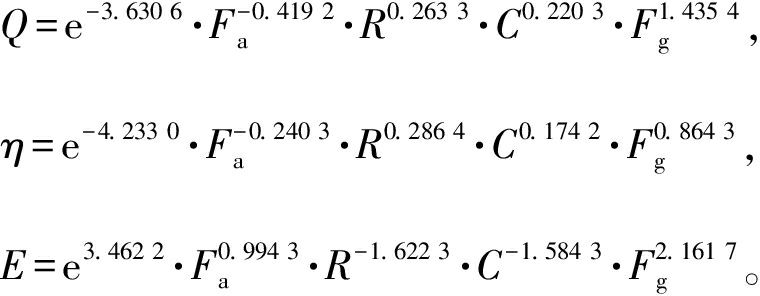
(7)
回归分析得到参变量间的复相关系数r和显著性值F如表3所示。
表3 模型相关系数与显著性值
Tab.3 Model correlation coefficient and significance value
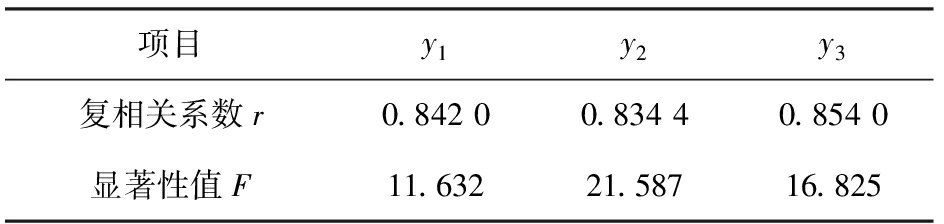
项目y1y2y3复相关系数r0.842 00.834 40.854 0显著性值F11.63221.58716.825
由表中数据可知，模型的相关系数(即模型拟合度)较为接近1，且模型的显著性值F均大于总体显著性检验值F0.90=7.622，说明模型的拟合效果好。
基于上述回归过程的分析，得到参数值变化的可行范围，利用遗传算法进一步扩大参数值的搜寻范围，通过模型输出与实际输出构成的误差函数值，不断修正模型中未知参数，直到误差函数取得极小值[13-14]。最终得到的数学模型为
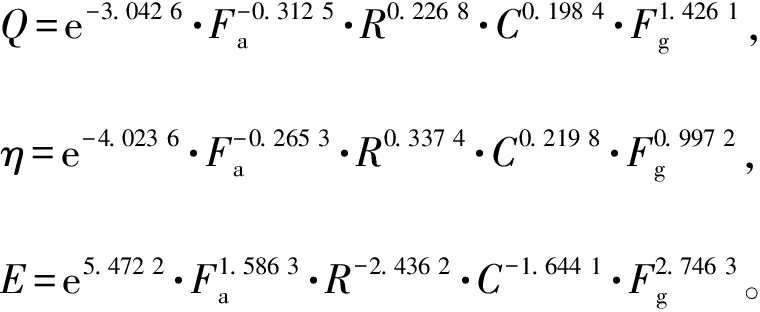
(8)
3 多目标优化数学模型的建立
3.1 决策变量
根据上述对磨矿性能影响因素分析，以及相似准数的演化，分别选取给料粒度特性Fa、介质的填充特性Fg、自转与公转的转速比R以及矿浆浓度C这4个决定性相似准数作为棒磨机的决策变量。
3.2 目标函数
多辊筒棒磨机的磨矿性能可由其产量、能耗和产物品质来衡量。本文进行棒磨机多目标优化设计的目的在于综合提高棒磨机的产量，提升产物品质，降低能耗。为了实现目标，将生产转化率Q、产品均一度指数E作为优化目标函数,则得到
MAX{Q}，
MAX{E}。
为了求解方便，将模型转化为求解1/Q、1/E的最小值问题，即可得到棒磨机磨矿性能的目标函数为
min(1/Q)=
(9)
min(1/E)=
(10)
3.3 约束条件
在上述目标函数分析中，着重考虑了棒磨机的产量及产物品质，为了保证设备的节能环保性能，应该兼顾到棒磨机的能耗，为此选取能源利用率模型作为一个约束条件。根据实际情况，能源利用率的约束为
75%≤η≤95%。
(11)
另外，其他各决策变量约束由具体的设计工艺参数来确定，具体分析如下：
1)转速率R和介质填充特性系数Fg约束。
在实际的磨矿生产过程中，为了更好地发挥介质作用，保证磨矿效果，理论上，细磨过程要求磨机以较低的转速运转，带动介质钢棒做泻落式运动，以实现对物料的研磨作用；粗磨过程则要求磨机高速运转，带动介质钢棒做抛落式运动，来加强对物料的冲击作用[15]。不同作用下介质运动状态示意图如图2所示。
实际上，要同时满足细磨和粗磨过程的要求是相矛盾的，因此需要进行权衡折中处理，寻求一个相对较为合理的转速率，使其磨矿效果尽可能达到最优。经过理论推导[16]，得出填充率与转速率之间的关系式为
(12)
在实际生产过程中，棒磨机的介质填充率的范围通常为30%～50%，从而根据式(12)可以求解出填充率与转速率的合理取值范围为
78%≤R≤93%，
(13)
30%≤φ≤69%。
(14)
由此得到介质填充特性系数约束为
1.5×107≤Fg≤2.8×107。
(15)
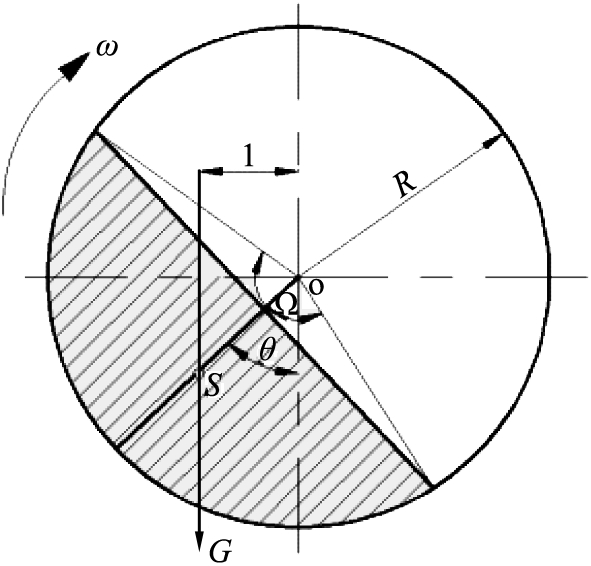
a 研磨作用下介质的泻落运动
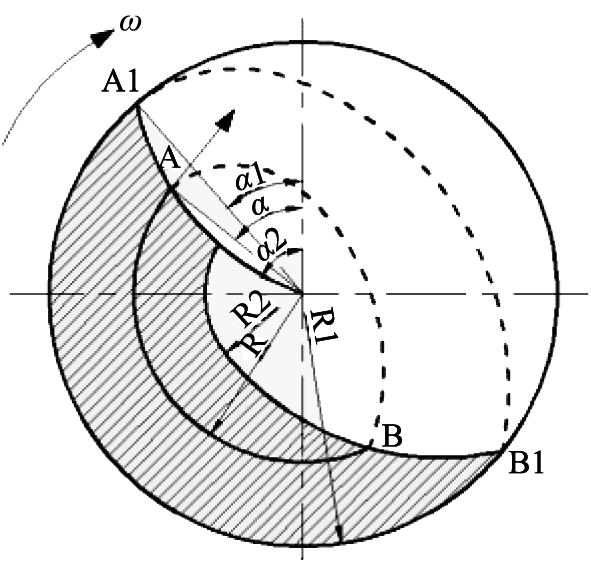
b 冲击作用下介质的抛落运动
图2 不同作用下介质运动状态示意图
Fig.2 Schematic diagram of medium motion state under different actions
2)矿浆浓度C约束。理论研究表明，棒磨机的适宜矿浆浓度一般在60%～85%，而实际生产过程中发现，棒磨机的磨矿浓度高于80%存在排料困难的问题，因此矿浆浓度不宜高于80%。故更有利于磨矿效率发挥的矿浆浓度范围为
60%≤C≤80%。
(16)
3)给料粒度特性系数Fa约束。棒磨机在磨矿过程中，物料总是以一定的粒度特性分布输送到棒磨机滚筒之内，受棒磨机滚筒直径和介质棒尺寸的限制，给料粒度不宜超过6 mm；为防止发生过粉碎现象，给料粒度也不宜低于0.074 mm。基于此，给料特性系数的约束范围为
1≤Fa≤1.8。
(17)
由此得到棒磨机磨矿过程的约束集合
75%≤η≤95% ，
78%≤R≤93% ，
30%≤φ≤69% ，
1.5×107≤Fg≤2.8×107 ，
60%≤C≤80% 。
3.4 多目标优化模型
根据以上分析，得到多辊筒棒磨机的多目标优化模型为
0.75≤η≤0.95，
(18)
1≤Fa≤1.8 ，
0.78≤R≤0.93 ，
1.5×107≤Fg≤2.8×107 ，
0.6≤C≤0.8 。
4 优化及结果分析
4.1 优化算法设计
根据上述所得到的辊筒棒磨机多目标优化模型，利用遗传算法进行求解。设计算法过程中，为了防止种群元素出现“近亲”交叉现象，保证种群的均匀分布和多样性，加快找到Pareto最优解的速度，在选择父代进行交叉以前，先计算2个父本之间的目标函数空间内的距离，并将其作为交叉限制条件，如果距离小于给定的值，则这2个父本不进行交叉；否则，允许交叉[17-18]。
结合棒磨机的工矿对磨矿性能的影响，在常规“遗传算法”求解的基础上，引入“交叉限制”条件，改进的遗传算法流程如图3所示。
设定种群的大小num=200、后代交叉比例为0.75、精英数目为20、最大迭代数为200、适应度函数偏差为1×10-6、交叉过滤限制值取为1。当种群进化完毕，得出多目标函数优化模型的Pareto解，并对所求得的解进行适应度检验。
最后利用TOPSIS法对求得多组Pareto解进行相对优劣评价，即对所求解进行规范化处理，然后从处理后的目标值中，选出2个目标函数最小值和最大值，分别作为正理想解和负理想解，计算每组目标值与正、负理想解间的距离和相对靠近度，通过比较相对靠近度，从中求得一组相对靠进度最佳的解作为最优解[19]。
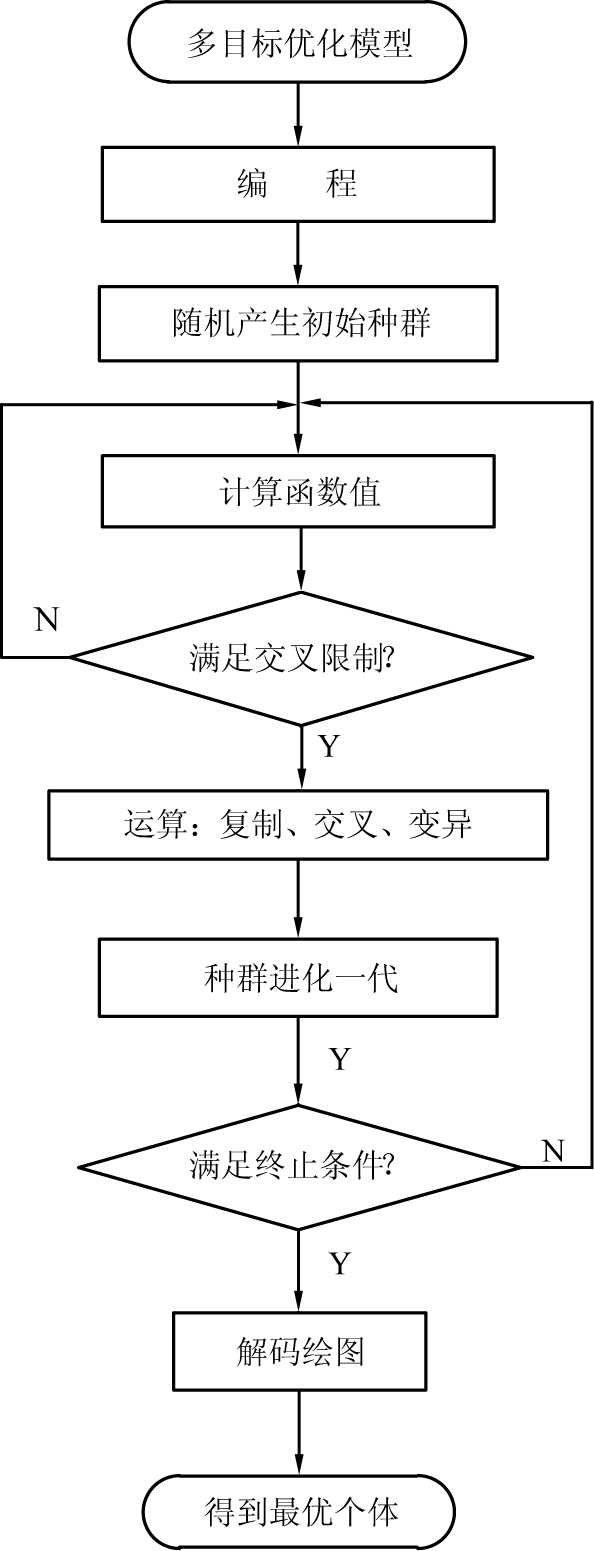
图3 改进的遗传算法流程图
Fig.3 Improved genetic algorithm flow chart
4.2 优化结果及分析
利用上述优化的遗传算法求解，得到多目标优化模型的Pareto解集如图4所示。
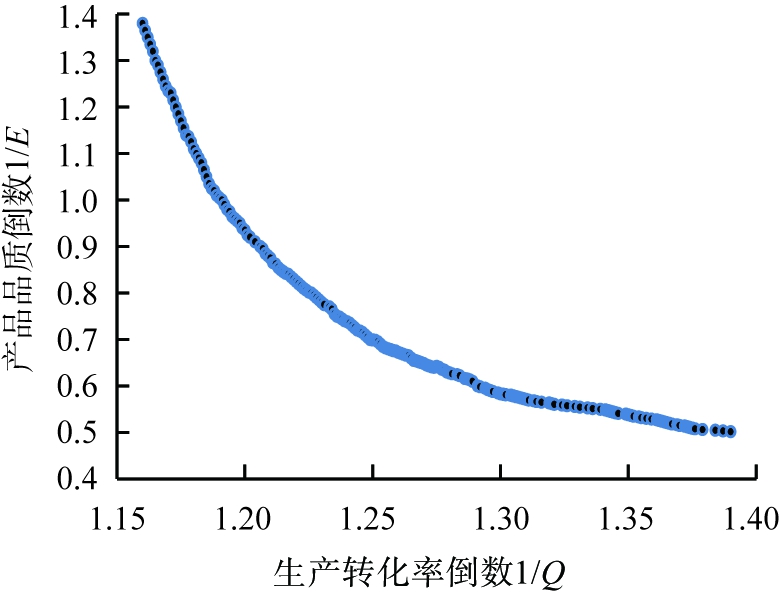
图4 棒磨机多目标优化模型的Pareto解
Fig.4 Pareto solution of multi-objective optimization model of rod mill
利用TOPSIS方法，对上述200组Pareto解进行评价，比较其相对靠进度，得到该模型的最优解为第72组，其对应的决策变量的值依次为：Fa=1.6，R=0.832 6，Fg=1.608×107,C=0.687,对所求得的最优个体进行适应度检验，得到系统适应度函数值变化曲线如下图5所示。
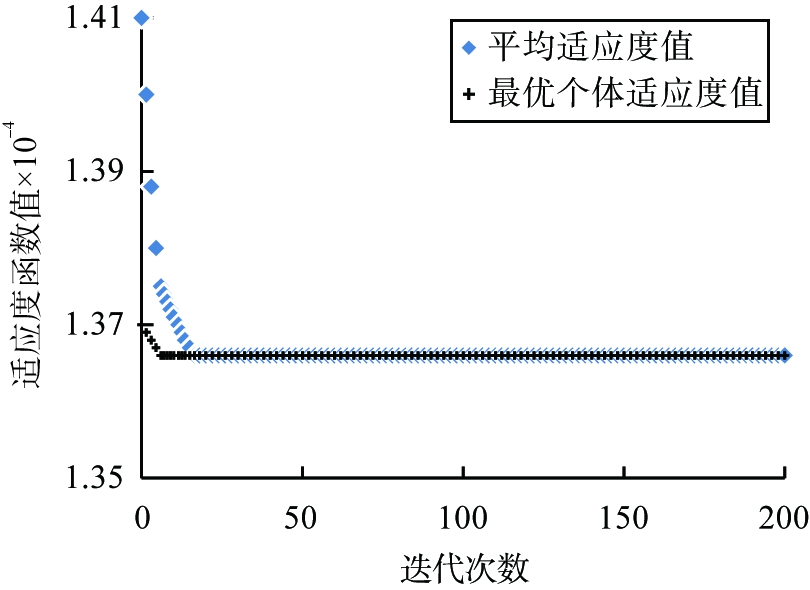
图5 系统适应度函数值变化曲线
Fig.5 System fitness function value curve
从图5中可以看出，随着迭代次数的增加，最优个体的适应度函数值不断减小，且收敛速度较快，最终趋于稳定，表明最终得到的最优个体适应程度较高，结果可信。
综合上述结果，结合“XMB-四辊五十筒棒磨机”在湖北省地质勘查装备中心进行测试对比，根据实际生产和测试记录数据，得到优化前后设计变量如表4所示，优化前后目标函数值如表5所示。
表4 设计变量优化结果
Tab.4 Design variable optimization result
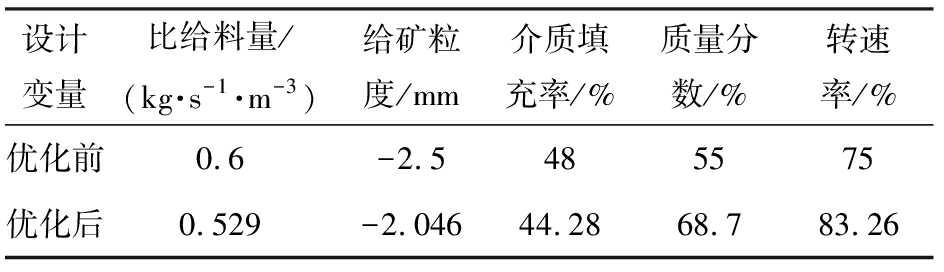
设计变量比给料量/(kg·s-1·m-3)给矿粒度/mm介质填充率/%质量分数/%转速率/%优化前0.6-2.5485575优化后0.529-2.04644.2868.783.26
表5 优化前后目标函数
Tab.5 Optimization before and after objective function
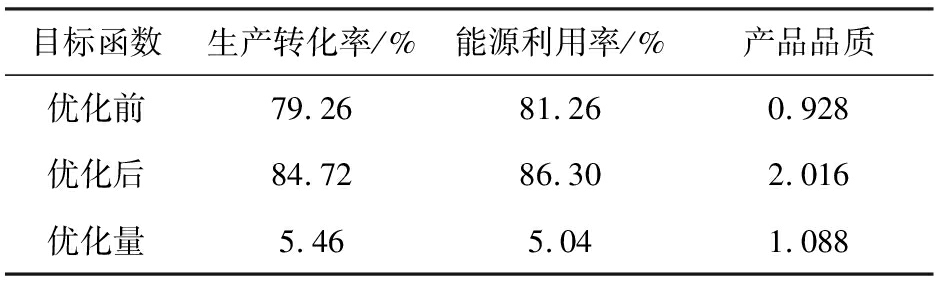
目标函数生产转化率/%能源利用率/%产品品质优化前79.2681.260.928优化后84.7286.302.016优化量5.465.041.088
根据表5数据，对比优化前后的目标函数值，棒磨机的生产转化率提高了5.46%，能源利用率提高了5.04%，产物的均一性指数增大了1.088，改善了棒磨机的综合性能，同时提升了磨矿产物品质。
为了进一步验证优化后的磨矿性能，以表4中优化后的设计变量为参考依据进行实验，得到的结果与表5中优化后的目标函数值相近。
综上所述，本文中得到了多辊筒棒磨机多目标优化问题的最优解，按照上述参数进行设定即可实现多辊筒棒磨机最优磨矿性能。
5 结论
1)基于多目标优化理论，结合无因次量分析方法，以提高棒磨机的产量，提升产物品质为目标，构建了多辊筒棒磨机的多目标优化模型。该模型合理规避了常规多目标解法目标权系数不易确定的难题，且直观完整地描述了棒磨机磨矿过程。
2)作者结合棒磨机的磨矿工况，对目标函数的求解是在常规遗传算法的基础之上增设交叉限制条件进行的，提高了算法效率，减少了求解时间，保证了Pareto最优解集的均匀性及多样性。
3)通过TOPSIS评价方法，分析求得多辊筒棒磨机磨矿过程多目标优化的最优解，优化后的棒磨机生产转化率提高了5.46%，能源的利用率提高了5.04%，矿磨产物的均一性指数增大了1.088，改善了棒磨机的综合性能，实现了节能环保的要求，达到了磨矿综合性能优化的目的。
[1]魏德洲. 固体物料分选学[M]. 北京： 冶金工业出版社，2000： 72-80.
[2]汤素燕，刘其瑞. 棒磨机工艺参数优化的研究[J]. 金属矿山，1994(7)：38-44.
[3]雷德明. 多目标智能优化算法及其应用[M]. 北京：科学出版社，2009：45-48.
[4]盖国胜，陈炳辰. 球磨过程无因次量群及数学模型组[J]. 矿冶工程，1994，14(2)：22-26.
[5]MITRA K, GOPINATH R.Multi-objective optimization of an industrial grinding operation using elitist non-dominated[J]. Chemical Engineering Science, 2004，59(2)：385-396.
[6]杨金林，莫凡，周文涛，等. 选择性磨矿研究概述[J]. 矿产综合利用，2017(5):1-6.
[7]刘长淼，赵登魁，吕子虎，等. 铝土矿在三辊四筒磨机中的磨矿行为初探[J]. 矿产保护与利用，2011(增刊)：28-31.
[8]刘志伟. 磨机磨矿效率影响因素分析[J]. 有色金属(选矿部分)，2018(4)：66-69.
[9]喻晓，王成伟，刘政，等. 用于水煤浆制备的大型棒磨机关键技术研究[J]. 矿山机械，2017(10)：37-40.
[10]梁灿彬，曹周键，陈陟陶. 量纲分析简介[J]. 大学物理，2017，36(12)：1-5.
[11]李之光. 相似与模化[M]. 北京： 国防工业出版社，1982： 61-69.
[12]叶菊兰，董海，张林进，等. 卧式行星磨粉磨过程的无因次量及数学模型分析[J]. 中国粉体技术，2013，19(6)：17-19.
[13]夏秀渝，周激流. 一种混合遗传算法及其在线性系统辨识中的应用[J]. 四川大学学报(工程科学版)，2005，37(1)：104-107.
[14]JOST F，KUDRSS M，KORKEL S，et al. A computational method for key-performance-indicator-based parameter identification of industrial manipulators[J]. Journal of Mathematics in Industry, 2017，7(1)： 9-11.
[15]韩佳宏，代淑娟，张作金，等. 钢锻作为磨矿介质的磨矿效果研究[J]. 矿山机械，2017，45(3)：38-41.
[16]杨金林，周文涛，马少健，等. 基于球磨机破碎能下最优磨矿参数研究[J]. 有色金属(选矿部分)，2016(5)：62-65.
[17]陈小庆，侯中喜，郭良民，等. 基于NSGA-Ⅱ的改进多目标遗传算法[J]. 计算机应用，2006，26(10)：2453-2456.
[18]林虹虹. 基于PARETO的改进遗传在多目标模型的研究[J]. 科技创新导报，2015(27)：46-47.
[19]杨威，庞永锋. 基于DEMATEL和TOPSIS的多值中智模糊多属性决策方法[J]. 模糊系统与数学，2018，32(3)：136-143.