旋流器是三相分离的设备之一,主要用于分级、脱水、除沙等作业[1-3],随着工业要求的不断提高,微细颗粒一直受到各大企业的青睐[4-5];但是由于微细颗粒在分离过程中受到的离心力较小,分离的效果不明显[6-7],因此微细颗粒一直没有得到广泛的应用。国外用D10mm和D25mm的微型旋流器对高岭土进行选矿,得到粒径小于2 μm的高岭土颗粒,质量分数占90%以上[8-9],但粒径小于1 μm颗粒分级仍然是个难题,而结构参数是决定旋流器分级效果的主要因素,因此研究旋流器的结构参数对流场及分离粒径的影响具有更实际的意义[10-12]。
锥角是旋流器最重要的结构参数之一。锥角越小,分级能力越强但同时伴随着内部湍流强度增大,不利于提高分离精度,锥角越大,处理量越大但分离精度不高[13-14]。相对于单锥角而言,双锥角旋流器能采用上端大锥角、下端小锥角串联的形式,这样可以提供更大的离心力,使微细颗粒能获得更大的离心推动力[15-16],因此合理选用锥角的形式和大小是旋流器结构优化设计的重要环节[17-18]。
本文中通过仿真计算流体力学 (computational fluid dynamics, CFD) 软件FLUENT对D8mm单锥角(3 °)微型旋流器和双锥角(5 °~3 °)微型旋流器进行了数值模拟,并进行实验验证,其结果对微型旋流器的结构优化设计有一定的指导意义。
1 微型旋流器
1.1 结构参数
图1为旋流器二维结构示意图。角锥比是指底流口直径与溢流口直径之比[19],本文中采用的角锥比为0.6,确定出单锥角的大小为3 °,为了提高分离粒径,采用上端大锥(5 °)与下端小锥(3 °)进行串联,以便更好地对比单锥与双锥旋流器的分离性能。

a 单锥旋流器
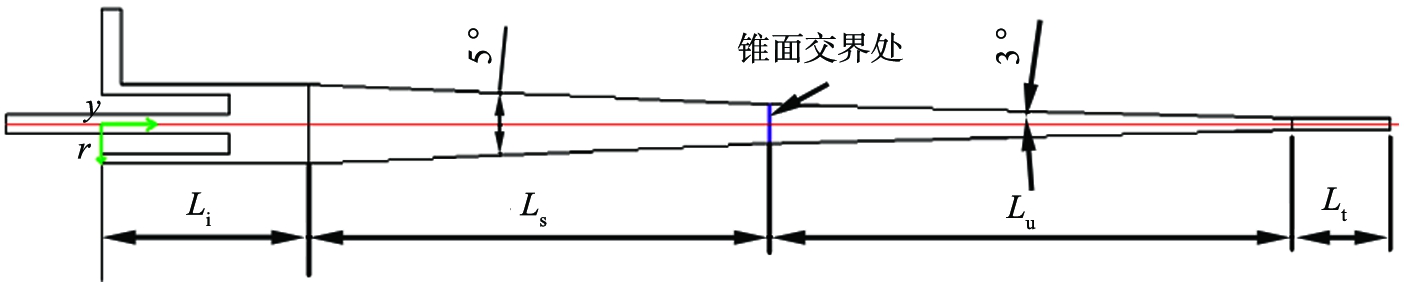
b 双锥旋流器
y—沿轴向方向;r—沿径向方向;Li—旋流器筒体高度;Ls—锥段高度;Lt—底流管长度; Lu—第2段锥段高度。
图1 旋流器二维示意图
Flg.1 Two dimensional diagram of hydrocyclone and wall function equation
单锥旋流器及壁面函数方程为
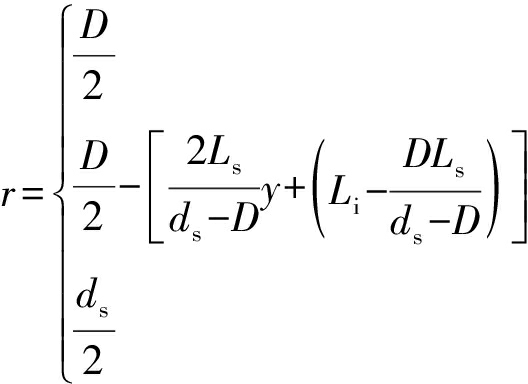
其中:
y<Li,
Li<y<Li+Ls,
y>Li+Ls,
式中:D为筒体直径;ds为底流口直径。
双锥旋流器及壁面函数方程为
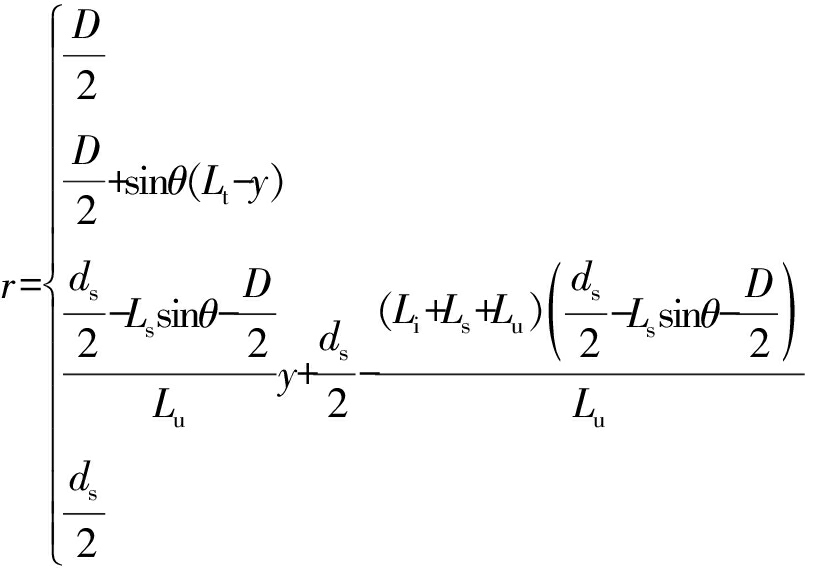
其中,
y<Li,
Li<y<Li+Ls,
Li+Ls<y<Li+Ls+Lu,
y>Li+Ls+Lu。
微型旋流器结构参数如表1所示。其中di为给料口直径,d0为溢流口直径,h0为溢流管插入深度,H为筒体高度。
表1 旋流器结构参数
Tab.1 Structure parameters of hydrocyclone

结构参数尺寸D/mm8di/mm2×1θ/(°)3 °5 °~3 °ds/mm1.2d0/mm2h0/mm13H/mm21
1.2 网格划分
将流体域的三维模型导入到ICEM-CFD软件中进行网格划分。为了提高计算精度,整个模型采用六面体网格生成方法。开展网格无关性验证,旋流器网格划数如图表2所示。
溢流口压力作为检验标准,发现单锥旋流器随着网格数的增加,溢流口压力不断变化,当增加到398 625和425 698时,溢流口压力基本不变,说明模拟结果不随网格数发生变化,同理得出双锥旋流器的最佳网格数,为了缩短模拟时间,单锥、双锥旋流器网格数分别选用398 625和418 625,网格划分如图2所示。
表2 旋流器网格划分数
Tab.2 Hydrocyclone grid number

旋流器类型网格划分数单锥115 689 226 873 346 512 398 625 425 698双锥165 847 263 525 368 957 418 625 452 368
图2 旋流器网格划分示意图
Fig.2 Diagram of hydrocyclone meshing
1.3 边界条件及参数选择
采用Fluent14.5软件对2种旋流器进行模拟分析,多相流模型采用Mixture模型,湍流模型为雷诺应力模型,压力速度耦合方式采用SIMPLE算法,压力离散格式为PRESTO,动量离散格式选用QUICK格式进行数值计算,湍动能和湍流耗散率采用二阶迎风格式。 由于壁面附近与湍流的区域中心部分存在差异较大,因此,为了便于提高精度,在模拟时选用标准壁面函数法求解壁面附近区域的流动。 给料口设为速度入口,底流口和溢流口设为压力出口,水相和颗粒相速度均为6 m/s,固相颗粒密度为4 650 kg/m3, 以进出口流量数值近似趋于相等作为计算收敛的判断依据。
2 模拟结果分析
数值模拟中加入5种不同粒径的硅酸锆颗粒,体积浓度见表3。
表3 不同颗粒的体积分数
Tab.3 Volume concentration of particles
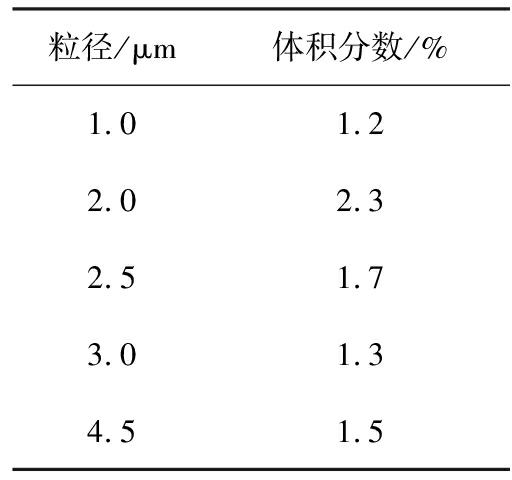
粒径/μm体积分数/%1.01.22.02.32.51.73.01.34.51.5
为了便于分析内部流场的变化,考虑柱段与锥段之间存在差异,分别选取不同截面进行分析,由于2个旋流器高度不同,选取单锥旋流器以底流口为基准面向上20、105.2 mm,双锥旋流器为23.29和84.78 mm,以保证2个旋流器截面的截面积相同。2个旋流器的特征线位置如图3所示。
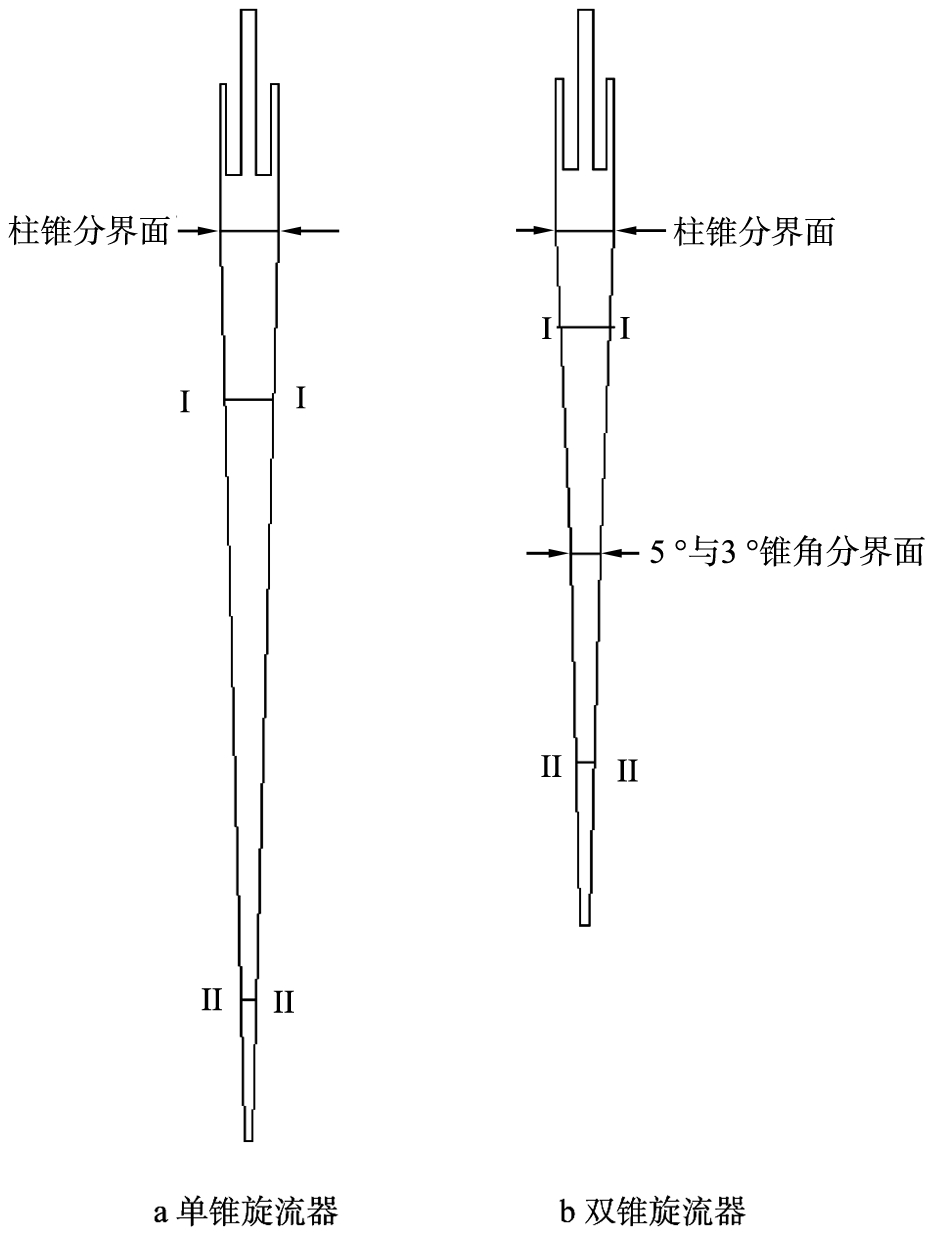
图3 旋流器特征线位置图
Fig.3 Hydrocyclone feature line location map
2.1 界面压力分布
压力是旋流器固液分离中的一项重要参数。超微细颗粒由于质量小,受到的离心力较小,如果压力较小则难以分离,因此需要增大压力来提高分离效果。图4为轴截面处的压力分布云图。
图5为2个不同截面处的压力分布图线。
从2个旋流器的轴截面压力云图可以看出,旋流器的静压力分布具有对称性,压力分布由器壁向轴心逐渐减小,在轴心处压力变为负值,这也是空气柱形成的原因。此外,双锥旋流器的径向压力梯度明显大于单锥旋流器,有利于微细颗粒的径向分离,压力越高,可以保证旋流器的的离心力场强度,提高颗粒的分离效果。
2.2 切向速度
切向速度是固液分离的主要动力源,其速度大小都高于轴向速度和径向速度,切向速度较大有利于两相的分离。图6为2个不同截面处的切向速度对比。 从分布图中看出,2个截面的速度的分布大致相同,成对称性图形,在旋流器中心位置处达到最大,沿器壁方向逐渐减小,在器壁位置处减小到零。从图6中还可以看出,2个截面处双锥旋流器的切向速度比单锥的大,在I—I截面处单锥、双锥旋流器的速度分别为7和10 m/s。
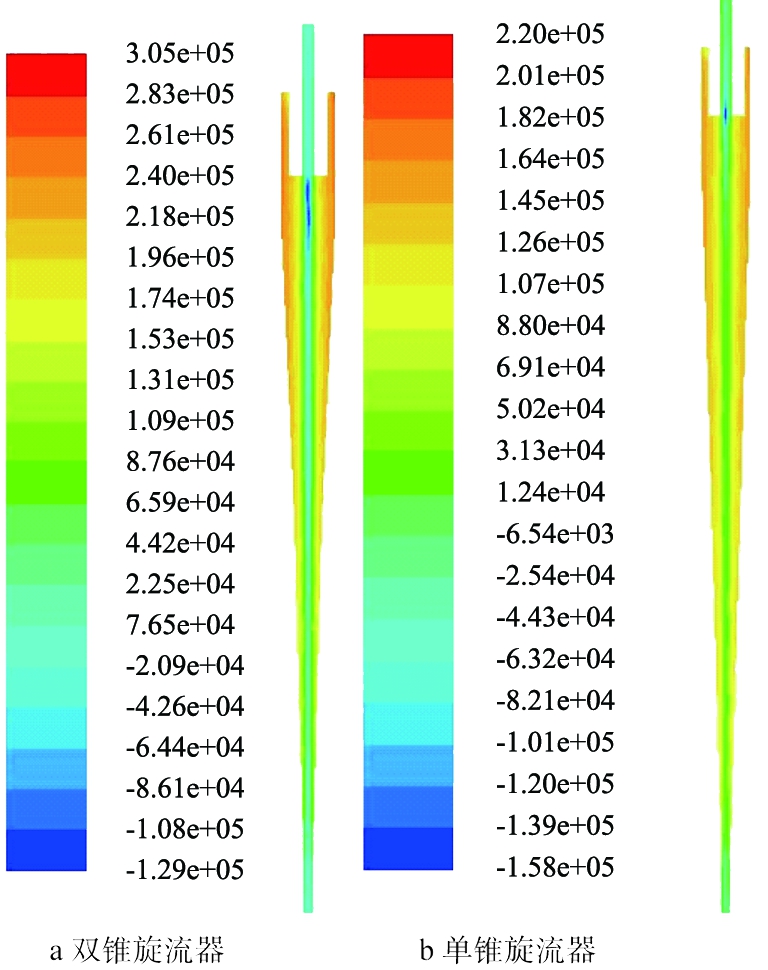
图4 轴截面压力云图
Fig.4 Axial pressure cloud diagram
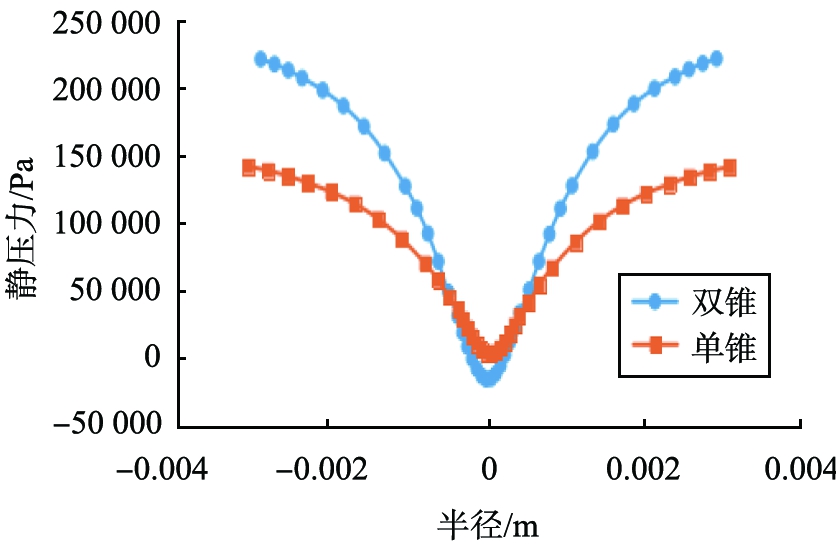
a I—I截面
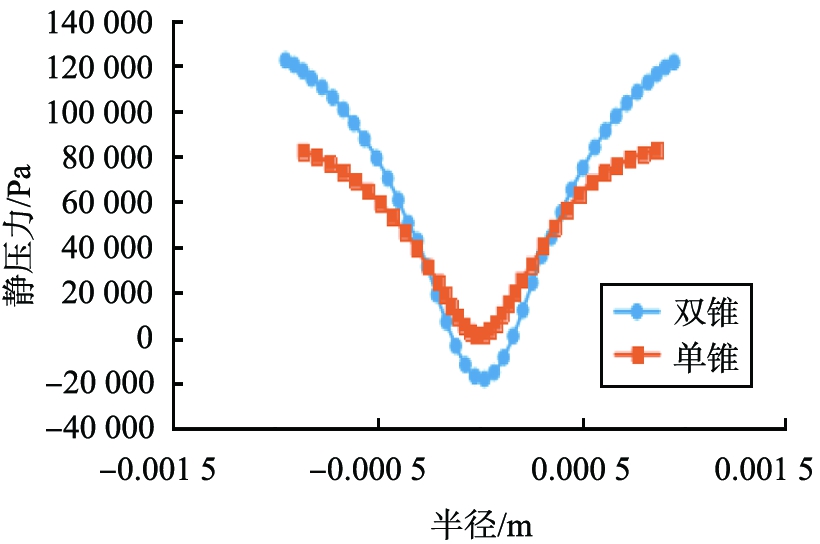
b II—II截面
图5 不同截面处静压力分布
Fig.5 Static pressure distribution lines at different sections
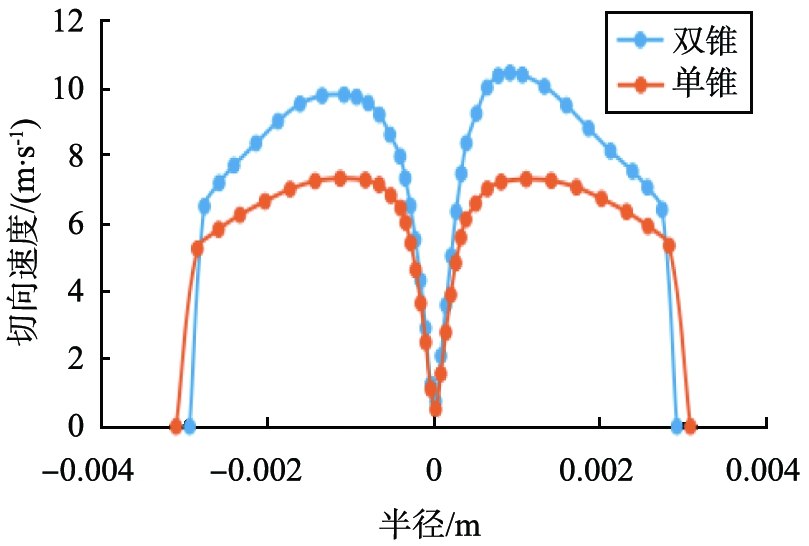
a I—I截面
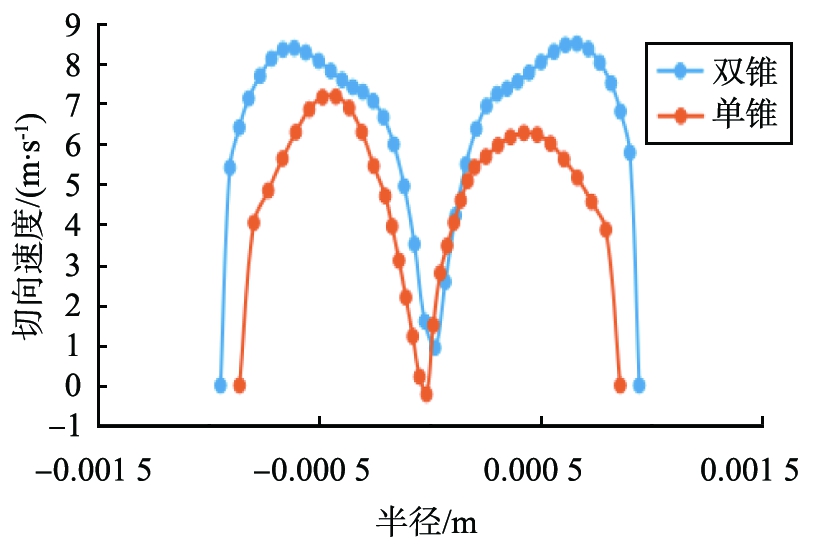
b II—II面
图6 不同截面处切向速度分布
Fig.6 Tangential velocity profile at different sections
根据向心力公式
F心![]()
可以看出,向心力与速度的平方成正比,在回转半径相同的情况下,双锥旋流器离心力是单锥旋流器的2.04倍,而微细颗粒分级需要更大的离心力推动才能将不同粒径的颗粒进行分离,并且分离粒径随着离心力的增大而减小,在相同的工况下可以减小分离粒径。
2.3 径向速度
旋流器内的径向流动主要沿器壁指向轴心,随着半径的减小而增大,在轴心处速度最大。径向速度是横向沉降的主要动力,与切向速度的规律基本类似,对分离性能有很大的影响,尤其是微细颗粒的分选对径向速度要求更高。
图7为旋流器内部不同截面的径向速度分布图线。由图看出,径向速度分布图线对称性较好,在器壁处速度为零,由器壁向内逐渐增大,在零速包络面位置处达到最大,其分布规律与常规的旋流器规律基本相同,双锥微型旋流器的径向速度大于单锥旋流器,这使得在径向的曳力较大,更利于微细颗粒进入内旋流,溢流中的细颗粒含量增多,减小溢流跑粗。
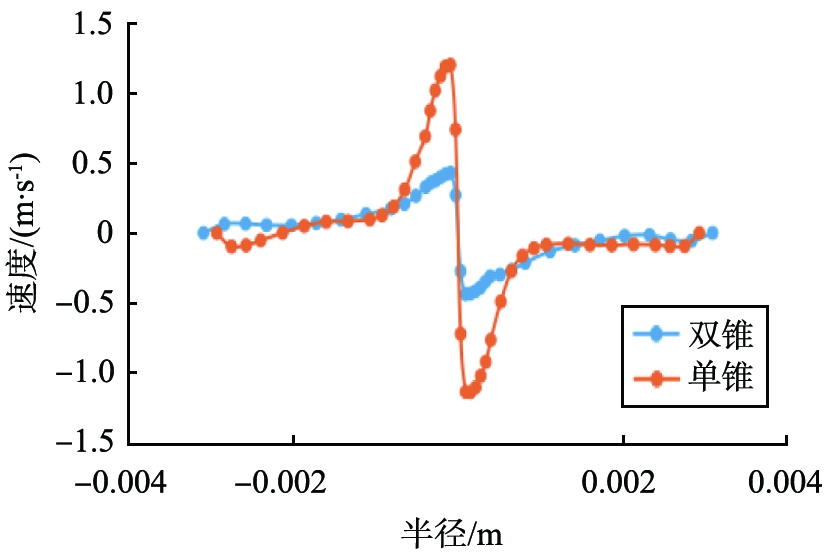
a I—I截面
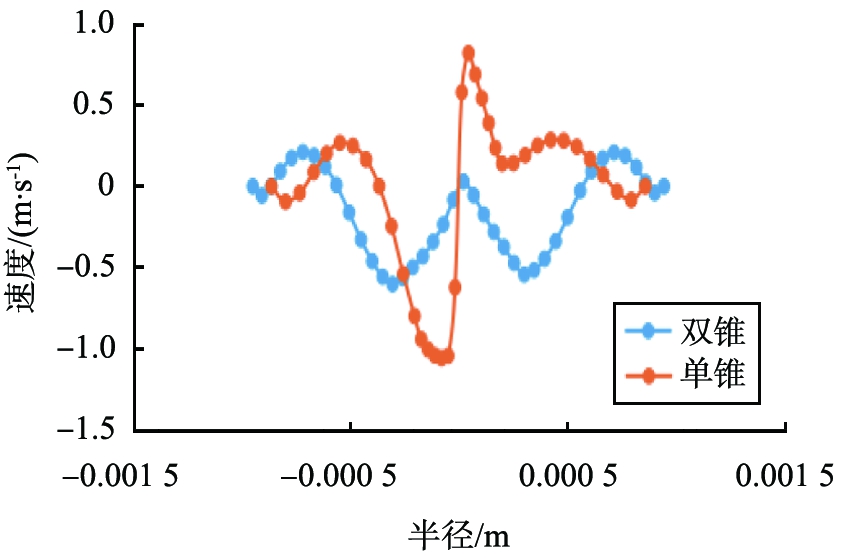
b II—II截面
图7 不同截面处径向速度分布
Fig.7 Radial velocity profile at different sections
2.4 颗粒分布对比
旋流器内的颗粒分布情况直接反应旋流器的分离性能,图8为2种颗粒的体积分数图线。从图8a可以看出双锥旋流器在底流口附近2.5 μm微粒体积分数明显小于单锥旋流器,进入底流口的微细颗粒明显减少,减少了底流夹细。从图8b可以看处,双锥旋流器在底流口附近4.5 μm微粒体积分数明显大于单锥旋流器,进入底流口的粗颗粒明显增多,有效减少了溢流跑粗。
2.5 分离粒径对比
旋流器的效率曲线表示给料中各种不同粒径物料进入沉砂(底流)的质量分数与相关粒径间的关系。分离粒径d50是分配率50%对应的颗粒粒径,是旋流器重要的质量指标。图9为2个旋流器模拟的分级效率曲线。从图中可以看出,单锥旋流器的d50为5.9 μm,双锥旋流器的d50为5 μm,分离粒径减小了0.9 μm。
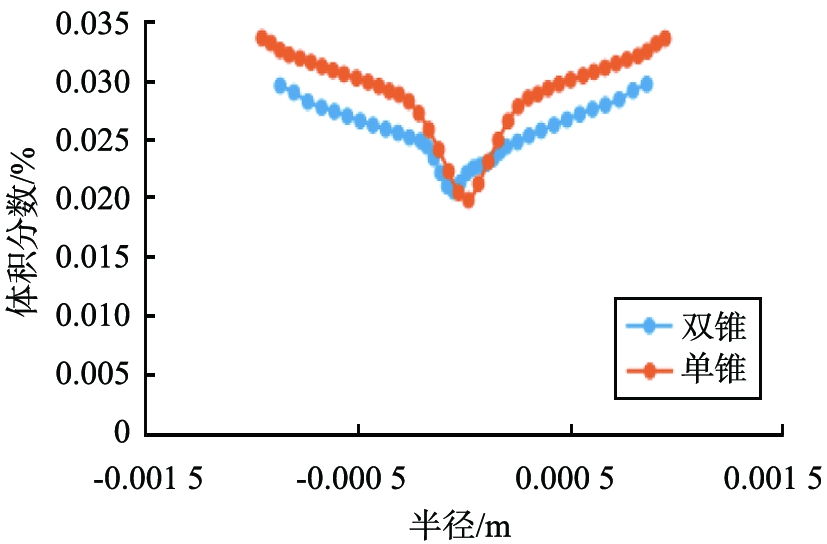
a 粒径为2.5 μm颗粒
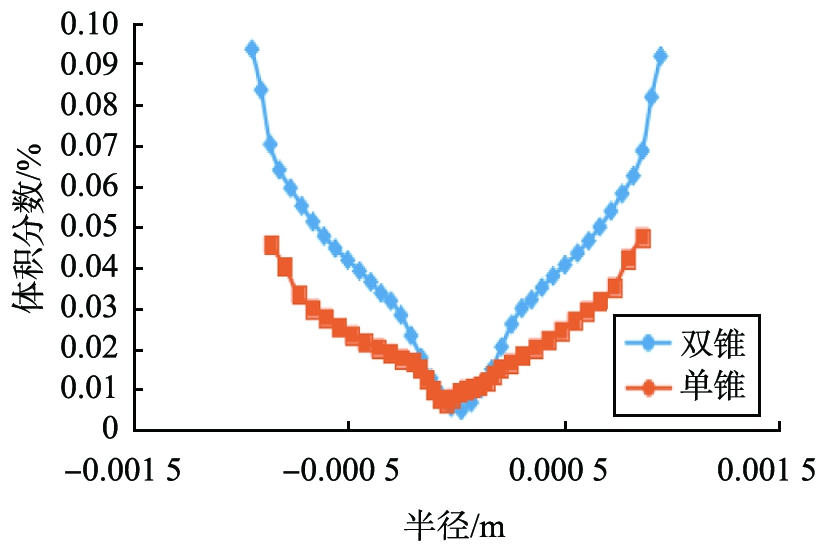
b 粒径为4.5 μm颗粒
图8 II—II截面处不同颗粒体积分数对比
Fig.8 Comparison of volume fraction of different particles at section II—II
3 实验
微细颗粒选用硅酸锆,物料质量浓度为8 g/L,入口压力为0.5 MPa,硅酸锆密度为4 650 kg/m3,表4为2种微型旋流器的浓度与产率。
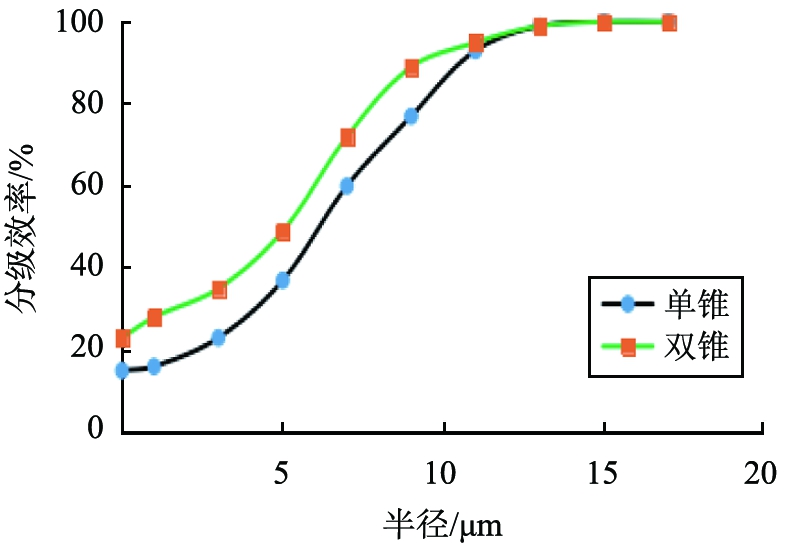
图9 模拟分级效率曲线
Fig.9 Simulate grading efficiency curve
从表中可以看出,双锥微型旋流器溢流的质量浓度减小了0.11 g/L,底流的增大了1.43,底流产率提高了6.36个百分点,分股比(底流体积流量与溢流体积流量的比值)的基本不变。
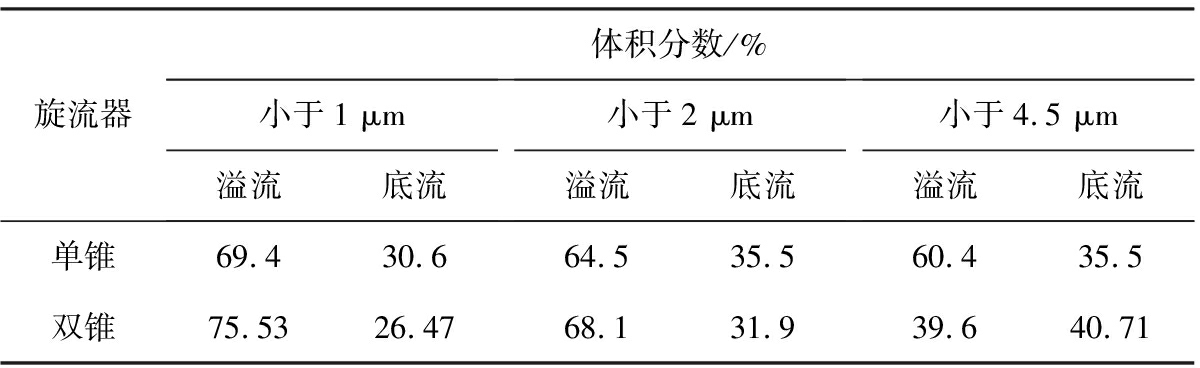
通过对比3种不同颗粒粒径的体积分数和分级效率来评定旋流器分级的效果。分别选取小于1、小于2、小于4.5 μm 3种粒径进行旋流器分级性能研究。
表5为3种颗粒体积分数。从表5中可以看出,小于1 μm微细颗粒的溢流体积分数为75.33%,比单锥旋流器溢流体积分数提高了5.93%,小于2 μm颗粒的溢流体积分数为68.1%,比单锥旋流器提高了3.6%,小于4.5 μm颗粒的底流体积分数为40.71%,比单锥旋流器提高了5.21%,有效地减少了底流夹细和溢流跑粗现象,实验结果与模拟结果吻合。
表4 浓度与产率值
Tab.4 Concentration and yield value

旋流器质量浓度/(g·L-1)溢流底流底流产率/%分股比单锥0.926.0352.130.392双锥0.816.3258.490.413
表5 3种颗粒体积分数
Tab.5 Particle volume fraction of 3 kinds
旋流器体积分数/%小于1 μm溢流底流小于2 μm溢流底流小于4.5 μm溢流底流单锥69.430.664.535.560.435.5双锥75.5326.4768.131.939.640.71
分离精度通常由分级效率曲线的陡度指数SI来表示,其定义式为
式中:d25为分级效率曲线上25%对应的颗粒粒径;d75为分级效率曲线上75%对应的颗粒粒径。
图10为试验分级效率曲线。
由图可知,单锥旋流器d25=3 μm,d75=7 μm。 双锥旋流器d25=2.3 μm,d75=6 μm。 单锥旋流器的陡度指数为0.43,双锥旋流器的陡度指数为0.38,由此可知双锥旋流器分离精度比单锥旋流器稍有降低,但从表4中可以得出双锥旋流器底流加细和溢流跑粗现象得到明显改善。
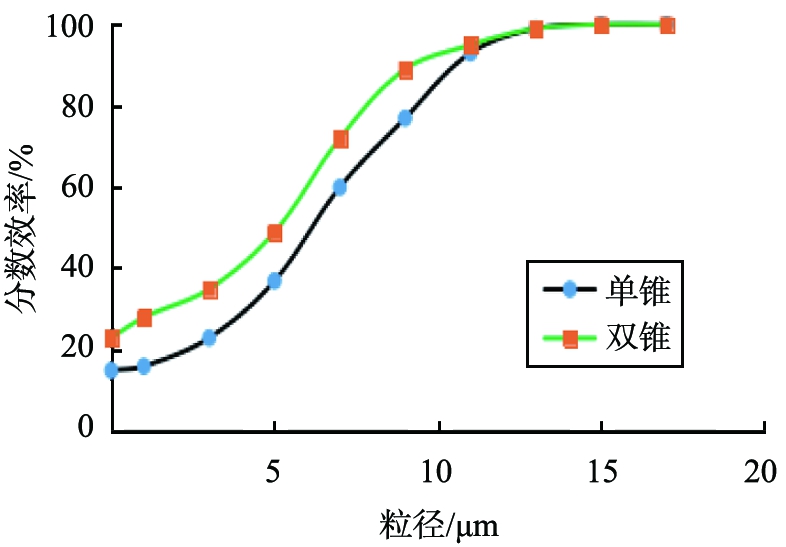
图10 实验分级效率曲线
Fig.10 Experiment grading efficiency curve
4 结论
1)通过CFD软件Fluent模拟显示,双锥旋流器的切向速度和径向速度都有所提高,在相同的工况下使微细颗粒具有更大的离心力,分离更加彻底。
2)通过模拟显示,双锥角微型旋流器分离粒径减小0.9 μm,溢流中小于1 μm产品含量质量分数提高6.13%,小于2 μm的提高3.6%,底流中小于4.5 μm产品质量分数提高5.21%,底流夹细和溢流跑粗现象得到明显改善。
3)实验证明双锥型微型旋流器分离粒径更小,分离效果更好。
[1]VAN OMMEN R. Krebs gMAX cyclones-for finer separations with larger diameter cyclones[J]. Aufbereitungs Technik, 2000, 41(9): 386-391.
[2]GHODRAT M, KUANG S B, YU A B, et al. Numerical analysis of hydrocyclones with different vortex finder configurations[J]. Minerals Engineering, 2014, 63: 117-132.
[3]KELSALL D F. A further study of the hydraulic cyclone[J]. Chemical Engineering Science, 1953, 2(6): 231-252.
[4]HSIEH K T, RAJAMANI R K. Mathematical model of the hydrocyclone based on physics of fluid flow[]. AICh E Journal, 1991, 37(5): 715-731.
[5]JIANG L Y, LIU P K, YANG H, et al. Short-circuit flow in hydrocyclones with arc-shaped vortex finders[J].Chemical Engineering & Technology, 2018, 41(9):1783-1792.
[6]褚良银,陈文梅. 水力旋流器固相颗粒径向速度研究[J]. 化工装备技术,1992, 13(4): 1-6.
[7]BRADLEY D. The hydrocyclone[M]. London: Pergamon Press, 1965:112-115.
[8]ZHANG Y K, LIU P K, XIAO L J, et al. Numerical simulation of a hydrocyclone with different diameters of vortex finder[J]. Energy Education Science and Technology Part A: Enegy Science and Research, 2014, 32(3): 2705-2712.
[9]GHODRAT M, KUANG S B, YU A B, et al. Numerical analysis of hydrocyclones with different conical section designs[J]. Minerals Engineering, 2014, 62(3): 74-84.
[10]OLSON T J, OMMEN R V. Optimizing hydrocyclone design using advanced CFD model[J]. Mineral Engineering, 2004(17):702-729.
[11]赵国庆,张明贤. 水力旋流器分离技术[M]. 北京:化学工业出版社,2003:262-269.
[12]DIKOV V A, SUKHANOV D E. Feasibility of hydrocyclones for combined cleaning of circulation and waste water[J]. Chemical and Petroleum Engineering, 2014, 49(9): 619-623.
[13]庞学诗. 水力旋流器技术与应用[M]. 北京: 中国石化出版社, 2010: 175-177.
[14]刘培坤,姜兰越,杨兴华,等. 抛物线型旋流器分离特性的数值模拟和试验研究[J]. 流体机械,2015(10): 3-6.
[15]曾志飞. 柱锥连接处扩经对水力旋流器性能的影响[J]. 矿冶工程, 2011, 31(2): 42-44.
[16]丁旭明, 王振波, 金有海. 两种入口结构旋流器性能对比试验研究[J]. 化工机械, 2004, 32(2): 69-71.
[17]董连平, 高建川, 杨宏丽, 等. 分级旋流器分选作用与分选旋流器分级作用试验研究[J]. 煤炭学报, 2014, 39(5): 954-960.
[18]李梅, 姚海生, 樊民强. 分级旋流器的分选作用[J]. 煤炭加工与综合利用, 2001(4): 7-9.
[19]王羕. 井下两级串联旋流器分离技术研究[D]. 大庆: 东北石油大学,2014.