在对岩石成分进行光谱分析时,需要将采集的样品粉碎研磨后,装入密闭容腔中进行混料处理,其目的是通过混合过程得到组成和性质均匀的矿粉,以保证光谱分析的效果[1]。混合效果的好坏直接影响着光谱分析的精度,所以对矿粉混合均匀性提出了更高的要求[2-3]。所谓混合,即矿粉微粒在外力的作用下发生运动速度和方向的改变,使粉体微粒均匀分布的操作过程[4-5]。由于混合过程中微粒的运动十分复杂,在如何提高微粒混合均匀度方面一直是如今研究的热点和难点,许多学者已进行了相关研究。梁增华等[6]针对钛粉在不同振动方向下的振动状态,通过仿真分析了钛粉填充密度的影响。任继良等[7]研究了颗粒运动轨迹对火药运动接触的影响,通过仿真分析其混合均匀性。张紫薇等[8]模拟了典型转速下三维滚筒内的碳球颗粒混合过程,分析研究滚筒内颗粒流态随时间的演化过程,展示不同颗粒流态下的颗粒混合结构特性。当前,在矿粉微粒的混合方法、混合均匀度及其混合效率等方面的关联性还有待深入研究。
为了提高微粒的混合均匀度和效率,本文在前人研究的基础上提出了一种混料方法,即在振动混料的条件下,向混料容器中加入一种搅拌介质,使其在混合过程中起到搅拌矿粉的作用,以获得更好的混料效果。通过EDEM软件建立微粒和搅拌介质仿真模型,模拟微粒在混料容器中的运动状态,将混合到一定程度的微粒进行试样分析,应用标准偏差和离散度来判断混料的效果,分析搅拌介质对微粒混合均匀度的影响,并通过振动混料实验对仿真结果进行验证。
1 固体介质的选用
针对矿粉微粒的混合特性,对其施加一定的机械外力,能够对微粒进行有效的重新排列来提高混合均匀性,这种机械外力可以统称为物料混合力,通过混合运动作用在矿粉微粒上[9-10]。
由于加入了搅拌介质,在混合过程中,它与矿粉微粒之间相互摩擦碰撞会产生磨损现象,从而影响光谱分析的效果,因此,原则上应选用耐磨且不与矿粉微粒发生反应的介质。
为了充分表达搅拌效果,该介质应悬浮在矿粉物料中,与矿粉一起受到物料混合力。当采用振动作为物料混合的驱动力,所需的混料运动将受到振幅和频率的影响,通过振动参数定性分析可知,密度太大的介质,会使振动幅度有减小的趋势,影响微粒在容腔中的运动;密度太小的介质,与微粒碰撞效果不明显,起不到搅拌的作用,因此,所选介质的密度应与实验矿粉的密度接近[11-12]。
同时还应考虑搅拌介质的几何尺寸,尺寸太大的介质因占用的空间大,会阻碍微粒混合的运动轨迹,微粒在运动中的相对位移就会减小,从而影响微粒混合的均匀性,因此,应避免选用尺寸较大的介质。
综合来看,选用玛瑙球作为搅拌介质较为合适[13]。主要是因为玛瑙的密度同矿粉的密度相近,且其主要成分是二氧化硅,即使在搅拌过程中发生元素渗透,也不影响光谱分析的效果。如实验需要将粒度为50~150 μm的矿料及粉状催化剂均匀混合,宜选用半径为2~3 mm的玛瑙球作为搅拌介质。实验时,可将2个坩埚密闭紧扣形成一个密闭容腔,模型如图1所示,呈杯状结构,底面半径为22 mm,高度为12 mm,将其密闭紧扣。把玛瑙球和被混物料放入其中,混合均匀后将玛瑙球取出以供实验用。
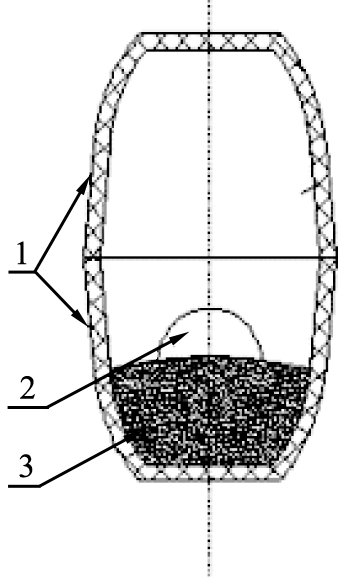
1—坩埚;2—玛瑙球;3—粉状光谱分析试样。
图1 微粉混合示意图
Fig.1 Mixed schematic diagram
2 建立颗粒接触模型
采用EDEM软件中的Hertz-Mindlin无滑动接触模型,其结构参数和物理意义如下:设半径分别为R1、R2的2个球形颗粒发生弹性接触,法向重叠的计算公式为
α=R1+R2-|r1-r2|,
(1)
式中:r1、 r2是2个颗粒球心位置矢量。
颗粒间的接触面为圆形,接触半径a为
(2)
式中, R*为等效粒子半径,可由下式求出
(3)
颗粒间的法向力Fn可由下式求得:
(4)
式中, E*为等效弹性模量,由下式求出
(5)
式中:E1、υ1、E2、υ2分别为颗粒1和颗粒2的弹性模量和泊松比。
法向阻尼力![]() 可由下式求得:
可由下式求得:
(6)
式中:m*为等效质量;![]() 设2个颗粒发生碰撞前的速度分别为v1、v2,发生碰撞时的法向单位矢量为n,则
设2个颗粒发生碰撞前的速度分别为v1、v2,发生碰撞时的法向单位矢量为n,则![]() 为相对速度的法向分量值,
为相对速度的法向分量值,![]() 和Sn分别为系数和法向刚度,
和Sn分别为系数和法向刚度,![]()
颗粒间切向力Ft可由下式求出:
Ft=-Stδ,
(7)
式中: δ为切向重叠量;St为切向刚度,由下式求出:
(8)
式中,G*为等效剪切模量,由下式求出:
(9)
式中G1和G2为2个颗粒的剪切模量。
颗粒间的切向阻尼力Ft可由下式求出:
(10)
式中![]() 是切向相对速度。
是切向相对速度。
3 几何模型和混合评价方法
3.1 几何模型
用Solidworks建立密闭坩埚三维模型导入到EDEM。由于矿粉微粒形状的复杂性,还原真实形态的仿真比较困难,因此在EDEM中采用简化模型,用3种不同的颗粒模型分别代表矿粉、粉状催化剂和玛瑙球,如图2、3所示。
3.2 微粒的生成方法
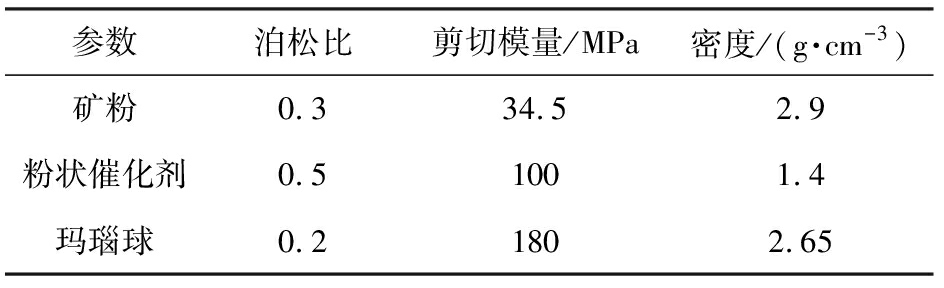
在Factory模块下建立3个颗粒场,Factory1中选择动态生成方式将矿粉微粒无限生成,直至距离坩埚底面大约5 mm的位置,从0.1 s开始生成颗粒。Factory2的颗粒场平面建立在距底面9.5 mm的位置,在矿粉微粒的基础上生成4 mm的粉状催化剂。在Factory3中选择static方式生成颗粒,在颗粒类型(type)选择玛瑙球。根据粉体微粒及振动的相关条件,设置微粒和玛瑙球的相关参数,如表1所示。
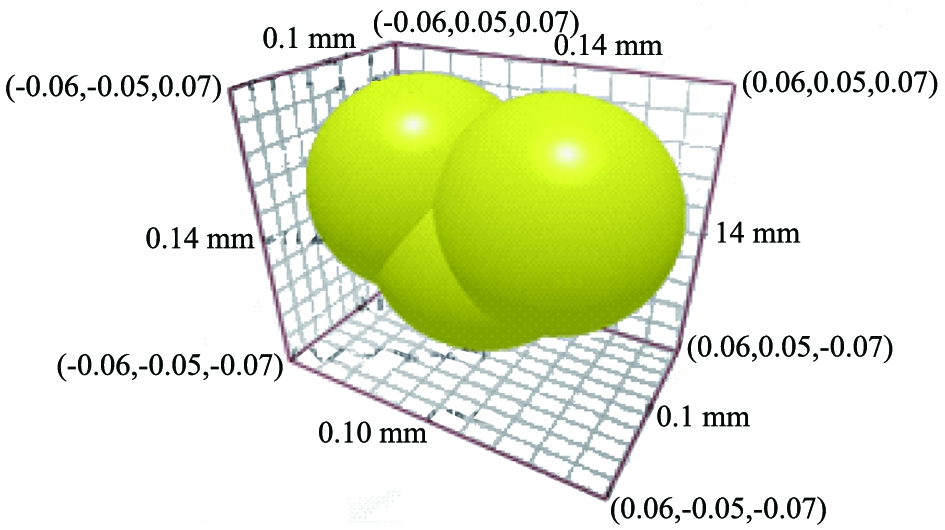
图2 矿粉或催化剂模型(粒径/75 μm)
Fig.2 Mineral powder or catalyst model (particle size 75 μm)
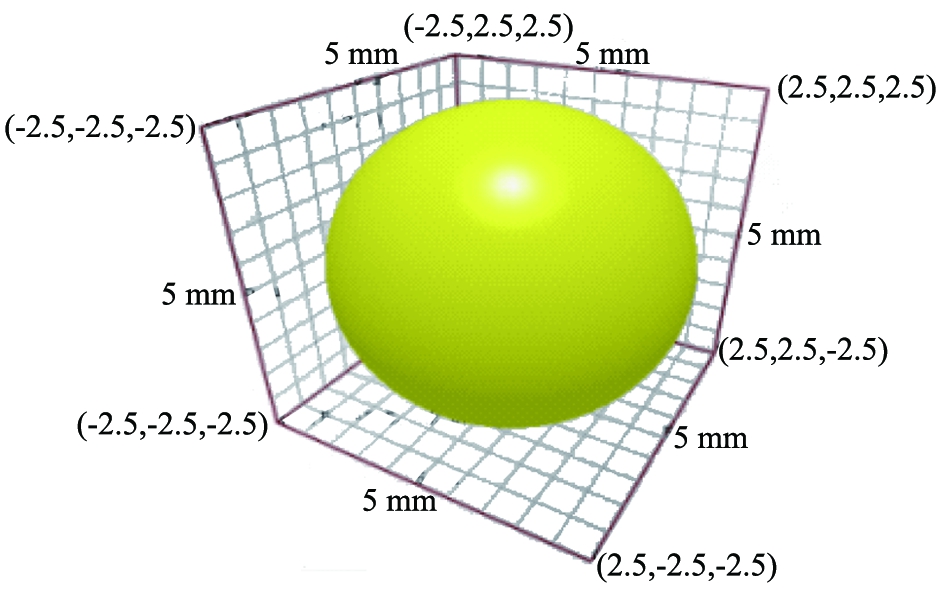
图3 玛瑙球模型(半径为2.5 mm)
Fig.3 Agate ball model (radius 2.5 mm)
表1 矿粉、催化剂和玛瑙球相关参数
Tab.1 Parameters of mineral powder,catalyst and agate ball
参数泊松比剪切模量/MPa密度/(g·cm-3)矿粉0.334.52.9粉状催化剂0.51001.4玛瑙球0.21802.65
3.3 3个指标的评价
利用标准偏差、混合度、混合指数对混合程度的高低进行评价[14]。在EDEM软件中,将密闭坩埚容器进行网络空间格划分,保证颗粒所占区域的网格类型近似相同。首先对坩埚建立4×4×4的空间格,导出各个时间段中每个空间格所占各种颗粒的数量,并计算出空间格中颗粒的总量,设xi为单元格中催化剂微粒所占的比例数,表示所有比例数的均值,本文选取催化剂为研究对象[15]。通过得到的数据对混合效果进行分析。标准偏差也称为均方差根,表示数据波动的幅度,其计算方法是为
(11)
标准偏差S值越小,说明数据波动的幅度越小,混合的效果就越好,但是,S值只与测定值和标准平均值的差值有关,而与各测定值的本身大小无关[16]。根据光谱分析实验的需要,在实验前抽样实测矿粉混合的均匀程度对光谱分析精度的影响,矿粉混合均匀度对应的S值应为0.05~0.06较合适。
实际上,当混合物的组分比例相差悬殊时,标准偏差就很难反映出混合效果了,还需引入离散度R来反应混合均匀程度。离散度的公式为
(12)
由于本文中所述的混料物的粒径为50~150 μm的矿料及粉状催化剂的组成比较接近,并无太大悬殊,因此,本文中仅以标准偏差S值作为混合均匀度的评价指标。
4 模拟结果分析与实际应用
利用EDEM软件模拟,对玛瑙球对矿粉微粒混合均匀度的影响进行分析。
4.1 玛瑙球数量对矿粉微粒均匀度的影响
在水平面上对密闭坩埚施加一个水平振动的机械外力。 通过对振动特性的研究,查阅参考相关文献[17],设定振动频率和振幅分别为2 kHz和0.5 mm时,坩埚混料较为合理。 在此基础上,玛瑙球的个数对坩埚内矿粉微粒的均匀性影响如图4所示。
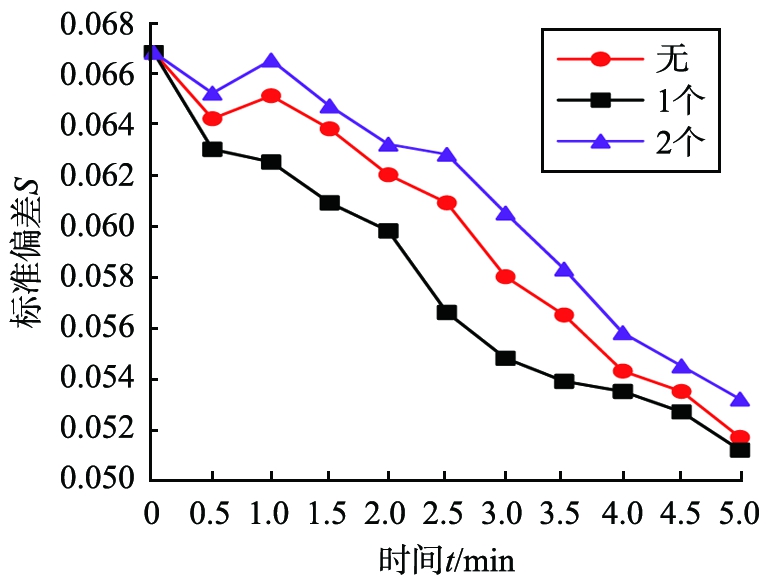
图4 玛瑙球数量对微粒混合均匀度的影响
Fig.4 Effect of agate bulb number on particle mixing uniformity
由图可知:1 min内,标准偏差会出现上下起伏现象,这是由于微粒之间发生碰撞有一个过渡的过程,之后微粒均匀性逐渐清晰,标准偏差随时间增加呈逐渐下降趋势。
2 min时,存放1个玛瑙球的坩埚仿真环境下,标准偏差为0.059 8,最先达到光谱分析的实验条件。不加玛瑙球的条件下,其标准偏差在2.5 min后才达到实验要求,而加入2个玛瑙球在3 min后才达到效果,相比不加玛瑙球的条件,混合速率更低,这是由于多个玛瑙球的体积过大,阻碍了微粒的运动轨迹,减少矿粉微粒的相对运动,矿粉微粒容易积成块状难以混合,即玛瑙球的数量应避免选用太多。
4 min之后,混合处于稳定,微粒混合基本达到均匀,这时玛瑙球对混料均匀度影响不大,所以,玛瑙球有助于矿粉微粒的混合,且时间在2.5 min左右,坩埚中加入1个玛瑙球较为优化。
4.2 翻面倾角对矿粉混合均匀度的影响
通过改变坩埚与水平面的倾斜角度,沿坩埚平面方向施加一维振动,并对坩埚施加一定的转速,这样可以把积压在坩埚底部的矿粉微粒实现翻面运动,从而判断其对混合均匀度的影响。
设定实验的振幅为0.5 mm,频率为2 kHz,转速为120 r/min,坩埚中放入1个玛瑙球。不同的倾角下,矿粉微粒混合均匀度的影响如图5所示。
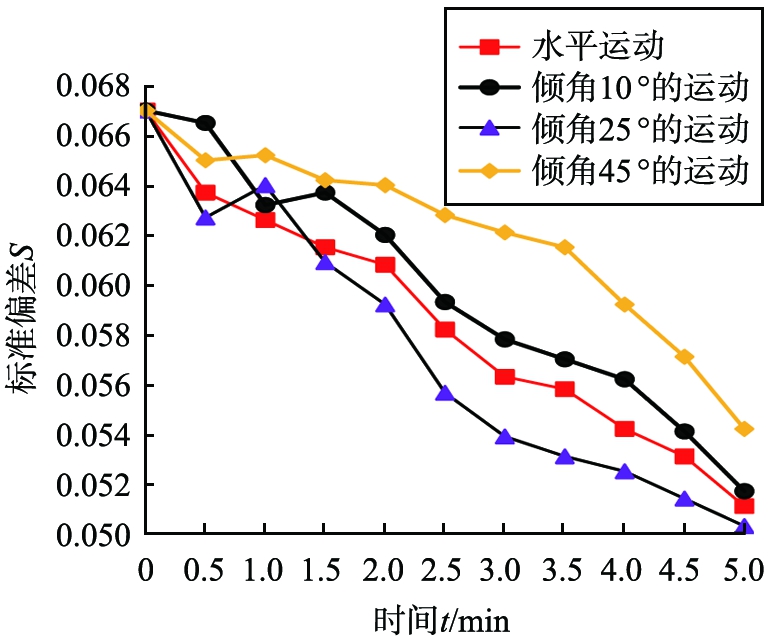
图5 翻面倾角对微粒混合均匀度的影响
Fig.5 Effect of face dip angle on mixing uniformity of particles
从图中可知:2 min时,倾角为25 °的坩埚标准偏差为0.059 2,最先达到试验要求,且2~3 min的混合效率明显优于其他状态下的混合效率,这是由于玛瑙球在上升过程中受到重力的作用而降低了上升幅度,在下降过程中受重力的作用加速下降,减少了微粒的振动幅度,倾斜一定角度能够使坩埚运动的速度方向与重力方向形成倾斜夹角,从而可以削弱重力的影响;当倾角为10 °较小时,微粒混合效果与水平振动基本相同,并未到达最佳混合效果;当倾角为45 °较大时,微粒的混合效果差,虽然削弱了重力的影响,但坩埚主要由底部的支撑转换为侧壁的支撑,玛瑙球的上升幅度会下降,微粒下降到一定的高度也无法下降,从而影响了微粒的混合均匀性。
所以,合理的偏转角度能够将重力作用转换到侧壁上面,使侧壁提供少量支撑力,从而有利于玛瑙球在坩埚中更好的搅拌混合微粒。综上所述,坩埚与水平面倾角为25 °左右时,能达到最佳混合效果。
4.3 振动混料试验
依据上述的模拟结果,制造了一台矿粉混料装置(如图6所示),混料盘的盘面与水平面成一定的倾角 (0~35 °)。

1—偏心振动轴;2—控制面板;3—混料盘。
图6 振动混料实验台
Fig.6 Vibration mixing test rig
在偏心轴的作用下实现沿盘面方向的一维振动(频率0~3 kHz、振幅0.3~0.8 mm)实现振动混料。混料盘还可围绕偏心轴作旋转运动(转速0~300 r/min),配合上述倾角,可实现混合料的翻面,从而提高混合效率。以上参数可根据实验需要进选取和调节。实验时,可将图1中的坩埚(装有需混合矿粉、催化剂和玛瑙球)安放在混料盘的圆孔中,此装置可存放多种实验矿粉的混料。启动机器可按设定参数实现自动混料,物料混合均匀后将玛瑙球取出以供实验用。
设定基本参数,以混料盘的安装孔全部装有坩埚后,且每个坩埚的矿粉都能快速混合均匀为前提。优选的实验参数为振动频率2 kHz、振幅0.3 mm,圆周转速120 r/min。
通过改变玛瑙球的数量和调节混料盘的倾角,将混合到各个时间点的微粒各选取10组样品,按照上述模拟空间格的方法,将样品尽量抹平在筛孔尺寸为0.074 mm的标准筛中,使微粒竟可能落在标准筛的空隙中, 把模拟空间格平面化。在计算机成像平面中,由于矿粉与催化剂微粒灰度相差较大,可以利用像素格分析法对标准筛进行拍照,使用计算机将照片分割成像素格再进行对比。由此方法得到各个时间段10组样品中催化剂微粒所占比例,通过公式(11)得到混合均匀度的标准偏差S值。
玛瑙球个数和倾角对矿粉混合均匀度的影响如图7—8所示。
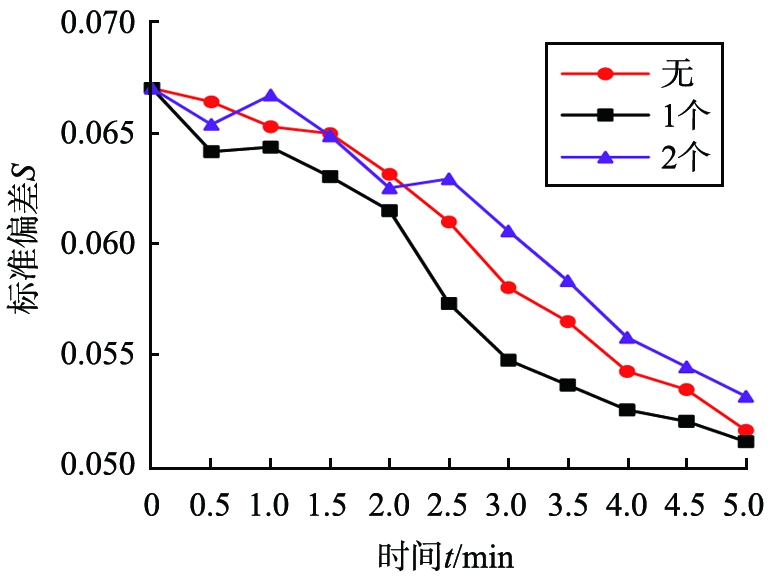
图7 玛瑙球数量对矿粉混合均匀度影响的对比
Fig.7 Comparison of influence of agate ball quantity on mixing uniformity of mineral powder
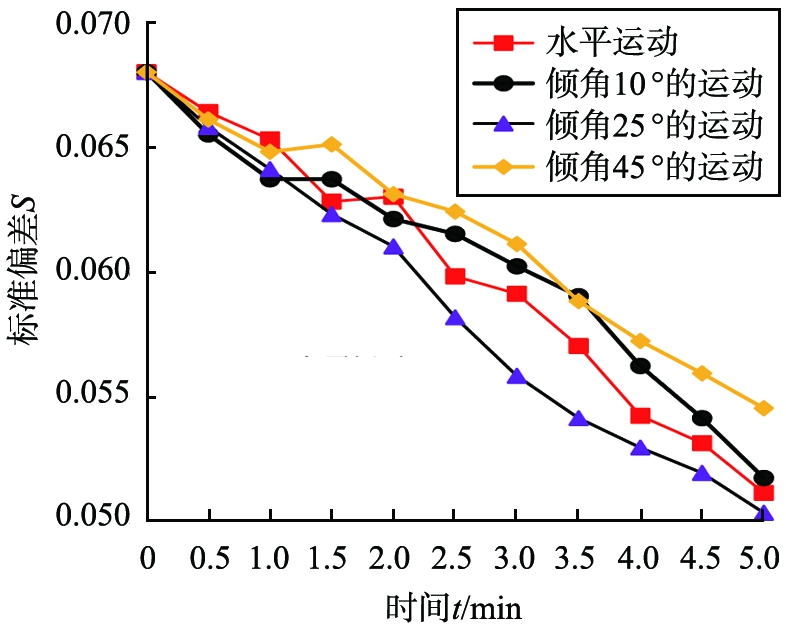
图8 矿粉混合均匀度的样品值对比下倾角翻面不同
Fig.8 Comparison of sample values of mineral powder mixing uniformity under different turning angles
由图可以清楚地看出,坩埚中放入1个玛瑙球,且混料盘的水平倾角为25 °时,最先满足实验标准条件(参照矿粉混合均匀度对应的S值),且时间为2.5 min左右时的混合效率最为明显;4 min后,混合趋于稳定,微粒均匀度基本达到饱和,且在实际操作时该装置运行平稳,实验效果良好。
通过实验还发现,采用该振动混料实验台,适当增加混料盘转速,混料效果更好。
综上所述:实验结果与虚拟仿真结果基本吻合,即玛瑙球在坩埚中起搅拌的作用,能够更好地混合矿粉微粒。
5 结论
1)玛瑙球的加入能充分发挥混料搅拌作用,可以高效地实现矿粉及催化剂的混合,优选的振动时间在2.5 min时只需在坩埚中加入1个玛瑙球。
2)合适的振动混料翻面倾角,能更好地发挥玛瑙球的搅拌作用,加快微粉混合均匀的速度、混合效率更高,优选的混料倾角为20~30 °。
3)实验结果反映了仿真模型的正确性,可为大批量混料作业的生产应用提供借鉴和参考。
[1]王雪莹, 王飞飞, 孙效轩, 等. 钛矿石与钛精矿X射线荧光光谱分析与化学分析用标准样品的研制[J]. 中国无机分析化学, 2018, 8(1): 21-28.
[2]李少华, 朱明亮, 张立栋, 等. 回转装置内三组元颗粒径向混合评价方法分析[J]. 化工进展, 2013, 32(6): 1224-1229.
[3]马宁, 李萌, 陈松, 等. 垂直振动激励下不同状态物料的宏观混合效果[J]. 科学技术与工程, 2016, 16(5): 207-211.
[4]戚华彪, 周光正, 于福海, 等. 颗粒物质混合行为的离散单元法研究[J]. 化学进展, 2015, 27(1): 113-124.
[5]范尚武, 徐永东, 张立同, 等. 振动频率和振动时间对粉料填充密度的影响[J]. 耐火材料, 2005(2): 123-125,129.
[6]梁增华, 刘邱祖, 马麟, 等. 基于EDEM的钛粉在振动成形中的填充密度模拟研究[J]. 粉末冶金工业, 2017, 27(4): 31-34.
[7]任继良, 李志鹏, 周忠勇, 等. 烟花火药成分的混合均匀性[J]. 中国粉体技术, 2014, 20(3): 25-29.
[8]张紫薇, 葛良, 桂南, 等. 转速对三维滚筒内颗粒混合特性的影响[J]. 中国科学院大学学报, 2017, 34(2): 218-225.
[9]JIANG Z H,LU K Q,HOU M Y,et al. Sandwich-like segregation in vertically vibrated binary granular mixtures[J]. Acta Physica Sinica, 2003,52(9): 2244-2248.
[10]GUI N,FAN J R,CEN K F. A macroscopic and microscopic study of particle mixing in a rotating tumbler[J]. Chemical Engineering Science,2010,65(10): 3034-3041.
[11]张立栋, 刘朝青, 于丁一, 等. 低转速回转滚筒内三组元颗粒混合机理[J]. 粉末冶金材料科学与工程, 2014, 19(6): 867-873.
[12]余学闯, 谌炎辉, 谢国进. 基于EDEM的不同颗粒粒径对物料安息角的影响研究[J]. 机械研究与应用, 2017, 30(6): 7-11.
[13]陶明, 徐海军. 玛瑙的结构、水含量和成因机制[J]. 岩石矿物学杂志, 2016, 35(2): 333-343.
[14]陶珍东,郑少华. 粉体工程与设备[M]. 3版. 北京: 化学工业出版社,2015.
[15]王振宇, 周伟, 杨利福, 等. 水平振动情况下颗粒系统振动分离机理的离散元数值研究[J]. 振动与冲击, 2016, 35(16): 24-29.
[16]赵啦啦, 刘初升, 闫俊霞, 等. 不同振动模式下颗粒分离行为的数值模拟[J]. 物理学报, 2010, 59(4): 2582-2588.
[17]刘永桥, 管声启, 柴彩彩. 基于EDEM的固体粉末物料振动下料过程分析[J]. 西安工程大学学报, 2017, 31(2): 278-282,288.