煤散料是一种典型的离散系统,目前国内外涉及到煤散料的输送状态和力学行为的研究,较多采用的是连续介质力学方法,通常将与采煤机械相互作用的煤料视为连续的整体[1],与离散系统本身的性质有所不同。
离散元法(DEM)在分析散体领域具有很大的优势,能够获得散料颗粒大量复杂的行为信息和不易测量的尺度行为信息[2],从细观层面了解其运动情况,对相关机械设备的设计优化具有指导意义。
颗粒材料参数的优化确定是进行离散元数值模拟的首要步骤。许多研究是基于文献中已有的或经验参数[3-6],但由于煤种、煤料大小、含水率情况等实际因素会对颗粒参数造成影响,仅从文献中得到的参数不能更为精确地模拟实际情况,因此,对颗粒参数优化的研究十分必要。离散元仿真参数主要包括2个部分,即材料的本征参数(剪切模量、泊松比和密度)和材料的接触参数(恢复系数、静摩擦系数和滚动摩擦系数)[7]。
对于不同的仿真参数,测定的方法有所不同。有些参数通过实验测定,如Barrios[8]通过自由下落实验和斜板实验分别测定了铁矿石颗粒的碰撞恢复系数和静摩擦系数。李洪昌等[9]、陆永光等[10]和冯斌[11]通过倾斜碰撞实验分别测定了水稻、花生荚果和马铃薯的恢复系数。有些参数通过虚拟优化得到,王云霞等[12]通过堆积角仿真试验,优化确定了玉米种子颗粒间静摩擦系数和滚动摩擦系数,韩燕龙等[13]采用圆筒抬升仿真试验优化确定了水稻颗粒的滚动摩擦系数。也有一些学者[14-15]不通过实际实验测定,将离散元仿真需要的所有参数或者经验所得的主要影响参数作为试验变量,经过大量仿真试验设计,得到与实验结果相一致的参数组合。这种参数优化方法,需设计大量的仿真试验,且最终得到的参数组合不唯一,与实际有较大差距,得到的结果缺乏普适性。
在借鉴国内外针对颗粒参数测定的研究基础上,本文中通过设计系列实验测定了煤的剪切模量、泊松比、密度、煤-煤恢复系数、煤-耐磨钢恢复系数和煤-耐磨钢静摩擦系数。由于煤的不规则外形,不能保证纯滚动,因此其滚动摩擦系数不易直接测定,通过仿真试验和实验相结合的方法进行优化;堆积角是表征散料流动、摩擦等特性的宏观参数[16-17],且堆积角的数据较容易获得,因此选用堆积角试验进行煤料的参数优化;基于响应面设计,以堆积角作为响应值,优化了煤-煤静摩擦系数、煤-煤滚动摩擦系数和煤-耐磨钢滚动摩擦系数,并设计了滑板实验装置进行仿真与实验的对比验证。优化所得参数为进一步研究煤矿机械和煤散料相互作用提供基础。
1 实验材料和方法
1.1 采用实验方法测定的煤散料参数
煤料的本征参数(剪切模量和密度)可通过实验测得。由于煤颗粒的不规则外形和各向异性,不能保证煤的纯滚动,因此可通过实验测得的接触参数包括煤-耐磨钢静摩擦系数、煤-煤以及煤-耐磨钢恢复系数。
1.1.1 剪切模量
选用煤为产自陕西榆林神木的长焰煤。将煤制成标准试样的直径为50 mm,长为100 mm,进行单轴压缩实验,煤单轴压缩应力-应变曲线如图1所示。

图1 煤单轴压缩应力-应变实验曲线
Fig.1 Experimental curve for coal stress and strain with uniaxial compression
选取图1中近似直线段MN,进行直线拟合,拟合直线斜率即为弹性模量(1 258.5 MPa),参考文献中泊松比0.3[1],剪切模量计算公式为
式中:G为剪切模量;E为弹性模量;v为泊松比。求得剪切模量为4.7×108Pa。
1.1.2 密度和煤-钢静摩擦系数
煤颗粒密度采用传统排水法测得,煤与耐磨钢间的静摩擦系数通过传统抬升斜板实验测得,考虑到煤颗粒的不规则外形,进行10次重复实验。
1.1.3 恢复系数
恢复系数表示了颗粒物料被碰撞后能恢复到其原始状态(碰撞前)的性能,定义为碰撞后法向分离速度与碰撞前法向接近速度的比值[18]。目前,关于农作物的恢复系数研究较多[9-11],但对煤颗粒的恢复系数研究较少。由于煤颗粒形状不规则,差异较大,因此恢复系数实验要进行大量的重复实验以减少误差干扰,选取50~60颗煤粒进行实验,选用的煤料粒径为6~8 mm,用实验筛筛出。图2为煤颗粒恢复系数测量原理示意图及测量装置。
基于运动学原理(图2a),设计了实验装置(图2b)来测定煤料与耐磨钢(煤料)的恢复系数。煤与耐磨板间的恢复系数通过煤碰撞耐磨板测得,煤颗粒间的恢复系数通过煤颗粒碰撞煤块测得。
图2a中h为煤颗粒开始自由下落到耐磨钢板的高度,经预实验测定,下落高度对恢复系数影响不大,取下落高度为500 mm。耐磨钢板倾角设置为45°,煤料碰撞到耐磨钢板反弹后做斜抛运动,可将其分解为2个方向的运动,水平面内以速度Vx做匀速运动,垂直面内做初速度Vy,加速度为重力加速度g的匀变速运动,最后落在接料板上。接料板上铺设了一层煤粉,目的是可以清晰的捕捉落点位置。其运动满足方程
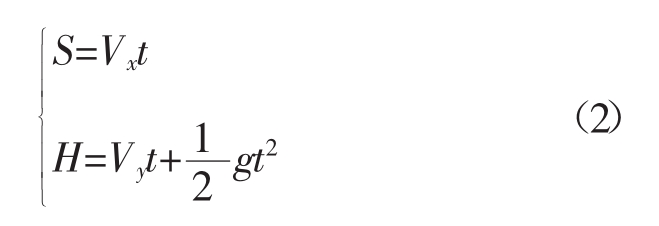
式中:S为煤颗粒碰撞斜板后在水平面内的位移;H为煤颗粒碰撞斜板后在垂直面内的位移。
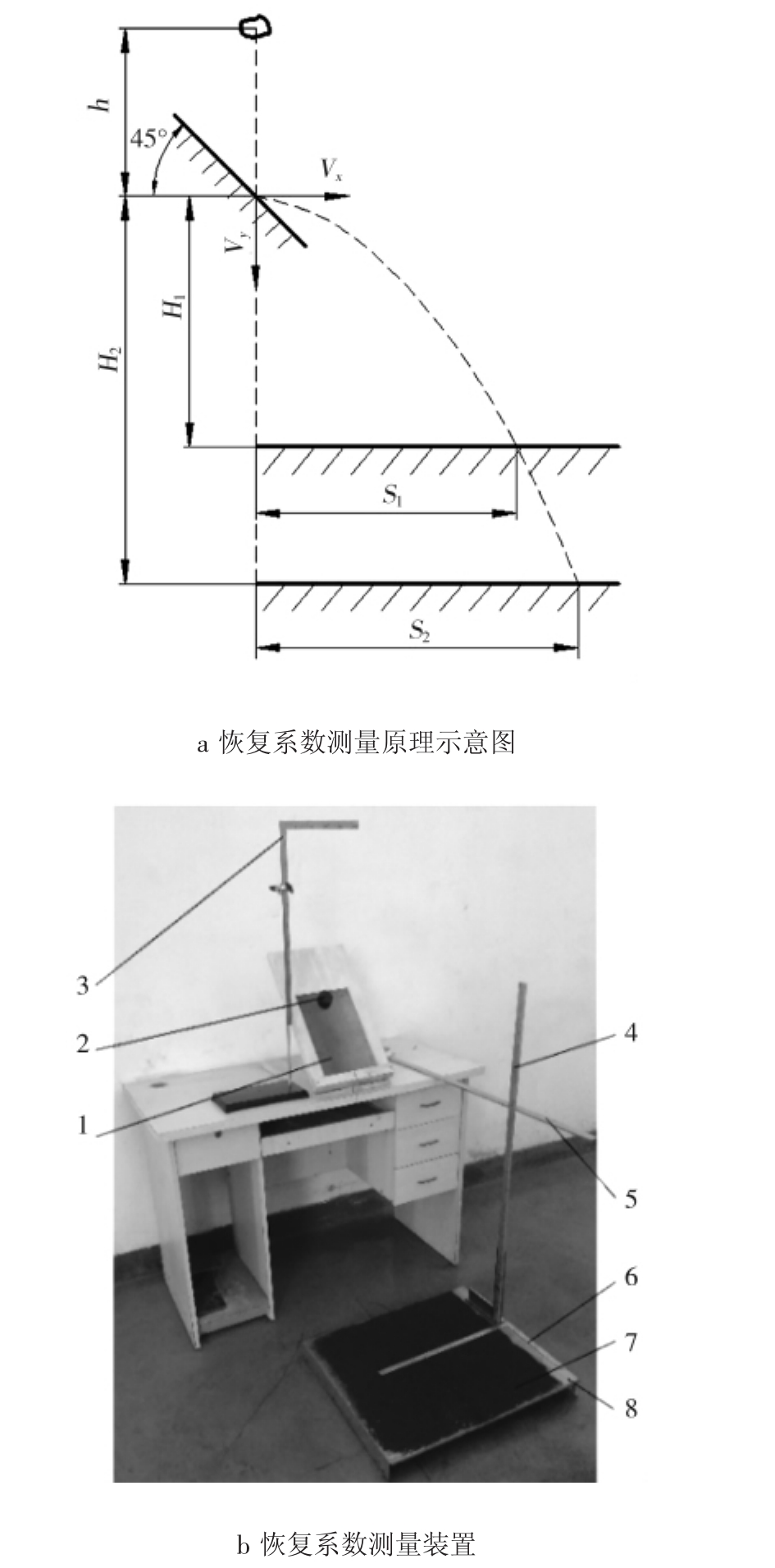
图2 煤颗粒恢复系数测量原理示意图及测量装置
Fig.2 Principle schematic and prototype of restitution coefficient measuring device for coal particles
1—耐磨钢板;2—煤块;3—下落高度标尺;4—垂度尺;5—水平位移尺1;6—水平位移尺2;7—煤粉8-接料板。
更改接料板的高度,测得在2个位置下煤粒的位移 S1、H1、S2、H2,可得到方程
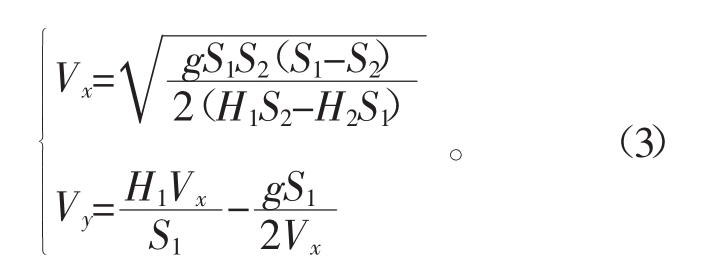
根据恢复系数的定义,得恢复系数

式中,Cr为恢复系数;Vn为碰撞后法向分离速度;Von为碰撞前法向接近速度![]()
1.2 采用仿真与实验对比方法进行煤散料优化
部分煤颗粒的接触参数包括煤-煤静摩擦系数、滚动摩擦系数以及煤-耐磨钢板滚动摩擦系数,通过实验不易测得,采用仿真与实验相结合的方法进行参数优化。参数优化流程图如图3所示。
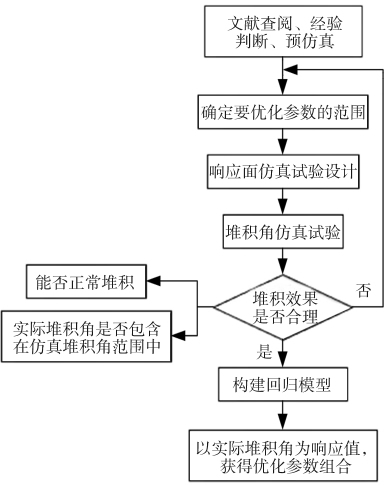
图3 参数优化流程图
Fig.3 Parameter optimization flow chart
1.2.1 仿真模型
1)煤颗粒离散元模型
由于煤颗粒形状不规则,因此统计了500 g粒径为6~8 mm的煤料,按相似形状进行分类统计,扁平状、类锥状、类块状质量各为75、120、305 g。为了与实际更为接近,在离散元软件EDEM中建立了3种颗粒模型,如图4所示为煤颗粒模型,颗粒模型尺寸按照实际煤料粒径范围随机生成,试验拟采用1 kg煤料。

图4 煤颗粒模型
Fig.4 Model of coal particles
2)离散元仿真参数设置
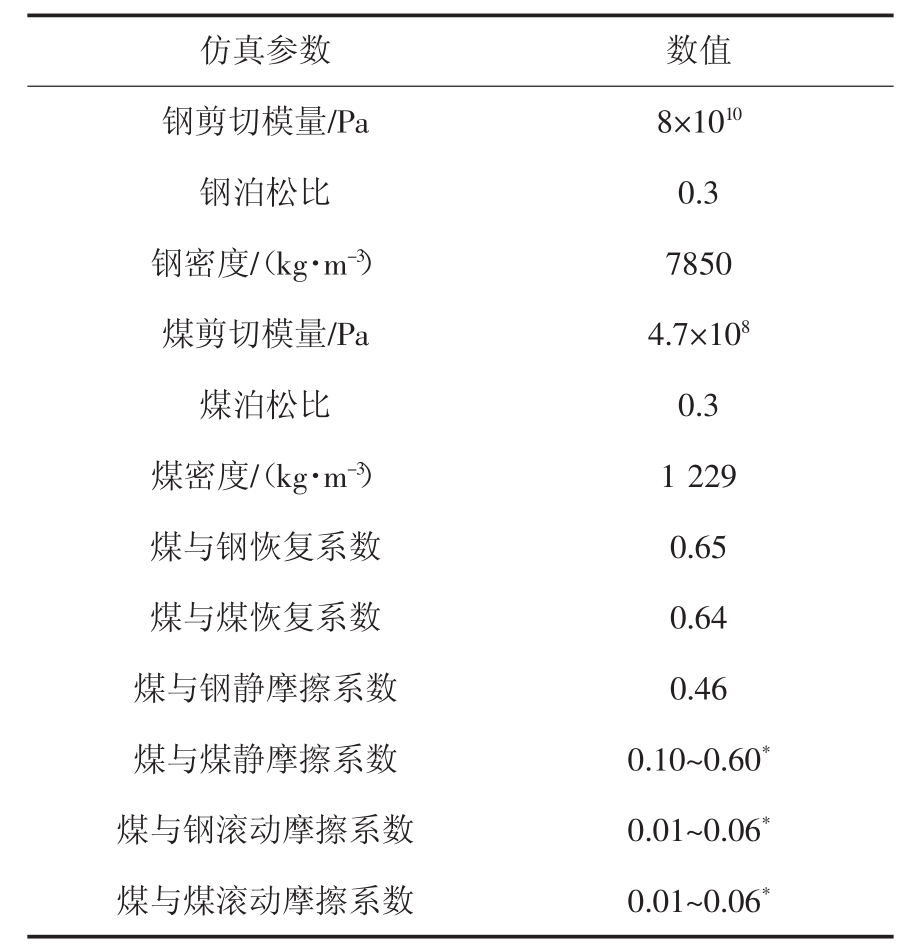
通过查阅文献[1],实验测定,仿真预试验,得到EDEM仿真所需参数如表1所示。
表1 EDEM仿真所需参数
Tab.1 Parameters required in EDEM simulation
注:*表示此项为试验变量
仿真参数 数值钢剪切模量/Pa 8×1010钢泊松比 0.3钢密度/(kg·m-3)7850煤剪切模量/Pa 4.7×108煤泊松比 0.3煤密度/(kg·m-3)1 229煤与钢恢复系数 0.65煤与煤恢复系数 0.64煤与钢静摩擦系数 0.46煤与煤静摩擦系数 0.10~0.60*煤与钢滚动摩擦系数 0.01~0.06*煤与煤滚动摩擦系数 0.01~0.06*
3)堆积仿真模型
在三维建模软件PROE中建立漏斗模型,并将其导入到EDEM中,堆积装置仿真模型如图5所示。在EDEM中定义模型材料属性。试验采用完全烘干后的煤料。基于 DEM 模型理论[2],采用 Hertz-Mindlin(no slip)模型,取重力加速度为9.81 m/s2。
图5 堆积装置仿真模型
Fig.5 Simulation model of stacking device
4)响应面设计试验
采用Design Expert软件,基于Box-Behnken试验设计原理,将3个试验变量进行响应面试验设计,选用3个中心点进行误差估计,共计15组仿真试验。
1.2.2 实验模型
研究采用的煤颗粒堆积实验装置如图6所示。在漏斗中加入1 kg的煤料,然后通过漏斗在耐磨板上形成近似锥形的颗粒堆,做3次重复实验。

图6 煤颗粒堆积实验装置
Fig.6 Coal particle accumulation test
为了减少人为测量导致的误差,更加准确地对堆积角进行测量,参考贾富国等[19]关于颗粒堆积角的图像处理方法,从4个方向对煤料堆进行拍照,然后利用MATLAB软件对堆积图像进行灰度化、二值化、提取边界轮廓,最后基于最小二乘法原理进行线性拟合得到堆积角。堆积角图像处理过程如图7所示。

图7 堆积角图像处理
Fig.7 Image processing of stacking angle
2 仿真结果与讨论
2.1 Box-Behnken仿真试验结果及分析
Box-Behnken仿真试验设计及其结果如表2所示。
表2 Box-Behnken仿真试验设计及结果
Tab.2 Design and results of Box-Behnken simulation test
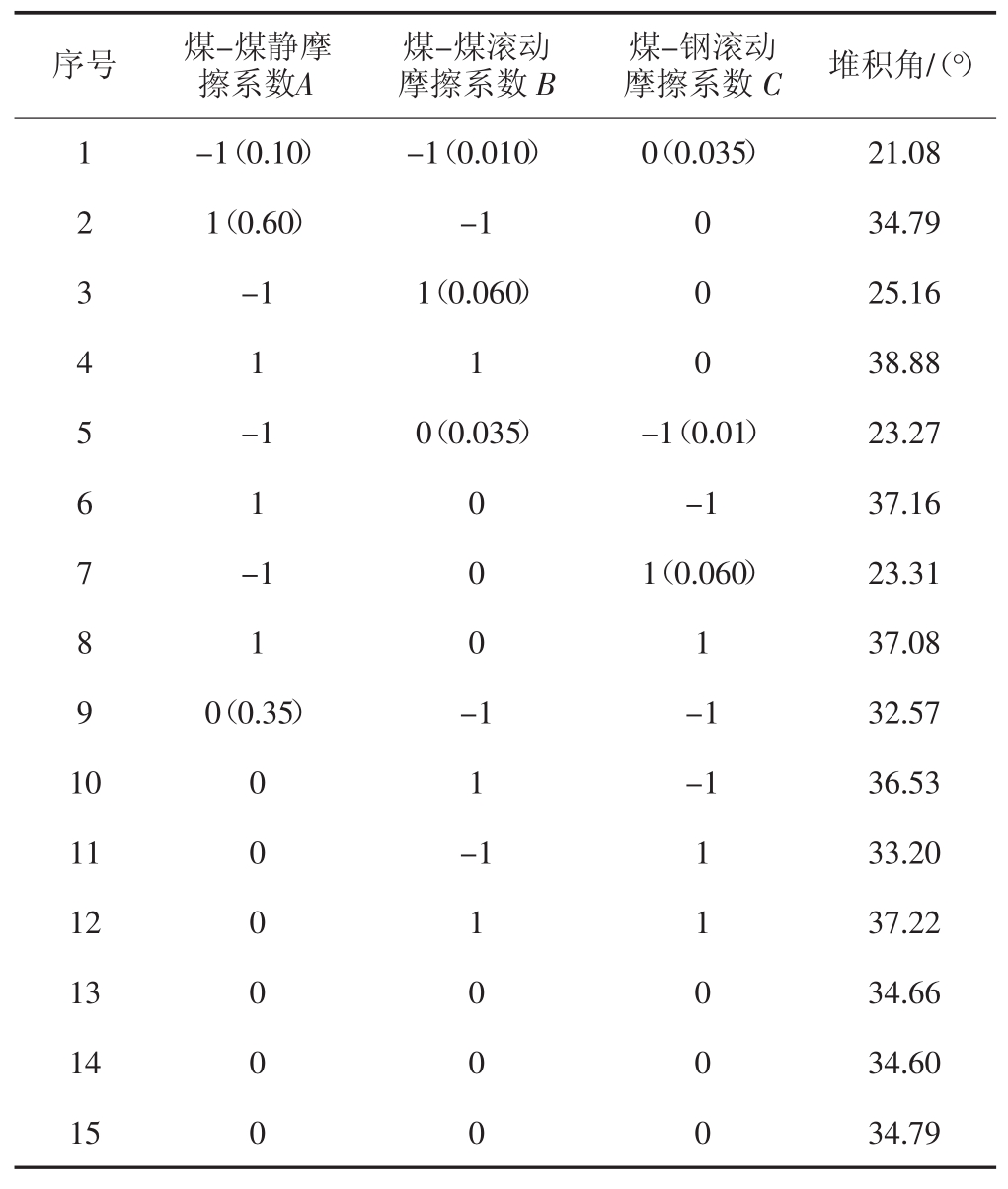
序号 煤-煤静摩擦系数A煤-煤滚动摩擦系数B煤-钢滚动摩擦系数C堆积角/(°)1 -1(0.10) -1(0.010) 0(0.035) 21.08 2 1(0.60) -1 0 34.79 3 -1 1(0.060) 0 25.16 4 1 1 0 38.88 5-1 0(0.035) -1(0.01) 23.27 6 1 0-1 37.16 7-1 0 1(0.060) 23.31 8 1 0 1 37.08 9 0(0.35) -1 -1 32.57 10 0 1 -1 36.53 11 0 -1 1 33.20 12 0 1 1 37.22 13 0 0 0 34.66 14 0 0 0 34.60 15 0 0 0 34.79
用Design-Expert软件建立煤散料堆积角与试验变量的二阶回归模型,得到其回归方程为

回归模型方差分析结果如表3所示,该拟合模型的P<0.000 1,表明用此模型来描述响应值与各参数值间的关系时,因变量与自变量间的关系极其显著;煤-煤静摩擦系数A、煤-煤滚动摩擦系数B、煤-煤静摩擦系数二次项A2对堆积角影响极显著;失拟项P=0.106 6>0.05,说明方程拟合良好。一般情况下,变异系数CV越高,试验的可靠性越低,该试验的变异系数为0.71%,表明了试验具有较好的可靠性。决定系数R2=0.999 5,校正决定系数R2adj=0.998 5,二者接近1,说明拟合方程可靠性高;精密度为95.428,表明该模型具有良好的精确度。
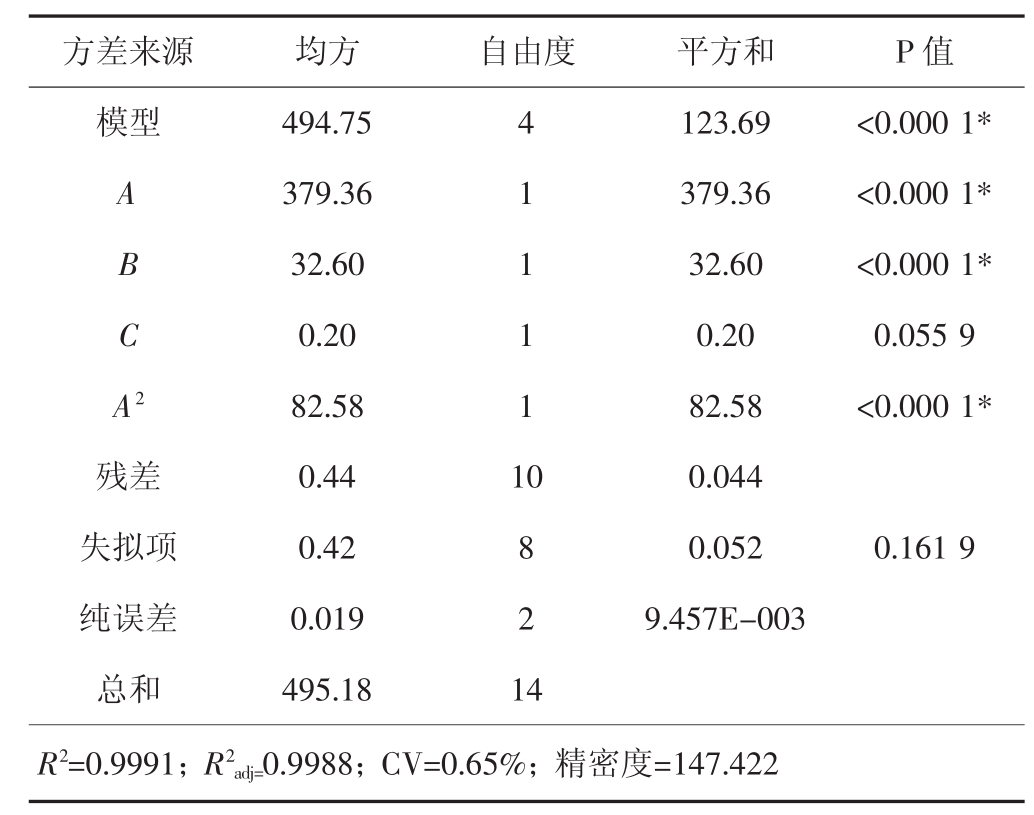
在保证回归模型显著、失拟项不显著的前提下,去除较不显著的项,对二阶回归模型进行优化,得到新的回归方程为
优化后的回归模型方差分析如表4所示。由表可知模型各项均得到优化。其变异系数降低到0.65%,可靠性增加;决定系数R2=0.999 1,校正决定系数![]() ,二者皆接近1,说明拟合方程可靠度提高;精密度增大到147.422,可以更准确的预测煤堆的堆积角。
,二者皆接近1,说明拟合方程可靠度提高;精密度增大到147.422,可以更准确的预测煤堆的堆积角。
表3 Box-Behnken试验设计的回归模型方差分析
Tab.3 ANOVA of regression model for Box-Behnken test
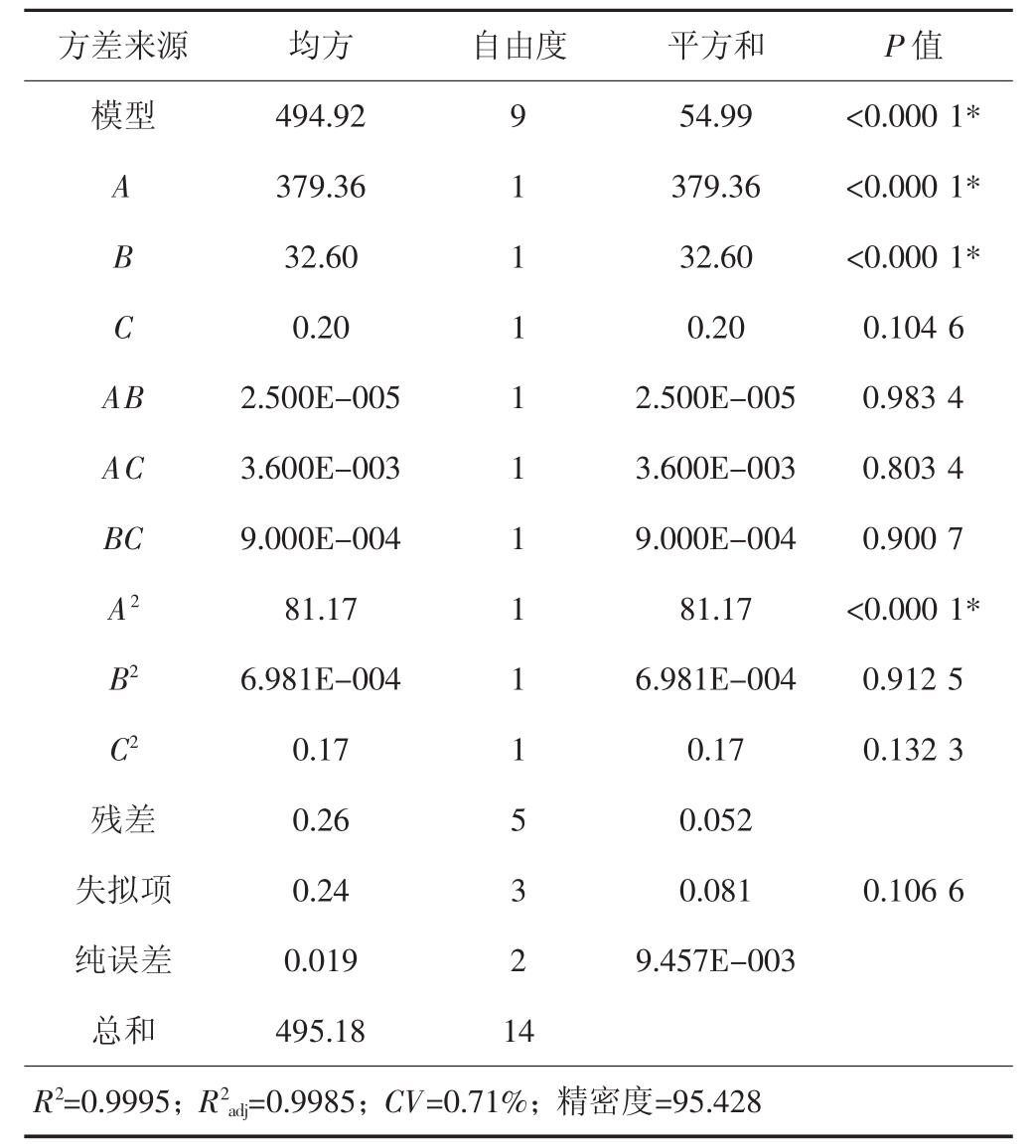
注:*表示该项显著(P<0.05)。
方差来源 均方 自由度 平方和 P值模型 494.92 9 54.99 <0.000 1*A 379.36 1 379.36 <0.000 1*B 32.60 1 32.60 <0.000 1*C 0.20 1 0.20 0.104 6 AB 2.500E-005 1 2.500E-005 0.983 4 AC 3.600E-003 1 3.600E-003 0.803 4 BC 9.000E-004 1 9.000E-004 0.900 7 A2 81.17 1 81.17 <0.000 1*B2 6.981E-004 1 6.981E-004 0.912 5 C2 0.17 1 0.17 0.132 3残差 0.26 5 0.052失拟项 0.24 3 0.081 0.106 6纯误差 0.019 2 9.457E-003总和 495.18 14 R2=0.9995;R2adj=0.9985;CV=0.71%;精密度=95.428
表4 Box-Behnken试验优化回归模型方差分析
Tab.4 ANOVA of modified regression model for Box-Behnken test
注:*表示该项显著(P<0.05)。
方差来源 均方 自由度 平方和 P值模型 494.75 4 123.69 <0.000 1*A 379.36 1 379.36 <0.000 1*B 32.60 1 32.60 <0.000 1*C 0.20 1 0.20 0.055 9 A2 82.58 1 82.58 <0.000 1*残差 0.44 10 0.044失拟项 0.42 8 0.052 0.161 9纯误差 0.019 2 9.457E-003总和 495.18 14 R2=0.9991;R2adj=0.9988;CV=0.65%;精密度=147.422
2.2 最优参数组合的确定
通过3次重复堆积试验,采用MATLAB图像处理技术,得到煤料的实际堆积角为34.28°。
利用Design-Expert的优化功能,在试验因素取值范围内以实际堆积角为响应值对优化后的回归模型进行求解,得到最优参数组合为:煤-煤静摩擦系数为0.329,煤-煤滚动摩擦系数为0.036,煤-耐磨钢滚动摩擦系数为0.032。
3 验证试验
滑板试验装置如图8所示,用于验证最优参数的准确性。滑板试验相比于漏斗试验,增加了煤颗粒的运动过程。将滑板试验装置通过PROE建模,然后导入到EDEM中,把通过实验测定参数与仿真优化参数作为离散元仿真参数,进行滑板试验的仿真模拟,同时进行相应的实验,重复3次。

图8 滑板试验装置
Fig.8 Device of skateboard test
1—侧挡板;2—调位孔;3—挡料板;4—料斗;5—碰撞板;6—前部观察板(透明的);7—底板。
由试验可得,仿真堆积角为28.14°,实验堆积角为28.51°,数值差异是1.3%,差异较小。实验与仿真试验堆积形态曲线对比如图9所示。由图可以看出:仿真与实验堆积轮廓形态曲线拟合较好,说明与实际情况较为相符。该参数可更好地为煤散料与煤矿机械相互作用的进一步模拟提供依据。
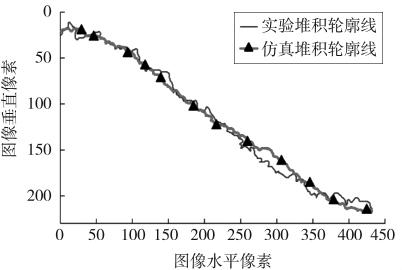
图9 实验与仿真试验堆积形态曲线对比
Fig.9 Comparison of accumulation state curve for simulation and actual tests
4 结论
1)通过单轴压缩实验测得了煤的剪切模量和泊松比,用排水法测得了煤的密度,用斜板抬升实验测得煤-耐磨钢的静摩擦系数,用斜碰实验测得了煤-煤和煤-钢的恢复系数。
2)根据Box-Behnken试验结果,建立了试验变量与堆积角间的回归模型并对其进行了优化。通过方差分析可知,煤-煤静摩擦系数、煤-煤滚动摩擦系数、煤-煤静摩擦系数的二次项对堆积角影响极为显著。
3)以实际堆积角作为响应值,对优化后的回归模型进行求解,优化确定了煤-煤静摩擦系数为0.329,煤-煤滚动摩擦系数为0.036,煤-钢滚动摩擦系数为0.032。
4)通过滑板试验对得到的优化参数进行验证,对比实验与仿真的堆积形态曲线,发现2条曲线拟合性较好,堆积角差异是1.3%,差异很小,从而说明针对煤料的参数优化方法是可行的。
[1]蔡柳.煤散料在刮板输送机中部槽内的运输状态与力学行为[D].太原:太原理工大学,2016.
[2]王国强,郝万军,王继新.离散单元法及其在EDEM上的实践[M].西安:西北工业大学出版社,2010.
[3]GONG Z Q,WANG D C,WANG G H,et al.Simulation analysis and design of vertical screw silage-conveyor based on EDEM[R].ASABE Annual International Meeting,2016.
[4]蔡柳,王学文,王淑平,等.煤散料在刮板输送机中部槽中的运动分布特征与作用力特性[J].煤炭学报,2016,41(S1):247-252.
[5]毛君,刘歆妍,陈洪月,等.基于EDEM的采煤机滚筒工作性能的仿真研究[J].煤炭学报,2017,42(4):1069-1077.
[6]WANG X W,LI B,YANG Z J.Analysis of the bulk coal transport state of a scraper conveyor using the discrete element method[J].Journal of Mechanical Engineering,2018,64(1):37-46.
[7]龚明.材料物料特性参数标定 [R].北京:EDEM用户大会报告,2013.
[8]BARRIOS G K P,CARVALHO R M D,KWADE A,et al.Contact parameter estimation for DEM simulation of iron ore pellet handling[J].Powder Technology,2013,248(2):84-93.
[9]李洪昌,高芳,李耀明,等.水稻籽粒物理特性测定[J].农机化研究,2014(3):23-27.
[10]陆永光,吴努,王冰,等.花生荚果碰撞模型中恢复系数的测定及分析[J].中国农业大学学报,2016,21(8):111-118.
[11]冯斌,孙伟,石林榕,等.收获期马铃薯块茎碰撞恢复系数测定与影响因素分析[J].农业工程学报,2017,33(13):50-57.
[12]王云霞,梁志杰,张东兴,等.基于离散元的玉米种子颗粒模型中间接触参数标定[J].农业工程学报,2016,32(22):36-42.
[13]韩燕龙,贾富国,唐玉荣,等.颗粒滚动摩擦系数对堆积特性的影响[J].物理学报,2014,63(17):165-171.
[14]刘凡一,张舰,李博,等.基于堆积试验的小麦离散元参数分析及标定[J].农业工程学报,2016,32(12):247-253.
[15]罗帅,袁巧霞,GOUDA S,等.基于JKR粘结模型的蚯蚓粪基质离散元法参数标定[J].农业机械学报,2018,49(4):343-350.
[16]吴爱详,孙业志,刘湘平.散体动力学理论及其应用[M].北京:冶金工业出版社,2002.
[17]GUO Z G,CHEN X L,LIU H F,et al.Theoretical and experimental investigation on angle of repose of biomass-coal blends[J].Fuel,2014,116(1):131-139.
[18]葛藤,贾智宏,周克栋.计算点面接触碰撞恢复系数的一种理论模型[J].机械设计与研究,2007,23(3):14-15.
[19]贾富国,韩燕龙,刘扬,等.稻谷颗粒物料堆积角模拟预测方法[J].农业工程学报,2014,30(11):254-260.