气力输送是用气体作为载体在密闭的管道中输送固体物料的一种输送技术,由于该技术具有布置灵活,使用简单,输送距离长,输送物料量大等优点,被广泛应用于粮食等散料的运输[1-2]。目前粮食颗粒的主要运输方式以稀相输送为主。然而,该种输送技术具有较高的能耗,管道的磨损和粉料破碎等缺陷,这些问题一直在困扰着气固两相流技术的发展[3-4]。对于稀相输送的不足,有研究人员提出了密相输送技术。文献[5-7]通过实验和仿真的方法对粉煤灰颗粒在密相条件下的气力输送进行相关研究,分析物料在管道内的流动特性,得出物料在管道中的流动规律,并找到使流体连续稳定流动的方法。经过研究发现密相输送技术拥有能耗低、固气比大和气固分离量小的优势,同时也存在易堵塞和气体膨胀等问题[8-9],研究人员发现解决这些问题最直接有效的办法是改变管径的大小。文献[10-11]分析变径管流场中的速度分布和管压降变化状况,得出使用合理尺寸的变径管能减少气蚀和振动等不利影响因素的结论;管径比和变径长度对变径管压降的影响规律。虽然对密相变径输送的相关研究较多,但是绝大部分都是以粒径为100 μm的粉煤灰等细小颗粒为输送对象,而针对粒径较大的粮食颗粒的研究较少,尤其是粮食颗粒的密相变径输送研究更为鲜见。鉴于此,利用FLUENT软件中的Euler双流体模型与k-ε湍流模型,对小麦颗粒在直管和变径长度不同的管道中进行流动特性的数值模拟,得出主要参数的变化对粮食颗粒在变径管中流动特性的影响。并将仿真模拟结果与实验数据相比较,验证其正确性。
1 数学模型
1.1 控制方程的建立
连续性方程是描述守恒量的偏微分方程,它是质量守恒定律在流体力学中的具体表述[12]。连续性方程在欧拉意义上的表达式可描述为:微元控制体密度的局部增长率与微元控制体单位体积流出的质量之和等于零。气相与固相的具体连续方程为
式中:αa、αs为气固两相的体积分数;ρa、ρs为气固两相的密度,kg/m3;va,vs分别为气固两相的速度,m/s。
流体微团的运动方程又称为动量方程,在欧拉意义上的表达式可描述为:微元控制体单位体积流体上的局部动量增长率与通过微元控制体的单位体积流体的动量输出量之和等于微元控制体上单位体积流体的质量力与表面力之和。气相与固相动量方程为
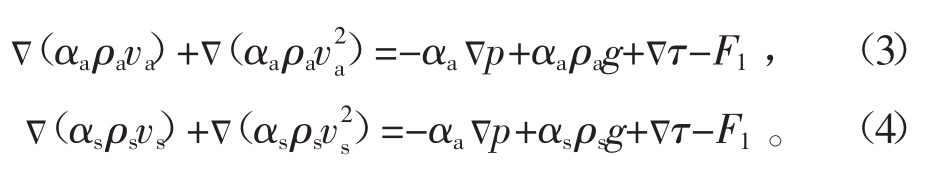
式中:P为压力,Pa;τ为应力张量;F1为两相间的作用力,其中相间阻力F2值最大且最为重要,其他相间力可忽略不计。
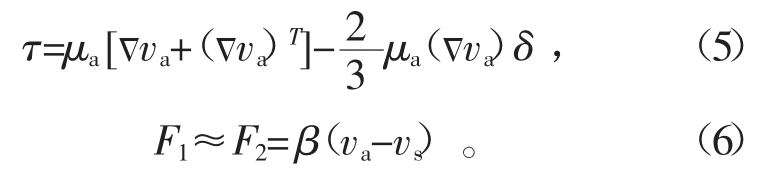
式中:μa为气体相的黏性系数;δ为克罗内克符号,此处取1;β为气固曳力系数,可用Ergun公式计算得到:
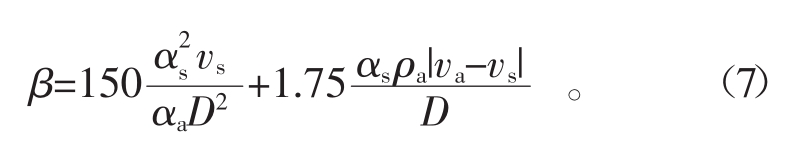
式中D为管道直径,m。
式(1)—(4)为计算流体动力学(CFD)的基本方程,根据动量与能量守恒的基本原理,描述两相在流动过程中体积分数、压力和速度等参数随着时间的变化。
1.2 湍流方程的选择
考虑到管道内的湍流作用强烈,故采用标准k-ε方程模型。模型需要求解k方程(湍流动能方程)及ε方程(湍流耗散方程)2个方程,
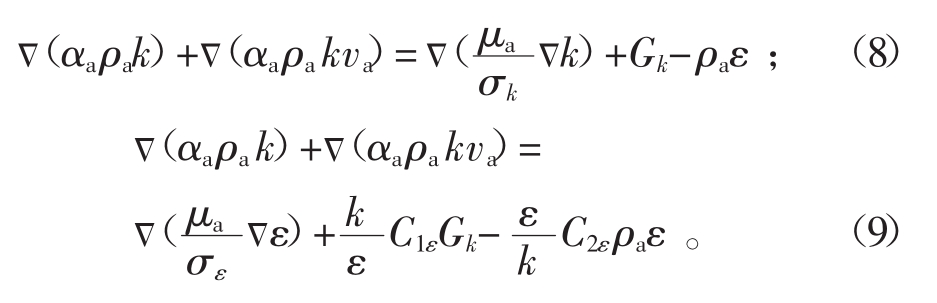
式中:k为单位质量流体湍流脉动动能;σk、σε分别为湍动能和湍动耗散率对应的普朗特数;Gk是湍动能;ε是湍动耗散率。
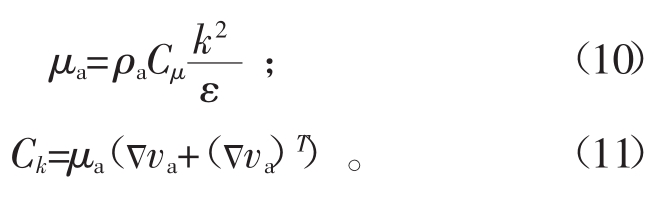
式中 Cμ=0.0845。
式(8)、(9)表示湍流对气力输送过程中能量的影响。k方程是湍流理论中最基本的方程之一,方程左端是湍流动能随时间变化率,它是由右端各项引起的。第1项为脉动能量的空间对流扩散;第2项是由于平均速度梯度引起的湍动能;第3项为湍流动能的耗散项,该项永远为负,即它使脉动动能减小而变成热能。ε方程是关于耗散项ε的微分方程。
2 数值仿真
2.1 几何模型的建立
用Workbench中的Geometry软件进行几何模型的建立,模型为4种不同的输送管道,管道模型几何尺寸如图1所示。
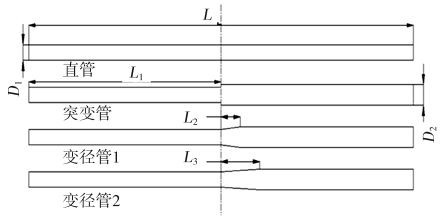
图1 管道模型几何尺寸示意图
Fig.1 Schematic diagram of pipe geometry
第1个管道为直管,管径D1=0.075 m,长度为L=3 m;后3种管道为不同的变径管,变径长度都为L1=1.5 m,变径后的管径为D2=0.1 m。其中变径管1的变径长度L2=0.15 m,变径管2的变径长度为L3=0.3 m。
2.2 计算网格的划分
用Workbench中的Mesh软件对所建立的模型进行网格划分。网格划分采用四面体网格,由于粮食颗粒直径较大,故网格最大尺寸为0.005 m,最小尺寸为0.003 m,在近壁面对网格进行加密。管道网格划分效果图见图2。
2.3 边界条件的设定
边界条件是数值计算过程中重要的一个环节,边界条件设定的好与否,直接关系到计算结果是否准确[13]。具体入口边界条件如表1所示。
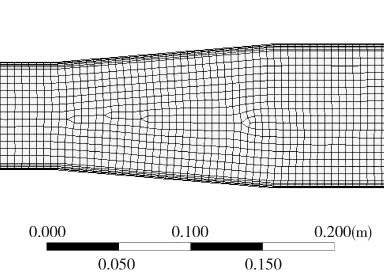
图2 管道网格划分效果图
Fig.2 Pipeline mesh renderings
表1 入口边界条件
Tab.1 Inlet boundary conditions
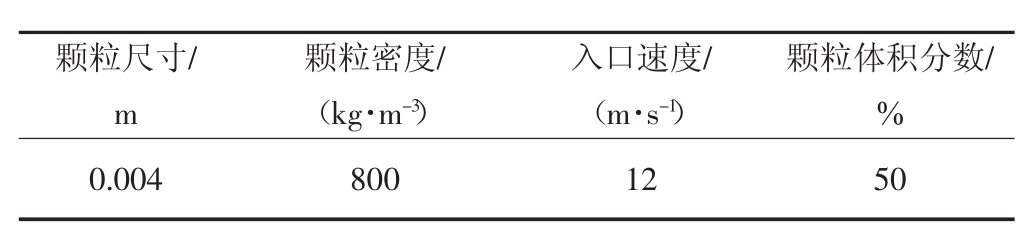
颗粒尺寸/m颗粒体积分数/%0.004 800 12 50颗粒密度/(kg·m-3)入口速度/(m·s-1)
3 结果与讨论
3.1 湍流强度在管道内的变化
湍流强度简称湍流度或湍强,反映脉动风速的相对强度,是描述大气湍流运动特性的最重要的特征量[14]。4种管道内的湍流强度如图3所示。
从图中可以看出,由于初始的边界条件相同,所有初始湍流强度均为11.3%;比较最终湍流强度,最小为变径管2,为127%;之后为变径管1的132%和突变管的140%,最大为直管的145%。
由图可以看出,湍流都发生在管道的后半段,这是因为气体速度的变大导致雷诺数的增大,从而使湍流强度变大,且湍流强度随着管道长度增大而增大,最大值都达到100%以上,最终平均值也在60%~80%之间,说明湍流对输送过程有较大的影响;对比图3a—d,3种变径管最终的湍流强度比直管要小,且湍流强度随时间的变化率也远远小于直管,说明变径管可以对湍流起到较好的控制效果。

图3 4种管道内的湍流强度
Fig.3 Turbulence intensity chart for four pipes
3.2 颗粒体积分数随管长的变化
颗粒体积分数能很好地展示颗粒在管道中的分布状况,通过不同的颗粒体积分数分布能够展示不同的流型[15-16]。体积分数随管长的变化如图4所示。
由图可以看出,4种管道中物料在入口处的体积分数为50%,随着管道长度的增加,由于重力大,动力小的原因,物料在0.5 m处开始与气体分离;在1 m处,大部分物料在管道底部流动,颗粒的体积分数接近1;在1.5 m的变径处,直管中颗粒体积分数没有太大变化,颗粒仍然在管道底部流动。其余3个管道由于管道口径从0.075 m增大至0.1 m,在变径处形成高低差,物料有一个下降的抛物线型的流动,突变管在变径管处,颗粒流下方的颗粒体积分布比上方的小,变径管2则正好相反,颗粒流下方的颗粒体积分布比上方的大,而变径管1颗粒流上下方的颗粒分布较为均匀。
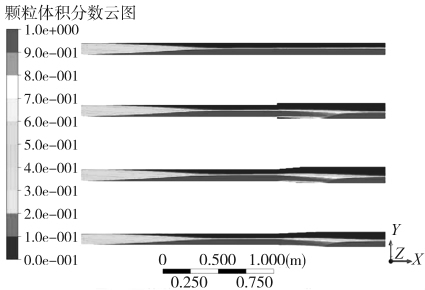
图4 颗粒体积分数随管长的变化
Fig.4 Distribution of volume fraction with tube length
从颗粒的体积分数可以推断出物料的流动类型是密相输送中的部分流;物料通过变径管时,颗粒体积分数发生变化,突变管由于管径变化过快,在变径处下方形成回流区,导致物料在此区域沉积,这会造成管道堵塞;变径管2由于变径长度过长,导致物料的流动不及变径管1均匀,从而会影响小麦颗粒的正常运输。
3.3 气体速度的变化规律
直管与突变管气体速度变化曲线如图5所示。对比图中曲线可以看出,直管内的气流速度沿管道方向单调持续增加,在管道尾段气流增长很快,在末端速度达到最大值18.29 m/s;突变管中的气流速度在管道长度1.5 m以前与直管上升趋势大致相同,通过变径之后,在1.5~2 m处,气体速度下降,降到13.42 m/s,然后持续增大,最终速度最大值达到15.94 m/s。
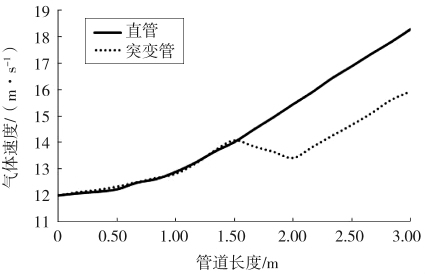
图5 直管与突变管气体速度变化曲线
Fig.5 Gas velocity curve between straight tube and abrupt tube
气体速度的持续增加,是由于在单一管径输送系统中,空气的初始速度确定后,输送过程中产生气流的连续膨胀,使气流速度不断增大;另外,由于固相在管道底部的缓慢流动,造成气体流动的通道变小,也会造成气流速度的不断增加。变径管造成气流速度的下降,是由于通过改变管径修正气流的连续膨胀引起的气流变化,使气流速度下降。从热力学原理角度进行分析,
式中:P0、P1为变径前后压力,Pa;T0、T1为变径前后温度,℃;V为气体体积流量,m3/s。
从式(12)可以看出,当其他条件一定时,气体速度与气体体积流量成正比,与管径的平方成反比。在本研究中,变径前后压力和温度相差不大,可以认为比值为1,而变径后气体体积流量变小,管径变大,直接导致气体速度的减小。
3种变径管的气体速度变化曲线如图6所示。在1.5 m之前,气体速度变化大致相同;在1.5 m时,气体速度都有所下降,突变管下降到12.89 m/s,变径管1下降到10.58 m/s,变径管2下降到11.23 m/s。对比3个数据,变径管1的降速效果最为明显。
突变管虽然管径变大,但是因为变化过快,使之在变径口下方产生气流涡旋,使变径前后压力和温度的比值变大,减弱降速效果;变径长度较大,管道直径比变径管1变化慢,影响气体速度随之变慢,导致降速效果没有变径管1理想。
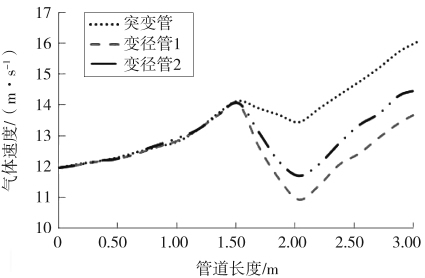
图6 3种变径管的气体速度变化曲线
Fig.6 Three adjustable tube gas velocity curve
3.4 压降曲线的变化规律
压力损失随管道长度的变化曲线如图7所示。从图中可以看出,压力损失最大值在管道出口处,其中直管为469.04 Pa,突变管为417.16 Pa,变径管1为349.72 Pa,变径管2为379.64 Pa;4种管道的压力损失都随着管道长度的增大而不断增大,变径管1的压力损失最小,其次为变径管2,然后为突变管,最后为直管。
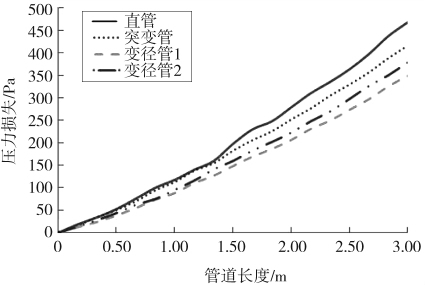
图7 压力损失随管道长度的变化曲线
Fig.7 Pressure loss curve with length of pipeline
上述结果产生的原因是在输送过程中气相与固相、固相与固相、固相与管壁、气相与管壁之间有相互作用,导致能量耗散以及湍能的耗散从而形成压力损失。湍流对压力损失的影响在式(8)和(9)中可以看出,由于湍流耗散项的存在,使得脉动动能减小,从而导致力压力损失的增大。而对于两相压力的变化,如式13所示。
式中:ΔPa、ΔPs是气相和固相的压力损失,Pa;λa是空气阻力系数,λs是小麦压力损失系数;ΔL为管道长度变化量,m。
从式(13)可以看出,在输送条件相同时,压力损失主要与两相速度,管道内径,空气阻力系数λa和小麦压力损失系数λs有关。其中两个阻力系数可以用公式求出。
λa的值与雷诺数(Re)有关:
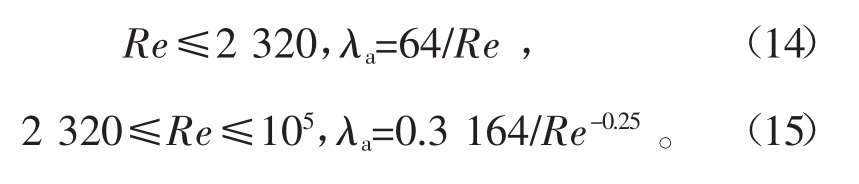
λs则与弗劳德数有关,它反应小麦与气体、小麦与管壁、小麦与小麦3种耦合关系的冲击和摩擦阻力的大小,
而几种管道在实验时,其他条件都大致相同,主要不同在于两相速度和管径。从式(13)中可以看出,物料在变径管中的压力损失是气相和固相流动所产生的压力损失的总和,压力损失与两相的速度呈正比,与管道内径呈反比,在3种管道的流动过程中,突变管与变径管1的管径大于直管,所以2种管道的压力损失相比直管会有所减小;而由图5可知,突变管中的气速比变径管2的大,导致压力损失大于变径管2;而变径管2的气速要大于变径管1,所以变径管1的压力损失要小于变径管2。
4 实验
实验装置为正压式连续气力输送系统,气力输送系统装置见图8。装置主要包含5大部分,气源、送料装置、输送管道、收料装置以及测量系统。其中气源采用罗茨风机,可以提供较大功率的气源;送料装置选用密闭式星型卸料器;输送管道为直径为0.075 m的水平无缝管道和垂直无缝管道,长度分别为10 m和5 m;收料装置为料仓,用的是旋转料仓,可以将物料与气体分离;测量系统包含电子秤,压力传感器和涡街流量器。电子秤用来测量物料输送量,压力传感器用来测量压差,涡街流量计用来测量气体的质量流量。
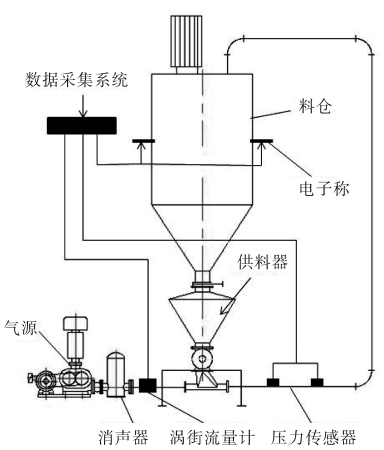
图8 气力输送系统装置
Fig.8 Pneumatic conveying system device diagram
实验测得压力损失随管道长度的变化曲线如图9所示。直管、突变管、变径管1和变径管2在出口处的压力损失值分别为439.21、413.36、346.23、379.64 Pa。
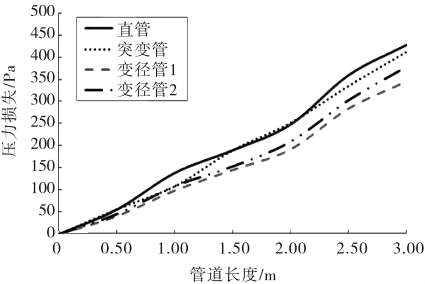
图9 实验测得压力损失随管道长度的变化曲线
Fig.9 Pressure loss curve with length of pipeline in the experiment
4种管道的压力损失的数值都在随着管道长度在不断增大;通过对比可以看出,在0~1.5 m前,4种变径管道压力损失大致相同,在通过1.5 m之后,4种管道产生较大的区别,直管和突变管的压力损失继续增大,变径管1和变径管2增大速度减慢,4种管道中压力损失最小的为变径管1,其次为变径管2和突变管,最大的为直管。
通过对比实验结果与模拟结果可以看出,2种实验所得压力损失变化曲线大致相同,因而可以证实其正确性。
5 结论
1)在气力输送过程中,初始颗粒体积分数较大且输送距离较长时,使用变径管可以防止物料在管底沉积,可以预防物料的堵塞。
2)当输送压力保持不变时,由于气体连续膨胀的原因,气体速度随着管道长度的增大而不断增大;变径管可以降低管道内的气体速度。
3)当管径比相同时,变径长度为0.15 m的变径管对管道内气体速度的减缓效果好于突变管和变径长度为0.3 m的管道,表明随着变径长度的增大,气体速度先减少后增大。
4)使用变径管能有效的减少总压力损失;颗粒体积分数和管径比相同时,突变管1的压降上升速度要小于突变管与变径管2,说明压降随着变径长度的增大先减小后增大。
参考文献(References):
[1]黄芬霞,靳世平.管道内颗粒气力输送的研究现状与热点分析[J].中国粉体技术,2017,23(5):87-92.
[2]霍征征,张东初,胡英杰.粮食稀相气力输送弯管段防磨减压的研究[J].机械科学与技术,2013,32(11):1680-1684
[3]MALLICK S S,WYPYCH P W.Minimum transport boundaries for pneumatic conveying of powders[J].Powder Technology,2009,194(3):181-186.
[4]杜俊,胡国明,方自强.稀相气力输送CFD-DEM仿真中两种模型的比较[J].海军工程大学学报,2015,27(2):57-60.
[5]BEHERA N,AGARWAL V K,JONES M G,et al.CFD modeling and analysis of dense phase pneumatic conveying of fine particles including particle size distribution[J].Powder Technology,2013,244(4):30-37.
[6]BEHERA N,AGARWAL V K,JONES M G,et al.Modeling and analysis of dilute phase pneumatic conveying of fine particles[J].Powder Technology,2013,249(11):196-204.
[7]刘敏,黄明明,丁小骄.小流量煤粉浓相气力输送特性[J].科学技术与工程,2016,16(20):169-174.
[8]SETIA G,MALLICK S S.Modelling fluidized dense-phase pneumatic conveying of fly ash[J].Powder Technology,2015,270(270):39-45.
[9]CHENG J,ZHANG N,LI Z,et al.Erosion Failure of Horizontal Pipe Reducing Wall in Power-Law Fluid Containing Particles via CFD DEM Coupling Method[J].Journal of Failure Analysis&Prevention,2017(5):1-14.
[10]ZHENG Y,RINOSHIKA A,YAN F.Multi-scale analysis on particle fluctuation velocity nearthe minimum pressure drop in a horizontal pneumatic conveying[J].Chemical Engineering Science,2012,72(16):94-107.
[11]王锟,段广彬,刘宗明.浓相气力输送水平渐扩管流动分析[J].流体机械,2012,40(7):7-10.
[12]李志华,彭宗祥,周云杰,等.散状物料在气力输送管道中的密相流动数值模拟与分析[J].硫磷设计与粉体工程,2012(5):32-35.
[13]GUNDOGDU M Y,KUTLAR A I,DUZ H.Analytical prediction of pressure loss through a sudden-expansion in two-phase pneumatic conveying lines[J].Advanced Powder Technology,2009,20(1):48-54.
[14]MCGLINCHEY D,COWELL A,CROWE R.CFD investigation of dense phase pneumatic conveying at a pipeline enlargement[J].Particuology,2012,10(2):176-183.
[15]MA A C,WILLIAMS K C,ZHOU J M,et al.Numerical study on pressure prediction and its main influence factors in pneumatic conveyors[J].Chemical Engineering Science, 2010, 65(23):6247-6258.
[16]CHEN J,LIU S,WU D,et al.Decoupling the joint effect of moisture and mass in dense phase pneumatic conveying[J].Flow Measurement&Instrumentation,2013,34(34):168-176.