颗粒包覆过程,即在颗粒的表面均匀包覆上一层功能材料,具有保护、缓释、提高环境相容性等用途。在工业生产中,尤其是制药行业应用广泛,同时也是高温气冷堆核燃料元件制备过程的重要环节。颗粒包覆是颗粒性能改进的主要方法之一,而包覆层的均匀性是颗粒包覆过程追求的目标。高温气冷堆核燃料元件采用的是4层包覆燃料颗粒,因为核燃料的固有安全特征设计,要求包覆层满足一定的技术指标,其中颗粒包覆层的均匀性则是决定高温气冷堆安全性的关键因素之一。
实验研究颗粒均匀包覆工艺是很重要的一个方面,如果通过数学建模和数值模拟,能分析出操作参数对颗粒均匀包覆的影响规律,可指导实验研究方向,减少实验次数。对颗粒包覆过程进行准确的数值模拟是研究均匀包覆机理的一种有效手段,进而可优化包覆过程,进行包覆工艺的放大,也是提高颗粒包覆过程经济性的有效途径。如何进行包覆过程的准确数值模拟,以往的研究给出了很多颗粒包覆过程数值模拟方法,但缺少比较系统和深入的对比研究[1]。
本文中首先分析了颗粒均匀包覆过程的主要特征,指出颗粒包覆过程的研究层次,即单颗粒表面均匀和全颗粒均匀2个层次,指出目前大量的模型仅局限在颗粒之间包覆层质量均匀的模拟研究。然后阐述不同数学模型的具体实施过程,指出其优势和劣势,重点对CFD-DEM方法包覆过程模拟进行深入分析,并基于运动-吸附-沉积机理发展新型包覆过程模拟方法。最后基于现有文献中的颗粒包覆过程数值模拟方法对比分析研究,指出包覆模拟研究的规律,给出了颗粒包覆过程准确数值模拟的发展趋势,即基于单颗粒尺度的表面均匀包覆机理研究和基于反应器尺度的物理场分布研究相耦合的多尺度研究方法。
1 颗粒包覆技术
目前工业上成功采用的主要有2种颗粒包覆过程,即流化床过程和转鼓过程,2种过程在核燃料制备过程中均有采用,如图1所示。高温气冷核反应堆采用的燃料元件由包覆燃料颗粒和石墨基体组成。其中陶瓷型二氧化铀(UO2)核燃料颗粒制成之后,需要在其表面均匀包覆上疏松热解炭层、内致密热解炭层、碳化硅层、外致密热解炭层(即3层结构各向同性(TRISO)颗粒制备,采用流化床过程)还需要颗粒表面均匀包覆上一层石墨层(即穿衣颗粒制备,采用转鼓过程),才能将之与石墨基体混合压制成燃料元件。TRISO颗粒包覆层是核燃料颗粒安全性第1道保障,而穿衣层则决定了颗粒在压制过程的完整性,因此,颗粒包覆过程,即在颗粒的表面均匀包覆上一层功能材料,是高温气冷堆燃料元件制备过程的重要环节,必须予以高度重视。颗粒包覆装置如图1所示,尽管流化床和转鼓2个过程差别较大,但是将其用于颗粒包覆过程具有内在的相似性,很多数值模拟方法可以在2个过程通用[2]。
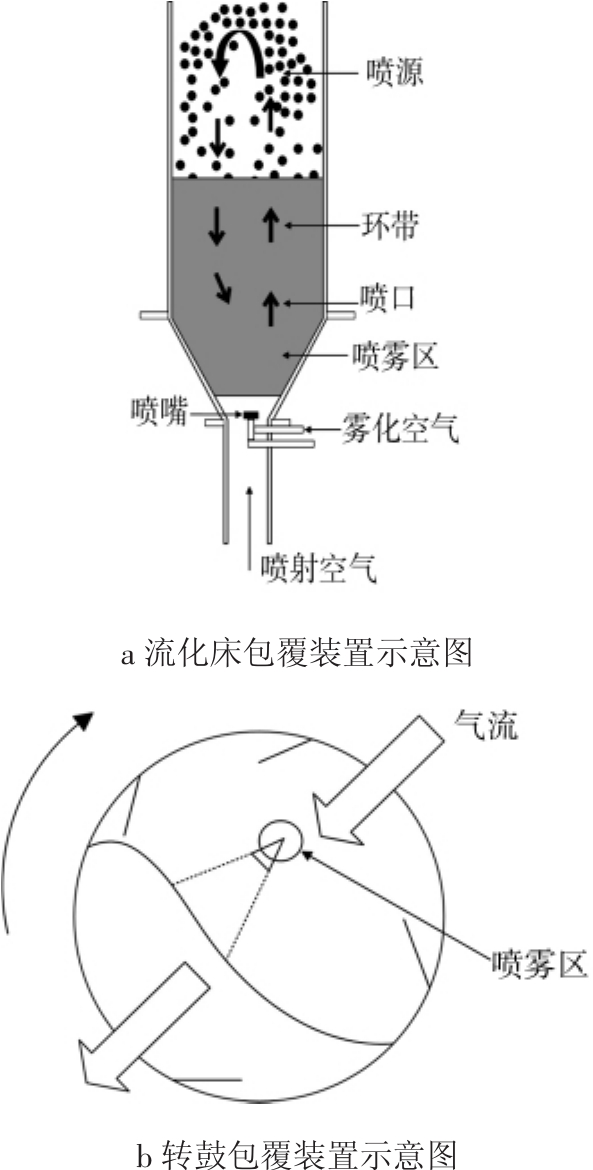
图1 颗粒包覆装置示意图
Fig.1 Schematic diagram of particle coating device
2 颗粒包覆层均匀性分析
颗粒包覆层是否均匀是颗粒包覆过程追求的目标,包括单颗粒均匀(颗粒内均匀)和全颗粒均匀(颗粒间均匀)2个方面。单颗粒均匀包覆指的是该颗粒上的包覆层性质均匀,包括厚度、密度、各向异性度等;全颗粒均匀包覆包括2个方面,一是每个颗粒上的包覆层质量均匀,二是每个颗粒上的包覆层性质均匀,如图2所示。

图2 颗粒包覆层均匀性分析
Fig.2 Analysis of particle coating uniformity
目前关于包覆过程的数值模拟多是针对全颗粒包覆层的质量均匀而言的,关于单颗粒性质均匀方面的数值模拟非常困难,研究较少,仅有针对单颗粒包覆层厚度均匀提出的一种耦合球谐函数的模拟方法。本文中针对全颗粒质量均匀包覆和单颗粒包覆层厚度均匀包覆提出的模型做详细的对比分析。
3 数值模拟方法
在颗粒间包覆层质量均匀方面,数值模拟方法包括表面更新模型(surface renewal model)、蒙特卡罗模拟方法(Monte-Carlo method)、分区群体平衡模型(compartment-based population balance model)、DEM-C-PBM模型(discrete element methodcompartment-population balance model)、CFD-DEM模型(computational fluid dynamics-discrete element method)等。在单颗粒性质均匀方面研究较少,仅有耦合球谐函数的CFD-DEM模型(CFD-DEM&spherical harmonic formulation)等少数方法。
3.1 全颗粒包覆均匀数值模拟
3.1.1 表面更新模型
颗粒包覆的一般过程是颗粒在不断运动的过程中循环往复通过含有待沉积产物的区域,待沉积产物附着在颗粒表面形成包覆层[3],基本原理见图3。
表面更新模型是一个基础的数学分析模型,起源于连续循环体系的数学分析[4],很早被用于分析颗粒包覆工艺参数的影响,其基本原理认为反应器内分为包覆区和非包覆区,颗粒每通过一次包覆区质量增加为xi,则通过n次后总的包覆质量为:
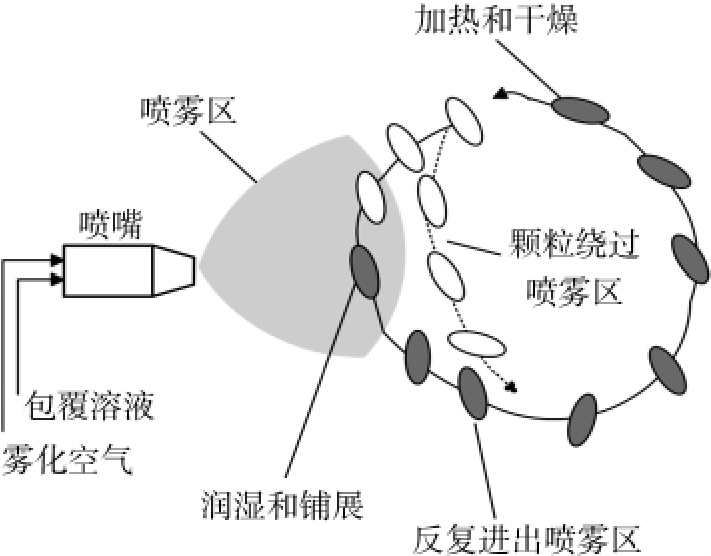
图3 颗粒包覆过程原理示意图
Fig.3 Schematic diagram of particle coating process
颗粒包覆质量均匀性,即变化系数c v,m(coefficient of variation)可以用颗粒包覆质量的标准偏差来表示,
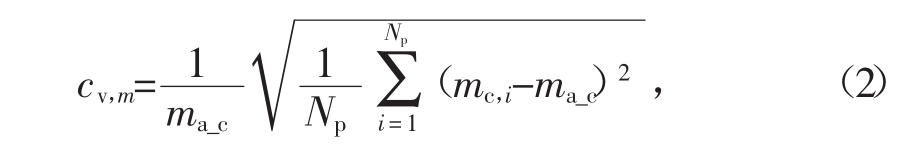
式中:N P是颗粒数量;m c,i是颗粒i的包覆层质量;m a_c是所有颗粒的包覆层平均质量。
经过数学推导,可得到颗粒包覆层质量的变化系数和单颗粒循环时间以及每次包覆量的关系
式中:μcpp和σcpp是在一次循环时间内全体颗粒每次通过包覆区的包覆层增加值的平均值和标准偏差;μct和σct分别是所有颗粒循环时间的平均值和标准偏差;T coat是颗粒总的包覆时间。
颗粒包覆层质量分布如图4所示。
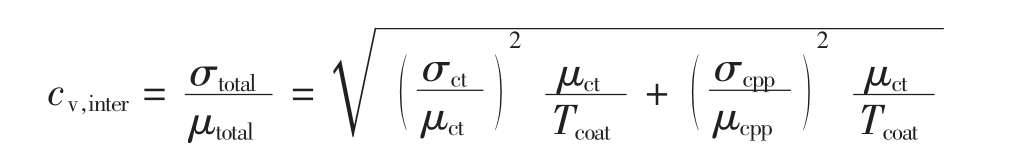
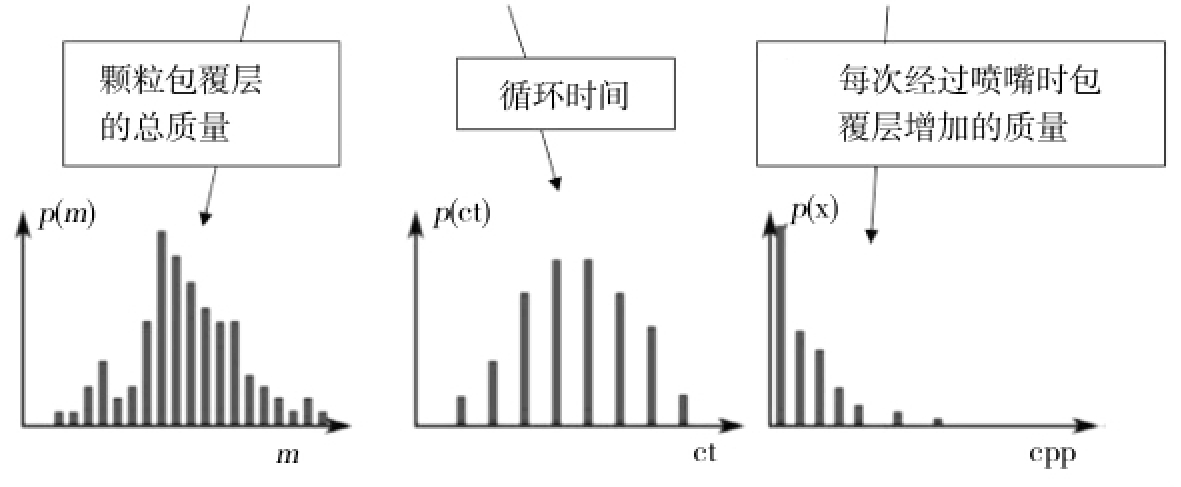
图4 颗粒包覆层质量分布
Fig.4 Mass distribution of particle coating layer
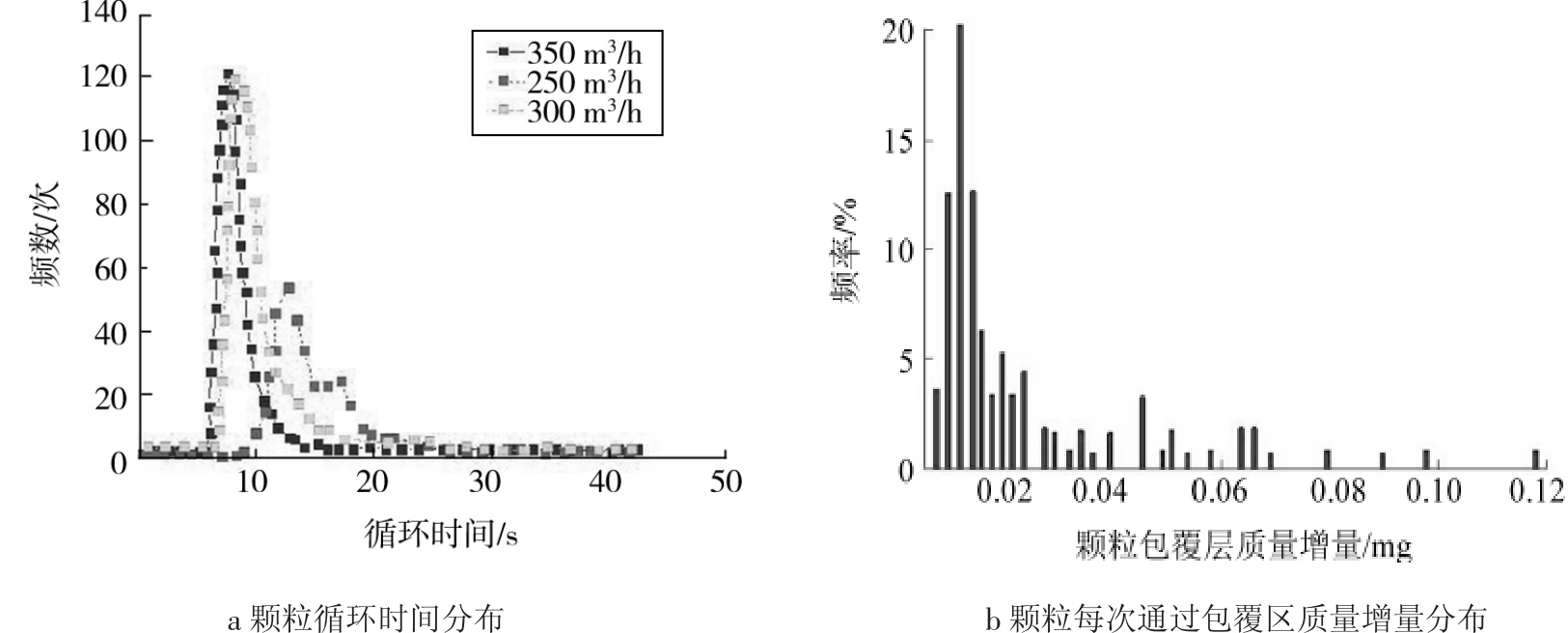
图5 颗粒循环时间分布及每次通过包覆区质量增量分布
Fig.5 Particle circulation-time distribution and coating-per-pass distribution
μct和σct可以通过加入磁性颗粒以及检测线圈、或者其他示踪方法,例如荧光增强颗粒示踪技术(PEPT)来获得,其测量相对比较容易,研究结论较多一些。μcpp和σcpp则可以通过加入一定颜色的包覆染料来测得,研究较少,可以给出包覆层不均匀性的主要起源,用于和实验结果进行分析。典型的研究例子是文献[5]中利用磁性颗粒示踪,并用反应器外部侧壁不同高度缠绕金属线圈来检测磁性颗粒的运动轨迹,获取颗粒循环时间分布,得到不同气速下的颗粒循环时间分布,如图5a所示。由图5a可以看出,气速越大,包覆层质量分布越集中。利用蓝色染料喷射包覆,用荧光光度计测量单次循环中(气速300 m3/h),每个颗粒通过包覆区的包覆层质量增量,得到其分布,如图5b所示,可以看出包覆层质量增量分布非常宽。
表面更新模型可以用于深入分析包覆过程影响因素,即2种决定因素对颗粒包覆均匀性的影响,认为包覆区内的浓度分布、颗粒之间的相互阻挡、颗粒运动的脉动不稳定性是决定包覆层增加量的不均匀分布的主要因素,并可以通过该模型的研究给出颗粒均匀包覆的改进方向,即取消高浓度包覆区、减少喷嘴附近的变化以及降低颗粒运动的脉动不稳定性等。文献[6]对此方法进行了发展,通过以轴向Peclet准数为特征的平流运动和扩散运动的组合来精确地描述颗粒的轴向运动,开发了基于更新理论的数学框架,并且获得颗粒间包覆层变化性的表达式,其解释了颗粒在涂布机内部的停留时间的变化。
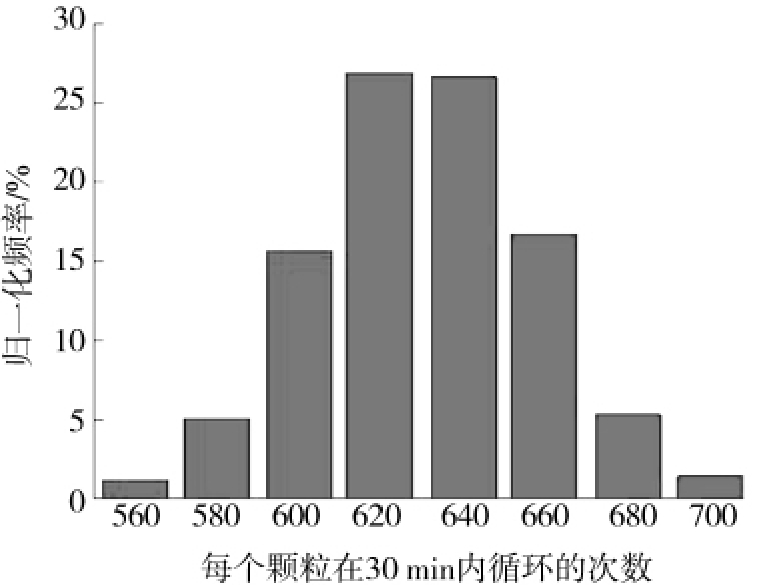
图6 利用蒙特卡罗方法计算得到的颗粒循环时间分布图
Fig.6 Particle circulation-time distribution calculated by Monte Carlo method
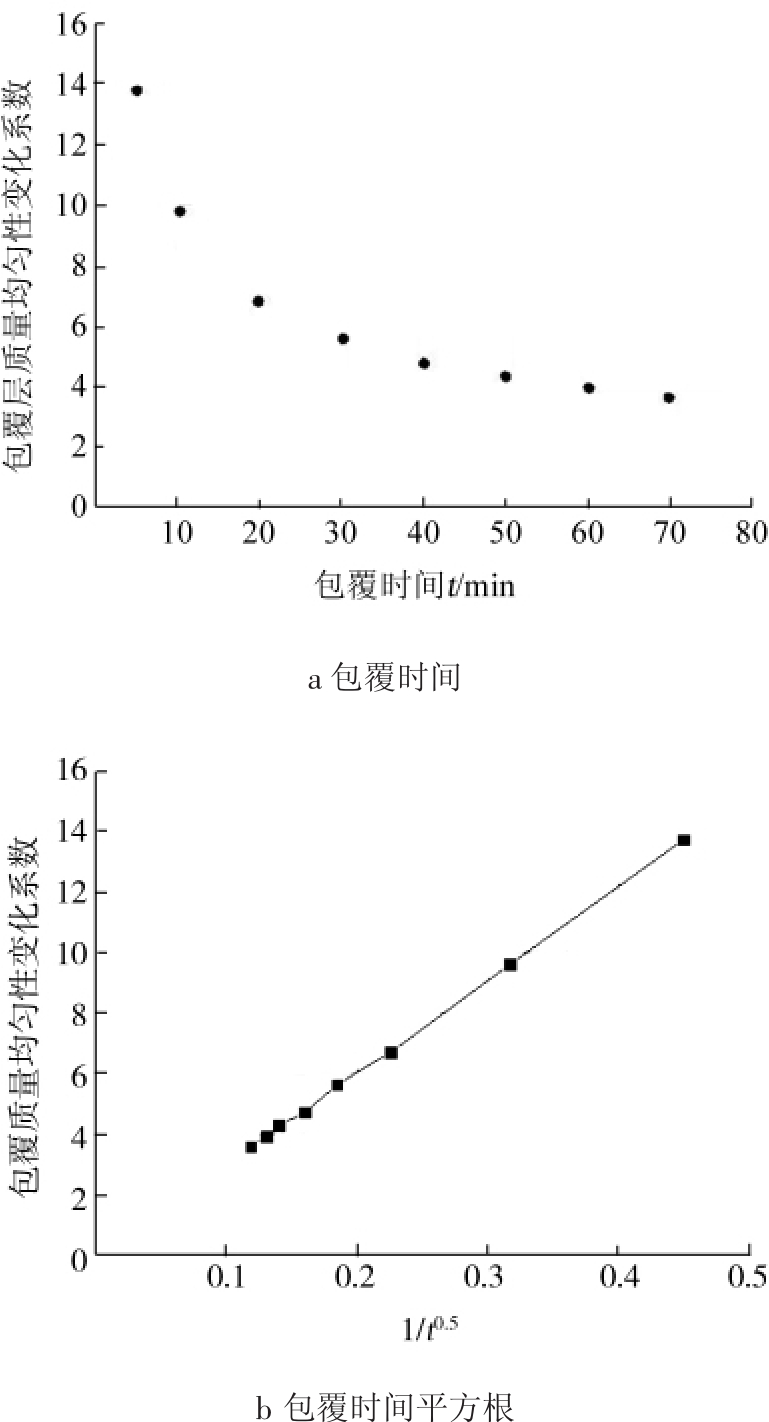
图7 包覆时间对颗粒包覆层质量变化的影响
Fig.7 Effect of coating time on mass coating variability
3.1.2 蒙特卡罗模拟方法
蒙特卡罗方法是基于重复的随机性采样的一种随机分析方法。此方法本身是普适性的,可以应用在不同领域,在包覆过程中的应用主要取决于颗粒随机运动行为和喷射通量的空间分布行为,文献[7-8]中曾用该方法研究颗粒包覆过程。蒙特卡罗方法模拟颗粒包覆过程的主要原理是:颗粒在包覆区和非包覆区之间循环往复运动,当颗粒通过包覆区时,每个颗粒表面的颗粒包覆层增量取决于颗粒暴露与喷口的截面积,局部喷射通量以及颗粒与喷射源之间的距离。当颗粒的初始位置选定后,颗粒在下一个时刻的位置取决于一个随机量决定的值。例如在文献[12]中对颗粒在导流板流化床中包覆均匀性进行了蒙特卡罗模拟,颗粒速度计算公式为
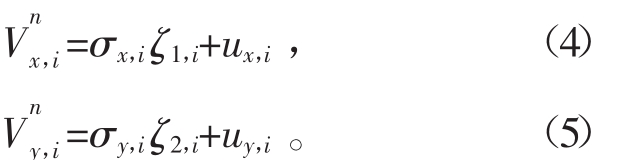
式中![]() 分别是颗粒n在x,y方向上位置i的速度;σx,i、σy,i分别是颗粒n在x,y方向上位置i的速度的标准偏差;ux,i和uy,i分别是颗粒n在x,y方向上位置i的速度的平均值,(x和y方向上颗粒速度的平均值和标准偏差分布可以从实验中获知);ζ1,i、ζ2,i是0~1之间的随机数。式(4)、(5)可对颗粒位置进行蒙特卡罗模拟,得到颗粒循环次数(时间)的分布图。文献中利用蒙特卡罗方法获得颗粒循环时间分布如图6所示[7]。
分别是颗粒n在x,y方向上位置i的速度;σx,i、σy,i分别是颗粒n在x,y方向上位置i的速度的标准偏差;ux,i和uy,i分别是颗粒n在x,y方向上位置i的速度的平均值,(x和y方向上颗粒速度的平均值和标准偏差分布可以从实验中获知);ζ1,i、ζ2,i是0~1之间的随机数。式(4)、(5)可对颗粒位置进行蒙特卡罗模拟,得到颗粒循环次数(时间)的分布图。文献中利用蒙特卡罗方法获得颗粒循环时间分布如图6所示[7]。
基于该颗粒循环时间分布图,通过实验测得的喷雾通量分布、喷雾区形状及面积大小、颗粒投影面积可以计算得到颗粒包覆质量均匀性变化系数与包覆时间之间的关系,如图7所示。由图可以看出,颗粒包覆质量均匀性变化系数cv,m与包覆时间函数1/t0.5成正比关系。
文献[9]中发展了一种蒙特卡洛方法,研究了实心圆锥和平行圆柱2种包覆区形状对模拟结果的影响,图8为2种模型中颗粒投影表面积离散化的示意图。结果发现实心圆锥模型的模拟效果没有平行圆柱模型好,并对喷射速度和导流板低端缝隙大小进行了影响因素分析,发现对于具有较低气体速度和间隙高度的情况,包覆层分布更宽。
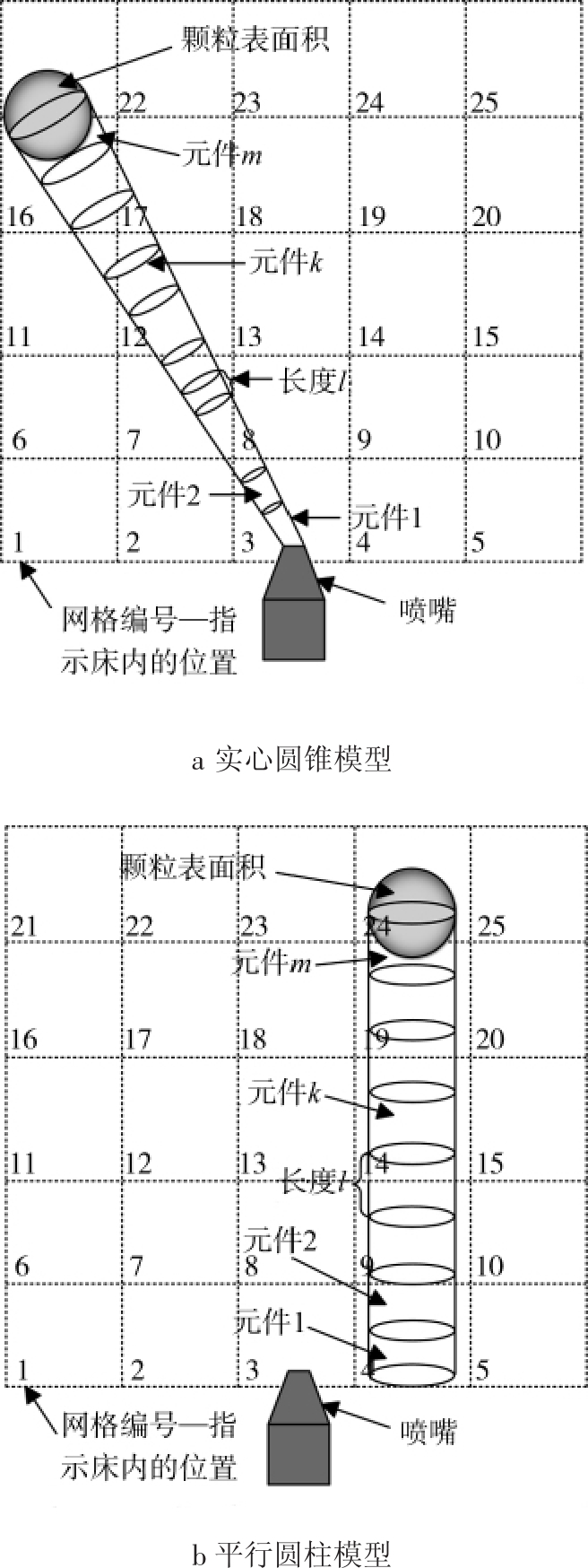
图8 不同模型中颗粒投影表面积离散化示意图
Fig.8 Schematic diagrams of discretization of particle projection area in different models
3.1.3 分区群体平衡模型
表面更新模型和蒙特卡罗方法模拟实质上都是二元分区模型,研究者将分区模型和群体平衡模型耦合,通过分析包覆过程的不同步骤,提出了多种类型的两室或多室群体平衡模型,用于预测多分散颗粒的包覆层质量分布。文献[10]中给出了一种较为简洁的处理方式,将整个反应器分成3种区域——有效包覆区G、有效干燥区F、非有效区E,如图9所示。
基于颗粒在每个区内混合均匀,颗粒不会磨损、破碎,颗粒不会跨过F区直接在G区和E区之间交换等假设,颗粒在G区和F区之间传递速率为a,在F区和E区之间传递速率为b,根据每个区的物质守恒可以给出区域间的颗粒群体平衡模型:
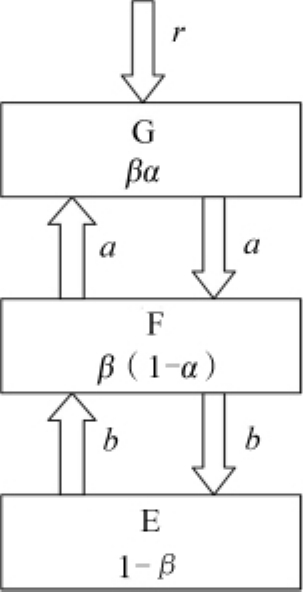
图9 分区群体平衡模型示意图
Fig.9 Schematic diagram of com partment-based population balance model
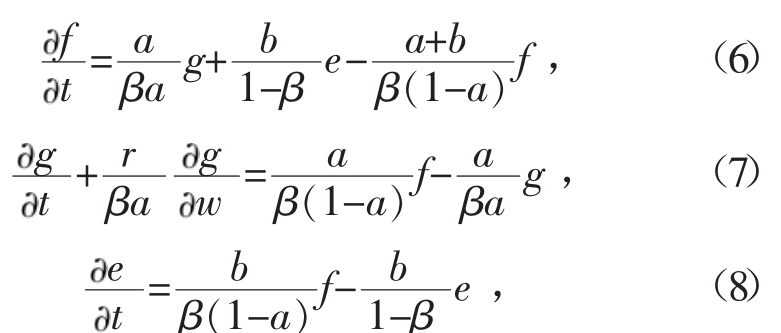
式中:f为F区群体密度函数;g为G区群体密度函数;e为E区群体密度函数;α为喷射的活性区占的分数;β为包覆过程整个床占的分数;r为包覆层质量增加速率;t代表时间;w代表包覆层质量。
通过上述模型可以研究包覆区的大小、包覆时间、单位时间的包覆增加量对包覆均匀性的影响规律。研究认为包覆质量是包覆时间的函数,考虑了颗粒流动的非均匀性带来的包覆变异系数变化。分区模型关键参数包括喷射区的相对尺寸、分区之间的流动速率、喷射速率以及喷射时间等。文献[10]中得到结果如图10所示。
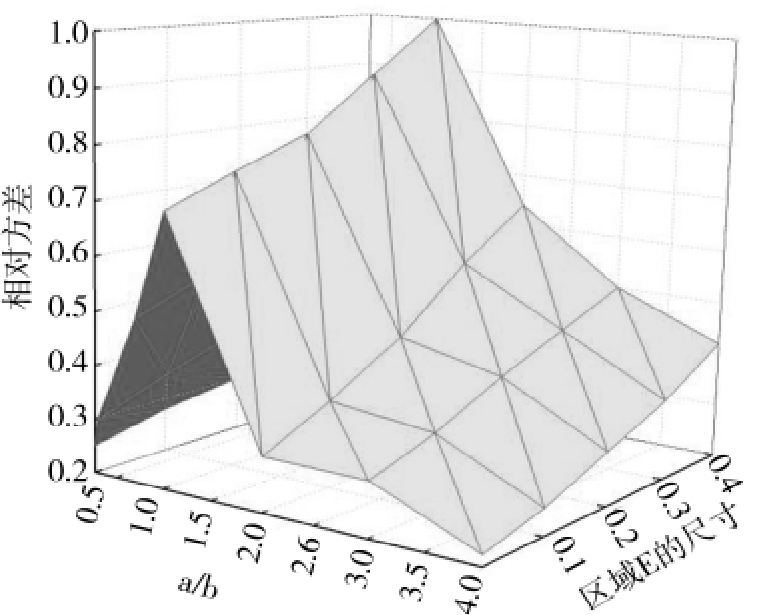
图10 以a/b和非活性区域尺寸为变量的包覆层质量分布的相对方差图
Fig.10 Variance of the coating distribution as a function of a/b and size of non-active domain
由图可以看出:如果包覆时间足够长,包覆层分布接近于正态分布;非包覆区的增加会增大包覆层的不均匀性;a和b相等时不均匀性最大,但是无论a和b哪个增大都会使得包覆分布更加均匀,但是a的增大,即有效干燥区和有效包覆区之间的传递速率增大,使得包覆分布均匀的效果更加明显;非活性区域尺寸的增大通常会导致涂层分布的变化的增加;若非活性区域内存在停滞,则会产生具有较大变化的涂层分布;区域之间转移速率的增加会使涂层分布变窄;当所有区域之间的颗粒转移速率相等时,产生最大的涂层变化;与活性干燥区域和非活性区域相比,活性干燥区域和活性喷雾区域之间的交换速率的增大会产生更窄的涂层分布。
文献[11]中还给出一种耦合DEM-C-PBM的分区模型,用于转鼓中颗粒包覆过程的数值模拟。如图11所示为在没有挡板的水平旋转鼓室中的颗粒流动。细黑线表示在短时间内的颗粒轨迹,箭头表示包覆机中的一般颗粒流动,喷雾区由靠近床自由表面的实心黑线标记,红色阴影区域表示被动床区域。在该模型中,靠近自由表面并且靠近鼓壁的颗粒以环形循环,其中在自由表面处有一小部分暴露于喷雾中;在颗粒床的中心附近还存在颗粒速度较小的区域;在外部循环区域和中心区域之间发生颗粒的连续交换。
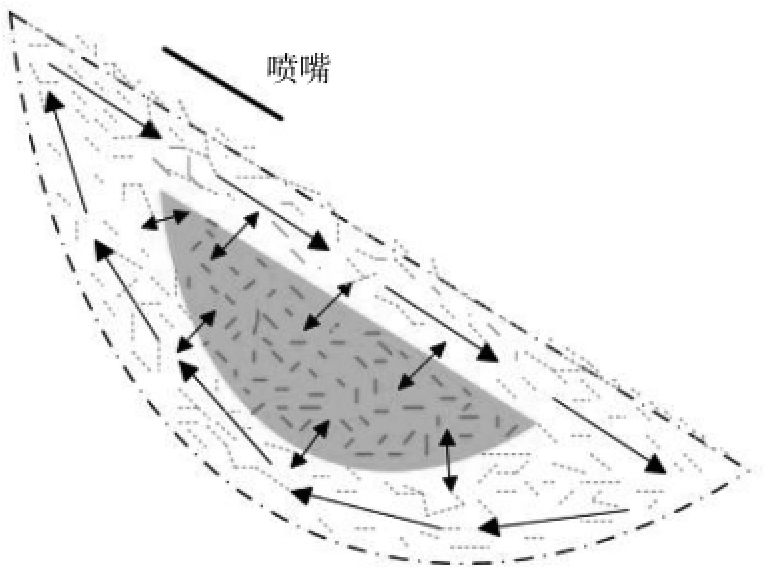
图11 旋转鼓室中颗粒流动示意图
Fig.11 Schematic diagram of flow of particles in a rotating drum
基于这种流动模式,在循环回路中的颗粒流动,包括喷雾区和一部分活性床区,如图12所示。参数α和β分别表示喷雾区域和床区域尺寸占颗粒总数的百分比,数量γ表示循环回路中床区占的百分数,循环回路中的颗粒的数量流速由N·loop循环给出,并且在活性区和被动床区的各个隔室之间交换颗粒的数量流量为N·exch/N B。这种耦合PBM的分区模型中的参数可由DEM数值模拟直接获得,形成基于DEM的参数评估分区PBM模型,可用于包覆过程模拟,是一种多尺度模型。
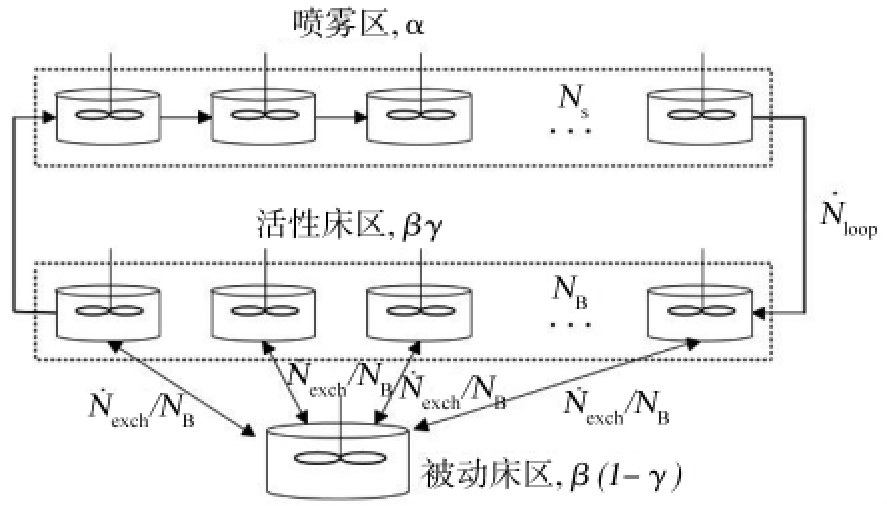
图12 旋转鼓室流动分区模型示意图
Fig.12 Schematic diagram of flow of compartmentpopulation particles in a rotating drum
3.1.4 CFD-DEM耦合模型
DEM是一种描述颗粒移动和碰撞行为的模拟方法。其可与CFD耦合,模拟颗粒-气体相互作用引起的各种现象,例如颗粒流态化行为等,称为CFD-DEM耦合模型[12-13]。DEM可以深入到单颗粒层次,所以可以准确地描述每个颗粒的变化和运动轨迹,尤其适应于包覆过程的数值模拟,这种算法的核心在于颗粒受力的计算。
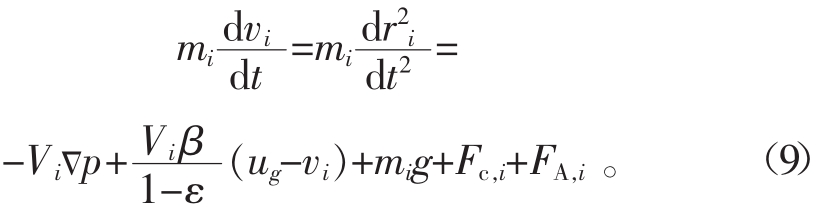
式中:mi为颗粒i的质量;vi为颗粒i的速度;ri为颗粒i的位置矢量;t为时间;p为压力;Vi为颗粒i的体积;β为相间动量传递系数;ε是孔隙率;ug为气体速度;g为重力加速度;F c,i为颗粒i受到的接触力;F A,i为颗粒i受到的颗粒之间的黏合力。
方程(9)右侧的力分别是由于压力梯度、阻力、重力、接触力和黏合颗粒之间的相互作用力。
关于CFD-DEM耦合模型用于颗粒运动体系数值模拟的工作已经有很多进展,研究人员将CFDDEM耦合模型和包覆区的分布结合起来,研究包覆参数的影响。例如文献[14]中对比分析了2种不同的包覆反应器构造对颗粒包覆均匀度的影响,如图13所示。结果表明,Wurster制粒机的特征在于具有比较窄的停留时间分布,而使用顶部喷雾制粒机则导致较宽的停留时间分布,这说明Wurster制粒机可以获得更加均匀的颗粒包覆分布。该模拟的核心还是将反应器区域先分成几个不同功能的区域,例如有效包覆区和非有效包覆区。颗粒在包覆区内的停留时间分布决定了颗粒包覆层的厚度,因而决定了颗粒包覆层质量的分布。
3.2 单颗粒包覆均匀数值模拟
以上均是对全体颗粒包覆质量均匀进行数值模拟和描述的方法,此类研究较多,而对单颗粒表面包覆均匀性的数值模拟研究较少。仅有的文献[15]中均采用DEM方法进行颗粒运动的数值模拟,然后耦合蒙特卡罗方法模拟计算了单颗粒表面沉积均匀性。具体方法是首先将颗粒表面离散化,如图14所示,颗粒表面包覆层质量m为表面积分,
式中:h为包覆层增加厚度;A是包覆层面积;ρ是包覆层密度。
假定颗粒在均匀的喷射场内,而颗粒的转动是随机的,因此与均匀流场碰撞的面是包覆层增加的面,即
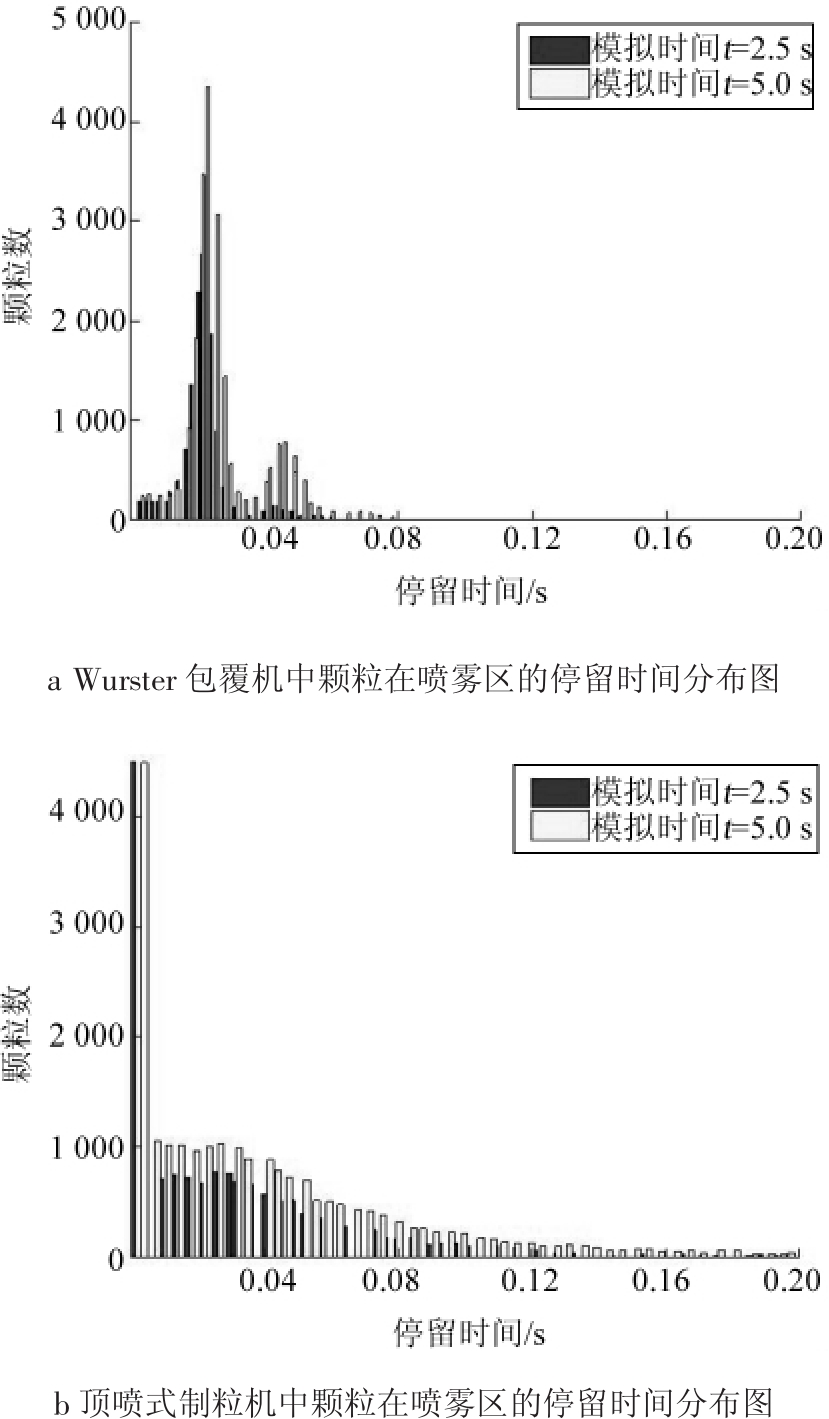
图13 不同包覆机中颗粒在喷雾区的停留时间分布
Fig.13 Residence time distribution of particles in spray zone of different coating devices
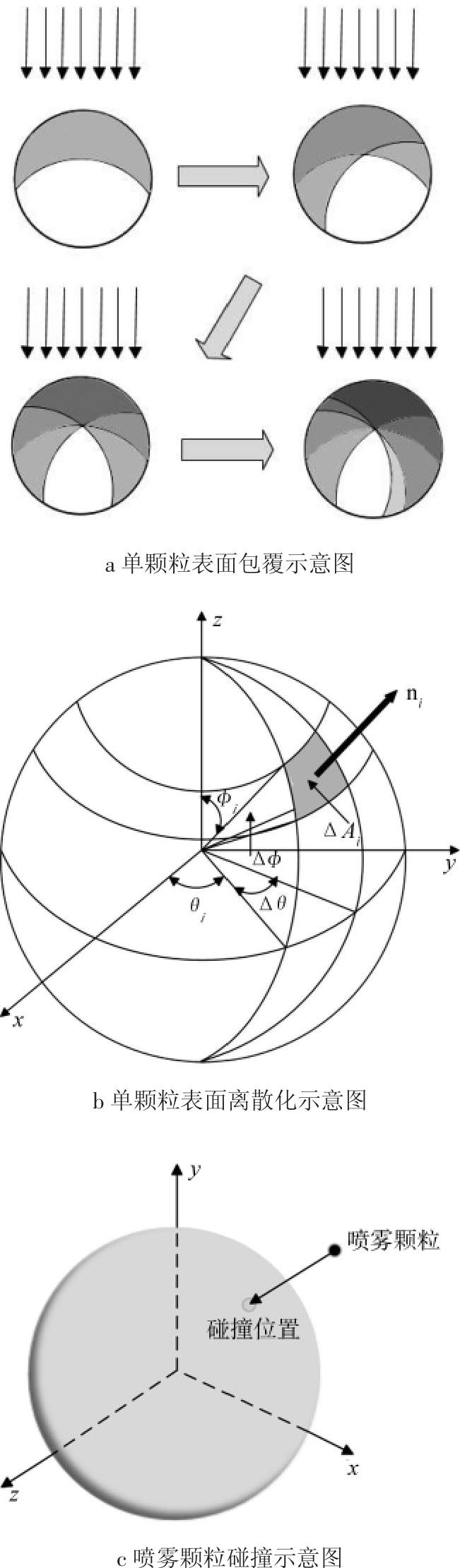
图14 耦合球谐函数的CFD-DEM模型示意图
Fig.14 Schematic diagram of CFD-DEM&spherical harmonic formulation model
式中:n是外延法向量,如图14b所示;u rel是颗粒与喷射场的相对运动速度。
计算出每一个离散面的包覆层增加厚度,即可以得到单颗粒表面包覆不均匀性的模拟计算。
文献[16]中另外一种模拟计算单颗粒表面沉积均匀性的模型是耦合球谐函数的CFD-DEM模型。在该模型中,也是首先将颗粒表面离散化,用颗粒表面分布函数来表示单颗粒表面沉积的均匀性,如图14所示。图14a表示将单个球形颗粒暴露于均匀喷雾,颗粒在涂层试验之间随机旋转,颗粒阴影表示颗粒表面的那部分上的膜厚度;图14b为单颗粒包覆均匀性模拟时的颗粒表面离散化示意图,面积为ΔA i的面板位于半径为R的球形颗粒上,面板的单位法向量为n i,相对于粒子的固定球体参照系测量角度分别为φp和θi;图14c表示喷雾颗粒在 φp、θp方向上与球表面上的点撞击。该模型采用的是液滴沉积原理,即假定沉积产物在包覆反应器内以液滴形式存在,当液滴与颗粒从一个角度碰撞时,液滴的体积会映射到颗粒表面上,形成包覆层。该映射方式的计算,即球体表面分布方式的计算是采用球面谐波函数的方式进行的。例如,如果考虑2个液滴(体积为V1和V2)沉积到颗粒表面的过程,则映射到颗粒表面的质量分别为V1g(θ)和V2g(θ),颗粒表面沉积产物的增加过程可以表示为
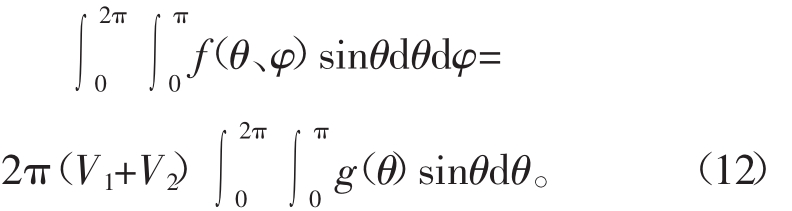
式中:f为颗粒表面沉积产物分布函数;g为正态分布函数。式子左边可以用球谐函数来表示,即得到颗粒表面沉积产物的分布。
将气体、颗粒、液滴用CFD-DEM进行模拟,将颗粒和液滴的碰撞、包覆过程用上式来描述,可以得到整个体系的颗粒包覆过程,最终模拟结果如图15所示,可以看出颗粒沉积变化系数与包覆时间、颗粒速度之间的关系。结果表明,当颗粒速度越大、包覆时间越长,则颗粒表面沉积变化系数越小,即表面包覆越均匀;完全随机覆盖的![]() 的理想斜率如图15中虚线所示。
的理想斜率如图15中虚线所示。
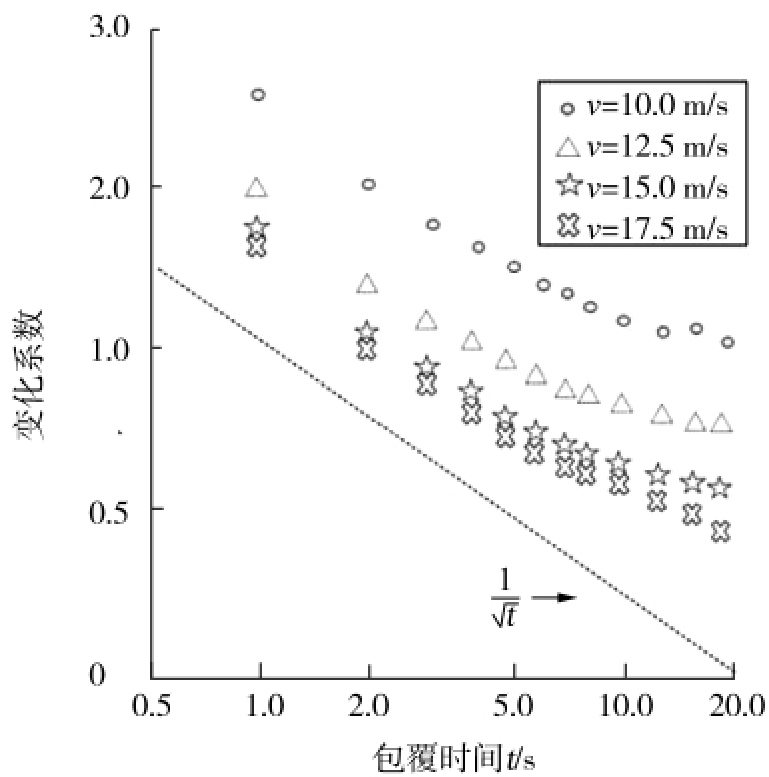
图15 CFD-DEM模拟结果示意图
Fig.15 Schematic diagram of CFD-DEM simulation results
4 模型比较分析
从上述模型比较分析来看,表面更新模型、蒙特卡罗模型、分区群体平衡模型都是全部颗粒描述性的模型,没有涉及颗粒包覆表面的演化细节过程,而CFD-DEM模型是单颗粒层次的模拟模型,可以准确描述颗粒的包覆层变化,例如可以考虑单个颗粒包覆质量的变化,耦合颗粒表面离散化分布函数,就可以对单颗粒包覆均匀性进行描述。另外,上述模型都是基于包覆反应器存在不同分区这一假设基础。分区概念是一种比较合理的近似,但仍是一种不精确的描述,实际上,包覆反应器内各个分区之间不可能有这么清晰的界限,这一点也始终是颗粒包覆模拟准确性受质疑的最大原因[1-2]。
基于以上对颗粒包覆过程数值模拟模型的分析,针对包覆燃料颗粒制备过程使用的流化床-化学气相沉积技术,我们提出了CFD-DEM-CVD模型,其基本思想是去除包覆反应器分区概念,将多组分气体化学反应浓度场、颗粒运动-吸附-沉积结合起来,用于分析在颗粒流化状态下化学气相沉积包覆反应过程,如图16所示。
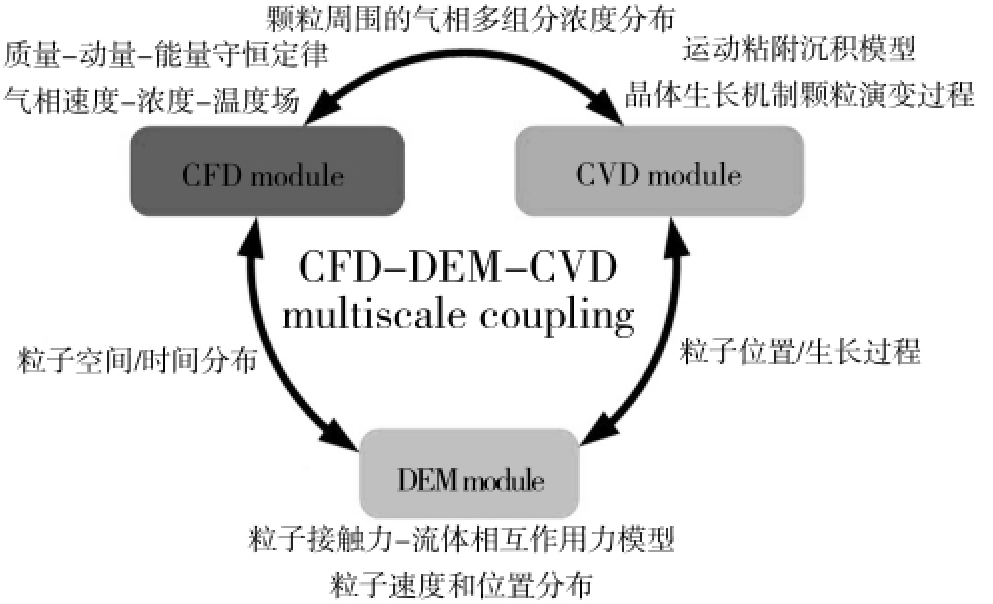
图16 CFD-DEM-CVD多尺度耦合模型示意图
Fig.16 Schematic diagram of CFD-DEM-CVD multiscale coupling model
在此模型中,颗粒生长速率与单位时间内颗粒扫过的体积以及颗粒周围的有效气体浓度成正比[17],即
式中:R为颗粒半径;k a为粘附系数;k r为沉积系数;粒子速度U p可以从DEM获得,邻近粒子的气体速度U f和有效气体浓度C eff可以从CFD获得,从而建立了CFD-DEM-CVD多尺度耦合模型概念。
目前我们已经实现了单相耦合,基于传统分区概念,将该模型用于分析颗粒在单孔喷动床的包覆区内的停留时间分布等行为,如图17所示。
从图中可以清楚地看到包覆颗粒和未包覆颗粒之间的混合行为,虽然整个区域分为有效包覆区和无效包覆区,但喷嘴床中颗粒快速混合,2 s后包覆过程变成一个整体,而包覆效率仅由操作和设备参数决定。
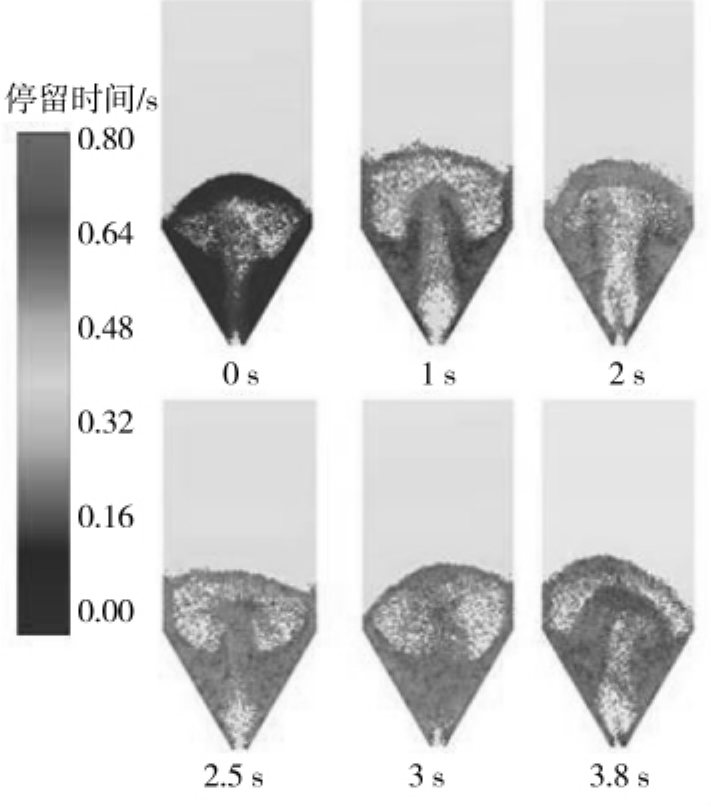
图17 不同包覆时间下颗粒包覆的模拟结果
Fig.17 Simulation results of particle coating at different coating time
5 结论
1)颗粒包覆均匀性研究包括2个层次,即全颗粒均匀包覆和单颗粒均匀包覆,目前文献研究主要集中在前者。
2)包覆过程数值模拟方法分为表面更新模型、蒙特卡罗模拟方法、分区群体平衡模型、DEM-C-PBM模型、CFD-DEM模型,其中CFD-DEM模型是单颗粒层次的数值模拟方法。
3)基于颗粒包覆数值模拟方法的比较分析,针对颗粒包覆过程的多场耦合特征,提出CFD-DEM-CVD多尺度模型,可以将宏观流体尺度、介观颗粒尺度、微观材料沉积尺度耦合起来,进行包覆过程数值模拟。
4)颗粒包覆过程准确数值模拟的未来发展趋势是基于单颗粒尺度的表面均匀包覆机理研究和基于反应器尺度的物理场分布研究相耦合的多尺度研究方法。
参考文献(
References):
[1]TOSCHKOFF G,KHINAST J G.Mathematical modeling of the coating process[J].International Journal of Pharmaceutics,2013,457(2):407-422.
[2]SAHNI E,CHAUDHURI B.Experimental and modeling approaches in characterizing coating uniformity in a pan coater:a literature review[J].Pharmaceutical Development and Technology,2012,17(2):134-147.
[3]DENISA C,HEMATIA M,CHULIAB D,et al.A model of surface renewal with application to the coating of pharmaceutical tablets in rotary drums[J].Powder Technology,2003,130(1):174-180.
[4]MANN U,RUBINOVITCH M,CROSBY E J.Characterization and analysisofcontinuousrecyclesystems[J].AICHEJournal,1979,27(5):873-882.
[5]SHELUKAR S,HO J,ZEGA J,et al.Identification and characterization of factors controlling tablet coating uniformity in a Wurstercoatingprocess[J].PowderTechnology,2000,110(1):29-36.
[6]KUMAR R,WASSGREN C.Inter-particle coating variability in a continuous coater[J].Chemical Engineering Science,2014,117:1-7.
[7]PANDEY P,KATAKDAUNDE M,TURTON R.Modeling weight variability in a pan coating process using Monte Carlo simulations[J].AAPS Pharm Sci Tech,2006,7(4):E1-E10.
[8]NAKAMURA H,ABE E,YAMADA N.Coating mass distributions of seed particles in a tumbling fluidized bed coater[J].Powder Technology,1998,99(1):140-146.
[9]KUSHAARI K,PANDEY P,SONG Y,et al.Monte Carlo simulations to determine coating uniformity in a Wurster fluidized bed coating process[J].Powder Technology,2006,166(2):81-90.
[10]MARONGA S J,WNUKOWSKI P.Modelling of the three-domain fluidized-bed particulate coating process[J].Chemical Engineering Science,1997,52(17):2915-2925.
[11]KUMAR R,FREIREICH B,WASSGREN C.DEM-compartmentpopulation balance model for particle coating in a horizontal rotating drum[J].Chemical Engineering Science,2015,125:144-157.
[12]CUNDALL P A,STRACK O D L.A discrete numerical model for granular assemblies[J].Geotechnique,1979,29(1):47-65.
[13]ZHU H P,ZHOU Z Y,YANG R Y,et al.Discrete particle simulation of particulate systems:theoretical developments[J].Chemical Engineering Science,2007,62(13):3378-3396.
[14]FRIES L,ANTONYUK S,HEINRICH S,et al.DEM-CFD modeling of a fluidizedbed spraygranulator[J].ChemicalEngineering Science,2011,66(11):2340-2355.
[15]FREIREICH B,WASSGREN C.Intra-particle coating variability:analysis and Monte-Carlo simulations[J].Chemical Engineering Science,2010,65(3):1117-1124.
[16]HILTON J E,YING D Y,CLEARY P W.Modelling spray coating using a combined CFD-DEM and spherical harmonic formulation[J].Chemical Engineering Science,2013,99(99):141-160.
[17]LIU M L,LIU R Z,WEN Y Y,et al.Investigation of the fluidized bed-chemical vapor deposition(FB-CVD)process using CFD-DEM method[C]//2014 proceeding of the HTR.Weihai,China:2014.